Behaviour Investigation of SMA-Equipped Bar Hysteretic Dampers Using Machine Learning Techniques
Abstract
:1. Introduction
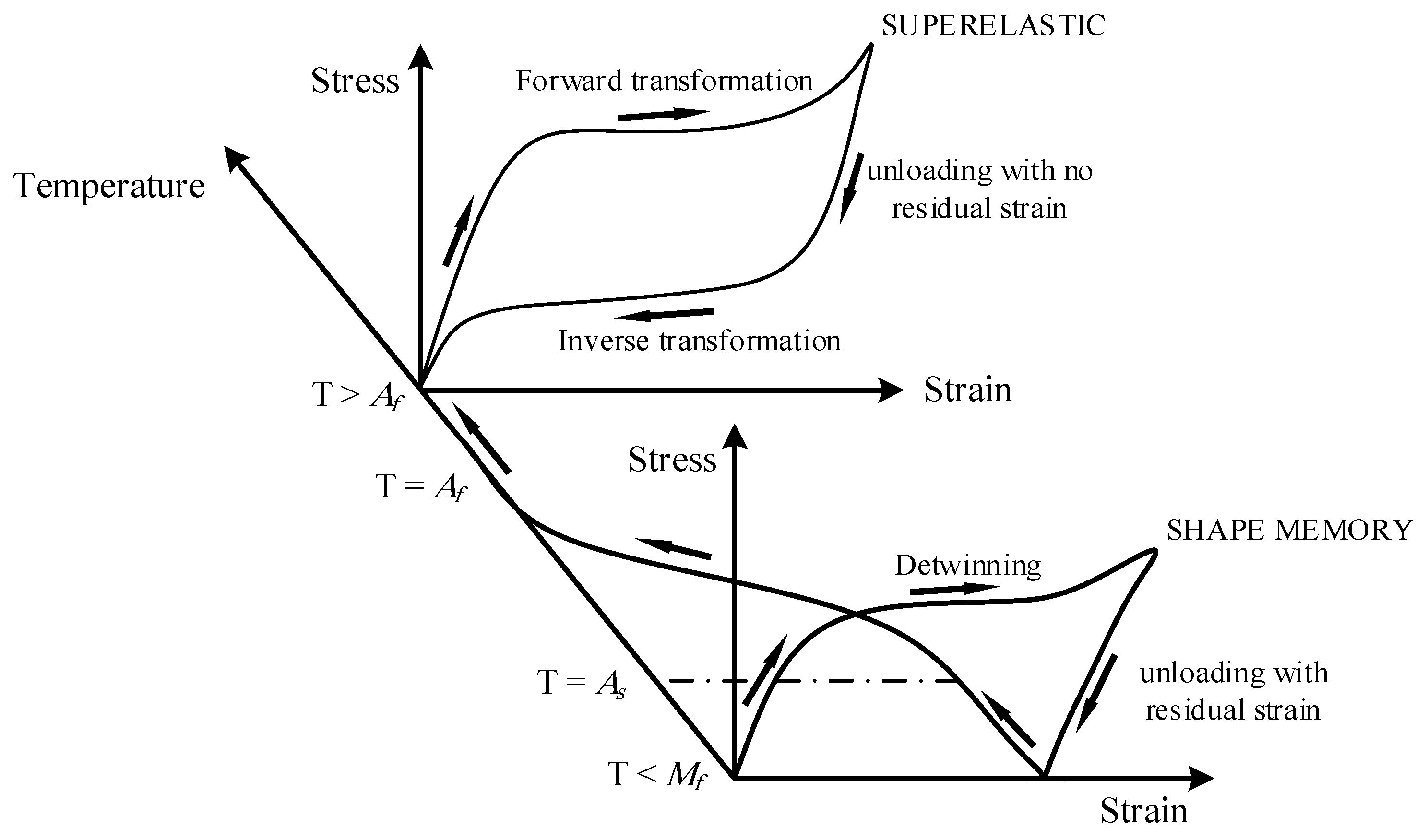
2. Shape Memory Alloys
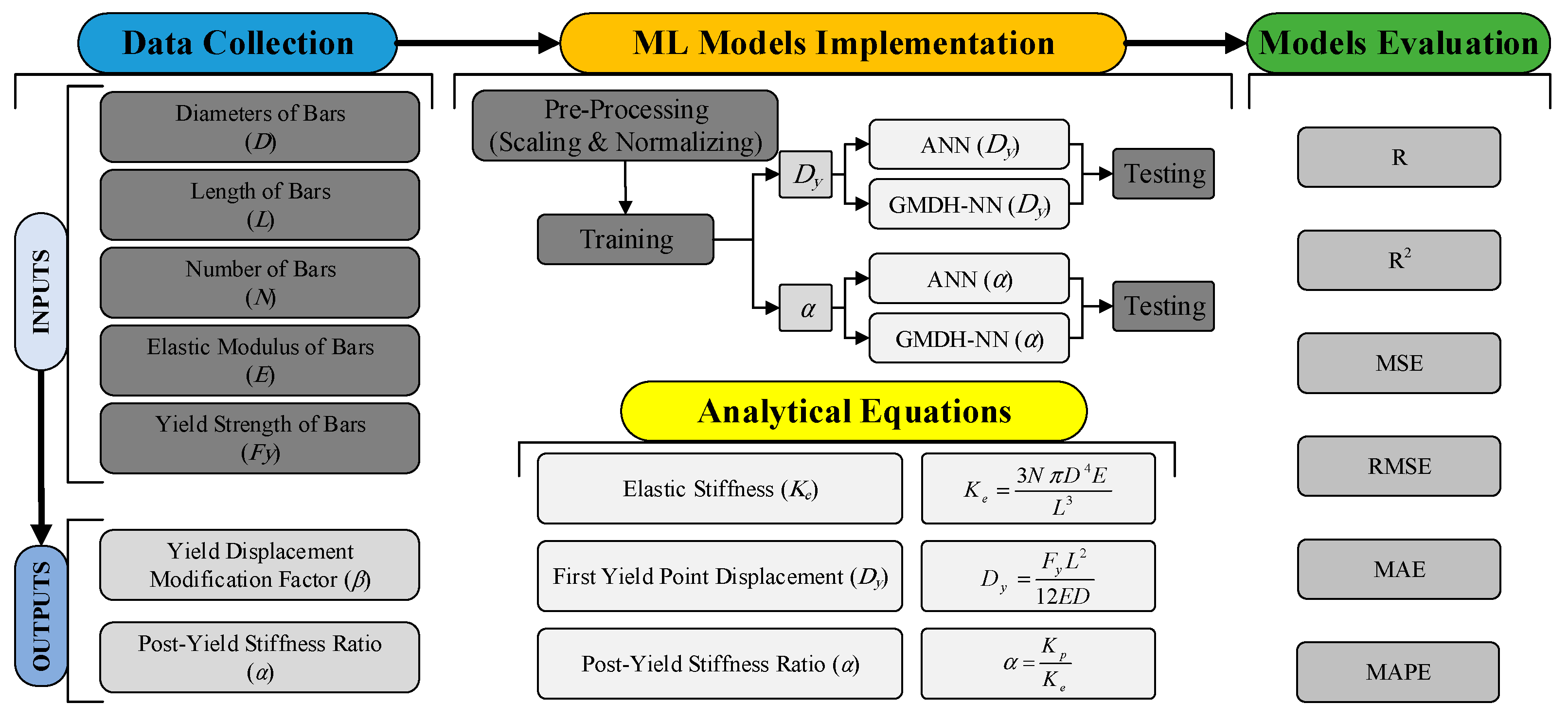
3. Methodology
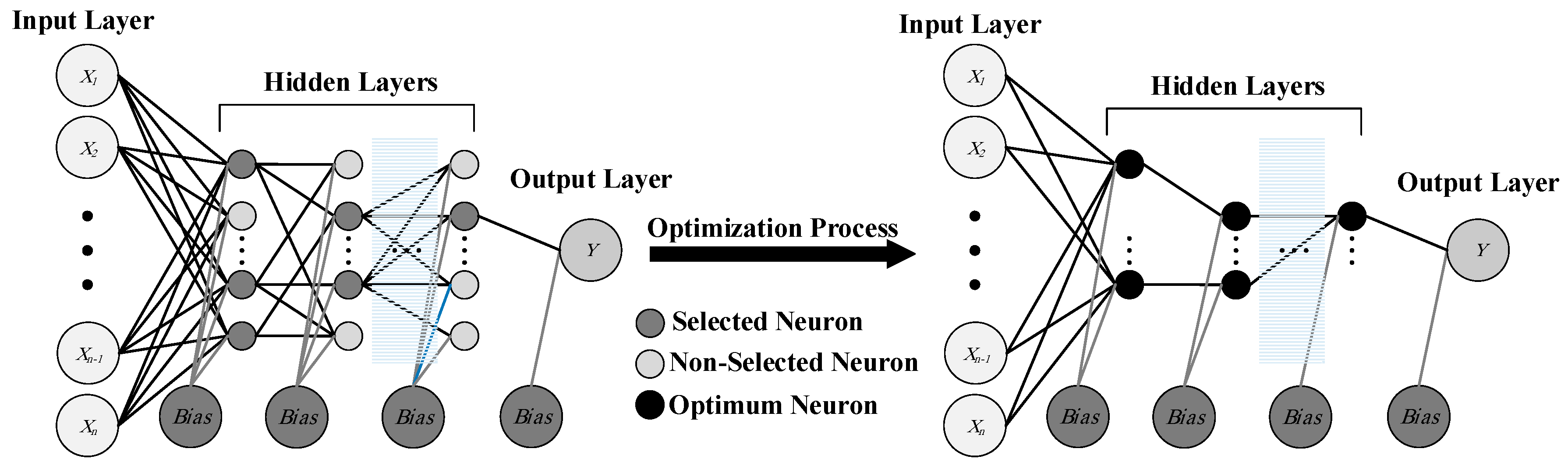
3.1. The Artificial Neural Networks (ANNs)
3.2. The Group Method of Data Handling (GMDH)
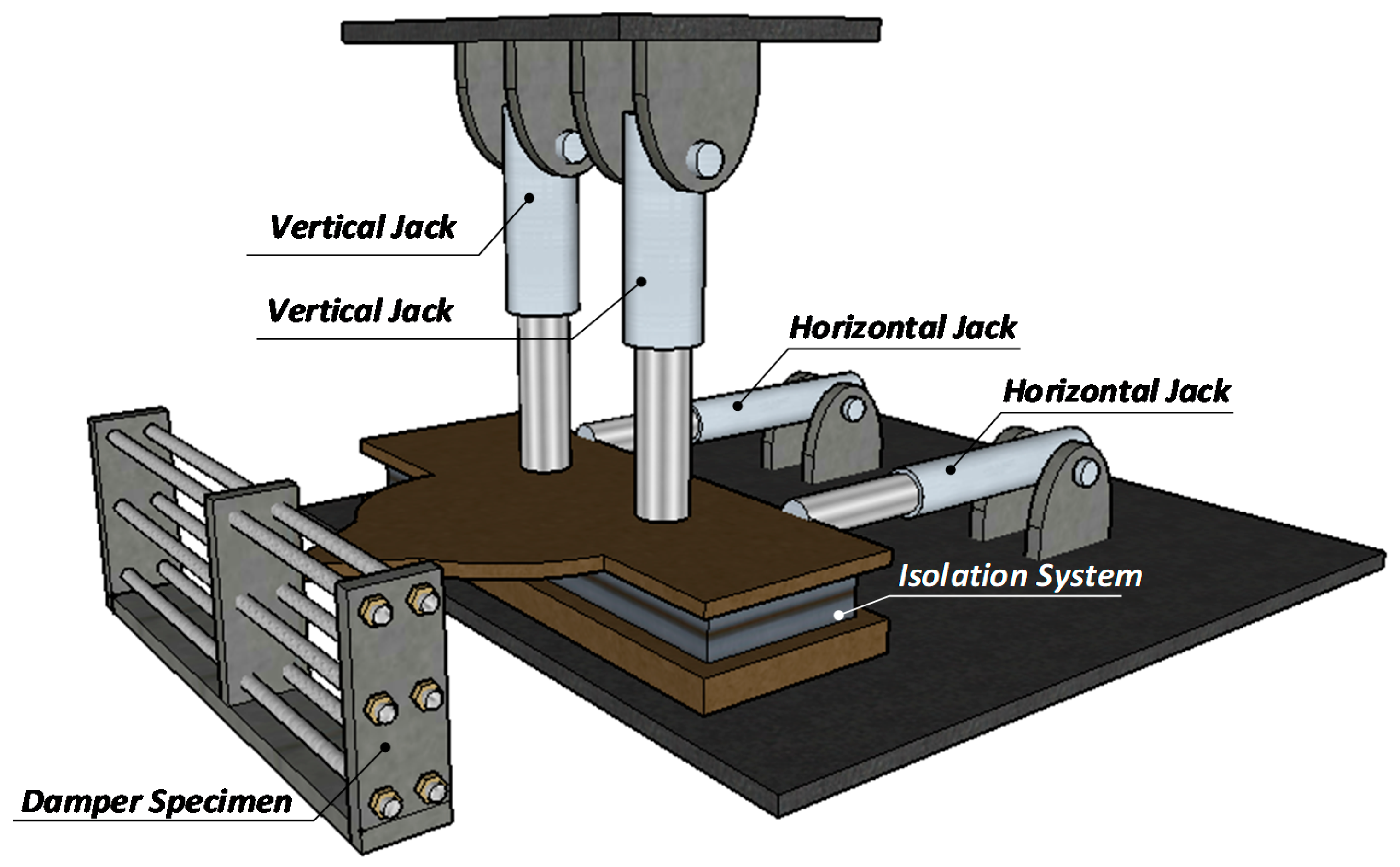
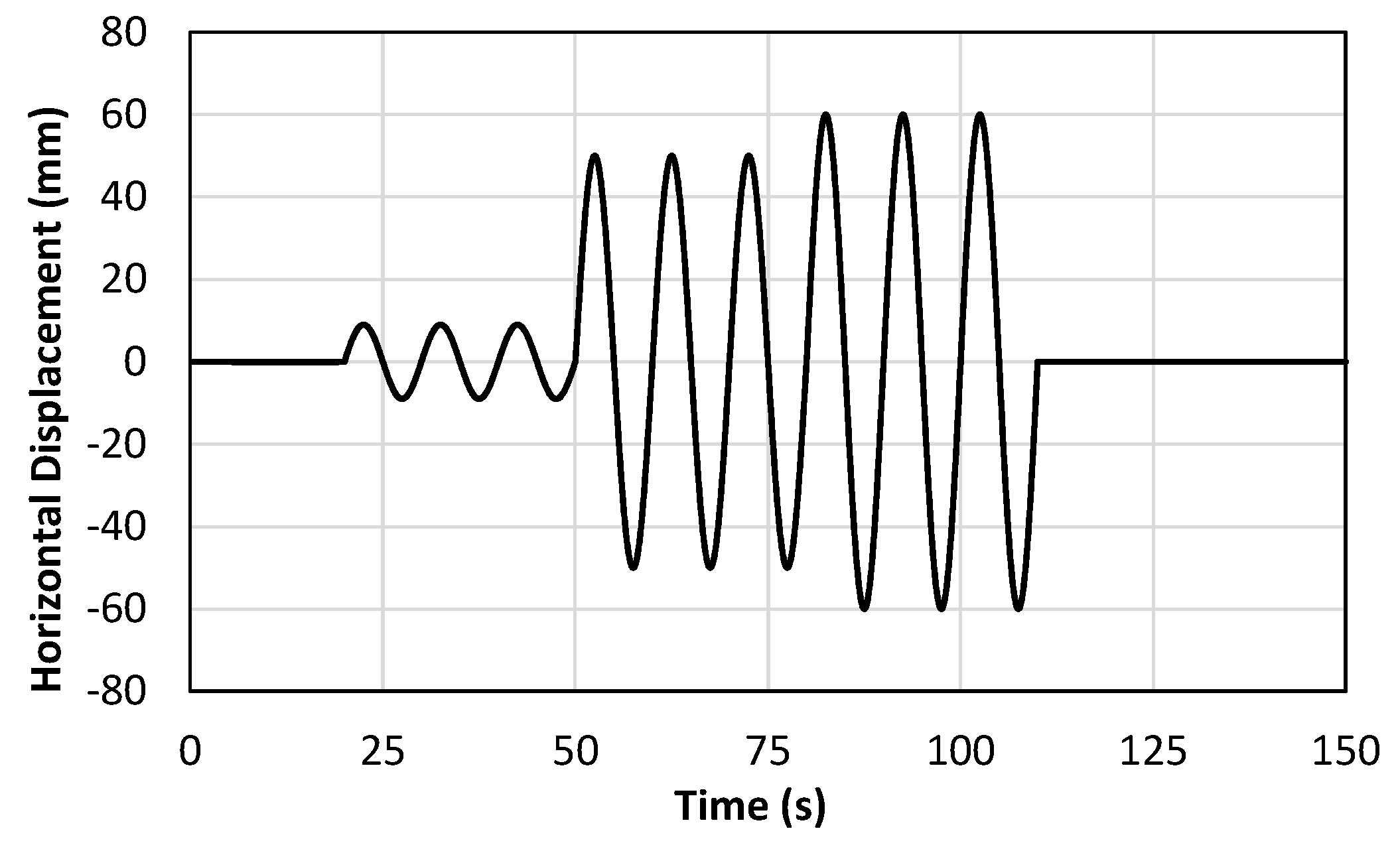
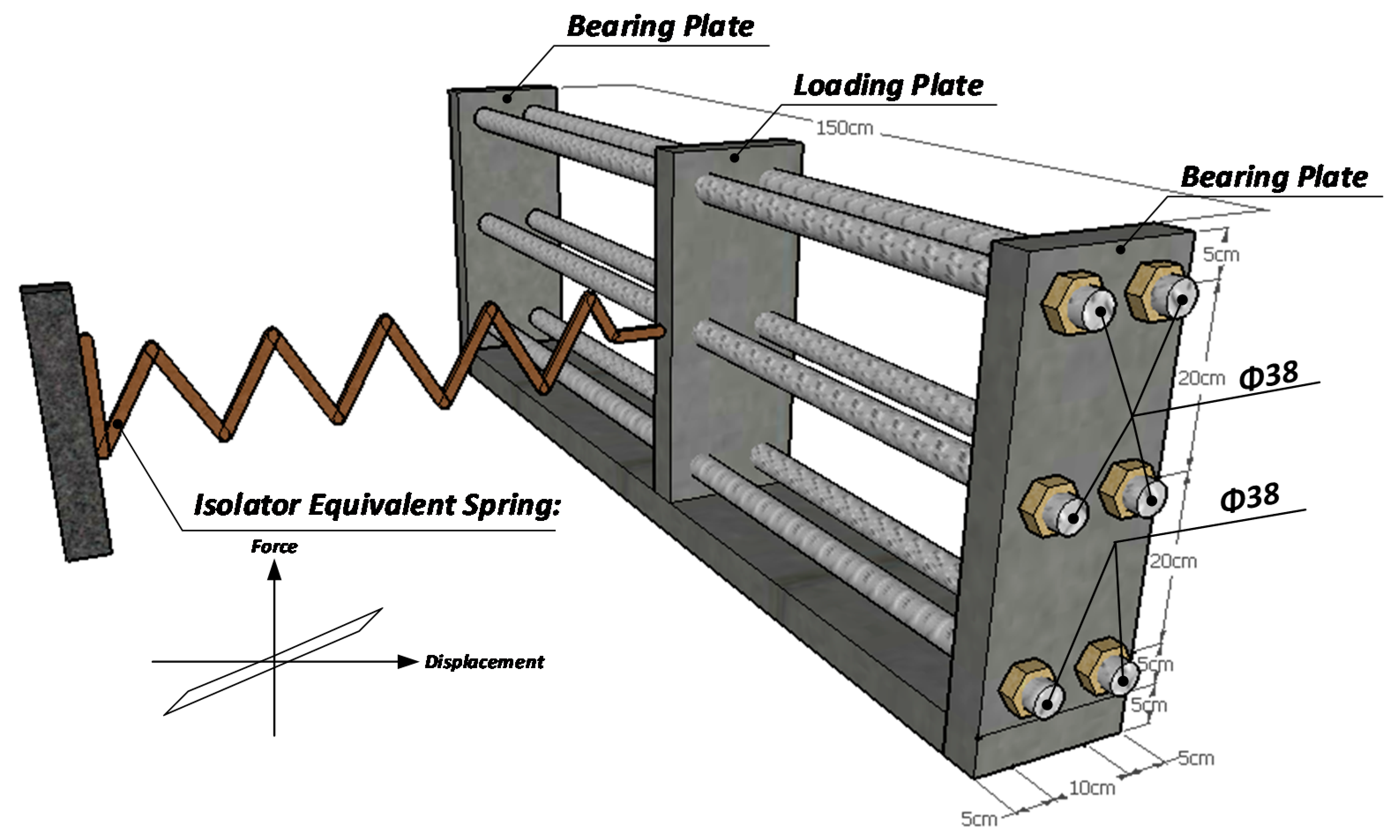
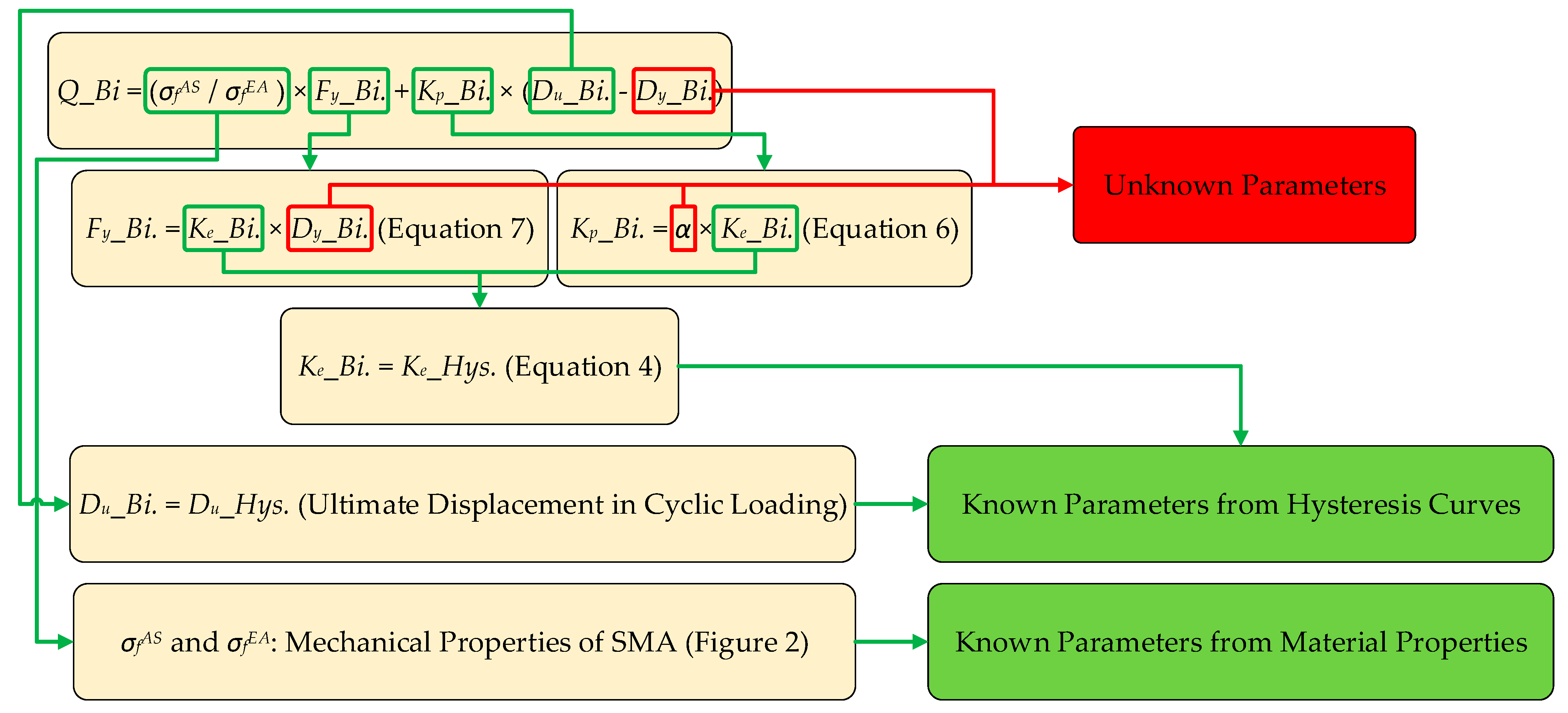
4. Experimental Specimens and Numerical Models
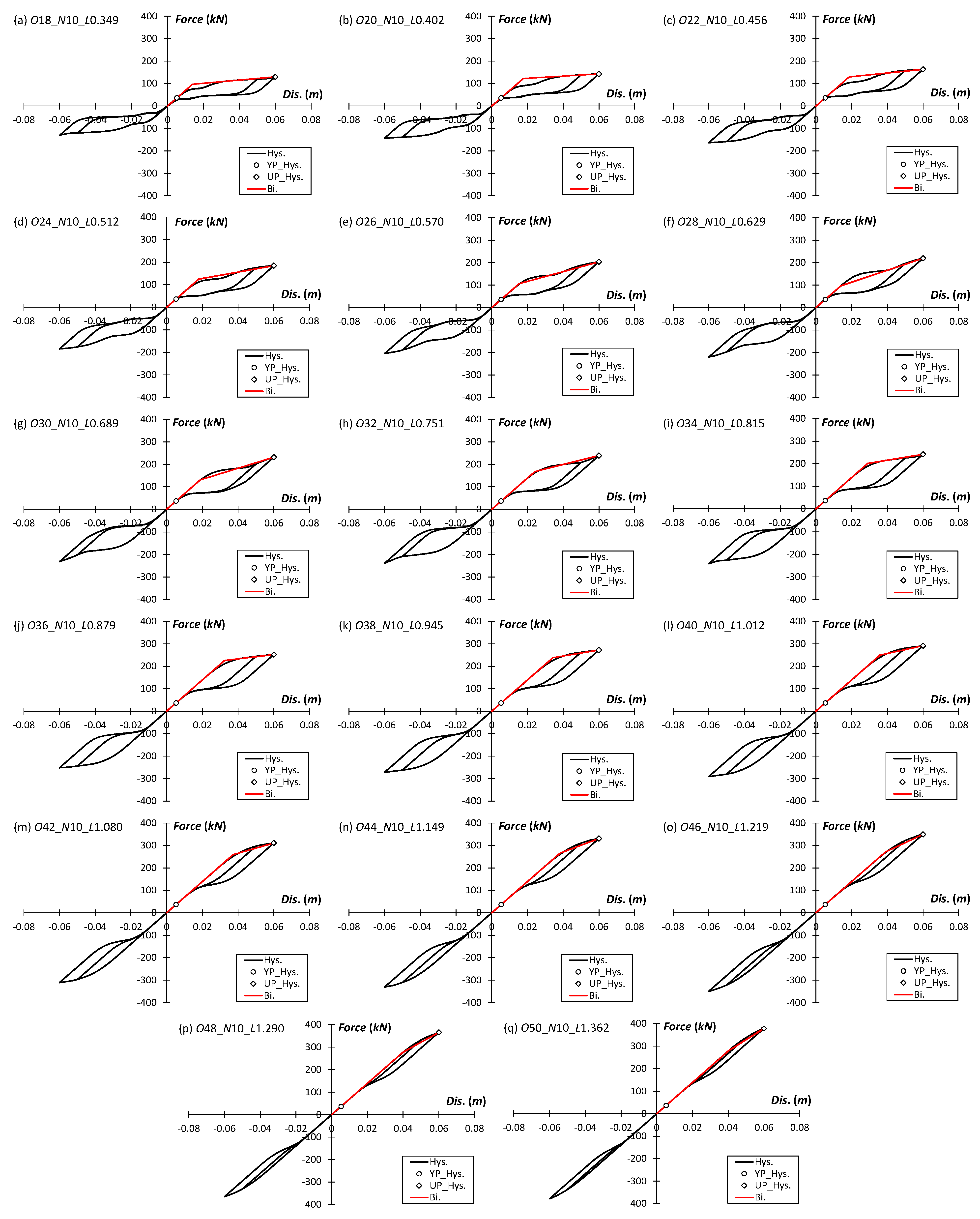
4.1. Experimental Specimens
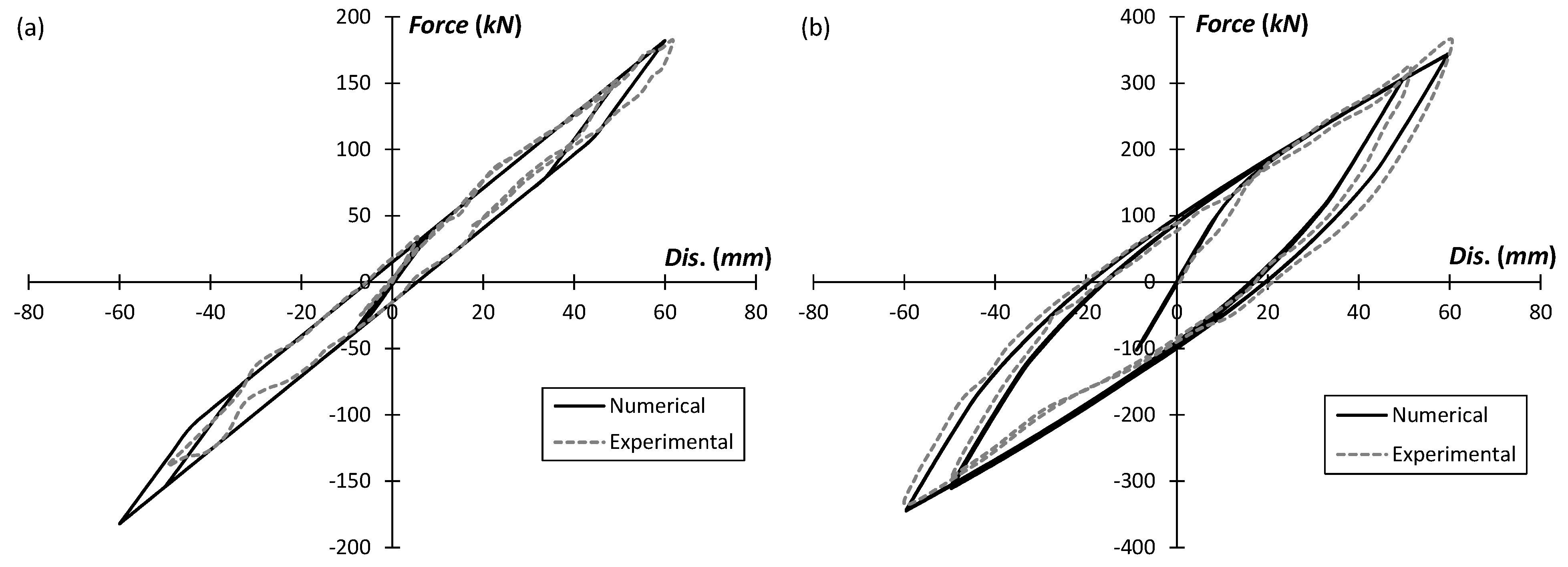
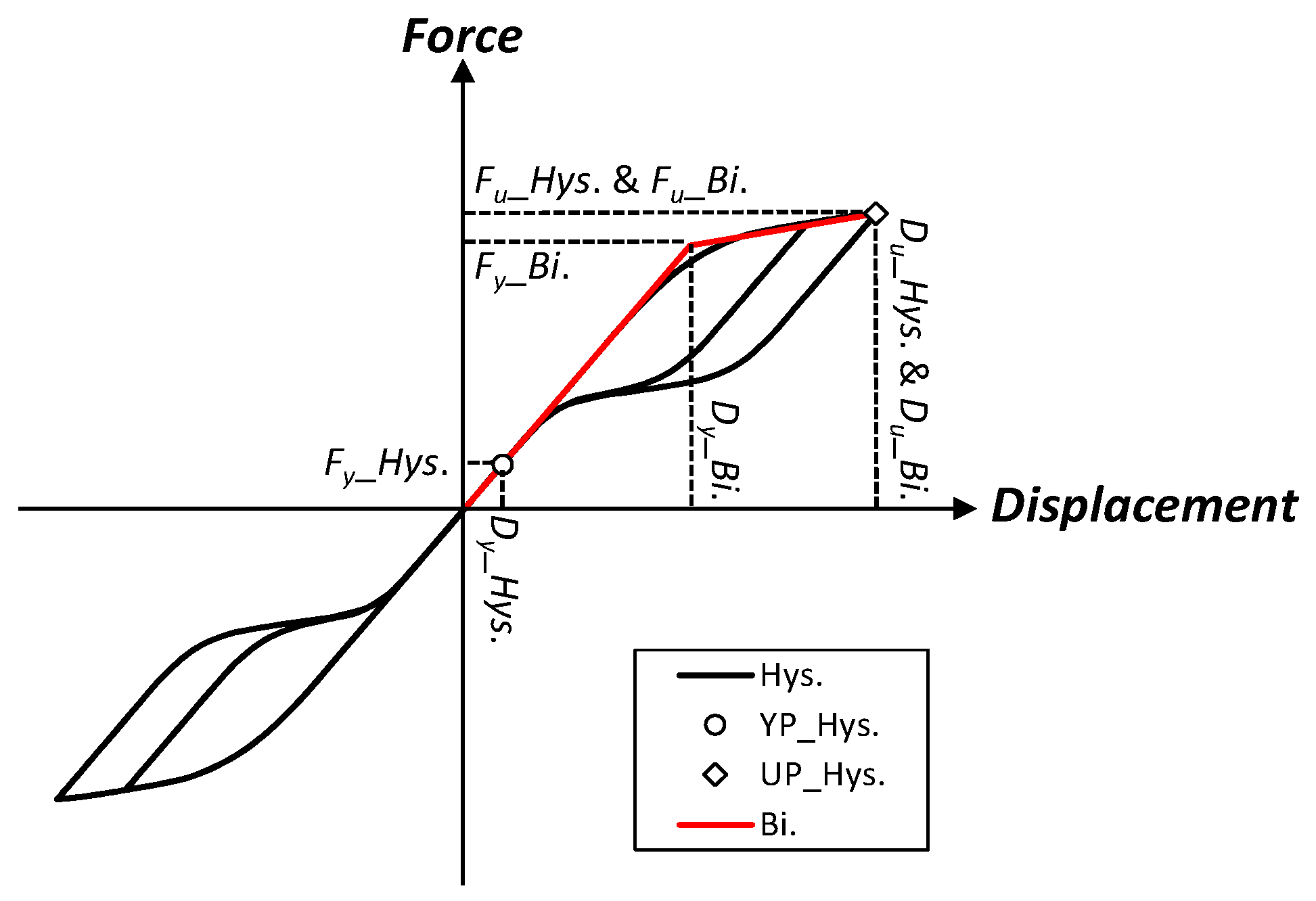
4.2. Numerical Models
5. Machine Learning Approaches
5.1. Numerical Database
5.2. Data Pre-Processing
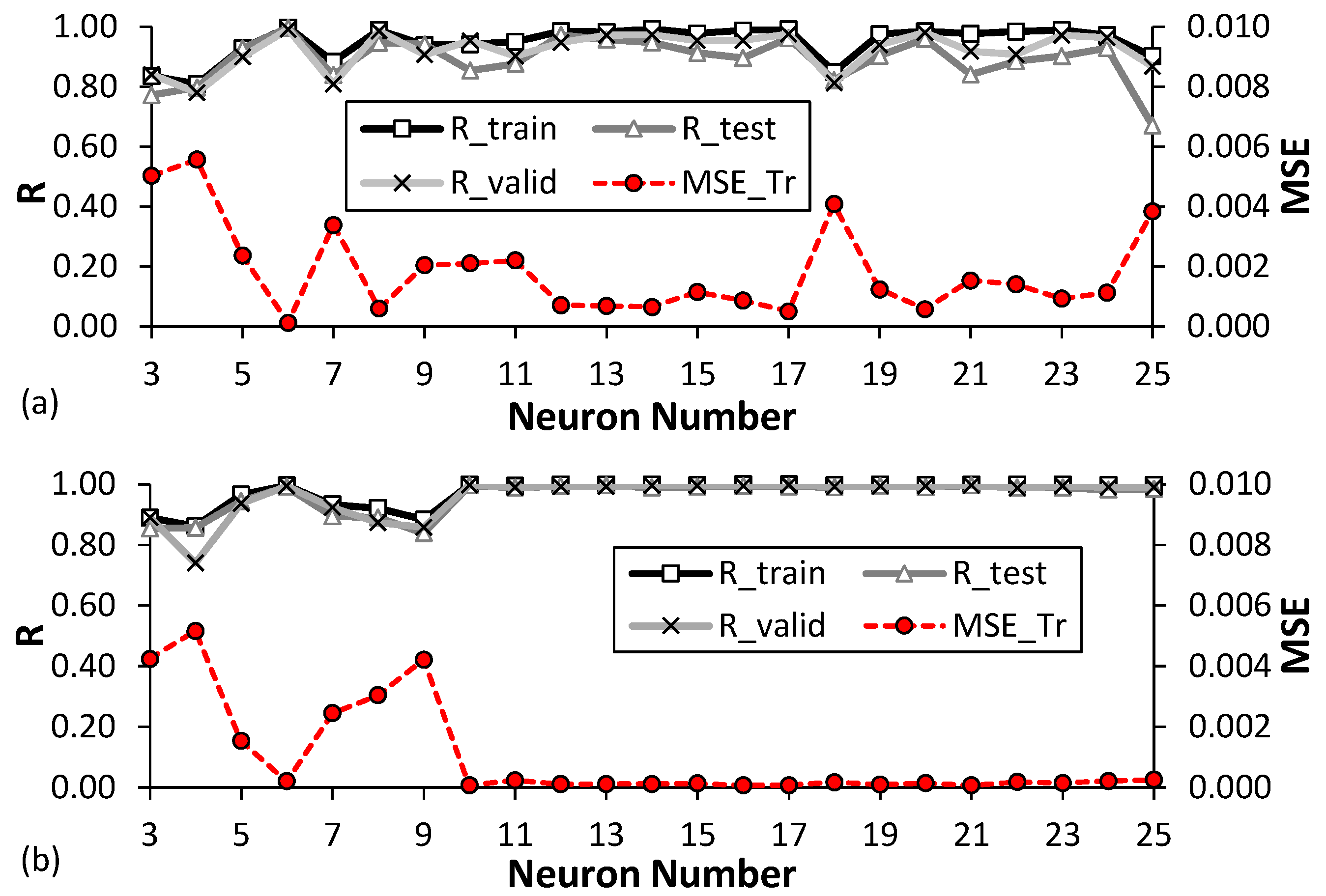
5.3. Proposed ANN Models
5.4. Proposed GMDH Models
5.5. ML Proposed Models Performances
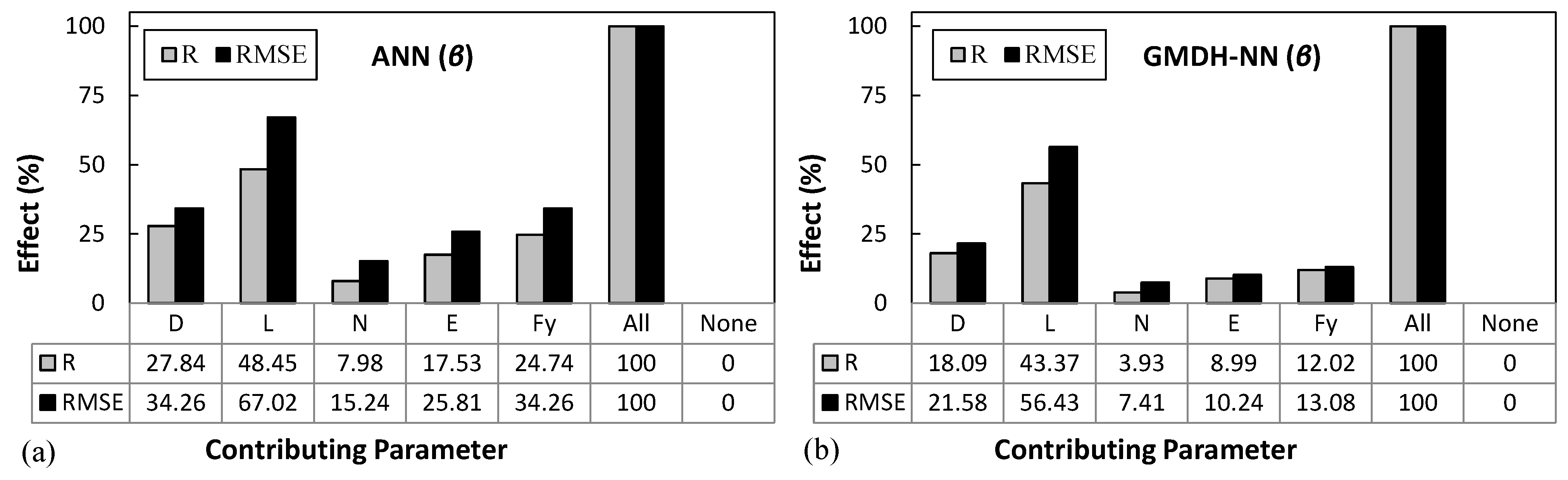
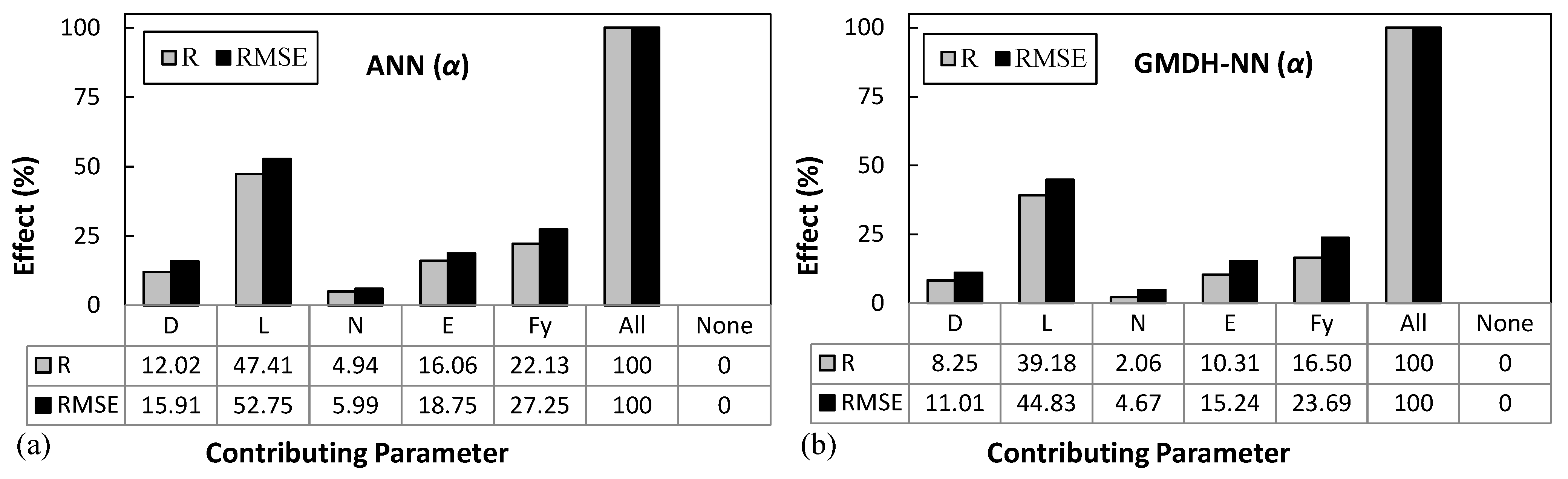
5.6. Sensitivity Analysis
5.7. Computational Costs
6. Conclusions
- As expected, by substituting SMA bars instead of steel bar in bar hysteretic dampers, no residual displacement could be seen in hysteretic curves, which shows the excellent performance of SMA-BHDs as added dampers to isolation systems.
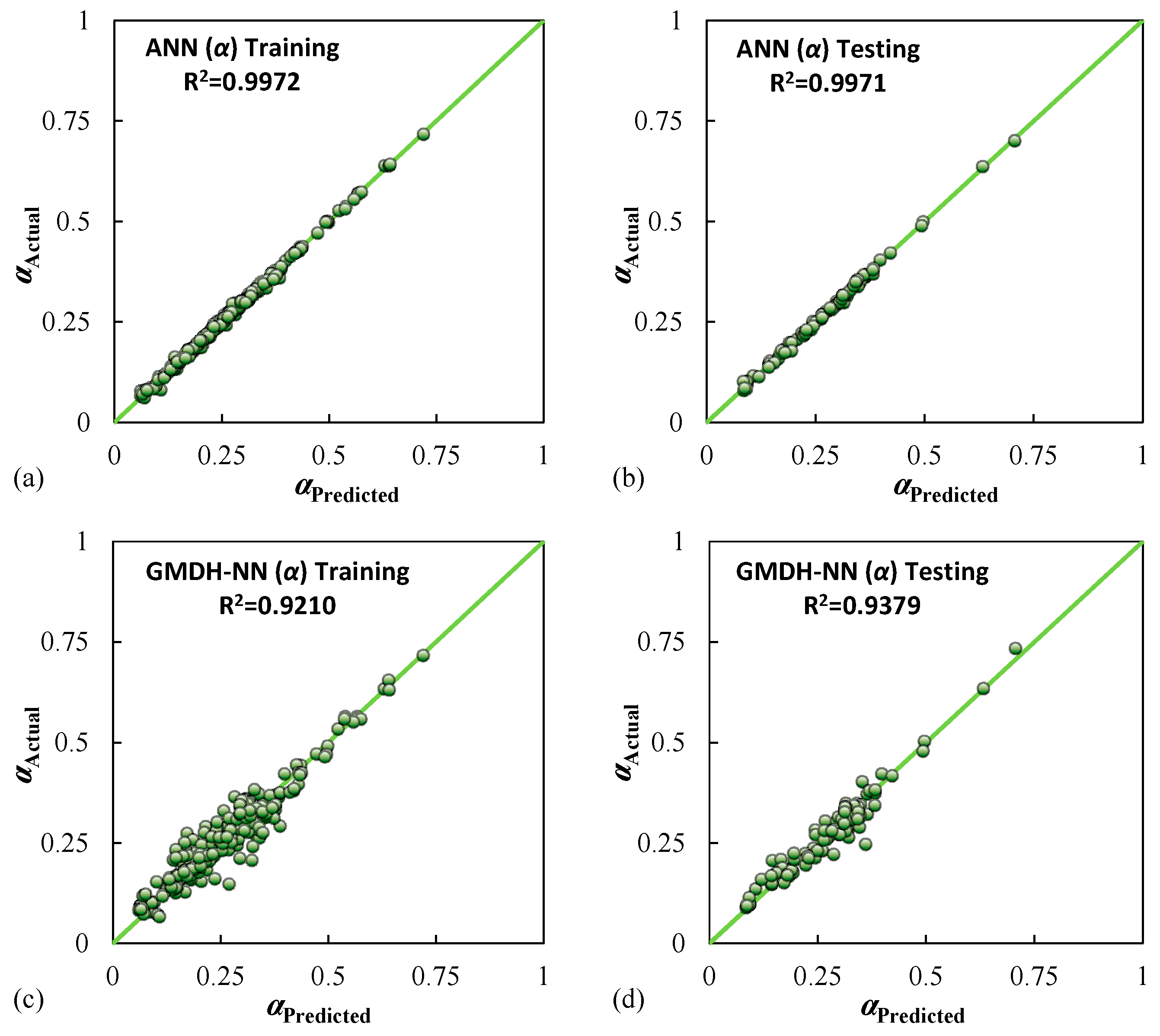
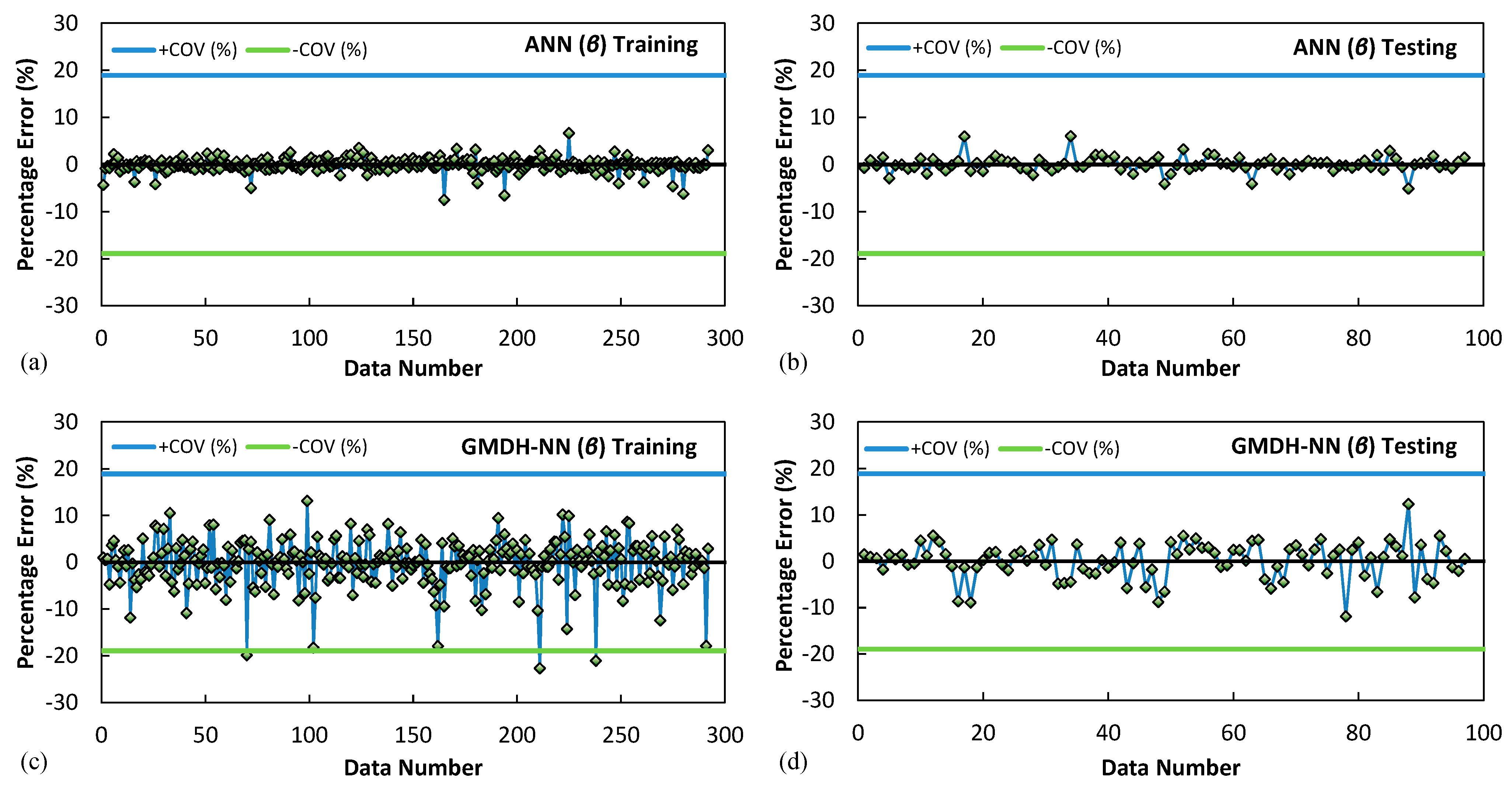
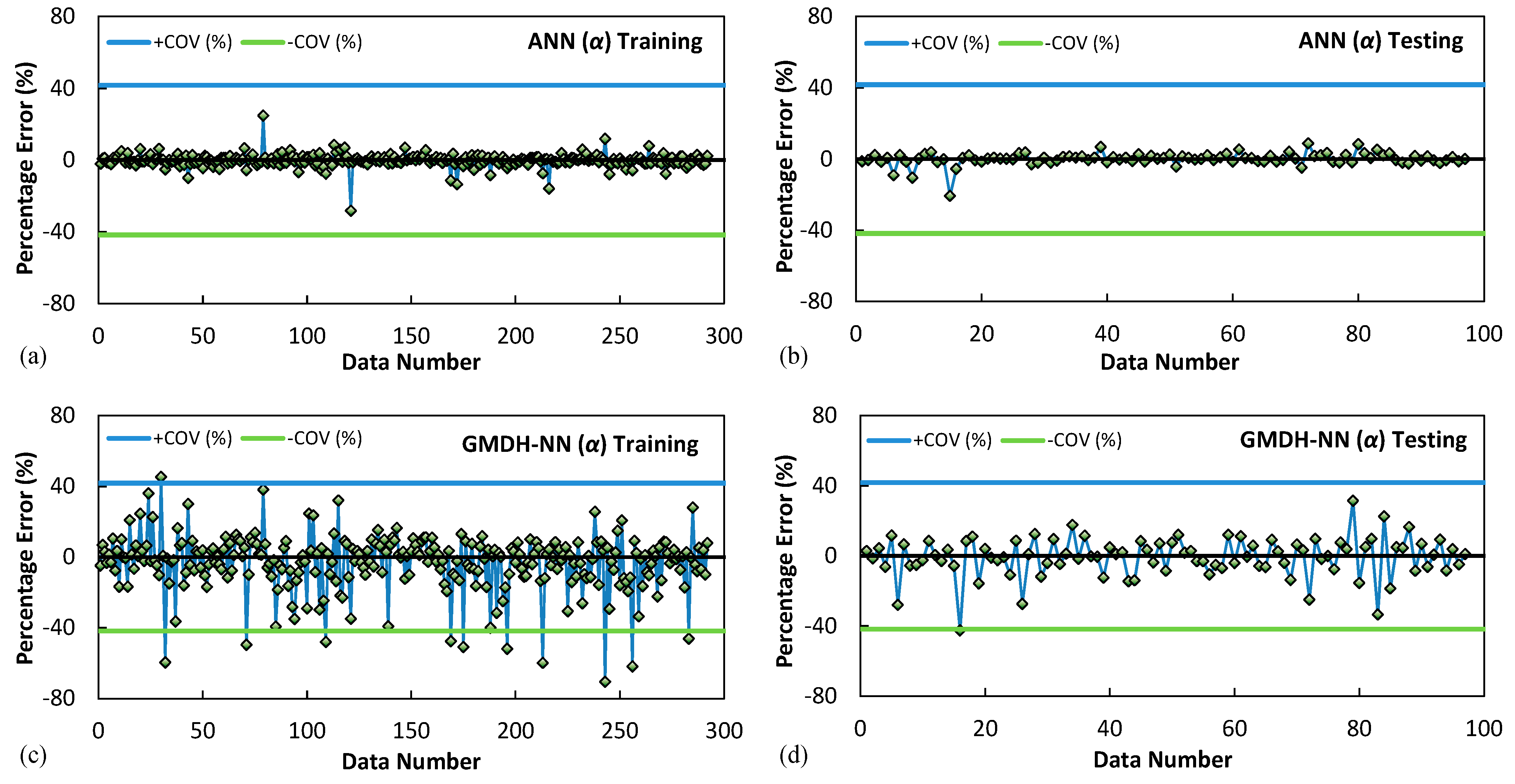
- Considering the ANN models with one hidden layer and varying neuron numbers between 3 to 25, the neural networks with 10 and 6 hidden neurons were selected as the optimised network structure for β and α parameters, respectively. The ANN (β) model has the R values of 0.9972, 0.9958, and 0.9916 in training, testing, and validation data sets and considerably small MSE values of 0.00012 and 0.00047, and MAPE values of 2.60% and 3.31%, in training and testing data sets, respectively. On the other hand, ANN (α) model has the R values of 0.9986, 0.9966, and 0.9972 in training, testing, and validation data sets and MSE values of 0.00007 and 0.00008, and MAPE values of 2.34% and 2.43%, in training and testing data sets, respectively.
- In the GMDH-NN models, similarly to ANN models, around 25% of all databases (97 data from 389 data) were randomly set aside for the test stage and considered unseen data. The results show that the proposed ANN models with higher R2 and lower error values in both the training and testing stages outperform the proposed GMDH-NN models. However, compared with the ANN model, GMDH-NN models present more user-friendly and easy-to-interpret closed-form equations.
- The sensitivity analysis of the input parameters in the developed ANN and GMDH-NN models for estimating both β and α parameters showed that the calculated SMA bars length (L) variable with higher R and RMSE values is the most influential input variable. Furthermore, the number of SMA bars (N) with lower impact values on the R and RMSE has the least effect.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jahangir, H.; Khatibinia, M.; Kavousi, M. Application of Contourlet Transform in Damage Localization and Severity Assessment of Prestressed Concrete Slabs. Soft Comput. Civ. Eng. 2021, 5, 39–67. [Google Scholar] [CrossRef]
- Santandrea, M.; Imohamed, I.A.O.; Jahangir, H.; Carloni, C.; Mazzotti, C.; De Miranda, S.; Ubertini, F.; Casadei, P. An investigation of the debonding mechanism in steel FRP-and FRCM-concrete joints. In Proceedings of the 4th Workshop on The New Boundaries of Structural Concrete, Capri Island, Italy, 29 September–1 October 2016; pp. 289–298. [Google Scholar]
- Karimipour, A.; Ghalehnovi, M. Influence of steel fibres on the mechanical and physical performance of self-compacting concrete manufactured with waste materials and fillers. Constr. Build. Mater. 2021, 267, 121806. [Google Scholar] [CrossRef]
- Ghalehnovi, M.; Karimipour, A.; Anvari, A.; de Brito, J. Flexural strength enhancement of recycled aggregate concrete beams with steel fibre-reinforced concrete jacket. Eng. Struct. 2021, 240, 112325. [Google Scholar] [CrossRef]
- Jahangir, H.; Karamodin, A. Structural Behavior Investigation Based on Adaptive Pushover Procedure. In Proceedings of the 10th National Congress on Civil Engineering, Tehran, Iran, 27–29 December 2015. [Google Scholar]
- Khaleghi, M.; Salimi, J.; Farhangi, V.; Moradi, M.J.; Karakouzian, M. Application of Artificial Neural Network to Predict Load Bearing Capacity and Stiffness of Perforated Masonry Walls. CivilEng 2021, 2, 4. [Google Scholar] [CrossRef]
- Hasani, H.; Ryan, K.L. Experimental Cyclic Test of Reduced Damage Detailed Drywall Partition Walls Integrated with a Timber Rocking Wall. J. Earthq. Eng. 2021, 1, 1–21. [Google Scholar] [CrossRef]
- Jahangir, H.; Esfahani, M.R. Structural Damage Identification Based on Modal Data and Wavelet Analysis. In Proceedings of the 3rd National Conference on Earthquake & Structure, Kerman, Iran, 17–18 October 2012. [Google Scholar]
- Jahangir, H.; Esfahani, M.R. Damage localization of Structures Using Adaptive Neuro-Fuzzy Inference System. In Proceedings of the 7th National Congress on Civil Engineering, Zahedan, Iran, 7 May 2013. [Google Scholar]
- Seyedi, S.R.; Keyhani, A.; Jahangir, H. An Energy-Based Damage Detection Algorithm Based on Modal Data. In Proceedings of the 7th International Conference on Seismologhy and Earthquake Engineering, International Institute of Earthquake Engineering and Seismology (IIEES), Tehran, Iran, 17–20 May 2015; pp. 335–336. [Google Scholar]
- Soong, T.; Dargush, G. Passive Energy Dissipation Systems in Structural Engineering; John Wiley Sons: London, UK, 1997. [Google Scholar]
- Castaldo, P. Integrated Seismic Design of Structure and Control Systems; Springer Tracts in Mechanical Engineering; Springer International Publishing: Cham, Switzerland, 2014; ISBN 978-3-319-02614-5. [Google Scholar]
- Michalski, R.S.; Carbonell, J.G.; Mitchell, T.M. Machine Learning: An Artificial Intelligence Approach; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Chen, Y.; Yan, J.; Feng, J.; Sareh, P. Particle Swarm Optimization-Based Metaheuristic Design Generation of Non-Trivial Flat-Foldable Origami Tessellations with Degree-4 Vertices. J. Mech. Des. 2021, 143, 011703. [Google Scholar] [CrossRef]
- Fan, W.; Chen, Y.; Li, J.; Sun, Y.; Feng, J.; Hassanin, H.; Sareh, P. Machine learning applied to the design and inspection of reinforced concrete bridges: Resilient methods and emerging applications. Structures 2021, 33, 3954–3963. [Google Scholar] [CrossRef]
- Di Cesare, A.; Ponzo, F.C.; Nigro, D. Assessment of the performance of hysteretic energy dissipation bracing systems. Bull. Earthq. Eng. 2014, 12, 2777–2796. [Google Scholar] [CrossRef]
- Javanmardi, A.; Ibrahim, Z.; Ghaedi, K.; Benisi Ghadim, H.; Hanif, M.U. State-of-the-Art Review of Metallic Dampers: Testing, Development and Implementation. Arch. Comput. Methods Eng. 2019, 27, 455–478. [Google Scholar] [CrossRef]
- Guerrero, J. Bandas amortiguadoras para muros de partición (damping strips for partition walls). In Proceedings of the Primer Congreso Nacional de Ingenieria Sısmica, Guadalajara, Mexico, 17 May 1965; pp. 75–85. [Google Scholar]
- Muto, K. Earthquake resistant design of 36-storied Kasumigaseki building. In Proceedings of the 4th World Conference of Earthquake Engineering, Santiago de, Chile, Chile, 13–18 January 1969; pp. 16–33. [Google Scholar]
- Kelly, J.M.; Skinner, R.I.; Heine, A.J. Mechanisms of energy absorption in special devices for use in earthquake resistant structures. Bull. N.Z. Soc. Earthq. Eng. 1972, 5, 63–88. [Google Scholar]
- Skinner, R.I.; Kelly, J.M.; Heine, A.J. Hysteretic dampers for earthquake-resistant structures. Earthq. Eng. Struct. Dyn. 1974, 3, 287–296. [Google Scholar] [CrossRef]
- Bergman, D.; Goel, S. Evaluation of Cyclic Testing of Steel-Plate Devices for Added Damping and Stifness; Department of Civil Engineering, University of Michigan: Michigan, MI, USA, 1987. [Google Scholar]
- Tsai, K.; Chen, H.; Hong, C.; Su, Y. Design of Steel Triangular Plate Energy Absorbers for Seismic-Resistant Construction. Earthq. Spectra 1993, 9, 505–528. [Google Scholar] [CrossRef]
- Tehranizadeh, M. Passive energy dissipation device for typical steel frame building in Iran. Eng. Struct. 2001, 23, 643–655. [Google Scholar] [CrossRef]
- Bakre, S.V.; Jangid, R.S.; Reddy, G.R. Optimum X-plate dampers for seismic response control of piping systems. Int. J. Press. Vessel. Pip. 2006, 83, 672–685. [Google Scholar] [CrossRef]
- Ming-Hsiang, S.; Wen-pei, S.; Cheer-Germ, G.O. Investigation of newly developed added damping and stiffness device with low yield strength steel. J. Zhejiang Univ. A 2004, 5, 326–334. [Google Scholar] [CrossRef]
- Shih, M.-H.; Sung, W.-P. A model for hysteretic behavior of rhombic low yield strength steel added damping and stiffness. Comput. Struct. 2005, 83, 895–908. [Google Scholar] [CrossRef]
- Han, Q.; Jia, J.; Xu, Z.; Bai, Y.; Song, N. Experimental Evaluation of Hysteretic Behavior of Rhombic Steel Plate Dampers. Adv. Mech. Eng. 2014, 6, 185629. [Google Scholar] [CrossRef]
- Chan, R.W.K.; Albermani, F. Experimental study of steel slit damper for passive energy dissipation. Eng. Struct. 2008, 30, 1058–1066. [Google Scholar] [CrossRef]
- Lee, C.-H.; Kim, J.; Kim, D.-H.; Ryu, J.; Ju, Y.K. Numerical and experimental analysis of combined behavior of shear-type friction damper and non-uniform strip damper for multi-level seismic protection. Eng. Struct. 2016, 114, 75–92. [Google Scholar] [CrossRef]
- Lee, J.; Kim, J. Development of box-shaped steel slit dampers for seismic retrofit of building structures. Eng. Struct. 2017, 150, 934–946. [Google Scholar] [CrossRef]
- Ahmadie Amiri, H.; Najafabadi, E.P.; Estekanchi, H.E. Experimental and analytical study of Block Slit Damper. J. Constr. Steel Res. 2018, 141, 167–178. [Google Scholar] [CrossRef]
- Köroğlu, M.A.; Köken, A.; Dere, Y. Use of different shaped steel slit dampers in beam to column connections of steel frames under cycling loading. Adv. Steel Constr. 2018, 14, 251–273. [Google Scholar]
- Jahangir, H.; Daneshvar Khorram, M.H.; Ghalehnovi, M. Influence of Geometric Parameters on Perforated Core Buckling Restrained Braces Behavior. J. Struct. Constr. Eng. 2018, 6, 75–94. (In Persian) [Google Scholar] [CrossRef]
- Bayat, K.; Shekastehband, B. Seismic performance of beam to column connections with T-shaped slit dampers. Thin-Walled Struct. 2019, 141, 28–46. [Google Scholar] [CrossRef]
- Liu, Y.; Aoki, T.; Shimoda, M. Strain Distribution Measurement of a Shear Panel Damper Developed for Bridge Structure. J. Struct. 2013, 2013, 1–11. [Google Scholar] [CrossRef]
- Deng, K.; Pan, P.; Sun, J.; Liu, J.; Xue, Y. Shape optimization design of steel shear panel dampers. J. Constr. Steel Res. 2014, 99, 187–193. [Google Scholar] [CrossRef]
- Sahoo, D.R.; Singhal, T.; Taraithia, S.S.; Saini, A. Cyclic behavior of shear-and-flexural yielding metallic dampers. J. Constr. Steel Res. 2015, 114, 247–257. [Google Scholar] [CrossRef]
- Deng, K.; Pan, P.; Li, W.; Xue, Y. Development of a buckling restrained shear panel damper. J. Constr. Steel Res. 2015, 106, 311–321. [Google Scholar] [CrossRef]
- Taherian, I.; Ghalehnovi, M.; Jahangir, H. Analytical Study on Composite Steel Plate Walls Using a Modified Strip Model. In Proceedings of the 7th International Conference on Seismologhy and Earthquake Engineering, Tehran, Iran, 17–20 May 2015. [Google Scholar]
- Qiu, C.; Zhang, Y.; Qu, B.; Dai, C.; Hou, H.; Li, H. Cyclic testing of seismic dampers consisting of multiple energy absorbing steel plate clusters. Eng. Struct. 2019, 183, 255–264. [Google Scholar] [CrossRef]
- Garivani, S.; Aghakouchak, A.A.; Shahbeyk, S. Numerical and experimental study of comb-teeth metallic yielding dampers. Int. J. Steel Struct. 2016, 16, 177–196. [Google Scholar] [CrossRef]
- Ciampi, V. Research and development of passive energy dissipation techniques for civil buildings in Italy. In Proceedings of the International Post—SMIRT Conference Seminar on Seismic Isolation, Passiver Energy Dissipation and Control of Vibration of Structures, Milan, Italy, 5 May 1995; pp. 1–15. [Google Scholar]
- Kato, S.; Kim, Y.-B.; Nakazawa, S.; Ohya, T. Simulation of the cyclic behavior of J-shaped steel hysteresis devices and study on the efficiency for reducing earthquake responses of space structures. J. Constr. Steel Res. 2005, 61, 1457–1473. [Google Scholar] [CrossRef]
- Kato, S.; Kim, Y.-B. A finite element parametric study on the mechanical properties of J-shaped steel hysteresis devices. J. Constr. Steel Res. 2006, 62, 802–811. [Google Scholar] [CrossRef]
- Oh, S.-H.; Song, S.-H.; Lee, S.-H.; Kim, H.-J. Seismic response of base isolating systems with U-shaped hysteretic dampers. Int. J. Steel Struct. 2012, 12, 285–298. [Google Scholar] [CrossRef]
- Deng, K.; Pan, P.; Wang, C. Development of crawler steel damper for bridges. J. Constr. Steel Res. 2013, 85, 140–150. [Google Scholar] [CrossRef]
- Maoshe, L.I.U.; Junlong, L.U. Analysis of Shear Stiffness of the Thin U-Shape Metal Damper [J]. J. Xi’an Univ. Technol. 2013, 29, 207–210. [Google Scholar]
- Deng, K.; Pan, P.; Su, Y.; Xue, Y. Shape optimization of U-shaped damper for improving its bi-directional performance under cyclic loading. Eng. Struct. 2015, 93, 27–35. [Google Scholar] [CrossRef]
- Bagheri, S.; Barghian, M.; Saieri, F.; Farzinfar, A. U-shaped metallic-yielding damper in building structures: Seismic behavior and comparison with a friction damper. Structures 2015, 3, 163–171. [Google Scholar] [CrossRef]
- Ene, D.; Kishiki, S.; Yamada, S.; Jiao, Y.; Konishi, Y.; Terashima, M.; Kawamura, N. Experimental study on the bidirectional inelastic deformation capacity of U-shaped steel dampers for seismic isolated buildings. Earthq. Eng. Struct. Dyn. 2016, 45, 173–192. [Google Scholar] [CrossRef]
- Wang, B.; Zhu, S. Superelastic SMA U-shaped dampers with self-centering functions. Smart Mater. Struct. 2018, 27, 055003. [Google Scholar] [CrossRef]
- Taiyari, F.; Mazzolani, F.M.; Bagheri, S. A proposal for energy dissipative braces with U-shaped steel strips. J. Constr. Steel Res. 2019, 154, 110–122. [Google Scholar] [CrossRef]
- Ghaedi, K.; Ibrahim, Z.; Javanmardi, A.; Rupakhety, R. Experimental Study of a New Bar Damper Device for Vibration Control of Structures Subjected to Earthquake Loads. J. Earthq. Eng. 2018, 25, 1–19. [Google Scholar] [CrossRef]
- Ghaedi, K.; Ibrahim, Z.; Javanmardi, A. A new metallic bar damper device for seismic energy dissipation of civil structures. IOP Conf. Ser. Mater. Sci. Eng. 2018, 431, 122009. [Google Scholar] [CrossRef]
- Aghlara, R.; Tahir, M.M. A passive metallic damper with replaceable steel bar components for earthquake protection of structures. Eng. Struct. 2018, 159, 185–197. [Google Scholar] [CrossRef]
- Golzan, S.B.; Langlois, S.; Legeron, F.P. Implementation of a Simplified Method in Design of Hysteretic Dampers for Isolated Highway Bridges. J. Bridg. Eng. 2017, 22, 04016127. [Google Scholar] [CrossRef]
- Jahangir, H.; Bagheri, M.; Delavari, S.M.J. Cyclic Behavior Assessment of Steel Bar Hysteretic Dampers Using Multiple Nonlinear Regression Approach. Iran. J. Sci. Technol. Trans. Civ. Eng. 2021, 45, 1227–1251. [Google Scholar] [CrossRef]
- Jahangir, H.; Esfahani, M.R. Numerical Study of Bond–Slip Mechanism in Advanced Externally Bonded Strengthening Composites. KSCE J. Civ. Eng. 2018, 22, 4509–4518. [Google Scholar] [CrossRef]
- Bagheri, M.; Chahkandi, A.; Jahangir, H. Seismic Reliability Analysis of RC Frames Rehabilitated by Glass Fiber-Reinforced Polymers. Int. J. Civ. Eng. 2019, 17, 1785–1797. [Google Scholar] [CrossRef]
- Jahangir, H.; Esfahani, M.R. Investigating loading rate and fibre densities influence on SRG—Concrete bond behaviour. Steel Compos. Struct. 2020, 34, 877–889. [Google Scholar] [CrossRef]
- Jahangir, H.; Esfahani, M.R. Experimental analysis on tensile strengthening properties of steel and glass fiber reinforced inorganic matrix composites. Sci. Iran. 2020, 28, 1152–1166. [Google Scholar] [CrossRef]
- Jahangir, H.; Esfahani, M.R. Strain of Newly–Developed Composites Relationship in Flexural Tests. J. Struct. Constr. Eng. 2018, 5, 92–107. (In Persian) [Google Scholar] [CrossRef]
- Gebretsadik, B.; Jadidi, K.; Farhangi, V.; Karakouzian, M. Application of Ultrasonic Measurements for the Evaluation of Steel Fiber Reinforced Concrete. Eng. Technol. Appl. Sci. Res. 2021, 11, 6662–6667. [Google Scholar] [CrossRef]
- Asgarian, B.; Moradi, S. Seismic response of steel braced frames with shape memory alloy braces. J. Constr. Steel Res. 2011, 67, 65–74. [Google Scholar] [CrossRef]
- Dolce, M.; Cardone, D.; Ponzo, F.C. Shaking-table tests on reinforced concrete frames with different isolation systems. Earthq. Eng. Struct. Dyn. 2007, 36, 573–596. [Google Scholar] [CrossRef]
- Andrawes, B.; DesRoches, R. Unseating prevention for multiple frame bridges using superelastic devices. Smart Mater. Struct. 2005, 14, S60–S67. [Google Scholar] [CrossRef]
- Farhangi, V.; Karakouzian, M. Design of bridge foundations using reinforced micropiles. In Proceedings of the IRF Global Road2Tunnel Conference & Expo, Las Vegas, NV, USA, 19–22 November 2019. [Google Scholar]
- Malakooti, A.; Maguire, M.; Thomas, R.J. Evaluating Electrical Resistivity as a Performance Based Test for Utah Bridge Deck Concrete (CAIT-UTC-NC35); Rutgers University, Center for Advanced Infrastructure and Transportation: Piscataway, NJ, USA, 2018. [Google Scholar]
- Song, G.; Ma, N.; Li, H.-N. Applications of shape memory alloys in civil structures. Eng. Struct. 2006, 28, 1266–1274. [Google Scholar] [CrossRef]
- Farahi, B.; Esfahani, M.; Sabzi, J. Experimental investigation on the behavior of reinforced concrete beams retrofitted with NSM-SMA/FRP. Amirkabir J. Civ. Eng. 2019, 51, 685–698. [Google Scholar] [CrossRef]
- Jahangir, H.; Bagheri, M. Evaluation of Seismic Response of Concrete Structures Reinforced by Shape Memory Alloys (Technical Note). Int. J. Eng. 2020, 33. [Google Scholar] [CrossRef]
- Karimipour, A.; Edalati, M. Shear and flexural performance of low, normal and high-strength concrete beams reinforced with longitudinal SMA, GFRP and steel rebars. Eng. Struct. 2020, 221, 111086. [Google Scholar] [CrossRef]
- Sabzi, J.; Esfahani, M.R.; Ozbakkaloglu, T.; Farahi, B. Effect of concrete strength and longitudinal reinforcement arrangement on the performance of reinforced concrete beams strengthened using EBR and EBROG methods. Eng. Struct. 2020, 205, 110072. [Google Scholar] [CrossRef]
- Jalali, A.; Cardone, D.; Narjabadifam, P. Smart restorable sliding base isolation system. Bull. Earthq. Eng. 2011, 9, 657–673. [Google Scholar] [CrossRef]
- Zafar, A.; Andrawes, B. Incremental dynamic analysis of concrete moment resisting frames reinforced with shape memory composite bars. Smart Mater. Struct. 2012, 21, 025013. [Google Scholar] [CrossRef]
- Alam, M.S.; Youssef, M.A.; Nehdi, M.L. Exploratory investigation on mechanical anchors for connecting SMA bars to steel or FRP bars. Mater. Struct. 2010, 43, 91–107. [Google Scholar] [CrossRef]
- Shrestha, B.; Li, C.; Hao, H.; Li, H. Performance-Based Seismic Assessment of Superelastic Shape Memory Alloy-Reinforced Bridge Piers Considering Residual Deformations. J. Earthq. Eng. 2017, 21, 1050–1069. [Google Scholar] [CrossRef]
- DesRoches, R.; McCormick, J.; Delemont, M. Cyclic Properties of Superelastic Shape Memory Alloy Wires and Bars. J. Struct. Eng. 2004, 130, 38–46. [Google Scholar] [CrossRef]
- Malécot, P.; Lexcellent, C.; Folte^te, E.; Collet, M. Shape Memory Alloys Cyclic Behavior: Experimental Study and Modeling. J. Eng. Mater. Technol. 2006, 128, 335–345. [Google Scholar] [CrossRef]
- Auricchio, F.; Sacco, E. A Superelastic Shape-Memory-Alloy Beam Model. J. Intell. Mater. Syst. Struct. 1997, 8, 489–501. [Google Scholar] [CrossRef]
- Seismosoft. Seismostruct V7.0—A Computer Program for Static and Dynamic Nonlinear Analysis of Framed Structures; Seismic Support, Inc.: Pavia, Italy, 2014. [Google Scholar]
- Roshani, M.M.; Kargar, S.H.; Farhangi, V.; Karakouzian, M. Predicting the effect of fly ash on concrete’s mechanical properties by ann. Sustainibility 2021, 13, 1469. [Google Scholar] [CrossRef]
- Ghaderi, A.; Morovati, V.; Dargazany, R. A physics-informed assembly of feed-forward neural network engines to predict inelasticity in cross-linked polymers. Polymers 2020, 12, 2628. [Google Scholar] [CrossRef]
- Rezazadeh Eidgahee, D.; Rafiean, A.H.; Haddad, A. A Novel Formulation for the Compressive Strength of IBP-Based Geopolymer Stabilized Clayey Soils Using ANN and GMDH-NN Approaches. Iran. J. Sci. Technol. Trans. Civ. Eng. 2019, 44, 219–229. [Google Scholar] [CrossRef]
- Moradi, M.J.; Khaleghi, M.; Salimi, J.; Farhangi, V.; Ramezanianpour, A.M. Predicting the compressive strength of concrete containing metakaolin with different properties using ANN. Meas. J. Int. Meas. Confed. 2021, 183, 109790. [Google Scholar] [CrossRef]
- Moradi, M.J.; Daneshvar, K.; Ghazi-nader, D.; Hajiloo, H. The prediction of fire performance of concrete-filled steel tubes (CFST) using artificial neural network. Thin—Walled Struct. 2021, 161, 107499. [Google Scholar] [CrossRef]
- Mashrei, M.A.; Seracino, R.; Rahman, M.S. Application of artificial neural networks to predict the bond strength of FRP-to-concrete joints. Constr. Build. Mater. 2013, 40, 812–821. [Google Scholar] [CrossRef]
- Ivakhnenko, A.G. The group method of data of handling; a rival of the method of stochastic approximation. Sov. Autom. Control. 1968, 13, 43–55. [Google Scholar]
- Muller, J.A.; Ivakhnenko, A.G. Self-organizing modelling in analysis and prediction of stock market. In Proceedings of the Second International Conference on Application of Fuzzy Systems and Soft Computing, ICAFS, Vienna, Austria, 29–30 August 1996; pp. 491–500. [Google Scholar]
- Ivakhnenko, A.G. Heuristic self-organization in problems of engineering cybernetics. Automatica 1970, 6, 207–219. [Google Scholar] [CrossRef]
- Auricchio, F.; Fugazza, D.; DesRoches, R. A 1D rate-dependent viscous constitutive model for superelastic shape-memory alloys: Formulation and comparison with experimental data. Smart Mater. Struct. 2007, 16, 39–50. [Google Scholar] [CrossRef]
- Shahin, M.A.; Maier, H.R.; Jaksa, M.B. Data Division for Developing Neural Networks Applied to Geotechnical Engineering. J. Comput. Civ. Eng. 2004, 18, 105–114. [Google Scholar] [CrossRef]
- Marquardt, D.W. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Rezazadeh Eidgahee, D.; Haddad, A.; Naderpour, H. Evaluation of shear strength parameters of granulated waste rubber using artificial neural networks and group method of data handling. Sci. Iran. 2019, 26, 3233–3244. [Google Scholar] [CrossRef] [Green Version]
- Ivakhnenko, A.G. Polynomial theory of complex systems. IEEE Trans. Syst. Man. Cybern. 1971, 1, 364–378. [Google Scholar] [CrossRef] [Green Version]
- Madala, H.R.; Ivakhnenko, A.G. Inductive Learning Algorithms for Complex Systems Modeling; cRc press: Boca Raton, FL, USA, 1994; Volume 368. [Google Scholar]
- Anastasakis, L.; Mort, N. The Development of Self-Organization Techniques in Modelling: A Review of the Group Method of Data Handling (GMDH); Department of Automatic Control & Systems Engineering, The University of Sheffield: Sheffield, UK, 2001. [Google Scholar]
- Gascón-Moreno, J.; Salcedo-Sanz, S.; Saavedra-Moreno, B.; Carro-Calvo, L.; Portilla-Figueras, A. An evolutionary-based hyper-heuristic approach for optimal construction of group method of data handling networks. Inf. Sci. 2013, 247, 94–108. [Google Scholar] [CrossRef]
- Jahangir, H.; Rezazadeh Eidgahee, D. A new and robust hybrid artificial bee colony algorithm—ANN model for FRP-concrete bond strength evaluation. Compos. Struct. 2021, 257, 113160. [Google Scholar] [CrossRef]
- Naderpour, H.; Rezazadeh Eidgahee, D.; Fakharian, P.; Rafiean, A.H.; Kalantari, S.M. A new proposed approach for moment capacity estimation of ferrocement members using Group Method of Data Handling. Eng. Sci. Technol. Int. J. 2020, 23, 382–391. [Google Scholar] [CrossRef]
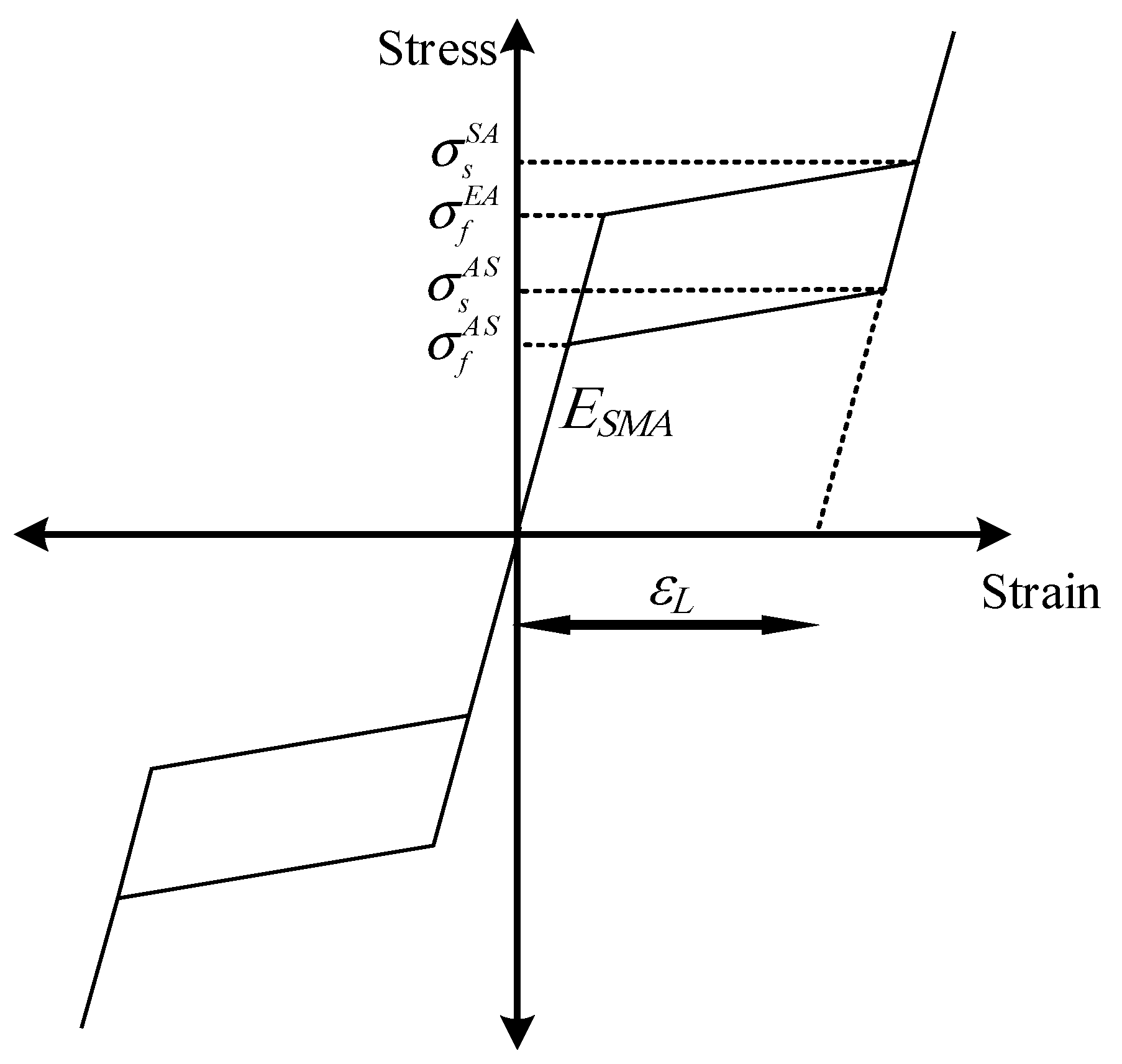





| Mechanical Property | Set 1 | Set 2 | Set 3 |
|---|---|---|---|
| ESMA (GPa) | 30 | 24.6 | 28 |
| εL (‰) | 4.8 | 4.10 | 4.25 |
| σfEA (Mpa) | 350 | 280 | 320 |
| σsSA (MPa) | 370 | 350 | 460 |
| σsAS (MPa) | 150 | 250 | 260 |
| σfAS (MPa) | 135 | 40 | 190 |
| Mechanical Property | Inputs | Outputs | |||||
|---|---|---|---|---|---|---|---|
| Statistical Feature | D (m) | L (m) | N | E (GPa) | Fy (MPa) | β_Bi. | α_Bi. |
| Min | 0.018 | 0.324 | 1 | 24.6 | 280 | 0.005 | 0.061 |
| Max | 0.050 | 1.362 | 10 | 30 | 350 | 0.040 | 0.720 |
| Ave | 0.037 | 0.728 | 6.286 | 27.658 | 318.274 | 0.022 | 0.268 |
| SD | 0.008 | 0.241 | 2.597 | 2.203 | 28.564 | 0.008 | 0.110 |
| CoV (%) | 24.016 | 32.901 | 41.303 | 8.010 | 8.977 | 36.725 | 41.720 |
| NN | MSE_Tr | MSE_Ts | MAPE_Tr | MAPE_Ts | R_train | R_test | R_valid |
|---|---|---|---|---|---|---|---|
| 3 | 0.00503 | 0.00663 | 18.86 | 19.80 | 0.8355 | 0.7715 | 0.8399 |
| 4 | 0.00556 | 0.00894 | 19.44 | 22.07 | 0.8089 | 0.7980 | 0.7799 |
| 5 | 0.00237 | 0.00518 | 9.16 | 10.76 | 0.9283 | 0.9274 | 0.8995 |
| 6 | 0.00012 | 0.00047 | 2.60 | 3.31 | 0.9972 | 0.9958 | 0.9916 |
| 7 | 0.00339 | 0.00362 | 11.91 | 12.12 | 0.8840 | 0.8388 | 0.8082 |
| 8 | 0.00059 | 0.00223 | 5.32 | 7.61 | 0.9884 | 0.9461 | 0.9847 |
| 9 | 0.00204 | 0.00420 | 9.84 | 13.16 | 0.9392 | 0.9413 | 0.9063 |
| 10 | 0.00211 | 0.00475 | 11.33 | 16.83 | 0.9410 | 0.8542 | 0.9528 |
| 11 | 0.00220 | 0.00424 | 12.12 | 17.43 | 0.9493 | 0.8766 | 0.9017 |
| 12 | 0.00071 | 0.00260 | 6.13 | 9.42 | 0.9849 | 0.9717 | 0.9470 |
| 13 | 0.00068 | 0.00186 | 5.88 | 8.75 | 0.9833 | 0.9568 | 0.9713 |
| 14 | 0.00065 | 0.00258 | 4.69 | 8.04 | 0.9930 | 0.9470 | 0.9733 |
| 15 | 0.00115 | 0.00240 | 8.12 | 11.35 | 0.9777 | 0.9123 | 0.9537 |
| 16 | 0.00086 | 0.00276 | 7.31 | 12.71 | 0.9875 | 0.8958 | 0.9543 |
| 17 | 0.00050 | 0.00206 | 5.64 | 10.36 | 0.9913 | 0.9617 | 0.9756 |
| 18 | 0.00408 | 0.00513 | 15.96 | 18.47 | 0.8495 | 0.8222 | 0.8120 |
| 19 | 0.00124 | 0.00412 | 9.47 | 15.32 | 0.9753 | 0.9034 | 0.9403 |
| 20 | 0.00057 | 0.00182 | 6.27 | 9.78 | 0.9853 | 0.9601 | 0.9806 |
| 21 | 0.00154 | 0.00389 | 9.40 | 14.16 | 0.9763 | 0.8408 | 0.9180 |
| 22 | 0.00140 | 0.00424 | 8.21 | 13.34 | 0.9841 | 0.8850 | 0.9081 |
| 23 | 0.00093 | 0.00265 | 6.02 | 10.57 | 0.9891 | 0.9017 | 0.9717 |
| 24 | 0.00112 | 0.00293 | 8.31 | 14.38 | 0.9713 | 0.9291 | 0.9634 |
| 25 | 0.00384 | 0.00753 | 15.56 | 20.61 | 0.9024 | 0.6701 | 0.8679 |
| NN | MSE_Tr | MSE_Ts | MAPE_Tr | MAPE_Ts | R_train | R_test | R_valid |
|---|---|---|---|---|---|---|---|
| 3 | 0.00424 | 0.00481 | 15.92 | 15.73 | 0.8892 | 0.8540 | 0.8898 |
| 4 | 0.00516 | 0.00569 | 19.52 | 18.71 | 0.8609 | 0.8567 | 0.7405 |
| 5 | 0.00154 | 0.00193 | 8.59 | 8.86 | 0.9656 | 0.9444 | 0.9369 |
| 6 | 0.00020 | 0.00030 | 4.11 | 4.30 | 0.9956 | 0.9917 | 0.9936 |
| 7 | 0.00245 | 0.00275 | 10.05 | 10.18 | 0.9330 | 0.8941 | 0.9229 |
| 8 | 0.00304 | 0.00347 | 10.89 | 11.10 | 0.9209 | 0.8901 | 0.8737 |
| 9 | 0.00421 | 0.00501 | 15.76 | 15.51 | 0.8839 | 0.8381 | 0.8575 |
| 10 | 0.00007 | 0.00008 | 2.34 | 2.43 | 0.9986 | 0.9966 | 0.9972 |
| 11 | 0.00023 | 0.00034 | 4.31 | 4.77 | 0.9954 | 0.9890 | 0.9904 |
| 12 | 0.00011 | 0.00015 | 2.82 | 3.20 | 0.9983 | 0.9938 | 0.9920 |
| 13 | 0.00011 | 0.00014 | 2.87 | 3.14 | 0.9981 | 0.9966 | 0.9927 |
| 14 | 0.00011 | 0.00021 | 2.70 | 2.94 | 0.9983 | 0.9890 | 0.9967 |
| 15 | 0.00013 | 0.00025 | 3.02 | 3.82 | 0.9978 | 0.9915 | 0.9943 |
| 16 | 0.00007 | 0.00009 | 2.13 | 2.45 | 0.9992 | 0.9939 | 0.9952 |
| 17 | 0.00007 | 0.00011 | 2.17 | 2.61 | 0.9992 | 0.9925 | 0.9967 |
| 18 | 0.00017 | 0.00037 | 2.91 | 3.47 | 0.9975 | 0.9906 | 0.9920 |
| 19 | 0.00009 | 0.00019 | 2.45 | 3.15 | 0.9991 | 0.9950 | 0.9941 |
| 20 | 0.00014 | 0.00020 | 2.92 | 3.39 | 0.9979 | 0.9895 | 0.9941 |
| 21 | 0.00007 | 0.00012 | 2.13 | 2.75 | 0.9991 | 0.9957 | 0.9958 |
| 22 | 0.00018 | 0.00044 | 2.61 | 3.81 | 0.9991 | 0.9893 | 0.9871 |
| 23 | 0.00015 | 0.00028 | 2.99 | 4.15 | 0.9980 | 0.9892 | 0.9943 |
| 24 | 0.00021 | 0.00034 | 3.23 | 3.99 | 0.9979 | 0.9812 | 0.9896 |
| 25 | 0.00025 | 0.00048 | 3.88 | 5.15 | 0.9972 | 0.9839 | 0.9894 |
| ANN Model | Neuron Number | Weight | Bias | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Wik | Wk | ||||||||
| D (m) | L (m) | N | E (Pa) | Fy (Pa) | bhk | b0 | |||
| ANN (β) | 1 | 3.965 | −20.960 | −0.619 | 0.187 | −0.620 | 10.051 | −17.347 | 10.821 |
| 2 | −1.108 | 4.541 | 0.132 | 0.415 | −0.837 | 3.784 | 1.343 | ||
| 3 | −1.193 | 5.374 | 0.216 | 1.576 | −1.959 | −1.853 | 0.845 | ||
| 4 | −2.051 | 8.078 | 0.261 | 0.024 | −0.998 | −5.004 | 3.198 | ||
| 5 | 1.008 | 0.108 | 0.645 | 0.208 | −0.059 | 1.520 | −2.189 | ||
| 6 | 2.392 | −9.337 | −0.315 | 1.584 | −0.635 | −3.428 | −3.944 | ||
| ANN (α) | 1 | 0.559 | −2.633 | −0.276 | 1.729 | −2.516 | −3.141 | 1.216 | 3.533 |
| 2 | 1.366 | −4.664 | −0.196 | −0.520 | 2.946 | −0.520 | 0.335 | ||
| 3 | 0.843 | −2.784 | −0.621 | −1.609 | −2.580 | −0.252 | 2.271 | ||
| 4 | −0.616 | 2.599 | 0.258 | −0.818 | 1.907 | −3.149 | −1.095 | ||
| 5 | 0.947 | −0.272 | 0.538 | 2.254 | 2.055 | 0.741 | 2.634 | ||
| 6 | −0.321 | −2.157 | 0.185 | −0.133 | 0.139 | −0.250 | −1.712 | ||
| 7 | −0.673 | 3.086 | 0.070 | −0.913 | −0.159 | −2.342 | 1.988 | ||
| 8 | −0.962 | 5.921 | 0.561 | 0.350 | 2.526 | −0.353 | 3.006 | ||
| 9 | −1.300 | 7.781 | 0.364 | 1.100 | −0.862 | −4.083 | 7.370 | ||
| 10 | 0.833 | −3.854 | −0.185 | 2.809 | −1.610 | −2.730 | −2.643 | ||
| Parameter | Method | Data Partition | R | R2 | MSE | RMSE | MAE | MAPE (%) |
|---|---|---|---|---|---|---|---|---|
| β | ANN (β) | Training | 0.9974 | 0.9949 | 0.00008 | 0.00903 | 0.00572 | 0.91 |
| Testing | 0.9917 | 0.9834 | 0.00024 | 0.01538 | 0.00773 | 1.18 | ||
| GMDH-NN (β) | Training | 0.9726 | 0.9459 | 0.00554 | 0.07441 | 0.05507 | 3.55 | |
| Testing | 0.9744 | 0.9494 | 0.00423 | 0.06507 | 0.05080 | 3.03 | ||
| α | ANN (α) | Training | 0.9986 | 0.9972 | 0.00004 | 0.00597 | 0.00444 | 2.23 |
| Testing | 0.9985 | 0.9971 | 0.00003 | 0.00578 | 0.00464 | 2.21 | ||
| GMDH-NN (α) | Training | 0.9597 | 0.9210 | 0.00100 | 0.03159 | 0.02334 | 10.90 | |
| Testing | 0.9685 | 0.9379 | 0.00070 | 0.02642 | 0.01991 | 8.16 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Farhangi, V.; Jahangir, H.; Eidgahee, D.R.; Karimipour, A.; Javan, S.A.N.; Hasani, H.; Fasihihour, N.; Karakouzian, M. Behaviour Investigation of SMA-Equipped Bar Hysteretic Dampers Using Machine Learning Techniques. Appl. Sci. 2021, 11, 10057. https://doi.org/10.3390/app112110057
Farhangi V, Jahangir H, Eidgahee DR, Karimipour A, Javan SAN, Hasani H, Fasihihour N, Karakouzian M. Behaviour Investigation of SMA-Equipped Bar Hysteretic Dampers Using Machine Learning Techniques. Applied Sciences. 2021; 11(21):10057. https://doi.org/10.3390/app112110057
Chicago/Turabian StyleFarhangi, Visar, Hashem Jahangir, Danial Rezazadeh Eidgahee, Arash Karimipour, Seyed Alireza Nedaei Javan, Hamed Hasani, Nazanin Fasihihour, and Moses Karakouzian. 2021. "Behaviour Investigation of SMA-Equipped Bar Hysteretic Dampers Using Machine Learning Techniques" Applied Sciences 11, no. 21: 10057. https://doi.org/10.3390/app112110057
APA StyleFarhangi, V., Jahangir, H., Eidgahee, D. R., Karimipour, A., Javan, S. A. N., Hasani, H., Fasihihour, N., & Karakouzian, M. (2021). Behaviour Investigation of SMA-Equipped Bar Hysteretic Dampers Using Machine Learning Techniques. Applied Sciences, 11(21), 10057. https://doi.org/10.3390/app112110057









