Classical and Quantum Gases on a Semiregular Mesh
Abstract
1. Introduction
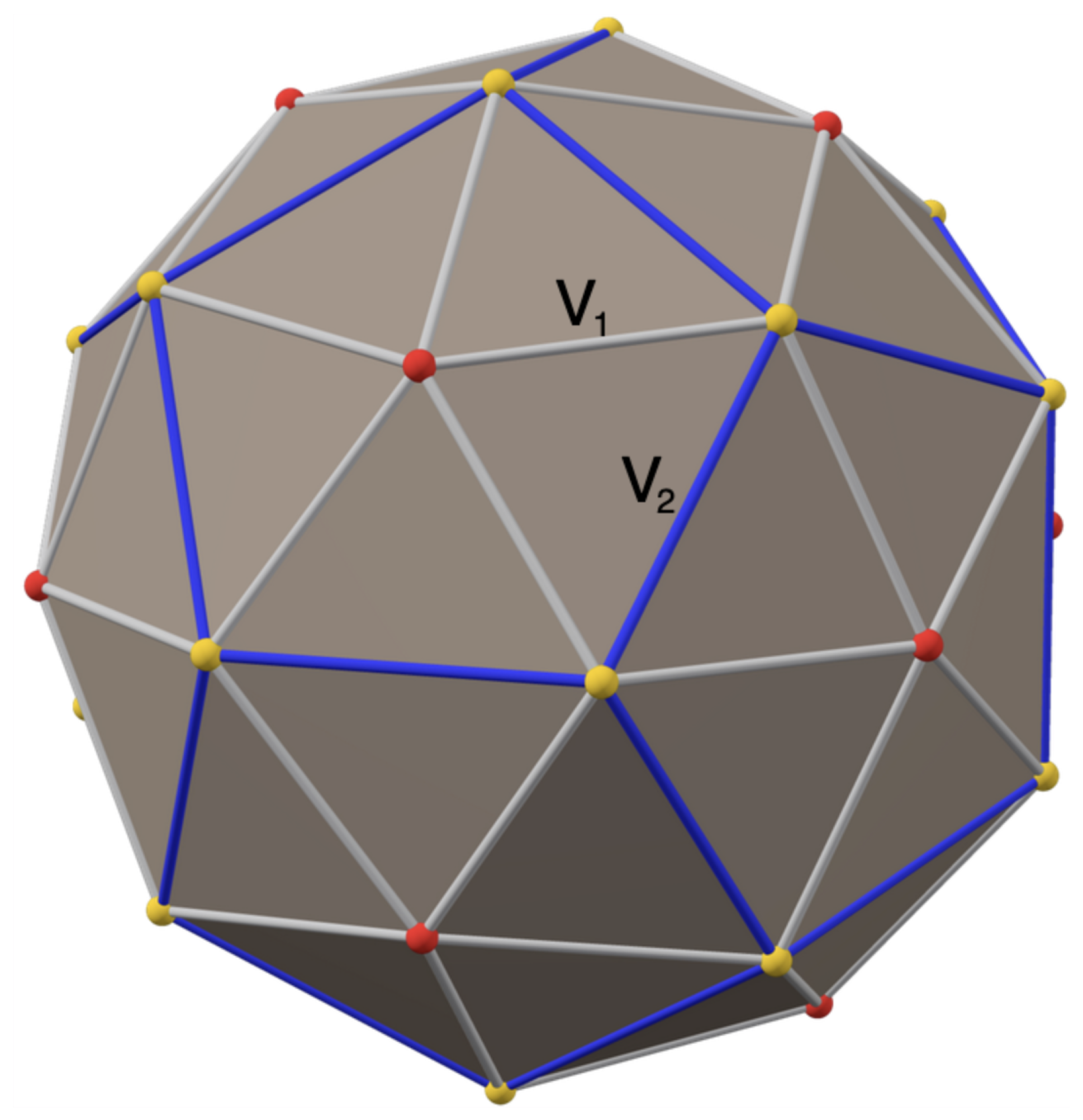
2. Lattice-Gas Models on a Spherical Mesh
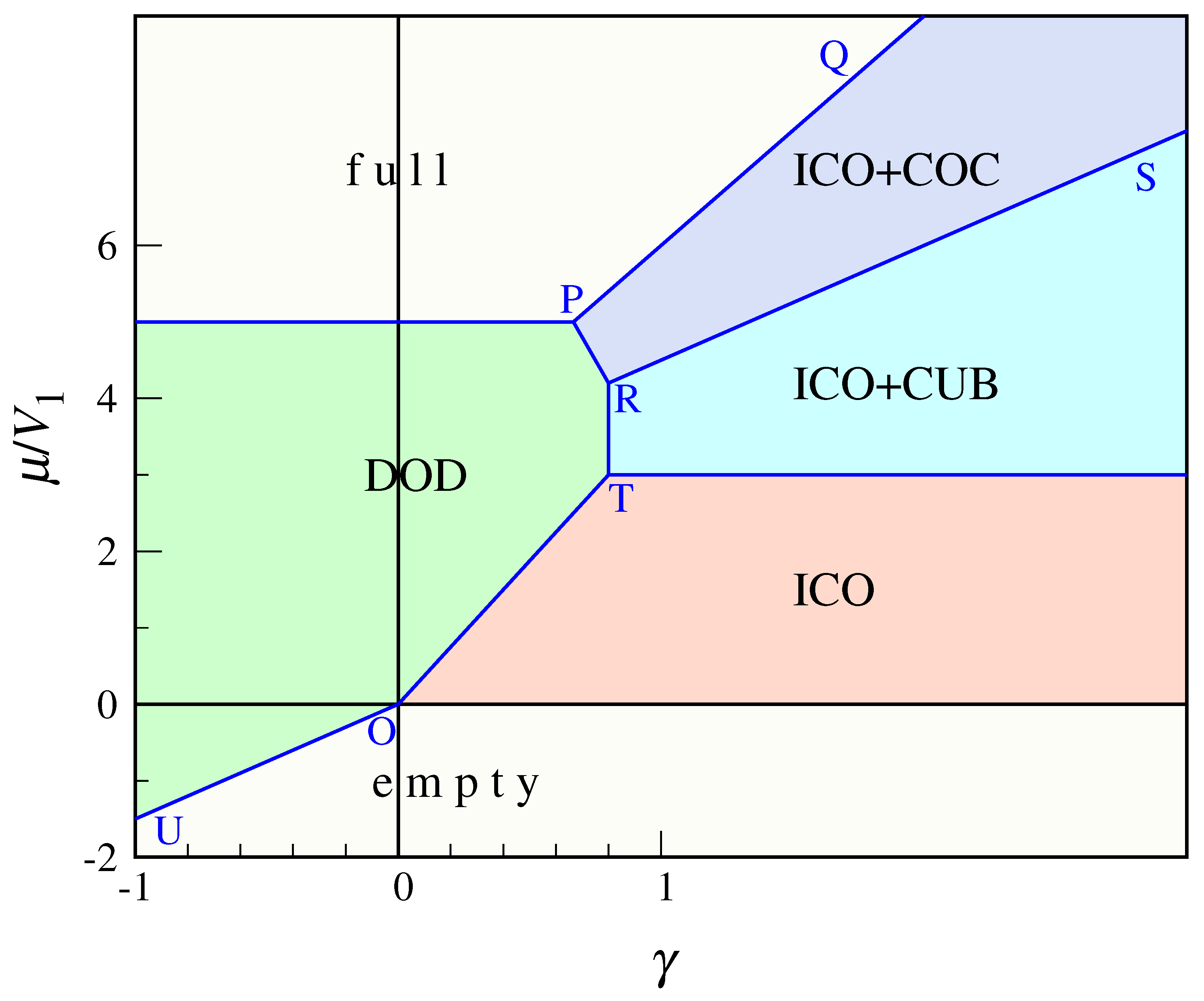
2.1. Zero-Temperature Phases
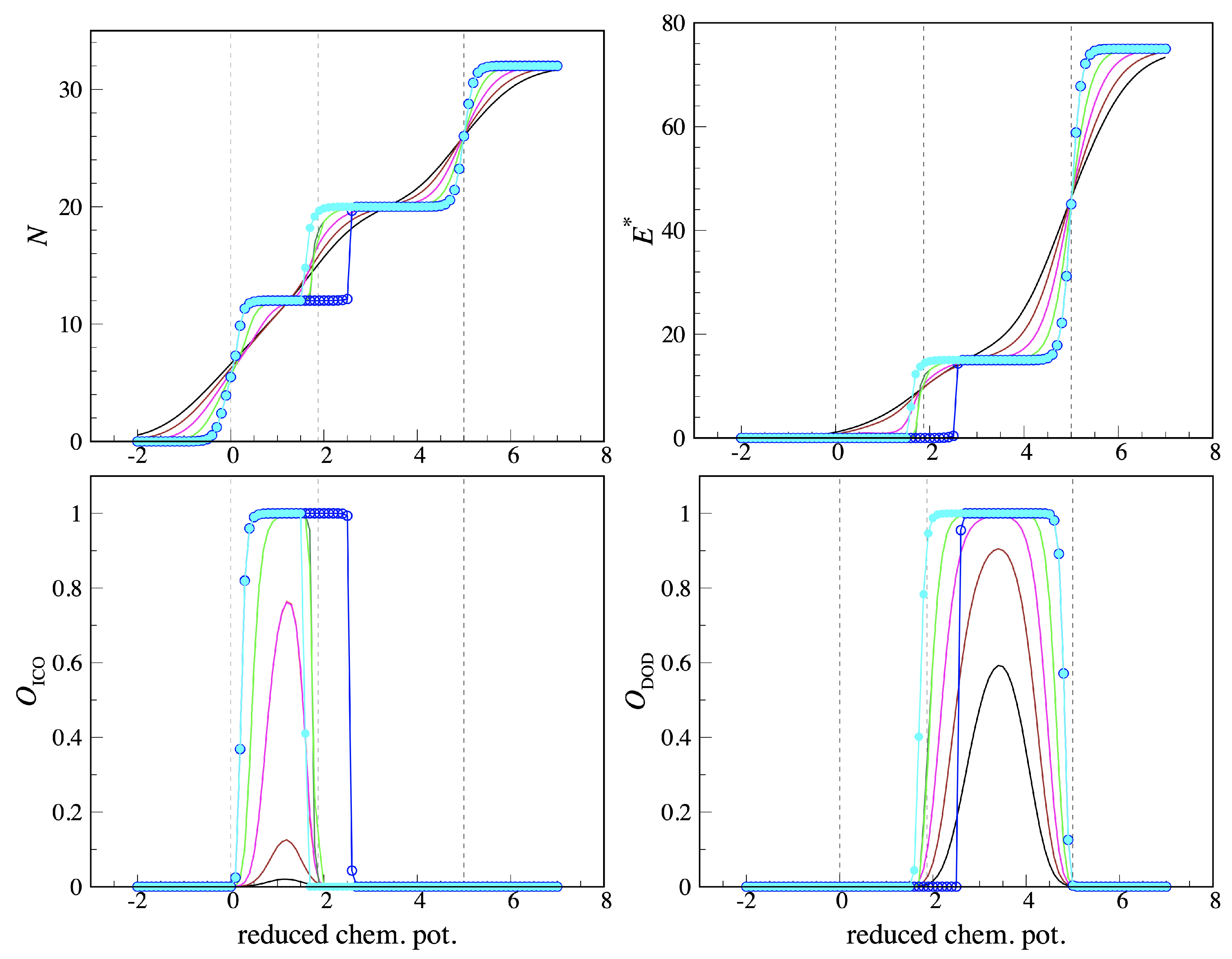
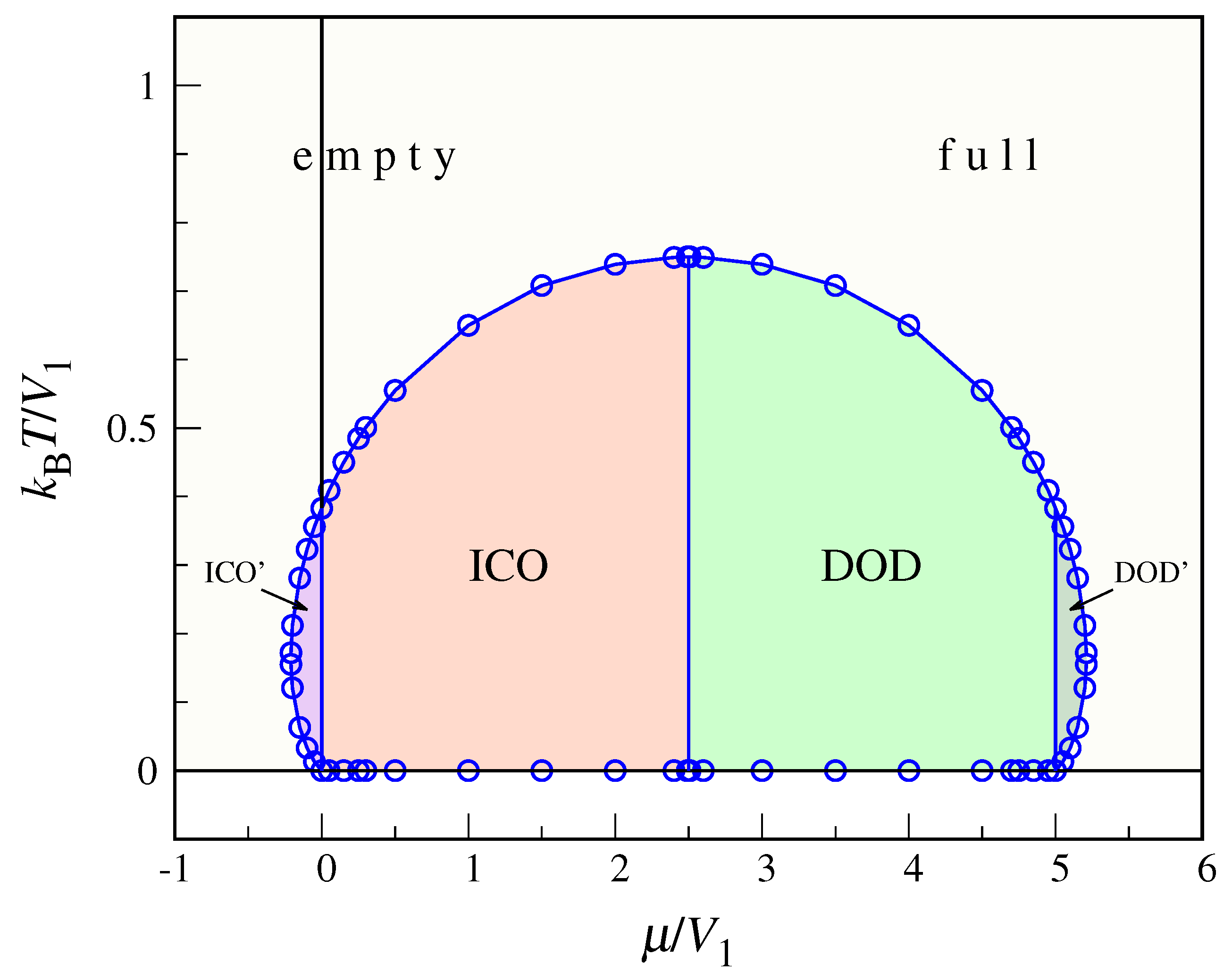
2.2. Finite-Temperature Behavior
3. Hard-Core Bosons on a Spherical Mesh: Extended Bose-Hubbard Model
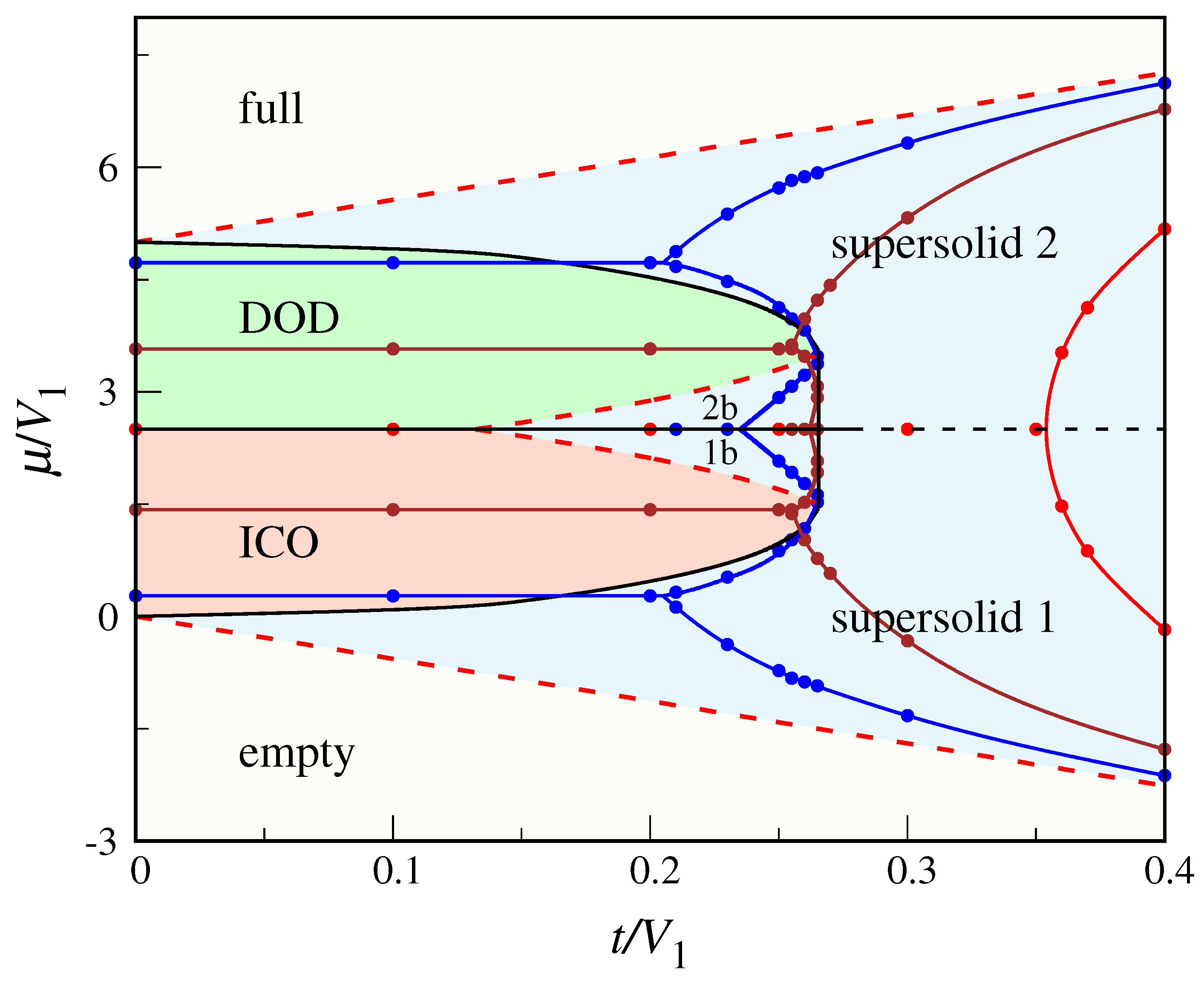
3.1. Decoupling Approximation
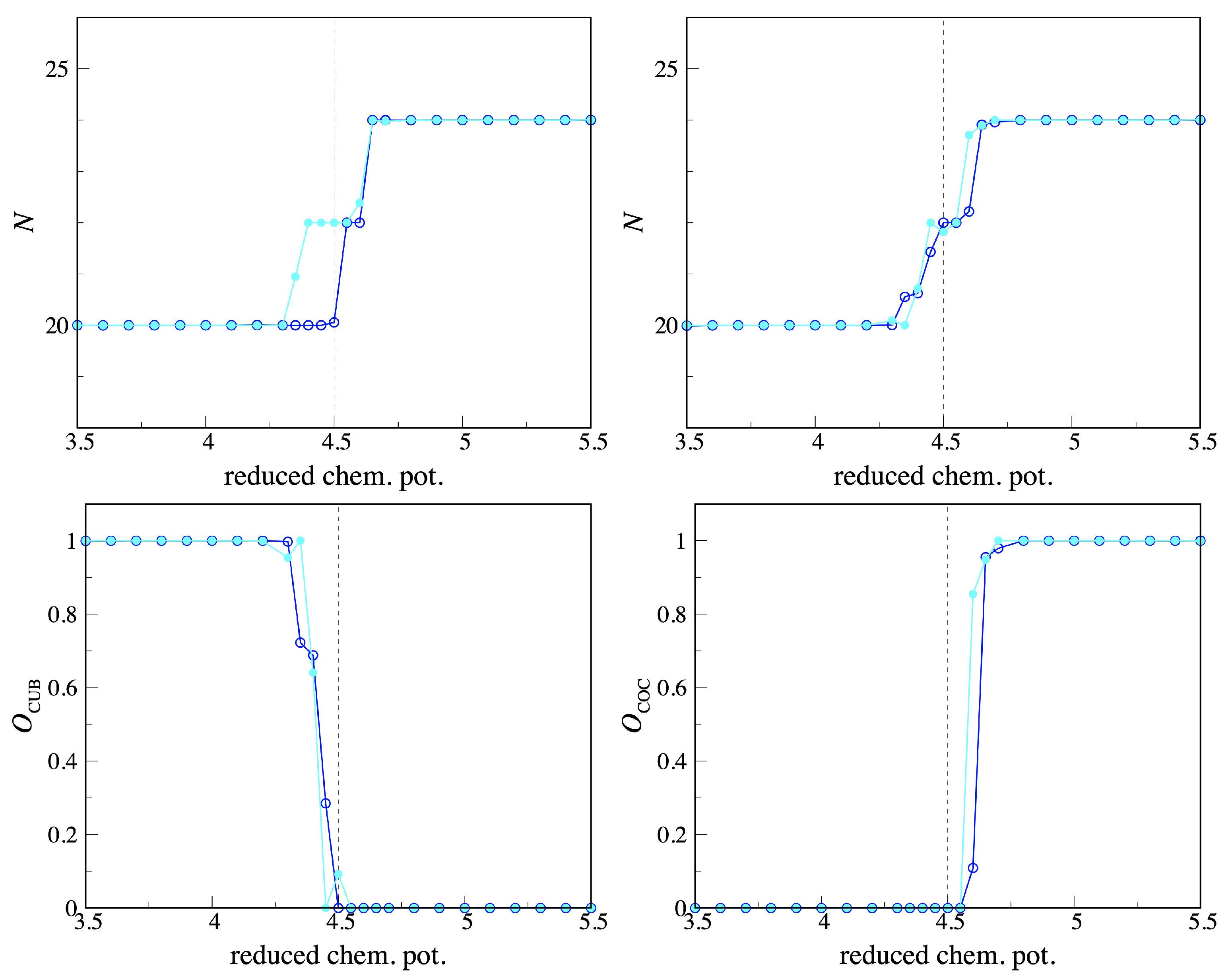
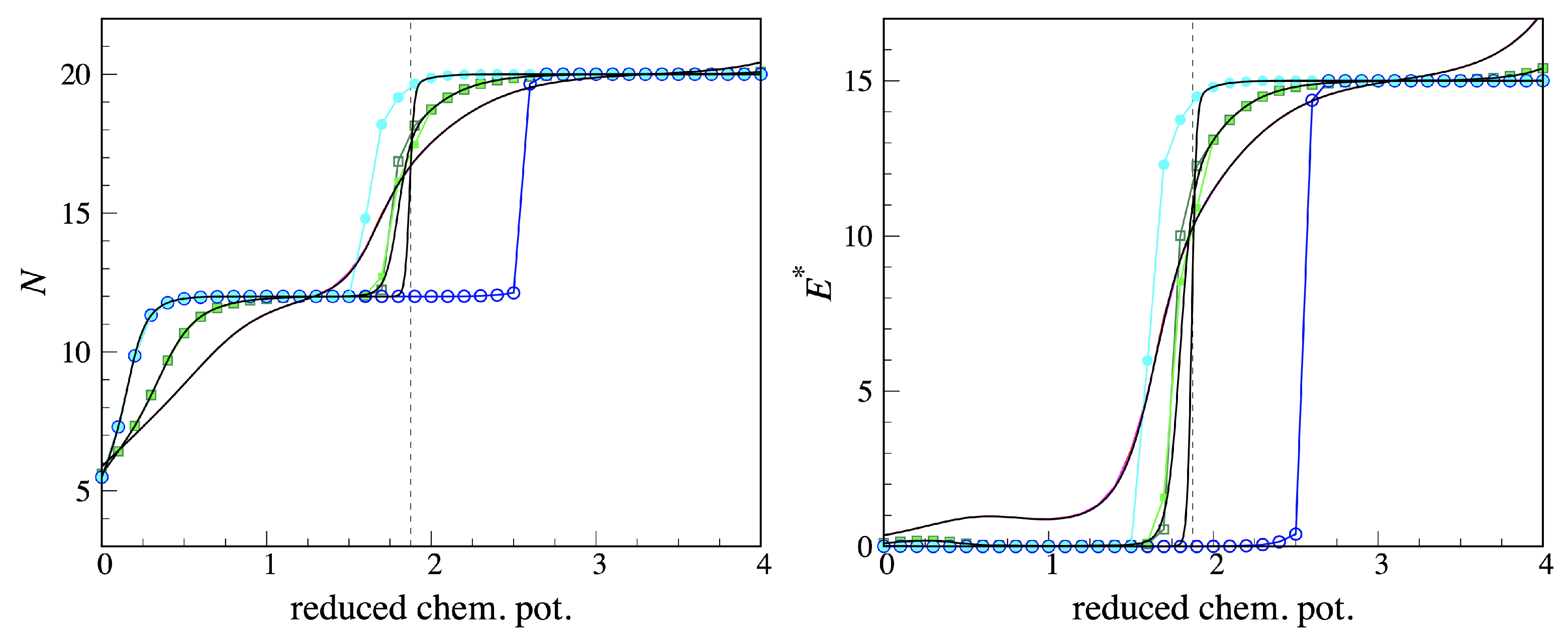
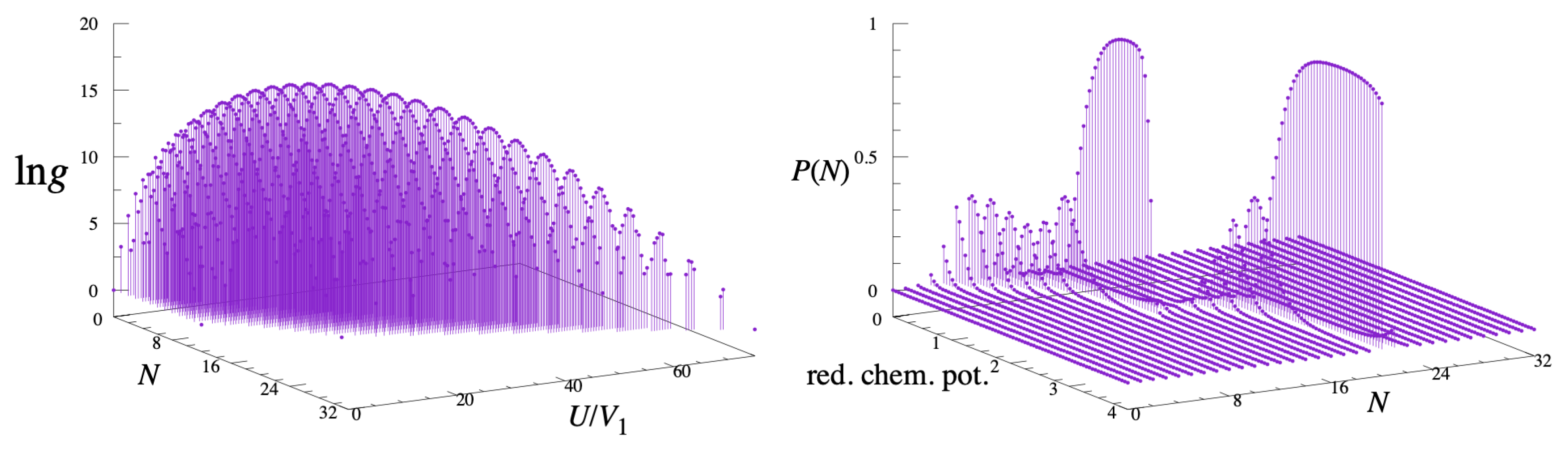
3.2. Numerical Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Calculation of Specific Heats
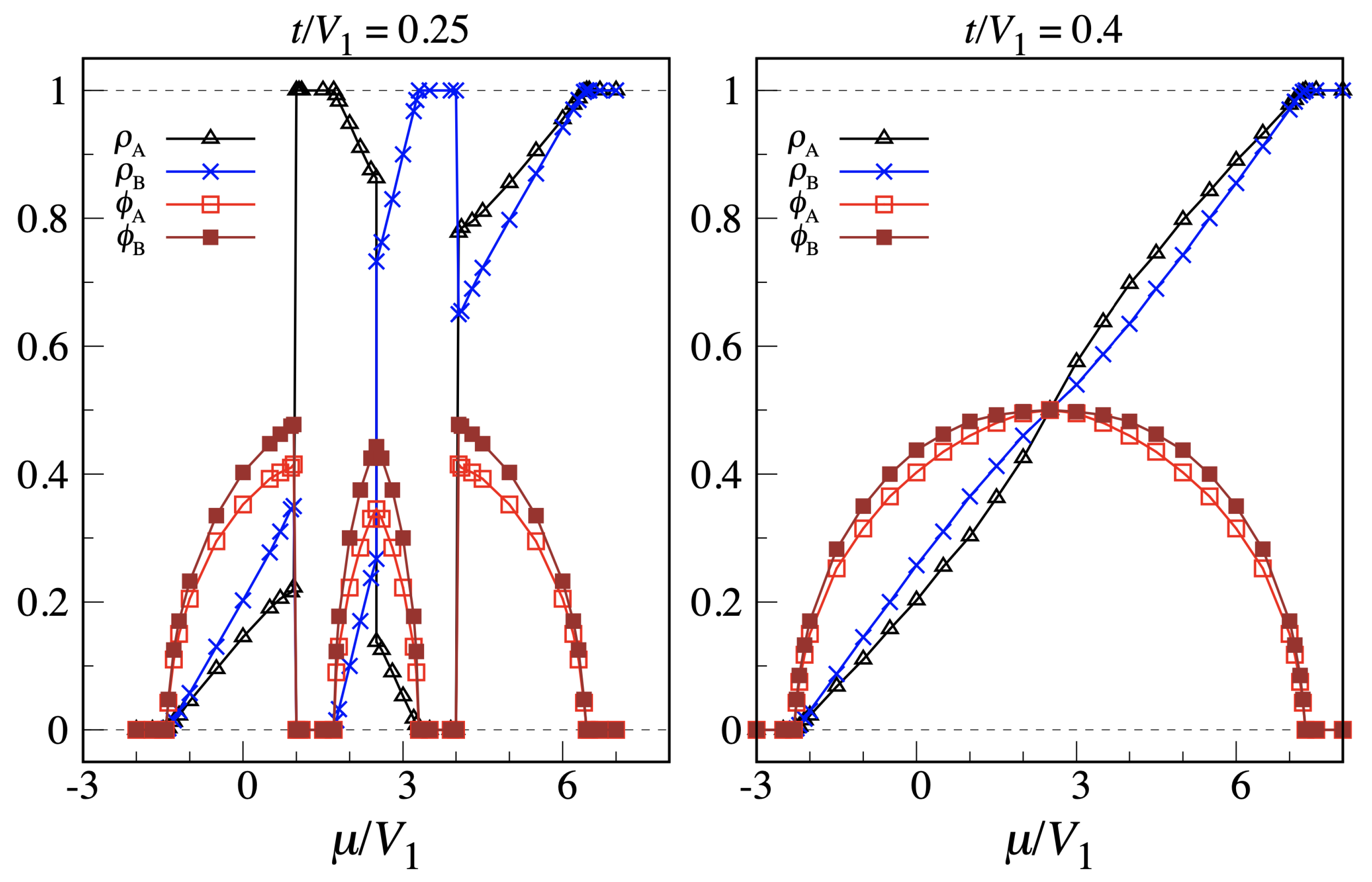
Appendix B. Order Parameters
References
- Post, A.J.; Glandt, E.D. Statistical thermodynamics of particles adsorbed onto a spherical surface. I. Canonical ensemble. J. Chem. Phys. 1986, 85, 7349–7358. [Google Scholar] [CrossRef]
- Prestipino Giarritta, S.; Ferrario, M.; Giaquinta, P.V. Statistical geometry of hard particles on a sphere. Phys. A 1992, 187, 456–474. [Google Scholar] [CrossRef]
- Prestipino Giarritta, S.; Ferrario, M.; Giaquinta, P.V. Statistical geometry of hard particles on a sphere: Analysis of defects at high density. Phys. A 1993, 201, 649–665. [Google Scholar] [CrossRef]
- Prestipino, S.; Speranza, C.; Giaquinta, P.V. Density anomaly in a fluid of softly repulsive particles embedded in a spherical surface. Soft Matter 2012, 8, 11708–11713. [Google Scholar] [CrossRef]
- Vest, J.-P.; Tarjus, G.; Viot, P. Glassy dynamics of dense particle assemblies on a spherical substrate. J. Chem. Phys. 2018, 148, 164501. [Google Scholar] [CrossRef] [PubMed]
- Guerra, R.E.; Kelleher, C.P.; Hollingsworth, A.D.; Chaikin, P.M. Freezing on a sphere. Nature 2018, 554, 346–350. [Google Scholar] [CrossRef]
- Franzini, S.; Reatto, L.; Pini, D. Formation of cluster crystals in an ultra-soft potential model on a spherical surface. Soft Matter 2018, 14, 8724–8739. [Google Scholar] [CrossRef]
- Dlamini, N.; Prestipino, S.; Pellicane, G. Self-Assembled Structures of Colloidal Dimers and Disks on a Spherical Surface. Entropy 2021, 23, 585. [Google Scholar] [CrossRef]
- Prestipino, S.; Giaquinta, P.V. Ground state of weakly repulsive soft-core bosons on a sphere. Phys. Rev. A 2019, 99, 063619. [Google Scholar] [CrossRef]
- Zobay, O.; Garraway, B.M. Atom trapping and two-dimensional Bose-Einstein condensates in field-induced adiabatic potentials. Phys. Rev. A 2004, 69, 023605. [Google Scholar] [CrossRef]
- Garraway, B.M.; Perrin, H. Recent developments in trapping and manipulation of atoms with adiabatic potentials. J. Phys. B At. Mol. Opt. Phys. 2016, 49, 172001. [Google Scholar] [CrossRef]
- Elliott, E.R.; Krutzik, M.C.; Williams, J.R.; Thompson, R.J.; Aveline, D.C. NASA’s Cold Atom Lab (CAL): System development and ground test status. Npj Microgravity 2018, 4, 16. [Google Scholar] [CrossRef] [PubMed]
- Lundblad, N.; Carollo, R.A.; Lannert, C.; Gold, M.J.; Jiang, X.; Paseltiner, D.; Sergay, N.; Aveline, D.C. Shell potentials for microgravity Bose-Einstein condensates. Npj Microgravity 2019, 5, 30. [Google Scholar] [CrossRef] [PubMed]
- Wannier, G.H. Antiferromagnetism. The Triangular Ising Net. Phys. Rev. 1950, 79, 357–364. [Google Scholar] [CrossRef]
- Toulouse, G. Theory of the frustration effect in spin glasses. Commun. Phys. 1977, 2, 115–119. [Google Scholar]
- Bloch, I.; Dalibard, J.; Zwerger, W. Many-body physics with ultracold gases. Rev. Mod. Phys. 2008, 80, 885–964. [Google Scholar] [CrossRef]
- Amico, L.; Boshier, M.; Birkl, G.; Minguzzi, A.; Miniatura, C.; Kwek, L.C.; Aghamalyan, D.; Ahufinger, V.; Andrei, N.; Arnold, A.S.; et al. Roadmap on Atomtronics. arXiv 2020, arXiv:2008.04439. [Google Scholar]
- Jaksch, D.; Bruder, C.; Cirac, J.I.; Gardiner, C.W.; Zoller, P. Cold Bosonic Atoms in Optical Lattices. Phys. Rev. Lett. 1998, 81, 3108–3111. [Google Scholar] [CrossRef]
- Greiner, M.; Mandel, O.; Esslinger, T.; Hänsch, T.W.; Bloch, I. Quantum phase transition from a superfluid to a Mott insulator in a gas of ultracold atoms. Nature 2002, 415, 39–44. [Google Scholar] [CrossRef] [PubMed]
- Windpassinger, P.; Sengstock, K. Engineering novel optical lattices. Rep. Prog. Phys. 2013, 76, 086401. [Google Scholar] [CrossRef]
- Barredo, D.; Lienhard, V.; de Léséleuc, S.; Lahaye, T.; Browaeys, A. Synthetic three-dimensional atomic structures assembled atom by atom. Nature 2018, 561, 79–82. [Google Scholar] [CrossRef] [PubMed]
- Browaeys, A.; Lahaye, T. Many-body physics with individually controlled Rydberg atoms. Nat. Phys. 2020, 16, 132–142. [Google Scholar] [CrossRef]
- Visual Polyhedra. Available online: http://dmccooey.com/polyhedra/ (accessed on 10 May 2021).
- Prestipino, S. Ultracold Bosons on a Regular Spherical Mesh. Entropy 2020, 22, 1289. [Google Scholar] [CrossRef]
- Wang, F.; Landau, D.P. Efficient, Multiple-Range Random Walk Algorithm to Calculate the Density of States. Phys. Rev. Lett. 2001, 86, 2050–2053. [Google Scholar] [CrossRef] [PubMed]
- Belardinelli, R.E.; Pereyra, V.D. Fast algorithm to calculate density of states. Phys. Rev. E 2007, 75, 046701. [Google Scholar] [CrossRef]
- Morita, T. On the lattice model of liquid helium proposed by Matsubara and Matsuda. Prog. Theor. Phys. 1957, 18, 462–466. [Google Scholar] [CrossRef][Green Version]
- Fisher, M.P.A.; Weichman, P.B.; Grinstein, G.; Fisher, D.S. Boson localization and the superfluid-insulator transition. Phys. Rev. B 1989, 40, 546–570. [Google Scholar] [CrossRef] [PubMed]
- Rokhsar, D.S.; Kotliar, B.G. Gutzwiller projection for bosons. Phys. Rev. B 1991, 44, 10328–10332. [Google Scholar] [CrossRef]
- Krauth, W.; Caffarel, M.; Bouchaud, J.-P. Gutzwiller wave function for a model of strongly interacting bosons. Phys. Rev. B 1992, 45, 3137–3140. [Google Scholar] [CrossRef]
- Batrouni, G.G.; Scalettar, R.T.; Zimanyi, G.T.; Kampf, A.P. Supersolids in the Bose-Hubbard Hamiltonian. Phys. Rev. Lett. 1995, 74, 2527–2530. [Google Scholar] [CrossRef]
- Van Otterlo, A.; Wagenblast, K.-H.; Baltin, R.; Fazio, R.; Schön, G. Quantum phase transitions of interacting bosons and the supersolid phase. Phys. Rev. B 1995, 52, 16176–16186. [Google Scholar] [CrossRef] [PubMed]
- Wessel, S.; Troyer, M. Supersolid Hard-Core Bosons on the Triangular Lattice. Phys. Rev. Lett. 2005, 95, 127205. [Google Scholar] [CrossRef] [PubMed]
- Kovrizhin, D.L.; Pai, G.V.; Sinha, S. Density wave and supersolid phases of correlated bosons in an optical lattice. Europhys. Lett. 2005, 72, 162–168. [Google Scholar] [CrossRef]
- Pollet, L.; Picon, J.D.; Büchler, H.P.; Troyer, M. Supersolid Phase with Cold Polar Molecules on a Triangular Lattice. Phys. Rev. Lett. 2010, 104, 125302. [Google Scholar] [CrossRef] [PubMed]
- Iskin, M. Route to supersolidity for the extended Bose-Hubbard model. Phys. Rev. A 2011, 83, 051606. [Google Scholar] [CrossRef]
- Tanzi, L.; Lucioni, E.; Famà, F.; Catani, J.; Fioretti, A.; Gabbanini, C.; Bisset, R.N.; Santos, L.; Modugno, G. Observation of a dipolar quantum gas with metastable supersolid properties. Phys. Rev. Lett. 2019, 122, 130405. [Google Scholar] [CrossRef]
- Böttcher, F.; Schmidt, J.-N.; Wenzel, M.; Hertkorn, J.; Guo, M.; Langen, T.; Pfau, T. Transient supersolid properties in an array of dipolar quantum droplets. Phys. Rev. X 2019, 9, 011051. [Google Scholar] [CrossRef]
- Chomaz, L.; Petter, D.; Ilzhöfer, P.; Natale, G.; Trautmann, A.; Politi, C.; Durastante, G.; van Bijnen, R.M.W.; Patscheider, A.; Sohmen, M.; et al. Long-lived and transient supersolid behaviors in dipolar quantum gases. Phys. Rev. X 2019, 9, 021012. [Google Scholar] [CrossRef]
- Leggett, A.J. Can a solid be “superfluid”? Phys. Rev. Lett. 1970, 25, 1543–1546. [Google Scholar] [CrossRef]
- Tanzi, L.; Maloberti, J.G.; Biagioni, G.; Fioretti, A.; Gabbanini, C.; Modugno, G. Evidence of superfluidity in a dipolar supersolid from nonclassical rotational inertia. Science 2021, 371, 1162–1165. [Google Scholar] [CrossRef]
- Kunimi, M.; Kato, Y. Mean-field and stability analyses of two-dimensional flowing soft-core bosons modeling a supersolid. Phys. Rev. B 2012, 86, 060510. [Google Scholar] [CrossRef]
- Macrì, T.; Maucher, F.; Cinti, F.; Pohl, T. Elementary excitations of ultracold soft-core bosons across the superfluid-supersolid phase transition. Phys. Rev. A 2013, 87, 061602. [Google Scholar] [CrossRef]
- Prestipino, S.; Sergi, A.; Bruno, E. Freezing of soft-core bosons at zero temperature: A variational theory. Phys. Rev. B 2018, 98, 104104. [Google Scholar] [CrossRef]
- Prestipino, S. Bose-Hubbard model on polyhedral graphs. Phys. Rev. A 2021, 103, 033313. [Google Scholar] [CrossRef]
- Sheshadri, K.; Krishnamurthy, H.R.; Pandit, R.; Ramakhrishnan, T.V. Superfluid and Insulating Phases in an Interacting-Boson Model: Mean-Field Theory and the RPA. Europhys. Lett. 1993, 22, 257–263. [Google Scholar] [CrossRef]
- Gheeraert, N.; Chester, S.; May, M.; Eggert, S.; Pelster, A. Mean-Field Theory for Extended Bose-Hubbard Model with Hard-Core Bosons. In Selforganization in Complex Systems: The Past, Present, and Future of Synergetics; Pelster, A., Wunner, G., Eds.; Springer: Zurich, Switzerland, 2016; pp. 289–296. [Google Scholar]
- Zhang, X.-F.; Dillenschneider, R.; Yu, Y.; Eggert, S. Supersolid phase transitions for hard-core bosons on a triangular lattice. Phys. Rev. B 2011, 84, 174515. [Google Scholar] [CrossRef]
- Van Oosten, D.; van der Straten, P.; Stoof, H.T.C. Mott insulators in an optical lattice with high filling factors. Phys. Rev. A 2003, 67, 033606. [Google Scholar] [CrossRef]
- Buonsante, P.; Vezzani, A. Phase diagram for ultracold bosons in optical lattices and superlattices. Phys. Rev. A 2004, 70, 033608. [Google Scholar] [CrossRef]
- Lu, X.; Yu, Y. Finite-temperature effects on the number fluctuation of ultracold atoms across the superfluid-to-Mott-insulator transition. Phys. Rev. A 2006, 74, 063615. [Google Scholar] [CrossRef]
- Capogrosso-Sansone, B.; Prokof’ev, N.V.; Svistunov, B.V. Phase diagram and thermodynamics of the three-dimensional Bose-Hubbard model. Phys. Rev. B 2007, 75, 134302. [Google Scholar] [CrossRef]
- Mahmud, K.W.; Duchon, E.N.; Kato, Y.; Kawashima, N.; Scalettar, R.T.; Trivedi, N. Finite-temperature study of bosons in a two-dimensional optical lattice. Phys. Rev. B 2011, 84, 054302. [Google Scholar] [CrossRef]
- Fang, S.; Chung, C.-M.; Ma, P.N.; Chen, P.; Wang, D.-W. Quantum criticality from in situ density imaging. Phys. Rev. A 2011, 83, 031605. [Google Scholar] [CrossRef]
- Prestipino, S.; Laio, A.; Tosatti, E. A fingerprint of surface-tension anisotropy in the free-energy cost of nucleation. J. Chem. Phys. 2013, 138, 064508. [Google Scholar] [CrossRef] [PubMed]
- Prestipino, S. The barrier to ice nucleation in monatomic water. J. Chem. Phys. 2018, 148, 124505. [Google Scholar] [PubMed]
- Prestipino, S.; Gazzillo, D.; Tasinato, N. Probing the existence of phase transitions in one-dimensional fluids of penetrable particles. Phys. Rev. E 2015, 92, 022138. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Gregorio, D.; Prestipino, S. Classical and Quantum Gases on a Semiregular Mesh. Appl. Sci. 2021, 11, 10053. https://doi.org/10.3390/app112110053
De Gregorio D, Prestipino S. Classical and Quantum Gases on a Semiregular Mesh. Applied Sciences. 2021; 11(21):10053. https://doi.org/10.3390/app112110053
Chicago/Turabian StyleDe Gregorio, Davide, and Santi Prestipino. 2021. "Classical and Quantum Gases on a Semiregular Mesh" Applied Sciences 11, no. 21: 10053. https://doi.org/10.3390/app112110053
APA StyleDe Gregorio, D., & Prestipino, S. (2021). Classical and Quantum Gases on a Semiregular Mesh. Applied Sciences, 11(21), 10053. https://doi.org/10.3390/app112110053






