Abstract
Groundwater is one of the primary sources for the daily water requirements of the masses, but it is subjected to contamination due to the pollutants, such as nitrate, percolating through the soil with water. Especially in built-up areas, groundwater vulnerability and contamination are of major concern, and require appropriate consideration. The present study develops a novel framework for assessing groundwater nitrate contamination risk for the area along the Karakoram Highway, which is a part of the China Pakistan Economic Corridor (CPEC) route in northern Pakistan. A groundwater vulnerability map was prepared using the DRASTIC model. The nitrate concentration data from a previous study were used to formulate the nitrate contamination map. Three machine learning (ML) models, i.e., Support Vector Machine (SVM), Multivariate Discriminant Analysis (MDA), and Boosted Regression Trees (BRT), were used to analyze the probability of groundwater contamination incidence. Furthermore, groundwater contamination probability maps were obtained utilizing the ensemble modeling approach. The models were calibrated and validated through calibration trials, using the area under the receiver operating characteristic curve method (AUC), where a minimum AUC threshold value of 80% was achieved. Results indicated the accuracy of the models to be in the range of 0.82–0.87. The final groundwater contamination risk map highlights that 34% of the area is moderately vulnerable to groundwater contamination, and 13% of the area is exposed to high groundwater contamination risk. The findings of this study can facilitate decision-making regarding the location of future built-up areas properly in order to mitigate the nitrate contamination that can further reduce the associated health risks.
1. Introduction
Groundwater is a significant natural resource, particularly in arid zones, due to the shortage of surface water resources and insignificant precipitation [1,2]. Consequently, the deterioration of the quality of groundwater, which is the source of drinking water for such areas, threatens the health of the local populations [3]. Approximately one-third of the global population consumes groundwater for various purposes, including agricultural, domestic, and industrial [4]. Several chemicals, including nitrate, can infiltrate the soil, and potentially pollute groundwater [5,6,7]. Therefore, safe drinking water supplies and deteriorating groundwater quality are key issues all over the globe [8]. The associated groundwater vulnerability and contamination risk valuation are essential for groundwater contamination mitigation [9].
Groundwater is the biggest source of drinking water in most developing countries, including Pakistan. Various risks are associated with this, ranging from basic perceptions to detailed impacts that are assessed and managed in various ways [10,11,12,13]. Employment and economic growth in Pakistan are primarily centered on agriculture. Gross domestic product (GDP) receives a substantial portion from agriculture and the associated industries [14].
Groundwater, a high source of water consumption in Pakistan, is polluted by various contaminants. Permeability of various substances through the soil, including nitrate concentrations, can hypothetically pollute the groundwater [5,6,7]. Positioned below the agricultural surface, nitrogen is the primary source of nitrate concentrations and associated water contaminations. Water acts as a carrier through the soil, as it can form a mixture with nitrate concentrations, and help it to reach the groundwater table. These nitrates can exist in a groundwater table for an extended time period, considering the continuous yearly nitrogen supply to the land surface [15].
A hydrogeochemical profile of higher fluoride (F-) in groundwater was examined in a study of Dragai in northern Pakistan by Rashid et al. [16], and it was found that fluorite is the primary source of F-contamination in groundwater. Zafar and Ahmad [17] examined the physicochemical characteristics in the Gilgit and Hunza rivers, in northern Pakistan. The analytical outcomes of the collected samples showed a high concentration of bicarbonates in the water. Maqsoom et al. [3] analyzed various hydrological attributes to assess the groundwater susceptibility to pollution in northern Pakistan. The results showed that almost 60% of the area has a high to moderate vulnerability to groundwater contamination. However, a similar study outlining the nitrate concentration locations has not been reported to date for Pakistan. The assessment of groundwater vulnerability and its nitrate contamination risk can aid water management authorities in performing the appropriate nitrate risk mitigation procedures.
Knowing the effects of groundwater vulnerability in areas where it is used as the public water supply source is essential to groundwater safety. There are dual risks to groundwater (over-extraction and adverse land use), therefore necessitating a dual nature of safety [18]. The risk assessment is not the same as the assessment for groundwater’s vulnerability to pollution. The idea of groundwater vulnerability is to assess the vulnerability of groundwater resources to being badly impacted by an enforced contaminant load from the surface [19]. There are two types of groundwater vulnerability, namely intrinsic and specific vulnerability. The ease with which a contaminant from the surface can reach and diffuse in groundwater can be specified as intrinsic vulnerability [20]. In comparison, specific vulnerability is exploited to ascertain the vulnerability of groundwater to an individual contaminant or a group of contaminants and their association [21]. The concept of vulnerability helps to identify groundwater regions in areas that are at high risk based on their vulnerability, so as to adopt appropriate risk management options. Moreover, it also reduces the communication space between the decision-makers, planners, and hydrogeologists, and helps in water management.
Several approaches have been utilized to assess the level of vulnerability and contamination of groundwater around the globe. These include index techniques, interpolation techniques, process-based models, and statistical models. In the index techniques, experts suggest a weight to each parameter in associated methods based on their knowledge. These techniques include the DRAV model [22], Susceptibility Index (SI) technique [23], GOD technique [24], ANIMO and EPIC models [25], and the DRASTIC model [2]. The interpolation methods utilize sensors and devices and indicator kriging (IK) based on geostatistical procedures using the kriging interpolation algorithm [26,27,28,29]. These are used to assess the groundwater pollution risk with ease. However, this method is constrained by the requirement of dense data collection points, and associated output uncertainty.
The process-based models are relatively complex, for example, the groundwater loading effects of agricultural management systems (GLEAMS) [30,31,32,33], the pesticide root zone model (PRZM-3) [30,31], the water flow and nitrate transport global model (WNGM) [34,35], and the groundwater flow model (MODFLOW) [36]. The critical drawbacks of these approaches are the important input data [37], and the restricted local scales applicability [38,39]. The statistical models follow a statistical linear and nonlinear regression approach [40]. These approaches model the contamination by analyzing the association between contaminant density and the specific contamination influencing parameters [41]. To entail causality, expert knowledge is required for expressive forecasts where reaching a consensus may present challenges.
Recently, the use of soft computing approaches such as artificial intelligence and several machine learning (ML) techniques have been considerably applied for predicting risks and hazards in environmental sciences [1,42,43,44,45,46,47]. ML, an application of artificial intelligence (AI), allows systems to automatically learn and improve from experience without being explicitly programmed [48]. It focuses on developing computer programs that can access data, and use it to learn for themselves. ML has been used in various fields and domains of science such as agricultural sciences [48], concrete properties prediction [46], bushfire analyses [49], and flood detection and management [13,50], among others. Nevertheless, the applications of ML techniques are very limited or do not exist for mapping the groundwater contamination risk in developing countries, particularly Pakistan.
This study does not claim that ML has not been used for groundwater assessment. In fact, it has been used for modeling groundwater level changes in agricultural regions of the USA [51]. Other examples include mapping the groundwater contamination risk of multiple aquifers [52], and predicting groundwater nitrate concentrations from spatial data [53]. Specific to nitrate assessments, ML has been used to assess nitrates in groundwater in many countries [10,31]. Rahmati et al. [54] used three advanced ML techniques, including K-nearest neighbor algorithm, random forest, and support-vector machines (SVM) to spatially model groundwater nitrate concentrations in Iran. De Filippis et al. [25] used a spatially distributed, physically-based modeling approach for estimating agricultural nitrate leaching into groundwater in Italy. Sajedi-Hosseini et al. [15] also used three ML techniques, including multivariate discriminant analysis (MDA), SVM, and boosted regression trees (BRT), for the probability of nitrate groundwater contamination occurrence in Iran. Several ML techniques have also been used in other fields. For example, ML has been used to construct environmental risk scores beyond standard linear models [55]. In addition, it has been used for engineering risk assessment [56,57], prediction of bioconcentration factors in fish and invertebrates [58], and general monitoring of the environment [49,59].
However, even studies that have used ML techniques for groundwater risk assessment miss the assimilated framework for groundwater risk and nitrate evaluation. In developing countries like Pakistan, no or few investigations exist that assessed nitrate contamination risk involving ML techniques. Therefore, this study attempts to fill the gap using a holistic framework for groundwater pollution risk assessment in northern Pakistan. With the advent of CPEC, the northern region is expected to see a boom in economic activities, and there will be an increase in anthropogenic movements there. In addition, new industrial and housing zones are being planned for the future.
Moreover, the area is a tourist spot for Pakistani nationals and mountain trackers from around the world. Touristic activities are expected to intensify, as the road infrastructure will be enhanced due to the CPEC. All of these anthropogenic activities will directly or indirectly influence the contamination of groundwater. Therefore, mapping the groundwater contamination risk for this area is of great importance. It will lay a road map for the policymakers to devise policies and regulations to protect this precious natural resource.
Previously, the DRASTIC method, which is an index method based on expert opinion, had been employed in the same study area by Maqsoom et al. [3]. The biggest disadvantage of this method is subjectivity, as the rating values are assumed based on expert opinion [60]. However, this study focuses on the assessment of three ML models: multivariate discriminant analysis (MDA), boosted regression trees (BRT), and support-vector machines (SVM), to predict the incidence of groundwater contamination in the same area in northern Pakistan. The present study evaluates groundwater contamination using ensemble incidence, and proposes a holistic framework for groundwater risk evaluation. It generates the risk map by combining pollution (nitrate concentration) probability (ML models), and vulnerability (DRASTIC method) maps. Accordingly, the study establishes the most efficient ML approach for groundwater contamination assessment among the practiced techniques. Moreover, it also computes the percentages of the areas that are under different risk zones. Thus, the authorities can use the pollution risk map of groundwater to address different issues of groundwater vulnerability.
2. Materials and Methods
2.1. Study Area
The region under investigation is a section of Karakoram Highway (KKH), which is 236 km long, and stretches from Gilgit to Khunjerab in northern Pakistan. The city of Gilgit is the capital of the Gilgit Baltistan region, while Khunjerab is a 4693 m high mountain pass in the Karakoram mountains, and is in a strategic position on the northern border of Pakistan and on the southwest border of China.
The KKH is being reconstructed under an economic initiative between Pakistan and China, called the China Pakistan Economic Corridor (CPEC). The deemed area for this study is a buffer of 20 km along the considered section of the KKH, which covers an area of approximately 4720 km2. The area is located between the longitudes and latitudes of 35.8819° N, 74.4643° E, and 36.8539° N, 75.4589° E, respectively, as can be seen from Figure 1. The region around KKH has diverse lithologies (igneous, metamorphic, and sedimentary), subterranean crevices, cracked and endured rock masses, high reliefs, seismic hazard zones, arid to monsoon climate, and locally high rates of tectonic activity.

Figure 1.
Map of the study area, showing the elevation and location of wells in the area.
The KKH is surrounded by the elevated mountains of the Karakoram and Himalayan mountainous ranges. The elevation of the buffer zone along the considered section of KKH for this study varies between 1294 m and 7330 m. The period of the winter season is comparatively greater due to heavy rainfall. The temperature of the region surrounding KKH varies from 10 °C to 38 °C throughout the year. The temperature throughout the year is fairly cold (10 °C), but it can reach 35 °C during summer, between June and August. The mean annual precipitation is 159 mm, as per Pakistan Meteorological Department (PMD) (https://www.pmd.gov.pk, accessed on 20 September 2021). The Hunza River flows through the Karakoram range from north to south, and runs alongside the KKH. The Hunza River is the main source of discharge, as shown in Figure 1. Groundwater levels are higher in the regions closer to the Hunza River, and lower in the regions which are farther away.
2.2. Methodology
A stepwise procedure has been visually explained as a flow chart in Figure 2. The first of this methodology is the vulnerability map formation, utilizing the DRASTIC model. The second step involves nitrate contamination map preparation using the nitrate concentration data from the study area. The third step is mapping the probability of contamination occurrence, utilizing three ML models, namely MDA, BRT, and SVM. The final step is the preparation of the groundwater risk map. The comprehensive methodological framework proposed in this study has been constructed using the subsequent sections.
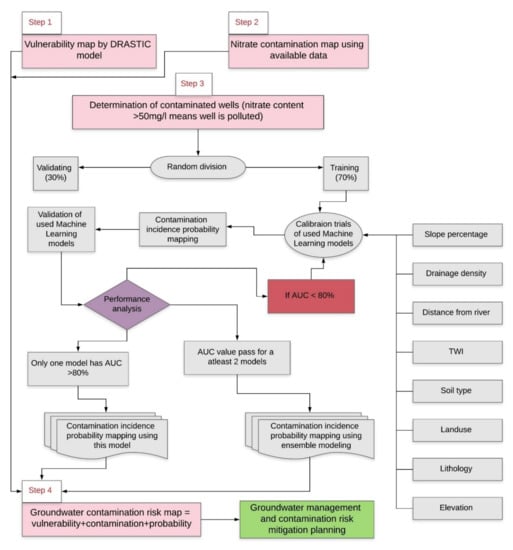
Figure 2.
Flowchart for the groundwater contamination risk mapping of the study area.
2.3. Groundwater Vulnerability Mapping through the DRASTIC Model
The DRASTIC approach has been utilized as a standard method for comparison with the ML techniques used in the current research in order to evaluate the vulnerability of groundwater to contamination. To assess the groundwater vulnerability, the data for different parameters are obtained from different government departments (for reference, see Maqsoom et al. [3]). The input parameters for mapping the groundwater vulnerability through the DRASTIC model comes from the word DRASTIC itself, where every word is an acronym that specifies a certain parameter: depth of water (D), net recharge (R), aquifer media (A), soil media (S), topography (T), vadose zone impact (I), and hydraulic conductivity (C) [61]. Initially, the parameters are allocated the value ratings (r) from 1 to 10, and then assigned weights (w) from 1 to 5 based on the existing literature [3,62]. The DRASTIC model is a collective multiplication of factor weights with their rates (r), as shown in Equation (1) [3,63]:
where w is the specific parameter weight with the rate (r) in the DRASTIC model, representing w and r for specific parameters. The assigned weight and rating values to each parameter provisional to their comparative importance are given in Table 1.

Table 1.
Drastic parameters their classes, ratings, and assigned weights.
2.4. Groundwater Nitrate Contamination Mapping
For mapping the nitrate concentration in the groundwater of the study area, this study uses nitrate concentration data from a previous study conducted in this region. Zafar and Ahmad [17] conducted a study to map the physicochemical characteristics in the Gilgit and Hunza Rivers, and collected 29 water samples from different locations of these rivers during July 2012. The analytical outcomes of the samples highlighted the elevated concentration of bicarbonates. The points in Figure 1 showing the location of the wells were used for the interpolation of the nitrate concentration values for the entire study area. The kriging interpolation technique in ArcGIS was utilized to map the nitrate concentration in the region. The kriging parameters utilized were as follows: universal interpolation type, prediction for the output surface type, the kernel function used was exponential, and the variable used was semi-variogram. Further, the lag number and lag size were 12 and 0.034, respectively. Moreover, the maximum and the minimum number of neighborhoods were 5 and 2, respectively.
2.5. Groundwater Contamination Probability Mapping through Machine Learning (ML) Techniques
2.5.1. Groundwater Contamination Conditioning Factors
Eight conditioning factors that influence groundwater contamination were selected, based on the literature for the probability mapping of groundwater contamination [50,64,65,66,67]. The selected parameters include slope, drainage, density, soil type, elevation, land use, lithology, distance to the river, and topographic wetness index (TWI). TWI is based on the groundwater flow arrangement, and measures the soil moisture [67,68]. The techniques and different sources used for collecting data used for the preparation of the individual factor maps are presented in Table 2.
The digital elevation model (STRM DEM) is used to produce the elevation, drainage density, distance from the river, TWI, and the slope percentage maps of the study area. The land use data is obtained from the Food and Agriculture Organization (FAO) land use map. Rahmati and Melesse [67] also assert that soil type has a considerate effect on subsurface flow and groundwater recharge. Groundwater hydrology characteristics are mainly dependent upon the lithology properties and geological formations of the specific terrain. As the considered study area is located in a mountainous region, and the geology is composed of rocks and soil, which influence water infiltration and discharge in their peculiar ways, it becomes important to consider them both. The soil type data and lithological details were extracted from the Geological maps of Pakistan, obtained from the Geological Survey of Pakistan. All of the maps were produced in an ArcGIS environment and with 30 m size pixels.
2.5.2. Boosted Regression Trees (BRT)
An effective ML procedure based on the statistical analysis is the BRT, or the stochastic gradient boosting [69]. The BRT technique combines multiple decision trees to produce a specific decision rule, rather than just a simple prediction to improve model accuracy and performance [70]. Boosting is a way to enhance the accuracy of the model. It is centered around the notion that it is simpler to locate and middle several rough rules of thumb than locating a specific, exact prediction rule [69,70]. BRT integrate significant benefits of tree-based techniques, processing distinct types of predictor variables, and accepting misplaced data. Fitting several trees in BRT helps to avert the major shortcoming of individual tree models: their comparatively inadequate predictive performance. In the case of BRT, the data transformation or elimination of outliers at the early stages is not required. These models can fit difficult nonlinear connections, and automatically manage interface effects among predictors. Even though BRT models are complicated, they can be recapitulated in forms that provide effective ecological comprehension, and their predictive performance is excellent, compared to most of the orthodox modelling models [69].

Table 2.
Sources and used techniques for calculating the factors.
Table 2.
Sources and used techniques for calculating the factors.
| Parameter | Source | Technique/Formula | Reference |
|---|---|---|---|
| Elevation | STRM DEM | 30 × 30 m DEM | [71] |
| Slope | STRM DEM | N = no. of contour cutting; i = contour interval | [72] |
| Drainage Density | STRM DEM | Proximity analysis | [73] |
| Landuse | FAO land use | Maximum likelihood | [74] |
| Distance to River | Google earth | Multiple buffer | [75] |
| TWI | STRM DEM | a = upslope contributing area (m2); b = slope in radians | [76] |
| Soil Data | Geological Maps of Pakistan | Proximity analysis | [73] |
| Lithology | Geological Maps of Pakistan | Proximity analysis | [73] |
2.5.3. Support Vector Machines (SVM)
SVM has also been utilized in this study, and was first presented by Cortes and Vapnik [77]. SVM is centered upon the statistical learning theory and structural risk minimization [77,78]. SVM methods utilize the bands and optimization algorithm to define a specific sample decision boundary, called the optimal decision boundary, by identifying the samples located in those boundaries. These sample boundaries are known as support vectors [77]. SVM utilizes typical adaptations such as nu-svc (nu classification), C-svc (C classification); nu-SVR (nu regression) [78], etc. The kernel types must be selected founded on the routine of the phenomena [79]. Radial basis functions (RBF) perform better than other kernel functions in groundwater analysis [78,79]. Based on the better performance, the present research utilized nu regression with RBF to predict groundwater contamination mapping.
2.5.4. Multivariate Discriminant Analysis (MDA)
The MDA procedure obtains and evaluates a linear composition by analyzing several variables that show clear discrimination among the selected independent variable assemblies [80]. This procedure involves the maximization of inter-group variance ratios to inter-group variance values. MDA represents the linear combination, as shown in Equation (2) [80]:
where x values represent the variable weights, and Y represents the overall score.
2.5.5. Implementation and Accuracy Assessment
This study implements the BRT, SVM, and MDA procedures through the SDM package in the R platform. To calibrate and test the models, the datasets are further divided randomly into the proportion of 70% (datasets utilized for calibration of the models) and 30% (datasets utilized for testing of the model), based on the literature [15,51,81,82,83,84]. The Receiver Operating Characteristic (ROC) curve technique and Area Under Curve (AUC) technique are utilized for the performance validation of the models [85,86,87,88]. Yesilnacar [89] defined the performance threshold value as AUC ≥ 80%, and the decision-making flow is illustrated in Figure 2. The possible outcomes of all three models utilized in the study are as follows:
- All of the models are operated, and the accuracy is assessed. The attained AUC is measured at less than 80% for all the models. Thus, all of the models are recalibrated to achieve the threshold value (a minimum AUC value of at least 80%);
- One model achieved an AUC value over 80%, and, without further calibration, it is utilized to map the groundwater contamination incidence probability;
- All of the remaining models achieved accuracy after further recalibration trials (AUC above 80%), and are used to map the groundwater contamination incidence probability without further recalibration procedures. An ensemble modeling process was utilized, which pools the outcomes of the single models, and produces synthesized results in order to achieve further accuracy [15]. In ensemble techniques, weighted incorporation of certain models is primarily employed, such as bagging and boosting. In the present study, the following equation is used to conduct the ensemble modeling:where EM represents the Ensemble models by evaluating AUC values of each model.
2.6. Groundwater Pollution Risk Mapping
Voudouris et al. [90] describe risk as an estimated possibility of an occurrence of a specific event, based on a specific group of factors. Thus, groundwater contamination risk can be forecasted by the overlaying of pollution, vulnerability, and probability maps as shown in Equation (4) [91]:
Risk = Vulnerability + Contamination + Probability
The risk evaluation procedure of the current study is centered upon the past research works [9,92], where the contamination, probability, and susceptibility maps were extracted by applying traditional statistical approaches.
3. Results and Discussions
3.1. Groundwater Contamination Vulnerability Mapping
The purpose of using the DRASTIC model in this study is to compare the DRASTIC model and the advanced ML approaches in order to establish a superior method for groundwater contamination assessment. The DRASTIC model has been used largely for groundwater contamination assessment in the past. This approach has been previously utilized in different parts of the world, including Iran, Pakistan, and India [2,3,10,69]. Maqsoom et al. [3] applied the DRASTIC model in the same study area, and produced the DRASTIC risk map of the area. The DRASTIC model was utilized to produce the groundwater vulnerability map, as shown in Figure 3.
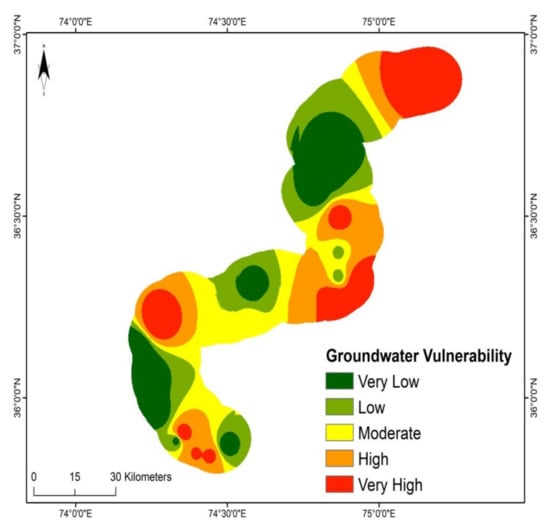
Figure 3.
Groundwater contamination vulnerability zones for the study area.
Equation (1) was utilized to obtain the DRASTIC Index (DI). In the groundwater vulnerability map, the DRASTIC index (DI) was categorized into five classes: very low, low, moderate, high, and very high, based on the level of vulnerability. Figure 3 shows that the northeast side of the area is exposed to high to very high vulnerability, whereas the southwest area has a considerably low vulnerability. However, the middle portion of the area has mostly moderate to high groundwater contamination vulnerability.
3.2. Groundwater Nitrate Concentration Mapping
The nitrate concentration in the study area is shown in Figure 4. This concentration was mapped using the data from a study previously conducted in this region [17]. The distribution of data points (wells) that were interpolated to obtain the nitrate concentration values for the study is shown in Figure 1. The highest and lowest nitrate densities recorded were (59.89 mg/L) and (5.04 mg/L), respectively, as presented in Figure 4. The World Health Organization (WHO) has set a threshold value of 50 mg/L for differentiating between polluted and non-polluted water resources [15]. Therefore, some of the study area wells can also be classified as polluted. In some parts of the area, the nitrate concentration is observed to be more than the threshold value of 50 mg/L. Figure 4 shows the nitrate concentration map. Figure 5, produced by the DRASTIC model, resembles Figure 4, as the areas that are more vulnerable to pollution also have greater nitrate concentrations.
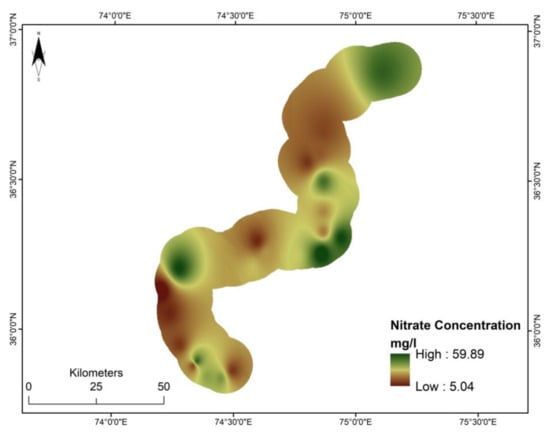
Figure 4.
Groundwater nitrate concentration map for the study area.

Figure 5.
Groundwater conditioning factors: (a) distance to river, (b) twi, (c) elevation, (d) slope, (e) land use, (f) soil type, (g) lithology, (h) drainage density.
3.3. Thematic Maps of Groundwater Contamination Conditioning Factors
The present study used eight conditioning factors for mapping a contamination probability map. The maps of the used conditioning factors are shown in Figure 5a–h. The central area of the buffer zone is very close to the Hunza River; therefore, the distance is not very far at the center, as can be seen from the map shown in Figure 5a.
The TWI map shown in Figure 5b demonstrates that a considerable percentage of the deliberated area has relatively high levels of wetness. The elevation values in the study area vary between 1294 m to 7330 m, and most of the high elevation regions are on the north side of the study area, as shown in Figure 5c. In addition, the study area has considerably diverse slopes due to its topography, as shown in Figure 5d. Figure 5e demonstrates six classes of land use in the region, including agriculture, bare areas, shrubs, urban area, snow, and water bodies, with a considerable proportion of bare areas and shrubs. Figure 5f shows that the soil of the considered study region is comprised of clay, loam sand, sandy clay, and silt, where silt is the most dominant soil type present. In addition, metamorphic rocks and granite gneiss are present in most study areas, as demonstrated in Figure 5g. The drainage density map in Figure 5h shows that the drainage density is considerably high in the central part of the buffer zone, where the Hunza River runs alongside the KKH, while traversing it at certain points.
3.4. Groundwater Contamination Incidence Probability Mapping
This research focuses on assessing the probability of groundwater nitrate contamination occurrence utilizing machine learning (ML) techniques such as SVM, BRT, and MDA. An ensemble modeling approach is applied for the production of groundwater contamination incidence probability mapping. There are a total of eight dependent factors that are analyzed and utilized in the current study. These datasets were used in the proportion of 70:30 to train and validate the three ML techniques practiced in this research, respectively.
In order to produce an effective groundwater contamination incidence probability map, all the models were taken through calibration trials to achieve a minimum AUC value of 80%. Table 3 indicates the model performance values for the prediction of the groundwater contamination incidence. The AUC values of different models varied from 0.82 to 0.86, with SVM being the most superior to the others. However, the corresponding AUC value for the ensemble model was 0.87. Being a reliability metric, the Kappa statistic ensured that the chance occurrence was minimized to zero for the good model presentation (0.55 < K < 0.85) [93].

Table 3.
Groundwater risk prediction map mean and variance values for models.
Table 3 demonstrates that the groundwater contamination probability maps were produced when all the models attained the threshold level of the AUC value. Among all of the models, the SVM model showed better performance as per the values of evaluation measures, including AUC, Kappa, and mean square error (AUC = 0.86, Kappa = 0.85, and MSE = 0.22). In the comparison of BRT (AUC = 0.85, Kappa = 0.84 and MSE = 0.22) and MDA (AUC = 0.82, Kappa = 0.81 and MSE = 0.19), BRT produces more efficient results than MDA. However, the ensemble techniques produce considerably better results than SVM, BRT, and MDA, as shown in Table 3 (AUC = 0.87, Kappa = 0.86, and MSE = 0.18).
Moreover, the variance and mean of all of the models are represented in Table 4. The variance of BRT and ensemble models (0.04 and 0.05, respectively) is considerably less than the variance of MDA and SVM models (0.09 and 0.08, respectively), as depicted in Table 4. The mean of the MDA model is also relatively greater than the other models (0.55). However, after the MDA model, the mean is greater for the ensemble model, followed by BRT (0.48) and SVM (0.47), as shown in Table 4.

Table 4.
Performance of models during testing datasets.
The groundwater contamination incidence probability maps were produced using the practiced models after achieving 80% accuracy. The produced maps are shown in Figure 6a–d. All of the maps show that the southern lower part of the study area has the most probability of groundwater contamination incidence. The regions on the northern side, where the elevation is low and the population is very scarce and widely distributed, have a low probability of groundwater contamination incidence. In all the contamination incidence maps, the regions of high probability have relatively low elevation and vegetation, a high drainage density, and agricultural and urbanization levels.
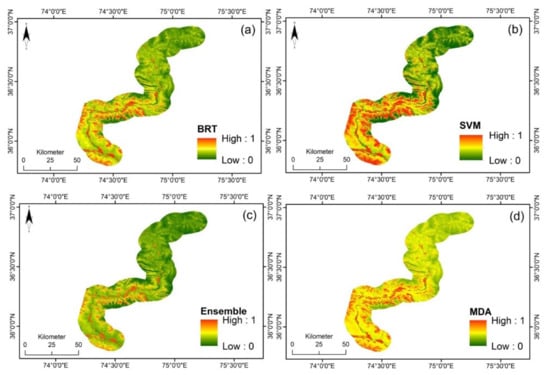
Figure 6.
Groundwater contamination incidence probability map: (a) BRT (b) SVM (c) ensemble (d) MDA.
The considerably non-efficient performance of the MDA model is due to the normal data algorithm being processed under the parametric routine, rather than through processing the nonlinear relationship amongst the variables [94]. Similarly, the non-parametric procedures, namely BRT and SVM, can analyze the nonlinear relationships of the data flow and produce considerably efficient results. SVM technique is a considerably efficient method, but obtaining critical variables through SVM techniques is a complex process, while the critical and efficient variables are assessed by the MDA model [94] for modeling. Moreover, the BRT method is a combination of boosting method and classification, and regression trees (CART) [69]. It provides a higher level of accuracy by competing for multiple decision trees to produce a specific model evaluation rule than a single non-efficient psychological prediction [70]. By analyzing the pros and cons of the predicted models, it has been shown that the combination of model predictions (ensemble modeling) can provide better results and prediction models [86,95]. This is also exhibited by the values demonstrated in Table 3.
3.5. Groundwater Contamination Risk Evaluation
This study seeks to locate and prioritize the most vulnerable regions in an area that could be the reason for groundwater contamination, and offers a scientific basis for groundwater protection and land use planning. ArcGIS Environment was utilized to produce the groundwater contamination risk map after obtaining the vulnerability (DRASTIC model), contamination (nitrate concentration), and probability maps (ML techniques) of the study area.
The map was further classified into five categories based on the occurrence, namely very low, low, moderate, high, and very high groundwater pollution risks, as shown in Figure 7. The northwestern region of the study area and the upper-middle region is mostly exposed to low to very low groundwater contamination risk. The main reason for the lower exposure is that most of the land here is composed of shrubs, and human settlements in these regions are scarce and highly dispersed. However, a very high to moderate level of nitrate groundwater contamination risk exists for the southwest and lower-middle regions of the study area. The main reason for this is the existence of wild animal waste and urban waste in these regions, due to the existence of human settlements.
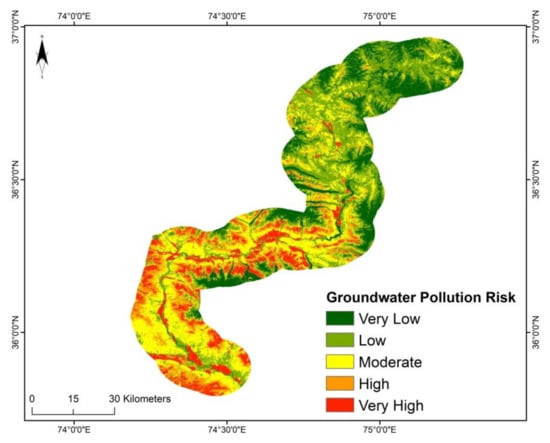
Figure 7.
Groundwater contamination risk map for the study area.
Moreover, the percentages of areas under different groundwater contamination risk classes are also measured and are shown in Table 5. The very low, low, moderate, high, and very high groundwater contamination risk classes encompass areas of 902.5, 1087.5, 1615, 427.5, and 617.5 km2, respectively. Thus, more than 50% of the area is exposed to moderate to very high groundwater contamination risk, as is evident from Table 5.

Table 5.
Area division by groundwater contamination risk for the study area.
The land use map does not demonstrate a considerable relationship with the nitrate contamination map. The groundwater vulnerability map and high nitrate contamination areas are also observed in the extreme northern part of the study area, where the population is not particularly dense, and is more scattered. The extreme northern area contains elevated snow-covered mountains, and has less vegetation cover. However, it has been found that the nitrate contaminants in snow and glaciers are the main source of contamination in this area. The high nitrate risk area includes the region of unconsolidated rocks. The area has many snowy glaciers that store a high amount of nitrates [96].
Moreover, the DRASTIC model does not consider the land use type, which shows the northern part as highly vulnerable. Furthermore, the major deposits in the area are silt and clay. Silt, constituting almost 70% of the area, restricts the water seepage due to the high compression. This is why the DRASTIC model does not show the southeastern part as more vulnerable. However, all of the ML models show that the northern part is less exposed, since the population in the majority of the area is considerably dispersed. In contrast, the areas with less vegetation and high land use are exposed to a fair amount of nitrate contamination.
Moreover, the study conducted by Maqsoom et al. [3] using the DRASTIC model and a modified version of the DRASTIC model (DRASTICA) for groundwater vulnerability assessment along the CPEC route also indicated that more than 50% of the area is exposed to very high to moderate groundwater contamination risk. The study also concluded that the areas with high vulnerability are those with high population density and anthropogenic activities, which shows that the outcomes are very much similar to the outcomes of the present study.
Furthermore, the study performed by Zafar and Ahmad [17], which examined the physicochemical characteristics in the Gilgit and Hunza rivers, northern Pakistan, by collecting 29 water samples from several locations of these rivers, also showed that the samples highlight a high intensity of bicarbonates. These results also correlate with the present study results, which show that the area has very high to moderate groundwater contamination. A similar approach has been implemented by Sajedi-Hosseini et al. [15] for assessing the probability of groundwater pollution occurrence in Lenjanat Plain, Iran. The outcomes of their study showed that accuracy for the three models (SVM, BRT, and MDA) ranged from 0.81 to 0.87. Thus, based on these arguments, it can be stated that the outcomes of this study are reasonable, and can be used by policymakers to pursue contamination mitigating measures.
Although the ML models in this study provided a fair and efficient result, the sampling and data collection procedure could be further optimized, and the study of soil types could be more detailed in future studies. The data collection and the sampling of the current study were limited due to a lack of financial resources, but improved sampling could be performed in the future for better results. The seasonal variation is also an important factor in achieving detailed accuracy. It includes the nitrate substance data, groundwater flow pattern, and the mean passage aquifer time [97]. To avoid nonlinear variation in the nitrate substance values and to achieve better accuracy, it is recommended that future studies should record the data monthly or quarterly in a specific year, in order to obtain a mean annual concentration for a specific sampling point. The current evaluation technique in this study is such that the nitrate contaminants are in a steady state, and not in a potential movement based on the downward gradient “disconnecting” the relationship between the two [98]. The fact that nitrate occurrence could be affected by the potential downgrade movement of the contaminants during the time interval is a major issue.
4. Conclusions
Groundwater is a major source for fulfilling household, agricultural, and industrial needs of water, but the leaching of pollutants from the surface are contaminating this natural resource. The assessment of contamination risk for the groundwater is an important approach to aid further mitigation and protective procedures. The study aims at assessing the groundwater nitrate contamination risk along the Karakoram Highway, which is now a part of the Chinese initiative CPEC. First, the groundwater vulnerability of the area is mapped using the DRASTIC model, and then the nitrate pollution is mapped using nitrate concentration data from a previously conducted study. Additionally, the study provides an innovative structure for assessing the probability of groundwater nitrate contamination incidence, based on ML techniques and the ensemble modeling method. The ML techniques utilized are SVM, MDA, and BRT. A total of eight groundwater conditioning factors were used to map the contamination incidence probability. The combination of the input maps such as pollution, probability, and vulnerability maps produced the groundwater nitrate contamination risk map that showed that the lower, central bottom, and traces of the upper regions are exposed to high to very high contamination risks. The model evaluation reveals that the ensemble technique outperforms the other techniques, including SVM, MDA, and BRT, in terms of AUC, Kappa, and MSE. The findings of this study are applicable in regional scale risk assessment for modern urbanization to mitigate health problems for the locale, and pollution risk management agencies could also utilize the groundwater contamination risk map to apply mitigation procedures. In agricultural land use areas, the nitrate contamination risk could be mitigated by using fewer nitrate fertilizers. In urban areas, household and industrial waste should not be disposed of in the water.
Author Contributions
Conceptualization, M.A., B.A., A.M., U.K., F.U., S.A. and M.I.; methodology, M.A., B.A., A.M., U.K., F.U., S.A. and M.I.; software, M.A., B.A., A.M. and S.A.; validation, M.A., B.A., A.M., U.K., F.U., S.A. and M.I.; formal analysis, M.A., B.A., A.M. and S.A.; investigation, M.A., B.A., A.M. and S.A.; resources, F.U. and M.I.; data curation, M.A., B.A., A.M., U.K., F.U., S.A. and M.I.; writing—original draft preparation, M.A., B.A., A.M. and S.A.; writing—review and editing, F.U. and M.I.; visualization, M.A., B.A., A.M., U.K., F.U., S.A. and M.I.; supervision, B.A., A.M., F.U. and M.I.; project administration, B.A., A.M., F.U. and M.I.; funding acquisition, F.U. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data is available with the second and third authors and can be shared with anyone upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Choubin, B.; Malekian, A.; Samadi, S.; Khalighi-Sigaroodi, S.; Hosseini, F.S. An ensemble forecast of semi-arid rainfall using large-scale climate predictors. Meteorol. Appl. 2017, 24, 376–386. [Google Scholar] [CrossRef] [Green Version]
- Neshat, A.; Pradhan, B.; Pirasteh, S.; Shafri, H.Z.M. Shafri; Estimating groundwater vulnerability to pollution using a modified DRASTIC model in the Kerman agricultural area, Iran. Environ. Earth Sci. 2014, 71, 3119–3131. [Google Scholar] [CrossRef]
- Maqsoom, A.; Aslam, B.; Khalil, U.; Ghorbanzadeh, O.; Ashraf, H.; Tufail, R.F.F.; Farooq, D.; Blaschke, T. A GIS-based DRASTIC Model and an Adjusted DRASTIC Model (DRASTICA) for Groundwater Susceptibility Assessment along the China–Pakistan Economic Corridor (CPEC) Route. ISPRS Int. J. Geo-Inf. 2020, 9, 332. [Google Scholar] [CrossRef]
- Rashid, A.; Guan, D.-X.; Farooqi, A.; Khan, S.; Zahir, S.; Jehan, S.; Khattak, S.A.; Khan, M.S.; Khan, R. Fluoride prevalence in groundwater around a fluorite mining area in the flood plain of the River Swat, Pakistan. Sci. Total Environ. 2018, 635, 203–215. [Google Scholar] [CrossRef] [Green Version]
- Hutchins, M.G.; Abesser, C.; Prudhomme, C.; Elliott, J.A.; Bloomfield, J.P.; Mansour, M.M.; Hitt, O.E. Combined impacts of future land-use and climate stressors on water resources and quality in groundwater and surface waterbodies of the upper Thames river basin, UK. Sci. Total Environ. 2018, 631, 962–986. [Google Scholar] [CrossRef]
- Hansen, B.; Thorling, L.; Schullehner, J.; Termansen, M.; Dalgaard, T. Groundwater nitrate response to sustainable nitrogen management. Sci. Rep. 2017, 7, 1–12. [Google Scholar] [CrossRef]
- Templeton, M.R.; Hammoud, A.S.; Butler, A.P.; Braun, L.; Foucher, J.-A.; Grossmann, J.; Boukari, M.; Faye, S.; Jourda, J.P. Nitrate Pollution of groundwater by pit latrines in developing countries. AIMS Environ. Sci. 2015, 2, 302. [Google Scholar] [CrossRef]
- Guo, X.; Zuo, R.; Shan, D.; Cao, Y.; Wang, J.; Teng, Y.; Fu, Q.; Zheng, B. Source apportionment of pollution in groundwater source area using factor analysis and positive matrix factorization methods. Hum. Ecol. Risk Assess. Int. J. 2017, 23, 1417–1436. [Google Scholar] [CrossRef]
- Shrestha, S.; Semkuyu, D.J.; Pandey, V.P. Assessment of groundwater vulnerability and risk to pollution in Kathmandu Valley, Nepal. Sci. Total Environ. 2016, 556, 23–35. [Google Scholar] [CrossRef]
- Ullah, F.; Sepasgozar, S.M.; Thaheem, M.J.; Wang, C.C.; Imran, M. It’s all about perceptions: A DEMATEL approach to exploring user perceptions of real estate online platforms. Ain Shams Eng. J. 2021. [Google Scholar] [CrossRef]
- Ullah, F.; Sepasgozar, S.M.; Shirowzhan, S.; Davis, S. Modelling users’ perception of the online real estate platforms in a digitally disruptive environment: An integrated KANO-SISQual approach. Telemat. Inform. 2021, 63, 101660. [Google Scholar] [CrossRef]
- Ullah, F. A beginner’s guide to developing review-based conceptual frameworks in the built environment. Architecture 2021, 1, 3. [Google Scholar] [CrossRef]
- Munawar, H.S.; Ullah, F.; Qayyum, S.; Heravi, A. Application of Deep Learning on UAV-Based Aerial Images for Flood Detection. Smart Cities 2021, 4, 65. [Google Scholar] [CrossRef]
- Hussain, Y.; Satgé, F.; Hussain, M.B.; Martinez-Carvajal, H.; Bonnet, M.-P.; Cárdenas-Soto, M.; Roig, H.L.; Akhter, G. Performance of CMORPH, TMPA, and PERSIANN rainfall datasets over plain, mountainous, and glacial regions of Pakistan. Theor. Appl. Climatol. 2018, 131, 1119–1132. [Google Scholar] [CrossRef]
- Sajedi-Hosseini, F.; Malekian, A.; Choubin, B.; Rahmati, O.; Cipullo, S.; Coulon, F.; Pradhan, B. A novel machine learning-based approach for the risk assessment of nitrate groundwater contamination. Sci. Total Environ. 2018, 644, 954–962. [Google Scholar] [CrossRef] [Green Version]
- Rashid, A.; Farooqi, A.; Gao, X.; Zahir, S.; Noor, S.; Khattak, J.A. Geochemical modeling, source apportionment, health risk exposure and control of higher fluoride in groundwater of sub-district Dargai, Pakistan. Chemosphere 2020, 243, 125409. [Google Scholar] [CrossRef]
- Zafar, M.; Ahmad, W. Water quality assessment and apportionment of northern Pakistan by multivariate statistical techniques, a case study. Int. J. Hydro. 2018, 2, 00040. [Google Scholar]
- Somaratne, N.; Zulfic, H.; Ashman, G.; Vial, H.; Swaffer, B.; Frizenschaf, J. Groundwater risk assessment model (GRAM): Groundwater risk assessment model for wellfield protection. Water 2013, 5, 1419–1439. [Google Scholar] [CrossRef] [Green Version]
- Foster, S.; Hirata, R.; Andreo, B. The aquifer pollution vulnerability concept: Aid or impediment in promoting groundwater protection? Hydrogeol. J. 2013, 21, 1389–1392. [Google Scholar] [CrossRef]
- Vrba, J.; Zaporozec, A. Guidebook on Mapping Groundwater Vulnerability; Heise: Hanover, Germany, 1994. [Google Scholar]
- Gogu, R.C.; Dassargues, A. Current trends and future challenges in groundwater vulnerability assessment using overlay and index methods. Environ. Geol. 2000, 39, 549–559. [Google Scholar] [CrossRef]
- Zhou, J.; Li, G.; Liu, F.; Wang, Y.; Guo, X. DRAV model and its application in assessing groundwater vulnerability in arid area: A case study of pore phreatic water in Tarim Basin, Xinjiang, Northwest China. Environ. Earth Sci. 2010, 60, 1055–1063. [Google Scholar] [CrossRef]
- Van Beynen, P.; Niedzielski, M.; Bialkowska-Jelinska, E.; Alsharif, K.; Matusick, J. Comparative study of specific groundwater vulnerability of a karst aquifer in central Florida. Appl. Geogr. 2012, 32, 868–877. [Google Scholar] [CrossRef]
- Foster, S. Fundamental Concepts in Aquifer Vulnerability, Pollution Risk and Protection Strategy; Netherlands Organization for Applied Scientific Research: The Hague, The Netherlands, 1987. [Google Scholar]
- De Filippis, G.; Ercoli, L.; Rossetto, R. A Spatially Distributed, Physically-Based Modeling Approach for Estimating Agricultural Nitrate Leaching to Groundwater. Hydrology 2021, 8, 8. [Google Scholar] [CrossRef]
- Narany, T.S.; Ramli, M.F.; Sulaiman, W.N.A.; Fakharian, K. Assessment of the Potential Contamination Risk of Nitrate in Groundwater Using Indicator Kriging (in Amol–Babol Plain, Iran). In From Sources to Solution; Springer: Berlin/Heidelberg, Germany, 2014; pp. 273–277. [Google Scholar]
- Stigter, T.Y.; Ribeiro, L.; Dill, A.C. Evaluation of an intrinsic and a specific vulnerability assessment method in comparison with groundwater salinisation and nitrate contamination levels in two agricultural regions in the south of Portugal. Hydrogeol. J. 2006, 14, 79–99. [Google Scholar] [CrossRef]
- Gong, G.; Mattevada, S.; O’Bryant, S. Comparison of the accuracy of kriging and IDW interpolations in estimating groundwater arsenic concentrations in Texas. Environ. Res. 2014, 130, 59–69. [Google Scholar] [CrossRef] [PubMed]
- Kaown, D.; Hyun, Y.; Bae, G.-O.; Lee, K.-K. Factors affecting the spatial pattern of nitrate contamination in shallow groundwater. J. Environ. Qual. 2007, 36, 1479–1487. [Google Scholar] [CrossRef] [PubMed]
- Akbar, T.A.; Lin, H.; DeGroote, J. Development and evaluation of GIS-based ArcPRZM-3 system for spatial modeling of groundwater vulnerability to pesticide contamination. Comput. Geosci. 2011, 37, 822–830. [Google Scholar] [CrossRef]
- Fontaine, D.D.; Havens, P.L.; Blau, G.E.; Tillotson, P.M. The role of sensitivity analysis in groundwater risk modeling for pesticides. Weed Technol. 1992, 6, 716–724. [Google Scholar] [CrossRef]
- Leonard, R.A.; Knisel, W.G.; Still, D.A. GLEAMS: Groundwater loading effects of agricultural management systems. Trans. ASAE 1987, 30, 1403–1418. [Google Scholar] [CrossRef]
- Leone, A.; Ripa, M.N.; Uricchio, V.; Deak, J.; Vargay, Z. Vulnerability and risk evaluation of agricultural nitrogen pollution for Hungary’s main aquifer using DRASTIC and GLEAMS models. J. Environ. Manag. 2009, 90, 2969–2978. [Google Scholar] [CrossRef]
- Bonton, A.; Rouleau, A.; Bouchard, C.; Rodríguez, M.J. Nitrate transport modeling to evaluate source water protection scenarios for a municipal well in an agricultural area. Agric. Syst. 2011, 104, 429–439. [Google Scholar] [CrossRef]
- Qin, R.; Wu, Y.; Xu, Z.; Xie, D.; Zhang, C. Assessing the impact of natural and anthropogenic activities on groundwater quality in coastal alluvial aquifers of the lower Liaohe River Plain, NE China. Appl. Geochem. 2013, 31, 142–158. [Google Scholar] [CrossRef]
- Nobre, R.; Filho, O.R.; Mansur, W.; Nobre, M.; Cosenza, C. Groundwater vulnerability and risk mapping using GIS, modeling and a fuzzy logic tool. J. Contam. Hydrol. 2007, 94, 277–292. [Google Scholar] [CrossRef] [PubMed]
- Iqbal, J.; Gorai, A.K.; Tirkey, P.; Pathak, G. Approaches to groundwater vulnerability to pollution: A literature review. Asian J. Water Environ. Pollut. 2012, 9, 105–115. [Google Scholar]
- Anane, M.; Abidi, B.; Lachaal, F.; Limam, A.; Jellali, S. GIS-based DRASTIC, Pesticide DRASTIC and the Susceptibility Index (SI): Comparative study for evaluation of pollution potential in the Nabeul-Hammamet shallow aquifer, Tunisia. Hydrogeol. J. 2013, 21, 715–731. [Google Scholar] [CrossRef]
- Garnier, M.; Porto, A.L.; Marini, R.; Leone, A. Integrated use of GLEAMS and GIS to prevent groundwater pollution caused by agricultural disposal of animal waste. Environ. Manag. 1998, 22, 747–756. [Google Scholar] [CrossRef] [PubMed]
- Johnson, T.D.; Belitz, K. Assigning land use to supply wells for the statistical characterization of regional groundwater quality: Correlating urban land use and VOC occurrence. J. Hydrol. 2009, 370, 100–108. [Google Scholar] [CrossRef]
- McLay, C.; Dragten, R.; Sparling, G.; Selvarajah, N. Predicting groundwater nitrate concentrations in a region of mixed agricultural land use: A comparison of three approaches. Environ. Pollut. 2001, 115, 191–204. [Google Scholar] [CrossRef]
- Choubin, B.; Malekian, A. Combined gamma and M-test-based ANN and ARIMA models for groundwater fluctuation forecasting in semiarid regions. Environ. Earth Sci. 2017, 76, 538. [Google Scholar] [CrossRef]
- Choubin, B.; Zehtabian, G.; Azareh, A.; Rafiei-Sardooi, E.; Sajedi-Hosseini, F.; Kişi, Ö. Precipitation forecasting using classification and regression trees (CART) model: A comparative study of different approaches. Environ. Earth Sci. 2018, 77, 314. [Google Scholar] [CrossRef]
- Nejad, S.G.; Falah, F.; Daneshfar, M.; Haghizadeh, A.; Rahmati, O. Delineation of groundwater potential zones using remote sensing and GIS-based data-driven models. Geocarto Int. 2017, 32, 167–187. [Google Scholar]
- Ullah, F.; Qayyum, S.; Thaheem, M.J.; Al-Turjman, F.; Sepasgozar, S.M. Risk management in sustainable smart cities governance: A TOE framework. Technol. Forecast. Soc. Chang. 2021, 167, 120743. [Google Scholar] [CrossRef]
- Maqsoom, A.; Aslam, B.; Gul, M.E.; Ullah, F.; Kouzani, A.Z.; Mahmud, M.A.; Nawaz, A. Using Multivariate Regression and ANN Models to Predict Properties of Concrete Cured under Hot Weather: A Case of Rawalpindi Pakistan. Sustainability 2021, 13, 10164. [Google Scholar] [CrossRef]
- Ullah, F.; Sepasgozar, S.M.; Thaheem, M.J.; Al-Turjman, F. Barriers to the digitalisation and innovation of Australian Smart Real Estate: A managerial perspective on the technology non-adoption. Environ. Technol. Innov. 2021, 101527. [Google Scholar] [CrossRef]
- Liakos, K.G.; Busato, P.; Moshou, D.; Pearson, S.; Bochtis, D. Machine learning in agriculture: A review. Sensors 2018, 18, 2674. [Google Scholar] [CrossRef] [Green Version]
- Ullah, F.; Khan, S.I.; Munawar, H.S.; Qadir, Z.; Qayyum, S. UAV Based Spatiotemporal Analysis of the 2019–2020 New South Wales Bushfires. Sustainability 2021, 13, 10207. [Google Scholar] [CrossRef]
- Atif, S.; Umar, M.; Ullah, F. Investigating the flood damages in Lower Indus Basin since 2000: Spatiotemporal analyses of the major flood events. Nat. Hazards 2021, 108, 2357–2383. [Google Scholar] [CrossRef]
- Sahoo, S.; Russo, T.A.; Elliott, J.; Foster, I. Machine learning algorithms for modeling groundwater level changes in agricultural regions of the US. Water Resour. Res. 2017, 53, 3878–3895. [Google Scholar] [CrossRef]
- Barzegar, R.; Moghaddam, A.A.; Deo, R.; Fijani, E.; Tziritis, E. Mapping groundwater contamination risk of multiple aquifers using multi-model ensemble of machine learning algorithms. Sci. Total Environ. 2018, 621, 697–712. [Google Scholar] [CrossRef] [PubMed]
- Knoll, L.; Breuer, L.; Bach, M. Large scale prediction of groundwater nitrate concentrations from spatial data using machine learning. Sci. Total Environ. 2019, 668, 1317–1327. [Google Scholar] [CrossRef]
- Rahmati, O.; Choubin, B.; Fathabadi, A.; Coulon, F.; Soltani, E.; Shahabi, H.; Mollaefar, E.; Tiefenbacher, J.; Cipullo, S.; Bin Ahmad, B.; et al. Predicting uncertainty of machine learning models for modelling nitrate pollution of groundwater using quantile regression and UNEEC methods. Sci. Total Environ. 2019, 688, 855–866. [Google Scholar] [CrossRef]
- Park, S.K.; Zhao, Z.; Mukherjee, B. Construction of environmental risk score beyond standard linear models using machine learning methods: Application to metal mixtures, oxidative stress and cardiovascular disease in NHANES. Environ. Health 2017, 16, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Ullah, F.; Al-Turjman, F. A conceptual framework for blockchain smart contract adoption to manage real estate deals in smart cities. Neural Comput. Appl. 2021, 14, 1–22. [Google Scholar] [CrossRef]
- Hegde, J.; Rokseth, B. Applications of machine learning methods for engineering risk assessment—A review. Saf. Sci. 2020, 122, 104492. [Google Scholar] [CrossRef]
- Miller, T.H.; Gallidabino, M.; MacRae, J.I.; Owen, S.F.; Bury, N.R.; Barron, L.P. Prediction of bioconcentration factors in fish and invertebrates using machine learning. Sci. Total Environ. 2019, 648, 80–89. [Google Scholar] [CrossRef] [PubMed]
- Hino, M.; Benami, E.; Brooks, N. Machine learning for environmental monitoring. Nat. Sustain. 2018, 1, 583–588. [Google Scholar] [CrossRef]
- Jafari, S.M.; Nikoo, M.R. Groundwater risk assessment based on optimization framework using DRASTIC method. Arab. J. Geosci. 2016, 9, 1–14. [Google Scholar] [CrossRef]
- Aller, L. DRASTIC: A Standardized System for Evaluating Ground Water Pollution Potential Using Hydrogeologic Settings; Robert S. Kerr Environmental Research Laboratory: Ada, OK, USA, 1985. [Google Scholar]
- Singh, A.; Srivastav, S.K.; Kumar, S.; Chakrapani, G.J. A modified-DRASTIC model (DRASTICA) for assessment of groundwater vulnerability to pollution in an urbanized environment in Lucknow, India. Environ. Earth Sci. 2015, 74, 5475–5490. [Google Scholar] [CrossRef]
- Rahman, A. A GIS based DRASTIC model for assessing groundwater vulnerability in shallow aquifer in Aligarh, India. Appl. Geogr. 2008, 28, 32–53. [Google Scholar] [CrossRef]
- Adiat, K.; Nawawi, M.; Abdullah, K. Assessing the accuracy of GIS-based elementary multi criteria decision analysis as a spatial prediction tool–a case of predicting potential zones of sustainable groundwater resources. J. Hydrol. 2012, 440, 75–89. [Google Scholar] [CrossRef]
- Golkarian, A.; Naghibi, S.A.; Kalantar, B.; Pradhan, B. Groundwater potential mapping using C5. 0, random forest, and multivariate adaptive regression spline models in GIS. Environ. Monit. Assess. 2018, 190, 149. [Google Scholar] [CrossRef]
- Park, I.; Kim, Y.; Lee, S. Groundwater productivity potential mapping using evidential belief function. Groundwater 2014, 52, 201–207. [Google Scholar] [CrossRef]
- Rahmati, O.; Melesse, A.M. Application of Dempster–Shafer theory, spatial analysis and remote sensing for groundwater potentiality and nitrate pollution analysis in the semi-arid region of Khuzestan, Iran. Sci. Total Environ. 2016, 568, 1110–1123. [Google Scholar] [CrossRef] [PubMed]
- Sajedi-Hosseini, F.; Choubin, B.; Solaimani, K.; Cerdà, A.; Kavian, A. Spatial prediction of soil erosion susceptibility using a fuzzy analytical network process: Application of the fuzzy decision making trial and evaluation laboratory approach. Land Degrad. Dev. 2018, 29, 3092–3103. [Google Scholar] [CrossRef]
- Elith, J.; Graham, C.H.; Anderson, R.P.; Dudík, M.; Ferrier, S.; Guisan, A.; Hijmans, R.J.; Huettmann, F.; Leathwick, J.R.; Lehmann, A.; et al. Novel methods improve prediction of species’ distributions from occurrence data. Ecography 2006, 29, 129–151. [Google Scholar] [CrossRef] [Green Version]
- Schapire, R.E. The boosting approach to machine learning: An overview. In Nonlinear Estimation and Classification; Springer: Berlin/Heidelberg, Germany, 2003; pp. 149–171. [Google Scholar]
- Saha, S.; Gayen, A.; Pourghasemi, H.R.; Tiefenbacher, J.P. Identification of soil erosion-susceptible areas using fuzzy logic and analytical hierarchy process modeling in an agricultural watershed of Burdwan district, India. Environ. Earth Sci. 2019, 78, 1–18. [Google Scholar] [CrossRef]
- Wentworth, C.K. A simplified method of determining the average slope of land surfaces. Am. J. Sci. 1930, 5, 184–194. [Google Scholar] [CrossRef]
- Pavelsky, T.M.; Smith, L.C. RivWidth: A software tool for the calculation of river widths from remotely sensed imagery. IEEE Geosci. Remote Sens. Lett. 2008, 5, 70–73. [Google Scholar] [CrossRef]
- Anderson, J.R. Land-use classification schemes. Photogramm. Eng. 1971, 37, 379–387. [Google Scholar]
- Nohani, E.; Moharrami, M.; Sharafi, S.; Khosravi, K.; Pradhan, B.; Pham, B.T.; Lee, S.; Melesse, A.M. Landslide susceptibility mapping using different GIS-based bivariate models. Water 2019, 11, 1402. [Google Scholar] [CrossRef] [Green Version]
- Habibi, V.; Ahmadi, H.; Jafari, M.; Moeini, A. Mapping soil salinity using a combined spectral and topographical indices with artificial neural network. PLoS ONE 2021, 16, e0228494. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support vector machine. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Choubin, B.; Darabi, H.; Rahmati, O.; Hosseini, F.S.; Klöve, B. River suspended sediment modelling using the CART model: A comparative study of machine learning techniques. Sci. Total Environ. 2018, 615, 272–281. [Google Scholar] [CrossRef] [PubMed]
- Arabgol, R.; Sartaj, M.; Asghari, K. Predicting nitrate concentration and its spatial distribution in groundwater resources using support vector machines (SVMs) model. Environ. Modeling Assess. 2016, 21, 71–82. [Google Scholar] [CrossRef]
- Hair, F.J.; Black, W.C.; Babin, B.J.; Anderson, R.E.; Tatham, L.R. Multivariate Data Analysis; Prentice Hall: Upper Saddle River, NJ, USA, 1998. [Google Scholar]
- Aslam, B.; Zafar, A.; Khalil, U.; Azam, U. Seismic activity prediction of the northern part of Pakistan from novel machine learning technique. J. Seismol. 2021, 25, 639–652. [Google Scholar] [CrossRef]
- Aslam, B.; Zafar, A.; Khalil, U. Correction to: Development of integrated deep learning and machine learning algorithm for the assessment of landslide hazard potential. Soft Comput. 2021, 25, 13795. [Google Scholar] [CrossRef]
- Fang, Z.; Wang, Y.; Peng, L.; Hong, H. Integration of convolutional neural network and conventional machine learning classifiers for landslide susceptibility mapping. Comput. Geosci. 2020, 139, 104470. [Google Scholar] [CrossRef]
- Naghibi, S.A.; Pourghasemi, H.R.; Dixon, B. GIS-based groundwater potential mapping using boosted regression tree, classification and regression tree, and random forest machine learning models in Iran. Environ. Monit. Assess. 2016, 188, 1–27. [Google Scholar] [CrossRef]
- Lee, S.; Kim, Y.-S.; Oh, H.-J. Application of a weights-of-evidence method and GIS to regional groundwater productivity potential mapping. J. Environ. Manag. 2012, 96, 91–105. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.; Oh, H.-J. Ensemble-Based Landslide Susceptibility Maps in Jinbu Area, Korea, in Terrigenous Mass Movements; Springer: Berlin/Heidelberg, Germany, 2012; pp. 193–220. [Google Scholar]
- Ozdemir, A. Using a binary logistic regression method and GIS for evaluating and mapping the groundwater spring potential in the Sultan Mountains (Aksehir, Turkey). J. Hydrol. 2011, 405, 123–136. [Google Scholar] [CrossRef]
- Razandi, Y.; Pourghasemi, H.R.; Neisani, N.S.; Rahmati, O. Application of analytical hierarchy process, frequency ratio, and certainty factor models for groundwater potential mapping using GIS. Earth Sci. Inform. 2015, 8, 867–883. [Google Scholar] [CrossRef]
- Yesilnacar, E.K. The Application of Computational Intelligence to Landslide Susceptibility Mapping in Turkey. Ph.D. Thesis, University of Melbourne, Parkville, Australia, 2005. [Google Scholar]
- Voudouris, K.; Kazakis, N.; Polemio, M.; Kareklas, K. Assessment of intrinsic vulnerability using DRASTIC model and GIS in Kiti aquifer, Cyprus. Eur. Water 2010, 30, 13–24. [Google Scholar]
- Dewan, A. Floods in a Megacity: Geospatial Techniques in Assessing Hazards, Risk and Vulnerability; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Neshat, A.; Pradhan, B.; Javadi, S. Risk assessment of groundwater pollution using Monte Carlo approach in an agricultural region: An example from Kerman Plain, Iran. Comput. Environ. Urban Syst. 2015, 50, 66–73. [Google Scholar] [CrossRef]
- Monserud, R.A.; Leemans, R. Comparing global vegetation maps with the Kappa statistic. Ecol. Model. 1992, 62, 275–293. [Google Scholar] [CrossRef]
- Xie, C.; Luo, C.; Yu, X. Financial distress prediction based on SVM and MDA methods: The case of Chinese listed companies. Qual. Quant. 2011, 45, 671–686. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Yousefi, S.; Kornejady, A.; Cerdà, A. Performance assessment of individual and ensemble data-mining techniques for gully erosion modeling. Sci. Total Environ. 2017, 609, 764–775. [Google Scholar] [CrossRef] [Green Version]
- Hastings, M.; Steig, E.J.; Sigman, D.M. Seasonal variations in N and O isotopes of nitrate in snow at Summit, Greenland: Implications for the study of nitrate in snow and ice cores. J. Geophys. Res. Atmos. 2004, 109, D20. [Google Scholar] [CrossRef]
- Jódar, J.; Lambán, L.J.; Medina, A.; Custodio, E. Exact analytical solution of the convolution integral for classical hydrogeological lumped-parameter models and typical input tracer functions in natural gradient systems. J. Hydrol. 2014, 519, 3275–3289. [Google Scholar] [CrossRef]
- Xu, T.; Gómez-Hernández, J.J. Joint identification of contaminant source location, initial release time, and initial solute concentration in an aquifer via ensemble Kalman filtering. Water Resour. Res. 2016, 52, 6587–6595. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).