Adaptive Tracking PID and FOPID Speed Control of an Elastically Attached Load Driven by a DC Motor at Almost Step Disturbance of Loading Torque and Parametric Excitation

Abstract

Adaptive tracking control of the speed of a very elastically attached circular load driven by a direct current motor accompanied with an adaptive conventional and a fractional-order Proportional Integral Derivative (PID) controller is studied. It refers to improving the closed-loop control system response of elastically coupled components of drivelines. The motor and the load mechatronic models and the block diagrams are constructed. Parameters of the PID controller in the model reference control are both constant, as well as vary in time. The adaptive control method is improved by the application of a new closed-loop control structure canceling error dynamics. A few competing control strategies are tested based on the application of two types low and high frequency stepwise increasing variations of loading torque and damping coefficient of motion. Moreover, the performance of the control strategies is verified by Integral Time-Weighted Absolute Error (ITAE) index, since their robustness is evaluated by applying a sine modulated triangle waves of selected electric parameters. Therefore, a dynamic forcing and parameter uncertainty is applied. Simulation results are compared for checking the proposed methods.

1. Introduction

Modeling of electric drives of machines and vehicles is currently one of the most explored fields of control engineering. Motion control systems are often equipped with permanent magnet induction machines working as driving components. In the electric part of a control system, the terminal voltage or the armature current is available for speed or position estimation, since, for the mechanical system state of driven inertia, the rotational displacement or velocity is measured with the use of additional sensors.

Control of the speed of a Direct Current (DC) motor with conventional Proportional Integral Derivative (PID) and non-conventional Artificial Neural Network (ANN) methods is taken into consideration in Reference [1]. Direct current motor model and performance indicators criteria are defined. For non-conventional method inverse model control schema is used, where a 3-layer Neural Network (NN) inverse model is trained by back-propagation algorithm. Considering the application of the motor in robotics, the study shows an interesting technique of improving the closed system’s dynamics, where there is no need to know the model parameters when designing the system control. Reference [2] applies an adaptive PID controller dependent on the extra blunder of a turn around control sign to comprehend non-linearity and parameter varieties. In both cases, the PID controller is tuned in MATLAB.

Adaptive tracking control taken into account also in this work proved its efficiency in Reference [3]. There can be found an adaptive velocity trajectory tracking control for a nonlinear shunt direct current electric machine subjected to unmeasurable variable loading torque and parametric uncertainty. Again, ANN and dynamical tracking error compensators are combined to avoid dependence on detailed mathematical models of uncertain nonlinear systems and significantly improve the controller robustness and efficiency. Other similar examples include: a sensorless speed tracking using an ANN [4], flatness-based control [5], or an adaptive backstepping control [6].

Similarly, in Reference [7], a comparative studies on different meta-heuristic type adaptive control for the speed regulation of the DC motor with parameters uncertainties are addressed. The work includes an overview with testing of several adaptive controllers based on the differential evolution, Particle Swarm Optimization (PSO), Bat Algorithm (BAT), Firefly Algorithm (FFA), and Wolf Search Algorithm (WSA) algorithms are proposed in the on-line tuning of the parameters used in calculating the motor control signal. Simulations show the efficacy of each control strategy.

Fractional-order brushless DC motor system is introduced in Reference [8], wherein there exist unknown dynamics, immeasurable states and chaotic oscillation. The authors propose an anti-oscillation and chaos control aimed at immeasurable states. The high-gain observers with fast convergence allowed to obtain information about system states. The system uncertainties are compensated using a finite-time echo state network with a weight to approximate uncertain dynamics, while its weight is tuned by a fractional-order adaptive law.

An FFA-based Fractional-Order PID (FOPID) controller is proposed in Reference [9] for a Brushless DC (BLDC) motor to achieve effective control of torque and speed. In a conventional control, the torque references are converted into current references and phase currents are controlled using current controllers. It is not effective, resulting in a ripple in the torque. The authors propose a direct instantaneous scheme in which reference torques are compared with those estimated directly and the error is given to FOPID controller tuned using the FFA technique.

A direct adaptive Fuzzy Logic Controller (FLC) studied in Reference [10] for precise control of the DC motor speed is estimated from two levels, where the lower level uses a Mamdani fuzzy controller and the upper level is an inverse model based on a Takagi–Sugeno approach. In this method, the output is used to adapt the parameters of the FLC in the lower level. The proposed controller is implemented using Arduino kit (also see References [11,12]). It has been proved that the proposed adaptive controller improves performance and disturbance of the response due to the load in the speed control of the DC motor.

In Reference [13], a bio-inspired adaptive control strategy based on an improved differential evolution is proposed for the speed regulation of the DC motor subject to parametric uncertainties. An optimization problem in this strategy of control is stated and solved on-line at each sampling time to obtain an optimal set of parameters that are used in the calculation of the control signal.

Reference [14] presents an active disturbance rejection controller for the BLDC motor. It compensates for the loading torque variations. Numerical simulations test and evaluate the performance of the proposed control algorithms in the presence of variable loading torque and noise. The simulation results demonstrated the good reconstruction of the speed trajectory in a challenging scenario of operation of the motor. A similar problem devoted to BLDC motors is related to a reduction of cogging torque [15].

1.1. Scope of the Selected Achievements

Each of the methodologies discussed above is unique. Here, we enumerate the main conclusions being important in the contents of our research.

• Neural networks elaborated in Reference [1] state an alternative to adaptive PID controllers [2] for identification of models and control for improving the system dynamics, as well.
• Knowledge of real-time estimation of disturbances and system parameters are unnecessary in Reference [3] to suppress time-varying disturbances of a higher order.
• The results found in Reference [7] confirm that the PSO-based controller is very promising.
• A fractional-order adaptive law presented in Reference [8] shows the path that we follow at a final stage of this work.
• FOPID controller is proposed in Reference [9] for BLDC motor to achieve effective control of torque and speed.
• An adaptive FLC considered in Reference [10] in the DC motor speed control improves disturbance rejection of the motor response due to the load.
• Active disturbance rejection controller considered in Reference [14] or even in Reference [15] for the BLDC motor can compensate variations of the loading or cogging torque.

1.2. The Improved Control Strategy Demonstrated in This Work

Control strategy presented in this study utilizes most of the approaches cited in Section 1.1. Moreover, it aims at an incremental development in this field of mechatronics. Opposite to the presented control problems, that are devoted to controlling of motor speed, this study does not focus on control of the DC motor speed directly, but in a different way, i.e., it is oriented on the regulation of the speed of an elastically attached load. Therefore, we assume to have a continuously measured position and velocity of the load. By this approach, we can focus our task on the maintenance of time characteristics of the load dynamics, not the motor directly, e.g., an optimal and oscillation free speeding up of a load of some inertia attached to the motor at the presence of an elastic coupling (a mass attached to a stretched wire states a similar problem; see Reference [16]). For instance, this problem has been extended also on the improvement of the system transient dynamical response due to appearance of time-varying characteristics of the motor viscous damping coefficient (viscoelastic damping structures are widely applied for vibration and disturbance reduction; see Reference [17]).

Unpredictable conditions of operation of the drivelines require leader-following multi-agent systems with the centralized event-triggering controller to regulate the speed of the networked multiple DC motor systems. In this context, the optimal Liner Quadratic Regulator (LQR) control of the system by minimizing the quadratic cost function and involving the determination of the performance index is applied in Reference [18].

2. The Physical Model

We will consider the mechatronic system schematically shown in Figure 1. It consists of a rigid DC motor and a mechanical load in the form of a solid disk with the mass moment of inertia $J_l$ (compare Reference [19]).

We begin deriving the equations for rotor dynamics and current distribution in the electrical system by defining the relationship between the torque $T_{ma}$ of the motor (“a” denotes the actual model) and the current $i_a$ in the motor’s armature circuit,

$$\begin{array}{c}\hfill T_{ma}\left(t\right)=K_t{i}_a\left(t\right).\end{array}$$

(1)

The parameters used in the work are listed in

Table 1. Parameters of the investigated motor model.

Parameter	Notation	Value	Unit
rotor inertia	$J_m$	$2.3·{10}^{-3}$	$\mathrm{kg}·{\mathrm{m}}^2$
load inertia	$J_l$	$10·J_m$	$\mathrm{kg}·{\mathrm{m}}^2$
motor damping	$b_m$	$1.2·{10}^{-4}$	$\mathrm{N}·\mathrm{m}·\mathrm{s}/\mathrm{rad}$
load damping	$b_l$	$0.02$	$\mathrm{N}·\mathrm{m}·\mathrm{s}/\mathrm{rad}$
torque constant	$K_t$	$0.5$	$\mathrm{N}·\mathrm{m}/\mathrm{A}$
inductance	L	$1.4·{10}^{-4}$	H
resistance	R	$0.9$	$\mathsf{\Omega }$
back-EMF	$K_b$	$0.5$	$\mathrm{V}·\mathrm{s}/\mathrm{rad}$
stiffness	$k_{rl}$	400	$\mathrm{N}·\mathrm{m}/\mathrm{rad}$
damping	$b_{rl}$	$0.01$	$\mathrm{N}·\mathrm{m}·\mathrm{s}/\mathrm{rad}$
reference control	$\beta$	1	$\mathrm{V}/\mathrm{rad}$

. The electromotive force $\mathcal{E}$ depends on the rotational speed in a linear manner,

$$\begin{array}{c}\hfill \mathcal{E}\left(t\right)=K_b{\dot{\theta }}_{ma}\left(t\right).\end{array}$$

(2)

Adding the moments of forces acting on the rotor shaft in the mechanical system and taking into account the moment of force from the damping of the mechanical system of the motor, we obtain:

$$J{\ddot{\theta }}_{ma}\left(t\right)=T_{ma}\left(t\right)-T_{la}\left(t\right)-b_m{\dot{\theta }}_{ma}\left(t\right),$$

(3)

$${\ddot{\theta }}_{ma}\left(t\right)={\displaystyle \frac{1}{J}}(K_t{i}_a\left(t\right)-T_{la}\left(t\right)-b_m{\dot{\theta }}_{ma}\left(t\right)).$$

(4)

Deriving the second differential equation describing the dynamics of current variations in the electrical system, we will use the second Kirchhoff’s law and the mathematical description of electronic components, i.e., the resistance R and the inductance L included in it (analytical calculations of parameters of permanent magnets motors are described in Reference [20]). Based on Kirchhoff’s second law, the sum of voltage drops on resistive elements in a closed circuit is equal to the sum of electromotive forces present in this circuit:

$$L{\dot{i}}_a\left(t\right)=u_a\left(t\right)-R{i}_a\left(t\right)-\mathcal{E}\left(t\right),$$

(5)

$${\dot{i}}_a\left(t\right)={\displaystyle \frac{1}{L}}(u_a\left(t\right)-R{i}_a\left(t\right)-K_b{\dot{\theta }}_{ma}),$$

(6)

where $u_a$ is defined by Equation (13).

The load is connected to the rotor by a flexible connector, which has damping and elastic properties dependent on the relative angular displacement and velocity, respectively, between the rotor and the disk-shaped inertial load.

Let the load moment $T_l$, operating in a flexible connection of both shafts, depends on the sum of its two components, i.e., the moment $T_{ls}$, resulting from the difference of angular positions $\delta {\theta }_a$ and the moment $T_{ld}$, resulting from the difference in angular velocities $\delta {\omega }_a$, which we write in the form

$$\begin{array}{cc}\hfill T_l\left(t\right)& =T_{ls}\left(t\right)+T_{ld}\left(t\right)\hfill \\ & =k_{rl}\delta {\theta }_a\left(t\right)+b_{rl}\delta {\omega }_a\left(t\right)\hfill \\ & =k_{rl}({\theta }_{ma}\left(t\right)-{\theta }_{la}\left(t\right))+b_{rl}({\dot{\theta }}_{ma}\left(t\right)-{\dot{\theta }}_{la}\left(t\right)).\hfill \end{array}$$

(7)

In Equation (7), the symbol ${\theta }_{la}$ denotes the angular displacement of the actual load’s shaft, while, based on the difference ${\theta }_{ma}-{\theta }_{la}$, we assume that the load keeps up with the force from the rotor shaft. Using this equation, one can write the equations of dynamics for the disk-shaped load in the actual system model:

$$\begin{array}{cc}\hfill J_l{\ddot{\theta }}_{la}\left(t\right)& +(b_l+b_{la}\left(t\right)){\dot{\theta }}_{la}\left(t\right)=(T_l\left(t\right)+T_{la}\left(t\right)),\hfill \\ \hfill {\ddot{\theta }}_{la}\left(t\right)& ={\displaystyle \frac{1}{J_l}}(k_{rl}({\theta }_{ma}\left(t\right)-{\theta }_{la}\left(t\right))+b_{rl}{\dot{\theta }}_{ma}\left(t\right)-(b_l+b_{rl}+b_{la}\left(t\right)){\dot{\theta }}_{la}\left(t\right)),\hfill \end{array}$$

(8)

where the introduced damping of rotational motion $b_{la}$, being a functionally changing additive term concerning the constant parameter $b_{rl}$ states for a parametric time-dependent uncertainty of the dynamical behavior of the driven load. This kind of complexity produces disturbance to the system, since it will change almost-discontinuously with some frequency. Similarly, the second almost-discontinuous forcing is introduced as the loading torque $T_{la}$, being an additive term with respect to $T_l$ given by Equation (7). These two factors have been selected as the most important for checking of effectiveness of the proposed control methods subject to a parametric and external disturbances.

Both, the current $i_a$ in Equation (3) for the mechanical subsystem and the angular speed of the rotor ${\dot{\theta }}_{ma}$ in the equation for the actual model of the electrical subsystem couple the dynamics of both subsystems, creating a mechatronic actual system being mathematically described by Equations (3)–(5) and (8). The elastic connection and the motor’s load interact dynamically, that makes the tested model closer to a real implementation.

The reference model, of which output is to be followed by the actual model is given by a similar set of the aforementioned equations, but after replacing index “a” with “r” and the input signal $u_a$ with $u_r$ given as a solution to the Equation (9).

3. The Trajectories of Disturbances

We have defined an actual system (see Equations (3)–(5) and (8)) with index and a reference system of the same structure.

The control task follows: the time trajectory of the rotational velocity of the actual load (not of the actual motor) has to be maintained as close as possible to the time trajectory of the reference model subject to the two mentioned disturbances coming from an addition to the external loading and uncertainty of a selected parameter.

The input reference trajectory $u_r\left(t\right)$ shown in green color in Figure 5 is formed by solving the discontinuous model:

$$\begin{array}{c}\hfill {\tau }_1{\tau }_2\frac{d^2{u}_r\left(t\right)}{d{t}^2}+({\tau }_1+{\tau }_2)\frac{d{u}_r\left(t\right)}{dt}+u_r\left(t\right)=u_s\left(t\right),\end{array}$$

(9)

where ${\tau }_1$ and ${\tau }_2$ are time constants, and the step of input voltage $u_i$ (e.g., $\{1.5,3,4.5,6,7.5\}$) is assumed on $j_u$ intervals based on the step function:

$$\begin{array}{c}\hfill u_s\left(t\right)=u_i\mathbf{1}\left(t\right)\mathrm{for}t\in (t_i,t_{i+1}],i=0,1,\cdots ,j_u.\end{array}$$

(10)

The two pyramid-shaped step functions of both aforementioned system disturbances $p_{la}\equiv \{T_{la}\vee b_{la}\}$ are found similarly by solving the following differential equation twice:

$$\begin{array}{c}\hfill {\tau }_1{\tau }_2\frac{d^2{p}_{la}\left(t\right)}{d{t}^2}+({\tau }_1+{\tau }_2)\frac{d{p}_{la}\left(t\right)}{dt}+p_{la}\left(t\right)=p_s\left(t\right),\end{array}$$

(11)

but their amplitudes ${\widehat{p}}_s\equiv \{T_s\vee b_s\}$ on the $j_s$ intervals form a discrete set of step input values (e.g., $\{0,0.3,0.6,0.9,0.6,0.3,0\}$), i.e.,

$$\begin{array}{c}\hfill p_s\left(t\right)={\widehat{p}}_s\mathbf{1}\left(t\right)\mathrm{for}t\in (t_i,t_{i+1}],i=0,1,\cdots ,j_s,\end{array}$$

(12)

that is passed through the second order filter with time constants ${\tau }_1$ and ${\tau }_2$ given by Equation (11).

The input voltage in the actual model open-loop control to the actual model follows:

$$\begin{array}{c}\hfill u_a\left(t\right)=u_r\left(t\right)+{\beta }_i({\theta }_{lr}\left(t\right)-{\theta }_{la}\left(t\right)),\end{array}$$

(13)

where $u_r\left(t\right)$ is a solution to the Equation (9), ${\beta }_i$ [V/rad] ($i=1,2$) is a constant, and ${\theta }_{lr}$ and ${\theta }_{la}$ are the angles of rotation of the reference and actual load, respectively.

4. Control Strategies

The servomechanism is a closed automatic control system that compensates for external forces and external or internal disturbances. The output signal can be position, speed or acceleration, i.e., angular or linear. The setpoint of one of these variables is compared by the transducer with the actual output signal and the resulting control deviation signal is fed to the correction element, after which it is amplified and then fed to the servo actuator input. The servo control system fulfils the task of minimizing the control error that occurs during step or pulse changes in the set value.

The servomechanism that is numerically studied in this research has the structure of a typical control system. It does not control the technological process but, as a rule, a single executive element in order to improve the performance of the executive line.

Nonlinear dynamics of servos containing integral components forces the necessity to use a proportional corrector with some high gain, and even three-state amplifiers.

The integrative nature of the actuator should provide theoretically zero static error. The high gain in the main circuit of the control system improves the follower properties of the system but reduces the stability margin. This can be improved by introducing, e.g., a proportional-differential controller or a proportional-integral-differential controller on the mainline. The PID controller will be implemented in this work.

In this work, we distinguish two realizations of closed-loop control strategy applied to assess the influence of various disturbances appearing in the reality, i.e., a sudden step increase of the loading torque, represented by $T_{la}$, and also the uncertainty of the rotor’s damping coefficient $b_{la}$. The two realizations presented below are based on two on-line adaptation techniques of parameters of the PID regulator. This continues the research [19] of low-speed voltage-input tracking control of a DC motor numerically modeled by a dynamical system with stick-slip friction.

One may note that by applying small values of stiffness and damping coefficients, the investigated dynamical system has been situated in a soft elastic and weak damping environment. It does control of the system more difficult due to the high tendency to oscillations that might be decisive for the performance of the control process.

Moreover, the system is parametric (parametrically uncertain) and externally forced, where the parameter of damping and external loading torque varies in time according to almost-discontinuous functions of frequency, respectively. The control strategies 2 and 3 described below are based on the nonlinear controller, making the whole closed-loop control dynamical system nonlinear.

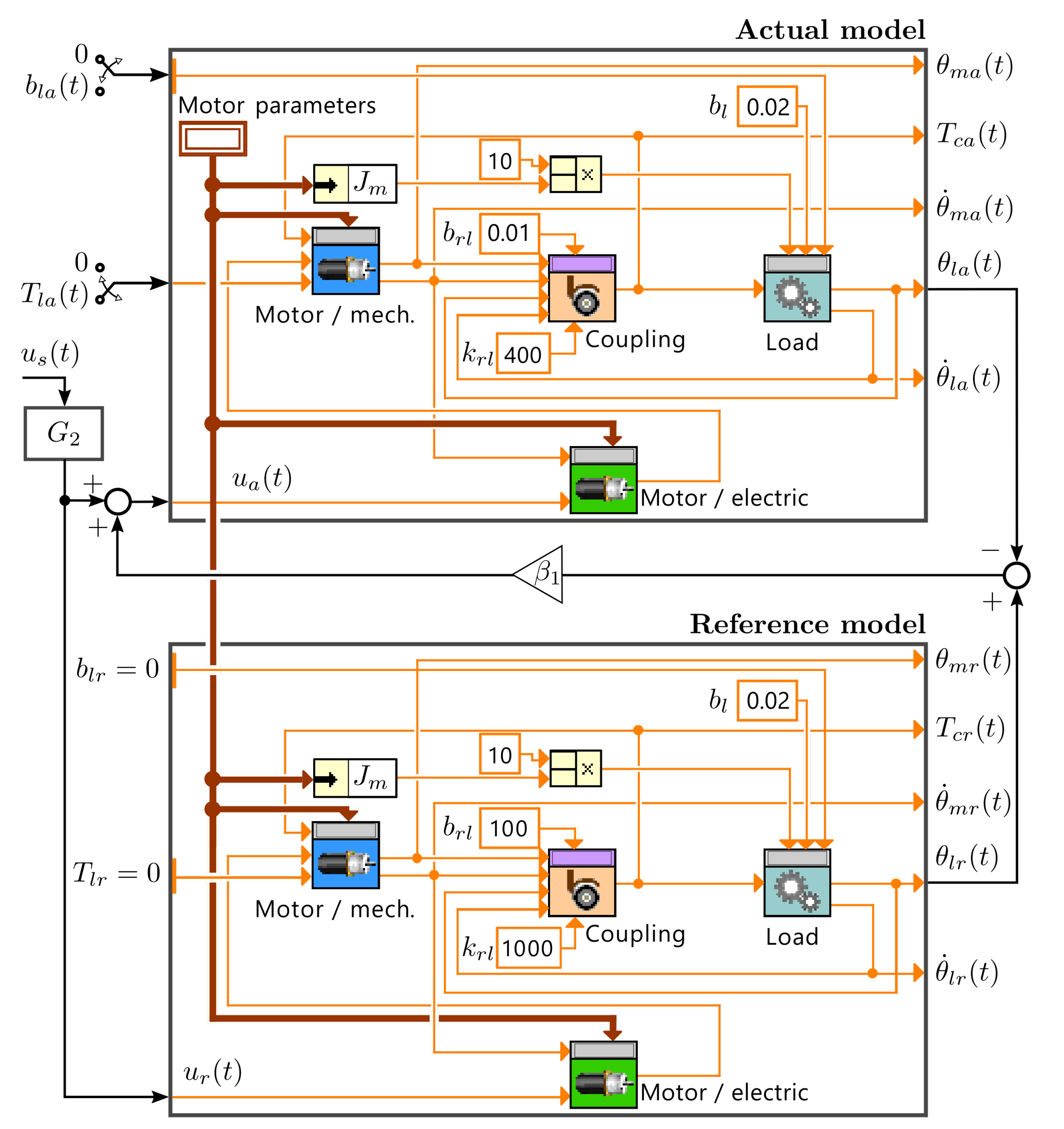
4.1. Block Diagram of the Object of Control

Figure 2 presents the object of control–actual model and the reference model to be followed by the actual. Although the rotational velocity ${\dot{\theta }}_{la}$ states the control variable, the difference between actual and reference states is taken and fed back to the actual model input.

The model is split into a few basic parts of the investigated mechatronic system, means the loading inertia visible as Load (see Equation (8)), the mechanical part of the motor visible as Motor/mechanical (see Equations (3) and (4)), and the electrical part visible as Motor / electric (see Equation (5)) and the visco-elastic element coupling shafts of the motor and the driven loading inertia, which is visible as Coupling; see Equation (7).

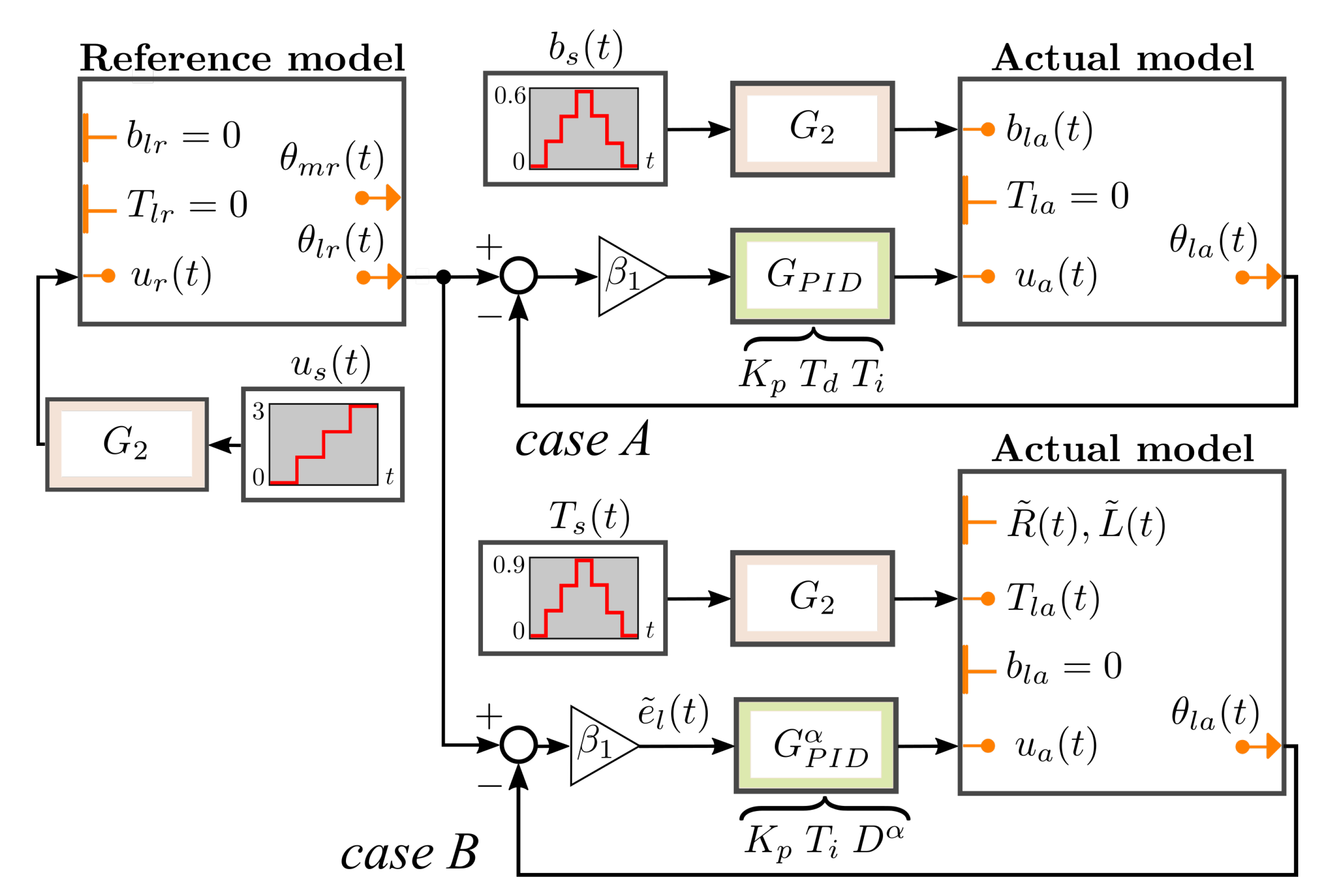
4.2. The First Strategy

The two analyzed models of the open-loop reference model tracking control system have been incorporated into the closed-loop model reference PID control system shown in Figure 3. As it can be seen, there are applied two kinds of disturbances, i.e., along the damping coefficient of load rotation $b_s\left(t\right)$ (case A), as well as along the loading torque $T_{la}\left(t\right)$, both changing almost-discontinuously with some frequency (low and high–doubled with respect to the lower one). This way, we introduce the next criterion of assessment of efficiency of the investigated control strategies.

Parameters of the classical PID are constant, being selected appropriately to achieve the best system response in both analyzed cases. Results of application of the control strategy are shown in Figures 6a,b and 10a,b.

The control law for the actual rotational velocity of the load is defined on time intervals obtained after splitting the time by appearance of step inputs of the reference control input $u_s\left(t\right)$ given by Equation (10) and the pyramid-shaped function of disturbances given by Equation (12), as it follows:

$$\begin{array}{cc}\hfill u_c\left(t\right)& ={\beta }_1({\theta }_{lr}\left(t\right)-{\theta }_{la}\left(t\right)),\hfill \\ \hfill u_a\left(t\right)& =K_p\left(u_c\left(t\right)+T_d\frac{d{u}_c\left(t\right)}{dt}+\frac{1}{T_i}{\int }_{t_j}^{t_{j+1}}{u}_c\left(\tau \right)d\tau \right)\hfill \end{array}$$

(14)

for $j=0,1,\cdots ,j_s+j_u$ and parameters $K_p$, $T_d$, and $T_i$ of the regulator. In the numerical simulation, the parameters of the regulator for both considered types of disturbance will be valued as follows: $K_p=300$, $T_i=1$, $T_d=2$, ${\beta }_1=1$.

4.3. The Second Strategy

This strategy is similar to the previous one but it differs in the derivative action implemented in $G_{PID}$, that is replaced by the fractional-order derivative (see $G_{PID}^{\alpha }$). It is computed in the following way.

The desired $\alpha$-order fractional derivative of the computed signal of error,

$$\begin{array}{c}\hfill e_l\left(t\right)={\theta }_{lr}\left(t\right)-{\theta }_{la}\left(t\right),{\tilde{e}}_l\left(t\right)={\beta }_1{e}_l\left(t\right),\end{array}$$

(15)

can be estimated using moments of a function.

The fractional derivative of order $\alpha$ will be approximated by a finite sum of N terms, including derivatives of integer order employing continuous expansion of the left Riemann-Liouville derivative.

According to Lemma 2.12 in Reference [21], let ${\tilde{e}}_l\left(t\right)\in C[a,b]$ and $0<\alpha <1$. Then, the left Riemann-Liouville fractional derivative ${}_{a}D_t^{\alpha }{\tilde{e}}_l\left(t\right))$ exists almost everywhere in $[a,b]$. Moreover, $t\in (a,b)$, ${}_{a}D_t^{\alpha }{\tilde{e}}_l\left(t\right)\in L_p[a,b]$, for $1\le p<1/\alpha$, and

$$\begin{array}{c}\hfill {}_{a}D_t^{\alpha }{\tilde{e}}_l\left(t\right)=\frac{1}{\mathsf{\Gamma }(1-\alpha )}\left[\frac{{\tilde{e}}_l\left(t\right)\left(a\right)}{{(t-a)}^{\alpha }}+{\int }_a^t{(t-\tau )}^{-\alpha }{\dot{\tilde{e}}}_l\left(\tau \right)d\tau \right].\end{array}$$

(16)

Integration of Equation (16) by parts yields

$$\begin{array}{cc}\hfill {}_{a}D_t^{\alpha }{\tilde{e}}_l\left(t\right)=& \frac{{\tilde{e}}_l\left(a\right){(t-a)}^{-\alpha }}{\mathsf{\Gamma }(1-\alpha )}+\frac{{(t-a)}^{1-\alpha }}{\mathsf{\Gamma }(2-\alpha )}\left[{\dot{\tilde{e}}}_l\left(a\right)+{\int }_a^t{C}^{\prime }\left(\tau \right){\ddot{\tilde{e}}}_l\left(\tau \right)d\tau \right],\hfill \end{array}$$

(17)

where, by definition

$$\begin{array}{c}\hfill C^{\prime }\left(\tau \right)={\left(1-\frac{\tau -a}{t-a}\right)}^{1-\alpha }.\end{array}$$

(18)

Since the condition $(\tau -a)\le (t-a)$ is satisfied, applying the binomial theorem to the function $C^{\prime }\left(\tau \right)$, one gets

$$\begin{array}{c}\hfill C^{\prime }\left(\tau \right)=\sum _{p=0}^{\infty }\frac{\mathsf{\Gamma }(p-1+\alpha )}{\mathsf{\Gamma }(\alpha -1)p!}{\left(\frac{\tau -a}{t-a}\right)}^p.\end{array}$$

(19)

Integration of Equation (17) by parts, including the definition (19) of the term $C^{\prime }\left(\tau \right)$ under the integral, gives

$$\begin{array}{cc}\hfill {}_{a}D_t^{\alpha }{\tilde{e}}_l\left(t\right)=& A\left(\alpha \right){(t-a)}^{-\alpha }{\tilde{e}}_l\left(t\right)+B\left(\alpha \right){(t-a)}^{1-\alpha }{\dot{\tilde{e}}}_l\left(t\right)-\sum _{p=2}^{\infty }C(\alpha ,p){(t-a)}^{1-\alpha -p}{V}_p\left({\tilde{e}}_l\left(t\right)\right),\hfill \end{array}$$

(20)

where, as it is defined in Reference [22], the moment of a function ${\tilde{e}}_l\left(t\right)\in C^2[a,b]$, for $p\in \mathbb{N}$ where $p\ge 2,t\ge a$, is given by the formula

$$\begin{array}{c}\hfill V_p\left({\tilde{e}}_l\left(t\right)\right)=(1-p){\int }_a^t{(\tau -a)}^{p-2}{\tilde{e}}_l\left(\tau \right)d\tau ,\end{array}$$

(21)

and

$$\begin{array}{cc}\hfill A\left(\alpha \right)=\frac{1}{\mathsf{\Gamma }(1-\alpha )}\left[1+\sum _{p=2}^{\infty }\frac{\mathsf{\Gamma }(p-1+\alpha )}{\mathsf{\Gamma }\left(\alpha \right)(p-1)!}\right]& ,B\left(\alpha \right)=\frac{1}{\mathsf{\Gamma }(2-\alpha )}\left[1+\sum _{p=1}^{\infty }\frac{\mathsf{\Gamma }(p-1+\alpha )}{\mathsf{\Gamma }(\alpha -1)p!}\right],\hfill \\ \hfill C(\alpha ,p)=& \frac{\mathsf{\Gamma }(p-1+\alpha )}{\mathsf{\Gamma }(2-\alpha )\mathsf{\Gamma }(\alpha -1)(p-1)!}.\hfill \end{array}$$

(22)

In this work, the above algorithm does not take into account any closed form function of ${\tilde{e}}_l\left(t\right)$. One assumes in the method that a finite discrete series of $n+1$ samples ${\tilde{e}}_l\left(t_j\right)$ is available at the time instants $t_j=jh$, for $j=0,\cdots ,n$, and the constant sampling period h. Therefore, in Equations (20) and (22), the time t is to be replaced with a j-th measurement sample at $t_j\in [t_0,t_n]$, while $t_0=a$ and $t_n=b$, and accordingly, ∞ is to be replaced with a finite number N of terms of approximation of the fractional left Riemann-Liouville derivative of order $\alpha$.

In the numerical simulation the parameters of the regulator for both considered types of disturbance will be valued as follows: $K_p=300$, $T_i=1$, ${\beta }_1=1$, $\alpha =0.7$ (the fractional derivative part), $t_{\mathrm{hr}}=0.2$ (the time horizon reset).

4.4. The Third Strategy

The adaptive controller $G_c^a$ shown in Figure 4 is a dynamic system with on-line parameter estimation. It updates an uncertain plant or controller’s parameters, while running with the use of the measured signal or even computed system response. The objective of such an approach is to obtain a consistent performance of a control system during operation in an inconsistent environment. Indirect control with an adaptation estimates plant parameters to update the controller’s parameters at the end after application of some updating rules. The procedure aims at a time convergence of the parameter values to the true unknowns. The direct adaptation estimates the controller’s parameters only since, in this work, we apply the second one.

In the third strategy below, we apply an adaptation represented by the block diagram shown in Figure 4.

In the problem of ${\dot{\theta }}_{lr}\left(t\right)$ reference trajectory to be followed by ${\dot{\theta }}_{la}\left(t\right)$ of the actual model of our multi-degree of freedom system, the model reference control engages a subsystem in which the input signal, being a difference $e_l\left(t\right))$–error of angular position of the driven load, is delivered to two adaptation blocks. The first one is responsible for estimation of the parameters of the controller operating on $e_l\left(t\right)$, while the second one uses the error of the driving motor position:

$$\begin{array}{c}\hfill e_m\left(t\right)={\theta }_{mr}\left(t\right)-{\theta }_{ma}\left(t\right),{\tilde{e}}_m\left(t\right)={\beta }_2{e}_m\left(t\right),\end{array}$$

(23)

both having a PID form.

Before the worked out signal of the difference of the two adaptive PID controller outputs will reach the actual model input $u_a\left(t\right)$, it is subject to the third dynamical action $G_{PI}$; see Figure 3. It computes a sum of a proportional and integral transformation of the error signal. The final step in the control subsystem is used to cancel the remaining non-compensated error dynamics. According to the procedure, the following adaptive control law (see adaptive control design methods and analysis in Reference [23]) is used in a modified form:

$$\begin{array}{cc}\hfill u_l\left(t\right)=& a^{|b{\tilde{e}}_l\left(t\right)|}+c{\dot{\tilde{e}}}_l\left(t\right)+I_l\left(t\right){\int }_{t_j}^{t_{j+1}}{\tilde{e}}_l\left(\tau \right)d\tau \hfill \\ \hfill u_m\left(t\right)=& a^{|b{\tilde{e}}_m\left(t\right)|}+c{\dot{\tilde{e}}}_m\left(t\right)+I_m\left(t\right){\int }_{t_j}^{t_{j+1}}{\tilde{e}}_m\left(\tau \right)d\tau \hfill \\ \hfill u_a\left(t\right)=& K_{pa}\left((u_l\left(t\right)-u_m\left(t\right))+\frac{1}{T_{ia}}{\int }_{t_j}^{t_{j+1}}(u_l\left(\tau \right)-u_m\left(\tau \right))d\tau \right),\hfill \end{array}$$

(24)

for $j=0,1,\cdots ,j_s+j_u$.

For adaptation of the time-dependent parameter of integral action $I_{·}\left(t\right)$, where “$·$” is to be replaced by “l” or “m”, the following adaptation for this part is applied:

$$\begin{array}{c}\hfill I_{·}\left(t\right)=\left\{\begin{array}{c}\frac{1}{D},\mathrm{for}D>f\hfill \\ d,\mathrm{for}D\le f,\hfill \end{array}\right.\end{array}$$

(25)

where $D=c|{\dot{\tilde{e}}}_{·}\left(t\right)|$. It is assumed that the constants: a, b, c, d, f are the same for both adaptation laws $u_l\left(t\right)$ and $u_m\left(t\right)$. In the numerical simulation the parameters of the regulator for both considered types of disturbance will be valued as follows: $a=250$, $b=8$, $c=8$, $d=0.001$, $f=0.02$, $K_{pa}=1$, $T_{ia}=1$, ${\beta }_i=1$.

5. Results

The results presented in this section are based on several numerical experiments performed with different forms of disturbance of the damping coefficient and additional loading torque, both increasing almost stepwise; low and, respectively, high frequency; and various controllers to obtain data of a comparative nature.

We investigate three types of controllers working in an open and closed model reference control system:

• classical PID—see Section 4.2,
• FOPID (PID${}^{\alpha }$)—see Section 4.3,
• adaptive PID with PI action at the second stage of error compensation—see Section 4.4.

Results of all numerical experiments are visualized (Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12) and assessed with the use of Integral Time-Weighted Absolute Error (ITAE) performance index summarized in

Table 2. The Integral Time-Weighted Absolute Error (ITAE) performance index for various numerical experiments.

ITAE	Controller	Control Loop	Disturbed Parameter	Disturbance Frequency	Figure
$0.0368$	PID	closed	$T_l$	low	Figure 6b
$0.0551$	Adaptive PID	closed	$T_l$	low	Figure 8b
$0.0839$	Adaptive PID	closed	$b_l$	low	Figure 8a
$0.0962$	FOPID	closed	$T_l$	low	Figure 7b
$0.1104$	PID	closed	$T_l$	high	Figure 10b
$0.1313$	Adaptive PID	closed	$T_l$	high	Figure 12b
$0.2210$	PID	closed	$b_l$	high	Figure 10a
$0.2263$	Adaptive PID	closed	$b_l$	high	Figure 12a
$0.2383$	FOPID	closed	$T_l$	high	Figure 11b
$0.4780$	FOPID	closed	$b_l$	low	Figure 7a
$0.7453$	–	open	$T_l$	high	Figure 9b
$1.2115$	FOPID	closed	$b_l$	high	Figure 11a
$1.4949$	–	open	$T_l$	low	Figure 5b
$1.5168$	PID	closed	$b_l$	low	Figure 6a
$1.9720$	–	open	$b_l$	high	Figure 9a
$2.4874$	–	open	$b_l$	low	Figure 5a

. Performance of each control system, as well as robustness of the best ones, with respect to variations of selected electric parameters of the mechatronic drive, is discussed in Section 6.

The selected motor model is described by the electromechanical parameters given in Table 1.

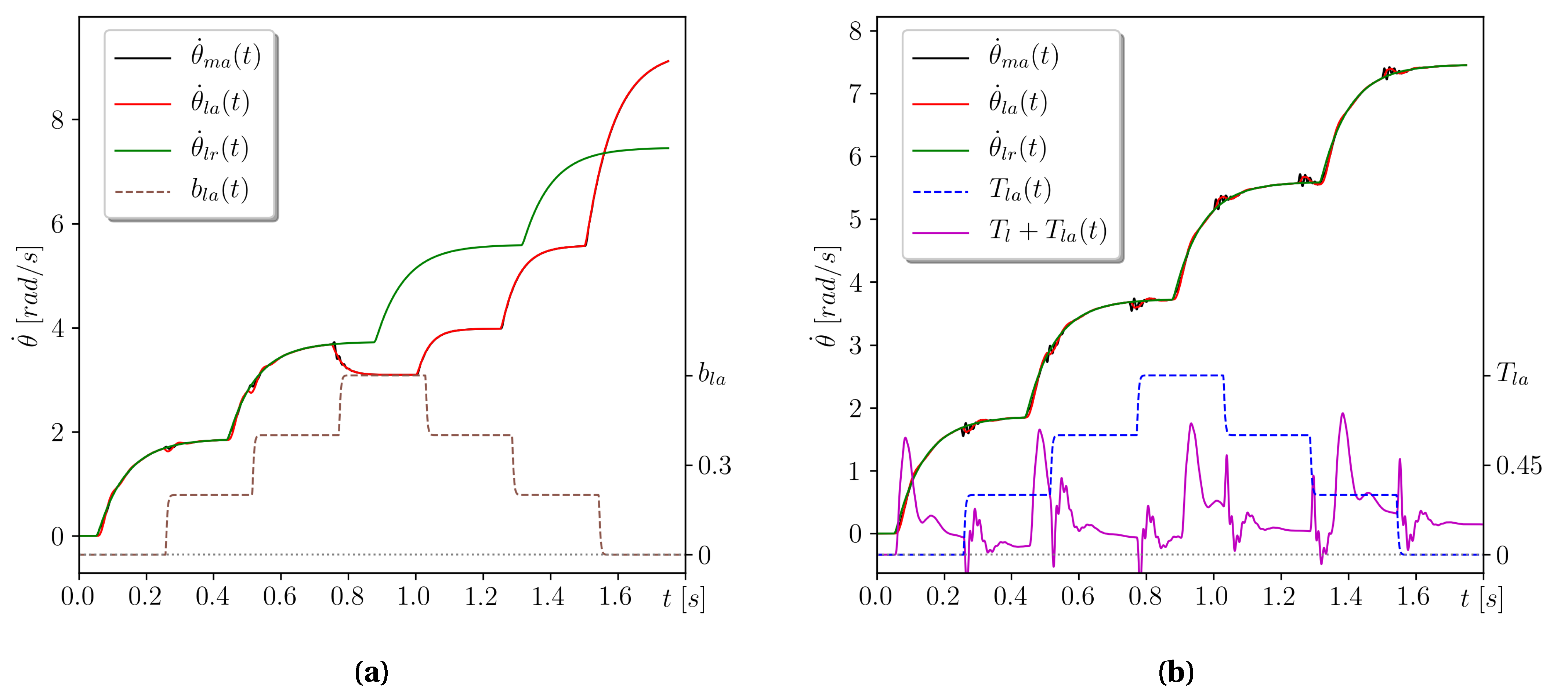
Numerical simulation of the investigated dynamical system for the motor parameters listed in Table 1 is conducted in time $t_f=1.75$ (s) at a step of integration $h=2·{10}^{-5}$ (s). It brings an interesting, but some anticipated solutions shown in Figure 5a,b. The dashed line represents a pyramid stepwise shaped variation of damping coefficient (Figure 5a) and variation of an additional loading torque (Figure 5b) in the motion of the driven load inertia; the green line is the time trajectory of velocity to be followed by the inertia, and the red line shows its actual position.

We see that both actual solutions are far from the required ones. It is important to note that also in both cases the disturbances are very harmful to the process, producing large temporary errors of the regulation. Together with the uncertainties of the parameter $b_{la}\left(t\right)$ and the loading torque $T_{la}\left(t\right)$, the control system has to deal with the stepwise second-order inertia increase of command velocity; see the green line. At these times, the motor’s actual velocity represented by the black line experiences some oscillations that incorporate some portion of error into the temporary states initiated by the smoothed steps of command rotational velocity.

6. Effectiveness of the Proposed Solutions

All numerical experiments were performed using the same parameters of the control object. The parameters $b_{la}$ and $T_{la}$, as well as control systems described in Section 4 treating control strategies, were changed. Additionally, two electric parameters, i.e., R and L, have been disturbed to supplement the analysis of robustness.

6.1. Estimating Performance of the Control System

When assessing the obtained results, it should be emphasized that some solutions become unstable at some point of the time response; see Figure 5a,b (open-loop control at low frequency of parametric and loading variation), Figure 6, Figure 9a,b and Figure 11a. It is worth emphasizing that the classical PID controller operating in a closed control system proved to be the best when controlling the rotational speed of the driven disk subjected to a variable additional load of low frequency $T_{la}$ (ITAE = 0.0368; see Table 2). On the other hand, the same controller, operating under the same conditions, failed during the variation of the damping parameter $b_{la}$ (ITAE = 1.5168), where a divergent response was obtained as the simulation time passed. The ITAE index has been computed numerically with the use of the $1/3$ Simpson’s rule.

It turns out that the proposed adaptive PID controller with PI compensation of the second stage error dynamics works very well in the presence of both considered types of disturbances, acting on the control object in the low-frequency regime.

Among the FOPID results, the best one is for a closed-loop control system in which the control object is subjected to a low-frequency disturbance of the torque loading the drive (ITAE = $0.0962$). In general, this type of controller does not perform well in the given operating conditions, and the convergence of the rotational speed to the given trajectory of the reference model is satisfactory.

It is important to note that after introducing the high-frequency disturbance characteristics of $b_{la}$ and $T_{la}$, the classical PID controller turned out to be the best.

Paying attention only to the local overshoots of the dynamic time responses, being in relation to the given reference time histories ${\dot{\theta }}_{rl}$, those shown in Figure 6b, Figure 7b, Figure 8a, and Figure 12a prove high efficiency of the tested controllers, of which the proposed adaptive PID with a second-stage PI compensation of error dynamics is found to be qualitatively the best.

6.2. Verifying Robustness of the Control System

In the last part of this work, one of the best solutions will be verified with regard to the robustness of the corresponding control system subject to a new test function— sine modulated triangle wave of periodic variations of two selected parameters of the electric model of the mechatronic drive, i.e., the resistance R and the inductance L:

$$\tilde{R}\left(t\right)=R(1-0.1{\tilde{y}}_{\mathrm{tr}}\left(t\right)),$$

(26)

$$\tilde{L}\left(t\right)=L(1+0.1{\tilde{y}}_{\mathrm{tr}}\left(t\right))$$

(27)

for the sine modulated amplitude of the triangle wave

$$\begin{array}{c}\hfill {\tilde{y}}_{\mathrm{tr}}\left(t\right)=\frac{4a}{f}\left|\left(\left(t-\frac{f}{4}\right)modf\right)-\frac{f}{2}\right|-a,\end{array}$$

(28)

where: $a=1+sin\left({\omega }_{\mathrm{t}r}t\right)$, $f=1/20$ (Hz)—amplitude and frequency, respectively; ${\omega }_{\mathrm{t}r}=2\pi ·5/t_f$ (rad/s)—angular frequency of basic modulation.

Analyzing the time histories presented in Figure 13, we conclude, that the selected configuration of a control system (see case B in Figure 3), including: two parametric uncertainties, variations of loading torque $T_{la}$ and a FOPID regulator is robust to about 10 percent variations about constant values $R=0.9$ ($\mathsf{\Omega }$) and $L=1.4·{10}^{-4}$ (H). At the presence of a maximal pulsation of the two parametric disturbances, there are visible only negligible local fluctuations of the rotational velocity of the load. It has been confirmed also for other solutions presented above that it does not significantly influence the stability and convergence of the tracking control.

7. Conclusions

The evaluated competing control strategies applied to the numerical complex and flexible test drive system taken into consideration in the study work well. One can choose one of them for different challenging scenarios of operation of the motor. The reference time trajectories of rotational speed variations in the form of an inertial rising and falling of step waves (pyramidal shape and alternately introduced low and high input amplitudes) are demanding for the tested induction machine. This made it possible to test and evaluate the behavior of this particular system under different conditions and with a different range of variable control values. The presented techniques of disturbance rejection have been tested on the motor but can be extended in future to BLDC motors, as well. The proposed control strategy could be used to deal with the nonlinear friction torques, which can be approximately deemed as damping disturbances. The adaptive control method has been improved by the application of a new compensating structure canceling error dynamics of the model at the second stage. Finalizing the work, performance and robustness of the control system have been successfully verified.