Conservation Integrals in Nonhomogeneous Materials with Flexoelectricity
Abstract
1. Introduction
- (i)
- The procedure used most widely is Noether theorem. Since Emmy Noether demonstrated the corresponding relation between the conservation integrals and the symmetries in 1918 [24], conservation integrals derived from the Noether theorem have been extensively developed by constructing different symmetries. Usually, according to Noether theorem, J-, M-, and L-integrals can be derived from the corresponding coordinate translation symmetry, scaling symmetry, and coordinate rotation symmetry, respectively. For instance, beginning with these symmetries, Knowles and Sternberg [25], and Fletcher [26], developed conservation laws in elastostatics and linear elastodynamics, respectively. Yang and Batra [27] obtained the conservation laws for linear piezoelectric materials. Other applications of Noether theorem can be found in second gradient electroelasticity [28], flexoelectric solids [29], dissipative electrochemomechanical coupling processes [30,31].
- (ii)
- The Neutral Action method for dissipative systems or nonhomogeneous solids. It is well known that the classical Noether’s theorem is only applicable to the Lagrangian systems. For systems without a Lagrangian, Honein et al. [32] developed a novel methodology called Neutral Action method to obtain the conservation laws directly from the partial differential equations. Then, their method was used to obtain conservation integrals for nonhomogeneous plane problems [33] and nonhomogeneous Bernoulli–Euler beams [34]. Nordbrock and Kienzer [35] applied the Neutral Action method to Schrödinger equation and found a new conservation law.
- (iii)
- The third type is called configurational force method or material force method in this manuscript, which originated from the energy-momentum tensor proposed by Eshelby [36]. The procedure is subjecting the Lagrangian density to the differential operators of grad, div, and curl, respectively [37]. Compared with the previous two methods, this method more easily obtains conservation laws for nonhomogeneous materials. For example, Kirchner [38] derived the energy-momentum tensor for nonhomogeneous anisotropic linearly elastic three-dimensional solids. Then, following this procedure, Lazar and Kirchner [39], Kirchner and Lazar [40], obtained the Eshelby stress tensor and conservation laws for gradient elasticity of nonhomogeneous, incompatible, linear, anisotropic media, and bone growth and remodeling, respectively. Recently, Agiasofitou and Lazar studied the elastic dislocations in elasticity [41] and electro-elastic dislocations in piezoelectric materials [42] through the conservation integrals derived from this method.
- (iv)
2. Basic Equations in Nonhomogeneous Flexoelectric Materials
3. Conservation Integrals Relevant to the Electric Gibbs Function
3.1. Application of Translation and J-Integral
3.2. Application of Dilatation and M-Integral
3.3. Application of Rotation and L-Integral
4. Conservation Integrals Derived from the Internal Energy
- (1)
- J-integral
- (2)
- M-integral
- (3)
- L-integral
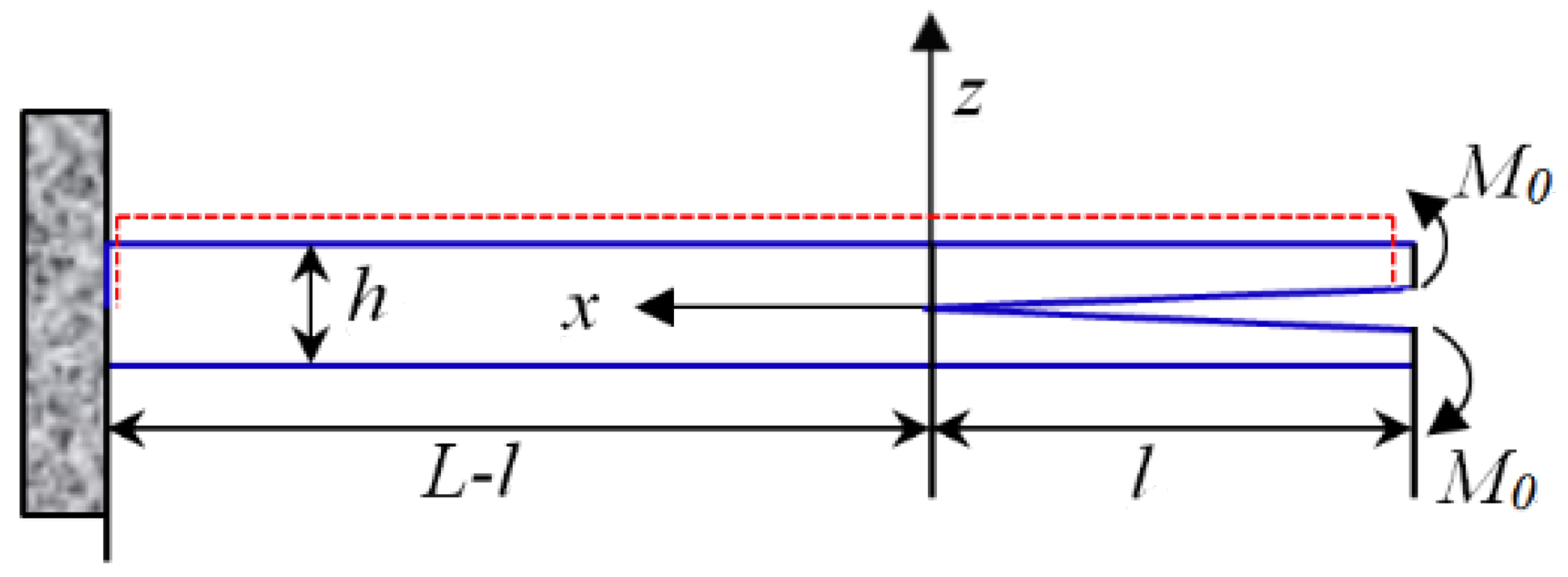
5. A Nonhomogeneous Bernoulli–Euler Beam Problem with Flexoelectricity
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kogan, S. Piezoelectric effect during inhomogeneous deformation and acoustic scattering of carriers in crystals. Sov. Phys. Solid State 1964, 5, 2069–2070. [Google Scholar]
- Askar, A.; Lee, P.; Cakmak, A. Lattice-dynamics approach to the theory of elastic dielectrics with polarization gradient. Phys. Rev. B 1970, 1, 3525. [Google Scholar] [CrossRef]
- Hu, S.; Shen, S. Variational principles and governing equations in nano-dielectrics with the flexoelectric effect. Sci. China Phys. Mech. Astron. 2010, 53, 1497–1504. [Google Scholar] [CrossRef]
- Shen, S.; Hu, S. A theory of flexoelectricity with surface effect for elastic dielectrics. J. Mech. Phys. Solids 2010, 58, 665–677. [Google Scholar] [CrossRef]
- Mindlin, R.D. Polarization gradient in elastic dielectrics. Int. J. Solids Struct. 1968, 4, 637–642. [Google Scholar] [CrossRef]
- Maranganti, R.; Sharma, P. Atomistic determination of flexoelectric properties of crystalline dielectrics. Phys. Rev. B 2009, 80. [Google Scholar] [CrossRef]
- Maranganti, R.; Sharma, P. Length scales at which classical elasticity breaks down for various materials. Phys. Rev. Lett. 2007, 98. [Google Scholar] [CrossRef]
- Sharma, N.D.; Maranganti, R.; Sharma, P. On the possibility of piezoelectric nanocomposites without using piezoelectric materials. J. Mech. Phys. Solids 2007, 55, 2328–2350. [Google Scholar] [CrossRef]
- Ma, W.; Cross, L.E. Large flexoelectric polarization in ceramic lead magnesium niobate. Appl. Phys. Lett. 2001, 79, 4420–4422. [Google Scholar] [CrossRef]
- Lu, J.; Lv, J.; Liang, X.; Xu, M.; Shen, S. Improved approach to measure the direct flexoelectric coefficient of bulk polyvinylidene fluoride. J. Appl. Phys. 2016, 119, 094104. [Google Scholar] [CrossRef]
- Ma, W.H.; Cross, L.E. Observation of the flexoelectric effect in relaxor Pb(Mg1/3Nb2/3)O3 ceramics. Appl. Phys. Lett. 2001, 78, 2920–2921. [Google Scholar] [CrossRef]
- Ma, W.H.; Cross, L.E. Strain-gradient-induced electric polarization in lead zirconate titanate ceramics. Appl. Phys. Lett. 2003, 82, 3293–3295. [Google Scholar] [CrossRef]
- Yan, X.; Huang, W.; Kwon, S.R.; Yang, S.; Jiang, X.; Yuan, F.-G. A sensor for the direct measurement of curvature based on flexoelectricity. Smart Mater. Struct. 2013, 22, 085016. [Google Scholar] [CrossRef]
- Huang, W.; Kwon, S.-R.; Zhang, S.; Yuan, F.-G.; Jiang, X. A trapezoidal flexoelectric accelerometer. J. Intell. Mater. Syst. Struct. 2014, 25, 271–277. [Google Scholar] [CrossRef]
- Hu, S.; Li, H.; Tzou, H. Flexoelectric responses of circular rings. J. Vib. Acoust. 2013, 135, 021003. [Google Scholar] [CrossRef]
- Tagantsev, A.K.; Yurkov, A.S. Flexoelectric effect in finite samples. J. Appl. Phys. 2012, 112, 044103. [Google Scholar] [CrossRef]
- Tagantsev, A.K. Piezoelectricity and flexoelectricity in crysttalline dielectrics. Phys. Rev. B 1986, 34, 5883–5889. [Google Scholar] [CrossRef]
- Tagantsev, A.K. Theory of flexoelectric effects in crystals. Zh. Eksp. I Teoretich. Fiz. 1985, 88, 2108–2122. [Google Scholar]
- Hu, S.L.; Shen, S.P. Electric field gradient theory with surface effect for nano-dielectrics. CMC Comput. Mat. Contin. 2009, 13, 63–87. [Google Scholar]
- Abdollahi, A.; Peco, C.; Millan, D.; Arroyo, M.; Catalan, G.; Arias, I. Fracture toughening and toughness asymmetry induced by flexoelectricity. Phys. Rev. B 2015, 92, 094101. [Google Scholar] [CrossRef]
- Fan, T.Y. Exact-solutions of semi-infinite crack in a strip. Chinese Phys. Lett. 1990, 7, 402–405. [Google Scholar]
- Sosa, H. Plane problems in piezoelectric media with defects. Int. J. Solids Struct. 1991, 28, 491–505. [Google Scholar] [CrossRef]
- Grentzelou, C.G.; Georgiadis, H.G. Balance laws and energy release rates for cracks in dipolar gradient elasticity. Int. J. Solids Struct. 2008, 45, 551–567. [Google Scholar] [CrossRef]
- Noether, E. Invariant variation problems. Math. Phys. Kl. 1918, 1, 235–257. [Google Scholar] [CrossRef]
- Knowles, J.K.; Sternberg, E. On a Class of Conservation Laws in Linearized and Finite Elastostatics; California Institute of Technology, Pasadena DIV of Engineering and Applied Science: Pasadena, CA, USA, 1971. [Google Scholar]
- Fletcher, D.C. Conservation laws in linear elastodynamics. Arch. Ration. Mech. An. 1976, 60, 329–353. [Google Scholar] [CrossRef]
- Yang, J.S.; Batra, R.C. Conservation-laws in linear piezoelectricity. Eng. Fract. Mech. 1995, 51, 1041–1047. [Google Scholar] [CrossRef]
- Kalpakides, V.K.; Agiasofitou, A.K. On material equations in second gradient electroelasticity. J. Elasticity 2002, 67, 205–227. [Google Scholar] [CrossRef]
- Tian, X.; Li, Q.; Deng, Q. The J-integral in flexoelectric solids. Int. J. Fract. 2019, 215, 67–76. [Google Scholar] [CrossRef]
- Yu, P.; Wang, H.; Chen, J.; Shen, S. Conservation laws and path-independent integrals in mechanical-diffusion-electrochemical reaction coupling system. J. Mech. Phys. Solids 2017, 104, 57–70. [Google Scholar] [CrossRef]
- Yu, P.F.; Chen, J.Y.; Wang, H.L.; Liang, X.; Shen, S.P. Path-independent integrals in electrochemomechanical systems with flexoelectricity. Int. J. Solids Struct. 2018, 147, 20–28. [Google Scholar] [CrossRef]
- Honein, T.; Chien, N.; Herrmann, G. On conservation-laws for dissipative systems. Phys. Lett. A 1991, 155, 223–224. [Google Scholar] [CrossRef]
- Honein, T.; Herrmann, G. Conservation laws in nonhomogeneous plane elastostatics. J. Mech. Phys. Solids 1997, 45, 789–805. [Google Scholar] [CrossRef]
- Chien, N.; Honein, T.; Herrmann, G. Conservation-laws for nonhomogeneous Bernoulli-Euler beams. Int. J. Solids Struct. 1993, 30, 3321–3335. [Google Scholar] [CrossRef]
- Nordbrock, U.; Kienzler, R. Conservation laws derived by the neutral-action method. Eur. Phys. J. D 2007, 44, 407–410. [Google Scholar] [CrossRef]
- Eshelby, J. The elastic energy-momentum tensor. J. Elast. 1975, 5, 321–335. [Google Scholar] [CrossRef]
- Kienzler, R.; Herrmann, G. On conservation laws in elastodynamics. Int. J. Solids Struct. 2004, 41, 3595–3606. [Google Scholar] [CrossRef]
- Kirchner, H. The force on an elastic singularity in a non-homogeneous medium. J. Mech. Phys. Solids 1999, 47, 993–998. [Google Scholar] [CrossRef]
- Lazar, M.; Kirchner, H.O.K. The Eshelby stress tensor, angular momentum tensor and dilatation flux in gradient elasticity. Int. J. Solids Struct. 2007, 44, 2477–2486. [Google Scholar] [CrossRef]
- Kirchner, H.O.K.; Lazar, M. The thermodynamic driving force for bone growth and remodelling: A hypothesis. J. R. Soc. Interface 2008, 5, 183–193. [Google Scholar] [CrossRef]
- Agiasofitou, E.; Lazar, M. Micromechanics of dislocations in solids: J-, M-, and L-integrals and their fundamental relation. Int. J. Eng. Sci. 2017, 114, 16–40. [Google Scholar] [CrossRef]
- Agiasofitou, E.; Lazar, M. Electro-elastic dislocations in piezoelectric materials. Philos. Mag. 2020, 100, 1059–1101. [Google Scholar] [CrossRef]
- Bueckner, H.F. Weight-functions and fundamental fields for the penny-shaped and the half-plane crack in 3-space. Int. J. Solids Struct. 1987, 23, 57–93. [Google Scholar] [CrossRef]
- Bueckner, H.F. Field singularities and related integral representations. In Methods of Analysis and Solutions of Crack Problems; Springer: New York, NY, USA, 1973; pp. 239–314. [Google Scholar]
- Yu, P.; Hu, S.; Shen, S. Electrochemomechanics with flexoelectricity and modelling of electrochemical strain microscopy in mixed ionic-electronic conductors. J. Appl. Phys. 2016, 120, 065102. [Google Scholar] [CrossRef]
- Li, X. Dual conservation-laws in elastostatics. Eng. Fract. Mech. 1988, 29, 233–241. [Google Scholar] [CrossRef]
- Cheperanov, G. Crack propagation in continuous media. J. Appl. Math. Mech. Transl. 1967, 31, 476–488. [Google Scholar]
- Yang, J. An Introduction to The Theory of Piezoelectrocity; Springer: New York, NY, USA, 2005. [Google Scholar]
- Maugin, G.A.; Epstein, M. The electroelastic energy momentum tensor. Proc. R. Soc. London Ser. A Math. Phys. Eng. Sci. 1991, 433, 299–312. [Google Scholar] [CrossRef]
- Dascalu, C.; Maugin, G.A. Energy-release rates and path-independent integrals in electroelastic crack-propagation. Int. J. Eng. Sci. 1994, 32, 755–765. [Google Scholar] [CrossRef]
- Reinhold Kienzler, G.H. Mechanics in Material Space: With Applications to Defect and Fracture Mechanics; Springer: Berlin/Heidelberg, Germany, 2000; p. 298. [Google Scholar]
- Li, Q.; Hu, Y.; Chen, Y. On the physical interpretation of the M-integral in nonlinear elastic defect mechanics. Int. J. Damage Mech. 2013, 22, 602–613. [Google Scholar]
- Wang, X.M.; Shen, Y.P. The conservation laws and path-independent integrals with an application for linear electro-magneto-elastic media. Int. J. Solids Struct. 1996, 33, 865–878. [Google Scholar] [CrossRef]
- Park, S.K.; Gao, X.L. Bernoulli-Euler beam model based on a modified couple stress theory. J. Micromech. Microeng. 2006, 16, 2355–2359. [Google Scholar] [CrossRef]
- Liang, X.; Hu, S.; Shen, S. Bernoulli-Euler dielectric beam model based on strain-gradient effect. J. Appl. Mech. 2013, 80, 044502. [Google Scholar] [CrossRef]
- Liang, X.; Hu, S.; Shen, S. A new Bernoulli-Euler beam model based on a simplified strain gradient elasticity theory and its applications. Compos. Struct. 2014, 111, 317–323. [Google Scholar] [CrossRef]
- Liang, X.; Hu, S.; Shen, S. Size-dependent buckling and vibration behaviors of piezoelectric nanostructures due to flexoelectricity. Smart Mater. Struct. 2015, 24, 105012. [Google Scholar] [CrossRef]
- Papargyri-Beskou, S.; Tsepoura, K.G.; Polyzos, D.; Beskos, D.E. Bending and stability analysis of gradient elastic beams. Int. J. Solids Struct. 2003, 40, 385–400. [Google Scholar] [CrossRef]
- Lazopoulos, K.A.; Lazopoulos, A.K. Bending and buckling of thin strain gradient elastic beams. Eur. J. Mech. A Solid 2010, 29, 837–843. [Google Scholar] [CrossRef]
- Shi, W.C.; Kuang, Z.B. Conservation laws in non-homogeneous electro-magneto-elastic materials. Eur. J. Mech. A Solid 2003, 22, 217–230. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, P.; Leng, W.; Suo, Y. Conservation Integrals in Nonhomogeneous Materials with Flexoelectricity. Appl. Sci. 2021, 11, 681. https://doi.org/10.3390/app11020681
Yu P, Leng W, Suo Y. Conservation Integrals in Nonhomogeneous Materials with Flexoelectricity. Applied Sciences. 2021; 11(2):681. https://doi.org/10.3390/app11020681
Chicago/Turabian StyleYu, Pengfei, Weifeng Leng, and Yaohong Suo. 2021. "Conservation Integrals in Nonhomogeneous Materials with Flexoelectricity" Applied Sciences 11, no. 2: 681. https://doi.org/10.3390/app11020681
APA StyleYu, P., Leng, W., & Suo, Y. (2021). Conservation Integrals in Nonhomogeneous Materials with Flexoelectricity. Applied Sciences, 11(2), 681. https://doi.org/10.3390/app11020681




