Adaptive Observer-Based Grid-Synchronization and Sequence Extraction Techniques for Renewable Energy Systems: A Comparative Analysis †
Abstract
1. Introduction
2. Problem Formulation
3. Overview of the Selected Techniques
3.1. Global Adaptive Observer (GAO)
3.1.1. Development of Phase Voltage Dynamical Model
3.1.2. Observer Design
3.2. Gain Normalized Adaptive Observer
3.3. SOGI-Type Adaptive Observer
3.3.1. Quadrature Signal-Based Dynamic Model Development
3.3.2. Observer Design
4. Results and Discussions
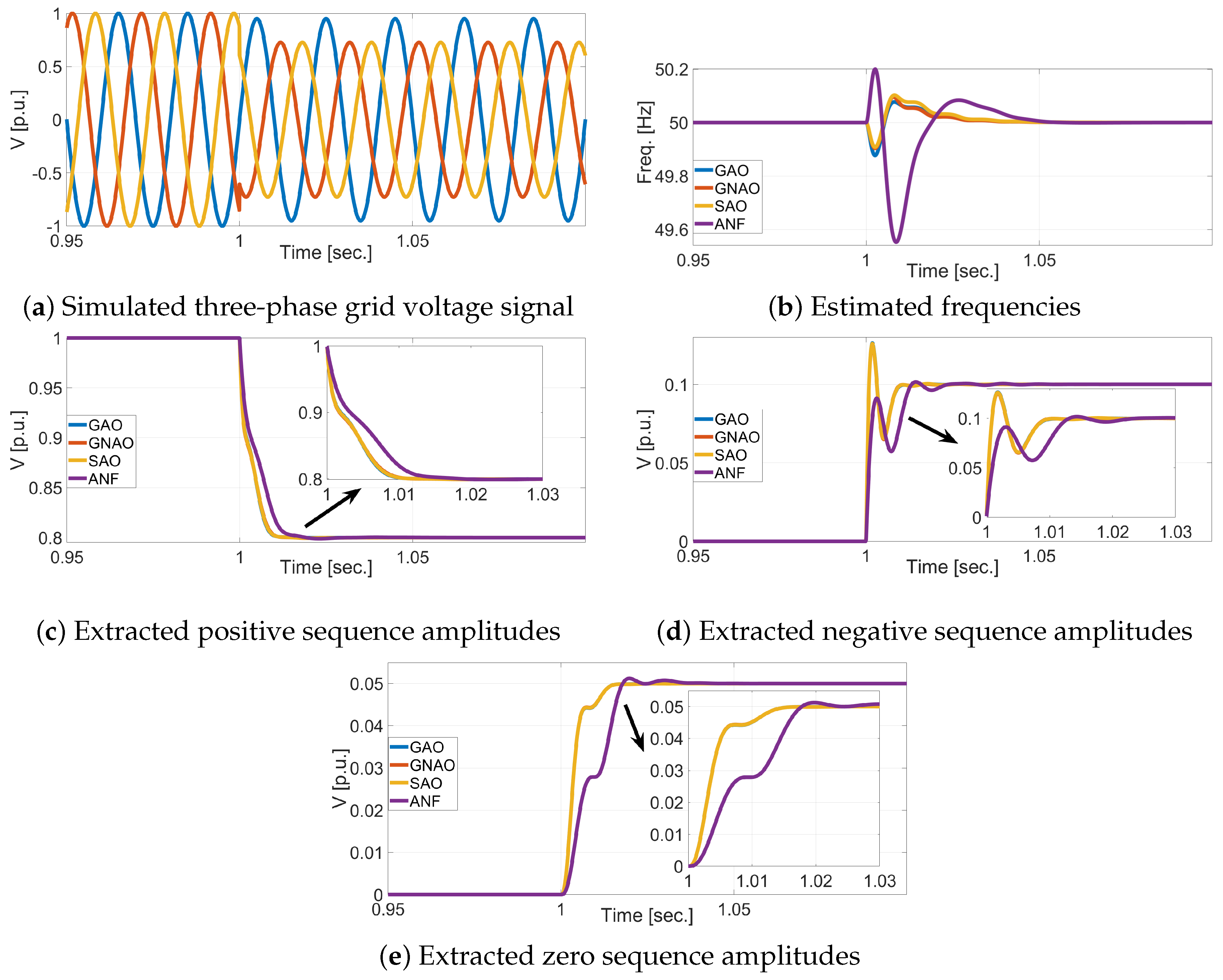
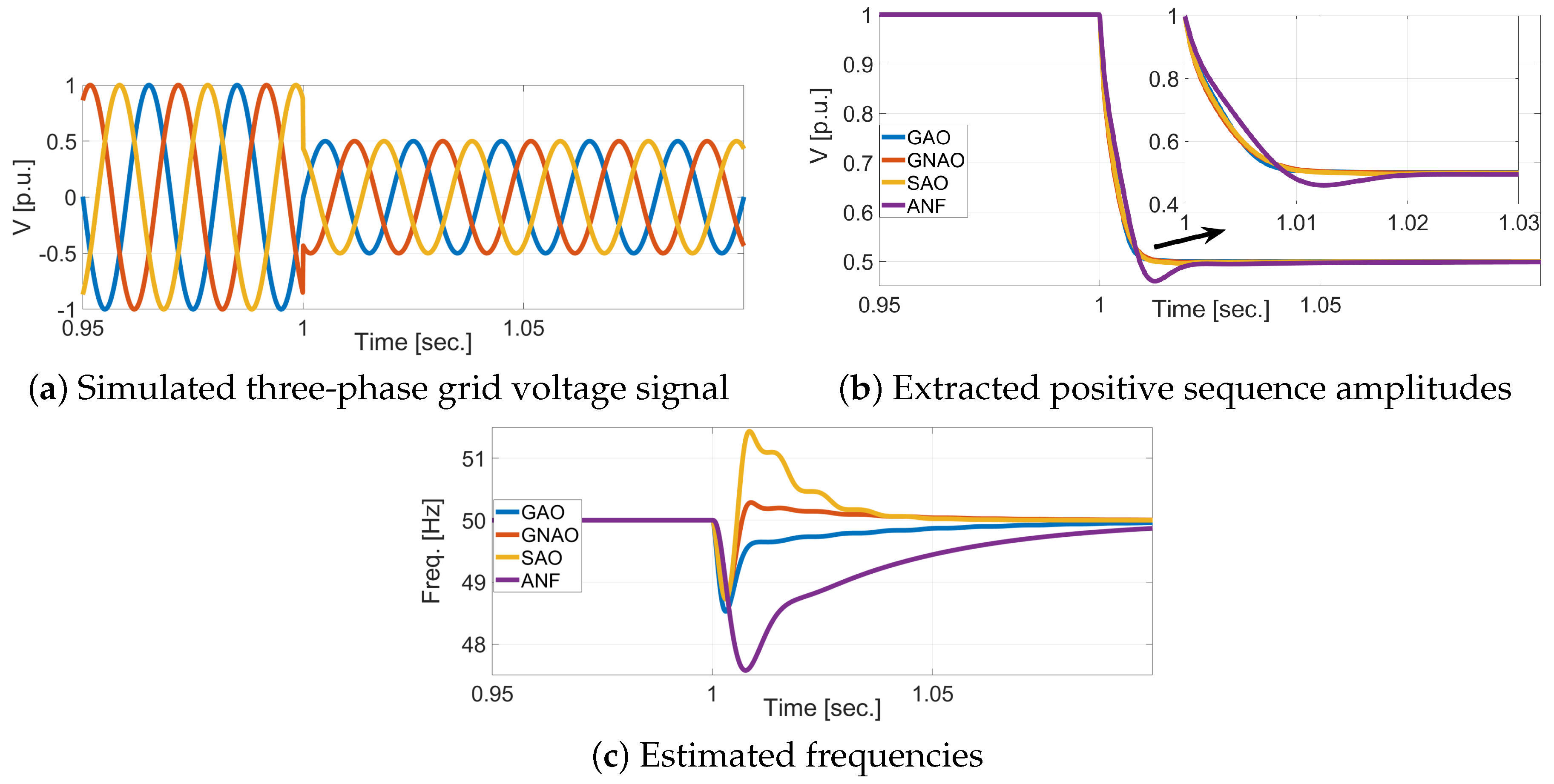
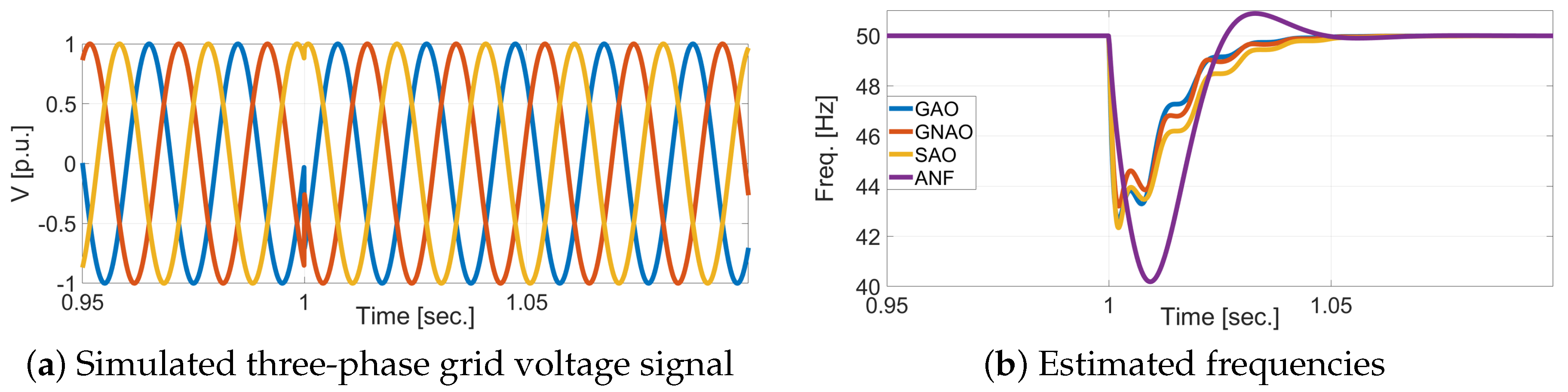
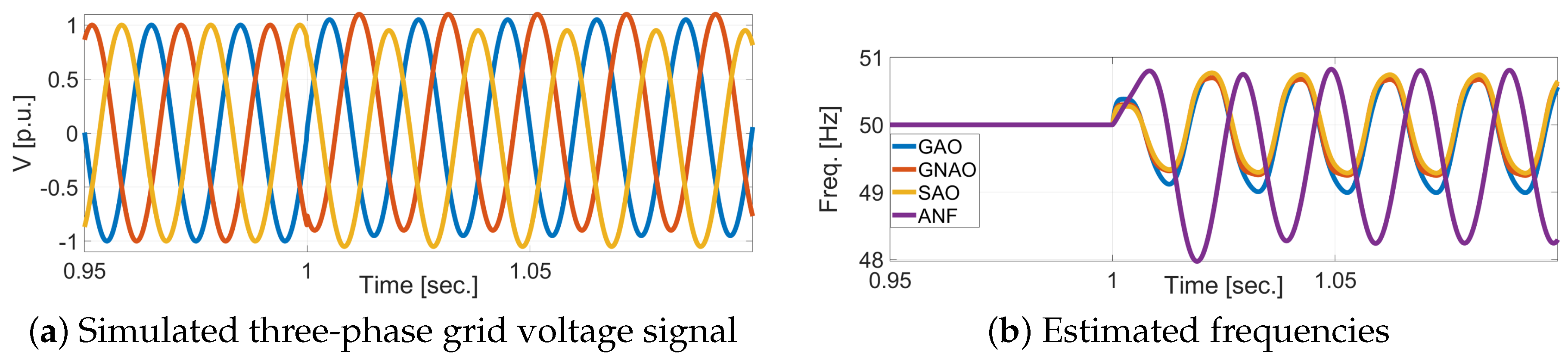
4.1. Simulation Results
- Test-I: Balanced to unbalanced grid,
- Test-II: Voltage sag,
- Test-III: Phase step change, and
- Test-IV: DC offset.
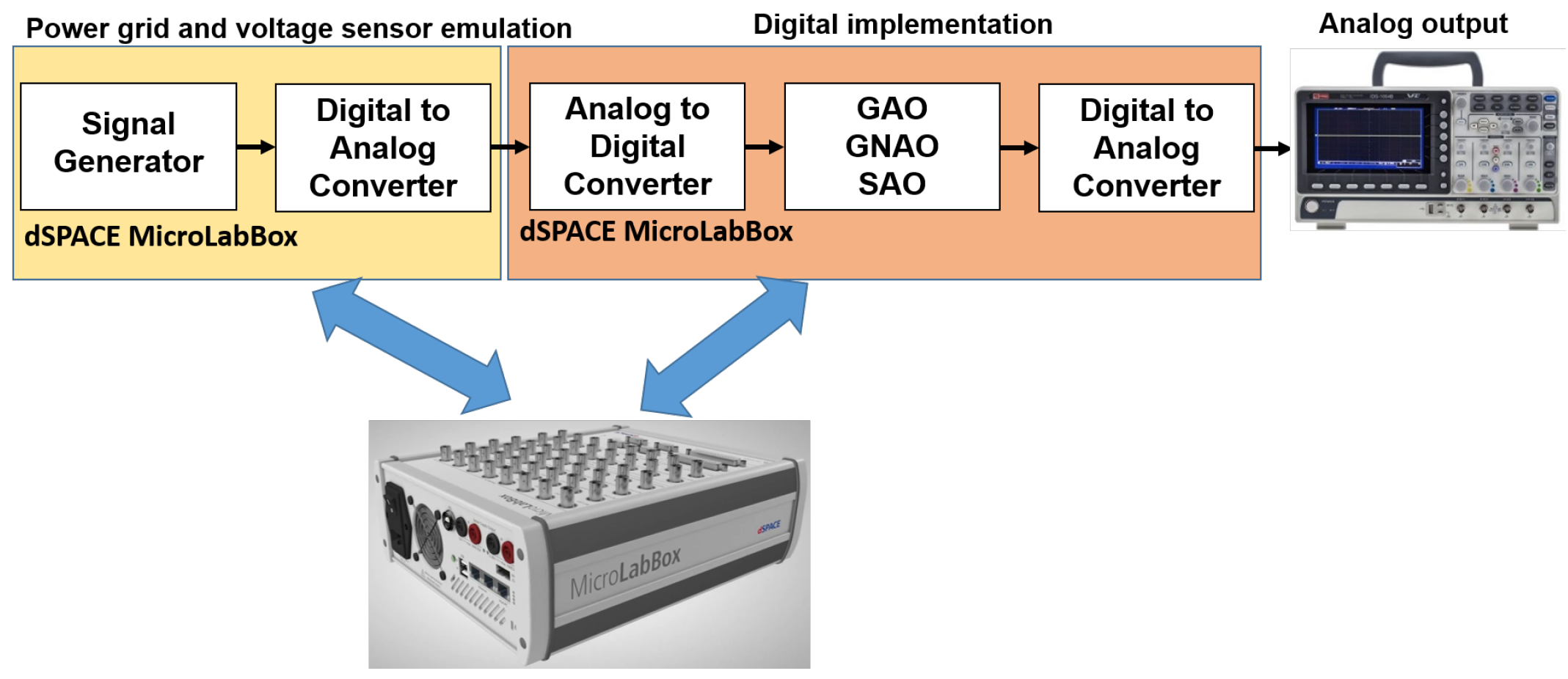
4.2. Experimental Results
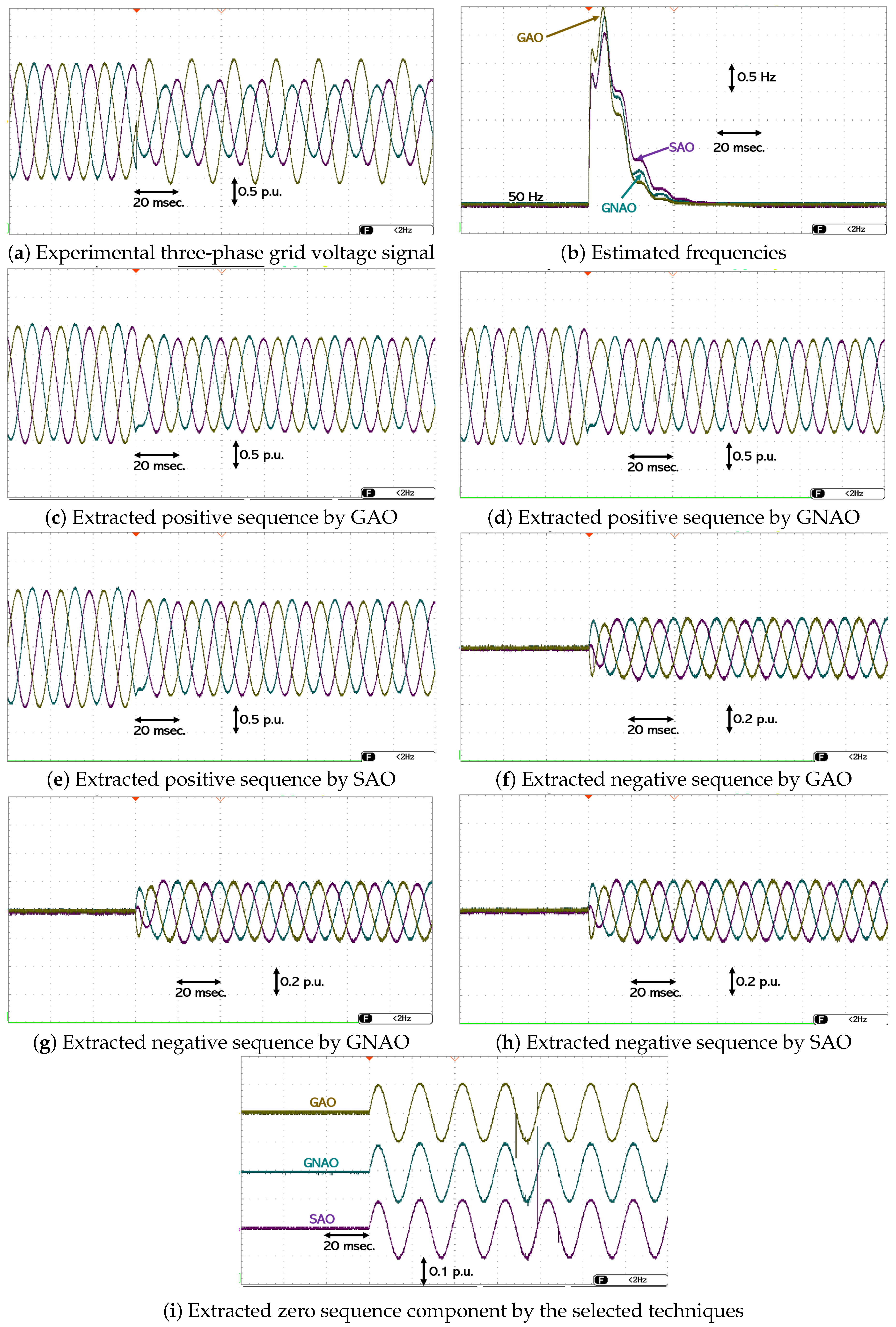
4.2.1. Unbalanced Grid
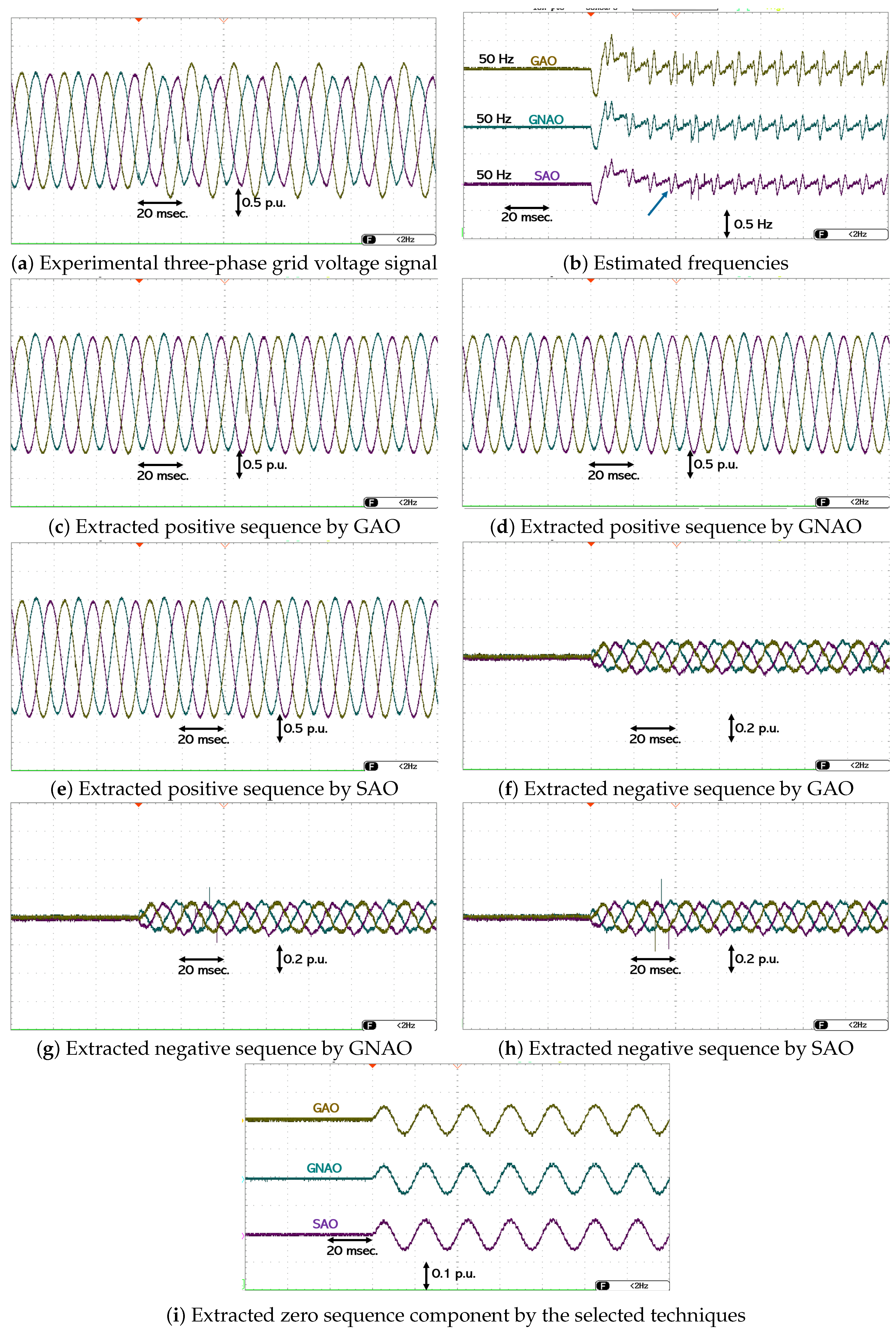
4.2.2. Unbalanced and Distorted Grid
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ouchen, S.; Betka, A.; Abdeddaim, S.; Menadi, A. Fuzzy-predictive direct power control implementation of a grid connected photovoltaic system, associated with an active power filter. Energy Convers. Manag. 2016, 122, 515–525. [Google Scholar] [CrossRef]
- Safa, A.; Berkouk, E.M.; Messlem, Y.; Gouichiche, A. A robust control algorithm for a multifunctional grid tied inverter to enhance the power quality of a microgrid under unbalanced conditions. Int. J. Electr. Power Energy Syst. 2018, 100, 253–264. [Google Scholar] [CrossRef]
- Ngo, T.; Biricik, S.; Basu, M. A Self-tuning Grid Synchronization Method for Active Power Filters. Electr. Power Components Syst. 2016, 44, 1947–1957. [Google Scholar] [CrossRef]
- Biricik, S.; Komurcugil, H.; Tuyen, N.D.; Basu, M. Protection of Sensitive Loads Using Sliding Mode Controlled Three-Phase DVR with Adaptive Notch Filter. IEEE Trans. Ind. Electron. 2018, 66, 5465–5475. [Google Scholar] [CrossRef]
- Biricik, S.; Redif, S.; Özerdem, Ö.C.; Khadem, S.K.; Basu, M. Real-time control of shunt active power filter under distorted grid voltage and unbalanced load condition using self-tuning filter. IET Power Electron. 2014, 7, 1895–1905. [Google Scholar] [CrossRef]
- Biricik, S.; Komurcugil, H.; Ahmed, H.; Babaei, E. Super Twisting Sliding Mode Control of DVR with Frequency-Adaptive Brockett Oscillator. IEEE Trans. Ind. Electron. 2020. [Google Scholar] [CrossRef]
- Biricik, S.; Komurcugil, H. Optimized sliding mode control to maximize existence region for single-phase dynamic voltage restorers. IEEE Trans. Ind. Inform. 2016, 12, 1486–1497. [Google Scholar] [CrossRef]
- Merai, M.; Naouar, M.W.; Slama-Belkhodja, I.; Monmasson, E. An adaptive PI controller design for DC-link voltage control of single-phase grid-connected converters. IEEE Trans. Ind. Electron. 2019, 66, 6241–6249. [Google Scholar] [CrossRef]
- Kukrer, O.; Bayhan, S.; Komurcugil, H. Model-Based Current Control Strategy with Virtual Time Constant for Improved Dynamic Response of Three-Phase Grid-Connected VSI. IEEE Trans. Ind. Electron. 2019, 66, 4156–4165. [Google Scholar] [CrossRef]
- Altin, N.; Ozdemir, S.; Komurcugil, H.; Sefa, I. Sliding-mode control in natural frame with reduced number of sensors for three-phase grid-tied LCL-interfaced inverters. IEEE Trans. Ind. Electron. 2018, 66, 2903–2913. [Google Scholar] [CrossRef]
- Rahman, M.M.; Hossain, S.; Rezwan, S. Dispatched Power and Unbalanced Operation of a Three-Phase NPC Based Double-Stage Grid Connected PV System. In Proceedings of the 2019 4th International Conference on Electrical Information and Communication Technology (EICT), Khulna, Bangladesh, 20–22 December 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–6. [Google Scholar]
- Chatterjee, A.; Mohanty, K.B. Current control strategies for single phase grid integrated inverters for photovoltaic applications—A review. Renew. Sustain. Energy Rev. 2018, 92, 554–569. [Google Scholar] [CrossRef]
- Guerrero-Rodríguez, N.; Rey-Boué, A.B.; Bueno, E.; Ortiz, O.; Reyes-Archundia, E. Synchronization algorithms for grid-connected renewable systems: Overview, tests and comparative analysis. Renew. Sustain. Energy Rev. 2017, 75, 629–643. [Google Scholar] [CrossRef]
- Jaalam, N.; Rahim, N.; Bakar, A.; Tan, C.; Haidar, A.M. A comprehensive review of synchronization methods for grid-connected converters of renewable energy source. Renew. Sustain. Energy Rev. 2016, 59, 1471–1481. [Google Scholar] [CrossRef]
- Jain, B.; Jain, S.; Nema, R. Control strategies of grid interfaced wind energy conversion system: An overview. Renew. Sustain. Energy Rev. 2015, 47, 983–996. [Google Scholar] [CrossRef]
- Amirat, Y.; Oubrahim, Z.; Ahmed, H.; Benbouzid, M.; Wang, T. Phasor Estimation for Grid Power Monitoring: Least Square vs. Linear Kalman Filter. Energies 2020, 13, 2456. [Google Scholar] [CrossRef]
- Ahmed, H.; Biricik, S.; Benbouzid, M. Linear Kalman Filter-Based Grid Synchronization Technique: An Alternative Implementation. IEEE Trans. Ind. Inform. 2020. [Google Scholar] [CrossRef]
- Choqueuse, V.; Belouchrani, A.; Auger, F.; Benbouzid, M. Frequency and phasor estimations in three-phase systems: Maximum likelihood algorithms and theoretical performance. IEEE Trans. Smart Grid 2018, 10, 3248–3258. [Google Scholar] [CrossRef]
- Mathuria, K.; Hussain, I.; Singh, B.; Kumar, N. A quadrature oscillator-based DT for accurate estimation of fundamental load current for PV system in distribution network. IEEE Trans. Ind. Inform. 2018, 15, 3324–3333. [Google Scholar] [CrossRef]
- Ahmed, H.; Biricik, S.; Benbouzid, M. Enhanced Frequency Adaptive Demodulation Technique For Grid-Connected Converters. IEEE Trans. Ind. Electron. 2020. [Google Scholar] [CrossRef]
- Chedjara, Z.; Massoum, A.; Massoum, S.; Wira, P.; Safa, A.; Gouichiche, A. A novel robust PLL algorithm applied to the control of a shunt active power filter using a self tuning filter concept. In Proceedings of the 2018 IEEE International Conference on Industrial Technology (ICIT); IEEE: Piscataway, NJ, USA, 2018; pp. 1124–1131. [Google Scholar]
- Bechouche, A.; Sediki, H.; Abdeslam, D.O.; Haddad, S. An adaptive neural PLL for grid synchronization. In Proceedings of the IECON 2012-38th Annual Conference on IEEE Industrial Electronics Society; IEEE: Piscataway, NJ, USA, 2012; pp. 4451–4456. [Google Scholar]
- Bobrowska-Rafal, M.; Rafal, K.; Jasinski, M.; Kazmierkowski, M. Grid synchronization and symmetrical components extraction with PLL algorithm for grid connected power electronic converters—A review. Bull. Pol. Acad. Sci. Tech. Sci. 2011, 59, 485–497. [Google Scholar] [CrossRef]
- Meral, M.E.; Çelik, D. Benchmarking simulation and theory of various PLLs produce orthogonal signals under abnormal electric grid conditions. Electr. Eng. 2018, 100, 1805–1817. [Google Scholar] [CrossRef]
- Meral, M.E.; Çelík, D. A comprehensive survey on control strategies of distributed generation power systems under normal and abnormal conditions. Annu. Rev. Control 2019, 47, 112–132. [Google Scholar] [CrossRef]
- Meral, M.E.; Celik, D. DSOGI-PLL based power control method to mitigate control errors under disturbances of grid connected hybrid renewable power systems. Adv. Electr. Electron. Eng. 2018, 16, 81–91. [Google Scholar] [CrossRef]
- Ahmed, H.; Pay, M.L.; Benbouzid, M.; Amirat, Y.; Elbouchikhi, E. Gain normalized adaptive observer for three-phase system. Int. J. Electr. Power Energy Syst. 2020, 118, 105821. [Google Scholar] [CrossRef]
- Shah, P.; Singh, B. Adaptive Observer Based Control for Roof-top Solar PV System. IEEE Trans. Power Electron. 2020, 35, 9402–9415. [Google Scholar] [CrossRef]
- Ahmed, H.; Pay, M.L.; Benbouzid, M.; Amirat, Y.; Elbouchikhi, E. Hybrid estimator-based harmonic robust grid synchronization technique. Electr. Power Syst. Res. 2019, 177, 106013. [Google Scholar] [CrossRef]
- Chishti, F.; Murshid, S.; Singh, B. Weak Grid Intertie WEGS With Hybrid Generalized Integrator for Power Quality Improvement. IEEE Trans. Ind. Electron. 2020, 67, 1113–1123. [Google Scholar] [CrossRef]
- Bendib, A.; Chouder, A.; Kara, K.; Kherbachi, A.; Barkat, S.; Issa, W. New modeling approach of secondary control layer for autonomous single-phase microgrids. J. Frankl. Inst. 2019, 356, 6842–6874. [Google Scholar] [CrossRef]
- Kherbachi, A.; Chouder, A.; Bendib, A.; Kara, K.; Barkat, S. Enhanced structure of second-order generalized integrator frequency-locked loop suitable for DC-offset rejection in single-phase systems. Electr. Power Syst. Res. 2019, 170, 348–357. [Google Scholar] [CrossRef]
- Safa, A.; Berkouk, E.M.; Messlem, Y.; Chedjara, Z.; Gouichiche, A. A Pseudo Open Loop Synchronization technique for heavily distorted grid voltage. Electr. Power Syst. Res. 2018, 158, 136–146. [Google Scholar] [CrossRef]
- Terriche, Y.; Guerrero, J.M.; Vasquez, J.C. Performance improvement of shunt active power filter based on non-linear least-square approach. Electr. Power Syst. Res. 2018, 160, 44–55. [Google Scholar] [CrossRef]
- Hackl, C.M.; Landerer, M. A Unified Method for Online Detection of Phase Variables and Symmetrical Components of Unbalanced Three-Phase Systems with Harmonic Distortion. Energies 2019, 12, 3243. [Google Scholar] [CrossRef]
- Ahmed, H.; Benbouzid, M. On the Enhancement of Generalized Integrator-based Adaptive Filter Dynamic Tuning Range. IEEE Trans. Instrum. Meas. 2020, 69, 7449–7457. [Google Scholar] [CrossRef]
- Chilipi, R.S.R.; Al Sayari, N.; Al Hosani, K.H.; Beig, A.R. Adaptive Notch Filter-Based Multipurpose Control Scheme for Grid-Interfaced Three-Phase Four-Wire DG Inverter. IEEE Trans. Ind. Appl. 2017, 53, 4015–4027. [Google Scholar] [CrossRef]
- Arya, S.R.; Maurya, R.; Naidu, T.A. Amplitude adaptive notch filter with optimized PI gains for mitigation of voltage based power quality problems. CPSS Trans. Power Electron. Appl. 2018, 3, 313–323. [Google Scholar] [CrossRef]
- Yazdani, D.; Mojiri, M.; Bakhshai, A.; Joos, G. A fast and accurate synchronization technique for extraction of symmetrical components. IEEE Trans. Power Electron. 2009, 24, 674–684. [Google Scholar] [CrossRef]
- Ahmed, H.; Benbouzid, M.; Ahsan, M.; Albarbar, A.; Shahjalal, M. Frequency Adaptive Parameter Estimation of Unbalanced and Distorted Power Grid. IEEE Access 2020, 8, 8512–8519. [Google Scholar] [CrossRef]
- Khalil, H.K. Nonlinear Control; Pearson Education North Asia Ltd.: Hong Kong, 2014. [Google Scholar]
| Characteristics | GAO | GNAO | SAO |
|---|---|---|---|
| Dynamic Performance | Very Fast | Very Fast | Very Fast |
| Voltage Sag Sensitivity | High | Low | Low |
| Harmonic Disturbance | Good | Very Good | Very Good |
| DC Offset Rejection | Good | Very Good | Very Good |
| Computational Complexity | Medium | High | Medium |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, H.; Benbouzid, M. Adaptive Observer-Based Grid-Synchronization and Sequence Extraction Techniques for Renewable Energy Systems: A Comparative Analysis. Appl. Sci. 2021, 11, 653. https://doi.org/10.3390/app11020653
Ahmed H, Benbouzid M. Adaptive Observer-Based Grid-Synchronization and Sequence Extraction Techniques for Renewable Energy Systems: A Comparative Analysis. Applied Sciences. 2021; 11(2):653. https://doi.org/10.3390/app11020653
Chicago/Turabian StyleAhmed, Hafiz, and Mohamed Benbouzid. 2021. "Adaptive Observer-Based Grid-Synchronization and Sequence Extraction Techniques for Renewable Energy Systems: A Comparative Analysis" Applied Sciences 11, no. 2: 653. https://doi.org/10.3390/app11020653
APA StyleAhmed, H., & Benbouzid, M. (2021). Adaptive Observer-Based Grid-Synchronization and Sequence Extraction Techniques for Renewable Energy Systems: A Comparative Analysis. Applied Sciences, 11(2), 653. https://doi.org/10.3390/app11020653






