1. Introduction
Cryptographic functions [
1,
2] are an integral part of cryptographic algorithms. The applications of these functions are observed in the round functions of the bock cipher, key generation algorithms, stream ciphers, message digest algorithms and many more [
1]. The cryptographic functions must possess some of the important characteristics such as non linearity, symmetricity, resiliency, propagation criterion, immune to correlation etc. Moreover, the introduction to the pseudo random number generator (PRNG) helps to provide randomness in the cipher outputs to increase confusion-diffusion property in the algorithm. Such randomness of the function provides robustness to withstand with correlation attacks [
3]. However, PRNGs have also faced different attacks in recent times [
4]. Therefore, there is an urge of generating a new random function which can provide the robustness against the attacks of evaluating differential, linear or non-linear cryptanalysis process for understanding the plaintext bits or key bits. In this paper, an analysis is executed on the properties of Symmetric Random Function Generator(SRFG).
Symmetric Boolean functions are very important for cryptography [
5]. Their outputs posses sepcial characteristics in cryptographic developments. Hamming distances of these outputs make use of proper correlation features as required. As the desirable properties of a cryptographic function is in objective, we have evaluated the propagation characteristics of the differentiations of SRFG outputs. Moreover, we have also analysed the immunity strength of SRFG: correlation immunity and algebraic immunity.
The organization of the paper is coherences in several sections. Introductory problem statement has been already shown in
Section 1. In the upcoming sections,
Section 2 reviews the works in the direction of cryptographic functional properties.
Section 3 shows the mathematical model of SRFG.
Section 4 describes explains the propagation criterion of SRFG.
Section 5 discusses about immunity of the functions.
Section 6 analyses the results, shows the statistical interpretaion and validation and,
Section 7 provides a logical conclusion.
2. Related Work
The algorithms in cryptography uses various types of cryptographic functions and transformations; these possess different factors which are important for designing such functions [
6]. For example, algebraic, random and heuristic contsructions of functions are important in this case. In paper [
7], the authors have discussed the propagation properties of Boolean functions. New properties are also identified which have the high strict avalanche criterion. The research work in [
8] analyses the inverse permutation on the field component functions. The weights of derivatives of the component functions also use Kloosterman sums. The authors in the paper [
9] show the property of aperiodic autocorrelation in Boolean function aspect and define the Aperiodic Propagation Criteria (APC). The work also shows the relation between aperiodic autocorrelation and the first derivative of the function.
The concept of correlation immunity in Boolean functions was introduced by Siegenthaler [
10]. Furthermore, this feature of Boolean functions has been considered to be an important characteristics for strong cryptographic algorithms and has been researched with concern as shown in [
11,
12,
13,
14]. Some of the contemporary research has been done to provide immunity to the functions both as correlation aspect and algebraic aspect. High algebraic immunity is a required factor for cryptographic algorithms to prevent algebraic attacks. Algebraic immunity must have a lower bound failing which functions must not be used in cryptography. Such a lower bound in evaluated in [
15]. The relation of algebraic immunity and extended algebraic immunity is researched in [
16,
17]. The bent functions are also in use for construction of a class of functions in infinity [
18]. The authors have considered only odd number of variables. Decomposition of the first-order correlation-immune Boolean functions is researched significantly [
19]. Following this, an enumerative encoded Boolean function is designed [
20]. In the paper [
21], optimal algebraic immunity construction strategy has been shown using vector spaces and m-sequences. Boolean functions can be presented into two hybrid classes [
22]. The magnitude of the inter-class algebraic immunity is maximum. It also prohibits resistance against algebraic attacks with high non-linearity. 1-resilient functions are also in existence. Algebraic immunity on balanced functions has been shown in the papers [
23,
24]. Vector valued functions over finite field has also experimented for maximum algebraic immunity in [
25].
Some of the recent developments in field of random and pseudo-random number generators have been reviewed. For example, the random number generation in [
26,
27] show the applications in BIST and IoT Applications. The later one is based on chaos and is validated by statistical tests. A pseudo random generator for cryptographic applications has been shown in [
28]. Several studies were carried out in this domain for validation of random numbers and generation of random numbers as shown in [
29,
30,
31,
32,
33]. Such studies show that random numbers are in real need for various applications and their design factors are also very important.
Symmetric Random Function Generator (SRFG) is random bit generator that produces the symmetric and balanced outputs [
34]. The authors have analysed the nonlinearity, resiliency, balancedness properties of SRFG. In our present work, we have extended the feature analsyis of SRFG with the explanation for propagation and immunity characteristics, security analysis and statistical testing. The main contribution of the presented research work are:
The analysis of propagation and immunity characteristics of SRFG.
Statistical testing on SRFG output-based NIST recommendations.
Security analysis for SRFG as a random number generator.
3. Symmetric Random Function Generator (SRFG)
The mathematical model of Symmetric Random Function Generator (SRFG) is shown in [
34]. It produces the balanced and symmetric outputs in consideration of number of 1’s and number of 0’s in the output string with variable input patterns. In this section we have mentioned some important mathematical expression as shown in [
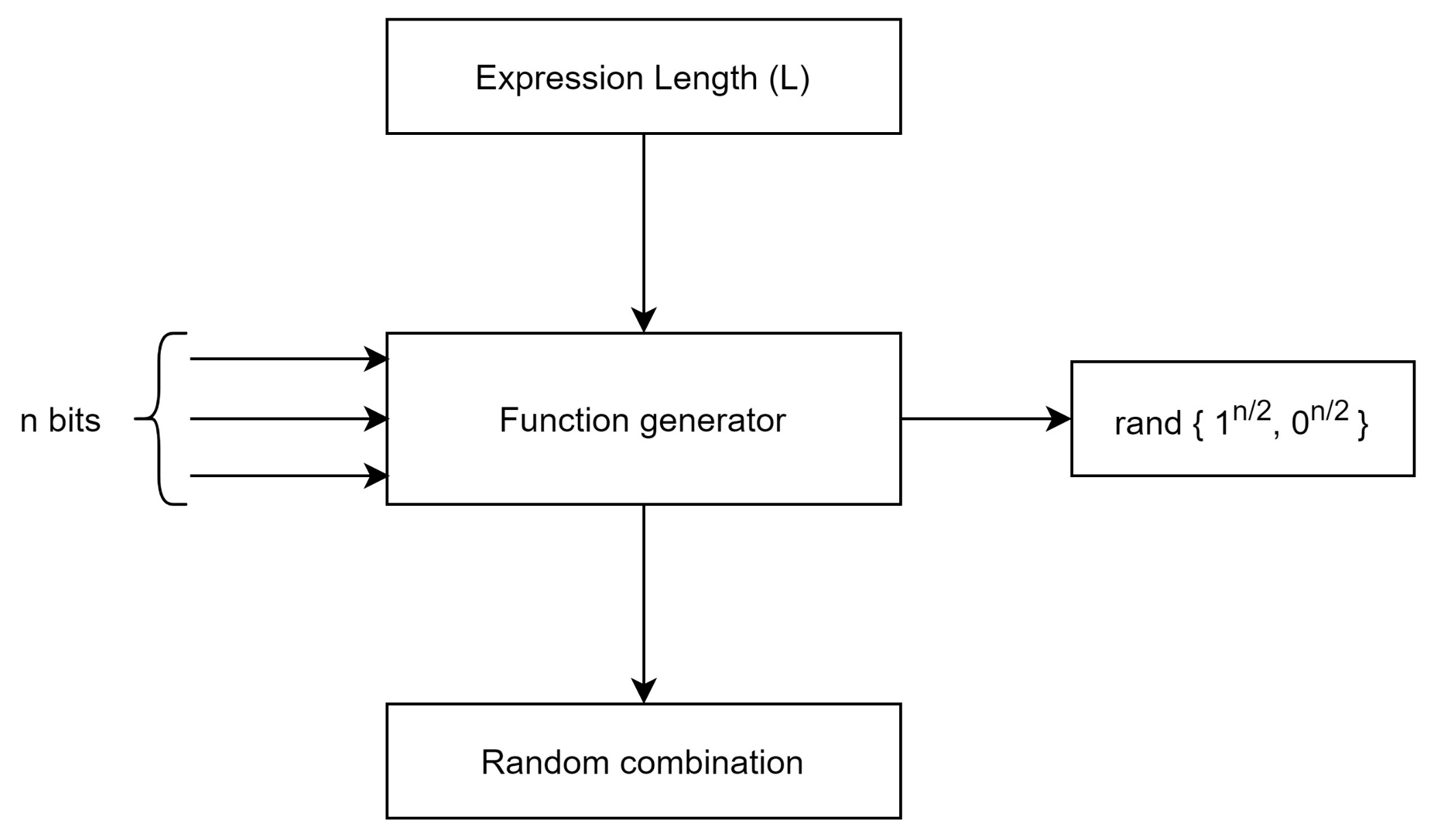
34] to make a clear understanding of propagation and immunity characteristic in next sections. The generalized mathematical expression for SRFG is given as:
where
i is number of gates (here, AND, OR, NOT and XOR GATEs are used with randomized selection) used in SRFG;
L represents the expression length. Expression length is defined as the number of the combined terms used in
f and ⊗ symbolizes the random combination. We show the logical model of SRFG in
Figure 1.
As randomness is the main criteria for a random number generator [
35], the SRFG generalized equation can be further granulated with
N input variables’ following a random selection as shown in Equation (
2).
The expanded structure and chaining of functions is shown in
Figure 2.
As per the shown model of SRFG in the literature, it uses a finite field and ⊗ denoted an operation on the field. SRFG inputs N variables, each of n bit vector . As the values in the vector is either 1 or 0, is a binary vector.
Furthermore, SRFG embodies a set of functions it generates as
is. All the functions map the elements from
into
where
. The output of SRFG is a vector which is a combination of
with
N variables. This vector is comprised of all the values
as the variables are randomly selected and represented as polynomial form of Algebraic Normal Form (ANF) [
36]. It is mathematically interpreted as:
with,
where
In coding theory and in cryptography, ANF considers a Boolean function as a multivariate polynomial. As the N inputs contain values in
, modulo
must be considered. Therefore, this polynomial has degree at most 1 in each input variable following that any monomial of this polynomial is the product of some input variables. For any
,
defines monomial as:
. Extending this monomial for L terms and random basis we obtain
.The proofs are given in [
36].
In SRFG, the outputs and input mapping correspond to a function
such that
. Following this, Equation (
3) is reconstructed as in Equation (
6).
where
and
.
is the elementary polynomial of degree
j with
N variables.
known as a simplified vector.
4. Propagation Criterion of SRFG
The derivatives of the cryptographic properties help in determining the propagation characteristics. All derivatives of the combined functions that output from SRFG are linearly equivalent. This is due to the equal number of 0s and 1s in the outputs equating with a hamming weight of . This is fixed for all the outputs of SRFG. The function f satisfies the propagation criterion of degree k and order m if any affine function is obtained from f with constant m input bits.
Let
and let
be such that
. Then,
and
are linearly equivalent. This signifies a linear permutation
of
such that
, where ∘ is composite function. The permutation
exists on
such that
. Since,
f is symmetric and balanced, we can have,
where ⊞ denotes addition over
.
Let k be an integer,
and
. Then the restriction of
to all affine subspaces
is given by:
The differential functions obtained from SRFG are also symmetric functions of
variables and weight is
. Moreover, simplified value vectors and ANF vectors for those differential symmetric are given for all
by
Let
. For any
with
, SRFG have the following relation.
Equation (
15) signifies
also follows the symmetric property. This infers that the partial derivatives of
f are also propagated with the propagation features. To calculate simplified ANF vector of
, we have decomposed the ANF of
f as given below.
Then, for any
and
, we have,
In Equation (
16),
is used to show that if any biased bit vector
b is included in SRFG function
f, it does not have any effect on output to disrupt the randomness features.
and
are used for selection of random bit patterns from the set of variables. In Equations (11)–(15),
deals with the derivatives showing that in the presence of any other bit vector
y, propagation feature is still preserved.
5. Immunity Feature of SRFG
Now, let’s discuss about the correlation immunity characteristics exhibited by the function generator’s outputs. Considering each of the
N input variable
as
n bit binary vector
,
for the combined symmetric and balanced function
f,
f is correlation immune if the following condition satisfies:
The set of all correlation immune functions of
N variables of
n bits each is denoted by
. Furthermore, the weight of correlation immune function
f of the generator is given by:
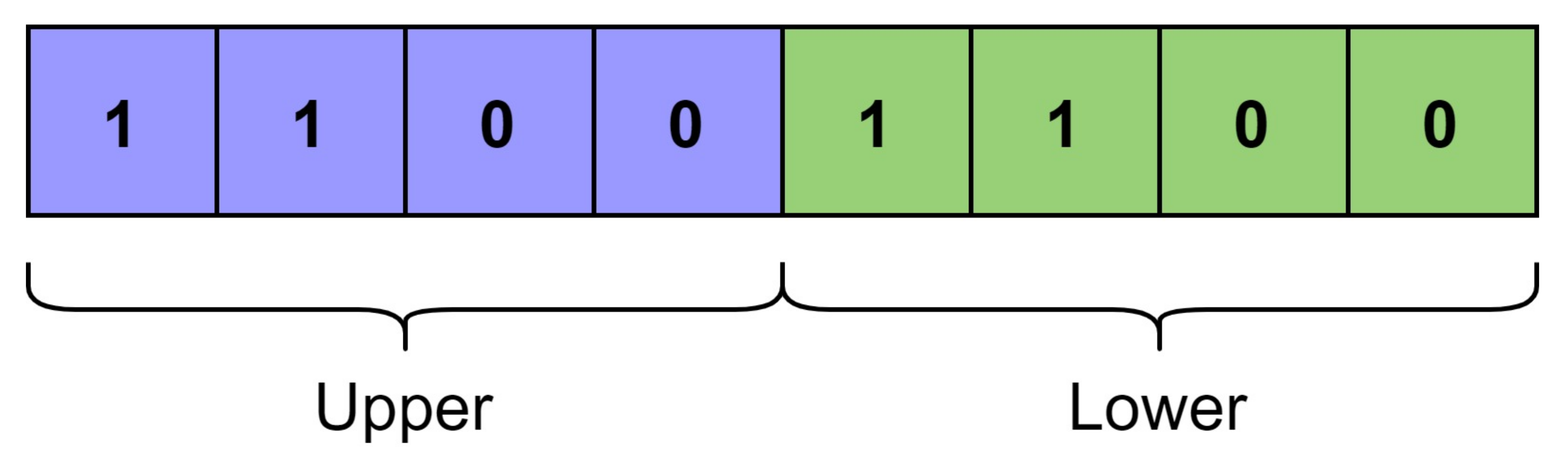
Let
and
be the upper and lower halves of equal length
for the function generator’s outputs as shown in
Figure 3. As,
,
. If there are
k places out of
1’s in the
where the corresponding positions in reverse of
, denoted as
, do not match. Therefore, the number of bits match with respect to 1 for the function is given as:
Following Equation (
20), we can also say that there are
k places out of
1’s in the
where the corresponding positions in
do not match. Therefore, the number of bits match with respect to 0 for the function is given as:
The correlation immune functions with the same values of form an equivalence class.
Proposition 1: Let
and
. Then
and
,
Apart from the correlation immunity, algebraic immunity is also a requirement for cryptographic algorithms. Algebraic immunity also is related with the annihilator of a function [
37]. This property helps the algorithm to prevent algebraic attacks [
38,
39] against the cryptographic algorithms.
We use the annihilators here. If
, any function of the set
is the annihilator of the function
f. The algebraic immunity of
f is denoted by
. It is defined as the minimum degree of all the nonzero annihilators of
f or
. The value of
is given as:
The idea is that for a given function
f on
N-variables, a reduced set of homogeneous linear equations is required by solving which one can decide whether there exist annihilators of
f at a specific degree [
40]. The experimented value for good designs of functions must possess the
f or
must not have any annihilator of degree more than
. SRFG exhibits this feature as the degree of SRFG functions is
. as they are balanced. As the SRGF outputs the symmetric function which are balanced and therefore minimum degree is always
. Therefore, the algebraic immunity of the outputs from SRGF is always
which is always optimal.
6. Results
We have executed an experiment for the SRFG to analyze the above mentioned properties. To evaluate these properties for SRFG and its output functions, we have implemented the model using concerning for two variable metrics: number of bits
n and number of expressions
L. The other parameters and metrics used for the experiments are summarized in
Table 1.
6.1. Performance of SRFG
The evaluation for the propagation criterion was measured with the introduced metric of criterion fraction. Criterion fraction is defined as: , where m is the number of bits in the input variable kept constant to get the propagation criterion of degree k. For the SRFG function generator as the output functions are balanced always, the value of k = and maximum number of bits we can keep constant is also . These values give the upper bound of criterion fraction as 1.
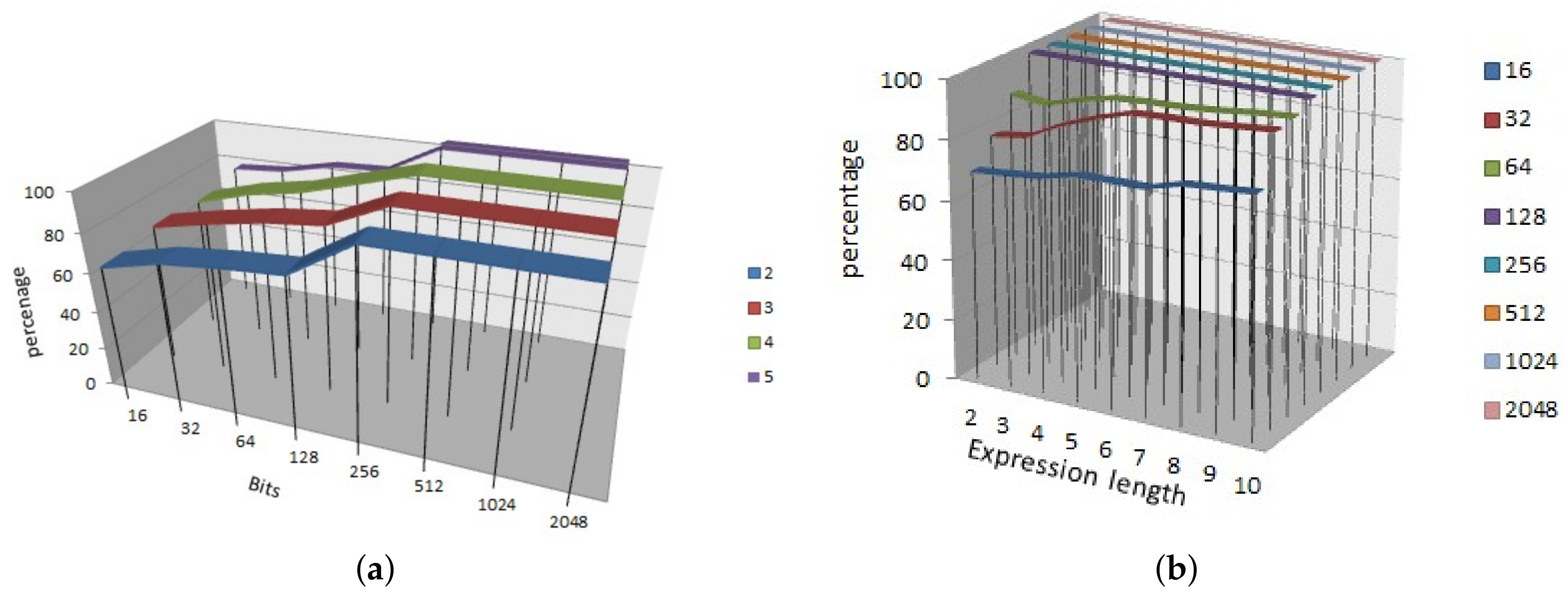
In
Figure 4, we showed the results of the propagation criterion for SRFG.
Figure 4a shows the result by varying the number of variables and number of bits of each variable. Similarly,
Figure 4b shows the result by varying the number of expression length and number of bits of each variable. It shows that more number of variables are providing more propagation; however, with the increasing number of bits propagation follows a steady output of 0.8 approximately. In both the cases, the results achieve more than 80% propagation criterion effect which reflects the strictly avalanche effect.
The correlation immunity characteristics were plotted in
Figure 5.
Figure 5a shows the result by varying the bits and number of variables from 2 to 5. It notifies that increasing number of bits is able to generate more immunity.
Figure 5b shows the result by varying the bits from 16 to 2048 and expression length from 2 to 10. We have noticed a new feature in both the cases that irrespective of the expression length and number of variables, SRFG is capable of producing 100% correlation immune functions with and after 128 bits. This makes the SRFG efficient and suitable for cryptographic algorithms.
The algebraic immunity of the SRFG generated functions are always at irrespective of the number of bits and number of expression length and therefore these parameters is not shown graphically explicitly.
6.2. Comparative Analysis
We chose some recent works from the literature for comparing the results and to validate the randomness efficiency of SRFG. The algorithms described in [
26,
27,
29,
31,
32,
33] exhibit true randomness and therefore have been considered for the comparison with SRFG. Another recent algorithm depicted in [
18] is also considered for comparison due to its related features. The comparison results shown in
Table 2 notify the order of the parameters considered for the evaluation. Percentage calculation in the table is based on 500 outputs of bit sequences from the random number generators.
Table 2 shows the fact that SRFG possess the three features significantly.
correlation immunity is possible because of balanced functions. The symmetric and balanced function in SRFG is therefore efficient for cryptographic primitives.
6.3. Statistical Analysis
The validation of the randomness has been executed by the test suite suggested by the NIST in the NIST 800-r1 document [
41]. To perform the tests the hypothesis has been set up for all the tests as:
Hypothesis 1. (null hypothesis): SRFG output sequences are significant for randomness.
Hypothesis 2. (alternate hypothesis): SRFG output sequences are non-significant for randomness.
For each of the applied tests, a choice or end is taken that acknowledges or dismisses the invalid theory which implies whether the SRFG is (or isn’t) ready to deliver randomness features, in light of the grouping that was created. For each test, an applicable randomness measurement is chosen and used to decide the value of acceptance or rejection of the invalid speculation. A test measurement esteem (
p-value) is figured on the information or arrangement of bits created by the SRFG. Practically, the explanation that factual theory testing works is that the reference appropriation and the basic worth are reliant on and created under a speculative suspicion of irregularity. In the event that the arbitrariness supposition that is, truth be told, valid for the current information, at that point the subsequent determined test measurement esteem on the information will have an extremely low likelihood (e.g., 0.01 ) of surpassing the basic worth. This estimation of 0.01 is likewise known as level of criticalness or level of significance. In the event that
p-value is more noteworthy than the degree of noteworthiness, we can acknowledge the invalid theory. The outline of the
p-values of the above said tests is given in
Table 3. We can observe that in all the above tests, the
p-values of the tests are greater than 0.01, the significance level of the tests. Therefore, the null hypothesis is accepted. This signifies that the SRFG has passed all the tests as per the recommendations by NIST test suite and the SRFG provides randomness in true significance.
SRFG is quite an interesting random number generator that possess all the required features of being used for cryptographic derivations with randomness features. The statistical test suite also validates the same. It can also be considered to be a post processing method for any other random number generators to provide immunity and eliminating bias and correlations. Furthermore, to validate the tests proportion of sequences passing, a test and uniformity was evaluated as per the NIST standards [
41]. The formula shown in the document to calculate the confidence interval level is used here. The confidence interval becomes:
where
,
is the significance level (0.01) and
m is the number of samples of bit sequences which is 800 in the experimented process. The Equation (
25) suggests that the proportion of the sequences under test should be more than 0.9794466. Out of 800 random samples tested, 799 samples have passed the tests of significance levels providing
p-values greater than 0.01 and thus, the proportion becomes
which is more than the confidence interval. Hence, SRFG is validated in proportioning the pass sequences to exhibit random features. The uniformity of the
p-values is also checked. Following the Goodness of Fit Distributional test as formulated in NIST document [
41], the
p-value for SRFG is measured as 0.001437 which is more than 0.0001. Hence, it is validated that the
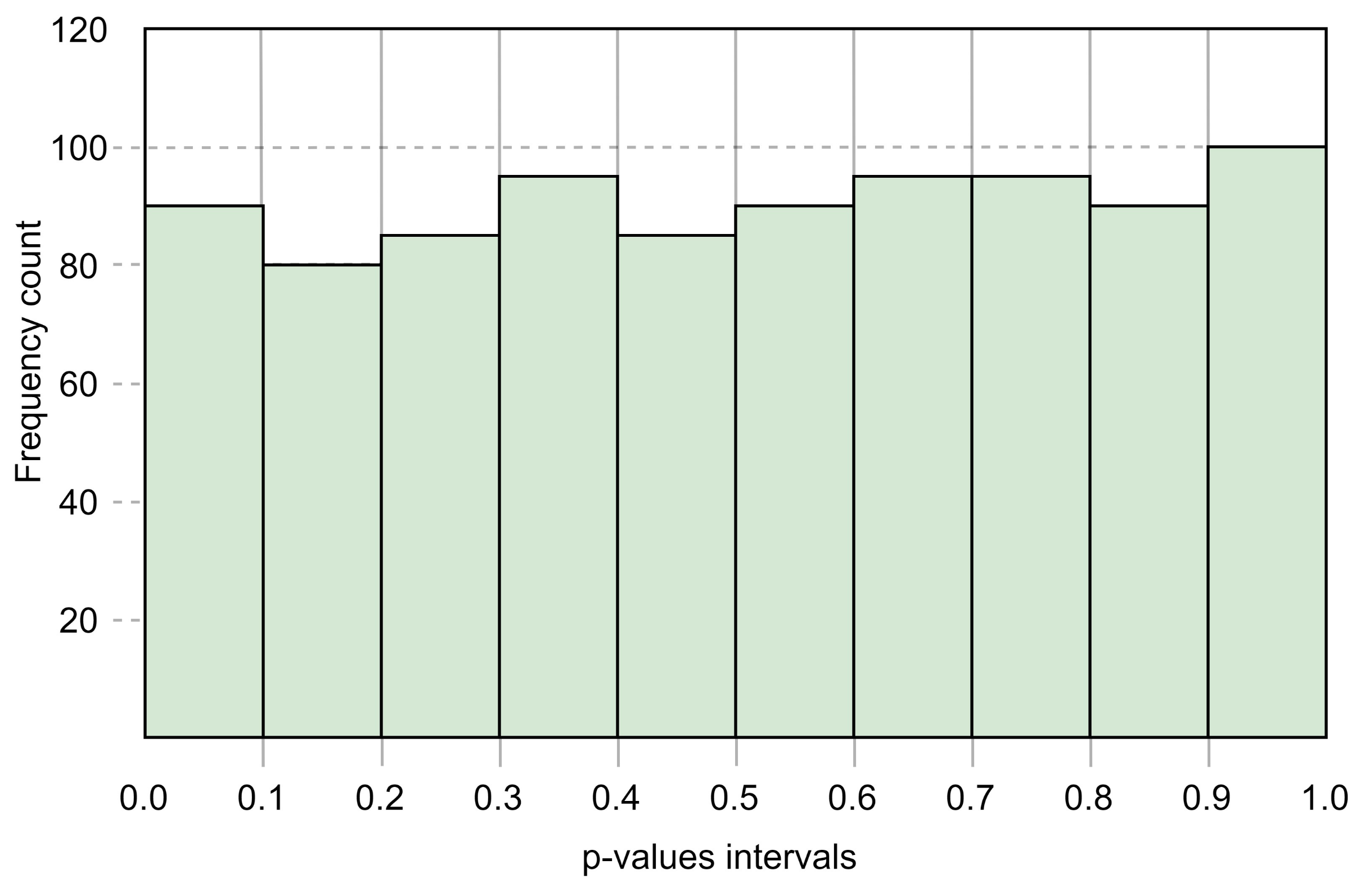
p-values are uniformly distributed. The distribution uniformity of the
p-values with 10 intervals and corresponding frequencies of
p-values are shown in
Figure 6.
6.4. Security Analysis
Generally, random number generators are a great help in key management of cryptosystems. Forward secrecy and backward secrecy are two important features that the random number generators should have to be used for key processing. Forward security ensures that any attacker who knows a sequential subset of old bit patterns is unable to derive the subsequent bit patterns. Backward security is defined with the assurance that an attacker with the knowledge of contiguous subset of bit patterns is unable to trace back the preceding bit patterns.
Let us assume two contiguous bit patterns as and each of n number of bits. As per the propagation criteria, at least bits are changed from an initial bit pattern to and bits from to . With the increasing number of iterations, the change of bits also increases. The maximum probability that a bit pattern of n bits can be derived from and is calculated as:
=, where r is the difference of bits in two contiguous bit patterns. For large number of bits and more differences in bit patterns . It signifies that SRFG is able to provide forward security.
Similarly, if an attacker knows bit pattern
and
and wants to trace
bit pattern with a random bit difference of
r, the probability that the bit pattern is revealed is:
Here, we assume that the attacker tries with sequence assuming that each sequence has bit difference r. Therefore, overall, bit difference becomes . With large number of bit differences between two contiguous bit patterns, the probability of discovering any previous bit pattern eventually becomes 0 and thus, SRFG preserves backward security.
For any random number generator, it is very important in cryptography to be immune against any distinguishing attack. Such an attack cryptanalyses on data encrypted or output by the system and distinguish it from random data. The correlation immunity and algebraic immunity provides strength to SRFG on this point. The statistical validation also supports SRFG’s indistinguishable property irrespective of inputs. For example: let us consider,
E is an encrypted output from SRFG and
S is a random bit pattern both of
n bits. By the immunity property, SRFG develops a difference of difference of
bits propagated from initial difference. Therefore, the probability of distinguishing attack is:
Therefore, SRFG is able to provide security parameters significantly and robust against cryptanalysis attacks; thus, efficient for cryptographic operations.