Combined Attenuation Zones of Combined Layered Periodic Foundations
Abstract
:1. Introduction
2. Computational Methods
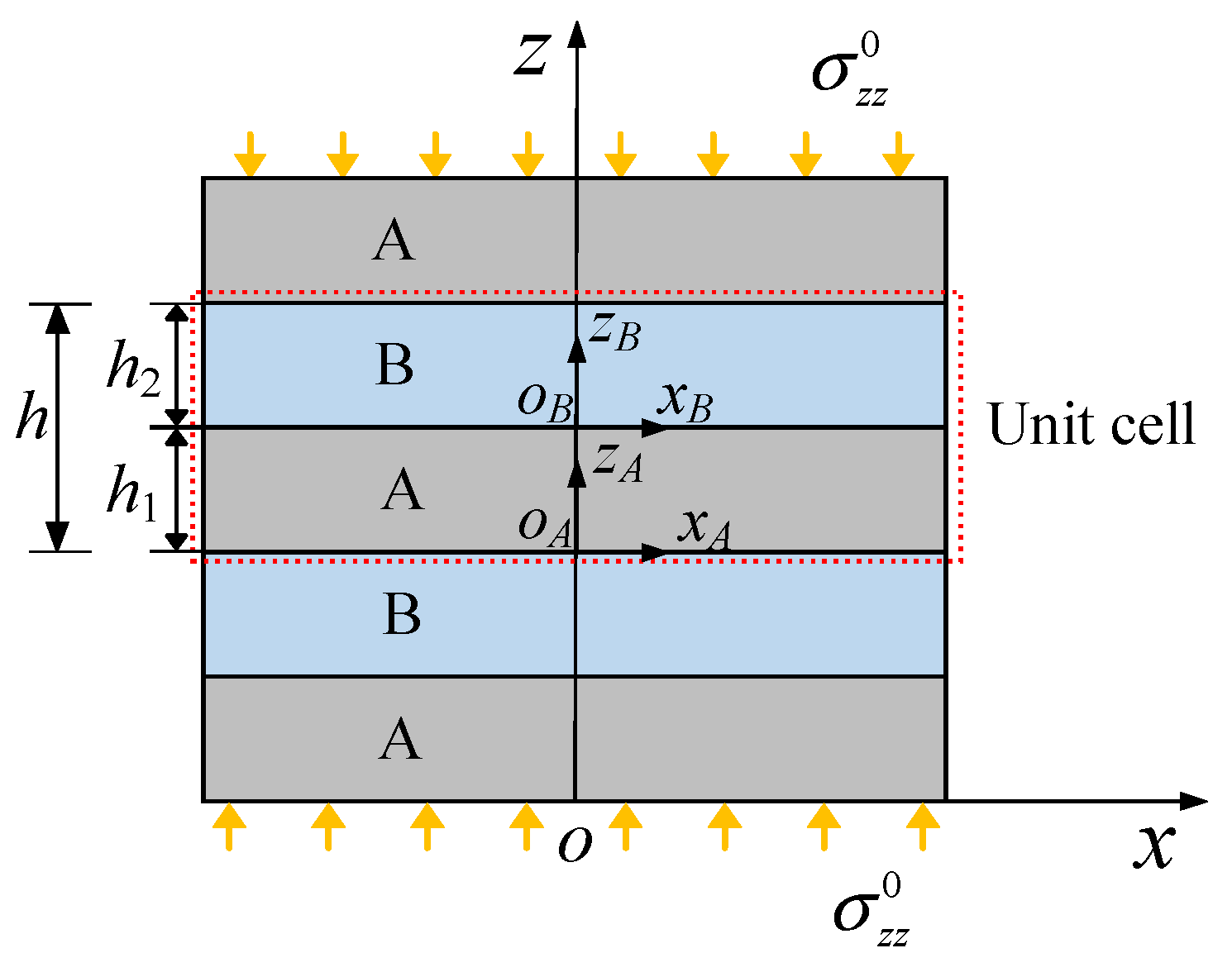
2.1. Dispersion Curves of SH Waves in Traditional LPFs with Identical Unit Cells
2.2. Frequency Response Functions of CLPFs
3. Results and Discussion
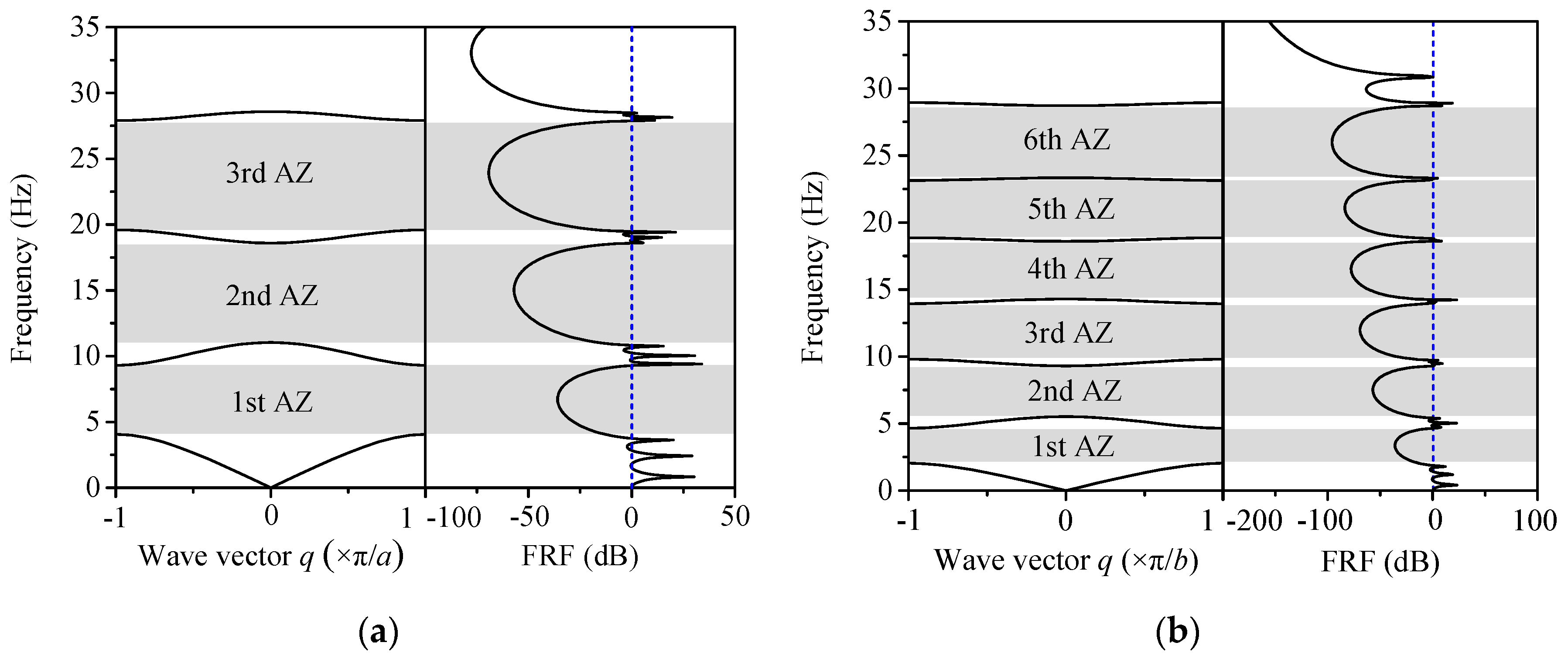
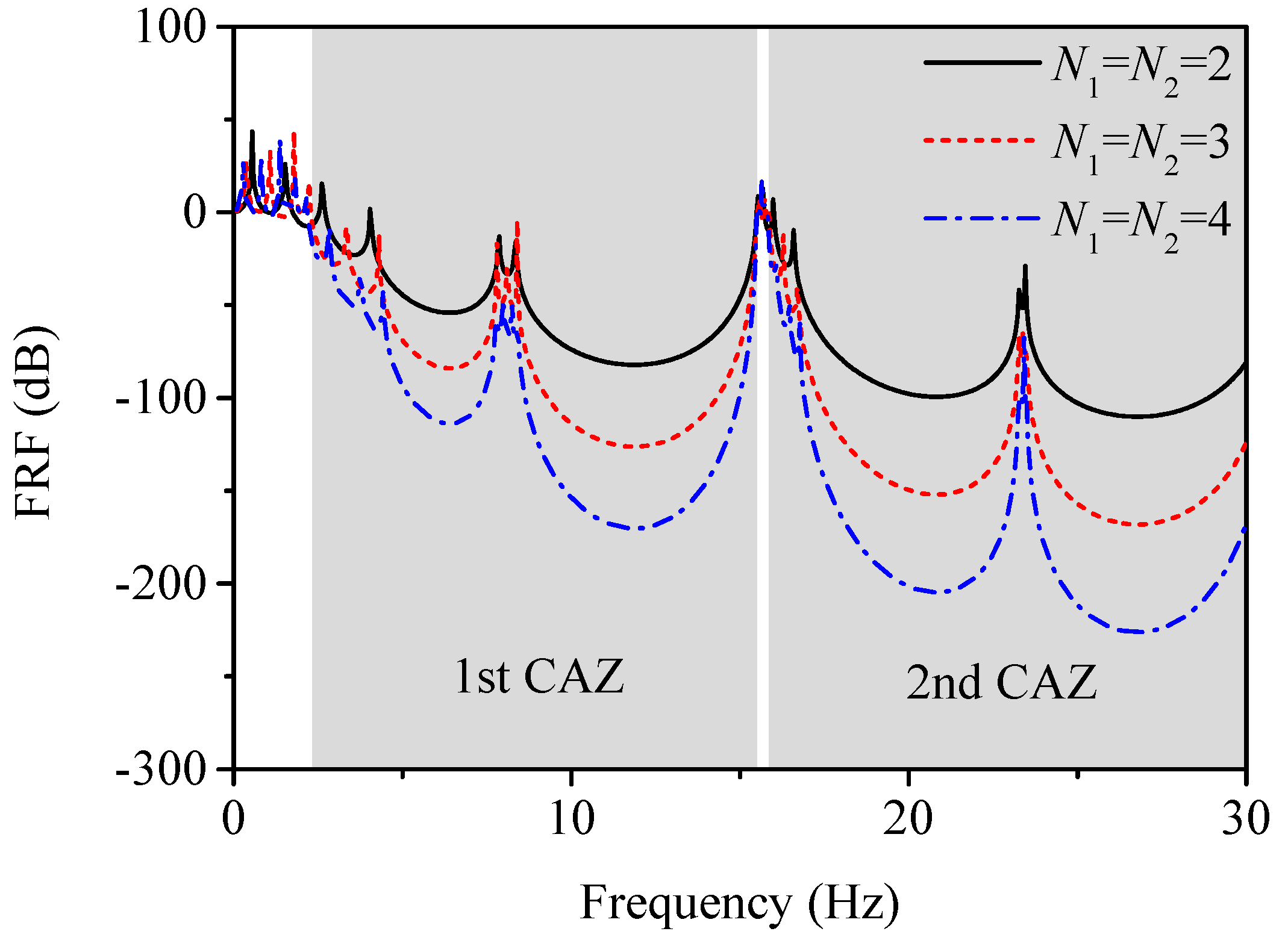
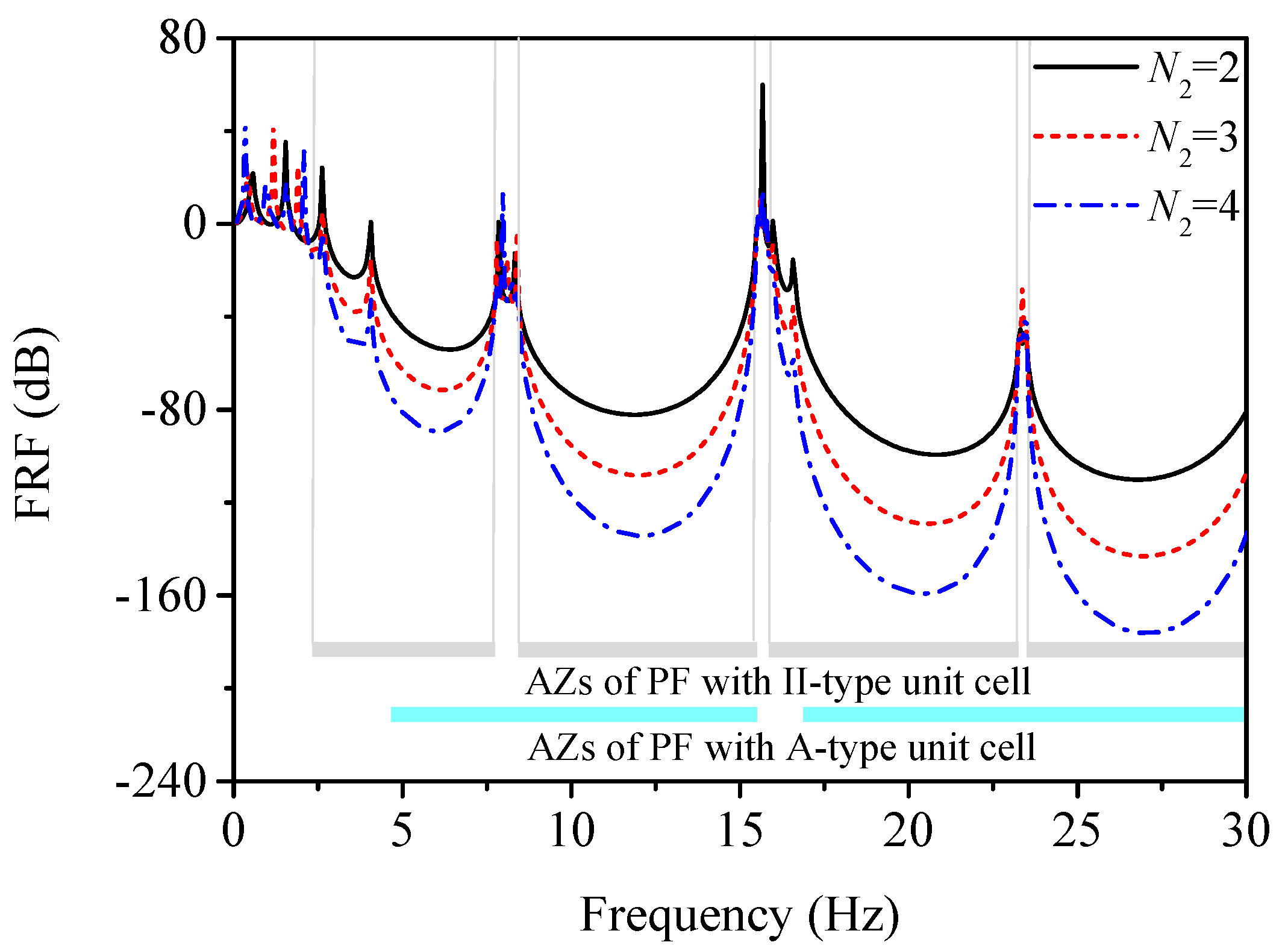
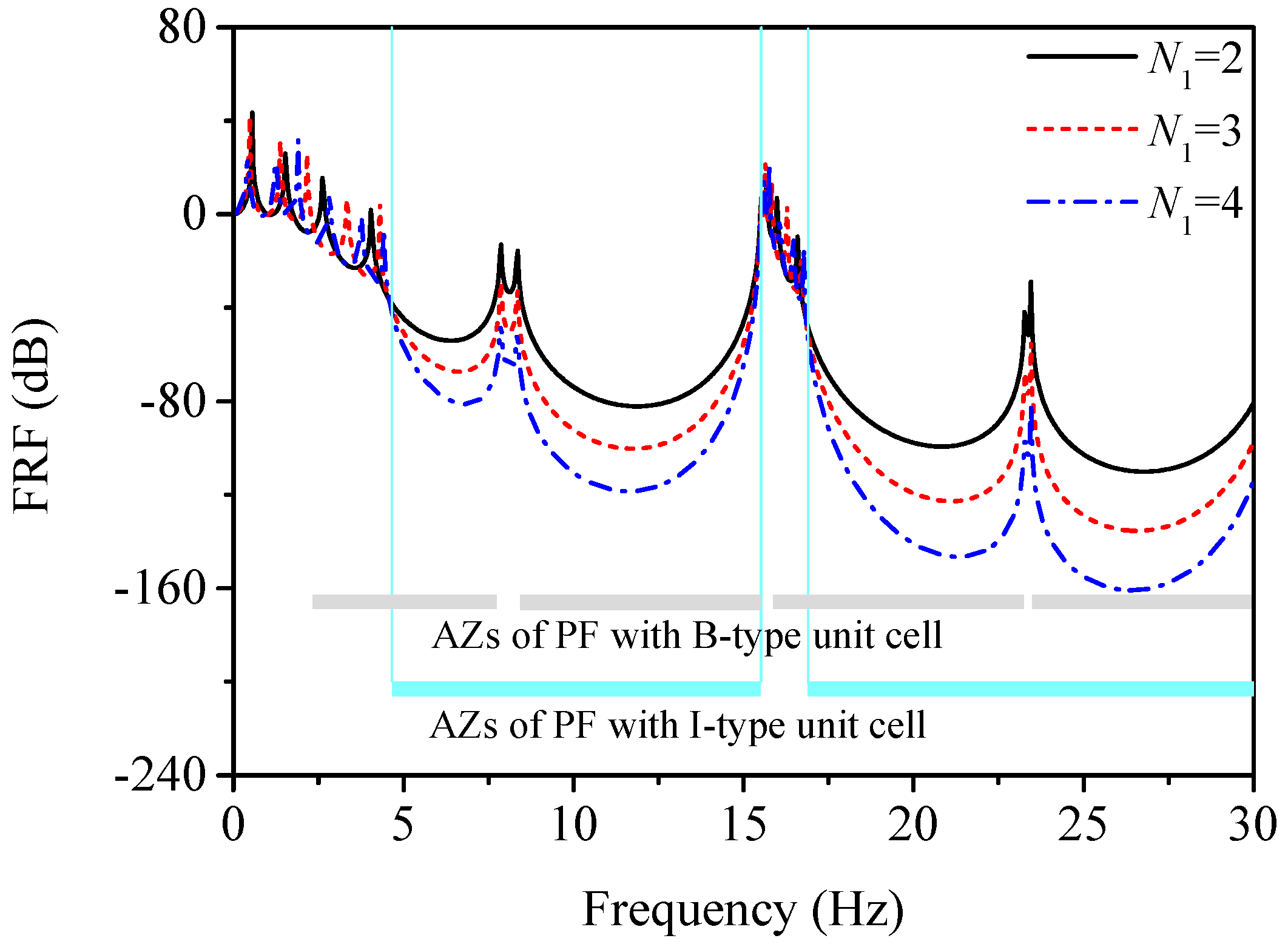
3.1. Attenuation Zones of Traditional LPFs with Identical Unit Cells
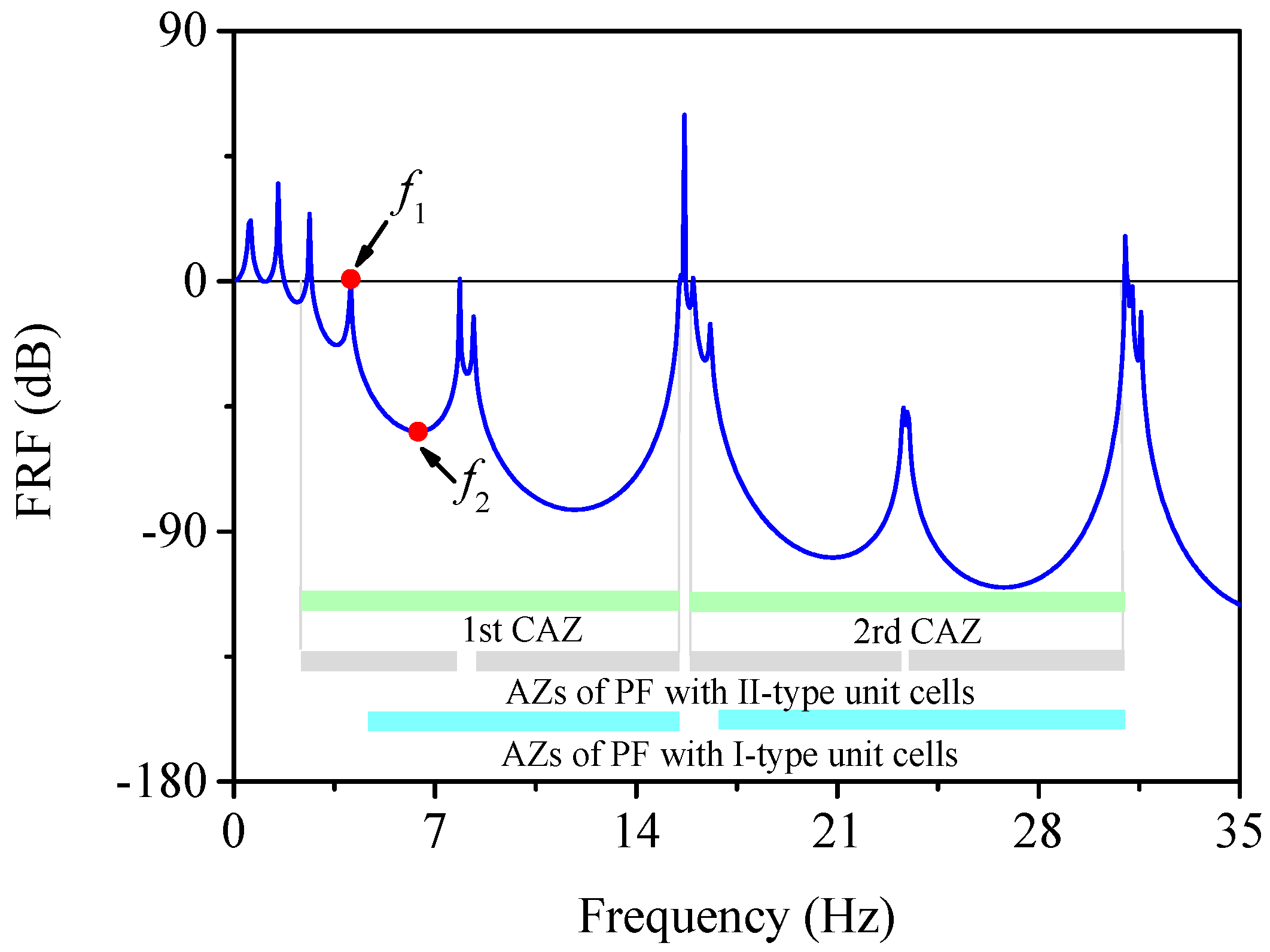
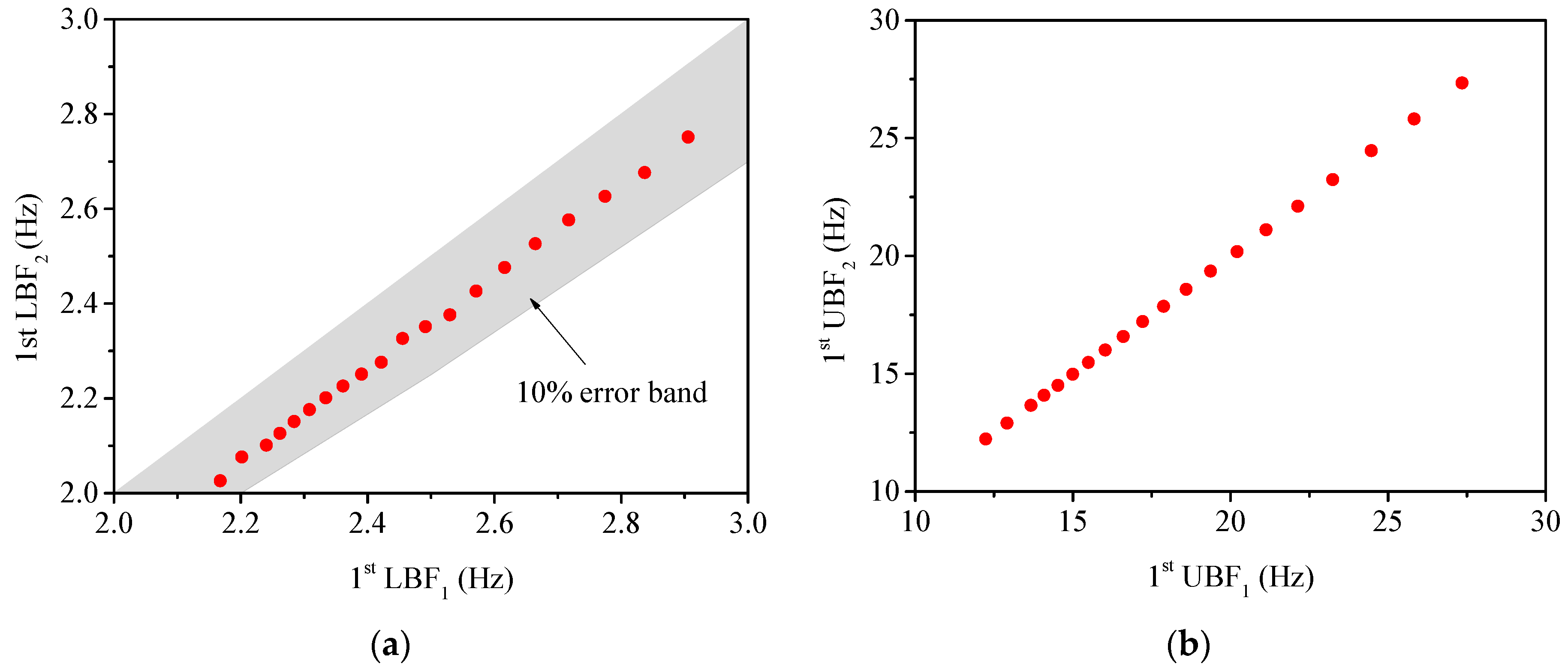
3.2. Combined Attenuation Zones of CLPFs
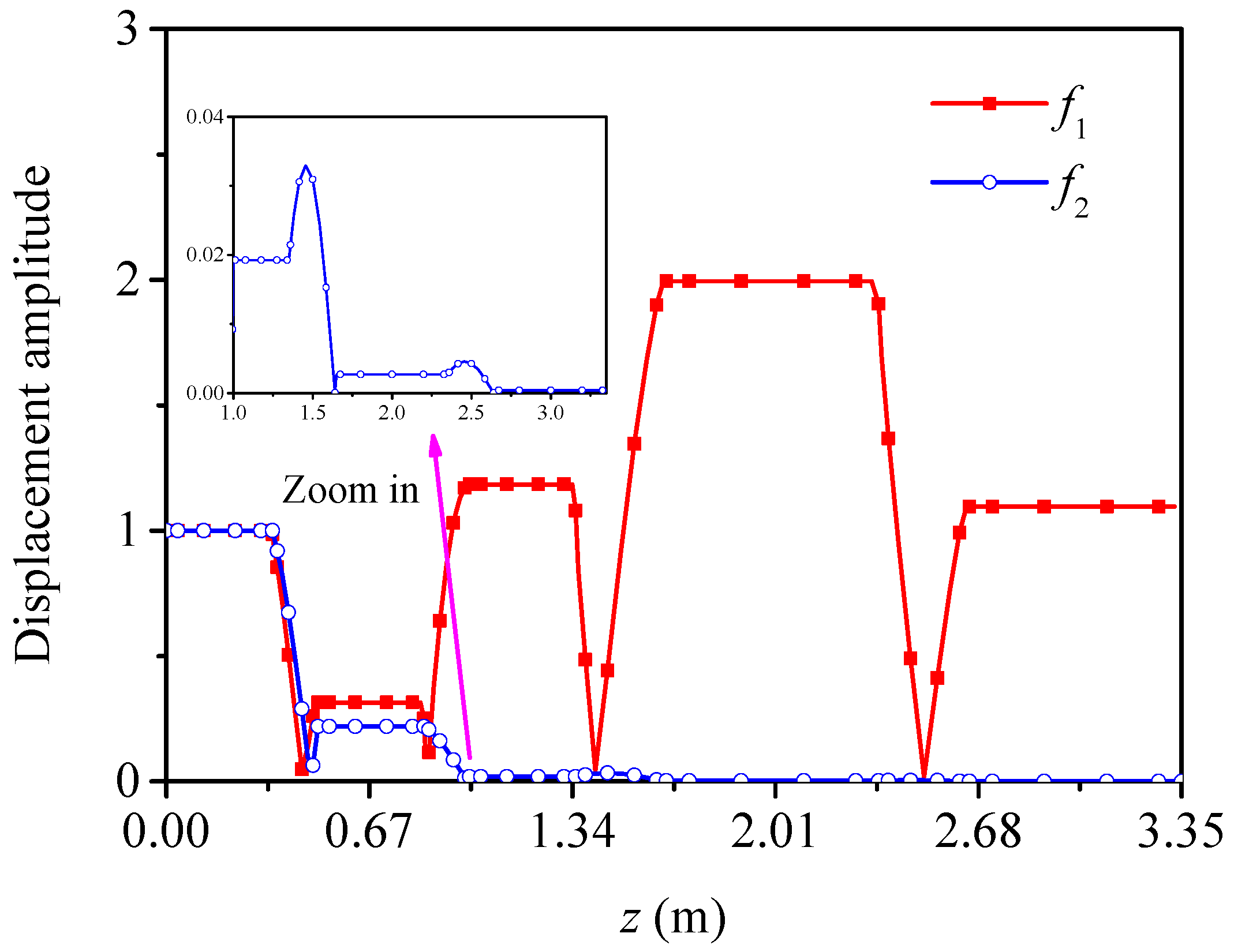
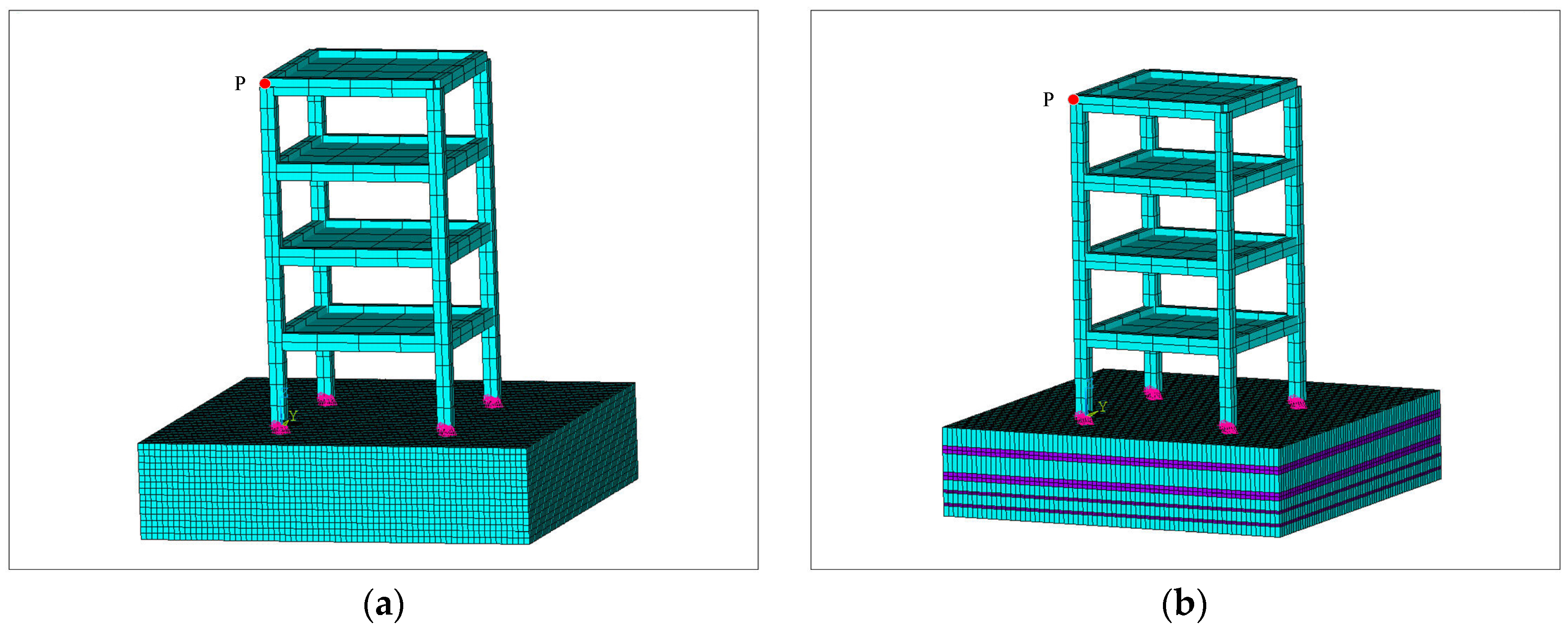
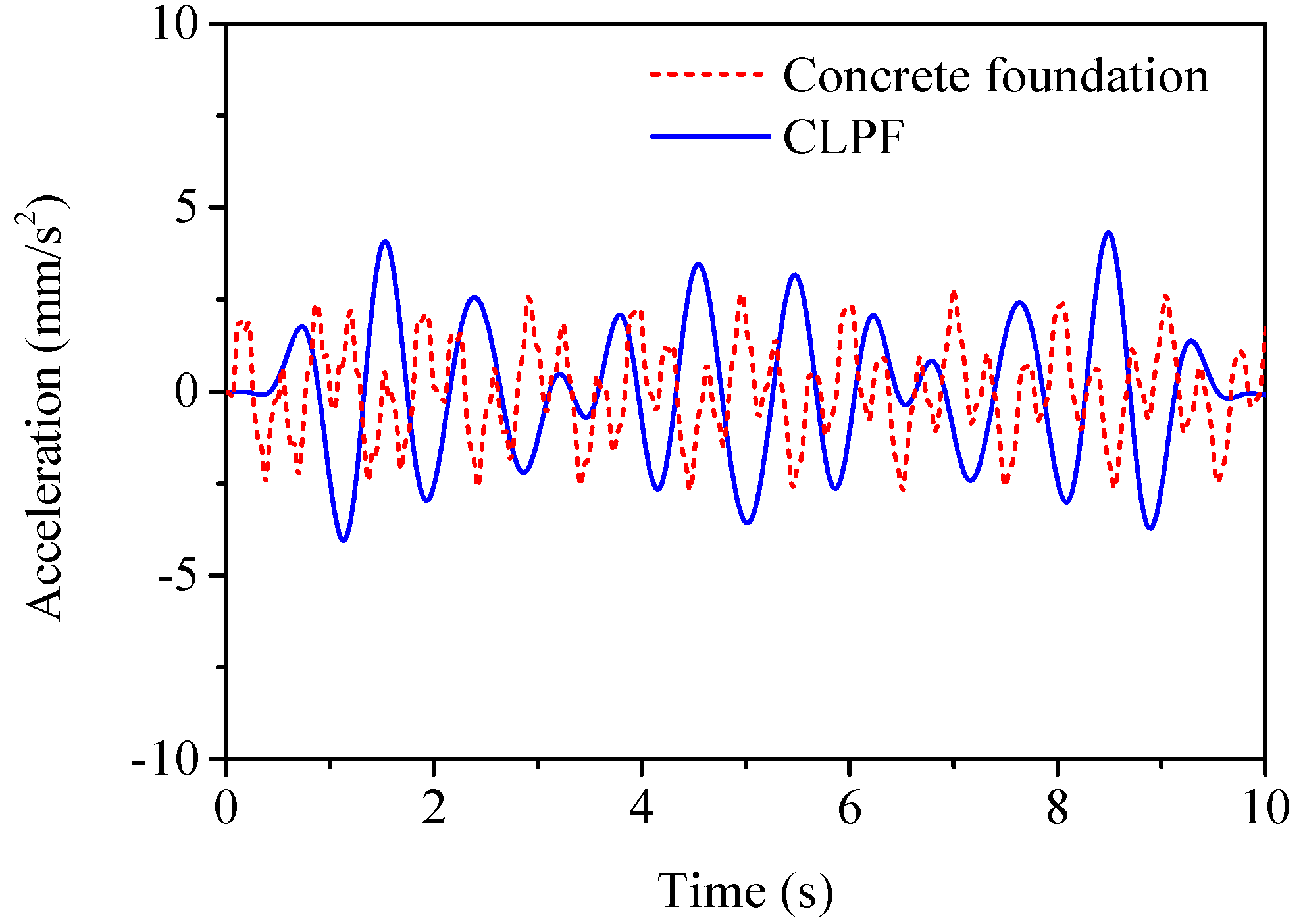
3.3. Seismic Performance of CLPFs
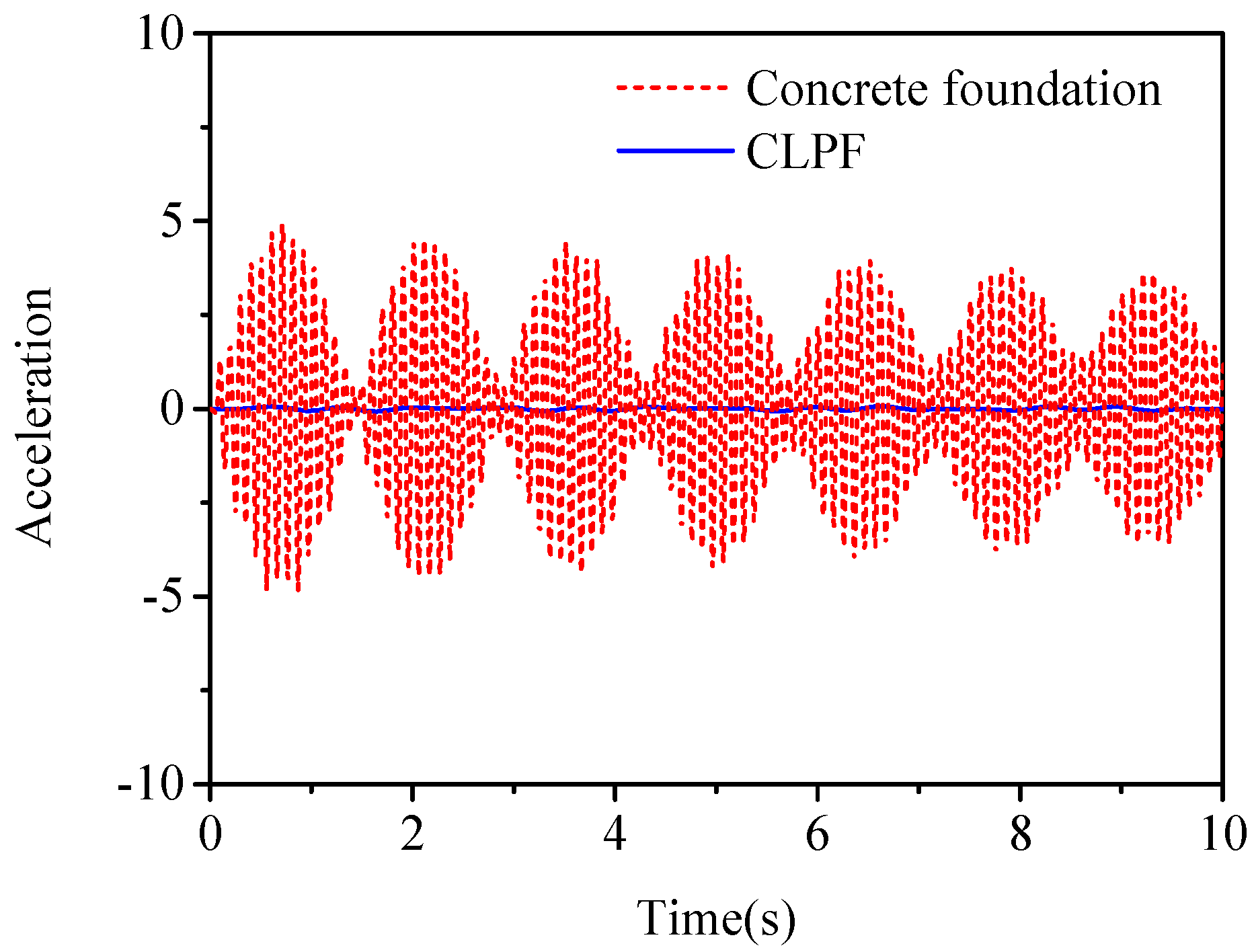
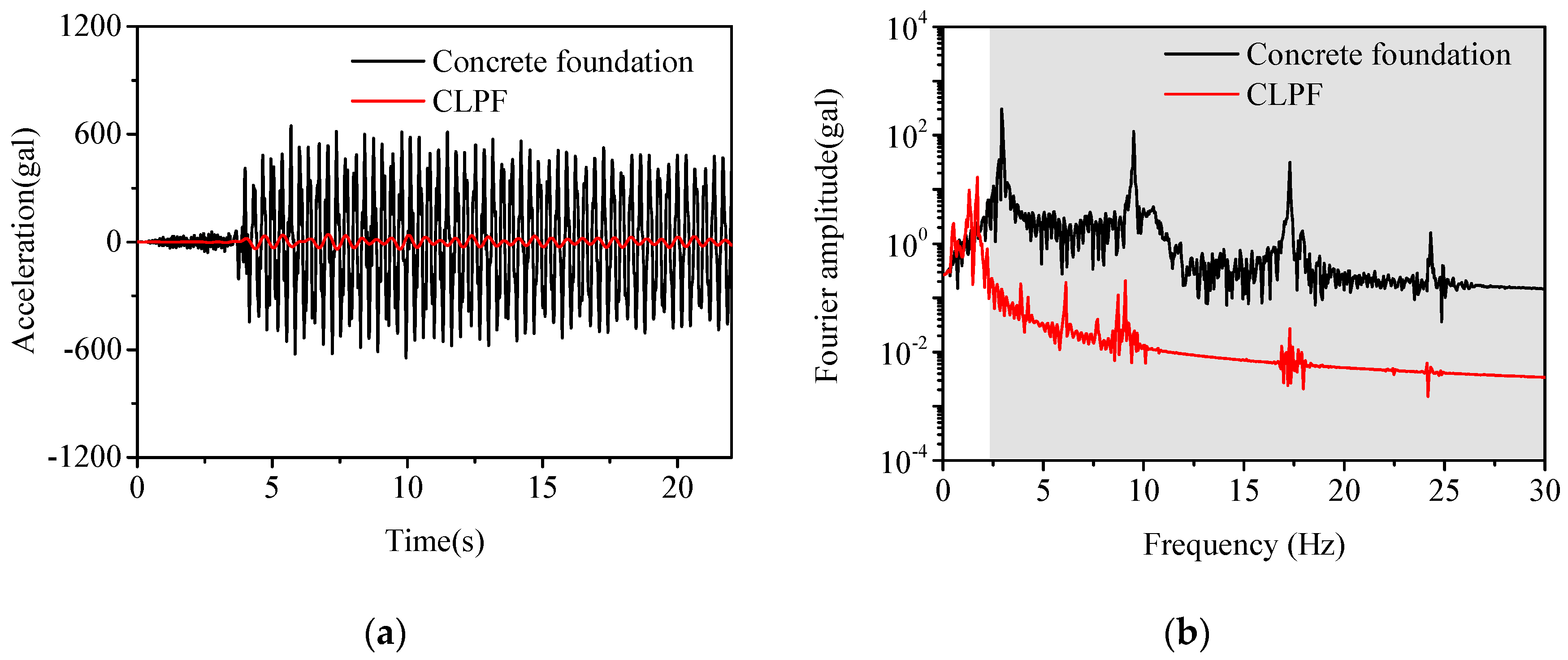
3.3.1. Time-Domain Response under Harmonic Excitations
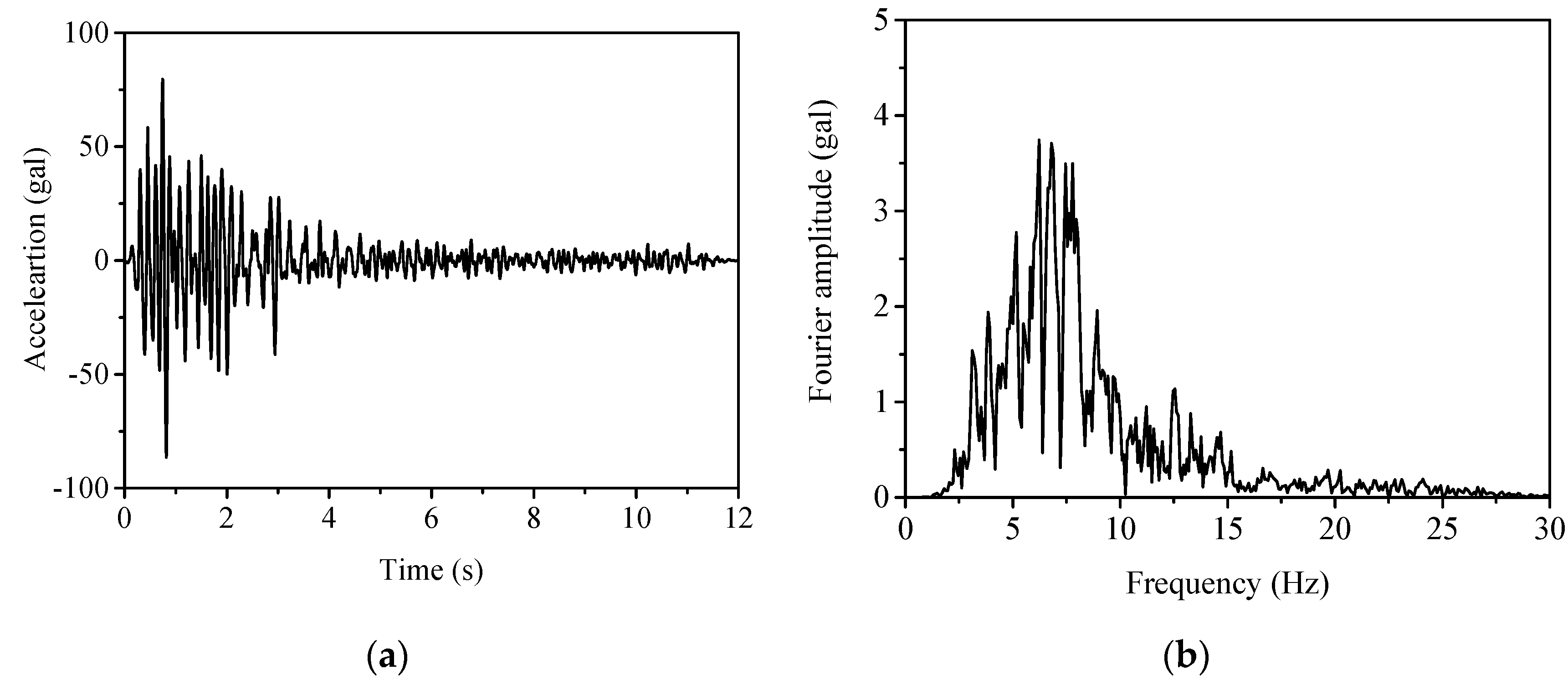
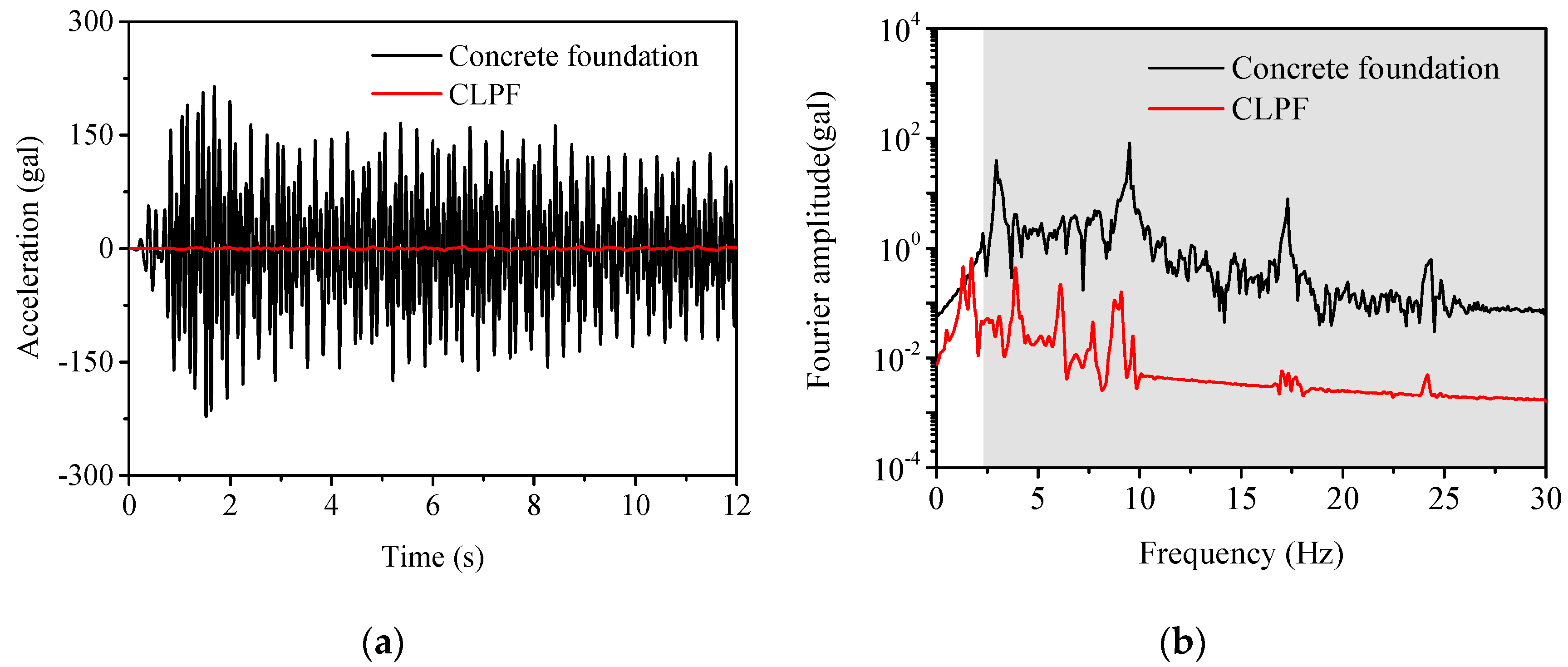
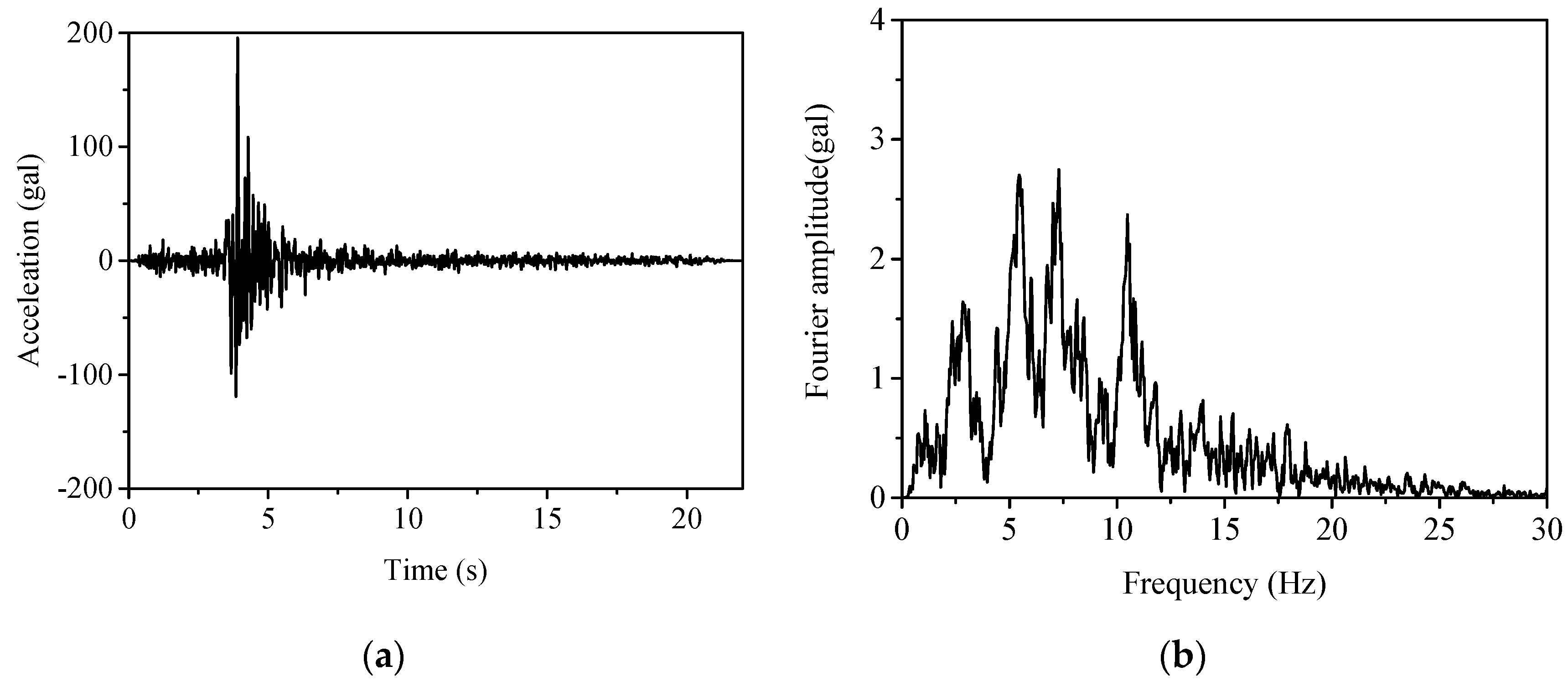
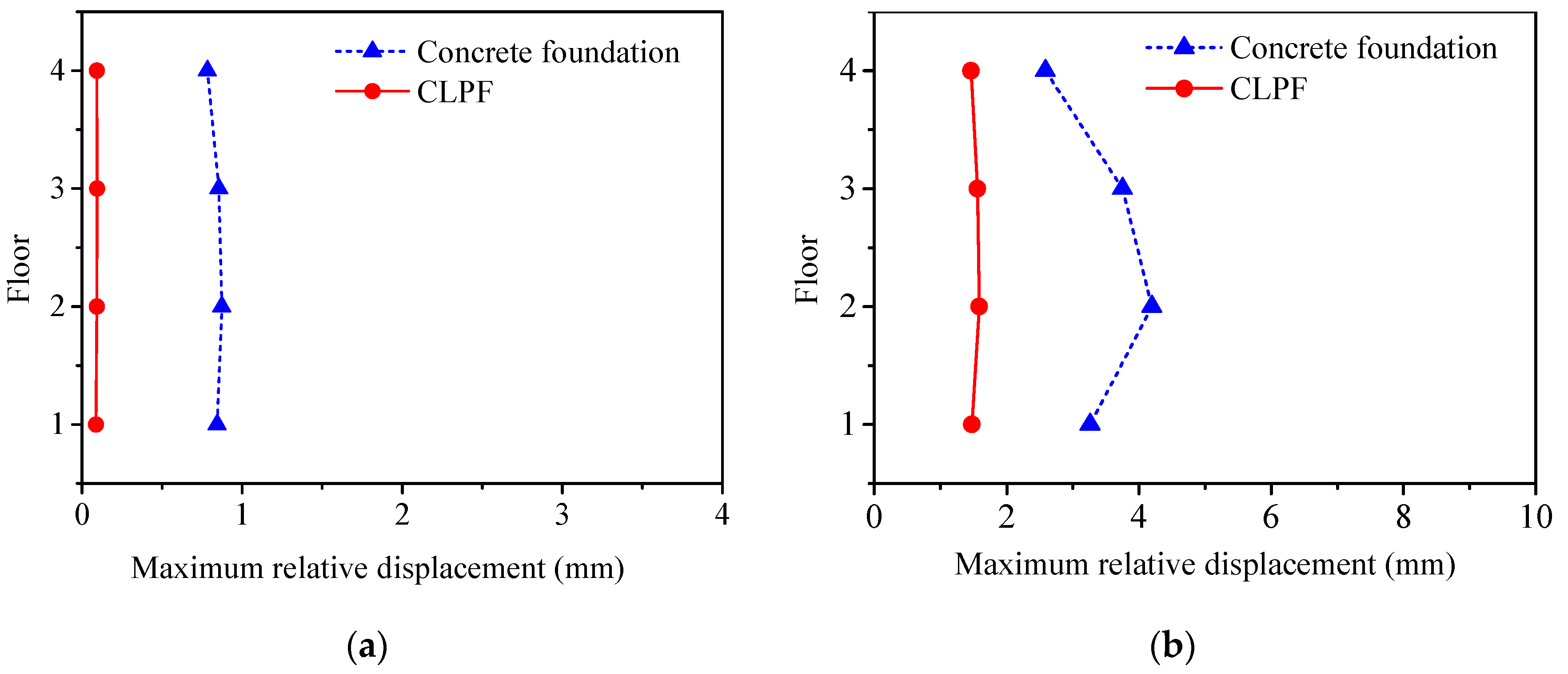
3.3.2. Time-Domain Response under Seismic Excitations
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Guo, Z.; Pan, J.; Sheng, M. Vibro-Acoustic performance of a sandwich plate with periodically inserted resonators. Appl. Sci. 2019, 9, 3651. [Google Scholar] [CrossRef] [Green Version]
- Qin, Q.; Sheng, M.; Guo, Z. Low-Frequency vibration and radiation performance of a locally resonant plate attached with periodic multiple resonators. Appl. Sci. 2020, 10, 2843. [Google Scholar] [CrossRef] [Green Version]
- Jia, G.F.; Shi, Z.F. A new seismic isolation system and its feasibility study. Earthq. Eng. Eng. Vib. 2010, 9, 75–82. [Google Scholar] [CrossRef]
- Basone, F.; Wenzel, M.; Bursi, O.S.; Fossetti, M. Finite locally resonant metafoundations for the seismic protection of fuel storage tanks. Earthq. Eng. Struct. Dyn. 2019, 48, 232–252. [Google Scholar] [CrossRef]
- Dertimanis, V.K.; Antoniadis, I.A.; Chatzi, E.N. Feasibility analysis on the attenuation of strong ground motions using finite periodic lattices of mass-in-mass barriers. J. Eng. Mech. 2016, 142, 04016060. [Google Scholar] [CrossRef]
- Bao, J.; Shi, Z.F.; Xiang, H.J. Dynamic responses of a structure with periodic foundations. J. Eng. Mech. 2012, 138, 761–769. [Google Scholar] [CrossRef]
- Witarto, W.; Wang, S.J.; Nie, X.; Mo, Y.L.; Shi, Z.F.; Tang, Y.; Kassawara, R.P. Analysis and design of one dimensional periodic foundations for seismic base isolation of structures. Int. J. Eng. Res. Appl. 2016, 6, 5–15. [Google Scholar]
- Yan, Y.Q.; Laskar, A.; Cheng, Z.B.; Menq, F.; Tang, Y.; Mo, Y.L.; Shi, Z.F. Seismic isolation of two dimensional periodic foundations. J. Appl. Phys. 2014, 116, 044908. [Google Scholar] [CrossRef]
- Huang, J.K.; Shi, Z.F.; Huang, W.X.; Chen, X.H. A periodic foundation with rotational oscillators for extremely low-frequency seismic isolation: Analysis and experimental verification. Smart Mater. Struct. 2017, 26, 035061. [Google Scholar] [CrossRef]
- Cheng, Z.B.; Shi, Z.F. Composite periodic foundation and its application for seismic isolation. Earthq. Eng. Struct. Dyn. 2018, 47, 925–944. [Google Scholar] [CrossRef]
- Liu, X.N.; Wang, Y.H.; Chen, Y.C. Attenuation zones of two dimensional periodic foundations including the effect of vertical loads. Appl. Sci. 2019, 9, 993. [Google Scholar] [CrossRef] [Green Version]
- Yan, Y.Q.; Cheng, Z.B.; Meng, F.; Mo, Y.L.; Tang, Y.; Shi, Z.F. Three dimensional periodic foundations for base seismic isolation. Smart Mater. Struct. 2015, 24, 075006. [Google Scholar] [CrossRef]
- Witarto, W.; Wang, S.J.; Yang, C.Y.; Wang, J.; Mo, Y.L.; Chang, K.C.; Tang, Y. Three-Dimensional periodic materials as seismic base isolator for nuclear infrastructure. AIP Adv. 2019, 9, 045014. [Google Scholar] [CrossRef] [Green Version]
- Sun, F.F.; Xiao, L.; Bursi, O.S. Quantification of seismic mitigation performance of periodic foundations with soil-structure interaction. Soil Dyn. Earthq. Eng. 2020, 132, 106089. [Google Scholar] [CrossRef]
- Xiong, C.; Shi, Z.F.; Xiang, H.J. Attenuation of Building Vibration using periodic foundations. Adv. Struct. Eng. 2012, 15, 1375–1388. [Google Scholar] [CrossRef]
- Xiang, H.J.; Shi, Z.F.; Wang, S.J.; Mo, Y.L. Periodic materials-based vibration attenuation in layered foundations: Experimental validation. Smart Mater. Struct. 2012, 21, 112003. [Google Scholar] [CrossRef]
- Shi, Z.F.; Cheng, Z.B.; Xiang, H.J. Seismic isolation foundations with effective attenuation zones. Soil Dyn. Earthq. Eng. 2014, 57, 143–151. [Google Scholar] [CrossRef]
- Liu, X.N.; Shi, Z.F.; Mo, Y.L.; Cheng, Z.B. Effect of initial stress on attenuation zones of layered periodic foundations. Eng. Struct. 2016, 121, 75–84. [Google Scholar] [CrossRef]
- Cheng, Z.B.; Shi, Z.F.; Palemo, A.; Xiang, H.J.; Guo, W. Seismic vibrations attenuation via damped layered periodic foundations. Eng. Struct. 2020, 211, 110427. [Google Scholar] [CrossRef]
- Witarto, W.; Nakshatrala, K.B.; Mo, Y.L. Global sensitivity analysis of frequency band gaps in one-dimensional phononic crystals. Mech. Mater. 2019, 134, 38–53. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.N.; Ren, Y.Q.; Song, X.R.; Witarto, W. A global sensitivity analysis method based on the Gauss-Lobatto integration and its application in layered periodic foundations with initial stress. Compos. Struct. 2020, 244, 112297. [Google Scholar] [CrossRef]
- Miniaci, M.; Krushynska, A.; Bosia, F.; Pugno, N.M. Large scale mechanical metamaterials as seismic shields. New J. Phys. 2016, 18, 083041. [Google Scholar] [CrossRef]
- Liu, H.; Kuang, Z.B.; Cai, Z.M. Propagation of Bleustein–Gulyaev waves in a prestressed layered piezoelectric structure. Ultrasonics 2003, 41, 397–405. [Google Scholar] [CrossRef]
- Zhong, H.Z.; Yu, T. A weak form quadrature element method for plane elasticity problems. Appl. Math. Model. 2009, 33, 3801–3814. [Google Scholar] [CrossRef]
- Liu, X.N.; Shi, Z.F.; Mo, Y.L. Attenuation zones of initially stressed periodic mindlin plates on an elastic foundation. Int. J. Mech. Sci. 2016, 115–116, 12–23. [Google Scholar] [CrossRef] [Green Version]
- Yuan, S.; Du, J.N. Upper bound limit analysis using the weak form quadrature element method. Appl. Math. Model. 2018, 56, 551–563. [Google Scholar] [CrossRef]
- Yuan, S.; Du, J.N. Effective stress-based upper bound limit analysis of unsaturated soils using the weak form quadrature element method. Comput. Geotech. 2018, 98, 172–180. [Google Scholar] [CrossRef]
- Meng, L.K.; Cheng, Z.B.; Shi, Z.F. Vibration mitigation in saturated soil by periodic pile barriers. Comput. Geosci. 2020, 117, 103251. [Google Scholar] [CrossRef]
- Peer Ground Motion Database. 2012. Available online: http://peer.berkeley.edu/peer_ground_motion_database (accessed on 14 July 2020).
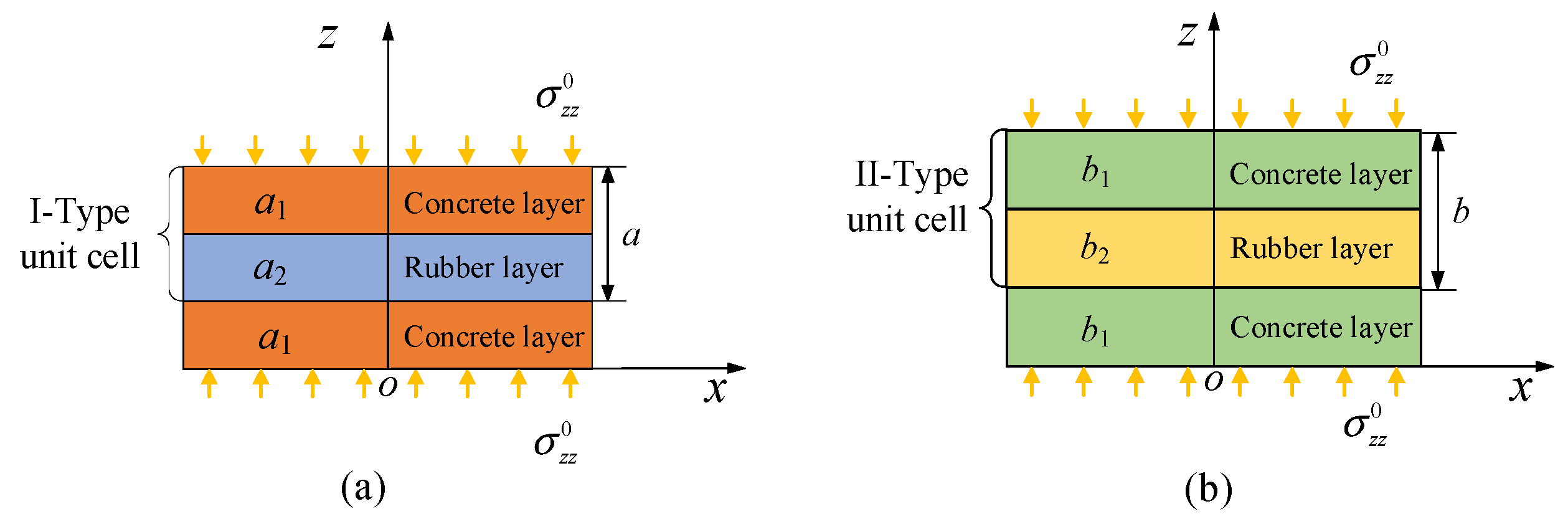
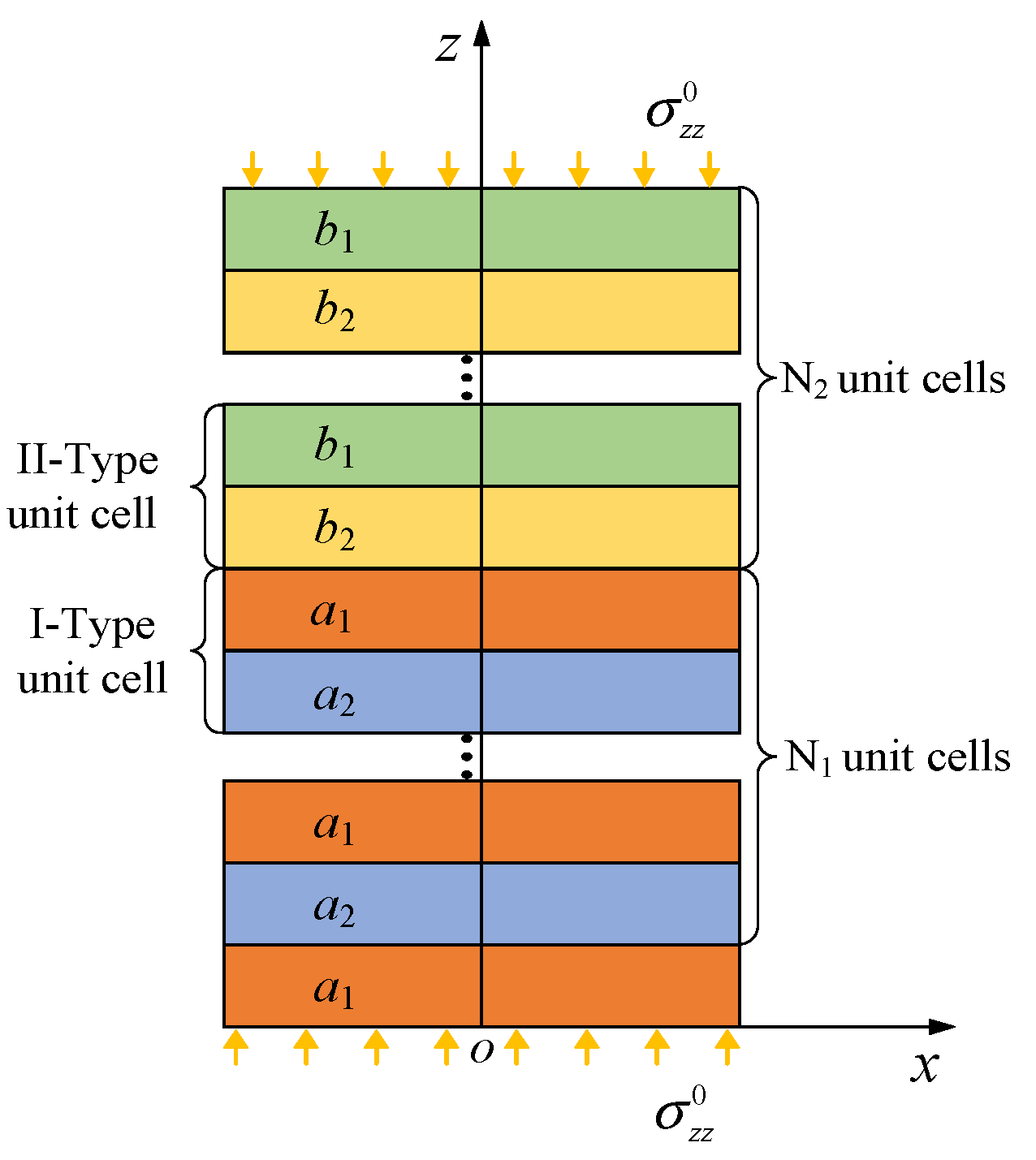


| Materials | Mass Density ρ (kg/m3) | Young Modulus E (GPa) | Poisson Ratio v |
|---|---|---|---|
| Concrete | 2300 | 25 | 0.330 |
| Rubber | 1300 | 1.37 × 10−4 | 0.463 |
| Earthquake (Record Place) | Magnitude (Date) | Acceleration Peak (Gal) |
|---|---|---|
| Whittier Narrows–02 (Big Tujunga Angeles Nat F) | 5.27 (4 October 1987) | 195.671 |
| Oroville–01 (Oroville Seismograph Station) | 5.89 (1 August 1975) | 86.434 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Ren, Y.; Song, X. Combined Attenuation Zones of Combined Layered Periodic Foundations. Appl. Sci. 2021, 11, 7114. https://doi.org/10.3390/app11157114
Liu X, Ren Y, Song X. Combined Attenuation Zones of Combined Layered Periodic Foundations. Applied Sciences. 2021; 11(15):7114. https://doi.org/10.3390/app11157114
Chicago/Turabian StyleLiu, Xinnan, Yiqiang Ren, and Xiaoruan Song. 2021. "Combined Attenuation Zones of Combined Layered Periodic Foundations" Applied Sciences 11, no. 15: 7114. https://doi.org/10.3390/app11157114
APA StyleLiu, X., Ren, Y., & Song, X. (2021). Combined Attenuation Zones of Combined Layered Periodic Foundations. Applied Sciences, 11(15), 7114. https://doi.org/10.3390/app11157114





