Semi-Supervised Time Series Anomaly Detection Based on Statistics and Deep Learning
Abstract
:1. Introduction
2. Background Knowledge
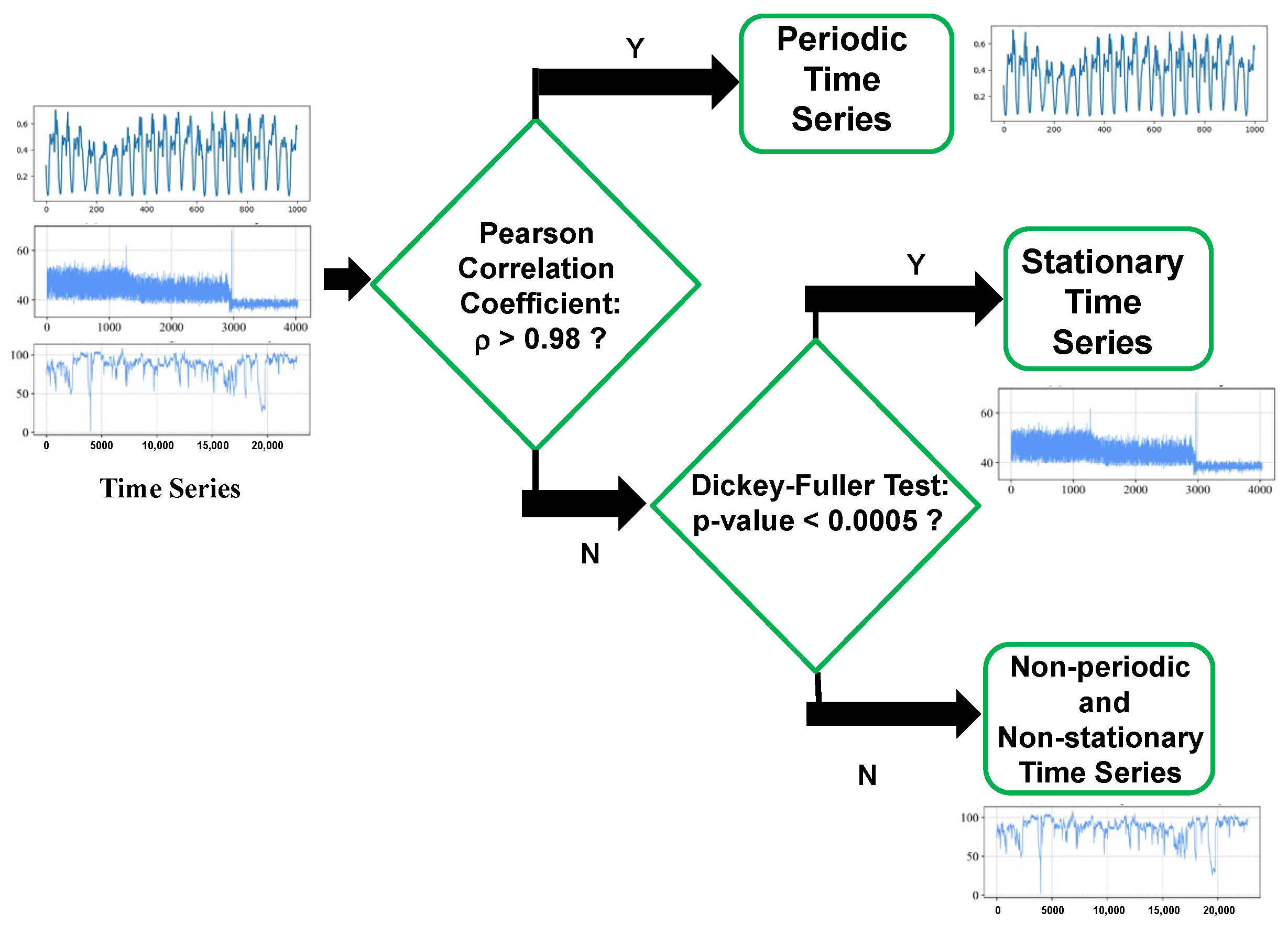
2.1. Time Series and Related Models
2.2. Pearson Correlation Coefficient
2.3. Dickey–Fuller Test
2.4. Discret Wavelet Transform
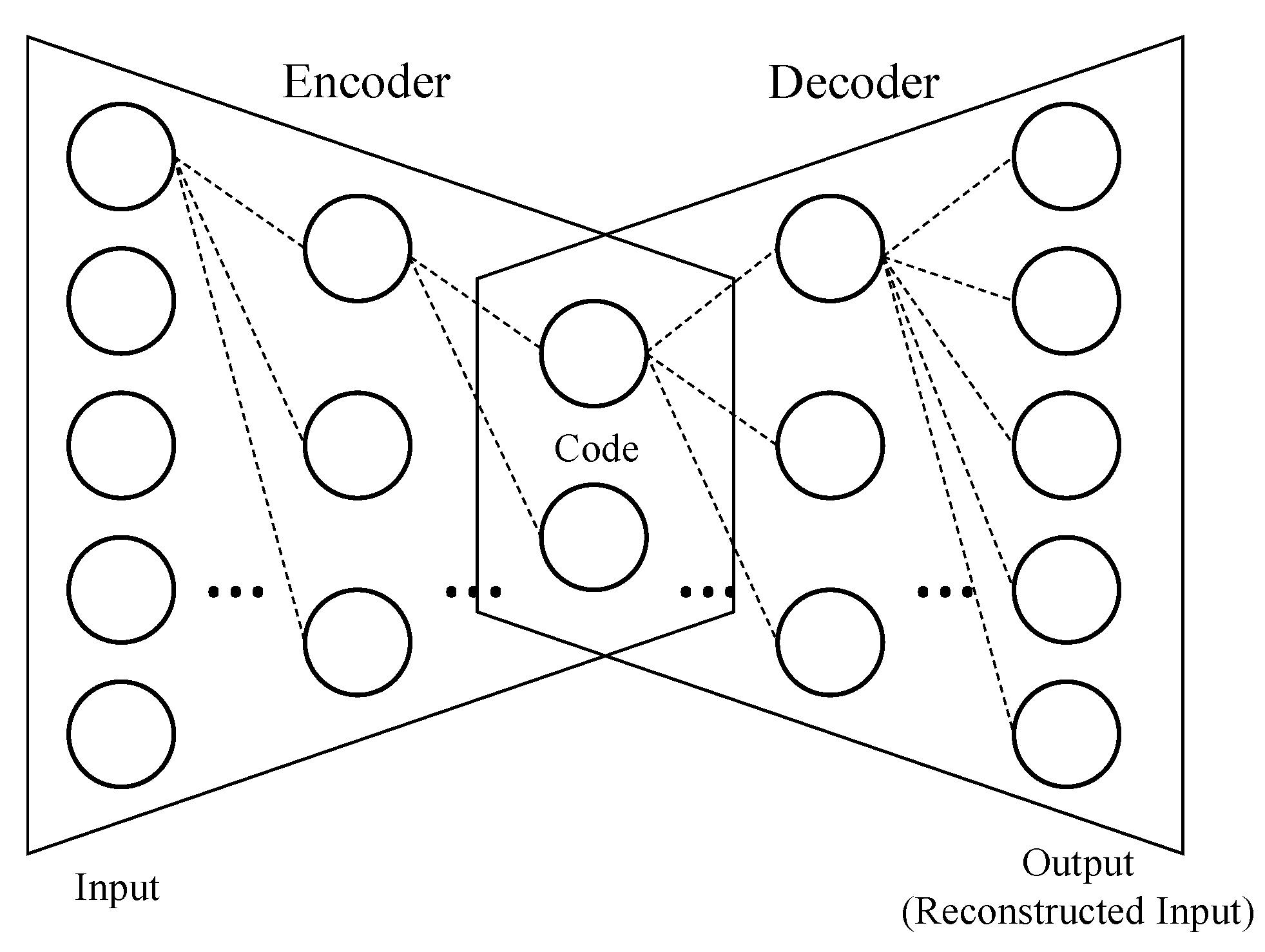
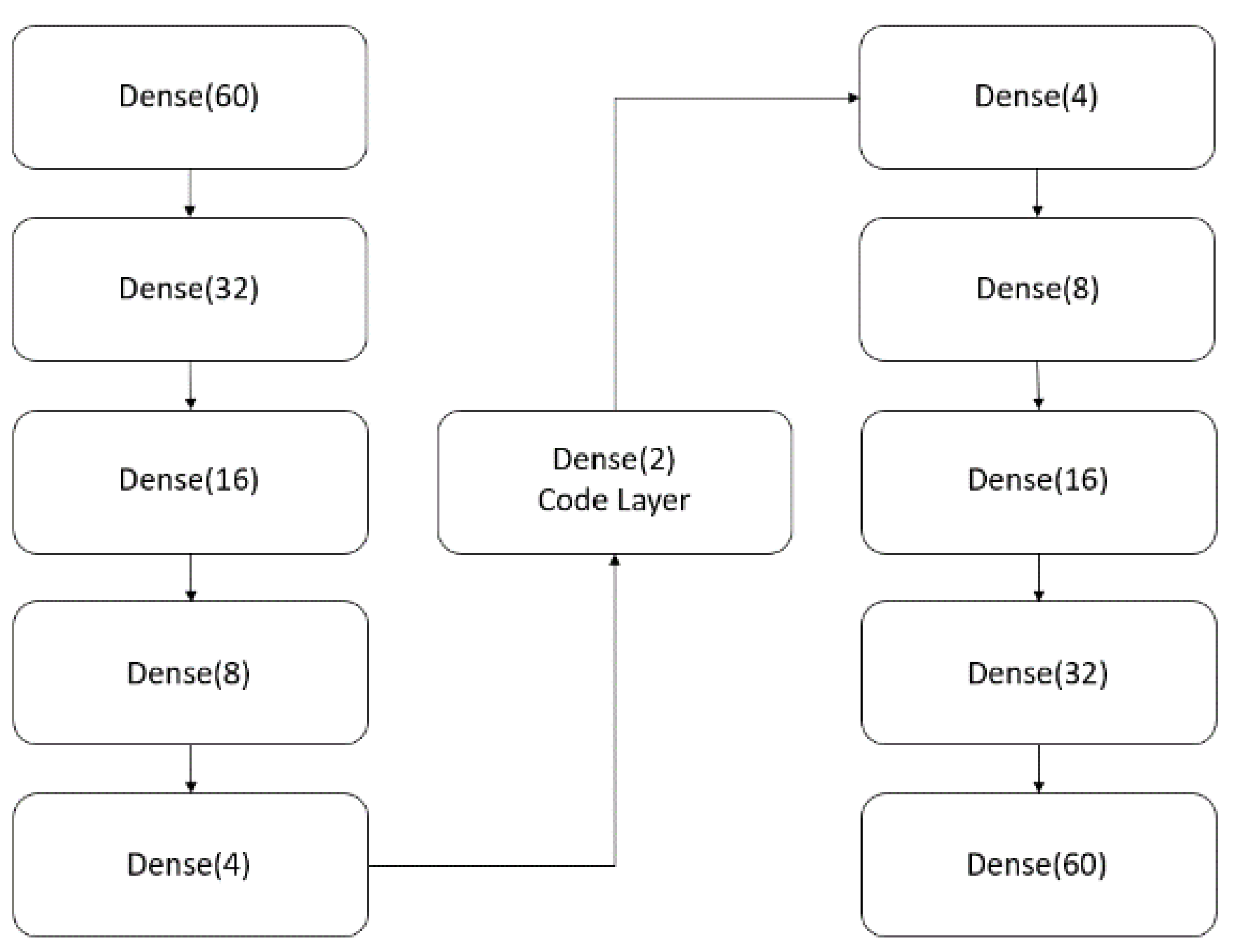
2.5. Autoencoder
3. Proposed Anomaly Detection Framework
3.1. Periodic Time Series Anomaly Detection
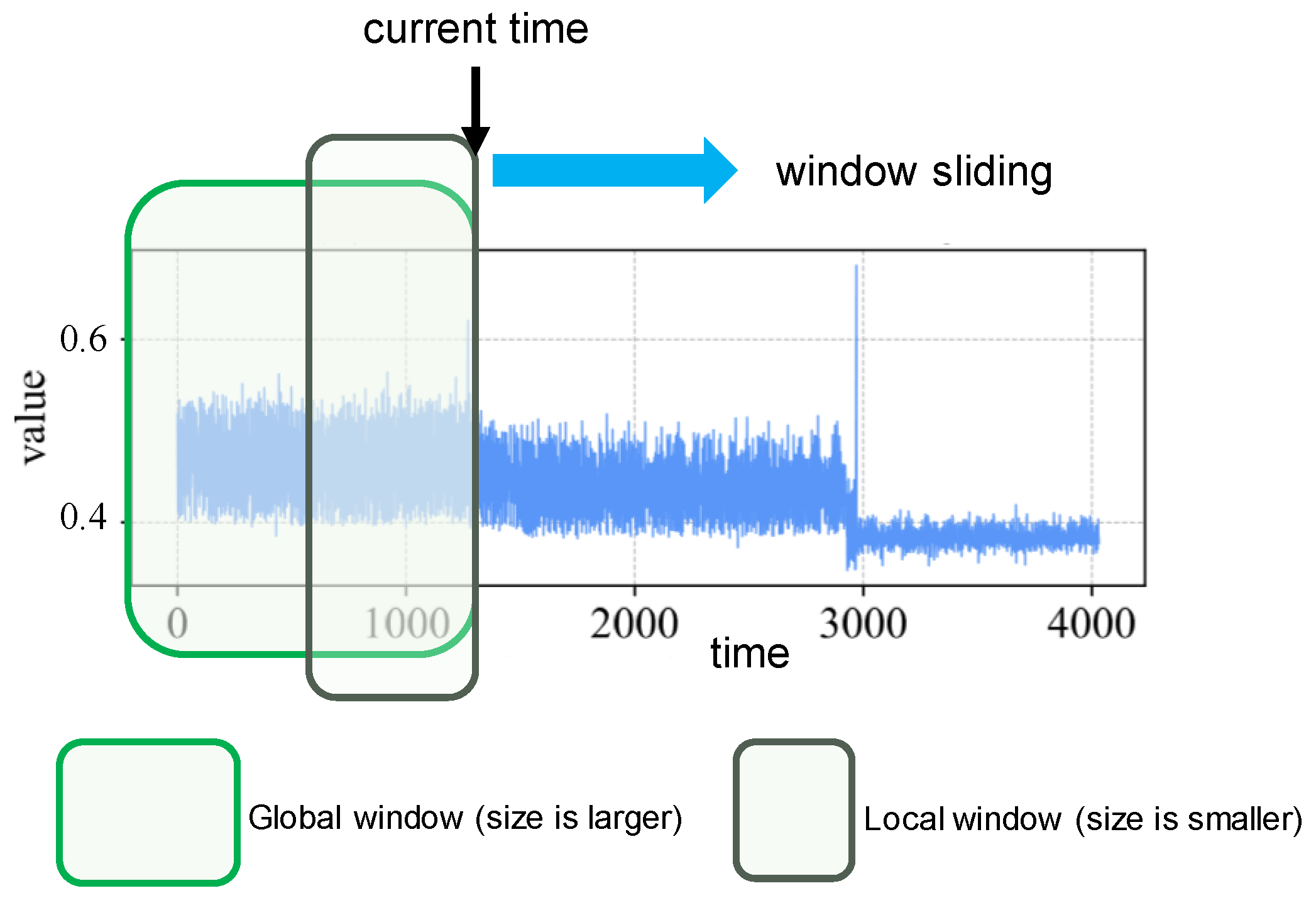
3.2. Stationary Time Series Anomaly Detection
3.3. Non-Periodic and Non-Stationary Time Series Anomaly Detection
3.4. Treshold Setting
3.5. Predecesors of Tri-CAD
4. Performance Evaluation and Comparison
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chandola, V.; Banerjee, A.; Kumar, V. Anomaly detection: A survey. ACM Comput. Surv. 2009, 41, 1–58. [Google Scholar] [CrossRef]
- Chalapathy, R.; Chawla, S. Deep learning for anomaly detection: A survey. arXiv 2019, arXiv:1901.03407. [Google Scholar]
- Zhang, J. Advancements of outlier detection: A survey. ICST Trans. Scalable Inf. Syst. 2013, 13, 1–26. [Google Scholar] [CrossRef] [Green Version]
- Gupta, M.; Gao, J.; Aggarwal, C.C.; Han, J. Outlier detection for temporal data: A survey. IEEE Trans. Knowl. Data Eng. 2013, 26, 2250–2267. [Google Scholar] [CrossRef]
- Pimentel, M.A.; Clifton, D.A.; Clifton, L.; Tarassenko, L. A review of novelty detection. Signal Process. 2014, 99, 215–249. [Google Scholar] [CrossRef]
- Zhao, Z.; Mehrotra, K.G.; Mohan, C.K. Online anomaly detection using random forest. In International Conference on Industrial, Engineering and Other Applications of Applied Intelligent Systems; Springer: Cham, Switzerland, June 2018; pp. 135–147. [Google Scholar]
- Beckman, R.J.; Cook, R.D. Outlier………. s. Technometrics 1983, 25, 119–149. [Google Scholar]
- Tripathi, A.; Yadav, D.R. Outlier detection in big data using optimized Orion technique. Int. J. Curr. Res. Life Sci. 2018, 7, 1204–1207. [Google Scholar]
- Al-khatib, A.A.; Balfaqih, M.; Khelil, A. A survey on outlier detection in Internet of Things big data. In Big Data-Enabled Internet of Things; IET Digital Library: London, UK, 2019; Chapter 11; pp. 225–272. [Google Scholar]
- Shahid, N.; Naqvi, I.H.; Qaisar, S.B. Characteristics and classification of outlier detection techniques for wireless sensor networks in harsh environments: A survey. Artif. Intell. Rev. 2015, 43, 193–228. [Google Scholar] [CrossRef]
- Van, N.T.; Thinh, T.N. An anomaly-based network intrusion detection system using deep learning. In Proceedings of the 2017 International Conference on System Science and Engineering (ICSSE), Ho Chi Minh City, Vietnam, 21–23 July 2017; pp. 210–214. [Google Scholar]
- Maimó, L.F.; Gómez, Á.L.P.; Clemente, F.J.G.; Pérez, M.G.; Pérez, G.M. A self-adaptive deep learning-based system for anomaly detection in 5G networks. IEEE Access 2018, 6, 7700–7712. [Google Scholar] [CrossRef]
- Lu, N.; Du, Q.; Sun, L.; Ren, P. Traffic-driven intrusion detection for massive MTC towards 5G networks. In Proceedings of the IEEE INFOCOM 2018-IEEE Conference on Computer Communications Workshops (INFOCOM WKSHPS), Honolulu, HI, USA, 15–19 April 2018; pp. 426–431. [Google Scholar]
- Choi, H.; Kim, M.; Lee, G.; Kim, W. Unsupervised learning approach for network intrusion detection system using autoencoders. J. Supercomput. 2019, 75, 5597–5621. [Google Scholar] [CrossRef]
- Choi, S.; Youm, S.; Kang, Y.S. Development of scalable on-line anomaly detection system for autonomous and adaptive manufacturing processes. Appl. Sci. 2019, 9, 4502. [Google Scholar] [CrossRef] [Green Version]
- Wang, P.; Yang, L.T.; Nie, X.; Ren, Z.; Li, J.; Kuang, L. Data-driven software defined network attack detection: State-of-the-art and perspectives. Inf. Sci. 2020, 513, 65–83. [Google Scholar] [CrossRef]
- Krishnaveni, S.; Vigneshwar, P.; Kishore, S.; Jothi, B.; Sivamohan, S. Anomaly-based intrusion detection system using support vector machine. In Artificial Intelligence and Evolutionary Computations in Engineering Systems; Springer: Singapore, 2020; pp. 723–731. [Google Scholar]
- Kubota, T.; Yamamoto, W. Anomaly detection from online monitoring of system operations using recurrent neural network. Procedia Manuf. 2019, 30, 83–89. [Google Scholar] [CrossRef]
- Lindemann, B.; Fesenmayr, F.; Jazdi, N.; Weyrich, M. Anomaly detection in discrete manufacturing using self-learning approaches. Procedia CIRP 2019, 79, 313–318. [Google Scholar] [CrossRef]
- Hsieh, R.J.; Chou, J.; Ho, C.H. Unsupervised online anomaly detection on multivariate sensing time series data for smart manufacturing. In Proceedings of the 2019 IEEE 12th Conference on Service-Oriented Computing and Applications (SOCA), Kaohsiung, Taiwan, 18–21 November 2019; pp. 90–97. [Google Scholar]
- Wu, J.; Zhao, Z.; Sun, C.; Yan, R.; Chen, X. Fault-attention generative probabilistic adversarial autoencoder for machine anomaly detection. IEEE Trans. Ind. Informatics 2020, 16, 7479–7488. [Google Scholar] [CrossRef]
- Nawaratne, R.; Alahakoon, D.; De Silva, D.; Yu, X. Spatiotemporal anomaly detection using deep learning for real-time video surveillance. IEEE Trans. Ind. Inform. 2019, 16, 393–402. [Google Scholar] [CrossRef]
- Singh, G.; Kapoor, R.; Khosla, A.K. Intelligent anomaly detection video surveillance systems for smart cities. In Driving the Development, Management, and Sustainability of Cognitive Cities; IGI Global: Hershey, PA, USA, 2019; pp. 163–182. [Google Scholar]
- Di Mauro, N.; Ferilli, S. Unsupervised LSTMs-based learning for anomaly detection in highway traffic data. In International Symposium on Methodologies for Intelligent Systems; Springer: Cham, Switzerland, October 2018; pp. 281–290. [Google Scholar]
- Xu, M.; Wu, J.; Wang, H.; Cao, M. Anomaly detection in road networks using sliding-window tensor factorization. IEEE Trans. Intell. Transp. Syst. 2019, 20, 4704–4713. [Google Scholar] [CrossRef]
- Malini, N.; Pushpa, M. Analysis on credit card fraud identification techniques based on KNN and outlier detection. In Proceedings of the 2017 Third International Conference on Advances in Electrical, Electronics, Information, Communication and Bio-Informatics (AEEICB), Chennai, India, 27–28 February 2017; pp. 255–258. [Google Scholar]
- Popat, R.R.; Chaudhary, J. A survey on credit card fraud detection using machine learning. In Proceedings of the 2018 2nd International Conference on Trends in Electronics and Informatics (ICOEI), Tirunelveli, India, 11–12 May 2018; pp. 1120–1125. [Google Scholar]
- Sheshasaayee, A.; Thomas, S.S. A purview of the impact of supervised learning methodologies on health insurance fraud detection. In Information Systems Design and Intelligent Applications; Springer: Singapore, 2018; pp. 978–984. [Google Scholar]
- Thill, M.; Däubener, S.; Konen, W.; Bäck, T. Anomaly detection in electrocardiogram readings with stacked LSTM networks. In Proceedings of the 19th Conference Information Technologies-Applications and Theory (ITAT 2019), Donovaly, Slovakia, 20–24 September 2019; pp. 17–25. [Google Scholar]
- Rastatter, S.; Moe, T.; Gangopadhyay, A.; Weaver, A. Abnormal Traffic Pattern Detection in Real-Time Financial Transactions (No 827). Available online: https://easychair.org/publications/preprint_open/CKvQ (accessed on 21 July 2021).
- Tam, N.T.; Weidlich, M.; Zheng, B.; Yin, H.; Hung NQ, V.; Stantic, B. From anomaly detection to rumour detection using data streams of social platforms. Proc. VLDB Endow. 2019, 12, 1016–1029. [Google Scholar] [CrossRef] [Green Version]
- Wu, H.S. A survey of research on anomaly detection for time series. In Proceedings of the 2016 13th International Computer Conference on Wavelet Active Media Technology and Information Processing (ICCWAMTIP), Chengdu, China, 16–18 December 2016; pp. 426–431. [Google Scholar]
- Islam, M.R.; Sultana, N.; Moni, M.A.; Sarkar, P.C.; Rahman, B. A comprehensive survey of time series anomaly detection in online social network data. Int. J. Comput. Appl. 2017, 180, 13–22. [Google Scholar]
- Cook, A.; Mısırlı, G.; Fan, Z. Anomaly detection for IoT time-series data: A survey. IEEE Internet Things J. 2019, 7, 6481–6494. [Google Scholar] [CrossRef]
- Blázquez-García, A.; Conde, A.; Mori, U.; Lozano, J.A. A review on outlier/anomaly detection in time series data. arXiv 2019, arXiv:2002.04236. [Google Scholar]
- Pearson, K. Notes on regression and inheritance in the case of two parents. Proc. R. Soc. Lond. 1895, 58, 240–242. [Google Scholar]
- Dickey, D.A.; Fuller, W.A. Distribution of the estimators for autoregressive time series with a unit root. J. Am. Stat. Assoc. 1979, 74, 427–431. [Google Scholar]
- Chui, C.K. An Introduction to Wavelets; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning Internal Representations by Error Propagation. Available online: https://apps.dtic.mil/sti/pdfs/ADA164453.pdf (accessed on 21 July 2021).
- Numenta Anomaly Benchmark. Available online: https://github.com/numenta/NAB (accessed on 15 March 2020).
- Xu, S.; Chan, H.K.; Zhang, T. Forecasting the demand of the aviation industry using hybrid time series SARIMA-SVR approach. Transp. Res. Part E Logist. Transp. Rev. 2019, 122, 169–180. [Google Scholar] [CrossRef]
- Cleveland, R.; Cleveland, W.S.; McRae, J.E.; Terpenning, I.J. STL: A seasonal-trend decomposition procedure based on loess (with discussion). J. Off. Stat. 1990, 6, 3–73. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Lee, S.; Kim, H.K. ADSaS: Comprehensive real-time anomaly detection system. In International Workshop on Information Security Applications; Springer: Cham, Switzerland, 2018; pp. 29–41. [Google Scholar]
- Kao, J.B.; Jiang, J.R. Anomaly detection for univariate time series with statistics and deep learning. In Proceedings of the 2019 IEEE Eurasia Conference on IOT, Communication and Engineering (ECICE), Yunlin, Taiwan, 3–6 October 2019; pp. 404–407. [Google Scholar]
- Li, Y.L.; Jiang, J.R. Anomaly detection for non-stationary and non-periodic univariate time series. In Proceedings of the 2020 IEEE Eurasia Conference on IOT, Communication and Engineering (ECICE), Yunlin, Taiwan, 23–25 October 2020; pp. 177–179. [Google Scholar]
- Ruppert, D.; Matteson, D.S. Time series models: Basics. In Statistics and Data Analysis for Financial Engineering; Springer: New York, NY, USA, 2015; pp. 307–360. [Google Scholar]
- Konasani, V.R.; Kadre, S. Time-series analysis and forecasting. In Practical Business Analytics Using SAS; Apress: Berkeley, CA, USA, 2015; pp. 441–507. [Google Scholar]
- Box GE, P.; Jenkins, G.M. Some comments on a paper by Chatfield and Prothero and on a review by Kendall. J. R. Stat. Society. Ser. A 1973, 136, 337–352. [Google Scholar] [CrossRef]
- Konasani, V.R.; Kadre, S. Multiple regression analysis. In Practical Business Analytics Using SAS; Apress: Berkeley, CA, USA, 2015; pp. 351–400. [Google Scholar]
- Cleveland, W.S.; Loader, C. Smoothing by local regression: Principles and methods. In Statistical Theory and Computational Aspects of Smoothing; Physica-Verlag HD: Heidelberg, Germany, 1996; pp. 10–49. [Google Scholar]
- Heymann, S.; Latapy, M.; Magnien, C. Outskewer: Using skewness to spot outliers in samples and time series. In Proceedings of the 2012 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining, Istanbul, Turkey, 26–29 August 2012; pp. 527–534. [Google Scholar]
- Alhakami, W.; ALharbi, A.; Bourouis, S.; Alroobaea, R.; Bouguila, N. Network anomaly intrusion detection using a nonparametric Bayesian approach and feature selection. IEEE Access 2019, 7, 52181–52190. [Google Scholar] [CrossRef]
- Hosseini, A.; Sarrafzadeh, M. Unsupervised prediction of negative health events ahead of time. In Proceedings of the 2019 IEEE EMBS International Conference on Biomedical & Health Informatics (BHI), Chichago, IL, USA, 19–22 May 2019; pp. 1–4. [Google Scholar]



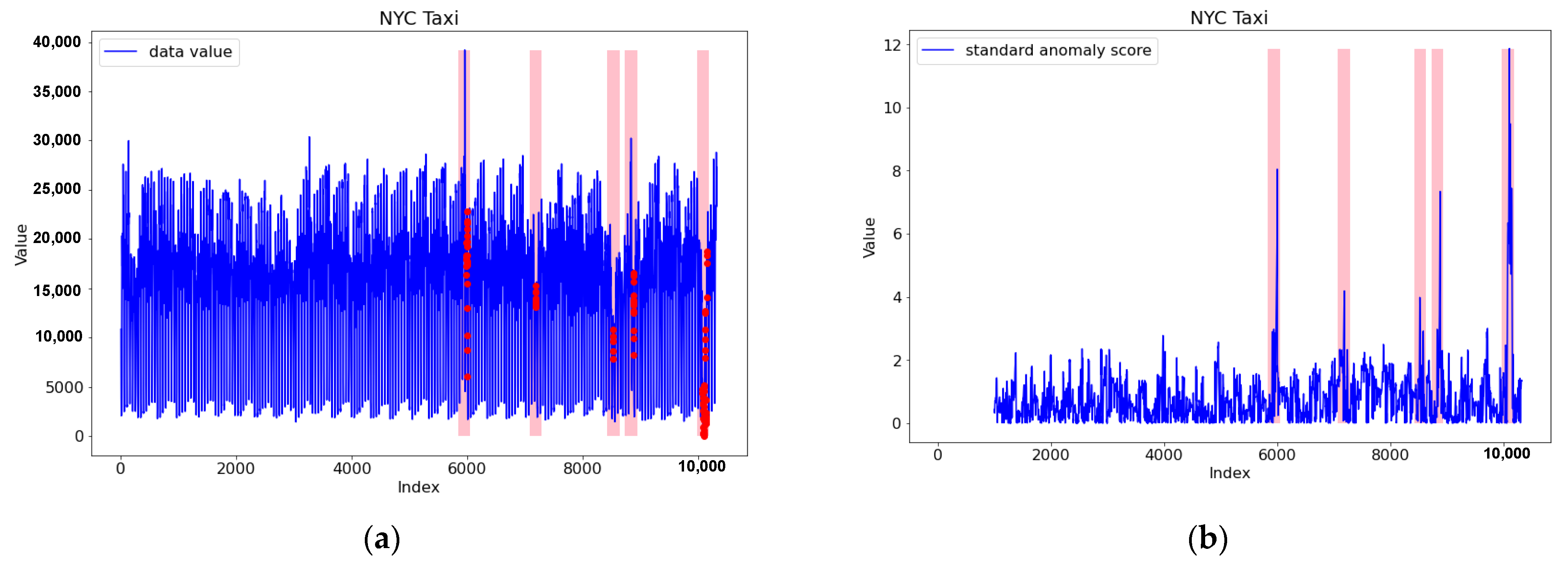

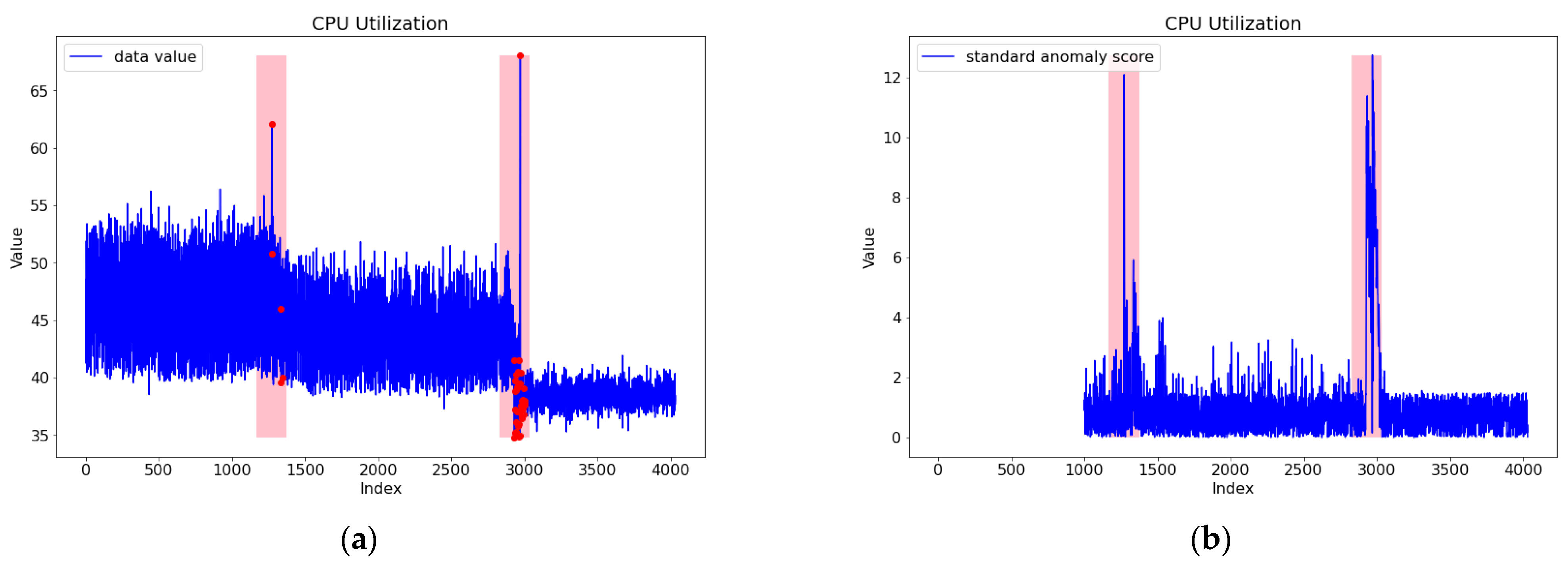
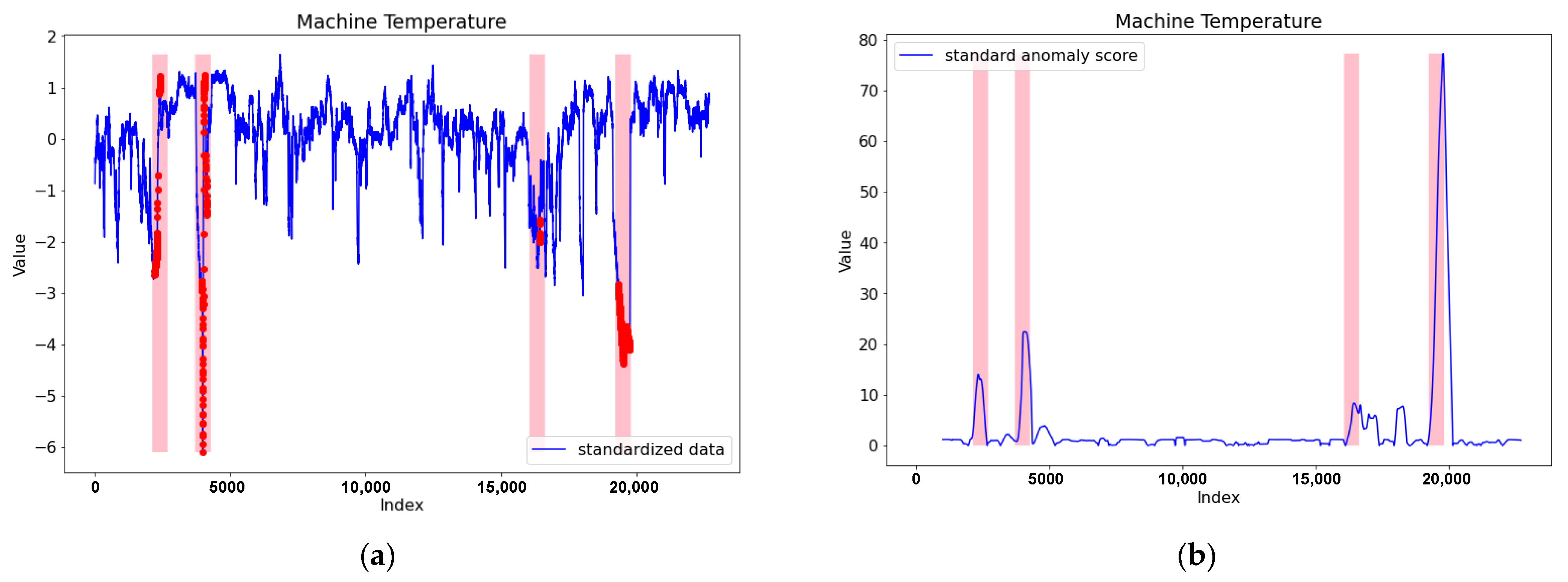


| Time Series | Class | Fixed Window Size (fws) | Metrics | STL only | SARIMA only | LSTM only | LSTM with STL | ADSaS | Proposed Framework Tri-CAD |
|---|---|---|---|---|---|---|---|---|---|
| NAB NYC Taxi | Class 1 | 206 | Precision Recall F1-score | 0.533 0.889 0.667 | 0.000 0.000 0.000 | 0.176 0.333 0.231 | 0.161 1.000 0.277 | 1.000 1.000 1.000 | 1.000 1.000 1.000 |
| NAB CPU Utilization | Class 2 | 200 | Precision Recall F1-score | 0.800 1.000 0.889 | 0.143 0.250 0.182 | 0.833 1.000 0.909 | 0.308 1.000 0.471 | 1.000 0.250 0.400 | 1.000 1.000 1.000 |
| NAB Machine Temperature | Class 3 | 566 | Precision Recall F1-score | 0.250 0.222 0.235 | 0.000 0.000 0.000 | 0.049 0.222 0.080 | 0.059 0.625 0.108 | 1.000 0.500 0.667 | 1.000 1.000 1.000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, J.-R.; Kao, J.-B.; Li, Y.-L. Semi-Supervised Time Series Anomaly Detection Based on Statistics and Deep Learning. Appl. Sci. 2021, 11, 6698. https://doi.org/10.3390/app11156698
Jiang J-R, Kao J-B, Li Y-L. Semi-Supervised Time Series Anomaly Detection Based on Statistics and Deep Learning. Applied Sciences. 2021; 11(15):6698. https://doi.org/10.3390/app11156698
Chicago/Turabian StyleJiang, Jehn-Ruey, Jian-Bin Kao, and Yu-Lin Li. 2021. "Semi-Supervised Time Series Anomaly Detection Based on Statistics and Deep Learning" Applied Sciences 11, no. 15: 6698. https://doi.org/10.3390/app11156698
APA StyleJiang, J.-R., Kao, J.-B., & Li, Y.-L. (2021). Semi-Supervised Time Series Anomaly Detection Based on Statistics and Deep Learning. Applied Sciences, 11(15), 6698. https://doi.org/10.3390/app11156698






