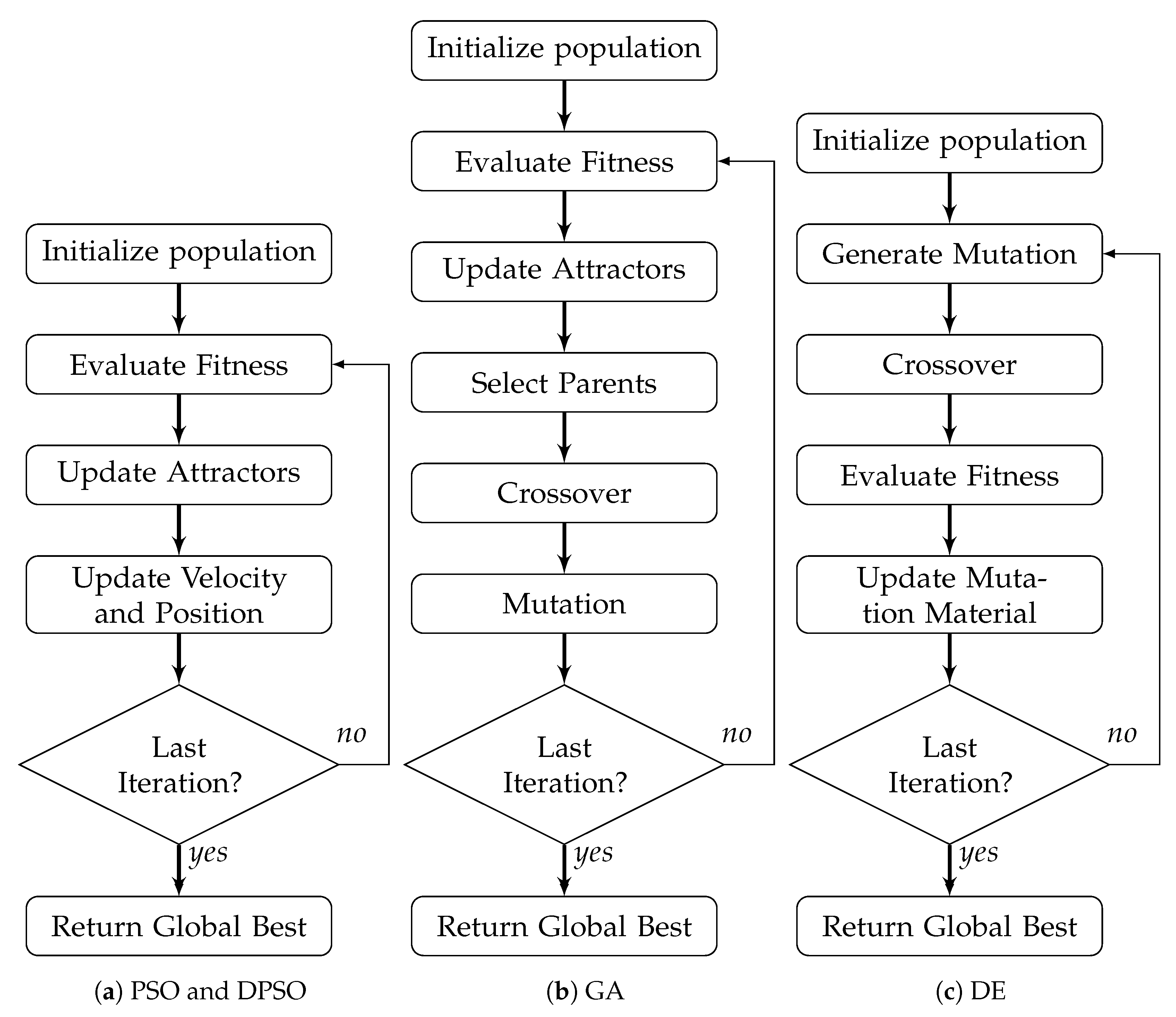
Appendix A. Additional Tables and Graphs
Table A1.
Global best self-tuning parameters for 7 dimensions.
Table A1.
Global best self-tuning parameters for 7 dimensions.
| DPSO | c0 | c1 | c2 | c3 | c4 | c5 | c6 |
| 0.862056 | 0.859008 | 0.620299 | 0.526893 | 0.103819 | 0.986512 | 0.801248 |
| PSO | | | | |
| 0.107710 | 0.741607 | 0.492210 | |
| GA | | | |
| 0.974085 | 0.558012 | |
| DE | | | |
| 0.251732 | 0.000000 | |
Table A2.
Global best self-tuning parameters for 14 dimensions.
Table A2.
Global best self-tuning parameters for 14 dimensions.
| DPSO | c0 | c1 | c2 | c3 | c4 | c5 | c6 |
| 0.507646 | 0.438668 | 1.000000 | 0.308361 | 1.000000 | 0.655705 | 0.970521 |
| PSO | | | | |
| 0.649608 | 0.594950 | 0.175723 | |
| GA | | | |
| 0.899098 | 0.233414 | |
| DE | | | |
| 0.470144 | 0.544929 | |
Table A3.
Global best self-tuning parameters for 21 dimensions.
Table A3.
Global best self-tuning parameters for 21 dimensions.
| DPSO | c0 | c1 | c2 | c3 | c4 | c5 | c6 |
| 0.734627 | 0.712416 | 0.891312 | 1.000000 | 0.767508 | 0.853393 | 0.786354 |
| PSO | | | | |
| 0.715330 | 0.386808 | 0.897650 | |
| GA | | | |
| 0.390245 | 0.092636 | |
| DE | | | |
| 1.000000 | 0.532237 | |
Table A4.
Fitness w.r.t. each function problem with 7 dimensions and the resulting ranking: rank 1 (best), rank 2, rank 3, and rank 4.
Table A4.
Fitness w.r.t. each function problem with 7 dimensions and the resulting ranking: rank 1 (best), rank 2, rank 3, and rank 4.
| Function | DPSO | PSO | GA | DE |
|---|
| Ave | 1.234 × 10 | 1.424 × 10 | 8.956 × 10 | 3.439 × 10 |
| Std | 2.252 × 10 | 2.910 × 10 | 0.000 | 1.342 × 10 |
| Ave | 1.641 × 10 | 3.849 × 10 | 1.326 × 10 | 2.560 × 10 |
| Std | 2.328 × 10 | 1.831 × 10 | 4.470 × 10 | 1.091 × 10 |
| Ave | 2.402 × 10 | 6.209 × 10 | 3.242 × 10 | 5.608 × 10 |
| Std | 9.313 × 10 | 2.289 × 10 | 1.397 × 10 | 2.328 × 10 |
| Ave | 1.257 × 10 | 2.950 × 10 | 9.232 × 10 | 3.505 × 10 |
| Std | 6.755 × 10 | 4.504 × 10 | 1.801 × 10 | 9.904 × 10 |
| Ave | 1.235 × 10 | 1.626 × 10 | 1.039 × 10 | 1.293 × 10 |
| Std | 0.000 | 6.104 × 10 | 1.526 × 10 | 0.000 |
| Ave | 9.617 × 10 | 3.099 × 10 | 1.026 × 10 | 5.356 × 10 |
| Std | 3.492 × 10 | 1.221 × 10 | 1.526 × 10 | 3.052 × 10 |
| Ave | 4.011 × 10 | 6.085 × 10 | 3.239 × 10 | 4.845 × 10 |
| Std | 1.421 × 10 | 2.132 × 10 | 1.421 × 10 | 3.553 × 10 |
| Ave | 4.172 × 10 | 6.060 × 10 | 3.821 × 10 | 2.000 × 10 |
| Std | 2.132 × 10 | 3.553 × 10 | 2.842 × 10 | 3.553 × 10 |
| Ave | 4.172 × 10 | 5.472 × 10 | 3.821 × 10 | 3.983 × 10 |
| Std | 2.132 × 10 | 3.553 × 10 | 2.842 × 10 | 1.421 × 10 |
| Ave | 1.007 | 1.248 × 10 | 2.851 × 10 | 6.054 × 10 |
| Std | 4.441 × 10 | 1.819 × 10 | 2.274 × 10 | 2.842 × 10 |
| Ave | 8.802 × 10 | 9.429 × 10 | 2.645 × 10 | 1.889 × 10 |
| Std | 7.276 × 10 | 4.366 × 10 | 1.091 × 10 | 0.000 |
| Ave | 1.179 × 10 | 1.303 × 10 | 1.277 × 10 | 4.141 × 10 |
| Std | 5.329 × 10 | 8.731 × 10 | 9.095 × 10 | 0.000 |
| Ave | 3.482 × 10 | 1.310 × 10 | 2.987 × 10 | 8.200 × 10 |
| Std | 2.842 × 10 | 0.000 | 7.105 × 10 | 4.263 × 10 |
| Ave | 2.288 × 10 | 1.189 × 10 | 5.204 × 10 | 1.364 × 10 |
| Std | 7.105 × 10 | 7.105 × 10 | 3.553 × 10 | 2.842 × 10 |
| Ave | 2.444 × 10 | 1.990 × 10 | 8.907 × 10 | 1.593 × 10 |
| Std | 0.000 | 1.137 × 10 | 1.421 × 10 | 5.329 × 10 |
| Ave | 1.913 × 10 | 2.357 | 1.956 | 1.945 |
| Std | 1.388 × 10 | 0.000 | 4.441 × 10 | 8.882 × 10 |
| Ave | 1.778 | 2.448 | 1.618 | 1.963 |
| Std | 1.332 × 10 | 1.332 × 10 | 8.882 × 10 | 1.332 × 10 |
| Ave | 1.000 | 2.051 | 1.782 | 1.924 |
| Std | 4.441 × 10 | 4.441 × 10 | 1.110 × 10 | 6.661 × 10 |
| Ave | 7.162 × 10 | 2.955 × 10 | 1.094 × 10 | 8.071 × 10 |
| Std | 5.684 × 10 | 1.705 × 10 | 0.000 | 4.263 × 10 |
| Ave | 2.052 × 10 | 6.003 × 10 | 6.232 × 10 | 3.490 |
| Std | 5.684 × 10 | 1.137 × 10 | 4.547 × 10 | 1.332 × 10 |
| Ave | 1.812 × 10 | 4.409 × 10 | 3.381 × 10 | 2.830 × 10 |
| Std | 1.137 × 10 | 2.274 × 10 | 5.684 × 10 | 1.705 × 10 |
| Ave | 2.223 × 10 | 1.836 × 10 | 4.693 × 10 | 9.548 |
| Std | 0.000 | 1.421 × 10 | 0.000 | 0.000 |
| Ave | 1.660 × 10 | 1.291 × 10 | 2.451 × 10 | 1.630 × 10 |
| Std | 1.066 × 10 | 5.684 × 10 | 1.421 × 10 | 7.105 × 10 |
| Ave | 6.700 | 1.643 × 10 | 2.302 × 10 | 8.036 |
| Std | 1.776 × 10 | 0.000 | 1.066 × 10 | 3.553 × 10 |
Table A5.
Fitness w.r.t. each function problem with 14 dimensions and the resulting ranking: rank 1 (best), rank 2, rank 3, and rank 4.
Table A5.
Fitness w.r.t. each function problem with 14 dimensions and the resulting ranking: rank 1 (best), rank 2, rank 3, and rank 4.
| Function | DPSO | PSO | GA | DE |
|---|
| Ave | 7.483 × 10 | 2.379 × 10 | 2.393 × 10 | 2.127 × 10 |
| Std | 0.000 | 4.657 × 10 | 9.375 × 10 | 8.527 × 10 |
| Ave | 7.640 × 10 | 1.753 × 10 | 1.680 × 10 | 3.327 × 10 |
| Std | 2.728 × 10 | 5.821 × 10 | 8.731 × 10 | 5.684 × 10 |
| Ave | 7.064 × 10 | 8.116 × 10 | 1.452 × 10 | 2.590 × 10 |
| Std | 1.164 × 10 | 3.603 × 10 | 2.684 × 10 | 0.000 |
| Ave | 2.018 × 10 | 1.638 × 10 | 1.943 × 10 | 2.578 × 10 |
| Std | 1.126 × 10 | 6.872 × 10 | 3.603 × 10 | 6.400 × 10 |
| Ave | 7.842 × 10 | 1.378 × 10 | 4.856 × 10 | 3.923 × 10 |
| Std | 2.749 × 10 | 0.000 | 1.526 × 10 | 1.221 × 10 |
| Ave | 4.560 × 10 | 8.607 × 10 | 2.788 × 10 | 3.949 × 10 |
| Std | 0.000 | 2.361 × 10 | 7.629 × 10 | 3.277 × 10 |
| Ave | 7.538 × 10 | 8.185 × 10 | 6.799 × 10 | 7.900 × 10 |
| Std | 0.000 | 4.263 × 10 | 4.263 × 10 | 1.421 × 10 |
| Ave | 8.224 × 10 | 8.116 × 10 | 6.852 × 10 | 6.462 × 10 |
| Std | 0.000 | 0.000 | 4.263 × 10 | 0.000 |
| Ave | 8.228 × 10 | 8.116 × 10 | 6.852 × 10 | 6.462 × 10 |
| Std | 4.263 × 10 | 0.000 | 4.263 × 10 | 0.000 |
| Ave | 1.963 × 10 | 5.403 × 10 | 2.195 × 10 | 3.387 × 10 |
| Std | 7.276 × 10 | 3.492 × 10 | 2.910 × 10 | 5.684 × 10 |
| Ave | 3.243 × 10 | 1.549 × 10 | 2.234 × 10 | 6.067 × 10 |
| Std | 2.183 × 10 | 1.164 × 10 | 1.397 × 10 | 4.547 × 10 |
| Ave | 7.982 × 10 | 2.034 × 10 | 2.279 × 10 | 8.108 × 10 |
| Std | 5.821 × 10 | 7.451 × 10 | 2.910 × 10 | 4.366 × 10 |
| Ave | 6.891 × 10 | 1.443 × 10 | 2.789 × 10 | 3.996 × 10 |
| Std | 1.421 × 10 | 6.821 × 10 | 1.705 × 10 | 2.842 × 10 |
| Ave | 7.068 × 10 | 7.193 × 10 | 2.165 × 10 | 1.123 × 10 |
| Std | 2.842 × 10 | 4.547 × 10 | 0.000 | 5.684 × 10 |
| Ave | 1.647 × 10 | 2.841 × 10 | 2.389 × 10 | 7.673 × 10 |
| Std | 8.527 × 10 | 1.705 × 10 | 1.137 × 10 | 4.263 × 10 |
| Ave | 2.256 | 3.689 | 2.932 | 3.500 |
| Std | 8.882 × 10 | 2.665 × 10 | 1.332 × 10 | 1.332 × 10 |
| Ave | 2.663 | 3.510 | 2.897 | 2.871 |
| Std | 0.000 | 1.332 × 10 | 1.332 × 10 | 4.441 × 10 |
| Ave | 2.540 | 2.970 | 2.960 | 3.017 |
| Std | 4.441 × 10 | 2.220 × 10 | 4.441 × 10 | 8.882 × 10 |
| Ave | 6.945 × 10 | 1.831 × 10 | 1.122 × 10 | 1.005 × 10 |
| Std | 1.137 × 10 | 9.095 × 10 | 2.274 × 10 | 6.821 × 10 |
| Ave | 1.708 × 10 | 2.040 × 10 | 6.648 × 10 | 5.270 |
| Std | 0.000 | 4.547 × 10 | 3.411 × 10 | 8.882 × 10 |
| Ave | 1.545 × 10 | 1.397 × 10 | 6.831 × 10 | 3.054 × 10 |
| Std | 8.527 × 10 | 0.000 | 0.000 | 0.000 |
| Ave | 2.142 × 10 | 7.904 × 10 | 3.584 × 10 | 2.357 × 10 |
| Std | 0.000 | 9.095 × 10 | 1.819 × 10 | 0.000 |
| Ave | 9.540 × 10 | 6.300 × 10 | 7.769 × 10 | 4.672 × 10 |
| Std | 4.263 × 10 | 7.105 × 10 | 1.137 × 10 | 2.132 × 10 |
| Ave | 5.050 × 10 | 5.681 × 10 | 1.995 × 10 | 3.500 × 10 |
| Std | 1.421 × 10 | 7.105 × 10 | 5.684 × 10 | 7.105 × 10 |
Table A6.
Fitness w.r.t. each function problem with 21 dimensions and the resulting ranking: rank 1 (best), rank 2, rank 3, and rank 4.
Table A6.
Fitness w.r.t. each function problem with 21 dimensions and the resulting ranking: rank 1 (best), rank 2, rank 3, and rank 4.
| Function | DPSO | PSO | GA | DE |
|---|
| 1.375 × 10 | 6.121 × 10 | 6.249 × 10 | 9.395 × 10 |
| Std | 0.000 | 0.000 | 0.000 | 3.815 × 10 |
| 2.600 × 10 | 2.824 × 10 | 2.417 × 10 | 5.773 × 10 |
| Std | 1.490 × 10 | 0.000 | 9.537 × 10 | 2.794 × 10 |
| 2.401 × 10 | 4.489 × 10 | 1.091 × 10 | 1.657 × 10 |
| Std | 8.731 × 10 | 9.766 × 10 | 3.725 × 10 | 6.400 × 10 |
| 2.028 × 10 | 5.324 × 10 | 5.551 × 10 | 8.484 × 10 |
| Std | 1.407 × 10 | 2.951 × 10 | 2.013 × 10 | 2.199 × 10 |
| 1.012 × 10 | 5.906 × 10 | 3.516 × 10 | 1.311 × 10 |
| Std | 3.815 × 10 | 2.441 × 10 | 2.147 × 10 | 6.872 × 10 |
| 2.981 × 10 | 2.988 × 10 | 7.175 × 10 | 1.038 × 10 |
| Std | 1.342 × 10 | 0.000 | 4.398 × 10 | 0.000 |
| 8.179 × 10 | 8.342 × 10 | 8.114 × 10 | 7.567 × 10 |
| Std | 1.421 × 10 | 0.000 | 1.421 × 10 | 2.842 × 10 |
| 7.943 × 10 | 8.394 × 10 | 8.307 × 10 | 8.329 × 10 |
| Std | 1.421 × 10 | 7.105 × 10 | 2.842 × 10 | 4.263 × 10 |
| 8.311 × 10 | 8.394 × 10 | 7.225 × 10 | 8.329 × 10 |
| Std | 0.000 | 7.105 × 10 | 4.263 × 10 | 4.263 × 10 |
| 1.220 × 10 | 3.937 × 10 | 5.202 × 10 | 2.246 × 10 |
| Std | 6.985 × 10 | 7.451 × 10 | 1.746 × 10 | 8.731 × 10 |
| 1.817 × 10 | 2.345 × 10 | 1.674 × 10 | 1.345 × 10 |
| Std | 5.821 × 10 | 1.118 × 10 | 6.985 × 10 | 0.000 |
| 2.353 × 10 | 1.266 × 10 | 8.217 × 10 | 3.199 × 10 |
| Std | 0.000 | 1.863 × 10 | 3.492 × 10 | 5.821 × 10 |
| 4.166 × 10 | 1.787 × 10 | 6.351 × 10 | 1.185 × 10 |
| Std | 1.137 × 10 | 2.274 × 10 | 1.137 × 10 | 4.547 × 10 |
| 5.709 × 10 | 7.462 × 10 | 5.936 × 10 | 7.634 × 10 |
| Std | 3.411 × 10 | 1.137 × 10 | 4.547 × 10 | 3.411 × 10 |
| 3.199 × 10 | 6.809 × 10 | 5.400 × 10 | 3.077 × 10 |
| Std | 5.684 × 10 | 3.411 × 10 | 4.547 × 10 | 0.000 |
| 3.883 | 3.941 | 3.740 | 3.517 |
| Std | 0.000 | 1.332 × 10 | 4.441 × 10 | 4.441 × 10 |
| 3.693 | 3.958 | 3.566 | 3.776 |
| Std | 1.332 × 10 | 4.441 × 10 | 0.000 | 4.441 × 10 |
| 3.045 | 3.731 | 3.764 | 2.943 |
| Std | 1.332 × 10 | 8.882 × 10 | 0.000 | 4.441 × 10 |
| 2.111 × 10 | 3.932 × 10 | 2.477 × 10 | 5.943 × 10 |
| Std | 1.364 × 10 | 1.819 × 10 | 1.364 × 10 | 0.000 |
| 9.646 × 10 | 1.594 × 10 | 3.848 × 10 | 7.506 × 10 |
| Std | 3.411 × 10 | 4.547 × 10 | 1.137 × 10 | 2.274 × 10 |
| 6.138 × 10 | 8.441 × 10 | 1.936 × 10 | 5.966 × 10 |
| Std | 2.274 × 10 | 5.684 × 10 | 1.364 × 10 | 4.547 × 10 |
| 2.518 × 10 | 1.894 × 10 | 6.016 × 10 | 5.172 × 10 |
| Std | 4.547 × 10 | 7.276 × 10 | 2.728 × 10 | 1.819 × 10 |
| 3.762 × 10 | 1.709 × 10 | 9.187 × 10 | 3.008 × 10 |
| Std | 5.684 × 10 | 5.684 × 10 | 3.638 × 10 | 4.547 × 10 |
| 3.401 × 10 | 1.415 × 10 | 6.376 × 10 | 2.164 × 10 |
| Std | 1.364 × 10 | 8.527 × 10 | 2.728 × 10 | 8.527 × 10 |
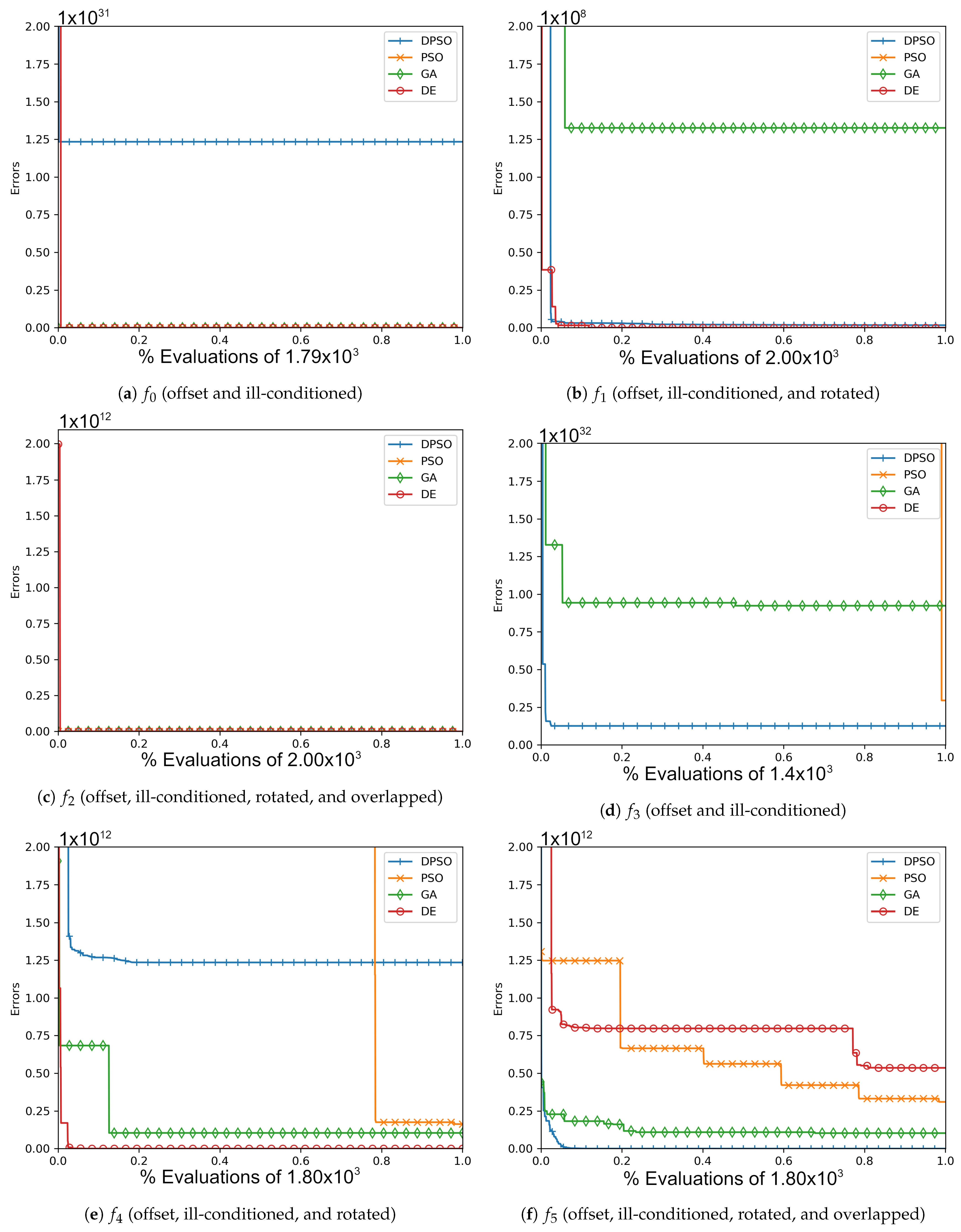
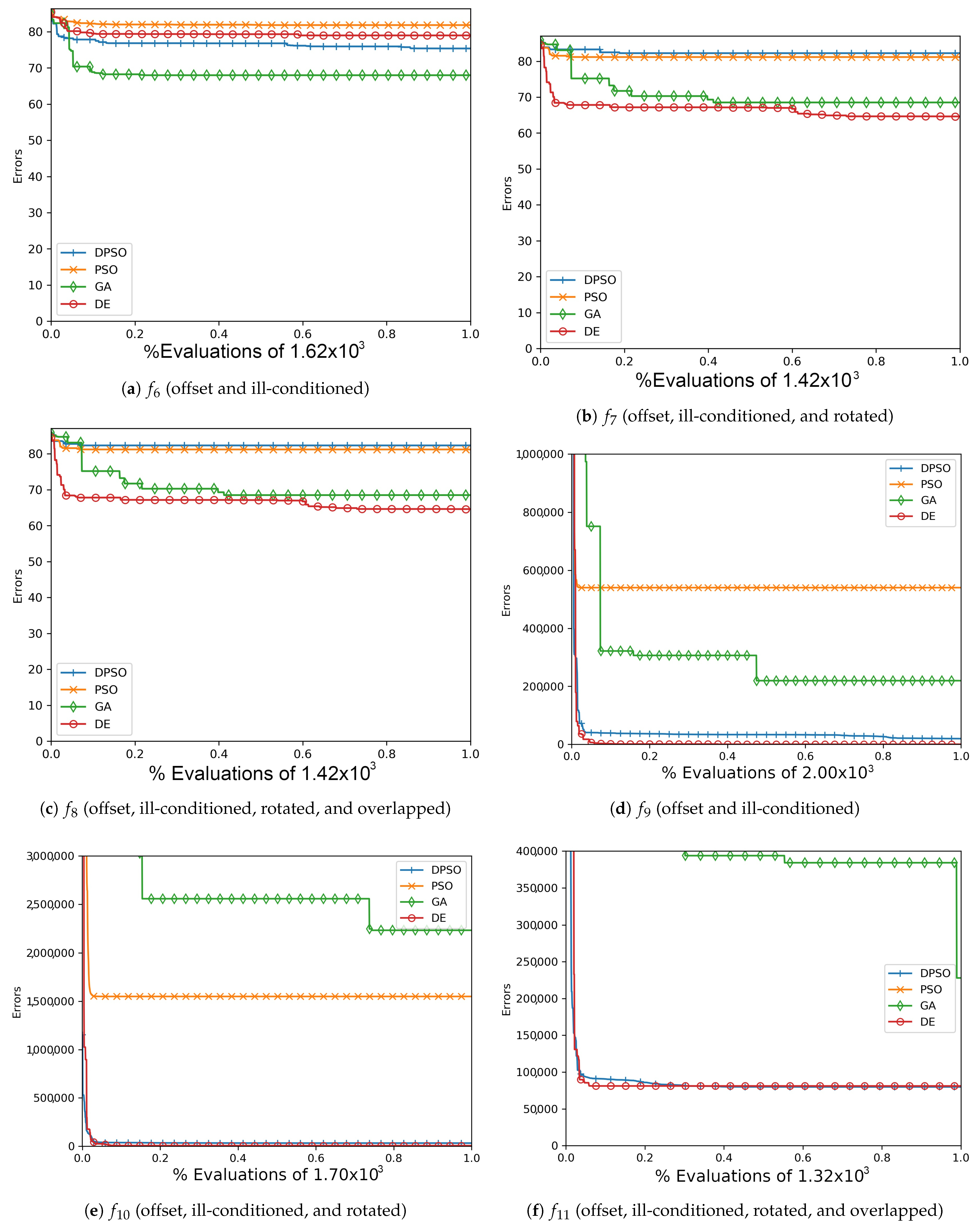
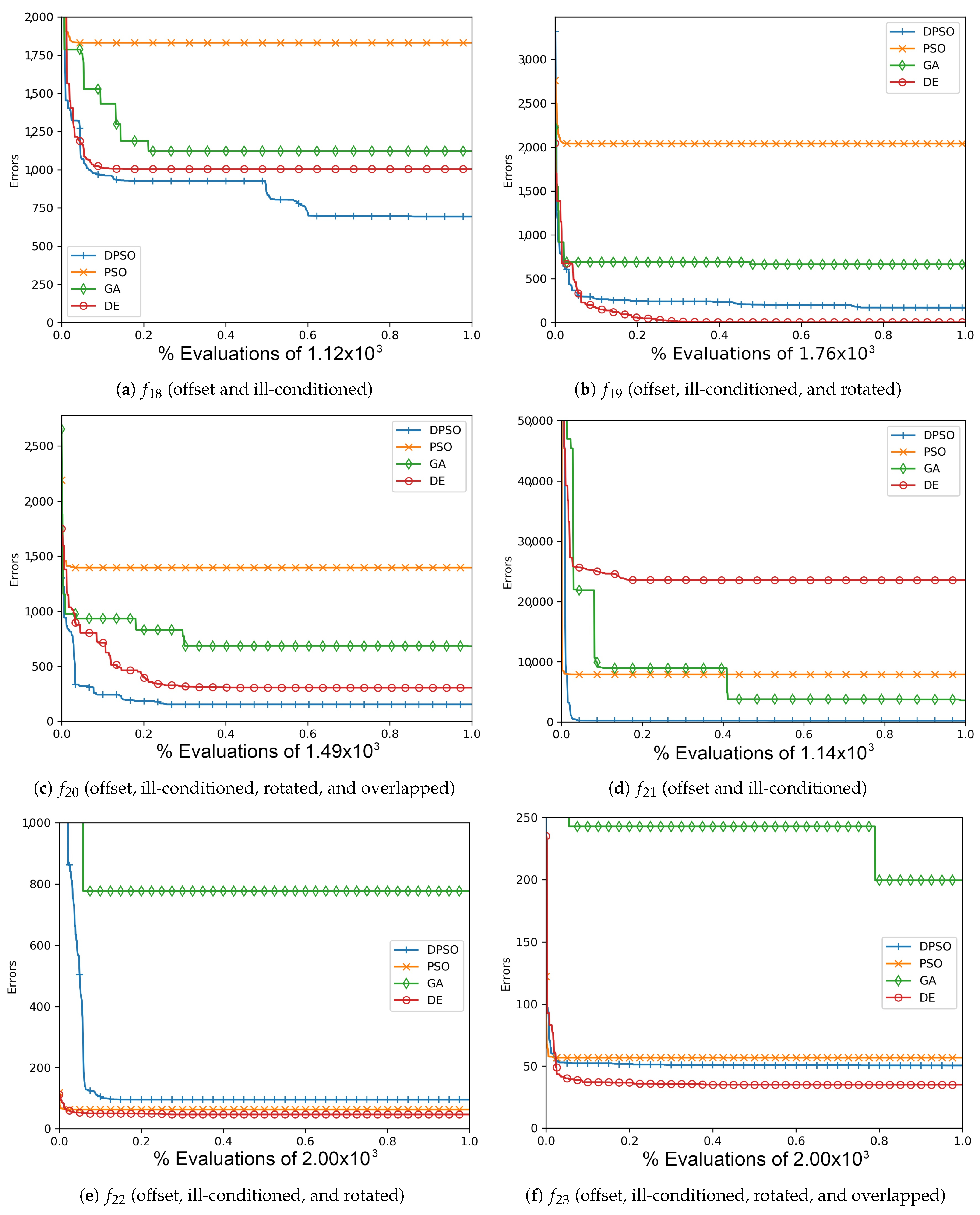
Figure A1.
The average In-Sample (, , ) and Elliptical (, , ) global best results over time for 7 dimensions.
Figure A1.
The average In-Sample (, , ) and Elliptical (, , ) global best results over time for 7 dimensions.
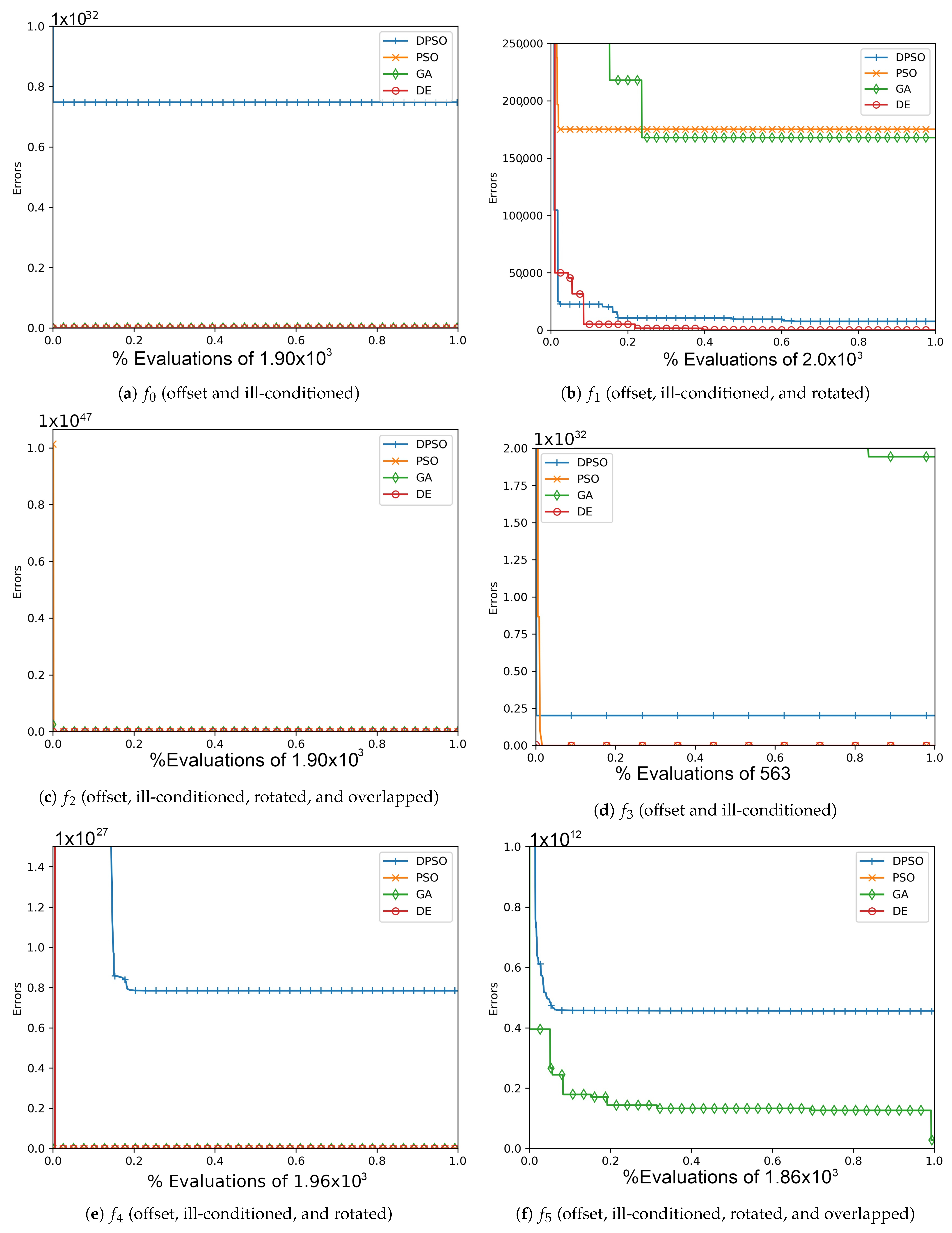
Figure A2.
The average In-Sample (, , ) and Elliptical (, , ) global best results over time for 14 dimensions.
Figure A2.
The average In-Sample (, , ) and Elliptical (, , ) global best results over time for 14 dimensions.
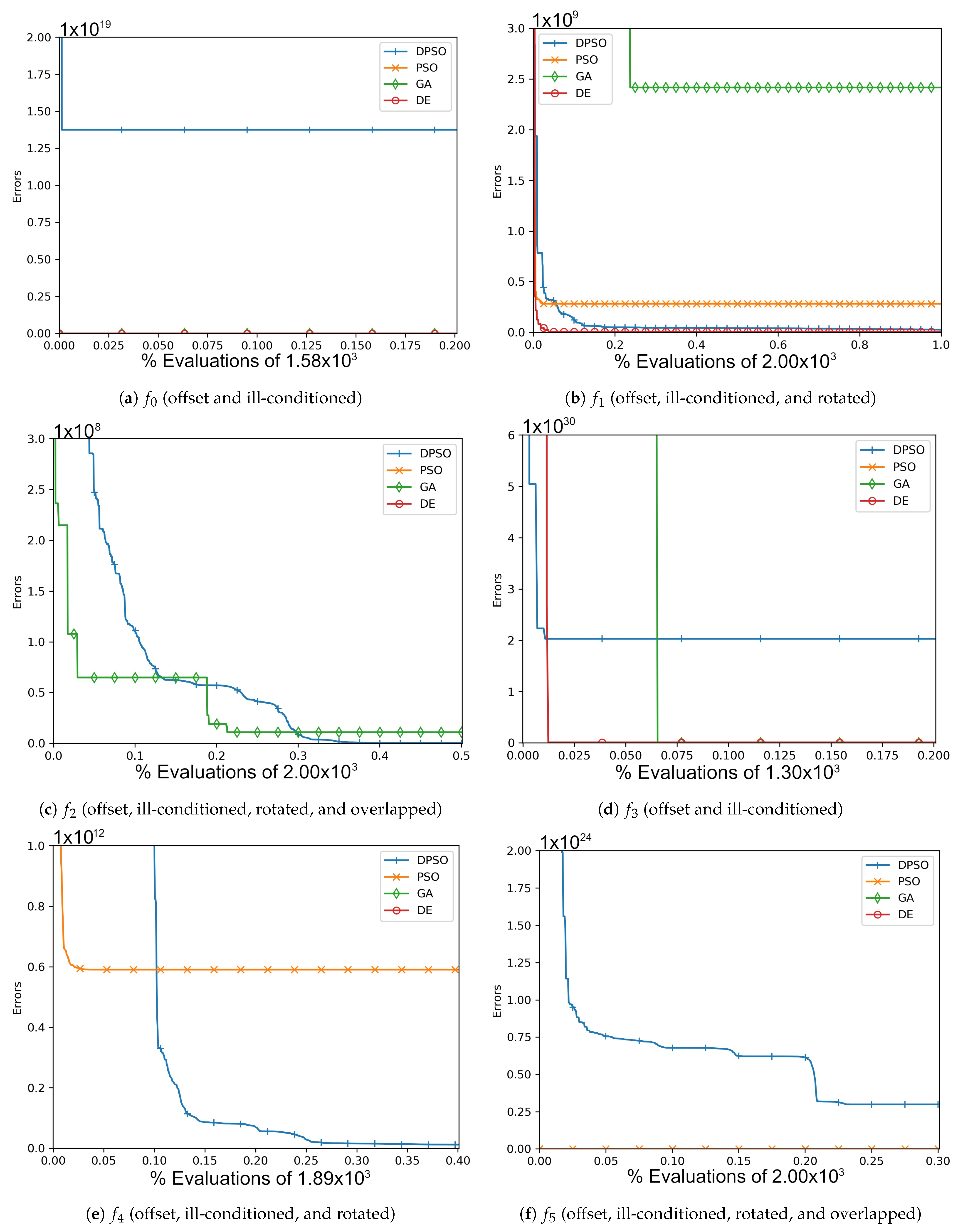
Figure A3.
The average In-Sample (, , ) and Elliptical (, , ) global best results over time for 21 dimensions.
Figure A3.
The average In-Sample (, , ) and Elliptical (, , ) global best results over time for 21 dimensions.
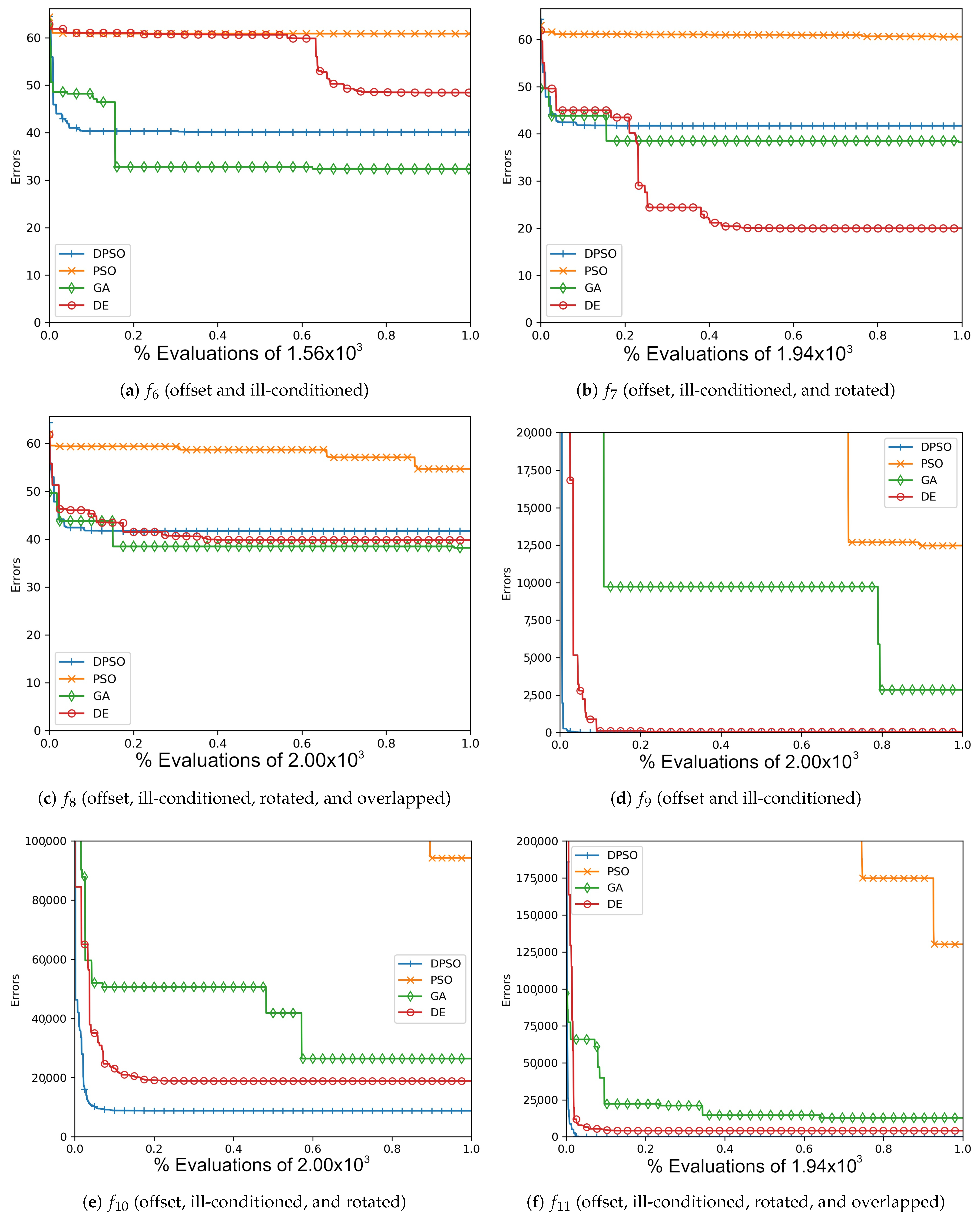
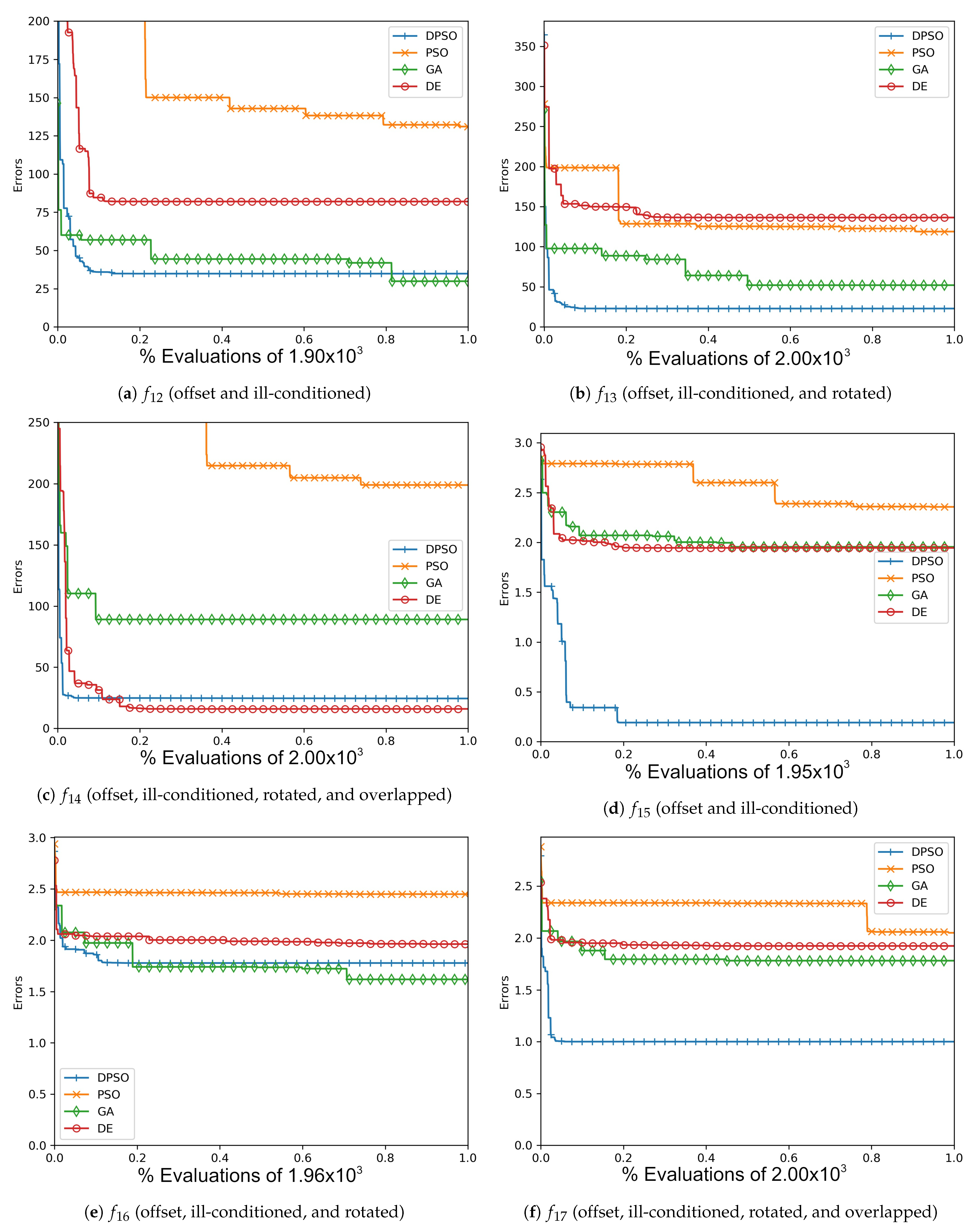
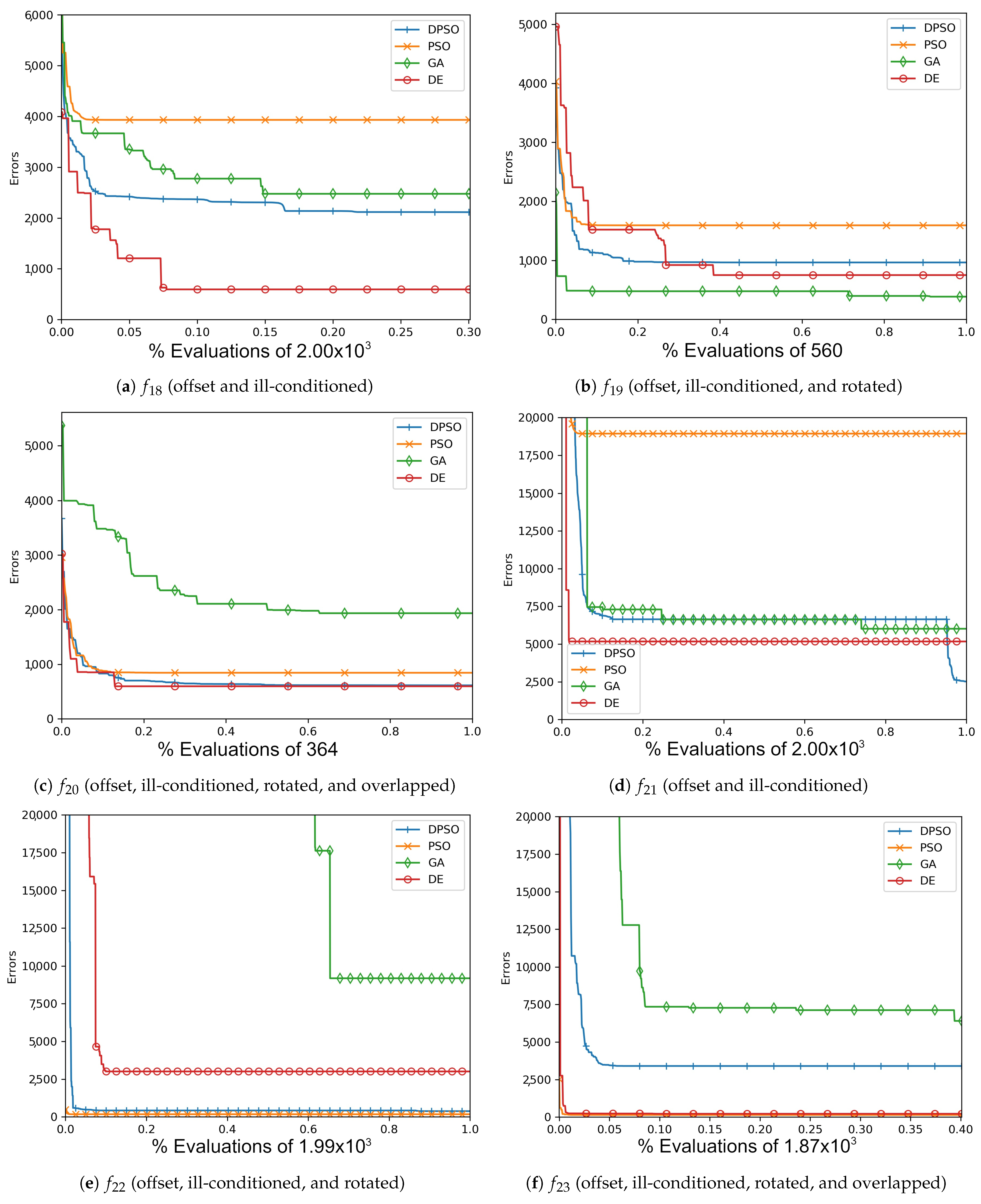
Figure A4.
The average Ackley (, , ) and Rosenbrock (, , ) global best results over time for 7 dimensions.
Figure A4.
The average Ackley (, , ) and Rosenbrock (, , ) global best results over time for 7 dimensions.
Figure A5.
The average Ackley (, , ) and Rosenbrock (, , ) global best results over time for 14 dimensions.
Figure A5.
The average Ackley (, , ) and Rosenbrock (, , ) global best results over time for 14 dimensions.
Figure A6.
The averageAckley (, , ) and Rosenbrock (, , ) global best results over time for 21 dimensions.
Figure A6.
The averageAckley (, , ) and Rosenbrock (, , ) global best results over time for 21 dimensions.
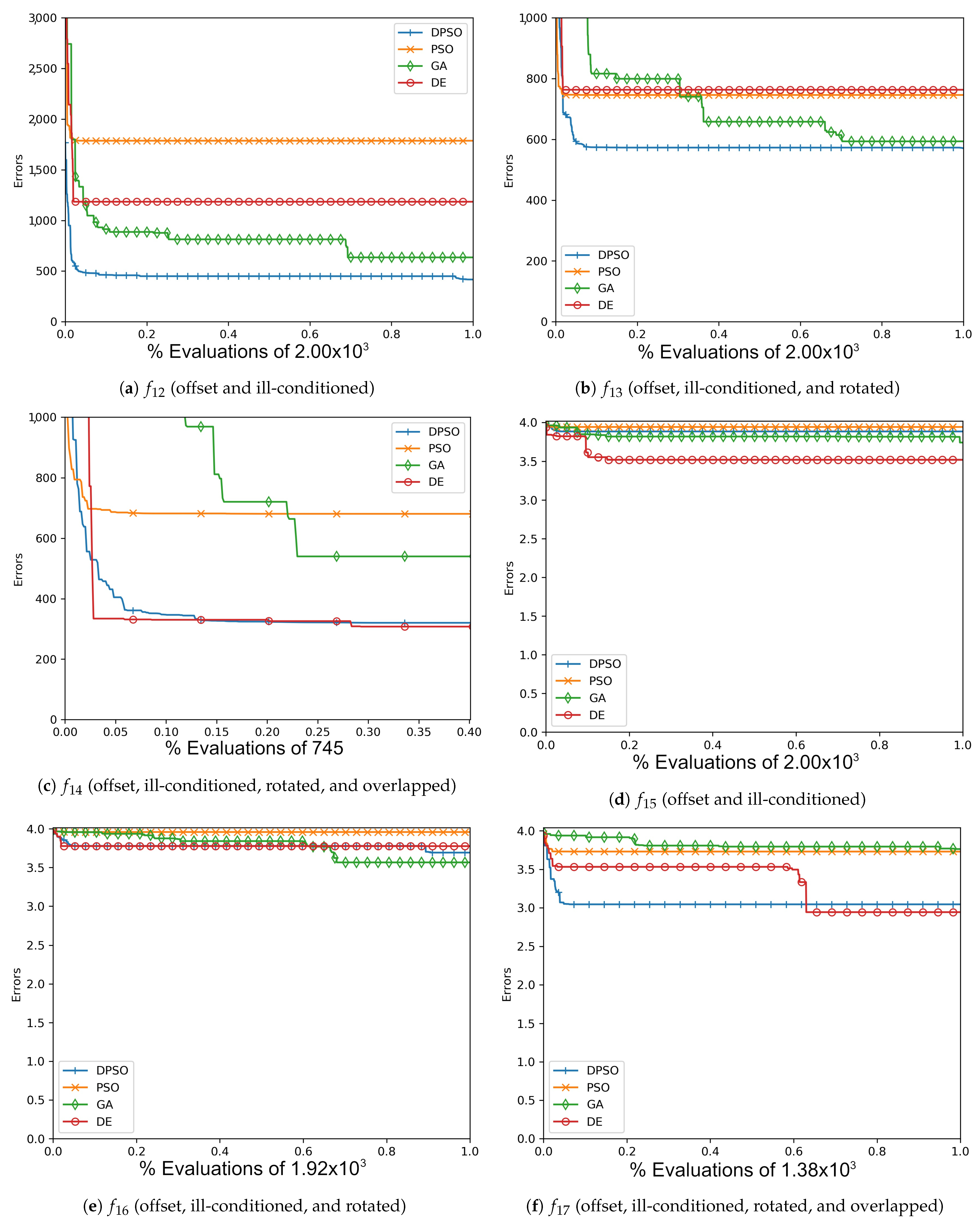
Figure A7.
The average Rastrigin (, , ) and Drop-Wave (, , ) global best results over time for 7 dimensions.
Figure A7.
The average Rastrigin (, , ) and Drop-Wave (, , ) global best results over time for 7 dimensions.
Figure A8.
The average Rastrigin (, , ) and Drop-Wave (, , ) global best results over time for 14 dimensions.
Figure A8.
The average Rastrigin (, , ) and Drop-Wave (, , ) global best results over time for 14 dimensions.
Figure A9.
The average Rastrigin (, , ) and Drop-Wave (, , ) global best results over time for 21 dimensions.
Figure A9.
The average Rastrigin (, , ) and Drop-Wave (, , ) global best results over time for 21 dimensions.
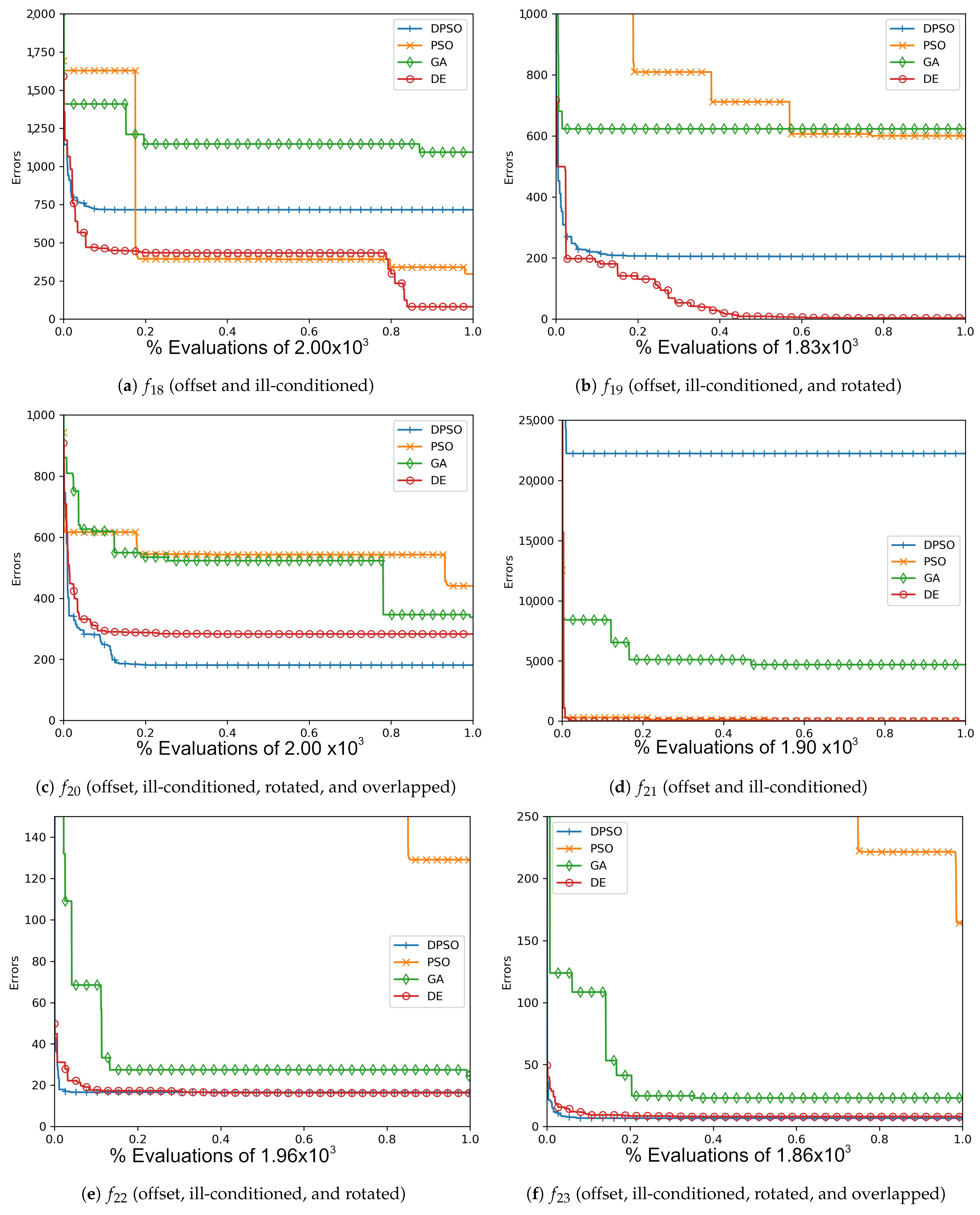
Figure A10.
The averageZero-Sum (, , ) and Salomon (, , ) global best results over time for 7 dimensions.
Figure A10.
The averageZero-Sum (, , ) and Salomon (, , ) global best results over time for 7 dimensions.
Figure A11.
The average Zero-Sum (, , ) and Salomon (, , ) global best results over time for 14 dimensions.
Figure A11.
The average Zero-Sum (, , ) and Salomon (, , ) global best results over time for 14 dimensions.
Figure A12.
The averageZero-Sum (, , ) and Salomon (, , ) global best results over time for 21 dimensions.
Figure A12.
The averageZero-Sum (, , ) and Salomon (, , ) global best results over time for 21 dimensions.