Abstract
The mechanical efficiency is a computed value for comparing the performance of the multi degrees-of-freedom geared transmissions of hybrid vehicles. Most of the current methods for estimating gear trains mechanical efficiency require the decomposition of gear transmissions in basic structural elements or planetary gear units (PGU). These are two degrees-of-freedom components whose mechanical efficiency has a deep influence on the overall device. The authors (E.L.E., E.P.) already evidenced that, under certain kinematic conditions, the classic Radzimovsky’s formulas, widely accepted for computing the mechanical efficiency of PGUs, are not adequate. In this paper, more general and reliable formulas for computing the mechanical efficiency are deduced. The proposed formulas herein, exploiting the concept of potential or virtual power, evidence the dependency between kinematics and efficiency. A numerical example compares our results with previous work on the subject.
1. Introduction
The multi degrees-of-freedom gear drive is a key component in hybrid vehicles. Its capability of managing power flows from different sources is of paramount importance for energy saving. For these reasons, the mechanical efficiency of planetary multi degrees-of-freedom planetary gear trains is a topic that received many contributions in recent times (e.g., [1,2,3,4,5,6,7,8,9,10,11,12,13,14]).
The analysis carried out herein offers a reliable approach toward a synthetic description of the relationship between kinematics conditions and gear train mechanical efficiency.
In this paper, the kinematic conditions governing the relationship between the algebraic signs of actual and virtual or potential powers are elucidated for the first time. Such an analysis has a significant influence on the casting of physically reliable and consistent formulas for the computation of mechanical efficiency in a two dof PGU (Planetary Gear Unit). Subsequently, two general formulas for mechanical efficiency computation in a two dof PGU are proposed. The differential unit is the building block of more complex planetary gear trains. Thus, the understanding of the two dof PGU basic mechanics influences the design of the entire planetary gear drive [15].
The approach adopted herein is based on the concept of virtual or potential power, at the base of thoughtful contributions on the mechanical efficiency of planetary gear trains [5,16,17,18,19,20,21,22]. The virtual power, a term coined by Chen and Angeles [17], or potential power, coined by Esmail [5], is the power measured by an observer on any arbitrary moving frame [23,24]. However, the use of kinematic inversion for torque and efficiency analysis on gear trains dates back to Macmillan [16]. In particular, he recognized that the torques acting on the PGU links and power losses are independent of the observer’s motion. The following quote is taken from [16]:
...our analysis is based upon an important principle relating to torques and the power lost in friction; this is the fact that magnitudes of the torques acting upon the various members of the gear are quite independent of the motion of the observer who measures them. In addition, the power lost, being determined solely by the internal torques and the relative motions of the wheels within the gear, is also independent of the observer’s motion.
Although Macmillan’s analysis was limited to one dof PGU, the importance of kinematic inversion in the gear trains mechanical efficiency analysis is well represented.
The present paper was stimulated by the discovery that, under certain kinematic conditions, the classic Radzimovsky formulas [15,25,26,27] for the computation of mechanical efficiency in a two dof gear unit are not valid anymore [28]. This situation may lead to an estimation of the overall mechanical efficiency flawed by errors.
As discussed by Pennestrì & Valentini [15], the Radzimovsky formulas consider the two dof epicyclic gear train as two single dof devices in parallel and crossed by a power-flow. These formulas are deduced after application of the general mechanical efficiency formula of a mechanical system composed of two parallel devices with a given mechanical efficiency and power-flow direction. However, with the introduction of the concept of virtual or potential power, the mechanical efficiency of an epicyclic gear train is reduced to that of an ordinary gear train. For this purpose, a kinematic inversion is introduced such that the observed motion of the gear carrier is canceled.
The orientation of power flow observed under such kinematic inversion may not be the same as one of epicyclic arrangement. This situation requires special attention and the algebraic expression of the overall mechanical efficiency should be set in a consistent manner. The new proposed formulas herein are of a general nature and do not suffer any of the mentioned pitfalls.
In this paper, the concept of virtual or potential power was applied to deduce two new general mechanical efficiency formulas that cover all the working modes of a two dof PGU:
- -
- Two driving members (i.e., those with positive powers) and one driven member (i.e., the one with negative power);
- -
- Two driven members and one driving member.
Our approach is based only on the application of mechanics first principles, namely, Willis’ formula, torque equilibrium, kinematic inversion, power balance and definition of mechanical efficiency. As a byproduct, general formulas of the power-flow ratios, for the case of a gear unit without power losses, are also deduced.
For the mechanical efficiency analysis, members with constant velocities and meshing losses only are considered. A constant mechanical efficiency is assumed for the unit working as an ordinary gear train. Moreover, the algebraic sign of the power-flow is not altered by friction.
On the basis of the previous hypotheses, two new compact formulas for the mechanical efficiency analysis of two dof PGU are deduced herein. The formulas can be adapted to any power flow arrangement within the PGU.
2. Power-Flow Ratios in a PGU
The PGU (see Figure 1) is composed of two mating gears and the gear carrier. Let us denote by x, y and z the three links of the PGU.
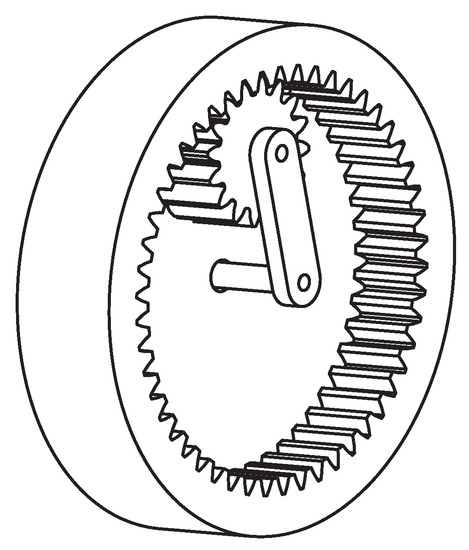
Figure 1.
Example of planetary gear unit (PGU) with internally meshing gears.
Angular speeds, torques and powers in a GPU are governed, respectively, by the well-known analytical conditions from Willis’ equation, torque equilibrium and power balance:
where and depend on the number of teeth ratio.
The readers will readily recognize (1a) as the Willis’ equation. In fact, setting z and x as the subscripts denoting the meshing gears and y the gear carrier, then
The comparison of (1a) with (2), yields and . Obviously, other subscript combinations are possible, with corresponding different analytical expressions of and . The choice x, y and z for the initial indistinct labeling all the moving bodies composing the PGU is justified by the advantage of condensing all possible cases for mechanical efficiency computation in two formulas only. In other words, what is lost in apparent initial abstraction is later gained in the results’ generality.
After some algebraic manipulation of (1) one obtains the following:
where , and are the powers sustained by links x, y and z, respectively. The power ratios deduced by Pennestrì & Freudenstein [29] are particular cases of the previous equations.
Under ideal conditions, in a PGU, the sign of powers is established prescribing the following: two angular speeds and one torque (kinematically driven PGU) or, alternatively, one angular speed and two torques (torque driven PGU) [30].
In a two dof PGU we distinguish the following working modes:
- -
- Two driving links (namely x and y, and ) and one driving link (namely z, );
- -
- Two driving links (namely x and y, and ) and one driving link (namely z, ).
In the current analysis, it is assumed that the presence of meshing losses does not alter the algebraic sign of actual power flows.
3. The Algebraic Sign of Virtual Power Flows
In a previous paper [28], the authors (E.L.E. and E.P. ) demonstrated that, under certain kinematic conditions, the Radzimovsky’s formulas do not hold. An analysis of power-flows algebraic signs is required to explain the limits for the Radzimovsky’s formulas and offer a more general alternative.
The following analysis will ascertain the algebraic sign correlation between the actual powers and and the virtual [17] or potential [5] powers, such as and . For instance, the potential power corresponds to the power which would be transmitted by the gear unit, operating in a rotating reference frame at which link j appears relatively fixed and at relative angular velocity , for link u. Therefore, the carrier potential power is measured under a kinematic inversion, making fixed the planet-carrier in the observer frame of reference. The potential power is the most important and basic principle of the mechanical efficiency analysis of differential devices).
Powers and have the same algebraic sign only if the following is true:
or
Similarly, and have the same algebraic sign only if the following are true:
or
There are two ranges consistent with inequality (6):
Moreover, we observe the following:
- -
- If , then is also negative.
- -
- If , then must be greater than one.
Case 1: and have opposite algebraic signs.
In this case, Equations (6) and (8) are both simultaneously valid. and , and have the same algebraic sign for any working mode, as depicted in the PGU block schemes shown in Figure 2 (1st working mode).
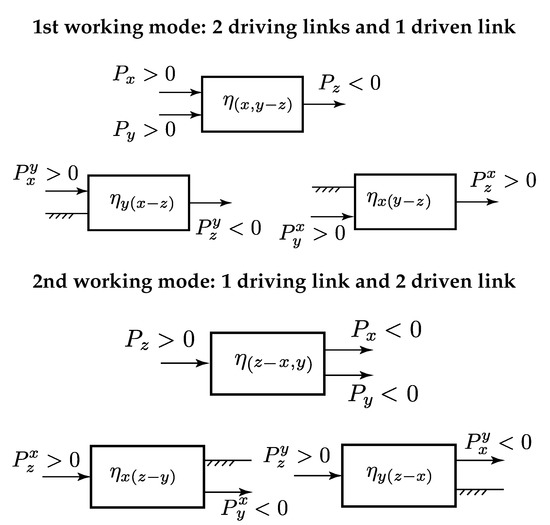
Figure 2.
Virtual power flow directions Kinematic condition: .
Case 2: and have the same algebraic sign, or .
Subcase 2a: When , then and have the same algebraic sign. The described situation is depicted in Figure 3, 1st working mode.
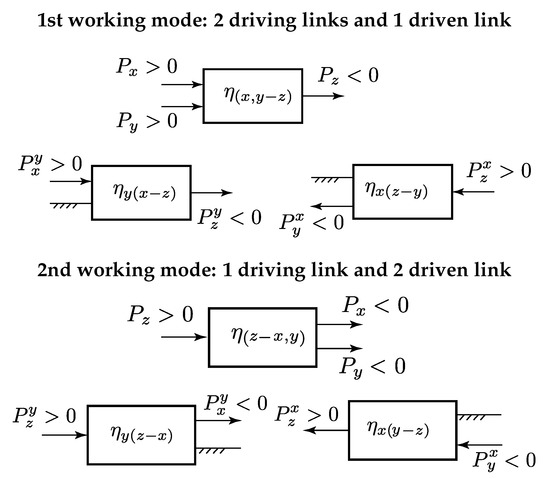
Figure 3.
Virtual power-flow directions for subcase 2a. Kinematic condition: and .
Subcase 2b: When , then and will have the same algebraic sign. The described situation is depicted in Figure 4, 1st working mode.
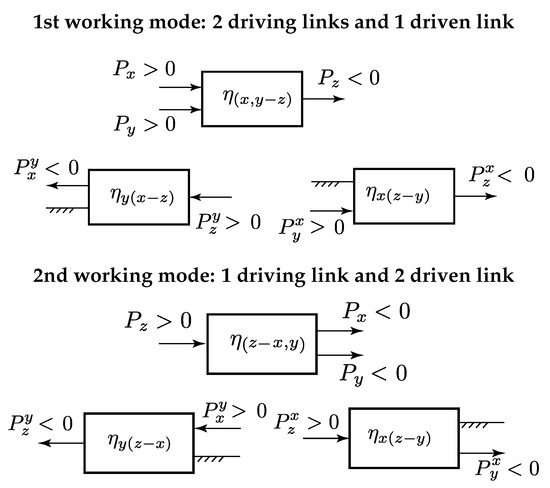
Figure 4.
Virtual power flow directions for subcase 2b. Kinematic condition: and .
The previous analysis can be summarized as follows:
- When and do not have the same algebraic sign, the power ratios and will have simultaneously the same algebraic sign. For all the links, the direction of the virtual power-flow is the same as the actual power flow (see Figure 2).
- When and have the same algebraic sign, power ratios and cannot have simultaneously the same algebraic sign. In particular, the condition is fulfilled when (See Figure 3). Conversely, the condition is fulfilled when .
4. The Modified Radzimovsky Formulas
4.1. Case x and y as Driving Links and z Driven Link
Let us consider the case of a two dof gear train with x and y as driving links (i.e., , and ).
Case 1: (see Figure 2, 1st working mode)
Under kinematic inversions that fix links x and y, respectively, assuming without loss of generality , the following relations hold (see 1st working mode of Figure 2):
The overall power balance condition is as follows:
Solving the system composed of the Equations (9), one obtains the following:
Subcase 2a: or (see Figure 3, 1st working mode)
Under kinematic inversions that fix links x and y, respectively, assuming without loss of generality , the following relations hold:
Solving the system composed of the Equations (9c) and (11), one obtains the following:
The proposed formula is more general than the one proposed by Radzimovsky (see Equation (11) of [26]).
When , the Equations (9b) and (11) are identically satisfied and Formula (13) is not valid. However, under these kinematic conditions, there is no meshing power loss. Under our hypotheses, the mechanical efficiency is equal to one.
4.2. Case x and y as Driven Links and z Driving Link
Let us consider the case of a two dof gear train with x and y as driven links (i.e., , and ), as shown in Figure 2, 2nd working mode. In this case the overall power balance equation is the following:
Case 1: (see Figure 2, 2nd working mode)
The following relations hold:
Solving the system composed of the Equations (15) and (16), one obtains the following:
Subcase 2a: and (see Figure 3, 2nd working mode)
The following relations hold:
Solving the system composed of the Equations (15) and (18), one obtains the following:
The proposed formula is more general than the one proposed by Radzimovsky (see Equation (25) of [26]).
The expressions of and , for all possible combinations of x, y and z, are listed in Table 1 of reference [1] (see also Appendix A).
5. Numerical Example
We consider the case of the gear unit, shown in Figure 5, with x and y driving links and the z-driven link. In particular, rpm and rpm.
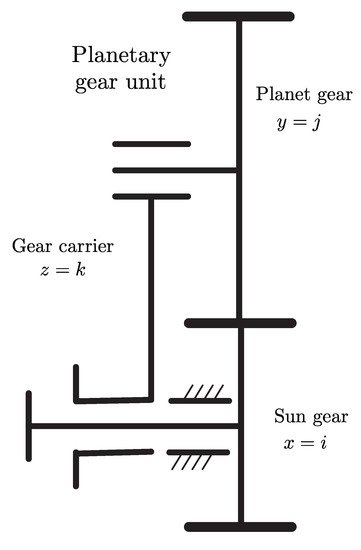
Figure 5.
Kinematic structure of the PGU analyzed.
For a planet gear ratio ,
and
Consequently, from Willis’ equation, follows rpm.
Since , the Formula (13) is applied. Considering the current value of , and assuming
the entries 3a and 5a of Table A1 of the Appendix A give, respectively, the following:
For the prescribed numerical data, the Formula (13) yields the following:
6. Conclusions
In this paper, the first novel result concerns the algebraic signs analysis of a virtual power-flow in a two dof PGU. It was shown that in a PGU, the virtual or potential powers, and , cannot have always the same algebraic sign. On the basis of this observation, new formulas for the computation of mechanical efficiency in a two dof PGU were deduced. The proposed formulas maintain their range of validity, also for cases not covered by the traditional Radzimovsky’s formulas. Therefore, our approach offers a more general and compact alternative. The results herein can be extended also to other types of differential devices.
It must be observed that the current approach is limited to meshing losses only under a stationary working mode. Future work should embody in the formulas also the bearing losses. Moreover, the present treatment is based on stationary conditions; however, often, the efficiency under transient conditions is required. In this case, the time variation of kinetic energy due to inertia forces needs to be included in the power balance.
Author Contributions
Conceptualization, E.L.E. and E.P.; methodology, E.L.E., M.C. and E.P.; validation, E.L.E., M.C. and E.P.; writing—original draft preparation, E.L.E., M.C. and E.P.; writing—review and editing, E.L.E., M.C. and E.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| dof | degree-of-freedom |
| Power of link , greater/less than zero when h is a driving/driven link in the absolute motion; | |
| Potential or virtual power of link x when link y is considered fixed; | |
| PGU | Planetary gear unit; |
| Planet gear ratio (+: internally meshing gears, −: externally meshing gears) | |
| Torque on link x | |
| Absolute angular velocity of link x | |
| Relative angular velocity of link x with respect to link y | |
| Mechanical efficiency of the one dof PGU when link x is fixed and links y and z are driving and driven links, respectively. | |
| Mechanical efficiency of the two dof PGU when operating with links x and y as driving links and z as driven. | |
| Mechanical efficiency of the two dof PGU when operating with links x and y as driven links and z as driving link. |
Appendix A
In Table A1 are reported the efficiencies of all possible kinematic inversions of a PGU [1].
The nomenclature of the table variables is as follows:
- and k: subscripts denoting the gears and gear carrier, respectively;
- : planet gear ratio;
Therefore, assuming (gear driving), (gear carrier driven), (fixed), , the mechanical efficiency of this gear arrangement is given by the entry 3a:
The efficiency of the ordinary gear train can be accurately computed in different ways. However, for a crude approximation, the Tuplin formula can be used:
where the + and − sign applies for external or internal meshing gears, respectively.

Table A1.
Efficiencies of single epicyclic spur-gear trains. : planet gear ratio.
Table A1.
Efficiencies of single epicyclic spur-gear trains. : planet gear ratio.
| Case | Driving | Driven | Fixed | ||
|---|---|---|---|---|---|
| 1 | i | j | k | ||
| 2 | j | i | k | ||
| 3a | i | k | j | ||
| 3b | i | k | j | ||
| 4a | k | i | j | ||
| 4b | k | i | j | ||
| 5a | j | k | i | ||
| 5b | j | k | i | ||
| 6a | k | j | i | ||
| 6b | k | j | i |
References
- Pennestrì, E.; Mariti, L.; Valentini, P.P.; Mucino, V. Efficiency evaluation of gearboxes for parallel hybrid vehicles: Theory and applications. Mech. Mach. Theory 2012, 49, 157–176. [Google Scholar] [CrossRef]
- Zhang, X.; Mi, C. Vehicle Power Management—Modeling, Control and Optimization; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Chen, C. Power flow analysis of compound epicyclic gear transmission: Simpson gear train. ASME J. Mech. Des. 2011, 133, 5. [Google Scholar] [CrossRef]
- Chen, C. Power flow and efficiency analysis of epicyclic gear transmission with split power. Mech. Mach. Theory 2013, 59, 96–106. [Google Scholar] [CrossRef]
- Esmail, E.L. Meshing efficiency analysis of two degree-of-freedom epicyclic gear trains. ASME J. Mech. Des. 2013, 138, 083301. [Google Scholar] [CrossRef]
- Jianying, L.; Qingchun, H. Power Analysis and Efficiency Calculation of the Complex and Closed Planetary Gears Transmission. Mech. Mach. Theory 2016, 100, 423–433. [Google Scholar] [CrossRef] [Green Version]
- Mohammadpour, M.; Theodossiades, S.; Rahnejat, H. Dynamics and efficiency of planetary gear sets for hybrid powertrains. Proc. IMechE Part C J. Mech. Sci. 2016, 230, 1359–1368. [Google Scholar] [CrossRef] [Green Version]
- Coaccioli, P. Pennestrì. Graph-Based Algorithm for the Evaluation of the Mechanical Efficiency of Epicyclic Gear Drive in Hybrid Scooters. In Graph-Based Modelling in Engineering. Mechanisms and Machine Science; Zawiślak, S., Rysiński, J., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2017; Volume 42, pp. 97–105. [Google Scholar]
- Yang, F.; Feng, J.; Zhang, H. Power flow and efficiency analysis of multi-flow planetary gear trains. Mech. Mach. Theory 2015, 92, 86–99. [Google Scholar] [CrossRef]
- Essam, E.L.; Juber, A.H.; Hussen, H.A. Power flow and efficiency analysis of multi-path transmission with planetary gear train. Int. J. Mech. Eng. Technol. 2018, 9, 412–423. [Google Scholar]
- Hussen, H.A.; Esmail, E.L.; Hussen, R.A. Power Flow Simulation for Two-Degree-of-Freedom Planetary Gear Transmissions with Experimental Validation. Model. Simul. Eng. 2020, 2020, 14. [Google Scholar] [CrossRef]
- De Carlo, M.; Mantriota, G. Electric vehicles with two motors combined via planetary gear train. Mech. Mach. Theory 2020, 148, 103789. [Google Scholar] [CrossRef]
- Ding, H.; Cai, C.; Chen, Z.; Ke, T.; Mao, B. Configuration Synthesis and Performance Analysis of 9-Speed Automatic Transmissions. Chin. J. Mech. Eng. 2020, 33, 21. [Google Scholar] [CrossRef]
- Mantriota, G.; Reina, G. Efficient Power-Split Powertrain for Full Electric Vehicles. In Mechanisms and Machine Science; Springer International Publishing: Berlin/Heidelberg, Germany, 2020; pp. 560–567. [Google Scholar] [CrossRef]
- Pennestrì, E.; Valentini, P.P. A review of formulas for the mechanical efficiency analysis of two degrees-of-freedom epicyclic gear trains. ASME J. Mech. Des. 2003, 125, 602–608. [Google Scholar] [CrossRef]
- Macmillan, R.H. Epicyclic gear efficiencies. Engineer 1949, 23, 727–728. [Google Scholar]
- Chen, C.; Angeles, J. Virtual-power flow and mechanical gear-mesh power losses of epicyclic gear trains. J. Mech. Des. Trans. ASME 2007, 129, 107–113. [Google Scholar] [CrossRef]
- Rotella, D.; Cammalleri, M. Power losses in power-split CVTs: A fast black-box approximate method. Mech. Mach. Theory 2018, 128, 528–543. [Google Scholar] [CrossRef]
- Esmail, E.L. Influence of the Operating Conditions of Two-Degree-of-Freedom Planetary Gear Trains on Tooth Friction Losses. ASME J. Mech. Des. 2018, 140, 054501. [Google Scholar] [CrossRef]
- Malashchenko, V.; Strilets, O.; Strilets, V.; Kłlysz, S. Investigation of the energy effectiveness of multistage differential gears when the speed is changed by the carrier. Diagnostyka 2019, 20, 57–64. [Google Scholar] [CrossRef]
- Cammalleri, M.; Castellano, A. Analysis of hybrid vehicle transmissions with any number of modes and planetary gearing: Kinematics, power flows, mechanical power losses. Mech. Mach. Theory 2021, 162, 104350. [Google Scholar] [CrossRef]
- Sun, Z.; Gao, B.; Sanada, K. Power Loss Evaluation of Automated Manual Transmission with Gearshift Assistant Mechanism. Int. J. Automot. Technol. 2021, 22, 441–454. [Google Scholar] [CrossRef]
- Chen, C.; Liang, T. Theoretic study of efficiency of two-DOFs of epicyclic gear transmission via virtual power. ASME J. Mech. Des. 2011, 133, 031007-1–031007-7. [Google Scholar] [CrossRef]
- Chen, C. Power analysis of epicyclic transmissions based on constraints. ASME J. Mech. Robot. 2012, 4, 041004-1–041004-11. [Google Scholar] [CrossRef]
- Radzimovsky, E.I. A Simplified Approach for Determing Power Losses and Efficiency of Planetary Gear Drives. Mach. Des. 1956, 28, 101–110. [Google Scholar]
- Radzimovsky, E.I. How to find efficiency, speed and power losses in planetary gear drives. Mach. Des. 1959, 31, 144–153. [Google Scholar]
- Pennestrì, E.; Freudenstein, F. The Mechanical Efficiency of Epicyclic Gear Trains. ASME J. Mech. Des. 1993, 115, 645–651. [Google Scholar] [CrossRef]
- Esmail, E.L.; Pennestrì, E.; Hussein Juber, A. Power Losses in Two-Degrees-of-Freedom Planetary Gear Trains: A Critical Analysis of Radzimovsky’s Formulas. Mech. Mach. Theory 2018, 128, 191–204. [Google Scholar] [CrossRef]
- Pennestrì, E.; Freudenstein, F. A Systematic Approach to Power-Flow and Static Force Analysis in Epicyclic Spur-Gear Trains. ASME J. Mech. Des. 1993, 115, 639–644. [Google Scholar] [CrossRef]
- Rabindran, D.; Tesar, D. Parametric design and power-flow analysis of parallel force/velocity actuators. ASME J. Mech. Robot. 2009, 1, 1–10. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).