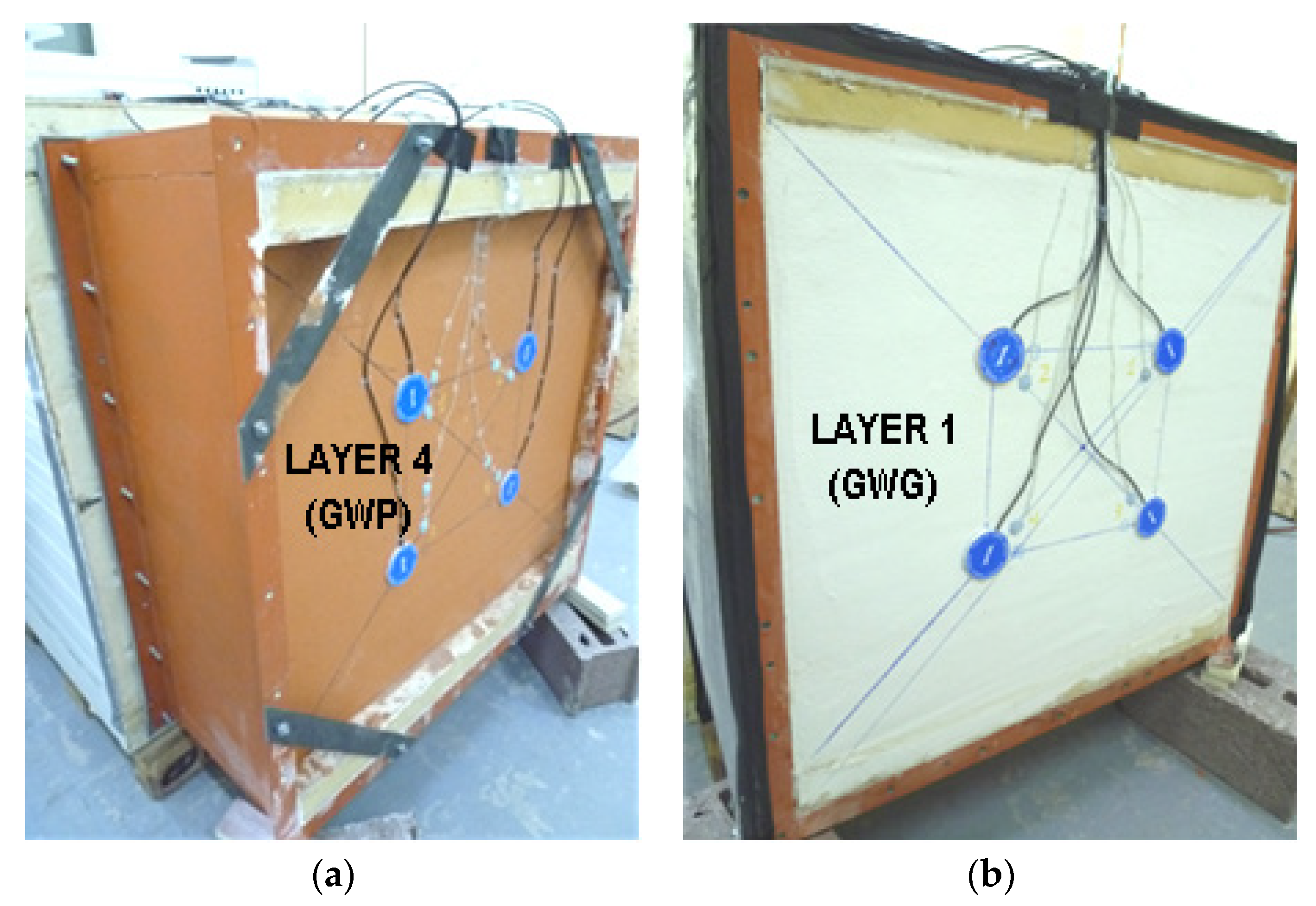
1. Introduction
Thermal comfort is one of the most valued concepts in the habitability of both residential and office buildings. Energy consumption is needed to achieve adequate thermal comfort, and the large energy demands of buildings have significant environmental impacts. Therefore, buildings must be designed to minimize heat loss through their enclosures and to reduce energy demands [
1].
Increasing the thermal resistance (
R, m
2K/W) of building enclosures is a well-known method to reduce heat loss. Thermal transmittance (
U-value, W/m
2K) is the inverse of the total resistance values of enclosure heat transfer (
Rtot). The
U-value is the rate of heat transfer (in watts) through 1 m
2 of a building element and is determined by the difference in temperature across the wall. Most building standards [
2] evaluate the
U-value of the materials that form the enclosure, characterizing their steady-state thermal physical properties. However, this method has the disadvantage of not accounting for the heat storage capacity of materials when environmental conditions change. In recent years, it has been concluded that it is not possible to design thermally efficient buildings based on
U-value alone. The determination of the transient thermal behavior of different construction solutions is receiving a great deal of interest in order to advance the concept of the thermal inertia of construction elements [
3].
Thermal inertia is the ability of a material to maintain the thermal energy it has been exposed to and to progressively release heat. Thermal inertia reduces the need to supply heated or cooled air, thus saving energy. Values of thermal inertia must be analyzed under real conditions of temperature and humidity, which vary over time. In addition, they must take the thermal storage capacity of each of the layers that constitute the constructive element to be analyzed into account. Using thermal inertia values, it will be possible to obtain more accurate values of thermal comfort than when using thermal transmittance alone. Previous studies on thermal inertia in Northern Italy showed that the difference in heating demands between low and high thermal inertia walls was about 10%. When considering cooling demands, the difference increased to 20% [
4]. Kossecka and Kosny [
5] stated that the difference in energy requirements between walls with different thermal efficiencies ranged between 2.3% and 11.3%, depending on the climate, with the difference being more pronounced in the case of an increased solar exposure and diurnal temperature differences. Asan and Sancaktar [
6] studied the influence of time lag and decrement factor on materials’ thermophysical properties, accounting for material thickness and its position in the wall. In addition, Asan [
7] also studied the effect of wall insulation thickness and position on the time lag and decrement factor, and determined the optimum insulation position to achieve the minimum decrement factor and maximum time lag. Ozel and Pithtili [
8] also established the optimum insulation location and its distribution in walls to improve thermal inertia. In a study by Di Perna et al. [
9], the influence of thermal mass placed on the inner side of a building envelope was assessed. Simultaneous monitoring was carried out on rooms with high internal heat loads (school classrooms), and the internal inertia of the envelope was varied using an insulating panel on the interior side. Ng et al. [
10] studied the most influential parameters in thermal inertia on lightweight concrete wall panels, and found that thermal diffusivity had a positive relationship with the thermal inertia of wall panels. Based on a 1D numerical model, Jin et al. [
11] studied the influence of heat flux on time lag and the decrement factor on the thermal properties and thickness of walls. They also reported the decrement factor for several building materials. Kontoleon et al. [
12] analyzed the impact of heat flux, concrete density, and conductivity on the decrement factor and time lag, and obtained the optimal decrement factor and time lag values for concretes with 950 kg/m
3 in wall assemblies with one layer of insulation. They also found that the placement of insulation into two layers improves the optimal decrement factor and time lag values using concretes with a density above 1200 kg/m
3. The best results were obtained by placing the insulation on the external surface and the center of the enclosure.
With respect to the heat transfer numerical simulation of concrete walls with cavities, del Coz et al. [
13,
14] and Gencel et al. [
15] focused on the evaluation of thermal transmittance properties and the optimization of construction elements under steady-state thermal conditions. These studies highlighted the importance of the size of holes and their distribution, and of radiation and convection phenomena in cavities. A study by Arendt et al. [
16] complemented these studies by taking into account dynamic thermal parameters, such as the decrement factor, time lag, and thermal conductivity. They used numerical and analytical models to determine that the optimal percentage of cavities to achieve ideal comfort conditions was between 45% and 65% with respect to the material volume. In contrast, thermal conductivity decreases proportionally with increased cavity volume. Zhang et al. [
17] concluded that the transient thermal performance of walls is optimal for thermal conductivity values lower than 1.0 W/mK. Their study was based on a reduction in material conductivity values using both block and hole filling, increasing the total thickness of the block and the number of cavities in parallel. Soret et al. [
18] proposed a numerical method to obtain the thermal inertia of a building’s components using its thermal insulation parameters in order to predict fire reaction behavior.
It is critical that the following factors be identified to obtain the thermal inertia properties of construction elements: layer distribution; thermo-physical characteristics of the materials used; temperature evolution; and the difference between indoor and outdoor thermal conditions.
In general, according to the existing literature mentioned above, high time lags and low decrement factor values are preferred to obtain optimal comfort conditions inside buildings. It can be concluded that interior thermal comfort conditions could vary significantly for envelopes with the same thermal resistances but with different densities.
The objective of this study was to analyze the thermal behavior under steady- and transient-state conditions of a wall made up of lightweight concrete blocks covered with layers of insulating materials. The material used in the block manufacturing has been shown to possess thermal and structural advantages, including a longer product life cycle than other construction materials, low structural weight, excellent behavior at high temperatures, and good thermal insulation values due to its low thermal conductivity [
19,
20]. In this study, experimental tests were performed in a 1 m
2 instrumented hot-box climatic chamber, and the material was subjected to variable temperature and humidity conditions to obtain thermal inertia values according to the ISO standard rule [
3]. We then created a finite element numerical model of a bi-dimensional wall section with holes, which was subjected to the temperature conditions established in the experimental test, both under steady- and transient-state conditions. We then compared the numerical and experimental findings and related them to standard thermal inertia results.
5. Conclusions
In this study, we presented experimental results and numerical simulations of a lightweight concrete wall with different insulation layers under transient- and steady-state temperature conditions. The purpose of this study was to compare thermal inertia behaviour of actual and numerical models of lightweight building walls. The numerical models were validated with experimental tests and numerical multicriteria optimizations using DOE.
The following conclusions can be drawn from the results of this study:
- (1)
Experimental results
- -
When the hot-box relative humidity is 70%, the measured thermal transmittance is 12% higher than at relative humidity of 30%. This demonstrates the importance of the moisture content in porous materials due to their hygroscopicity. In this sense, it is necessary to obtain the material thermal properties at specific humidity contents and account for the moisture transport inside multilayer walls. Moreover, the laboratory ambient conditions and the wall construction process can produce a non-uniform moisture content inside blocks and layers, affecting the thermal results.
- -
Thermal transmittance in steady-state tests was higher than the empirical value calculated following the ISO 6946 standard [
2], with differences ranging from 5 to 15%. Consequently, moisture content must be taken into account to obtain the thermal conductivity values of each layer of porous materials, in this case, Layer 3 (LWMA) and Layer 2 (LWBA25).
- -
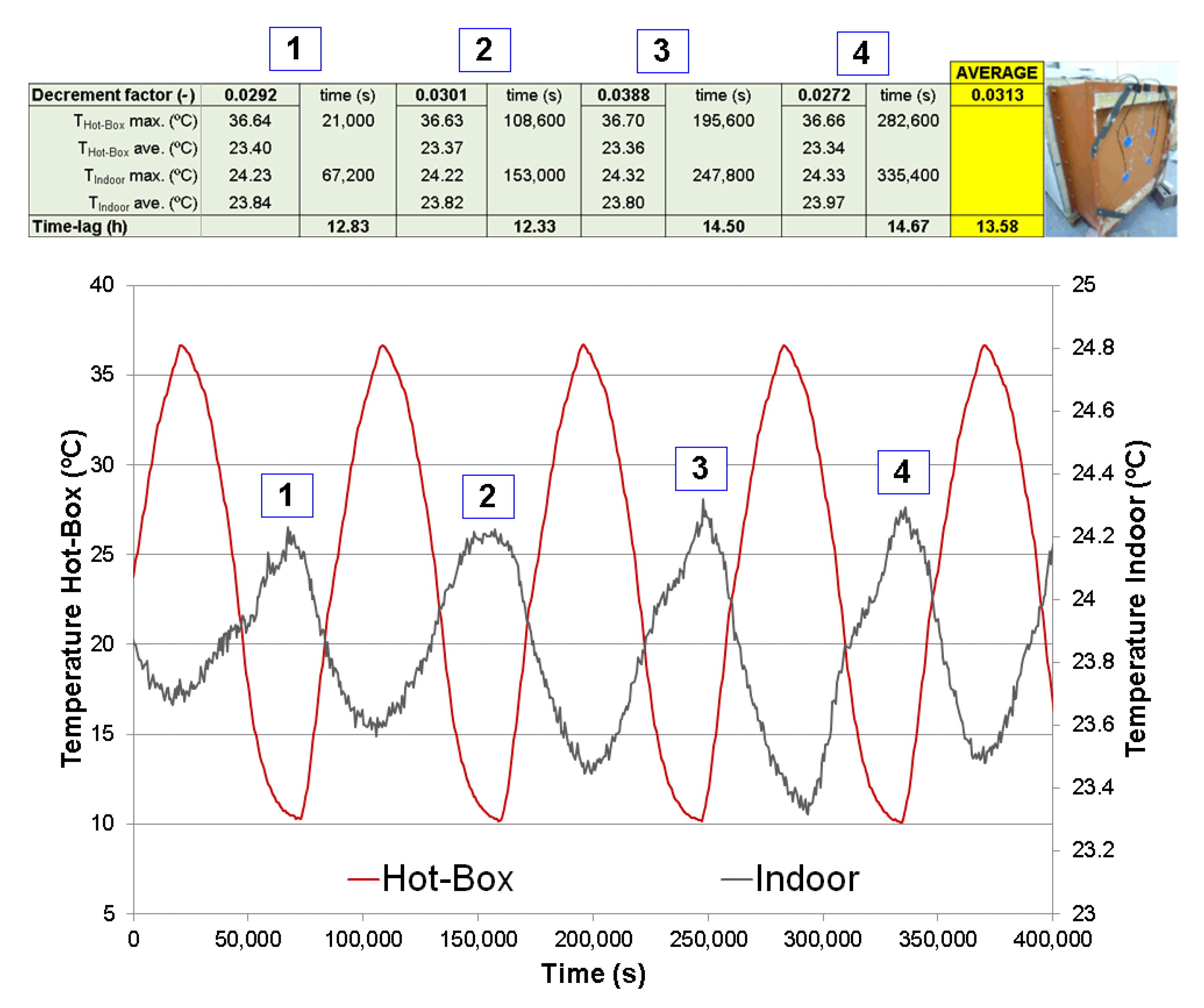
Transient thermal tests in different thermal flux directions showed significant differences in terms of time lag (1.25 h difference) and decrement factor (23% difference). Thermal inertia values were, therefore, strongly affected by the multilayer wall composition.
- -
According to the thermal inertia tests, Layer 3 (LWMA) was appropriate to be exposed to the outdoor conditions. This material had the lowest density, thermal conductivity, thermal diffusivity and heat capacity in the multi-layer wall. With this configuration, a high time lag and low decrement factor were obtained, so the optimal indoor conditions were reached. Thus, materials with lower values in terms of density and thermal properties are recommended to be used at outdoor conditions.
- -
Empirical dynamic thermal inertia parameters exhibited lower time lag and higher decrement factor values than the experimental results. In the empirical formulation, the decrement factor is given by the periodic thermal transmittance divided by the static thermal transmittance of layers with homogeneous materials. In this work, lightweight concrete blocks with cavities were not homogeneous. Their dynamic thermal behavior was not calculated accurately by the empirical formulation. Consequently, the ISO-13786 standard [
3] provides more restrictive designs than the experimental ones, and further research is required in this field.
- (2)
Numerical simulation
- -
A bidimensional FEM model, including conduction, convection and radiation, was used to simulate both steady- and transient-state thermal conditions in a multi-layer wall. The average temperature and heat flux of the block in the middle of the wall was used to obtain numerical results for the thermal transmittance, time lag, and decrement factor.
- -
Two DOE analyses were performed to determine the most influential parameters and obtain accurate material thermal properties similar to the experimental behavior.
- -
Sensitivity analysis obtained from the first DOE under steady-state conditions showed that the three most important input parameters were the thermal conductivity of Layer 3 (LWMA), the thermal conductivity of Layer 2 (LWBA25), and the emissivity of the cavities in the block.
- -
A multicriteria optimization based on second DOE analysis under transient thermal conditions was used to fit the experimental and numerical results. Thermal flux amplitude and phase Equation were used as an objective function according to Equation (11). From this optimization, the thermal conductivity of Layer 3 (LWMA) and Layer 2 (LWBA25) was obtained and used in FEM numerical models for transient- and steady-state analyses.
- (3)
Numerical, empirical and experimental comparison
- -
Numerical and empirical thermal transmittance results of steady-state analyses were in good agreement, showing differences of less than 6%.
- -
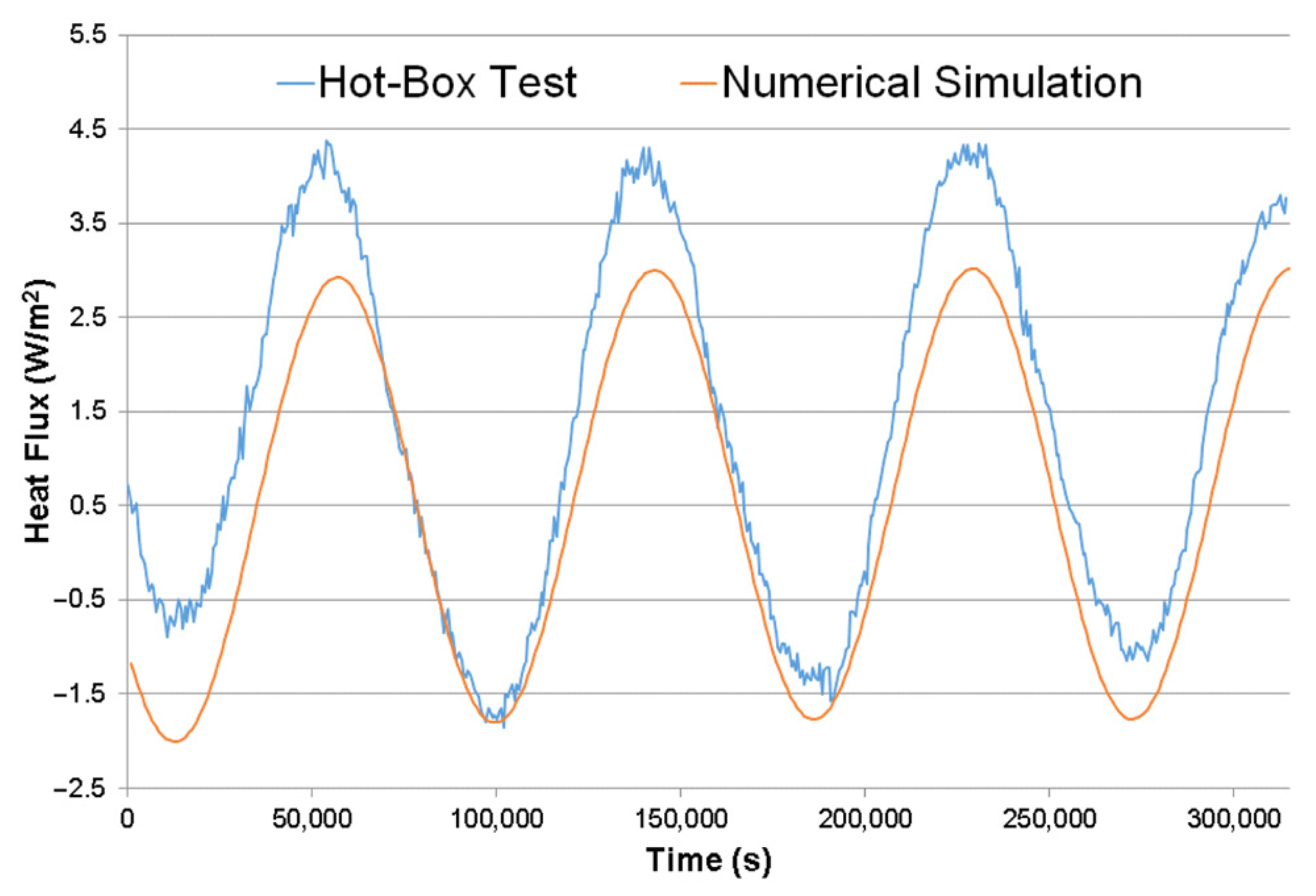
In the transient-state numerical analysis, the temperature amplitude on the indoor face of the wall was lower than the experimental amplitude. Thus, the numerical decrement factor was lower than the value obtained experimentally or empirically. More research is necessary to better understand this effect in the transient state. In this sense, numerical FEM models could be solved with a different time discretization (smaller time steps and lower heat tolerance). In addition, dynamic heat transfer phenomena inside cavities, specifically convection and radiation, must be deeply studied.
- -
Numerical and experimental time lags showed good agreement, with a difference of less than 3% between values. However, results of empirical calculations presented lower values.
This study presents a new hybrid numerical and experimental methodology based on a double DOE analyses including a multicriteria optimization over a FEM two-dimensional multi-layer wall. With the help of experimental tests, it is possible to build an accurate numerical model able to predict the steady-state and dynamic performance of walls made of porous materials, including air cavities.
Furthermore, as shown in previous works [
19,
20,
33,
34], the moisture content in porous materials has a great influence on the thermal performance of this type of lightweight concrete wall. The thermal conductivity is related to the characteristics of the pore structure and internal moisture distribution. Future studies should focus on the development of coupled numerical models, taking into account hygrothermal transport [
19] and dynamic heat transfer within cavities. They could also analyze other wall compositions in order to validate the empirical formulation indicated in the Standard [
3].
Finally, the numerical model developed in this work is an original contribution and a useful tool to simulate the steady-state and dynamic response of multi-layer building walls under different environmental conditions.