Short-Term Load Forecasting Using an Attended Sequential Encoder-Stacked Decoder Model with Online Training
Abstract
1. Introduction
- short-term: from a few minutes until one week ahead
- mid-term: from one week until one year ahead
- long-term: from one year until several years ahead
- a novel and simplified definition of the attention scoring function
- a novel online training procedure for sequence data on the base of transfer learning. This training procedure is especially important in the field of very dynamically changing load patterns.
- a high accuracy achieved on real data provided by NYISO
- an evaluation with different methods including linear regression, Hidden Markov Models and different recurrent neural network architectures
2. Materials and Methods
2.1. Data Used
2.2. Recurrent Network with Long Short-Term Memory Cell
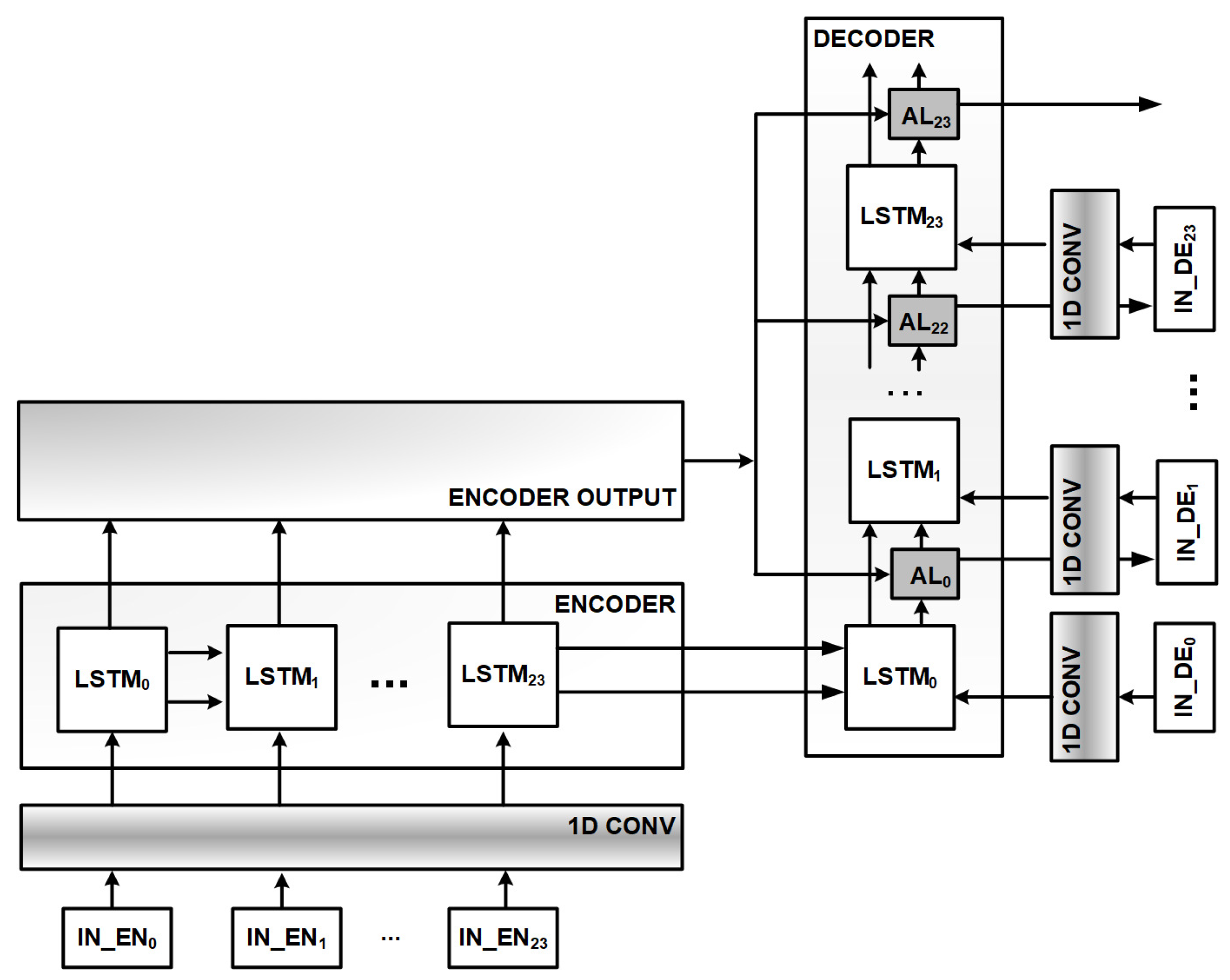
2.3. Encoder-Decoder and Attention
2.4. Application of the Attended Encoder-Decoder to the Short-Term Load Forecasting
2.4.1. Training Data
- daily minimum ambient temperature and wet bulb
- daily maximum ambient temperature and wet bulb
- daily minimum next day ambient temperature and wet bulb
- load power one hour before the intended forecast start before forecast start
- the type of the day (working day, weekend or holiday)
- the length of the day
- the type of the day concerning the ambient temperature (hot, cold, regular day)
2.4.2. Application of Encoder-Decoder Architecture
- the hour h,
- the load power from hour (for decoder the previous predicted value),
- the ambient temperature and wet bulb from hour h,
- the day of the week (0–6),
- the type of the day concerning the temperature (hot, cold, regular),
- the type of the day concerning holiday or working day,
- the length of the day
2.4.3. Attention Score Function
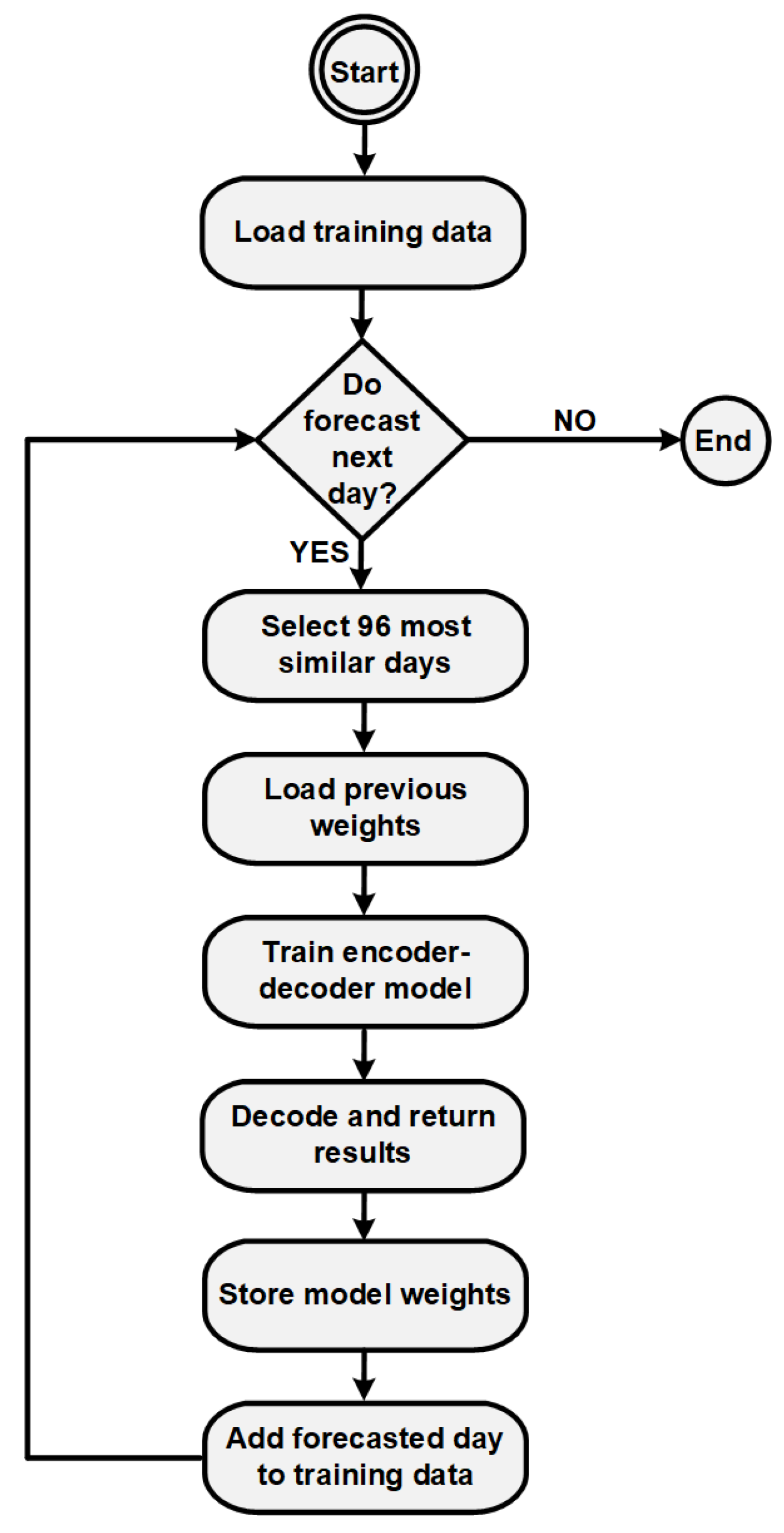
2.4.4. Online Training—A Piecewise Learning of the Underlying Function
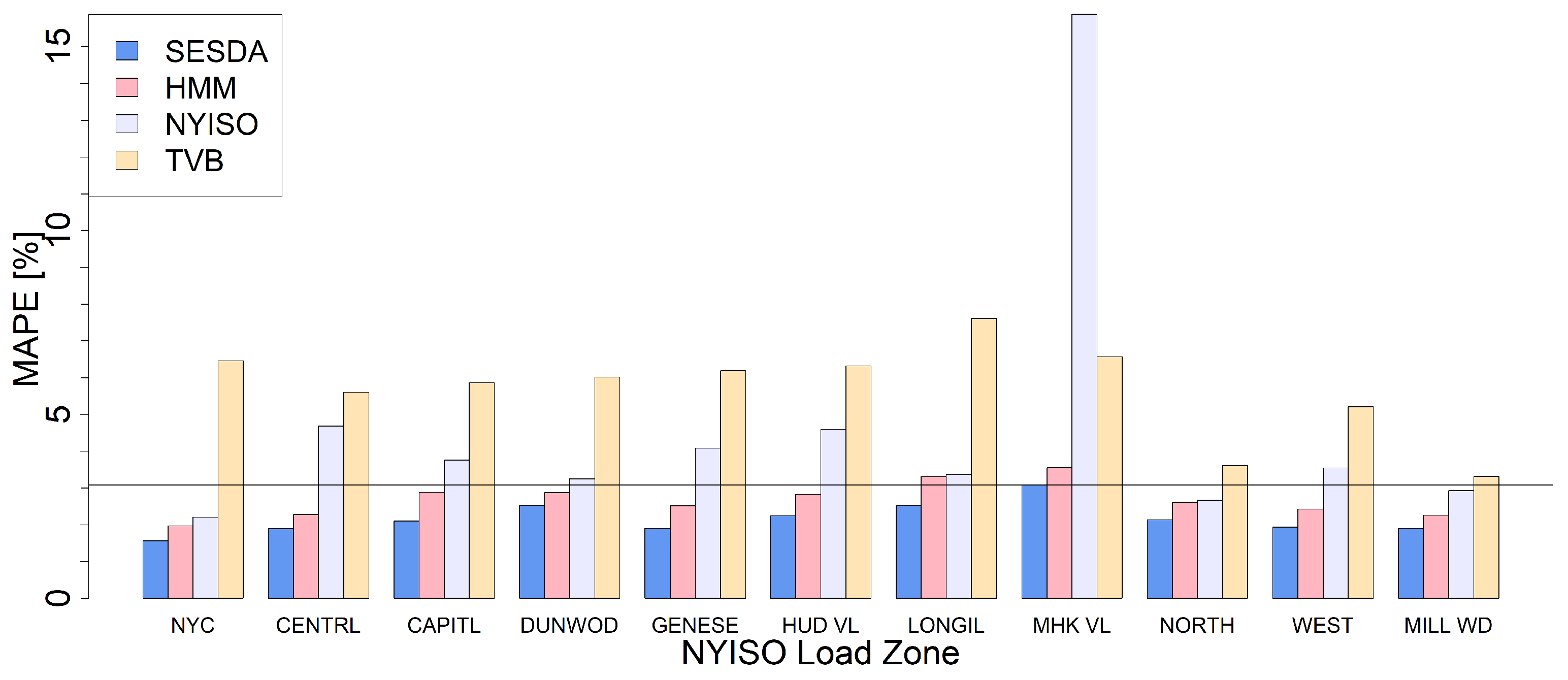
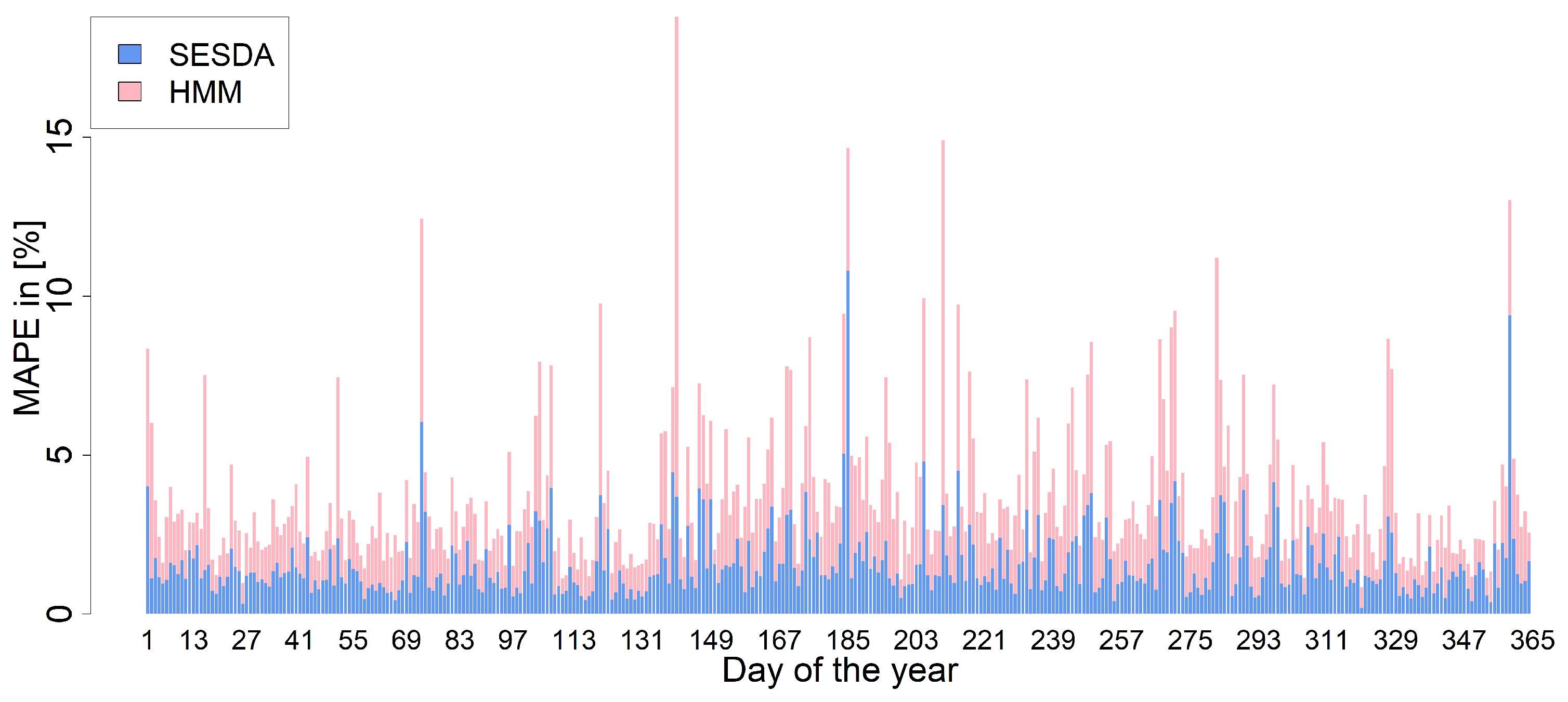
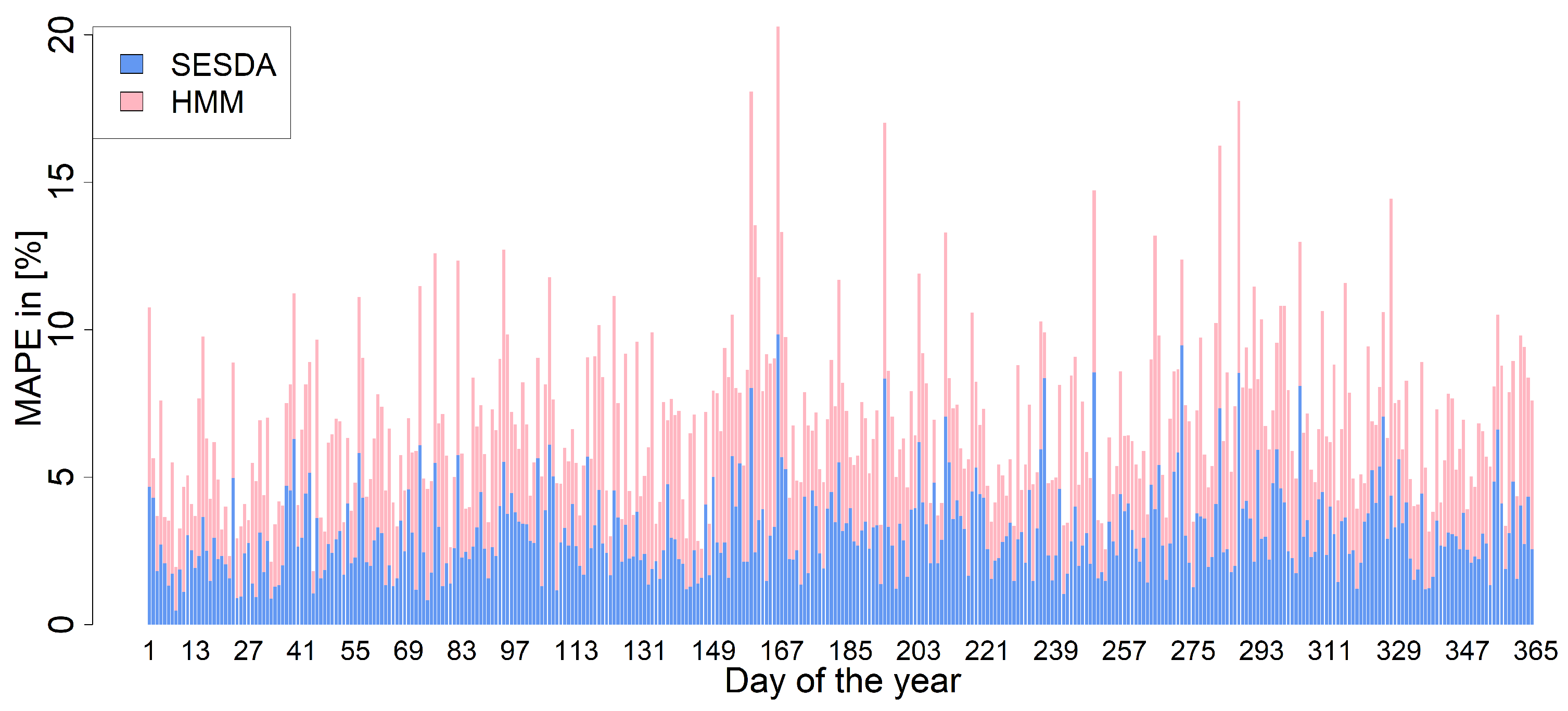
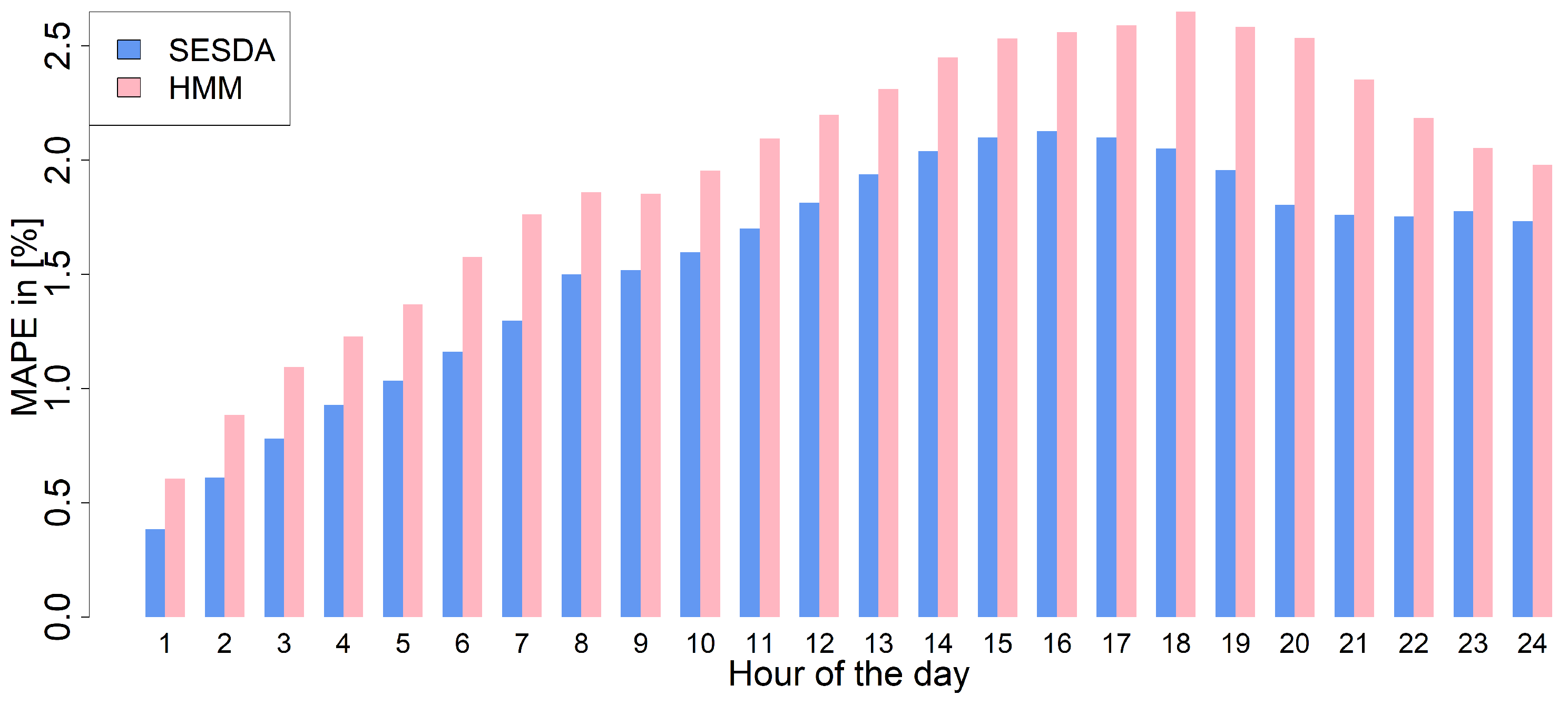
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
References
- Srivastava, A.K.; Pandey, A.S. Short-term load forecasting methods: A review. In Proceedings of the 2016 International Conference on Emerging Trends in Electrical Electronics & Sustainable Energy Systems (ICETEESES), Sultanpur, India, 11–12 March 2016; pp. 130–138. [Google Scholar]
- Papalexopoulos, A.D.; Hesterberg, T.C. A regression-based approach to short-term system load forecasting. IEEE Trans. Power Syst. 1990, 5, 1535–1547. [Google Scholar] [CrossRef]
- Hong, T. Short Term Electric Load Forecasting; North Carolina State University: Raleigh, NC, USA, 2010. [Google Scholar]
- Trull, O.; García-Díaz, J.C.; Troncoso, A. Application of Discrete-Interval Moving Seasonalities to Spanish Electricity Demand Forecasting during Easter. Energies 2019, 12, 1083. [Google Scholar] [CrossRef]
- Shilpa, G.; Sheshadri, G. Short-Term Load Forecasting Using ARIMA Model For Karnataka State Electrical Load. Int. J. Eng. Res. Dev. 2017, 13, 75–79. [Google Scholar]
- Mpawenimana, I.; Pegatoquet, A.; Roy, V.; Rodriguez, L.; Belleudy, C. A comparative study of LSTM and ARIMA for energy load prediction with enhanced data preprocessing. In Proceedings of the 2020 IEEE Sensors Applications Symposium (SAS), Sundsvall, Sweden, 2–4 August 2020; pp. 1–6. [Google Scholar]
- Singhal, R.; Choudhary, N.K.; Singh, N. Short-Term Load Forecasting Using Hybrid ARIMA and Artificial Neural Network Model. In Advances in VLSI, Communication, and Signal Processing; Lecture Notes in Electrical Engineering; Dutta, D., Kar, H., Kumar, C., Bhadauria, V., Eds.; Springer: Berlin/Heidelberg, Germany, 2020; pp. 935–947. [Google Scholar]
- Ganguly, P.; Kalam, A.; Zayegh, A. SHORT TERM LOAD FORECASTING USING FUZZY LOGIC. In Proceedings of the 2016 International Symposium on Electrical Engineering (ISEE), Hong Kong, China, 14 December 2017; pp. 1–7. [Google Scholar]
- Al-Kandari, A.M.; Soliman, S.A.; El-Hawary, M. Fuzzy short-term electric load forecasting. Int. J. Electr. Power Energy Syst. 2004, 26, 111–122. [Google Scholar] [CrossRef]
- Ding, N.; Benoit, C.; Foggia, G.; Besanger, Y.; Wurtz, F. Neural Network-Based Model Design for Short-Term Load Forecast in Distribution Systems. IEEE Trans. Power Syst. 2016, 31, 72–81. [Google Scholar] [CrossRef]
- Tian, C.; Ma, J.; Zhang, C.; Zhan, P. A Deep Neural Network Model for Short-Term Load Forecast Based on Long Short-Term Memory Network and Convolutional Neural Network. Energies 2018, 11, 3493. [Google Scholar] [CrossRef]
- Peng, T.M.; Hubele, N.F.; Karady, G. Advancement Short-Term in the Application of Neural Networks for Load Forecasting. Trans. Power Syst. 1992, 7, 250–257. [Google Scholar] [CrossRef]
- Kiartzis, S.; Bakirtzis, A.; Petridis, V. Short-term load forecasting using neural networks. Electr. Power Syst. Res. 1995, 33, 1–6. [Google Scholar] [CrossRef]
- Wu, W.; Liaob, W.; Miaoa, J.; Du, G. Using Gated Recurrent Unit Network to Forecast Short-Term Load Considering Impact of Electricity Price. In Proceedings of the 10th International Conference on Applied Energy (ICAE2018), Hong Kong, China, 22–25 August 2018; pp. 3369–3374. [Google Scholar]
- Zheng, J.; Xu, C.; Zhang, Z.; Li, X. Electric Load Forecasting in Smart Grid Using Long-Short-Term-Memory based Recurrent Neural Network. In Proceedings of the 2017 51st Annual Conference on Information Sciences and Systems (CISS), Baltimore, MD, USA, 22–24 March 2017; pp. 1–6. [Google Scholar]
- Kuo, P.H.; Huang, C.J. A High Precision Artificial Neural Networks Model for Short-Term Energy Load Forecasting. Energies 2018, 11, 213. [Google Scholar] [CrossRef]
- Bouktif, S.; Fiaz, A.; Ouni, A.; Serhani, M.A. Optimal Deep Learning LSTM Model for Electric Load Forecasting using Feature Selection and Genetic Algorithm: Comparison with Machine Learning Approaches. Energies 2018, 11, 1636. [Google Scholar] [CrossRef]
- Bouktif, S.; Fiaz, A.; Ouni, A.; Serhani, M.A. Multi-Sequence LSTM-RNN Deep Learning and Metaheuristics for Electric Load Forecasting. Energies 2020, 13, 391. [Google Scholar] [CrossRef]
- Bianchi, F.M.; Maiorino, E.; Kampffmeyer, M.C.; Rizzi, A.; Jenssen, R. Recurrent Neural Networks for Short-Term Load Forecasting. An Overview and Comparative Analysis; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Lu, K.; Meng, X.R.; Sun, W.X.; Zhang, R.G.; Han, Y.K.; Gao, S.; Su, D. GRU-based Encoder-Decoder for Short-term CHP Heat Load Forecast. IOP Conf. Ser. Mater. Sci. Eng. 2018, 392, 1–7. [Google Scholar] [CrossRef]
- Bahdanau, D.; Cho, K.H.; Bengio, Y. Neural Machine Translation by Jointly Learning to Align and Translate. arXiv 2015, arXiv:1409.0473. [Google Scholar]
- Sehovac, L.; Grolinger, K. Deep Learning for Load Forecasting: Sequence to Sequence Recurrent Neural Networks with Attention. IEEE Access 2020, 8, 36411–36426. [Google Scholar] [CrossRef]
- Meng, Z.; Xu, X. A Hybrid Short-Term Load Forecasting Framework with an Attention-Based Encoder–Decoder Network Based on Seasonal and Trend Adjustment. Energies 2019, 12, 4612. [Google Scholar] [CrossRef]
- Jin, X.B.; Zheng, W.Z.; Kong, J.L.; Wang, X.Y.; Bai, Y.T.; Su, T.L.; Lin, S. Deep-Learning Forecasting Method for Electric Power Load via Attention-Based Encoder-Decoder with Bayesian Optimization. Energies 2021, 14, 1596. [Google Scholar] [CrossRef]
- Pan, S.J.; Yang, Q. A Survey on Transfer Learning. IEEE Trans. Knowl. Data Eng. 2010, 22, 1345–1359. [Google Scholar] [CrossRef]
- Hooshmand, A.; Sharma, R. Energy Predictive Models with Limited Data using Transfer Learning. arXiv 2019, arXiv:1906.02646. [Google Scholar]
- Ribeiro, M.; Grolinger, K.; ElYamany, H.; Higashino, W.A.; Capretz, M. Transfer learning with seasonal and trend adjustment for cross-building energy forecasting. Energy Build. 2018, 165, 352–363. [Google Scholar] [CrossRef]
- NYISO. Load Data. 2019. Available online: https://www.nyiso.com/load-data (accessed on 26 May 2021).
- Henselmeyer, S.; Grzegorzek, M. Short-term load forecasting with discrete state Hidden Markov Models. J. Intell. Fuzzy Syst. 2020, 38, 2273–2284. [Google Scholar] [CrossRef]
- Mandal, P.; Senjyu, T.; Urasaki, N.; Funabashi, T. A neural network based several-hour-ahead electric load forecasting using similar days approach. Electr. Power Energy Syst. 2006, 28, 367–373. [Google Scholar] [CrossRef]
- Yurafsky, D.; Martin, J. Speech and Language Processing; Prentice Hall: Upper Saddle River, NJ, USA, 2008. [Google Scholar]
- Operations, N.E.M. Day Ahead Scheduling Manual. 2017. Available online: https://www.nyiso.com/documents/20142/2923301/dayahd_schd_mnl.pdf/0024bc71-4dd9-fa80-a816-f9f3e26ea53a (accessed on 26 May 2021).
- Liu, B. Short Term Load Forecasting with Recency Effect: Models and Applications; ProQuest, UMI Dissertation Publishing: Ann Arbor, MI, USA, 2016. [Google Scholar]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems. arXiv 2015, arXiv:1603.04467. [Google Scholar]
- Chollet, F. Keras. 2015. Available online: https://keras.io (accessed on 26 May 2021).
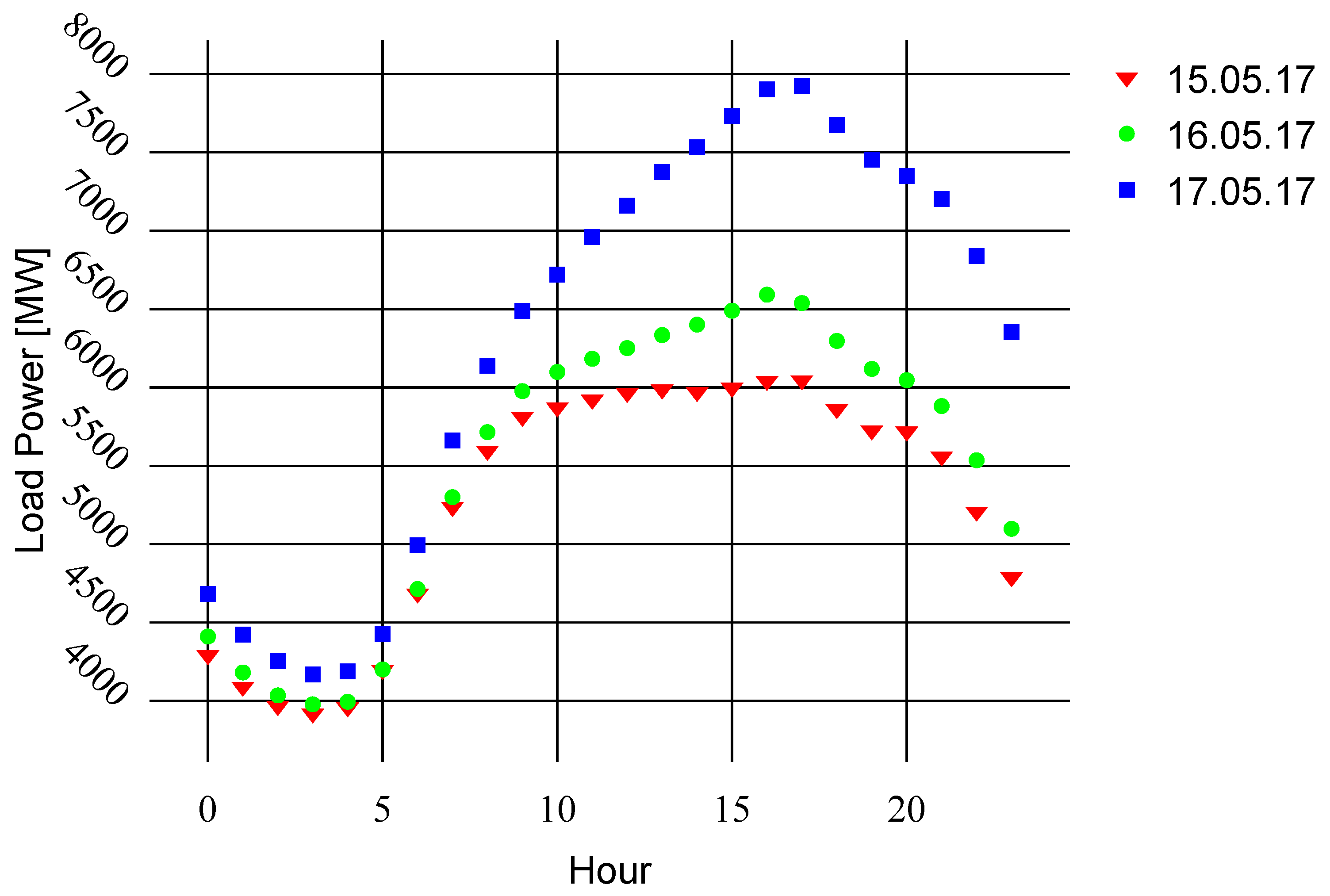
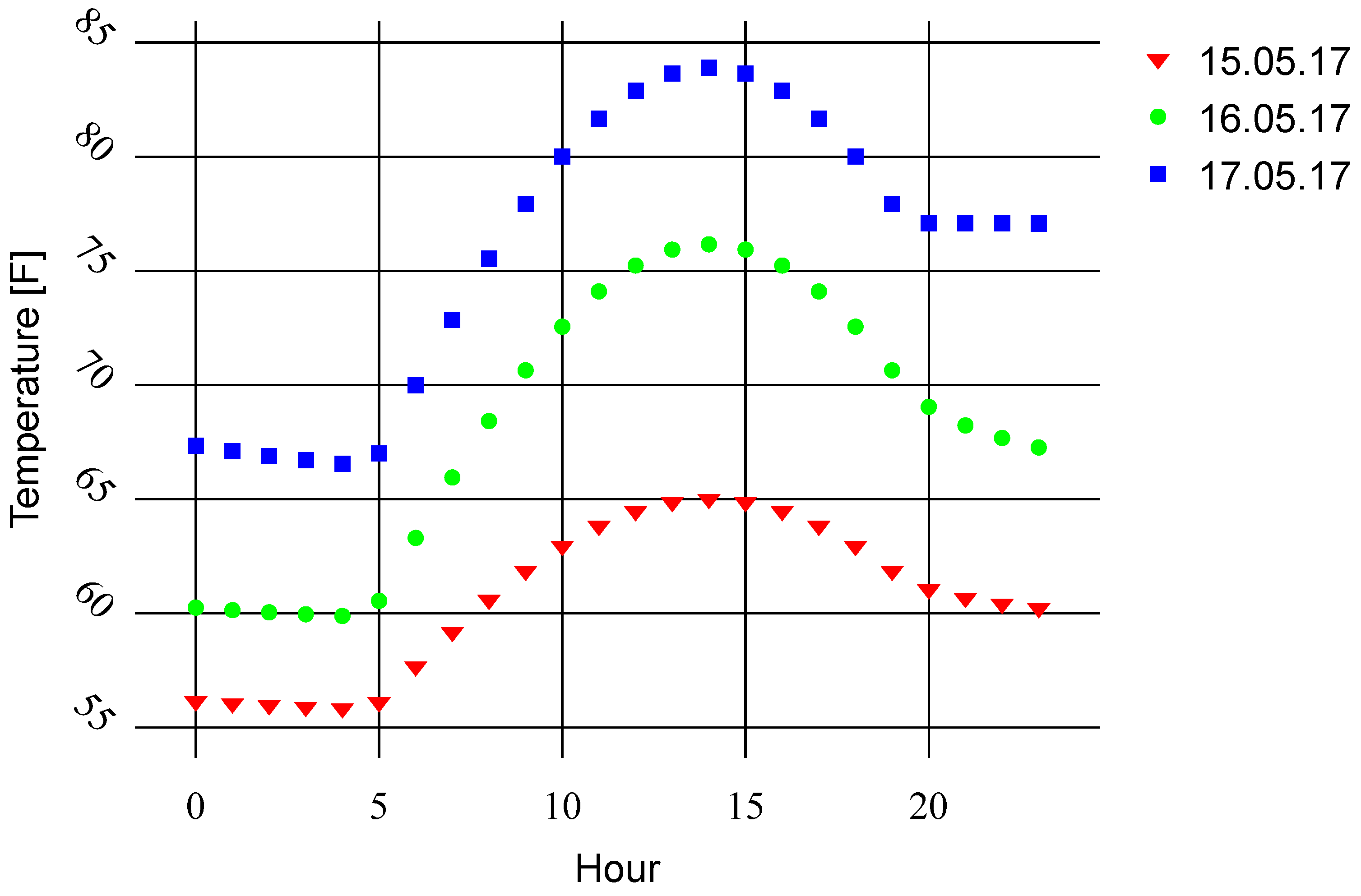
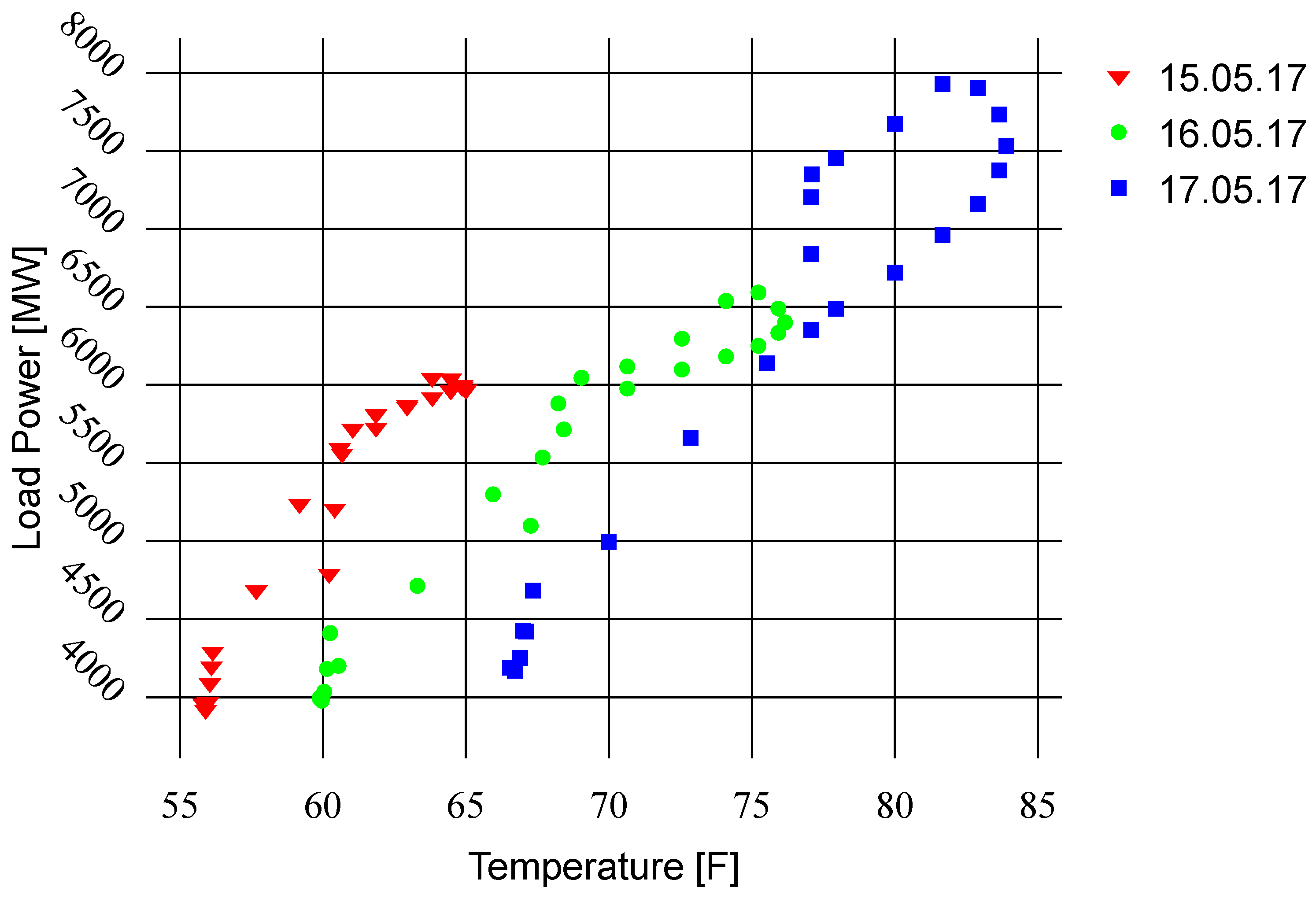

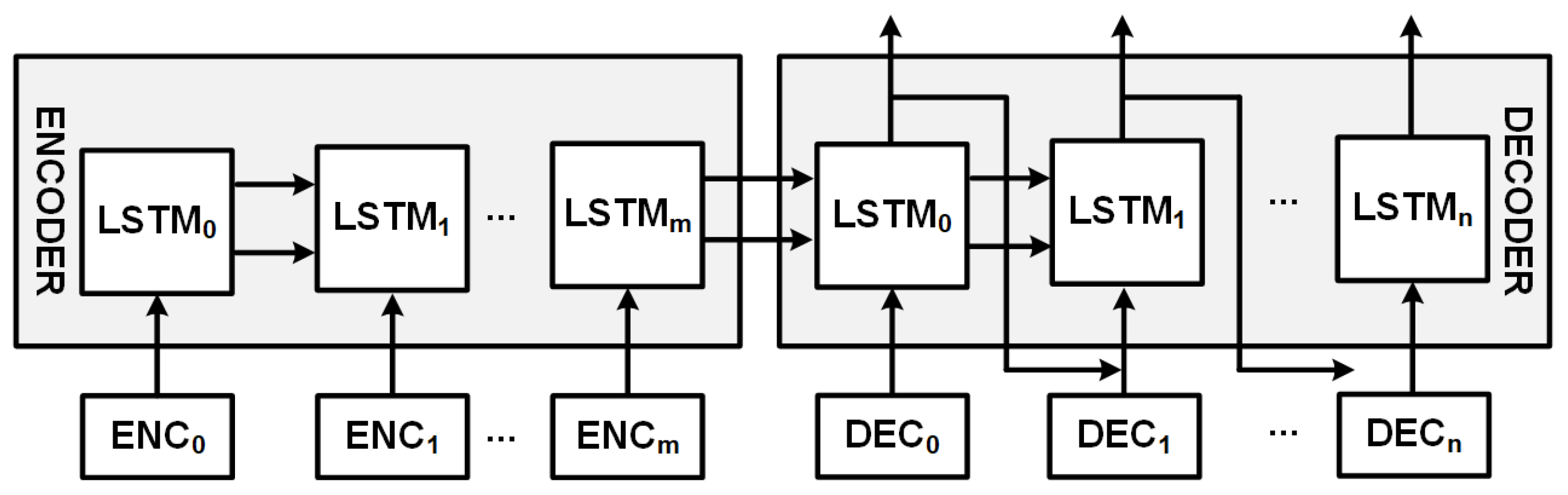
| Zone Name | Zone ID | Average Load [MW] |
|---|---|---|
| Capital | CAPITL | 1450 |
| Central | CENTRL | 1900 |
| Dunwoodie | DUNWOOD | 780 |
| Genese | GENESE | 1200 |
| Hudson Valley | HUD VL | 1200 |
| Long Island | LONGIL | 2500 |
| Millwood | MILL VD | 770 |
| Mohawk Valley | MHK VL | 980 |
| New York City | NYC | 6000 |
| North | NORTH | 590 |
| West | WEST | 1800 |
| Method Name | MAPE |
|---|---|
| Sequential Encoder Stacked Decoder with Attention | 1.52 |
| Sequential Encoder-Decoder with Attention | 1.66 |
| Sequential Encoder-Decoder | 1.72 |
| LSTM | 1.75 |
| NARX | 2.16 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Henselmeyer, S.; Grzegorzek, M. Short-Term Load Forecasting Using an Attended Sequential Encoder-Stacked Decoder Model with Online Training. Appl. Sci. 2021, 11, 4927. https://doi.org/10.3390/app11114927
Henselmeyer S, Grzegorzek M. Short-Term Load Forecasting Using an Attended Sequential Encoder-Stacked Decoder Model with Online Training. Applied Sciences. 2021; 11(11):4927. https://doi.org/10.3390/app11114927
Chicago/Turabian StyleHenselmeyer, Sylwia, and Marcin Grzegorzek. 2021. "Short-Term Load Forecasting Using an Attended Sequential Encoder-Stacked Decoder Model with Online Training" Applied Sciences 11, no. 11: 4927. https://doi.org/10.3390/app11114927
APA StyleHenselmeyer, S., & Grzegorzek, M. (2021). Short-Term Load Forecasting Using an Attended Sequential Encoder-Stacked Decoder Model with Online Training. Applied Sciences, 11(11), 4927. https://doi.org/10.3390/app11114927







