Featured Application
The proposed decomposition-ensemble learning model can be efficiently used to enhance the prediction accuracy of landslide displacement prediction and can also be extended to other difficult forecasting tasks in the geosciences with extremely complex nonlinear data characteristics.
Abstract
As vital comments on landslide early warning systems, accurate and reliable displacement prediction is essential and of significant importance for landslide mitigation. However, obtaining the desired prediction accuracy remains highly difficult and challenging due to the complex nonlinear characteristics of landslide monitoring data. Based on the principle of “decomposition and ensemble”, a three-step decomposition-ensemble learning model integrating ensemble empirical mode decomposition (EEMD) and a recurrent neural network (RNN) was proposed for landslide displacement prediction. EEMD and kurtosis criteria were first applied for data decomposition and construction of trend and periodic components. Second, a polynomial regression model and RNN with maximal information coefficient (MIC)-based input variable selection were implemented for individual prediction of trend and periodic components independently. Finally, the predictions of trend and periodic components were aggregated into a final ensemble prediction. The experimental results from the Muyubao landslide demonstrate that the proposed EEMD-RNN decomposition-ensemble learning model is capable of increasing prediction accuracy and outperforms the traditional decomposition-ensemble learning models (including EEMD-support vector machine, and EEMD-extreme learning machine). Moreover, compared with standard RNN, the gated recurrent unit (GRU)-and long short-term memory (LSTM)-based models perform better in predicting accuracy. The EEMD-RNN decomposition-ensemble learning model is promising for landslide displacement prediction.
1. Introduction
Landslides are a ubiquitous global hazard [1] posing significant threats to life and property. The statistics data show that landslide disasters affected 5 million people and caused total damage of 4.7 billion US dollars during the period from 2000 to 2020 [2]. As shown in Figure 1, China, the USA, Japan, Nepal, and India are the most landslide-prone regions [3], among which China suffers the most landslide disasters. In the past two decades, landslides have killed 3706 people and caused over 2 billion US dollars of estimated damage to China. Landslide early warning has proven to be the most effective measure for landslide mitigation [4,5], and landslide displacement prediction has been catching extensive attention from practitioners and scholars because of its significant importance in early landslide warning systems [6,7]. However, due to the inherent nonlinear characteristics of landslide monitoring data, achieving the desired prediction accuracy remains highly difficult and challenging. Therefore, it is essential to develop an effective and accurate prediction model to improve the performance of landslide displacement prediction, thus aiding landslide mitigation.
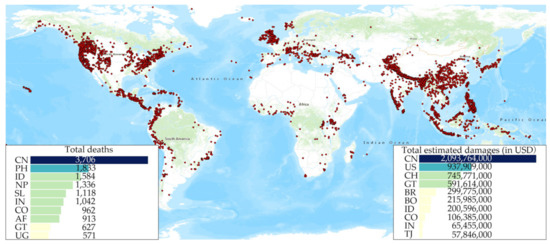
Figure 1.
Spatial distribution of landslide disasters during the period from 2000 to 2020. Each dot represents a single landslide. The insets show the total deaths and total estimated damages. (Source: https://public.emdat.be/data, accessed on 2 December 2020).
A variety of landslide displacement prediction models have been proposed since the pioneering work of Saito [8]. These prediction models generally fall into two main groups: Physics-based models and data-driven models [9]. Physics-based models generally require a clear understanding of the physical processes that involve a large amount of input, sophisticated mathematical tools, and significant user expertise. Therefore, the generalization ability of physics-based models is limited [4].
Recently, data-driven models, including artificial neural networks (ANNs) [10], decision trees [4], extreme learning machines (ELMs) [11,12], support vector machines (SVMs) [13,14,15], quantile regression neural networks [16], random forest (RF) [17], and kernel-based ELMs and SVMs [9,18,19], have attracted attention in landslide displacement prediction. These studies have demonstrated that a data-driven model is capable of providing satisfactory predictions by recognizing movement patterns in historical monitoring data and establishing a mapping between input and output displacements without the requirement of complex physical processes. Recent applications have demonstrated the feasibility of data-driven models to capture nonlinear relationships and to model landslide dynamic processes based on historical model data; however, limitations remain.
First, in most data-driven models, the input variables that have an important influence on the accuracy of landslide displacement prediction [9] are selected based on a priori expert knowledge, trial and error, or linear cross-correlation [9,12]. Nevertheless, a priori expert knowledge of landslide systems is biased [20], or not always available, or even when available, knowledge acquisition tends to be a difficult and time-consuming process. Generally, input variable selection via trial and error is a brute-force process that is computationally expensive, especially for data-driven models with large input candidates. The most commonly used linear correlation coefficients only evaluate linear correlation and cannot reveal the nonlinear relationships that are generally involved in data-driven models. Therefore, a clear need exists for a systematic input variable selection process that does not rely on a priori expert knowledge, is computationally inexpensive, and can describe nonlinear relationships.
Second, conventional data-driven models ignore the intrinsic temporal dependency, which involves the effect of preceding actions on present actions [21,22]. Actually, measured landslide displacement data contain temporal dependencies [23,24].
The abovementioned limitations can be addressed from the following perspectives. The first is to utilize mutual information index describing nonlinear relationships by the amount of related information that is jointly owned by two or more variables [25] for input variable selection. The second solution is to recognize intrinsic temporal dependencies by deploying advanced modeling techniques. A promising solution is the recurrent neural network (RNN) [26]. The temporal dependency in monitoring data can be captured by adopting a sequential approach, thereby improving the ability to model dynamic systems. In addition, the “decomposition-ensemble” learning paradigm can also be considered a promising tool for analyzing series with complex nonlinearity characteristics and enhancing prediction accuracy [27,28,29,30,31]. The effectiveness of the “decomposition-ensemble” has already been confirmed in a variety of fields.
Based on the “decomposition-ensemble” principle, a novel “decomposition-ensemble” learning model integrating EEMD and RNN was proposed in this study to enhance the performance of landslide displacement prediction. The Muyubao landslide located in the Three Gorges Reservoir area was selected as a case study to verify the performance of the proposed model.
2. Study Area and Datasets
2.1. Overview of the Muyubao Landslide
The Muyubao landslide, an ancient landslide, is located in Zigui County, Hubei Province and is situated on the right bank of the Yangtze River (see Figure 2 for landslide location). The length and width of the landslide are approximately 1500 m and 1200 m, respectively. The landslide is 50 m thick on average. The landslide covers approximately 2 million m2 in the planar area and has a volume of approximately 90 million m3. The altitude at the toe of the landslide is 100 m, and the altitude at the crown is 520 m (see Figure 2 for the landslide geological profile). The Muyubao landslide mainly slides in a direction of 20 degrees from North. The borehole analysis reveals that the Muyubao landslide slide along a soft coal layer with an average thickness of 0.2 m. The landslide materials are distributed in two layers: The upper Quaternary deposit and the lower highly disturbed rock mass (Figure 2). The underlaid bedrock is mudstone and sandstone of the Jurassic Xiangxi Formation.
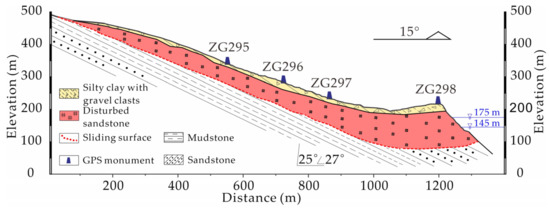
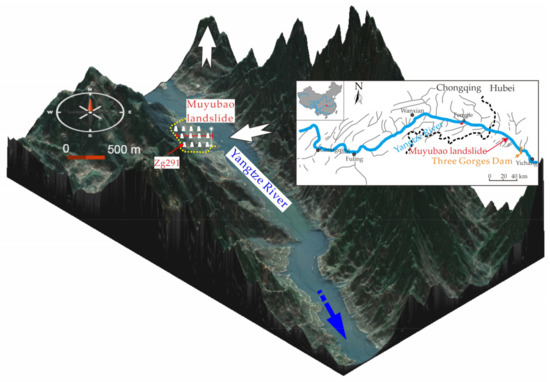
Figure 2.
Location and geological profile of the Muyubao landslide, Three Gorges Reservoir area.
2.2. Data Collection
The ancient Muyubao landslide was reactivated by the impoundment of the Three Gorges Reservoir in September 2006. A landslide monitoring system consisting of twelve GPS survey monuments was installed on the landslide mass (see Figure 2 for GPS monument locations) to monitor landslide movement. Nearly 13 years of monitoring data from October 2006 to October 2018 were acquired. According to the monitoring data, the maximum landslide displacement occurred at ZG291 with a cumulative displacement of 2437.36 mm. The landslide displacement at ZG291, reservoir level in the Yangtze River, and rainfall intensity are shown in Figure 3. As shown, the Muyubao landslide exhibits step-like deformation. Sharp increments of displacement occur mainly from November to March, with the reservoir level decreasing from 175 m to 165 m.
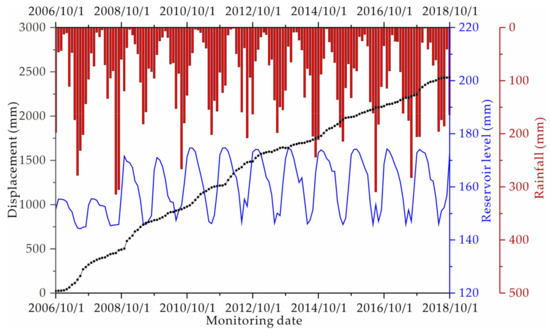
Figure 3.
Time series of landslide displacement at ZG291, reservoir level, and rainfall intensity during the monitoring period from October 2006 to October 2018.
3. Methodology
3.1. Ensemble Empirical Mode Decomposition
Empirical mode decomposition (EMD) is an approach to decompose nonlinear signals into a finite number of simple components called intrinsic mode functions (IMFs). These components form a complete and nearly orthogonal basis for the original signal. The main idea of EMD is repeatedly subtracting the local mean from the original signal. EEMD was improved from EMD to overcome modal aliasing problems by adding white noise [32], and it has been widely used for the decomposition of nonlinear and nonstationary signals [33]. EEMD has the advantages of robust self-adaptability and local variation. As shown in Figure 4, the EEMD decomposition process can be briefly described as the following steps:
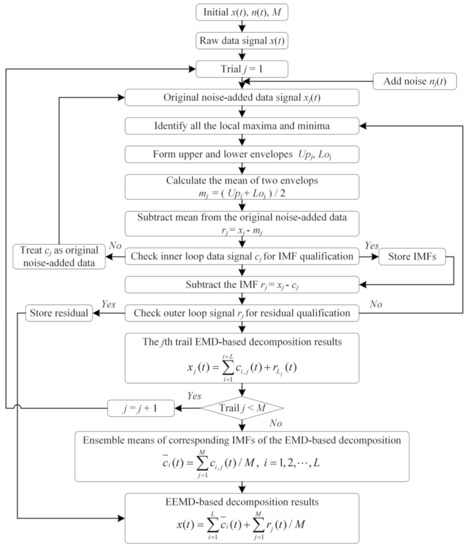
Figure 4.
Schematic diagram of the EEMD decomposition process.
Add a random noise signal to the original raw data to obtain the noise-added data signal
- (1)
- Use EMD to decompose the noise data into some IMFs:where is the ith IMF of noise-added data in the jth decomposition and is the corresponding residue.
- (2)
- Perform M trials by repeating steps (1) and (2) with diverse white noise.
- (3)
- Calculate the mean values of the corresponding IMFs and residue as follows:
3.2. Maximal Information Coefficient (MIC)
Compared with the traditional statistical indexes such as the Pearson coefficient, MIC allows to detect various correlation relationships including linear, non-linear, functional, and non-functional relationships. Secondly, the MIC is designed to maintain similar results even in presence of equal levels noise of different types [34,35].
For continuous variables x and y, the MIC between x and y is described by the following formula:
where presents the marginal probability of x, presents the marginal probability of y, presents the joint probability density function of x and y, and nx, ny is the number of bins of the partition of the x- and y-axis. An MIC of zero indicates that there is no dependence between the concerned variables, while MIC of one implies a stronger relationship [36]. Based on previous research, the final input variables with MICs greater than 0.1 [37,38] were selected from input candidates for model training.
3.3. Recurrent Neural Network
An RNN is an artificial neural network wherein adjacent hidden neurons are connected [39]. These recurrent structures of RNNs can transfer time dependence through hidden units and consider temporal correlations. There are three main types of RNNs: Standard RNN, long short-term memory (LSTM), and gated recurrent unit (GRU) (Figure 5).
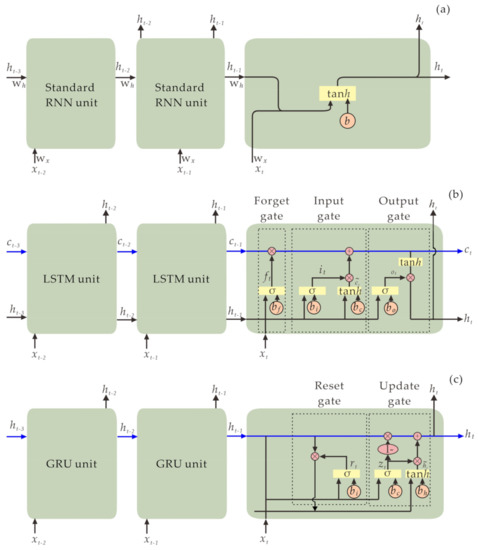
Figure 5.
Basic structures of RNN units: (a) Standard RNN; (b) LSTM; (c) GRU.
3.3.1. Standard RNN
A standard RNN is a simple and powerful RNN. Figure 5a shows the typical structure of a standard RNN. xt is the input vector at time step t and ht is the hidden state of RNN cell at time step t, which is computed based on the hidden state (ht–1) at the previous time step t–1 and the input vector (xt) at the current time step t. Formally, the output of the hidden units of the standard RNN can be formulated as follows:
The final output of RNN depends on not only the input of the current time step but also the calculated of the hidden layer in the previous time step. Theoretically, RNN can take advantage of all information no matter how long the sequences are. However, according to previous studies, because of the vanishing gradient problem, standard RNNs are suitable only for short-term dependencies [39,40].
3.3.2. LSTM
LSTM was improved to overcome the gradient disappearance problem [41] in standard RNN [42]. Figure 5b shows the basic structure of LSTM. A typical LSTM cell consists of one unit state and three types of gates: Input gate (it), output gate (ot), and forget gate (ft). These three gates act as filters, serving different purposes. The input gate (it) determines what new information is going to be stored in the cell state (Ct). The output gate (ot) specifies what information from the cell state (Ct) is used as output. The forget gate (ft) determines what information will be moved away from the cell state (Ct). More formally, the outputs of the input gate (it), output gate (ot), and forget gate (ft) can be formulated as follows:
The current cell state (Ct) can be formulated as follows:
The unit state can be described by the following formula:
The LSTM unit (ht) can be formulated as follows:
where , , , and are the linear correlation coefficient matrices; , , , and are the coefficient matrices of the input variable; denotes the sigmoid activation function; and , , , and are the bias terms of the corresponding formula.
3.3.3. GRU
GRU was developed by [43] to simplify LSTM. Figure 5c shows the basic structure of GRU. A typical GRU unit contains two types of gates: A reset gate (rt) and an update gate (zt). The reset gate (rt) controls how much information from the previous state is written into the current candidate hidden layer vector . The smaller the reset gate (rt), the less information from the previous state is written. The update gate (zt) is used to control the degree to which the state information ht−1 at the previous time step t − 1 will be brought into the current time step t. The larger the value of the update gate (zt), the more the state information at the previous time step is brought in. The reset gate (rt) and update gate (zt) can be defined by the following formula:
The candidate hidden layer vector is defined as follows:
The output of the GRU unit can be formulated as follows:
where , , , and are the weight matrices; and are the bias terms.
3.4. Decomposition-Ensemble Learning Model for Landslide Displacement Prediction
Based on the principle of the “decomposition-ensemble” methodology, a three-step learning model integrating EEMD and RNN can be formulated for landslide displacement prediction. As shown in Figure 6, the proposed EEMD-RNN learning model mainly consists of the following steps: Data decomposition, individual prediction, and ensemble prediction.
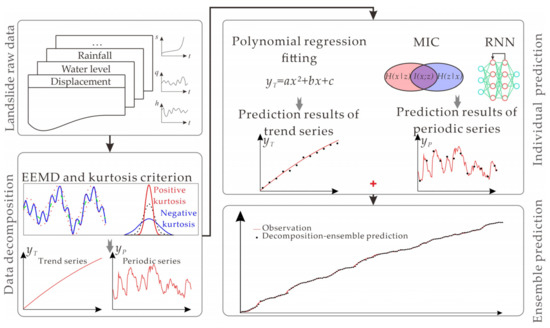
Figure 6.
Overall process of the decomposition-ensemble learning model based on EEMD and RNN.
3.4.1. Data Decomposition
The data decomposition technique is useful for the accurate prediction of landslide displacement, as it can reduce the complexity and improve the interpretability of nonlinear time series. In the present study, EEMD and kurtosis criteria were applied for landslide displacement decomposition and construction of trend and periodic components for further landslide displacement prediction.
Kurtosis is a dimensionless parameter [44,45] describing the waveform peak that is formulated as follows:
where M is the signal length, presents the average of the signal, and presents the standard deviation. A decomposed component with a higher kurtosis retains more deformation characteristics.
EEMD was used to decompose the landslide displacement data shown in Figure 3 into six IMFs and one residual (Figure 7). According to previous works [32], the noise added to the original signal and the maximum number of iterations were set to 0.2 and 100, respectively. The decomposed IMFs oscillate in descending order. The corresponding kurtoses for the decomposition components are listed in Table 1. The obtained kurtoses indicate that the decomposed residual term retains the overall deformation trend of the original time series with the largest kurtosis. Therefore, the residual component was treated as the main trend series for further landslide displacement prediction. The periodic series was obtained by subtracting the trend series from the original series [15]. As shown in Figure 7, the obtained trend components (yT) and periodic components (yP) show two characteristics: The trend components show an approximate monotonic increase in displacement with time, and the periodic components exhibit characteristics of a chaotic time series.
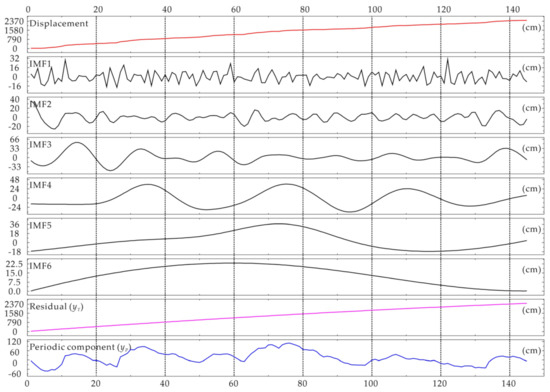
Figure 7.
Decomposition results of landslide displacement using the EEMD method and time series of original landslide displacement and the trend and periodic components.

Table 1.
The kurtoses for the decomposition components.
3.4.2. Individual Prediction
In the present study, 124 measurements from October 2006 to January 2017 were used as the training set for the prediction model, and 21 measurements from February 2017 to October 2018 were treated as testing data. According to previous research on landslide displacement prediction [46,47], the trend components are mainly controlled by internal geological conditions and can be perfectly predicted by polynomial regression fitting. In contrast, the periodic component is mainly controlled by external triggering factors, such as rainfall intensity and reservoir fluctuation. The major difficulty in landslide displacement prediction is accurate prediction of the periodic components. Therefore, polynomial regression fitting was treated as an individual prediction model to predict trend components. The trend component shown in Figure 7 can be fitted as follows:
The coefficient of determination (R2) for the trend component is 1000, which indicates a perfect model for the prediction of the trend component.
Aiming at interpreting the behaviors between input candidates and model outputs and excluding irrelevant and redundant variables to develop accurate and cost-effective prediction models [48], the RNN with MIC-based input variable selection was implemented for individual prediction of periodic components. Based on previous research related to landslide displacement prediction [49], seven commonly used variables were selected as input candidates, including three state candidates and four trigger candidates. The selected four trigger input candidates are one-month antecedent rainfall (x1), two-month antecedent rainfall (x2), average values of reservoir level for the current month (x3), and reservoir fluctuation for the current month (x4). The state candidates are displacement in the past month (x5), displacement of landslides in the past two months (x6), and displacement of landslides in the past three months (x7). Pair plots and MICs between the input candidates and periodic components are shown in Figure 8. The pair plots show an approximately linear dependency between the periodic components (yP) and state candidates (x5, x6, and x7). The MICs indicate that the seven input candidates have significant dependency on the periodic components, with MIC values larger than 0.2. Therefore, seven input candidates were treated as the input for individual prediction of periodic components.
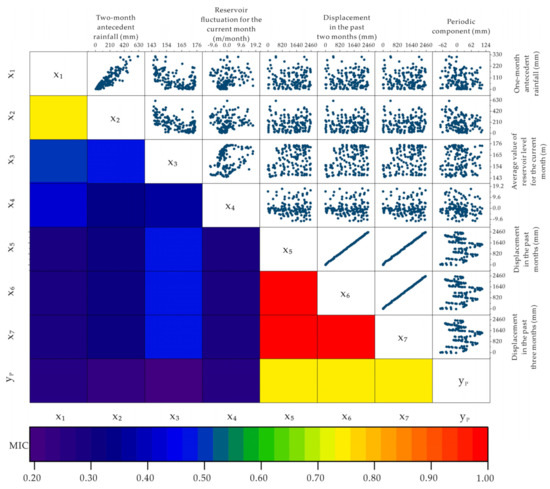
Figure 8.
Pair plots and MICs between the input candidates and periodic components.
The landslide measurements were first normalized in the range of 0 to 1 by min-max feature scaling. After the outputs from the EEMD-RNN approach were renormalized, the final displacement predictions were obtained. The simple trial and error method was adopted for the parameter tuning in RNN, GRU, and LSTM networks. The results from trial-and-error analysis show that RNN, GRU, and LSTM networks with one hidden layer for landslide displacement prediction is better than using a multi-layer network. Therefore, one hidden layer with topologies of 7-50-1, 7-55-1, and 7-50-1 was set up for RNN, LSTM, and GRU in the present study. The epoch strategy referring to the process by which all data are sent into the network to complete an iterative calculation was adopted. The epoch sizes were set to 1000, 400, and 100, respectively. Moreover, learning rate scheduling was adopted for faster convergence and convergence to a better minimum [50]. The corresponding learning rate parameters for RNN, LSTM, and GRU were set to 0.6, 0.7, and 0.5, respectively. More details about the parameter settings in the comparative studies are shown in Table 2.

Table 2.
Parameter settings in the comparative studies.
3.4.3. Ensemble Prediction
The final ensemble predictions of landslide displacement were obtained by aggregating the predictions of trends and periodic components. A comparative analysis was conducted with the following decomposition-ensemble learning model: EEMD-based RNN, EEMD-LSTM, EEMD-GRU, EEMD-SVM, EEM-ELM, and EMD-LSTM. The parameters of the different models used in the comparative studies are listed in Table 2. The model comparative processes were performed in RStudio Version 1.2.5042 running on an Intel(R) Core (TM) i5-6300HQ CPU @ 2.3 GHz with 4 GB RAM.
3.5. Evaluation Metrics
In the present study, six evaluation metrics, namely the mean absolute error (MAE), mean square error (MSE), mean absolute percentage error (MAPE), normalized root mean square error (NRMSE), coefficient of determination (R2), and Kling-Gupta efficiency (KGE), were applied to evaluate the model performance. These evaluation metrics are defined as follows:
where N is the quantity of deformation monitoring data; presents the measured values of landslide displacement; is predicted values of landslide displacement; and represent the mean values of observations and predictions; r is the linear relative coefficient between simulated displacement values and observed displacement values ; is a metric of the relative variability between predicted and observed displacement; and is the ratio between the average predicted displacement to the average observed displacement. The MAE is the average of the absolute errors between the predicted values and actual values, which reflects the actual predicted value error. The MSE is the expected value of the square of the difference between the predicted values and actual values, which evaluates the degree of variability in the data. The MAPE further considers the radio between error and the actual value. In general, the smaller the MAE, MSE, and MAPE values, the better the model performs. The NRMSE allows to read the errors in a more understandably way, since it is a non-dimensional parameter. The R2 measures the linear relationship between the predicted values and actual values of a dependent variable, whereby a high value of R2 (up to one) signposts a perfect model. The KGE values range from negative infinity to 1. It can evaluate the model performance from three perspective views: Correlation, bias, and variability [51,52]. For an ideal prediction model, the value of KGE should be as close to 1 as possible.
4. Results and Discussion
The final ensemble predictions from EEMD-RNN, EEMD-LSTM, EEMD-GRU, EEMD-SVM, EEMD-ELM, and EMD-LSTM are shown in Figure 9. The evaluation metrics, including MAE, MSE, MAPE, NRMSE, R2, and KGE, are shown in Figure 10. As shown, satisfactory predictions were achieved, with R2 values greater than 0.98, which demonstrate the effectiveness of the “decomposition-ensemble” learning model.
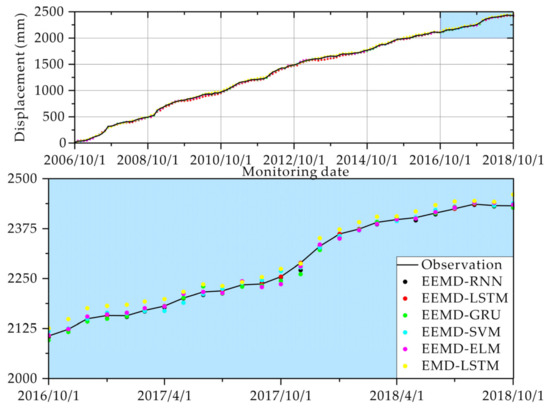
Figure 9.
Time series plots of observed and predicted landslide displacement. The training set is shown with the white background, while the testing set is shown with the blue background.
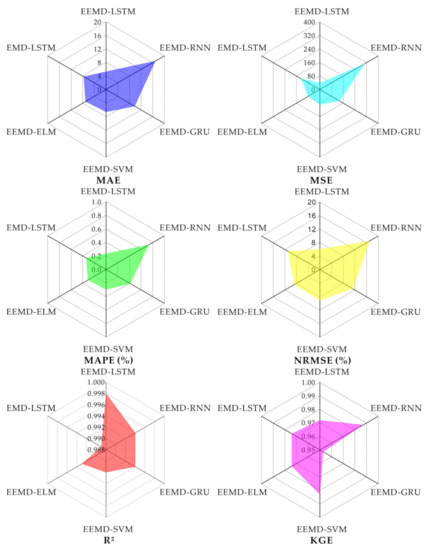
Figure 10.
Comparison of model performance in terms of MAE, MSE, MAPE, NRMSE, R2, and KGE.
4.1. Comparison of EEMD-SVM, EEMD-ELM, and EEMD-RNNs
As shown in Figure 10, in terms of correlation (R2), there are no significant differences among the models. For standard RNN, SVM, and ELM, the values of R2 are 0.994, 0.992, and 0.993, respectively, and the values of KGE are 0.987, 0.983, and 0.974, respectively. In terms of KGE, predictions with less bias and variability were achieved by the RNN-type network than SVM and ELM because recurrent networks provide higher nonlinearity. Moreover, landslide movements are essentially suspended during the dry season. Because static models can only learn current information and can only learn from a portion of historical data, static approaches, including ELM and SVM, provide unreasonable results. The suspended movement characteristics can be approximated well using dynamic RNN approaches through connections of adjacent hidden neurons and learning from a fully historical sequence.
4.2. Comparison of EEMD-Based Standard RNN, LSTM and GRU
As shown in Figure 10, LSTM has higher prediction accuracy than GRU, both of which are better than standard RNN. For the standard RNN, LSTM, and GRU models, the MAE values are 16.935, 5.357, and 9.8425, respectively, and the NRMSE values are 6.1, 11.3, and 17, respectively. The evaluation metrics in Figure 10 illustrate that the prediction accuracy of the LSTM and GRU models is better than that of the standard RNN model. The problem of gradient disappearance in standard RNN is the primary cause for this performance distinction. The LSTM and GRU approaches are more practicable for landslide displacement prediction because of the gated unit structures.
In this study, the GRU model consumes 47.66 s to train, while the LSTM model consumes 201.75s, an increase of nearly three times the computational cost due to the complex network structure. The comparative analysis shows that the LSTM and GRU models provide equally satisfactory performance for landslide displacement prediction, but GRU is more efficient because of its simpler network structure.
4.3. Comparison of EMD-LSTM and EEMD-LSTM
As shown in Figure 10, the R2 and KGE of EMD-LSTM are lower than those of the EEMD-LSTM decomposition-ensemble learning model. The lower performance statistics of the EMD-LSTM decomposition-ensemble learning model are caused mainly by the mode mixing problem in EMD.
Figure 11 compares the model performance for the periodic component in terms of R2 when varying the training data size: The model performance improves with the data capacity of the training set. The outperformance of EEMD-LSTM over EEMD-based static methods, including ELM and SVM, is not remarkable when the training dataset is smaller than 80%. This can be explained as follows: Compared to traditional models, more parameters must be tuned in the LSTM-based prediction model. Therefore, more input data are required to maintain the model performance.
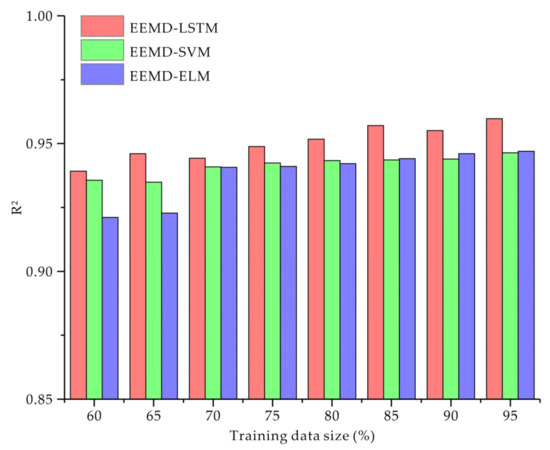
Figure 11.
Comparison of model performance for periodic components in terms of R2 when varying the training set size.
The case study from the Muyubao landslide shows that the hybrid EEMD-RNN decomposition-ensemble learning model is promising for accurate prediction of landslide displacement by combining the advantages of EEMD and RNN. The main advantages of the proposed EEMD-based RNN decomposition-ensemble learning model can be outlined as follows:
The MIC-based input variable selection is a systematic process without any a priori expert knowledge, computationally inexpensive, and capable of describing the nonlinear relationships. The performance of prediction model is able to be improved by EEMD decomposition of complicated forecasting problems into several easier ones, and the temporal dependency in complicated monitoring data is captured by adopting a RNN approach, thereby improving the ability to model dynamic systems.
Although the EEMD-RNN decomposition-ensemble learning model has potential for the accurate prediction of landslide displacement, it has inherent limitations associated with data-driven approaches, including lack of transparency and a requirement for large quantities of training data [53,54].
5. Conclusions
According to the decomposition-ensemble principle, a novel three-step decomposition-ensemble learning model integrating EEMD and RNN was proposed for landslide displacement prediction. The experimental results from the Muyubao landslide in the Three Gorges Reservoir area demonstrate that the proposed EEMD-RNN decomposition-ensemble learning model is capable of increasing prediction accuracy and outperforms traditional decomposition-ensemble learning models (including EMD-LSTM, EEMD-SVM, and EEMD-ELM) in terms of prediction accuracy. Moreover, the GRU- and LSTM-based models perform better than standard RNN by providing equally satisfactory performance in terms of predicting accuracy. Due to the simpler structure, GRU is more efficient than standard RNN and LSTM. Therefore, in practical application, EEMD-GRU learning model is more suitable for medium-term to long-term horizon displacement prediction of reservoir landslide in the Three Gorges Reservoir area. In addition to landslide displacement prediction, the proposed EEMD-RNN decomposition-ensemble learning model can also be extended to other difficult forecasting tasks in geosciences with extremely complex nonlinear data characteristics.
Author Contributions
The work was carried out in collaboration between all the authors. X.N. and J.M. guided and supervised this research; Y.W., J.Z., H.C. and H.T. performed the field investigation; X.N. wrote the original draft; and X.N. and J.M. reviewed and edited the draft. All authors have contributed to, seen, and approved the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Major Program of National Natural Science Foundation of China (Grant No. 42090055), Chongqing Geo-disaster Prevention and Control Center (Grant No. 20C0023), Science and Technology Projects of the Huaneng Lancang River Hydropower Co., Ltd. (Grant No. HNKJ18-H24), and the National Natural Science Foundation of China (Grant Nos. 41702328 and 42090055). All support is gratefully acknowledged.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data used in this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Froude, M.J.; Petley, D.N. Global fatal landslide occurrence from 2004 to 2016. Nat. Hazards Earth Syst. Sci. 2018, 18, 2161–2181. [Google Scholar] [CrossRef]
- Cred, F. EM-DAT. The OFDA/CRED International Disaster Database; Université Catholique de Louvain: Brussels, Belgium, 2011; Available online: www.emdat.be (accessed on 2 December 2020).
- Li, W.; Liu, C.; Scaioni, M.; Sun, W.; Chen, Y.; Yao, D.; Chen, S.; Hong, Y.; Zhang, K.; Cheng, G. Spatio-temporal analysis and simulation on shallow rainfall-induced landslides in China using landslide susceptibility dynamics and rainfall ID thresholds. Sci. China Earth Sci. 2017, 60, 720–732. [Google Scholar] [CrossRef]
- Ma, J.; Tang, H.; Liu, X.; Hu, X.; Sun, M.; Song, Y. Establishment of a deformation forecasting model for a step-like landslide based on decision tree C5.0 and two-step cluster algorithms: A case study in the Three Gorges Reservoir area, China. Landslides 2017, 14, 1275–1281. [Google Scholar] [CrossRef]
- Ma, J.; Tang, H.; Liu, X.; Wen, T.; Zhang, J.; Tan, Q.; Fan, Z. Probabilistic forecasting of landslide displacement accounting for epistemic uncertainty: A case study in the Three Gorges Reservoir area, China. Landslides 2018, 15, 1145–1153. [Google Scholar] [CrossRef]
- Picarelli, L.; Behavior, S.; Regime, P.P.; Mechanisms, L.; Mechanics, L. Landslides—Disaster Risk Reduction; Springer: Cham, Switzerland, 2009. [Google Scholar]
- Hu, X.; Wu, S.; Zhang, G.; Zheng, W.; Liu, C.; He, C.; Liu, Z.; Guo, X.; Zhang, H. Landslide displacement prediction using kinematics-based random forests method: A case study in Jinping Reservoir Area, China. Eng. Geol. 2021, 283, 105975. [Google Scholar] [CrossRef]
- Saito, M. Forecasting the Time of Occurrence of a Slope Failure. In Proceedings of the 6th International Conference on Soil Mechanics and Foundation Engineering, Montreal, QC, Canada, 8–15 September 1965; pp. 537–541. [Google Scholar]
- Ma, J.; Niu, X.; Tang, H.; Wang, Y.; Wen, T.; Zhang, J. Displacement prediction of a complex landslide in the Three Gorges Reservoir Area (China) using a hybrid computational intelligence approach. Complexity 2020, 2020. [Google Scholar] [CrossRef]
- Du, J.; Yin, K.; Lacasse, S. Displacement prediction in colluvial landslides, Three Gorges Reservoir, China. Landslides 2013, 10, 203–218. [Google Scholar] [CrossRef]
- Lian, C.; Zeng, Z.; Yao, W.; Tang, H. Extreme learning machine for the displacement prediction of landslide under rainfall and reservoir level. Stoch. Environ. Res. Risk Assess. 2014, 28, 1957–1972. [Google Scholar] [CrossRef]
- Cao, Y.; Yin, K.; Alexander, D.E.; Zhou, C. Using an extreme learning machine to predict the displacement of step-like landslides in relation to controlling factors. Landslides 2016, 13, 725–736. [Google Scholar] [CrossRef]
- Huang, F.; Huang, J.; Jiang, S.; Zhou, C. Landslide displacement prediction based on multivariate chaotic model and extreme learning machine. Eng. Geol. 2017, 218, 173–186. [Google Scholar] [CrossRef]
- Miao, F.; Wu, Y.; Xie, Y.; Li, Y. Prediction of landslide displacement with step-like behavior based on multialgorithm optimization and a support vector regression model. Landslides 2018, 15, 475–488. [Google Scholar] [CrossRef]
- Wen, T.; Tang, H.; Wang, Y.; Lin, C.; Xiong, C. Landslide displacement prediction using the GA-LSSVM model and time series analysis: A case study of Three Gorges Reservoir, China. Nat. Hazards Earth Syst. Sci. 2017, 17, 2181–2198. [Google Scholar] [CrossRef]
- Ma, J.; Liu, X.; Niu, X.; Wang, Y.; Wen, T.; Zhang, J.; Zou, Z. Forecasting of Landslide Displacement Using a Probability-Scheme Combination Ensemble Prediction Technique. Int. J. Environ. Res. Public Health 2020, 17, 4788. [Google Scholar] [CrossRef]
- Li, C.D.; Criss, R.E.; Fu, Z.Y.; Long, J.J.; Tan, Q.W. Evolution characteristics and displacement forecasting model of landslides with stair-step sliding surface along the Xiangxi River, three Gorges Reservoir region, China. Eng. Geol. 2021, 283, 105961. [Google Scholar] [CrossRef]
- Han, H.; Shi, B.; Zhang, L. Prediction of landslide sharp increase displacement by SVM with considering hysteresis of groundwater change. Eng. Geol. 2021, 280, 105876. [Google Scholar] [CrossRef]
- Zhou, C.; Yin, K.; Cao, Y.; Intrieri, E.; Ahmed, B.; Catani, F. Displacement prediction of step-like landslide by applying a novel kernel extreme learning machine method. Landslides 2018, 15, 2211–2225. [Google Scholar] [CrossRef]
- Brandt, L.A.; Benscoter, A.M.; Harvey, R.; Speroterra, C.; Bucklin, D.; Romañach, S.S.; Watling, J.I.; Mazzotti, F.J. Comparison of climate envelope models developed using expert-selected variables versus statistical selection. Ecol. Model. 2017, 345, 10–20. [Google Scholar] [CrossRef]
- Messinger, D.S.; Mattson, W.I.; Todd, J.T.; Gangi, D.N.; Myers, N.D.; Bahrick, L.E. Temporal dependency and the structure of early looking. PLoS ONE 2017, 12, e0169458. [Google Scholar] [CrossRef]
- Wu, J.; Zeng, W.; Yan, F. Hierarchical Temporal Memory method for time-series-based anomaly detection. Neurocomputing 2018, 273, 535–546. [Google Scholar] [CrossRef]
- Rahimi, M.; Shafieezadeh, A.; Wood, D.; Kubatko, E.J.; Dormady, N.C. Bayesian calibration of multi-response systems via multivariate Kriging: Methodology and geological and geotechnical case studies—ScienceDirect. Eng. Geol. 2019, 260, 105248. [Google Scholar] [CrossRef]
- Samia, J.; Temme, A.; Bregt, A.; Wallinga, J.; Guzzetti, F.; Ardizzone, F.; Rossi, M. Do landslides follow landslides? Insights in path dependency from a multi-temporal landslide inventory. Landslides 2017, 14, 547–558. [Google Scholar] [CrossRef]
- Liu, H.; Chen, C. Spatial air quality index prediction model based on decomposition, adaptive boosting, and three-stage feature selection: A case study in China. J. Clean. Prod. 2020, 265, 121777. [Google Scholar] [CrossRef]
- Fan, C.; Wang, J.; Gang, W.; Li, S. Assessment of deep recurrent neural network-based strategies for short-term building energy predictions. Appl. Energy 2019, 236, 700–710. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, J. A novel decomposition-ensemble model for forecasting short-term load-time series with multiple seasonal patterns. Appl. Soft Comput. 2018, 65, 478–494. [Google Scholar] [CrossRef]
- Yu, L.; Dai, W.; Tang, L. A novel decomposition ensemble model with extended extreme learning machine for crude oil price forecasting. Eng. Appl. Artif. Intel. 2016, 47, 110–121. [Google Scholar] [CrossRef]
- Yu, L.; Wang, Z.; Tang, L. A decomposition–ensemble model with data-characteristic-driven reconstruction for crude oil price forecasting. Appl. Energy 2015, 156, 251–267. [Google Scholar] [CrossRef]
- Niu, M.; Hu, Y.; Sun, S.; Liu, Y. A novel hybrid decomposition-ensemble model based on VMD and HGWO for container throughput forecasting. Appl. Math. Model. 2018, 57, 163–178. [Google Scholar] [CrossRef]
- Zuo, G.; Luo, J.; Wang, N.; Lian, Y.; He, X. Decomposition ensemble model based on variational mode decomposition and long short-term memory for streamflow forecasting. J. Hydrol. 2020, 585, 124776. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. A study of the characteristics of white noise using the empirical mode decomposition method. Proc. Math. Phys. Eng. Sci. 2004, 460, 1597–1611. [Google Scholar] [CrossRef]
- Li, G.; Hu, Y. An enhanced PCA-based chiller sensor fault detection method using ensemble empirical mode decomposition based denoising. Energy Build. 2019, 183, 311–324. [Google Scholar] [CrossRef]
- Zhang, Y.; Jia, S.; Huang, H.; Qiu, J.; Zhou, C. A novel algorithm for the precise calculation of the maximal information coefficient. Sci. Rep. 2014, 4, 1–5. [Google Scholar] [CrossRef]
- Kinney, J.B.; Atwal, G.S. Equitability, mutual information, and the maximal information coefficient. Proc. Natl. Acad. Sci. USA 2014, 111, 3354–3359. [Google Scholar] [CrossRef]
- Reshef, D.N.; Reshef, Y.A.; Finucane, H.K.; Grossman, S.R.; McVean, G.; Turnbaugh, P.J.; Lander, E.S.; Mitzenmacher, M.; Sabeti, P.C. Detecting novel associations in large data sets. Science 2011, 334, 1518–1524. [Google Scholar] [CrossRef]
- Lu, F.; Chen, Z.; Liu, W.; Shao, H. Modeling chlorophyll-a concentrations using an artificial neural network for precisely eco-restoring lake basin. Ecol. Eng. 2016, 95, 422–429. [Google Scholar] [CrossRef]
- Tian, W.; Zhibo, C.; Yuqun, F.; Weinan, Q.; Zhihua, L.; Chao, Z. Sensitivity analysis of influencing factors of induced electricity based on MIC in double-circuit transmission line. Electr. Meas. Instrum. 2020, 1–7. Available online: https://kns.cnki.net/kcms/detail/23.1202.TH.20201016.1612.010.html (accessed on 2 December 2020).
- Wei, X.; Zhang, L.; Yang, H.-Q.; Zhang, L.; Yao, Y.-P. Machine learning for pore-water pressure time-series prediction: Application of recurrent neural networks. Geosci. Front. 2021, 12, 453–467. [Google Scholar] [CrossRef]
- Pascanu, R.; Mikolov, T.; Bengio, Y.O. On the difficulty of training Recurrent Neural Networks. JMLR.org 2013, 1211, 5063. [Google Scholar]
- Jun, M.A.; Ding, Y.; Cheng, J.; Jiang, F.; Wan, Z. A Temporal-Spatial Interpolation and Extrapolation Method Based on Geographic Long Short-Term Memory Neural Network for PM2.5. J. Clean. Prod. 2019, 237, 117729. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Cho, K.; Van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv 2014, arXiv:1406.1078. [Google Scholar]
- Alam, S.S.; Bhuiyan, M.I.H. Detection of seizure and epilepsy using higher order statistics in the EMD domain. IEEE J. Biomed. Health Inform. 2013, 17, 312–318. [Google Scholar] [CrossRef]
- Li, Y.; Xu, M.; Liang, X.; Huang, W. Application of bandwidth EMD and adaptive multiscale morphology analysis for incipient fault diagnosis of rolling bearings. IEEE Trans. Ind. Electron. 2017, 64, 6506–6517. [Google Scholar] [CrossRef]
- Zhang, J.; Tang, H.; Tannant, D.D.; Lin, C.; Xia, D.; Liu, X.; Zhang, Y.; Ma, J. Combined forecasting model with CEEMD-LCSS reconstruction and the ABC-SVR method for landslide displacement prediction. J. Clean. Prod. 2021, 293, 126205. [Google Scholar] [CrossRef]
- Zhang, J.; Tang, H.; Tao, W.; Ma, J.; Tan, Q.; Xia, D.; Liu, X.; Zhang, Y. A Hybrid Landslide Displacement Prediction Method Based on CEEMD and DTW-ACO-SVR—Cases Studied in the Three Gorges Reservoir Area. Sensors 2020, 20, 4287. [Google Scholar] [CrossRef] [PubMed]
- Fang, W.; Huang, S.; Huang, Q.; Huang, G.; Meng, E.; Luan, J. Reference evapotranspiration forecasting based on local meteorological and global climate information screened by partial mutual information. J. Hydrol. 2018, 561, 764–779. [Google Scholar] [CrossRef]
- Li, L.; Wu, Y.; Miao, F.; Xue, Y.; Huang, Y. A hybrid interval displacement forecasting model for reservoir colluvial landslides with step-like deformation characteristics considering dynamic switching of deformation states. Stoch. Environ. Res. Risk Assess. 2020, 1–24. [Google Scholar] [CrossRef]
- Senior, A.; Heigold, G.; Ranzato, M.; Yang, K. An Empirical Study of Learning Rates in Deep Neural Networks for Speech Recognition. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 6724–6728. [Google Scholar] [CrossRef]
- Chen, Y.; Yuan, H. Evaluation of nine sub-daily soil moisture model products over China using high-resolution in situ observations. J. Hydrol. 2020, 588, 125054. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Khosravi, K.; Mao, L.; Kisi, O.; Yaseen, Z.M.; Shahid, S. Quantifying hourly suspended sediment load using data mining models: Case study of a glacierized Andean catchment in Chile. J. Hydrol. 2018, 567, 165–179. [Google Scholar] [CrossRef]
- Xu, S.; Niu, R. Displacement prediction of Baijiabao landslide based on empirical mode decomposition and long short-term memory neural network in Three Gorges area, China. Comput. Geosci. 2018, 111, 87–96. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).