Free Electron Laser High Gain Equation and Harmonic Generation
Abstract
1. Introduction
- (a)
- From the first of Equation (1), we obtain the lowest order (in the field strength) expansion of , namelywhere is the detuning parameter.
- (b)
- Inserting in the second of Equation (1) and averaging on the electron-field phase , we getwhere the averages have been taken by considering the e-beam mono-energetic and without spatial and angular dispersion, thereby getting
- (i)
- Absence of an initial bunching ( constant); in this case Equation (3) reduces toThe underlying physics is that energy modulation and consequent bunching are due to the input coherent seed .
- (ii)
- Nonconstant and emergence of non zero coefficients; the field may grow in a seedless mode, induced by the initial bunching coefficient, as illustrated below.
2. Algorithmic and Analytical Solutions of the FEL Integral Equation
- (i)
- The solution of the cubic equation can be written aswhere are the roots of the third-degree algebraic equation
- (ii)
- The amplitudes are fixed by the initial conditions, as shown below.
- (iii)
- Equation (12) is cast in the more convenient form
- (iv)
- The coefficient is obtained from Equation (13). It can be written aswhich after multiplying by and summing on the index j, yields the recursionand which for the higher order terms () is generalized as
- (a)
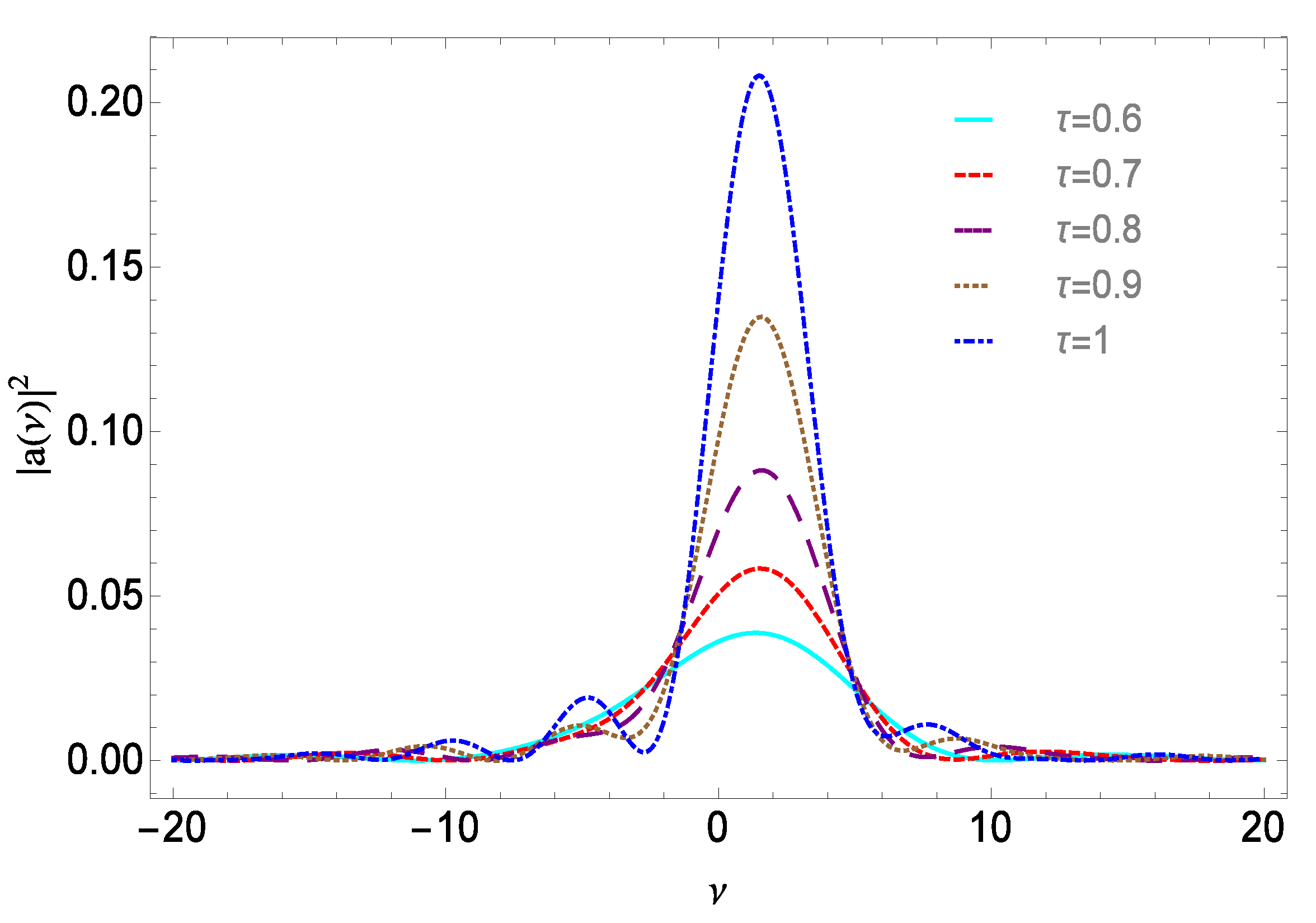
- The Fang–Torre formula (this Formula appeared in an unpublished manuscript by H. Fang, and was later derived with minor refinements by A. Torre, and reported in [27]) valid for , :The square modulus of yields the intensity growth as a function of the dimensionless time and of the detuning parameter. Regarding Equation (19) we find
- (b)
- The field growing from a bunching coefficient associated with the electron distribution and the solution of the evolution problem reads:
- (i)
- Quantities such as and should be replaced byand it is worth noting that the number of undulator periods does not appear anymore in the definition of the new dimensionless quantities (see below for further comments);
- (ii)
- Quantities involving the product of and , written in the new variables, read
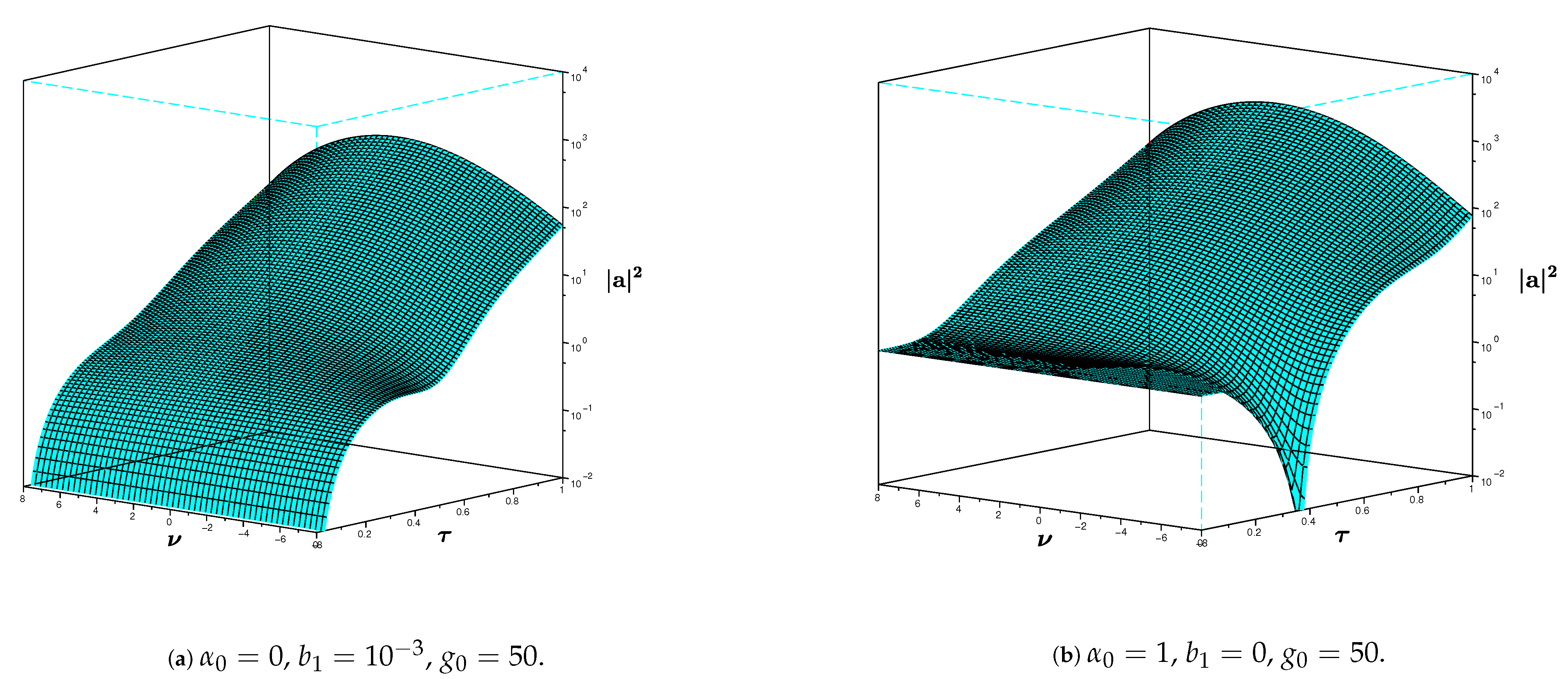
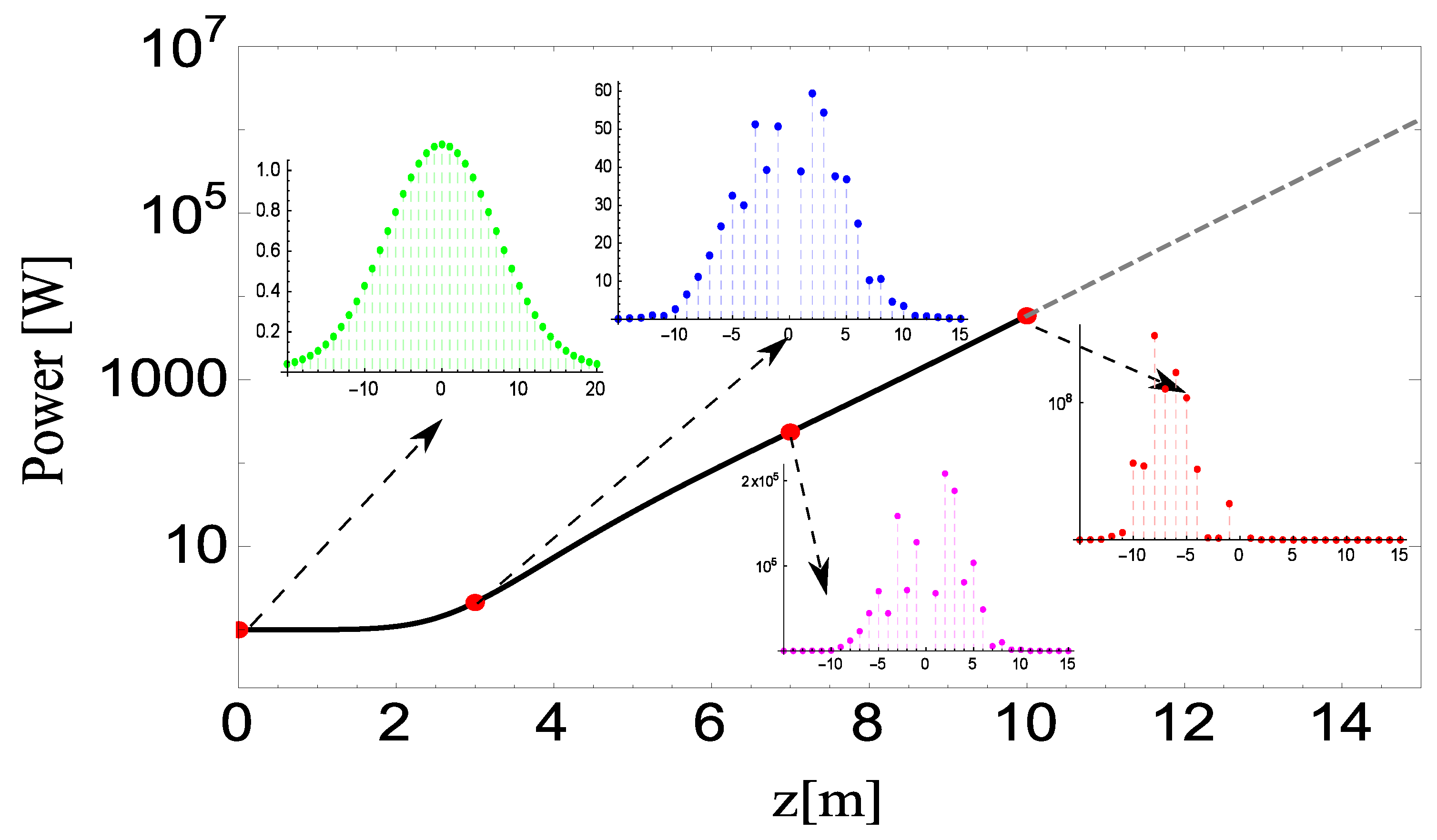
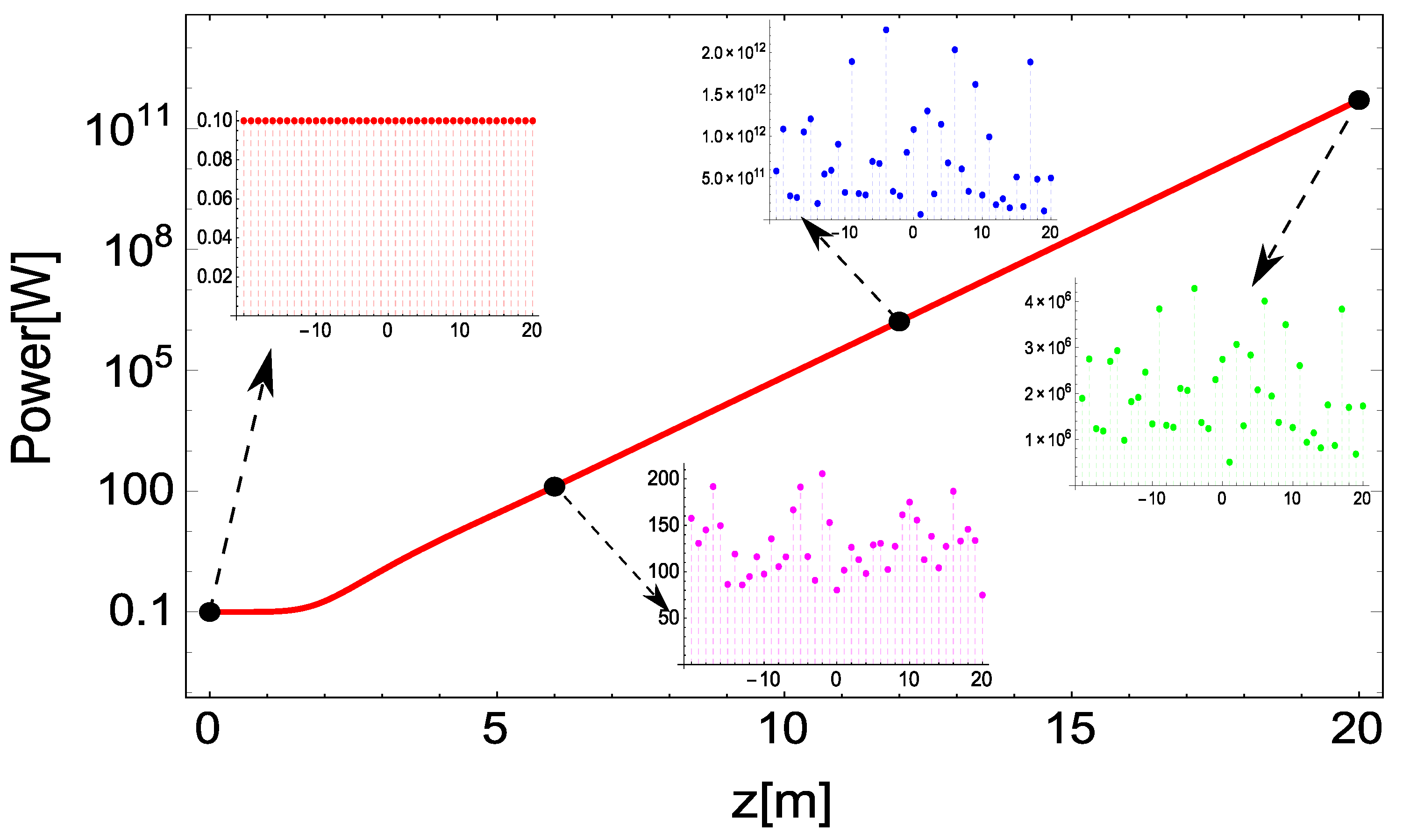
3. High Gain FEL Equations and Harmonic Generation
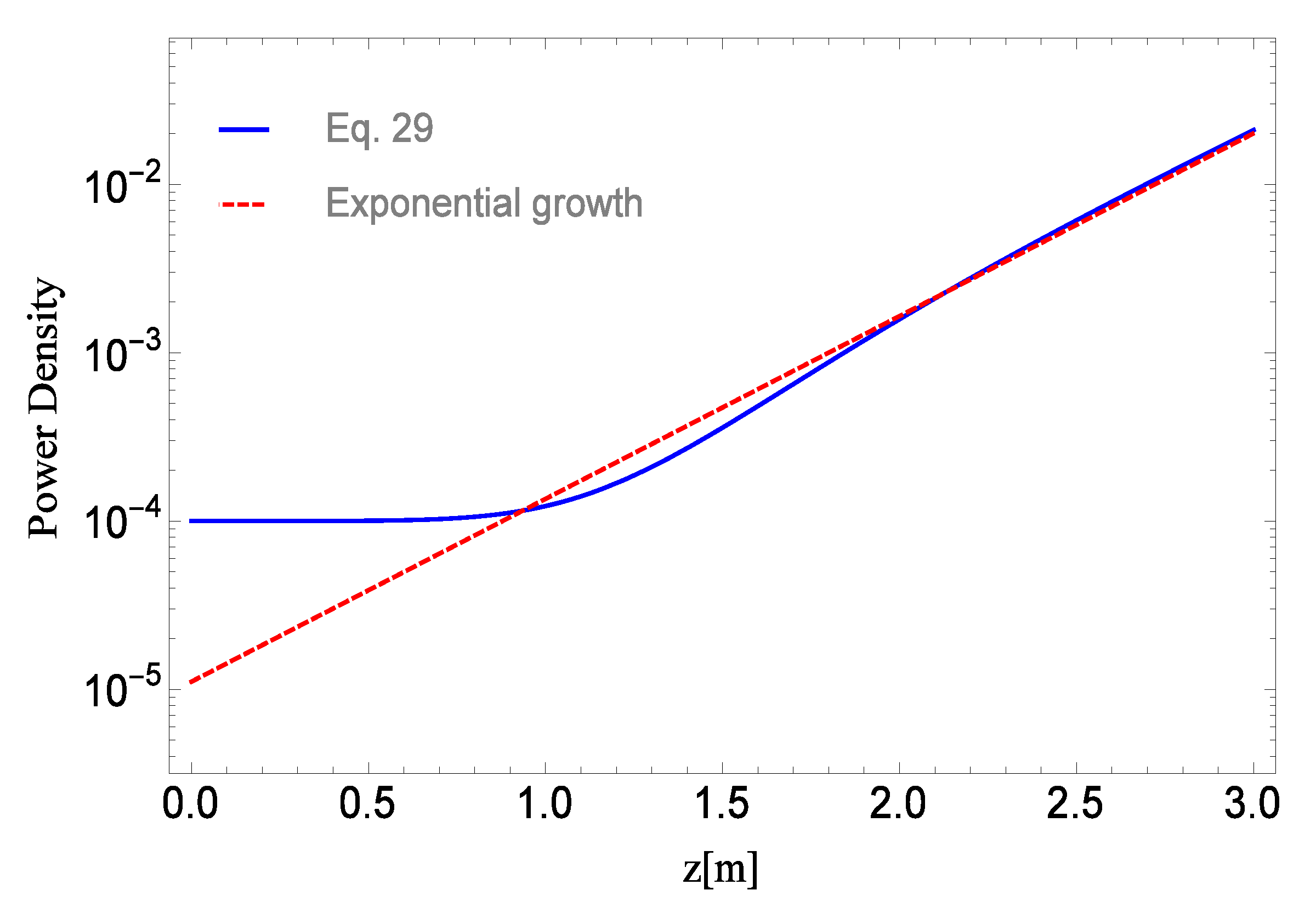
4. Inhomogeneous Broadening Partial Amplitudes and High Gain Equation
- (a)
- The wave packet is shifted back by a quantityThis means that the optical packet is moving back with respect to the bunch frame propagating at velocity c, the associated group velocity isThe radiation moves slower than c, by the effect of the interaction itself. The gain dilution due to the energy spread counteracts the velocity slow down with respect to the case of negligible energy spread.The complex refraction index derived from Equation (56) can be written as
- (b)
- The optical packed undergoes a longitudinal diffusion specified bywhich ensures that in one gain length the additional packet width is essentially a coherence length. This effect has been studied in the theory of mode-locked operation within the context of the oscillator theory; the relevant discussion can be found in [2].
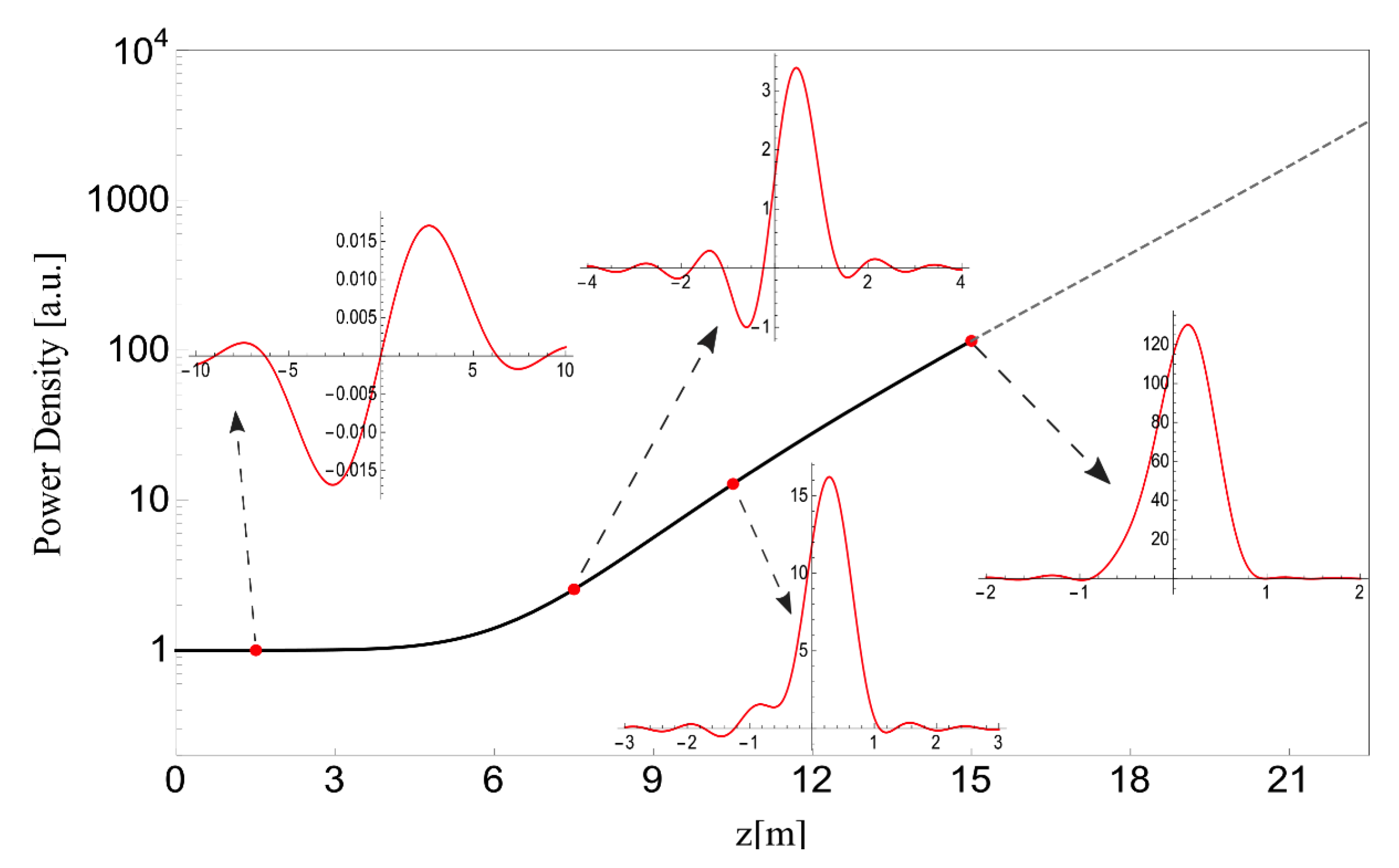
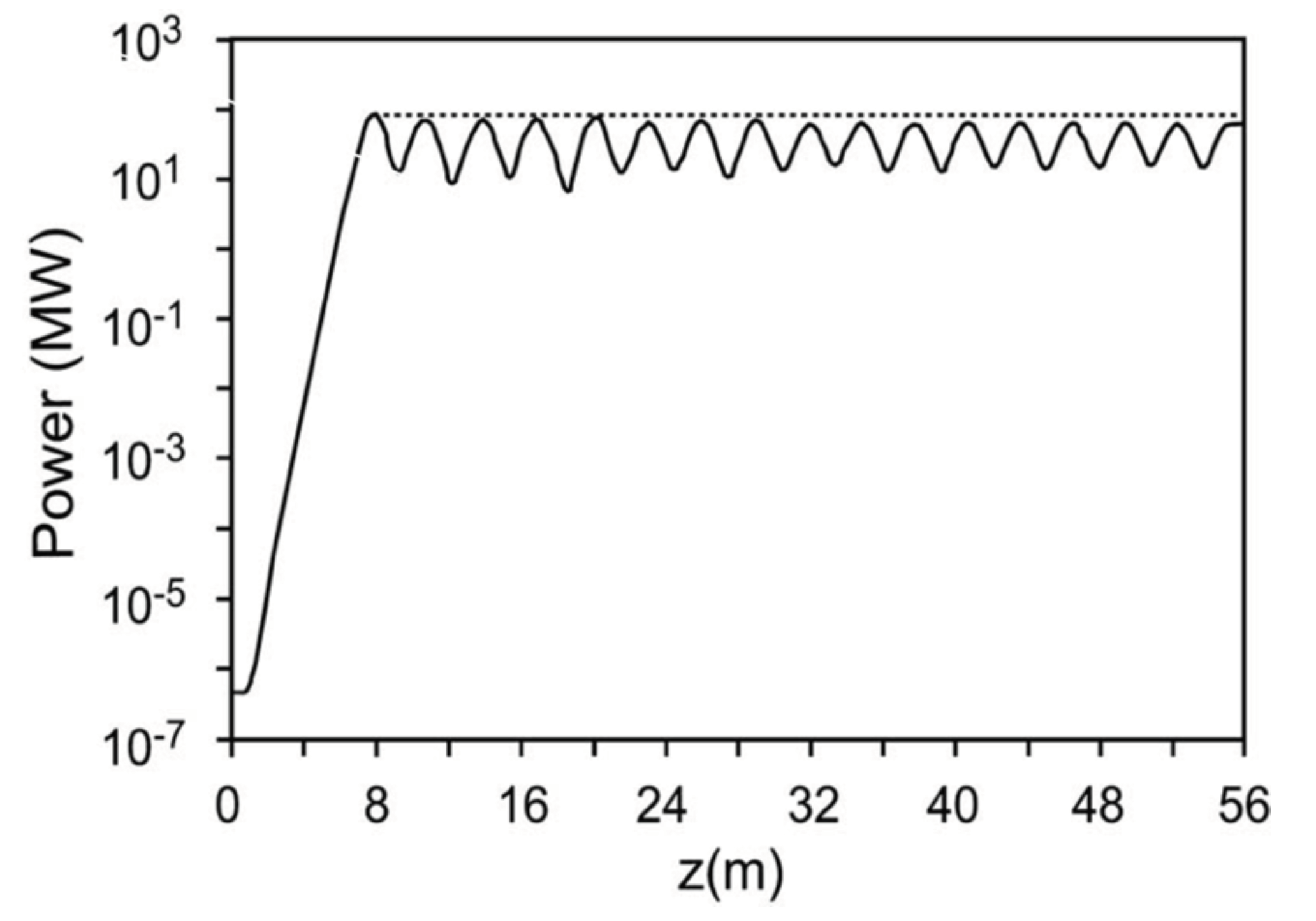
5. Slice Evolution
6. Final Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Madey, J.M.J. Stimulated Emission of Bremsstrahlung in a Periodic Magnetic Field. J. Appl. Phys. 1971, 42, 1906. [Google Scholar] [CrossRef]
- Dattoli, G.; Di Palma, E.; Pagnutti, S.; Sabia, E. Free Electron coherent sources: From microwave to X-rays. Phys. Rep. 2018, 739, 1–51. [Google Scholar] [CrossRef]
- Neyman, P.J.; Colson, W.B.; Gottschalk, S.C.; Todd, A.M.M.; Blau, J.; Cohn, K. Free Electron Lasers in 2017. In Proceedings of the 38th International Free Electron Laser Conference, FEL2017, Santa Fe, NM, USA, 20–25 August 2017; Available online: https://accelconf.web.cern.ch/fel2017/papers/mop066.pdf (accessed on 17 December 2020).
- Rossbach, J.; Schneider, J.R.; Wurth, W. 10 years of pioneering X-ray science at the Free-Electron Laser FLASH at DESY. Phys. Rep. 2019, 808, 1–74. [Google Scholar] [CrossRef]
- Topics. Available online: https://lcls.slac.stanford.edu/ (accessed on 17 December 2020).
- Topics. Available online: https://www.elettra.trieste.it/lightsources/fermi/machine.html (accessed on 17 December 2020).
- Topics. Available online: http://xfel.riken.jp/eng/ (accessed on 17 December 2020).
- Colson, W.B. Free Electron Laser Theory. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 1977. [Google Scholar]
- Colson, W.B. Classical Free Electron Laser Theory, Laser Handbook; Colson, W.B., Pellegrini, C., Renieri, A., Eds.; North-Holland: Amsterdam, The Netherlands, 1990; Volume VI. [Google Scholar]
- Saldin, E.L.; Schneidmiller, E.V.; Yurkov, M.V. The Physics of Free Electron Lasers; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar] [CrossRef]
- Kim, K.J.; Huang, Z.; Lindberg, R. Synchrotron Radiation and Free Electron Lasers; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar] [CrossRef]
- Bergmann, U.; Yachandra, V.; Yano, J. X-ray Free Electron Laser: Applications in Materials, Chemistry and Biology; Royal Society of Chemistry: Cambridge, UK, 2017; ISBN 978-1-84973-100-3. [Google Scholar]
- Dattoli, G.; Doria, A.; Sabia, E.; Artioli, M. Charged Beam Dynamics, Particle Accelerators and Free Electron Lasers; IOP Publishing Ltd.: Bristol, UK, 2017. [Google Scholar]
- Szarmes, E.B. Classical Theory of Free-Electron Lasers; IOP Publishing Ltd.: Bristol, UK, 2017. [Google Scholar]
- Jaeschke, E.; Khan, S.; Schneider, J.R.; Hastings, J.B. Synchrotron Light Sources and Free-Electron Lasers; Springer: Berlin/Heidelberg, Germany, 2016; ISBN 978-3-319-14393-4. [Google Scholar]
- Behrens, C.; Schmüser, P.; Dohlus, M.; Rossbach, J. Free-Electron Lasers in the Ultraviolet and X-ray Regime; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Dattoli, G.; Ottaviani, P.L. Fel Small Signal Dynamics and Electron Beam Prebunching; ENEA Internal Report, RT/INN/93/10; ENEA: Frascati, Italy, 1993. [Google Scholar]
- Dattoli, G.; Ottaviani, P.L.; Pagnutti, S. Booklet for FEL Design: A Collection of Practical Formulae; ENEA—Edizioni Scientifiche: Frascati, Italy, 2007. [Google Scholar]
- Bonifacio, R.; Pellegrini, C.; Narducci, L.M. Collective instabilities and high-gain regime in a free electron laser. Opt. Commun. 1984, 50, 373–378. [Google Scholar] [CrossRef]
- Haus, H. Quantum Electronics, Noise in Free Electron Laser Amplifier. IEEE J. Quantum Electron. 1981, 17, 1427–1435. [Google Scholar] [CrossRef]
- Dattoli, G.; Marino, A.; Renieri, A.; Romanelli, F. Progress in the Hamiltonian picture of the free-electron laser. IEEE J. Quantum Electron. 1981, 17, 1371–1387. [Google Scholar] [CrossRef]
- Petelin, M.I. On the theory of ultrarelativistic cyclotron self-resonance masers. Radiophys. Quantum Electron. 1974, 17, 686–690. [Google Scholar] [CrossRef]
- Nusinovich, G. Introduction to the Physics of Gyrotrons; The John Hopkins University Press: Baltimore, MD, USA, 2004. [Google Scholar]
- Bratman, V.L.; Ginzburg, N.S.; Petelin, M.I. Common properties of free electron lasers. Opt. Commun. 1979, 30, 409–412. [Google Scholar] [CrossRef]
- Di Palma, E.; Sabia, E.; Dattoli, G.; Licciardi, S.; Spassovsky, I. Cyclotron auto resonance maser and free electron laser devices: A unified point of view. J. Plasma Phys. 2017, 83, 905830102. [Google Scholar] [CrossRef]
- Caloi, R.; Ciocci, F.; Dattoli, G.; Torre, A. The High-Gain FEL Equation: An Inexpensive Numerical Algorithm. Il Nuovo Cimento B 1991, 106, 627–640. [Google Scholar] [CrossRef]
- Dattoli, G.; Renieri, A.; Torre, A. Lecture on Free Electron Laser Theory and Related Topics; World Scientific: Singapore, 1990. [Google Scholar]
- Tremaine, A.J.; Rosenzweig, B.; Anderson, S.; Frigola, P.; Hogan, M.; Murokh, A.; Pellegrini, C.; Nguyen, D.C.; Sheffield, R.L. Observation of Self-Amplified Spontaneous-Emission-Induced Electron-Beam Microbunching Using Coherent Transition Radiation. Phys. Rev. Lett. 1998, 81, 5816. [Google Scholar] [CrossRef]
- Nguyen, D.C.; Sheffield, R.L.; Fortgang, C.M.; Kinross-Wright, J.M.; Ebrahim, N.A.; Goldstein, J.C. A High-Power compact Regenerative Amplifier FEL. In Proceedings of the 17th PAC Conference, Vancouver, BC, Canada, 12–16 May 1997; p. 897. Available online: https://cds.cern.ch/record/909415?ln=it (accessed on 17 December 1997).
- Dattoli, G.; Cabrini, S.; Giannessi, L. Simple Model of Gain Saturation in Free Electron Laser. Phys. Rev. A 1991, 44, 8433. [Google Scholar] [CrossRef] [PubMed]
- Dattoli, G. Logistic function and evolution of free-electron-laser oscillators. J. Appl. Phys. 1998, 84, 2393–2398. [Google Scholar] [CrossRef]
- Dattoli, G.; Ottaviani, P.L. Semi-analytical models of Free Electron Laser Saturation. Opt. Comm. 2002, 204, 283–297. [Google Scholar] [CrossRef]
- Dattoli, G.; Giannessi, L.; Ottaviani, P.L.; Ronsivalle, C. Semi-analytical model of self-amplified spontaneous-emission free-electron lasers, including diffraction and pulse-propagation effects. J. Appl. Phys. 2004, 95, 3206–3210. [Google Scholar] [CrossRef]
- Shih, C.C.; Yariv, A. Inclusion of Space-Charge Effects with Maxwell’s Equations in the Single-Particle Analysis of Free-Electron Lasers. IEEE J. Quantum Electron. 1981, 17, 1387–1394. [Google Scholar] [CrossRef]
- Dattoli, G.; Torre, A.; Centioli, C.; Richetta, M. Free Electron Laser Operation in the Intermediate Gain Region. IEEE J. Quantum Electron. 1989, 25, 2327–2331. [Google Scholar] [CrossRef]
- Elias, L.R.; Fairbank, W.M.; Madey, J.M.J.; Schwettman, H.A.; Smith, T.I. Observation of Stimulated Emission of Radiation by Relativistic Electrons in a Spatially Periodic Transverse Magnetic Field. Phys. Rev. Lett. 1976, 36, 717. [Google Scholar] [CrossRef]
- Deacon, D.A.G.; Elias, L.R.; Madey, J.M.J.; Ramian, G.J.; Schwettman, H.A.; Smith, T.I. First Operation of a Free-Electron Laser. Phys. Rev. Lett. 1977, 38, 892–894. [Google Scholar] [CrossRef]
- Colson, W.B. The nonlinear wave equation for higher harmonics in free-electron lasers. IEEE J. Quantum Electron. 1981, 17, 1417–1427. [Google Scholar] [CrossRef]
- Dattoli, G.; Ottaviani, P.L.; Pagnutti, S. Non Linear Harmonic Generation in high gain free electron laser. J. Appl. Phys. 2005, 97, 113102. [Google Scholar] [CrossRef]
- Dattoli, G.; Ottaviani, P.L.; Pagnutti, S. The PROMETEO Code: A flexible tool for Free Electron Laser study. Il Nuovo Cimento C 2009, 32, 283–287. [Google Scholar]
- Gallardo, J.C.; Elias, L.R.; Dattoli, G.; Renieri, A. Integral equation for the laser field in a long-pulse free-electron laser. Phys. Rev. A 1987, 36, 3222. [Google Scholar] [CrossRef]
- Colson, W.B.; Dattoli, G.; Ciocci, F. Angular-gain spectrum of free-electron lasers. Phys. Rev. A 1985, 31, 828. [Google Scholar] [CrossRef]
- Giannessi, L. Seeding and Harmonic Generation in Free-Electron Lasers. In Synchrotron Light Sources and Free-Electron Lasers; Springer: Berlin/Heidelberg, Germany, 2016; pp. 195–223. ISBN 978-3-319-14393-4. [Google Scholar]
- Lambert, G.; Hara, T.; Garzella, D.; Tanikawa, T.; Labat, M.; Carre, B.; Kitamura, H.; Shintake, T.; Bougeard, M.; Inoue, S.; et al. Injection of harmonics generated in gas in a free electron laser providing intense and coherent extreme-ultraviolet light. Nat. Phys. 2008, 4, 296–300. [Google Scholar] [CrossRef]
- Colson, W.B.; Gallardo, J.C.; Bosco, P.M. Free-electron-laser gain degradation and electron-beam quality. Phys. Rev. A 1986, 34, 4875. [Google Scholar] [CrossRef]
- Dattoli, G.; Ottaviani, P.L.; Segreto, A.; Altobelli, G. Free electron laser gain: Approximant forms and inclusion of inhomogeneous broadening contributions. J. Appl. Phys. 1995, 77, 6162. [Google Scholar] [CrossRef]
- Dattoli, G.; Giannessi, L.; Torre, A.; Segreto, A. The pulse propagation problem in free electron lasers: Gain parametrization formulae. J. Appl. Phys. 1996, 79, 6729. [Google Scholar] [CrossRef]
- Bonifacio, R.; McNeil, B.W.J.; Pierini, P. Superradiance in the high-gain free-electron laser. Phys. Rev. A 1989, 40, 4467. [Google Scholar] [CrossRef]
- Saldin, E.L.; Schneidmiller, E.A.; Yurkov, M.V. Diffraction effects in the self-amplified spontaneous emission FEL. Opt. Commun. 2000, 186, 185–209. [Google Scholar] [CrossRef]
- Saldin, E.L.; Schneidmiller, E.A.; Yurkov, M.V. Properties of the third harmonic of the radiation from self-amplified spontaneous emission free electron laser. Phys. Rev. Spec. Top. Accel. Beams 2006, 9, 030702. [Google Scholar] [CrossRef]
- Dattoli, G.; Sabia, E.; Ottaviani, P.L.; Pagnutti, S.; Petrillo, V. Longitudinal dynamics of high gain free electron laser amplifiers. Phys. Rev.Spec. Top. Accel. Beams 2013, 16, 030704. [Google Scholar] [CrossRef]
- Merminga, L.; Morton, P.L.; Seeman, J.; Spence, W.L. Transverse phase space in the presence of dispersion. In Proceedings of the 1991 Institute of Electrical and Electronics Engineers (IEEE) Particle Accelerator Conference (PAC), San Francisco, CA, USA, 6–9 May 1991; Volume 910506, pp. 461–463. [Google Scholar]
- Dowell, D.H.; Bolton, P.R.; Clendenin, J.E.; Emma, P.; Gierman, S.M.; Graves, W.S.; Limborg, C.G.; Murphy, B.F.; Schmerge, J.F. Slice emittance measurements at the SLAC Gun Test Facility. Nucl. Instrum. Meth. A 2003, 507, 327–330. [Google Scholar] [CrossRef]
- Ferrario, M.; Alesini, D.; Bellaveglia, M.; Benfatto, M.; Boni, R.; Boscolo, M.; Castellano, M.; Chiadroni, E.; Clozza, A.; Cultrera, L.; et al. Recent results of the SPARC FEL experiments. In Proceedings of the 31st FEL Conference Liverpool, Liverpool, UK, 23–28 August 2009. [Google Scholar]
- Bettoni, S.; Aiba, M.; Beutner, B.; Pedrozzi, M.; Prat, E.; Reiche, S.; Schietinger, T. Preservation of low slice emittance in bunch compressors. Phys. Rev. Accel. Beams 2016, 19, 034402. [Google Scholar] [CrossRef]
- Dattoli, G.; Giannessi, L.; Torre, A. Unified view of free-electron laser dynamics and of higher-harmonics electron bunching. J. Opt. Soc. Am. 1993, 10, 2136–2143. [Google Scholar] [CrossRef]
- Dattoli, G.; Giannessi, L.; Ottaviani, P.L. Free electron laser small signal dynamics and inclusion of electron-beam energy phase correlation. J. Appl. Phys. 1999, 86, 1710–1715. [Google Scholar] [CrossRef]
- Dattoli, G.; Giannessi, L.; Ottaviani, P.L.; Pagnutti, S. Energy Phase Correlation and Pulse Dynamics in Short Bunch High Gain FELs. Opt. Commun. 2010, 285, 710–714. [Google Scholar] [CrossRef]
- Dattoli, G.; Sabia, E.; Ronsivalle, C.; Del Franco, M.; Petralia, A. Slice emittance, projected emittance and properties of the SASE FEL radiation. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2012, 671, 51–61. [Google Scholar] [CrossRef]
- Bonifacio, R.; De Salvo, L.; Pierini, P. Large harmonic bunching in a high-gain free-electron laser. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1990, 293, 627–629. [Google Scholar] [CrossRef]
- Dattoli, G.; Ottaviani, P.L.; Pagnutti, S. High gain amplifiers: Power oscillations and harmonic generation. J. Appl. Phys. 2007, 102, 033103. [Google Scholar] [CrossRef]
- Giannessi, L.; Musumeci, P.; Spampinati, S. Nonlinear pulse evolution in seeded free-electron laser amplifiers and in free-electron laser cascades. J. Appl. Phys. 2005, 98, 043110. [Google Scholar] [CrossRef]
- Yang, X.; Mirian, N.; Giannessi, L. Postsaturation dynamics and superluminal propagation of a superradiant spike in a free-electron laser amplifier. Phys. Rev. Accel. Beams 2020, 23, 010703. [Google Scholar] [CrossRef]
- Gardelle, J.; Labrouche, J.; Marchese, G.; Rullier, J.L.; Villate, D. Analysis of the beam bunching produced by a free electron laser. Phys. Plasmas 1996, 3, 4197. [Google Scholar] [CrossRef]
- Dattoli, G.; Ottaviani, P.L.; Pagnutti, S. Theory of High Gain Free Electron Laser, operating with segmented undulators. J. Appl. Phys. 2006, 99, 044907. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dattoli, G.; Di Palma, E.; Licciardi, S.; Sabia, E. Free Electron Laser High Gain Equation and Harmonic Generation. Appl. Sci. 2021, 11, 85. https://doi.org/10.3390/app11010085
Dattoli G, Di Palma E, Licciardi S, Sabia E. Free Electron Laser High Gain Equation and Harmonic Generation. Applied Sciences. 2021; 11(1):85. https://doi.org/10.3390/app11010085
Chicago/Turabian StyleDattoli, Giuseppe, Emanuele Di Palma, Silvia Licciardi, and Elio Sabia. 2021. "Free Electron Laser High Gain Equation and Harmonic Generation" Applied Sciences 11, no. 1: 85. https://doi.org/10.3390/app11010085
APA StyleDattoli, G., Di Palma, E., Licciardi, S., & Sabia, E. (2021). Free Electron Laser High Gain Equation and Harmonic Generation. Applied Sciences, 11(1), 85. https://doi.org/10.3390/app11010085





