Three-Dimensional, Time-Dependent Analysis of High- and Low-Q Free-Electron Laser Oscillators
Abstract
1. Introduction
2. Numerical Formulation
2.1. The MINERVA Simulation Code
2.2. Analytical Models for Static Magnetic Fields
2.3. Performance of the MINERVA FEL Code
2.3.1. The SPARC SASE FEL
2.3.2. The LCLS SASE FEL
2.4. The Optical Propagation Code OPC
2.4.1. Optical Elements
2.4.2. Modeling Mirrors
3. Some Considerations for Optical Resonators Used in Free-Electron Lasers
4. Low-Gain/High- Oscillators
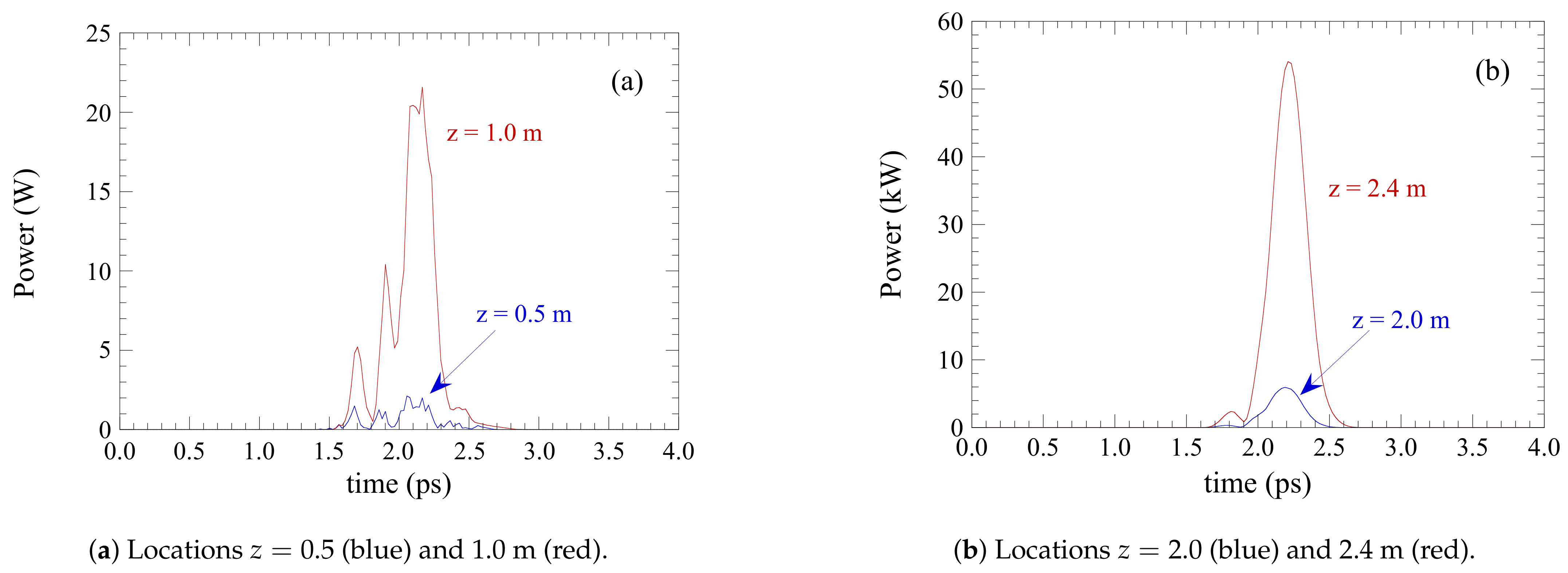
4.1. The IR-Demo Experiment at JLab
4.2. The 10-kW Upgrade Experiment at JLab
5. High-Gain/Low- Oscillators
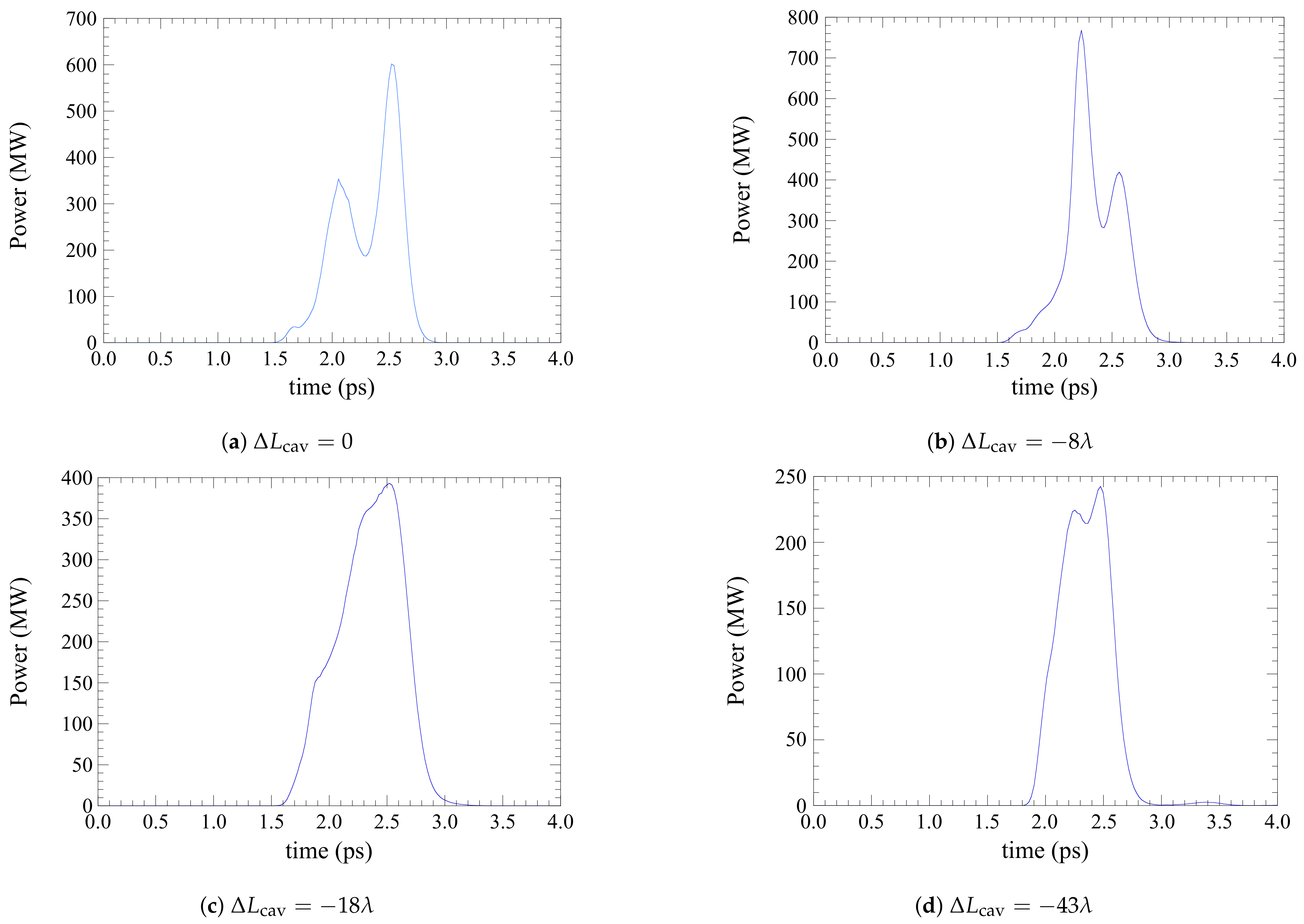
5.1. An Infrared RAFEL
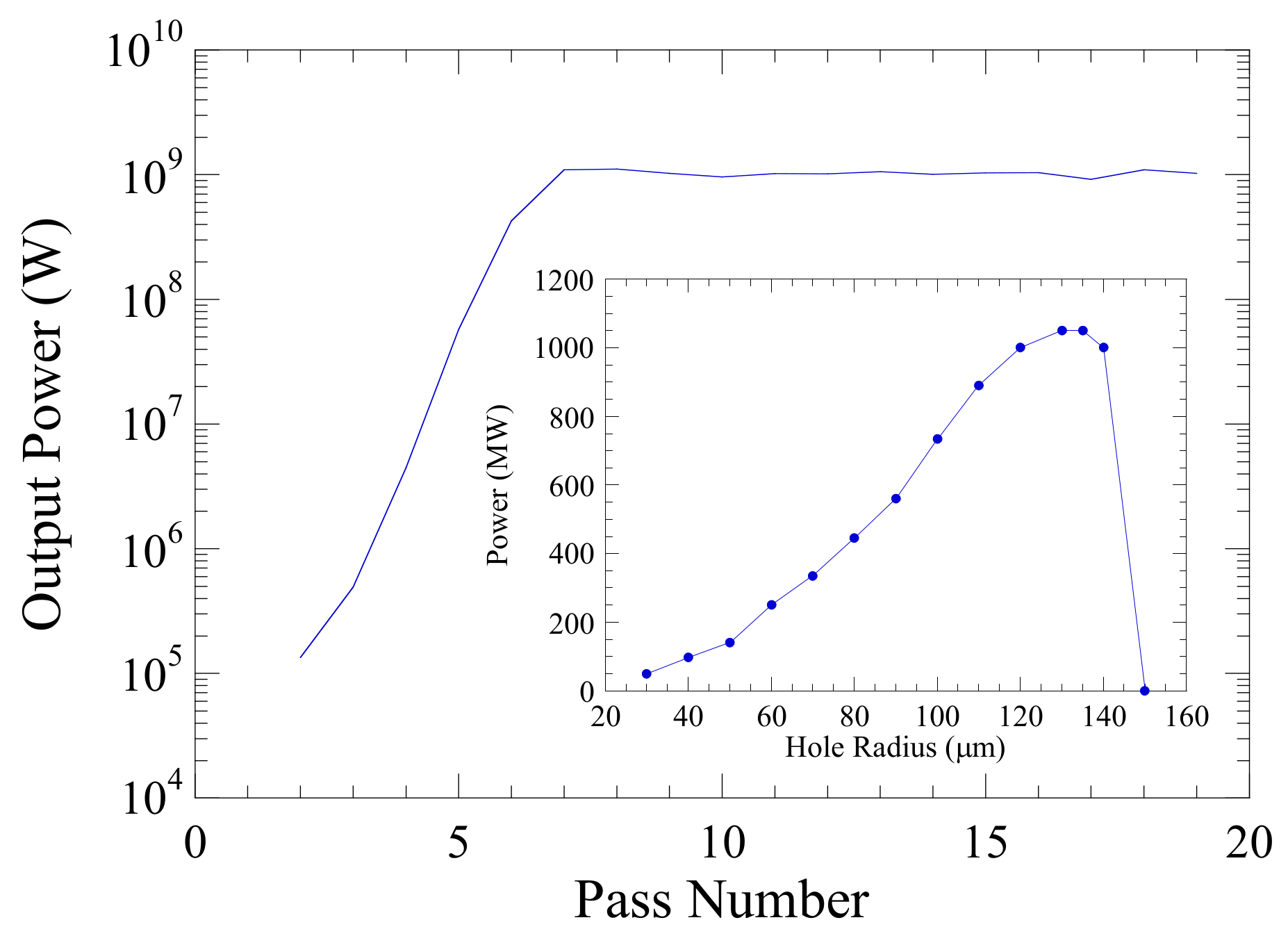
5.2. An X-ray RAFEL
6. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BPM | beam position monitor |
| CRL | compound refractive lens |
| CW | continuous wave |
| FEL | free-electron laser |
| FELO | free-electron laser oscillator |
| FODO | focusing and defocusing |
| FWHM | full width at half maximum |
| HGHG | high gain harmonic generation |
| IR | infrared |
| JLab | Thomas Jefferson National Accelerator Facility |
| LCLS | linac coherent light source |
| linac | linear accelerator |
| RAFEL | regenerative amplifier free-electron laser |
| RF | radio frequency |
| rms | root mean square |
| SASE | self-amplified spontaneous emission |
| SDE | source dependent expansion |
| SPARC | sorgente pulsata ed amplificata di radiazione coerente |
| VUV | vacuum ultraviolet |
| XFELO | X-ray free-electron laser |
References
- Freund, H.P.; Antonsen, T.M., Jr. Principles of Free Electron Lasers, 3rd ed.; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Moore, G.T. The high-gain regime of the free electron laser. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1985, 239, 19–28. [Google Scholar] [CrossRef]
- Deacon, D.A.G.; Elias, L.R.; Madey, J.M.J.; Ramian, G.J.; Schwettman, H.A.; Smith, T.I. First operation of a free-electron laser. Phys. Rev. Lett. 1977, 38, 892–894. [Google Scholar] [CrossRef]
- Elias, L.R.; Fairbank, W.M.; Madey, J.M.J.; Schwettman, H.A.; Smith, T.I. Observation of stimulated emission of radiation by relativistic electrons in a spatially periodic transverse magnetic field. Phys. Rev. Lett. 1976, 36, 717–720. [Google Scholar] [CrossRef]
- Phillips, R.M. History of the Ubitron. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1988, 272, 1–9. [Google Scholar] [CrossRef]
- Elias, L.R.; Ramian, G.; Hu, J.; Amir, A. Observation of single-mode operation in a free-electron laser. Phys. Rev. Lett. 1986, 57, 424–427. [Google Scholar] [CrossRef]
- Ramian, G. The new UCSB free-electron lasers. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1992, 318, 225–229. [Google Scholar] [CrossRef]
- Gover, A.; Faingersh, A.; Eliran, A.; Volshonok, M.; Kleinman, H.; Wolowelsky, S.; Yakover, Y.; Kapilevich, B.; Lasser, Y.; Seidov, Z.; et al. Radiation measurements in the new tandem accelerator FEL. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2004, 528, 23–27. [Google Scholar] [CrossRef]
- Gover, A.; Pinhasi, Y. Electrostatic-accelerator free-electron lasers. In Electrostatic Accelerators: Fundamentals and Applications; Springer: Berlin/Heidelberg, Germany, 2005; pp. 378–390. [Google Scholar] [CrossRef]
- Minehara, E.J.; Sawamura, M.; Nagai, R.; Kikuzawa, N.; Sugimoto, M.; Hajima, R.; Shizuma, T.; Yamauchi, T.; Nishimori, N. JAERI superconducting RF linac-based free-electron laser-facility. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2000, 445, 183–186. [Google Scholar] [CrossRef]
- Neil, G.R.; Behre, C.; Benson, S.V.; Bevins, M.; Biallas, G.; Boyce, J.; Coleman, J.; Dillon-Townes, L.A.; Douglas, D.; Dylla, H.F.; et al. The JLab high power ERL light source. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2006, 557, 9–15. [Google Scholar] [CrossRef]
- Thomas, A.W.; Williams, G.P. The free electron laser at Jefferson Lab: The technology and the science. Proc. IEEE 2007, 95, 1679–1682. [Google Scholar] [CrossRef]
- Thompson, N.R.; Clarke, J.A.; Craig, T.; Dunning, D.J.; Kolosov, O.V.; Moss, A.; Saveliev, Y.M.; Surman, M.; Tovee, P.D.; Weightman, P. Status of the Alice IR-FEL: From ERL demonstrator to user facility. In Proceedings of the 37th International Free Electron Laser Conference; JACoW Publishing: Daejeon, Korea, 2015; pp. 379–383. [Google Scholar] [CrossRef]
- Vinokurov, N.A.; Arbuzov, V.S.; Chernov, K.N.; Davidyuk, I.V.; Dementyev, E.N.; Dovzhenko, B.A.; Getmanov, Y.V.; Knyazev, B.A.; Kolobanov, E.I.; Kondakov, A.A.; et al. Novosibirsk high-power THz FEL facility. In Proceedings of the 2016 International Conference Laser Optics (LO); IEEE: Piscataway, NJ, USA, 2016; pp. R10–R14. [Google Scholar] [CrossRef]
- Shevchenko, O.A.; Melnikov, A.R.; Tararyshkin, S.V.; Getmanov, Y.V.; Serednyakov, S.S.; Bykov, E.V.; Kubarev, V.V.; Fedin, M.V.; Veber, S.L. Electronic modulation of THz radiation at NovoFEL: Technical aspects and possible applications. Materials 2019, 12, 3063. [Google Scholar] [CrossRef]
- Smith, T.I.; Frisch, J.C.; Rohatgi, R.; Schwettman, H.A.; Swent, R.L. Status of the SCA-FEL. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1990, 296, 33–36. [Google Scholar] [CrossRef]
- Van der Wiel, M.J.; van Amersfoort, P.W.; Team, F. FELIX: From laser to user facility. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1993, 331, ABS30–ABS33. [Google Scholar] [CrossRef]
- Tomimasu, T.; Saeki, K.; Miyauchi, Y.; Oshita, E.; Okuma, S.; Wakita, K.; Kobayashi, A.; Suzuki, T.; Zako, A.; Nishihara, S.; et al. The FELI FEL facilities—Challenges at simultaneous FEL beam sharing systems and UV-range FELs. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1996, 375, 626–631. [Google Scholar] [CrossRef]
- Ortega, J.M. The CLIO infrared FEL facility. Synchrotron Radiat. News 1996, 9, 20–33. [Google Scholar] [CrossRef]
- Ortega, J.M. Operation and extension to far-infrared of the CLIO FEL facility. Jpn. J. Appl. Phys. 2002, 41, 20–28. [Google Scholar] [CrossRef]
- Schwettman, H.A.; Smith, T.I.; Swent, R.L. The Stanford picosecond FEL center. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1996, 375, 662–663. [Google Scholar] [CrossRef]
- Horiike, H.; Tsubouchi, N.; Awazu, K.; Asakawa, M.; Heya, M. Status of the Institute of Free-Electron Laser, Osaka University. Jpn. J. Appl. Phys. 2002, 41, 10–14. [Google Scholar] [CrossRef][Green Version]
- Tanaka, T.; Hayakawa, K.; Hayakawa, Y.; Sato, I.; Science, Q. Guiding optics system for LEBRA FEL user facility. In Proceedings of the 26th International Free Electron Laser Conference; JACoW Publishing: Trieste, Italy, 2004; pp. 427–430. [Google Scholar]
- Van der Zande, W.J.; Jongma, R.T.; van der Meer, L.; Redlich, B. FELIX facility: Free electron laser light sources from 0.2 to 75 THz. In Proceedings of the 2013 38th International Conference on Infrared, Millimeter, and Terahertz Waves (IRMMW-THz); IEEE: Piscataway, NJ, USA, 2013; pp. 1–2. [Google Scholar] [CrossRef]
- Schöllkopf, W.; Gewinner, S.; Junkes, H.; Paarmann, A.; von Helden, G.; Bluem, H.; Todd, A.M.M. The new IR and THz FEL facility at the Fritz Haber Institute in Berlin. In Proceedings of the SPIE Proceedings Volume 9512—Advances in X-ray Free-Electron Lasers Instrumentation III; Biedron, S.G., Ed.; SPIE: Prague, Czech Republic, 2015; p. 95121L. [Google Scholar] [CrossRef]
- Zen, H.; Suphakul, S.; Kii, T.; Masuda, K.; Ohgaki, H. Present status and perspectives of long wavelength free electron lasers at Kyoto University. Phys. Procedia 2016, 84, 47–53. [Google Scholar] [CrossRef]
- Klopf, J.M.; Zvyagin, S.; Helm, M.; Kehr, S.C.; Lehnert, U.; Michel, P.; Pashkin, A.; Schneider, H.; Seide, W.; Winnerl, S. FELBE—Upgrades and status of the IR/THz FEL user facility at HZDR. In Proceedings of the 2018 43rd International Conference on Infrared, Millimeter, and Terahertz Waves (IRMMW-THz); IEEE: Piscataway, NJ, USA, 2018; pp. 1–2. [Google Scholar] [CrossRef]
- Li, M.; Yang, X.; Xu, Z.; Wu, D.; Wang, H.; Xiao, D.; Shu, X.; Lu, X.; Huang, W.; Dou, Y. China’s First Tera-Hertz Free Electron Laser Oscillator. In Proceedings of the 2018 International Conference on Microwave and Millimeter Wave Technology (ICMMT); IEEE: Chengdu, China, 2018; pp. 1–3. [Google Scholar] [CrossRef]
- Schöllkopf, W.; Gewinner, S.; Todd, A.M.M.; Colson, W.B.; de Pas, M.; Dowell, D.; Gottschalk, S.C.; Junkes, H.; Rathke, J.W.; Schultheiss, T.J.; et al. The FHI FEL upgrade design. In Proceedings of the 39th International Free-Electron Laser Conference; JACoW Publishing: Geneva, Switzerland, 2019; pp. 52–55. [Google Scholar] [CrossRef]
- Zhao, Z.; Li, H.; Jia, Q.; He, Z.; Zhu, Y. Proposal of an operation mode of FELiChEM for generating high-power ultra-short infrared FEL pulses. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2020, 984, 164634. [Google Scholar] [CrossRef]
- Gallerano, G.P.; Doria, A.; Giovenale, E.; Renieri, A. Compact free electron lasers: From Cerenkov to waveguide free electron lasers. Infrared Phys. Technol. 1999, 40, 161–174. [Google Scholar] [CrossRef]
- Jeong, Y.U.; Kazakevitch, G.M.; Lee, B.C.; Park, S.H.; Cha, H.J. Laboratory-scale wide-band FIR user facility based on a compact FEL. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2004, 528, 88–91. [Google Scholar] [CrossRef]
- Hara, T.; Couprie, M.E.; Garzella, D.; Nahon, L.; Marsi, M.; Bakker, R.; Billardon, M. Progress of the Super-ACO storage ring free electron laser in the UV as a source for users. J. Electron Spectrosc. Relat. Phenom. 1996, 80, 317–320. [Google Scholar] [CrossRef]
- Litvinenko, V.N.; Burnham, B.; Park, S.H.; Wu, Y.; Cataldo, R.; Emamian, M.; Faircloth, J.; Goetz, S.; Hower, N.; Madey, J.M.J.; et al. First UV/visible lasing with the OK-4/Duke storage ring FEL. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1998, 407, 8–15. [Google Scholar] [CrossRef]
- Hosaka, M.; Katoh, M.; Mochihashi, A.; Shimada, M.; Takashima, Y.; Hara, T. High power deep UV lasing on the UVSOR-II storage ring FEL. In Proceedings of the 28th International Free Electron Laser Conference; JACoW Publishing: Berlin, Germany, 2006; pp. 368–370. [Google Scholar]
- Wu, Y.K.; Vinokurov, N.A.; Mikhailov, S.; Li, J.; Popov, V. High-gain lasing and polarization switch with a distributed optical-klystron free-electron laser. Phys. Rev. Lett. 2006, 96, 224801. [Google Scholar] [CrossRef]
- Wu, Y.K. Accelerator physics research and light source development programs at Duke University. In Proceedings of the 2007 IEEE Particle Accelerator Conference (PAC); IEEE: Piscataway, NJ, USA, 2007; pp. 1215–1217. [Google Scholar] [CrossRef]
- Edwards, G.S.; Allen, S.J.; Haglund, R.F.; Nemanich, R.J.; Redlich, B.; Simon, J.D.; Yang, W.C. Applications of free-electron lasers in the biological and material sciences. Photochem. Photobiol. 2007, 81, 711–735. [Google Scholar] [CrossRef]
- Neyman, P.J.; Colson, W.B.; Gottshalk, S.C.; Todd, A.M.M. Free electron lasers in 2017. In Proceedings of the 38th International Free-Electron Laser Conference; JACoW Publishing: Sante Fe, NM, USA, 2017; pp. 204–209. [Google Scholar] [CrossRef]
- Newnam, B.; Warren, R.; Sheffield, R.; Stein, W.; Lynch, M.; Fraser, J.; Goldstein, J.; Sollid, J.; Swann, T.; Watson, J.; et al. Optical performance of the Los Alamos free-electron laser. IEEE J. Quantum Electron. 1985, 21, 867–881. [Google Scholar] [CrossRef]
- Bamford, D.J.; Deacon, D.A.G. Measurement of the coherent harmonics emitted in the Mark III free electron laser. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1989, 285, 23–30. [Google Scholar] [CrossRef]
- O’Shea, P.G.; Bender, S.C.; Carlsten, B.E.; Early, J.W.; Feldman, D.W.; Lumpkin, A.H.; Feldman, R.; Goldstein, J.C.; McKenna, K.; Martineau, R.; et al. Performance of the APEX free-electron laser at Los Alamos National Laboratory. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1993, 331, 62–68. [Google Scholar] [CrossRef]
- Prazeres, R.; Berset, J.M.; Glotin, F.; Jaroszynski, D.A.; Ortega, J.M. Optical performance of the CLIO infrared FEL. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1993, 331, 15–19. [Google Scholar] [CrossRef]
- Van der Meer, A.F.G.; Bakker, R.J.; van der Geer, C.A.; Oepts, D.; van Amersfoort, P.W.; Gillespie, W.A.; Martin, P.F.; Saxon, G. Optimization of the FELIX accelerator with respect to laser performance. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1993, 331, 282–286. [Google Scholar] [CrossRef]
- O’Shea, P.G.; Bender, S.C.; Byrd, D.A.; Early, J.W.; Feldman, D.W.; Fortgang, C.M.; Goldstein, J.C.; Newnam, B.E.; Sheffield, R.L.; Warren, R.W.; et al. Demonstration of ultraviolet lasing with a low energy electron beam. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1994, 341, 7–11. [Google Scholar] [CrossRef][Green Version]
- Nguyen, D.C.; Gierman, S.M.; Goldstein, J.C.; Kinross-Wright, J.M.; Kong, S.H.; Plato, J.G.; Russell, S.J.; Sheffield, R.L.; Sigler, F.E.; Sherwood, B.A.; et al. Recent progress of the compact AFEL at Los Alamos. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1995, 358, 27–30. [Google Scholar] [CrossRef]
- Xie, J.; Zhuang, J.; Huang, Y.; Li, Y.; Lin, S.; Ying, R.; Zhong, Y.; Zhang, L.; Wu, G.; Zhang, Y.; et al. The saturation of the Beijing FEL. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1995, 358, 256–259. [Google Scholar] [CrossRef]
- Berryman, K.W.; Smith, T.I. First lasing, capabilities, and flexibility of FIREFLY. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1996, 375, 6–9. [Google Scholar] [CrossRef]
- Minehara, E.J.; Sugimoto, M.; Sawamura, M.; Nagai, R.; Kikuzawa, N.; Yamanouchi, T.; Nishimori, N. A 0.1 kW operation of the JAERI superconducting RF linac-based FEL. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1999, 429, 9–11. [Google Scholar] [CrossRef]
- Neil, G.R.; Benson, S.; Biallas, G.; Bohn, C.L.; Douglas, D.; Dylla, H.F.; Evans, R.; Fugitt, J.; Gubeli, J.; Hill, R.; et al. First operation of an FEL in same-cell energy recovery mode. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2000, 445, 192–196. [Google Scholar] [CrossRef]
- Lumpkin, A.H.; Tokar, R.L.; Dowell, D.H.; Lowrey, A.R.; Yeremian, A.D.; Justice, R.E. Improved performance of the Boeing/LANL FEL experiment. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1990, 296, 169–180. [Google Scholar] [CrossRef]
- Jeong, Y.U.; Lee, B.C.; Kim, S.K.; Cho, S.O.; Cha, B.H.; Lee, J.; Kazakevitch, G.M.; Vobly, P.D.; Gavrilov, N.G.; Kubarev, V.V.; et al. First lasing of the KAERI compact far-infrared free-electron laser driven by a magnetron-based microtron. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2001, 475, 47–50. [Google Scholar] [CrossRef]
- Wu, D.; Li, M.; Yang, X.; Wang, H.; Luo, X.; Shen, X.; Xiao, D.; Wang, J.; Li, P.; Li, X.; et al. First Lasing of the CAEP THz FEL facility driven by a superconducting accelerator. J. Phys. Conf. Ser. 2018, 1067, 032010. [Google Scholar] [CrossRef]
- Oepts, D.; van der Meer, A.F.G.; Bakker, R.J.; van Amersfoort, P.W. Selection of single-mode radiation from a short-pulse free-electron laser. Phys. Rev. Lett. 1993, 70, 3255–3258. [Google Scholar] [CrossRef] [PubMed]
- Billardon, M.; Elleaume, P.; Lapierre, Y.; Ortega, J.M.; Bazin, C.; Bergher, M.; Marilleau, J.; Petroff, Y. The Orsay storage ring free electron laser: New results. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1986, 250, 26–34. [Google Scholar] [CrossRef]
- Kulipanov, G.; Litvinenko, V.N.; Pinaev, I.; Popik, V.; Skrinsky, A.N.; Sokolov, A.S.; Vinokurov, N.A. The VEPP-3 storage-ring optical klystron: Lasing in the visible and ultraviolet regions. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1990, 296, 1–3. [Google Scholar] [CrossRef]
- Yamada, K.; Yamazaki, T.; Sugiyama, S.; Tomimasu, T.; Ohgaki, H.; Noguchi, T.; Mikado, T.; Chiwaki, M.; Suzuki, R. Visible oscillation of storage-ring free electron laser on TERAS. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1992, 318, 33–37. [Google Scholar] [CrossRef]
- Yamazaki, T.; Yamada, K.; Sugiyama, S.; Ohgaki, H.; Sei, N.; Mikado, T.; Noguchi, T.; Chiwaki, M.; Suzuki, R.; Kawai, M.; et al. First lasing of the NIJI-IV storage-ring free-electron laser. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1993, 331, 27–33. [Google Scholar] [CrossRef]
- Takano, S.; Hama, H.; Isoyama, G. Gain Measurement of a free electron laser with an optical klystron on the UVSOR storage ring. Jpn. J. Appl. Phys. 1993, 32, 1285–1289. [Google Scholar] [CrossRef]
- Couprie, M.E.; Garzella, D.; Billardon, M. Operation of the Super-ACO free-electron laser in the UV range at 800 MeV. Europhys. Lett. (EPL) 1993, 21, 909–914. [Google Scholar] [CrossRef]
- Trovò, M.; Clarke, J.A.; Couprie, M.E.; Dattoli, G.; Garzella, D.; Gatto, A.; Giannessi, L.; Günster, S.; Kaiser, N.; Marsi, M.; et al. Operation of the European storage ring FEL at ELETTRA down to 190 nm. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2002, 483, 157–161. [Google Scholar] [CrossRef]
- Nölle, D.; Garzella, D.; Geisler, A.; Gianessi, L.; Hirsch, M.; Quick, H.; Ridder, M.; Schmidt, T.; Wille, K. First lasing of the FELICITA I FEL at DELTA. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2000, 445, 128–133. [Google Scholar] [CrossRef]
- Sei, N.; Ogawa, H.; Yamada, K. Lasing of infrared free-election lasers using the storage ring NIJI-IV. Opt. Lett. 2009, 34, 1843–1845. [Google Scholar] [CrossRef]
- Benson, S.; Biallas, G.; Bohn, C.; Douglas, D.; Dylla, H.F.; Evans, R.; Fugitt, J.; Hill, R.; Jordan, K.; Krafft, G.; et al. First lasing of the Jefferson Lab IR Demo FEL. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1999, 429, 27–32. [Google Scholar] [CrossRef]
- Neil, G.R.; Bohn, C.L.; Benson, S.V.; Biallas, G.; Douglas, D.; Dylla, H.F.; Evans, R.; Fugitt, J.; Grippo, A.; Gubeli, J.; et al. Sustained kilowatt lasing in a free-electron laser with same-cell energy recovery. Phys. Rev. Lett. 2000, 84, 662–665. [Google Scholar] [CrossRef]
- Nishimori, N.; Hajima, R.; Nagai, R.; Minehara, E.J. High extraction efficiency observed at the JAERI free-electron laser. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2001, 475, 266–269. [Google Scholar] [CrossRef]
- Hajima, R.; Shizuma, T.; Sawamura, M.; Nagai, R.; Nishimori, N.; Kikuzawa, N.; Minehara, E.J. First demonstration of energy-recovery operation in the JAERI superconducting linac for a high-power free-electron laser. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2003, 507, 115–119. [Google Scholar] [CrossRef]
- Antokhin, E.A.; Akberdin, R.R.; Arbuzov, V.S.; Bokov, M.A.; Bolotin, V.P.; Burenkov, D.; Bushuev, A.A.; Veremeenko, V.F.; Vinokurov, N.A.; Vobly, P.D.; et al. First lasing at the high-power free electron laser at Siberian center for photochemistry research. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2004, 528, 15–18. [Google Scholar] [CrossRef]
- Benson, S.; Beard, K.; Biallas, G.; Boyce, J.; Bullard, D.; Coleman, J.; Douglas, D.; Dylla, F.; Evans, R.; Evtushenko, P.; et al. High power operation of the JLab IR FEL driver accelerator. In Proceedings of the 2007 IEEE Particle Accelerator Conference (PAC); IEEE: Piscataway, NJ, USA, 2007; pp. 79–81. [Google Scholar] [CrossRef]
- Shevchenko, O.A.; Vinokurov, N.A.; Arbuzov, V.S.; Chernov, K.N.; Deichuly, O.I.; Dementyev, E.N.; Dovzhenko, B.A.; Getmanov, Y.V.; Gorbachev, Y.I.; Knyazev, B.A.; et al. The Novosibirsk free electron laser facility. In Proceedings of the AIP Conference Proceedings 2299-Synchrotron and Free Electron Laser Radiation; AIP: Novosibirsk, Russia, 2020; p. 020001. [Google Scholar] [CrossRef]
- Vinokurov, N.A.; Sknnsky, A.N. Optical Range Klystron Oscillator Using Ultrarelativistic Electrons; Preprint 77-59; Institute of Nuclear Physics: Novosibirsk, Russia, 1977. [Google Scholar]
- Deacon, D.A.G.; Billardon, M.; Elleaume, P.; Ortega, J.M.; Robinson, K.E.; Bazin, C.; Bergher, M.; Velghe, M.; Madey, J.M.J.; Petroff, Y. Optical klystron experiments for the ACO storage ring free electron laser. Appl. Phys. B Photophys. Laser Chem. 1984, 34, 207–219. [Google Scholar] [CrossRef]
- Yamazaki, T.; Yamada, K.; Sugiyama, S.; Ohgaki, H.; Tomimasu, T.; Noguchi, T.; Mikado, T.; Chiwaki, M.; Suzuki, R. Lasing in visible of a storage-ring free electron laser at ETL. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1991, 309, 343–347. [Google Scholar] [CrossRef]
- Takano, S.; Hama, H.; Isoyama, G. Lasing of a free electron laser in the visible on the UVSOR storage ring. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1993, 331, 20–26. [Google Scholar] [CrossRef]
- Yamazaki, T.; Yamada, K.; Sei, N.; Ohgaki, H.; Sugiyama, S.; Mikado, T.; Suzuki, R.; Noguchi, T.; Chiwaki, M.; Ohdaira, T.; et al. Lasing in the ultraviolet region with the NIJI-IV storage-ring free-electron laser. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1995, 358, 353–357. [Google Scholar] [CrossRef]
- Wu, Y.K.; Mikhailov, S.; Li, J.; Popov, V.; Vinokurov, N.A.; Gavrilov, N.G.; Shevchenko, O.A.; Vobly, P.D.; Kulipanov, G.N. First lasing and initial operation of a circularly polarized optical klystron OK-5 fel and a variably polarized distributed optical klystron DOK-1 FEL at DUKE. In Proceedings of the 27th International Free Electron Laser Conference; Nuhn, H.D., Ed.; JACoW Publishing: Paolo Alto, CA, USA, 2005; pp. 407–410. [Google Scholar]
- Cutolo, A.; Benson, S.V.; Schultz, J.F.; Madey, J.M. Cavity dumping for free electron lasers. Appl. Opt. 1989, 28, 3177–3182. [Google Scholar] [CrossRef]
- Benson, S.V.; Madey, J.M.J.; Szarmes, E.B.; Bhowmik, A.; Metty, P.; Curtin, M. A demonstration of loss modulation and cavity dumping in a free-electron-laser oscillator. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1990, 296, 762–768. [Google Scholar] [CrossRef]
- Bhowmik, A.; Curtin, M.S.; McMullin, W.A.; Benson, S.V.; Madey, J.M.J.; Richman, B.A.; Vintro, L. Initial results from the free-electron-laser master oscillator/power amplifier experiment. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1990, 296, 20–24. [Google Scholar] [CrossRef]
- Takahashi, S.; Ramian, G.; Sherwin, M.S. Cavity dumping of an injection-locked free-electron laser. Appl. Phys. Lett. 2009, 95, 234102. [Google Scholar] [CrossRef]
- Rana, R.; Klopf, J.M.; Ciano, C.; Singh, A.; Winnerl, S.; Schneider, H.; Helm, M.; Pashkin, A. Gold implanted germanium photoswitch for cavity dumping of a free-electron laser. Appl. Phys. Lett. 2021, 118, 011107. [Google Scholar] [CrossRef]
- Burghoorn, J.; Kaminski, J.P.; Strijbos, R.C.; Klaassen, T.O.; Wenckebach, W.T. Generation of subnanosecond high power far infrared pulses using a FEL pumped passive resonator. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1992, 318, 85–86. [Google Scholar] [CrossRef]
- Smith, T.I.; Haar, P.; Schwettman, H.A. Pulse stacking in the SCA/FEL external cavity. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1997, 393, 245–251. [Google Scholar] [CrossRef]
- Faatz, B.; Haselhoff, E.H.; Zhulin, V.I.; van Amersfoort, P.W. Pulse stacking in FELIX. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1994, 341, ABS136. [Google Scholar] [CrossRef]
- Marks, H.S.; Lurie, Y.; Dyunin, E.; Gover, A. Enhancing electron beam radiative energy extraction efficiency in free-electron laser oscillators through beam energy ramping. IEEE Trans. Microw. Theory Tech. 2017, 65, 4218–4224. [Google Scholar] [CrossRef]
- Xu, Y.; Jia, Q.; Li, H. Efficiency enhancement of RF-linac based free electron laser oscillator with electron beam energy ramping. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2019, 940, 448–452. [Google Scholar] [CrossRef]
- Jaroszynski, D.A.; Oepts, D.; van der Meer, A.F.G.; van Amersfoort, P.W.; Colson, W.B. Consequences of short electron-beam pulses in the FELIX project. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1990, 296, 480–484. [Google Scholar] [CrossRef]
- Bakker, R.J.; van der Geer, C.A.J.; Jaroszynski, D.A.; van der Meer, A.F.G.; Oepts, D.; van Amersfoort, P.W.; Anderegg, V.; van Son, P.C. Agility of FELIX regarding wavelength and micropulse shape. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1993, 331, 79–83. [Google Scholar] [CrossRef]
- Knippels, G.M.H.; Bakker, R.J.; van der Meer, A.F.G.; Jaroszynski, D.A.; Oepts, D.; van Amersfoort, P.W.; Hovenier, J.N. Dynamic cavity desynchronisation in FELIX. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1994, 341, ABS26–ABS27. [Google Scholar] [CrossRef]
- Song, S.B.; Kim, S.K.; Choi, J.S.; Hahn, S.J. Dynamic cavity desynchronization in a shout pulse free-electron laser resonator. J. Korean Phys. Soc. 2000, 37, 209–214. [Google Scholar]
- Sumitomo, Y.; Hajima, R.; Hayakawa, Y.; Sakai, T. Simulation of short-pulse generation from a dynamically detuned IR-FEL oscillator and pulse stacking at an external cavity. J. Phys. Conf. Ser. 2019, 1350, 012040. [Google Scholar] [CrossRef]
- Zen, H.; Ohgaki, H.; Hajima, R. High-extraction-efficiency operation of a midinfrared free electron laser enabled by dynamic cavity desynchronization. Phys. Rev. Accel. Beams 2020, 23, 070701. [Google Scholar] [CrossRef]
- Sprangle, P.; Tang, C.M.; Manheimer, W.M. Nonlinear formulation and efficiency enhancement of free-electron lasers. Phys. Rev. Lett. 1979, 43, 1932–1936. [Google Scholar] [CrossRef]
- Kroll, N.; Morton, P.; Rosenbluth, M. Free-electron lasers with variable parameter wigglers. IEEE J. Quantum Electron. 1981, 17, 1436–1468. [Google Scholar] [CrossRef]
- Bosco, P.; Colson, W.B. Spontaneous radiation from relativistic electrons in a tapered undulator. Phys. Rev. A 1983, 28, 319–327. [Google Scholar] [CrossRef]
- Edighoffer, J.A.; Neil, G.R.; Hess, C.E.; Smith, T.I.; Fornaca, S.W.; Schwettman, H.A. Variable-wiggler free-electron-laser oscillation. Phys. Rev. Lett. 1984, 52, 344–347. [Google Scholar] [CrossRef]
- Curtin, M.; Bhowmik, A.; Brown, J.; McMullin, W.; Metty, P.; Benson, S.V.; Madey, J.M.J. Initial results of operating the Rocketdyne undulator in a tapered configuration. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1990, 296, 69–74. [Google Scholar] [CrossRef]
- Jaroszynski, D.A.; Prazeres, R.; Glotin, F.; Ortega, J.M.; Oepts, D.; van der Meer, A.F.G.; Knippels, G.M.H.; van Amersfoort, P.W. Free-electron laser efficiency enhancement, gain enhancement, and spectral control using a step-tapered undulator. Phys. Rev. Lett. 1995, 74, 2224–2227. [Google Scholar] [CrossRef]
- Benson, S.; Gubeli, J.; Neil, G.R. An experimental study of an FEL oscillator with a linear taper. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2001, 475, 276–280. [Google Scholar] [CrossRef][Green Version]
- Asgekar, V.; Lehnert, U.; Michel, P. A tapered undulator experiment at the ELBE far infrared hybrid-resonator oscillator free electron laser. Rev. Sci. Instrum. 2012, 83, 015116. [Google Scholar] [CrossRef]
- Saldin, E.L.; Schneidmiller, E.A.; Yurkov, M.V. The features of an FEL oscillator with a tapered undulator. Opt. Commun. 1993, 103, 297–306. [Google Scholar] [CrossRef]
- Christodoulou, A.; Lampiris, D.; Polykandriotis, K.; Colson, W.B.; Crooker, P.P.; Benson, S.; Gubeli, J.; Neil, G.R. Free-electron-laser oscillator with a linear taper. Phys. Rev. E 2002, 66, 056502. [Google Scholar] [CrossRef]
- Dattoli, G.; Pagnutti, S.; Ottaviani, P.L.; Asgekar, V. Free electron laser oscillators with tapered undulators: Inclusion of harmonic generation and pulse propagation. Phys. Rev. Spec. Top. Accel. Beams 2012, 15, 030708. [Google Scholar] [CrossRef]
- Ottaviani, P.L.; Pagnutti, S.; Dattoli, G.; Sabia, E.; Petrillo, V.; van der Slot, P.J.M.; Biedron, S.G.; Milton, S.V. Deep saturated free electron laser oscillators and frozen spikes. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2016, 834, 108–117. [Google Scholar] [CrossRef]
- Colson, W.B. Free-electron lasers operating in higher harmonics. Phys. Rev. A 1981, 24, 639–641. [Google Scholar] [CrossRef]
- Colson, W.B. The nonlinear wave equation for higher harmonics in free-electron lasers. IEEE J. Quantum Electron. 1981, 17, 1417–1427. [Google Scholar] [CrossRef]
- Becker, W. Increasing the frequency of a free electron laser by means of a linearly polarized magnetic field. Z. Phys. B Condens. Matter 1981, 42, 87–94. [Google Scholar] [CrossRef]
- Benson, S.V.; Madey, J.M.J. Demonstration of harmonic lasing in a free-electron laser. Phys. Rev. A 1989, 39, 1579–1581. [Google Scholar] [CrossRef] [PubMed]
- Bamford, D.J.; Deacon, D.A.G. Harmonic-generation experiments on the Mark III free electron laser. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1990, 296, 89–97. [Google Scholar] [CrossRef]
- Prazeres, R.; Ortega, J.M. Enhancement of the free-electron coherent harmonic generation by use of the dispersive function on a storage ring. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1990, 296, 436–441. [Google Scholar] [CrossRef]
- Prazeres, R.; Guyot-Sionnest, P.; Ortega, J.M.; Jaroszynski, D.; Billardon, M.; Couprie, M.E.; Velghe, M.; Petroff, Y. Production of VUV coherent light by harmonic generation with the optical klystron of super-ACO. IEEE J. Quantum Electron. 1991, 27, 1061–1068. [Google Scholar] [CrossRef]
- Jaroszynski, D.A.; Prazeres, R.; Glotin, F.; Marcouillé, O.; Ortega, J.M. Coherent harmonic production using a two-section undulator FEL. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1996, 375, 456–459. [Google Scholar] [CrossRef]
- Hayakawa, Y.; Sato, I.; Hayakawa, K.; Tanaka, T.; Yokoyama, K.; Sakai, T.; Kanno, K.; Ishiwata, K.i.; Hashimoto, E. Simultaneous measurement of the fundamental and third harmonic FEL at LEBRA. Jpn. J. Appl. Phys. 2002, 41, 54–57. [Google Scholar] [CrossRef]
- Yamada, K.; Yamazaki, T.; Sei, N.; Ohgaki, H.; Mikado, T.; Sugiyama, S.; Kawai, M.; Yokoyama, M. Observation of higher harmonics in the NIJI-IV FEL. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1998, 407, 193–197. [Google Scholar] [CrossRef]
- Neil, G.R.; Benson, S.V.; Biallas, G.; Gubeli, J.; Jordan, K.; Myers, S.; Shinn, M.D. Second harmonic FEL oscillation. Phys. Rev. Lett. 2001, 87, 084801. [Google Scholar] [CrossRef]
- Hajima, R.; Nagai, R.; Nishimori, N.; Kikuzawa, N.; Minehara, E.J. Third-harmonic lasing at JAERI-FEL. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2001, 475, 43–46. [Google Scholar] [CrossRef]
- Litvinenko, V.N. New results and prospects for harmonic generation in storage ring FELs. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2003, 507, 265–273. [Google Scholar] [CrossRef]
- Hayakawa, Y.; Sato, I.; Hayakawa, K.; Tanaka, T.; Yokoyama, K.; Kanno, K.; Sakai, T.; Ishiwata, K.; Nakao, K.; Hashimoto, E. Characteristics of the fundamental FEL and the higher harmonic generation at LEBRA. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2003, 507, 404–408. [Google Scholar] [CrossRef]
- De Ninno, G.; Danailov, M.B.; Diviacco, B.; Ferianis, M.; Trovo, M.; Giannessi, L. Coherent harmonic generation using the ELETTRA storage-ring optical klystron. In Proceedings of the Proceedings of the 26th International Free Electron Laser Conference; JACoW Publishing: Trieste, Italy, 2004; pp. 237–240. [Google Scholar]
- Sei, N.; Ogawa, H.; Yamada, K. Third harmonic lasing in a storage ring free-electron laser. J. Phys. Soc. Jpn. 2010, 79, 093501. [Google Scholar] [CrossRef]
- Kubarev, V.V.; Kulipanov, G.N.; Shevchenko, O.A.; Vinokurov, N.A. Third harmonic lasing on terahertz NovoFEL. J. Infrared Millim. Terahertz Waves 2011, 32, 1236–1242. [Google Scholar] [CrossRef]
- Jaroszynski, D.A.; Prazeres, R.; Glotin, F.; Ortega, J.M. Two-color free-electron laser operation. Phys. Rev. Lett. 1994, 72, 2387–2390. [Google Scholar] [CrossRef]
- Prazeres, R.; Glotin, F.; Insa, C.; Jaroszynski, D.A.; Ortega, J.M. Two-colour operation of a free-electron laser and applications in the mid-infrared. Eur. Phys. J. At. Mol. Opt. Phys. 1998, 3, 87–93. [Google Scholar] [CrossRef]
- Wu, Y.K.; Yan, J.; Hao, H.; Li, J.Y.; Mikhailov, S.F.; Popov, V.G.; Vinokurov, N.A.; Huang, S.; Wu, J. Widely tunable two-color free-electron laser on a storage ring. Phys. Rev. Lett. 2015, 115, 184801. [Google Scholar] [CrossRef]
- Yan, J.; Hao, H.; Li, J.Y.; Mikhailov, S.F.; Popov, V.G.; Vinokurov, N.A.; Huang, S.; Wu, J.; Günster, S.; Wu, Y.K. Storage ring two-color free-electron laser. Phys. Rev. Accel. Beams 2016, 19, 070701. [Google Scholar] [CrossRef]
- Zako, A.; Kanazawa, Y.; Konishi, Y.; Yamaguchi, S.; Nagai, A.; Tomimasu, T. Simultaneous two-color lasing in the mid-IR and far-IR region with two undulators and one RF linac at the FELI. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1999, 429, 136–140. [Google Scholar] [CrossRef]
- Swent, R.L.; Berryman, K.W.; Schwettman, H.A.; Smith, T.I. Applications of wavelength agility in an FEL facility. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1991, 304, 272–275. [Google Scholar] [CrossRef]
- Smith, T.I.; Crosson, E.R.; James, G.E.; Schwettman, H.A.; Swent, R.L. Multi-color, multi-user operation at the Stanford free electron laser center. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1998, 407, 151–156. [Google Scholar] [CrossRef]
- Knippels, G.M.H.; Mols, R.F.X.A.M.; van der Meer, A.F.G.; Oepts, D.; van Amersfoort, P.W. Intense far-infrared free-electron laser pulses with a length of six optical cycles. Phys. Rev. Lett. 1995, 75, 1755–1758. [Google Scholar] [CrossRef] [PubMed]
- Knippels, G.M.H.; van der Meer, A.F.G.; Oepts, D.; van Amersfoort, P.W. Generation of frequency-chirped optical pulses in a large-slippage free-electron laser. IEEE J. Quantum Electron. 1997, 33, 10–17. [Google Scholar] [CrossRef]
- Calderón, O.G.; Kimura, T.; Smith, T.I. Modulated desynchronism in short pulse free-electron laser oscillators. Phys. Rev. Spec. Top. Accel. Beams 2000, 3, 090701. [Google Scholar] [CrossRef]
- Hajima, R.; Nagai, R. Generation of a self-chirped few-cycle optical pulse in a FEL oscillator. Phys. Rev. Lett. 2003, 91, 024801. [Google Scholar] [CrossRef]
- McNeil, B.W.J.; Thompson, N.R. Cavity resonator free electron lasers as a source of stable attosecond pulses. EPL (Europhys. Lett.) 2011, 96, 54004. [Google Scholar] [CrossRef]
- Hajima, R. Few-cycle infrared pulse evolving in FEL oscillators and its application to high-harmonic generation for attosecond ultraviolet and X-ray pulses. Atoms 2021, 9, 15. [Google Scholar] [CrossRef]
- Bonifacio, R.; Pellegrini, C.; Narducci, L. Collective instabilities and high-gain regime in a free electron laser. Opt. Commun. 1984, 50, 373–378. [Google Scholar] [CrossRef]
- Hahn, S.J.; Lee, J.K. Bifurcations in a short-pulse free-electron laser oscillator. Phys. Lett. A 1993, 176, 339–343. [Google Scholar] [CrossRef]
- Bakker, R.J.; Jaroszynski, D.A.; van der Meer, A.F.G.; Oepts, D.; van Amersfoort, P.W. Short-pulse effects in a free-electron laser. IEEE J. Quantum Electron. 1994, 30, 1635–1644. [Google Scholar] [CrossRef]
- Piovella, N.; Chaix, P.; Shvets, G.; Jaroszynski, D.A. Analytical theory of short-pulse free-electron laser oscillators. Phys. Rev. E 1995, 52, 5470–5486. [Google Scholar] [CrossRef]
- Jaroszynski, D.A.; Chaix, P.; Piovella, N.; Oepts, D.; Knippels, G.M.H.; van der Meer, A.F.G.; Weits, H.H. Superradiance in a short-pulse free-electron-laser oscillator. Phys. Rev. Lett. 1997, 78, 1699–1702. [Google Scholar] [CrossRef]
- Hajima, R.; Nishimori, N.; Nagai, R.; Minehara, E.J. Analyses of superradiance and spiking-mode lasing observed at JAERI-FEL. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2001, 475, 270–275. [Google Scholar] [CrossRef]
- Nishimori, N.; Hajima, R.; Iijima, H.; Kikuzawa, N.; Minehara, E.; Nagai, R.; Nishitani, T.; Sawamura, M. FEL oscillation with a high extraction efficiency at JAEA ERL FEL. In Proceedings of the 28th International Free Electron Laser Conference; JACoW Publishing: Berlin, Germany, 2006; pp. 265–272. [Google Scholar]
- Duris, J.; Musumeci, P.; Sudar, N.; Murokh, A.; Gover, A. Tapering enhanced stimulated superradiant oscillator. Phys. Rev. Accel. Beams 2018, 21, 080705. [Google Scholar] [CrossRef]
- Jaroszynski, D.A.; Bakker, R.J.; van der Meer, A.F.G.; Oepts, D.; van Amersfoort, P.W. Experimental observation of limit-cycle oscillations in a short-pulse free-electron laser. Phys. Rev. Lett. 1993, 70, 3412–3415. [Google Scholar] [CrossRef]
- Knippels, G.M.H.; van der Meer, A.F.G.; Mols, R.F.X.A.M.; Oepts, D.; van Amersfoort, P.W.; Jaroszynski, D.A. Influence of a step-tapered undulator field on the optical pulse shape of a far-infrared free-electron laser. IEEE J. Quantum Electron. 1996, 32, 896–904. [Google Scholar] [CrossRef]
- De Ninno, G.; Fanelli, D.; Bruni, C.; Couprie, M.E. Chaotic dynamics in a storage-ring free electron laser. Eur. Phys. J. D 2003, 22, 269–277. [Google Scholar] [CrossRef]
- Kiessling, R.; Colson, W.B.; Gewinner, S.; Schöllkopf, W.; Wolf, M.; Paarmann, A. Femtosecond single-shot timing and direct observation of subpulse formation in an infrared free-electron laser. Phys. Rev. Accel. Beams 2018, 21, 080702. [Google Scholar] [CrossRef]
- Colson, W.B. Optical pulse evolution in the Stanford free-electron laser and in a tapered wiggler. In Free-Electron Generators of Coherent Radiation (Physics of Quantum Electronics); Jacobs, S.F., Moore, G., Pilloff, H.S., Sargent, M., III, Scully, M.O., Spitzer, R., Eds.; Addison-Wesley Publishing Co: Reading, MA, USA, 1982; Volume 8, pp. 457–488. [Google Scholar]
- Blau, J.; Wong, R.K.; Colson, W.B. Ultra-short pulse free electron laser oscillators. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1995, 358, 441–443. [Google Scholar] [CrossRef]
- Blau, J.; Cohn, K.; Colson, W.B. Four-dimensional models of free-eletron laser amplifiers and oscillators. In Proceedings of the 37th International Free Electron Laser Conference; Kang, H., Kim, D.E., Schaa, V.W., Eds.; JACoW Publishing: Daejeon, Korea, 2015; pp. 607–614. [Google Scholar] [CrossRef]
- Amir, A.; Knox-Seith, J.F.; Warden, M. Bandwidth narrowing of the UCSB FEL by injection seeding with a cw laser. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1991, 304, 12–16. [Google Scholar] [CrossRef]
- Oepts, D.; Bakker, R.J.; Jaroszynski, D.A.; van der Meer, A.F.G.; van Amersfoort, P.W. Induced and spontaneous interpulse phase locking in a free-electron laser. Phys. Rev. Lett. 1992, 68, 3543–3546. [Google Scholar] [CrossRef]
- Szarmes, E.B.; Madden, A.D.; Madey, J.M.J. Optical phase locking of a 286-GHz harmonically mode-locked free-electron laser. J. Opt. Soc. Am. B 1996, 13, 1588–1597. [Google Scholar] [CrossRef]
- Takahashi, S.; Ramian, G.; Sherwin, M.S.; Brunel, L.C.; van Tol, J. Submegahertz linewidth at 240 GHz from an injection-locked free-electron laser. Appl. Phys. Lett. 2007, 91, 174102. [Google Scholar] [CrossRef]
- Evain, C.; Szwaj, C.; Bielawski, S.; Couprie, M.E.; Hosaka, M.; Mochihashi, A.; Katoh, M. Suppression of self-pulsing instabilities in free-electron lasers using delayed optical feedback. Phys. Rev. Spec. Top. Accel. Beams 2012, 15, 040701. [Google Scholar] [CrossRef]
- Hajima, R.; Nagai, R. Generating carrier-envelope-phase stabilized few-cycle pulses from a free-electron laser oscillator. Phys. Rev. Lett. 2017, 119, 204802. [Google Scholar] [CrossRef]
- Shvets, G.; Wurtele, J.S. Generation of ultrashort radiation pulses by injection locking a regenerative free-electron-laser amplifier. Phys. Rev. E 1997, 56, 3606–3610. [Google Scholar] [CrossRef]
- Boehmer, H.; Caponi, M.Z.; Munch, J. Fel operation with prebunched electron beam. In Proceedings of the 4th International Topical Conference on High-Power Electron and Ion Beam Research & Technology; Doucet, H., Buzzi, J.M., Eds.; EcolePolytechnique: Palaiseau, France, 1981; pp. 947–952. [Google Scholar]
- Boscolo, I.; Stagno, V. A study of a transverse optical klystron experiment in Adone (TOKA). Nucl. Instrum. Methods Phys. Res. 1982, 198, 483–496. [Google Scholar] [CrossRef]
- Schnitzer, I.; Gover, A. The prebunched free electron laser in various operating gain regimes. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1985, 237, 124–140. [Google Scholar] [CrossRef]
- Yu, L.H. Generation of intense uv radiation by subharmonically seeded single-pass free-electron lasers. Phys. Rev. A 1991, 44, 5178–5193. [Google Scholar] [CrossRef]
- Allaria, E.; Appio, R.; Badano, L.; Barletta, W.A.; Bassanese, S.; Biedron, S.G.; Borga, A.; Busetto, E.; Castronovo, D.; Cinquegrana, P.; et al. Highly coherent and stable pulses from the FERMI seeded free-electron laser in the extreme ultraviolet. Nat. Photonics 2012, 6, 699–704. [Google Scholar] [CrossRef]
- Kim, K.J.; Shvyd’ko, Y.V.; Reiche, S. A proposal for an X-ray free-electron laser oscillator with an energy-recovery linac. Phys. Rev. Lett. 2008, 100, 244802. [Google Scholar] [CrossRef]
- Sheffield, R.L.; Gray, E.R.; Fraser, J.S. The Los Alamos photoinjector program. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1988, 272, 222–226. [Google Scholar] [CrossRef]
- Dowell, D.H.; Davis, K.J.; Friddell, K.D.; Tyson, E.L.; Lancaster, C.A.; Milliman, L.; Rodenburg, R.E.; Aas, T.; Bemes, M.; Bethel, S.Z.; et al. First operation of a photocathode radio frequency gun injector at high duty factor. Appl. Phys. Lett. 1993, 63, 2035–2037. [Google Scholar] [CrossRef]
- Arnold, N.D.; Attig, J.; Banks, G.; Bechtold, R.; Beczek, K.; Benson, C.; Berg, S.; Berg, W.; Biedron, S.G.; Biggs, J.; et al. Observation and analysis of self-amplified spontaneous emission at the APS low-energy undulator test line. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2001, 475, 28–37. [Google Scholar] [CrossRef]
- Rossbach, J.; Schneider, J.R.; Wurth, W. 10 years of pioneering X-ray science at the free-electron laser FLASH at DESY. Phys. Rep. 2019, 808, 1–74. [Google Scholar] [CrossRef]
- Allaria, E.; Badano, L.; Bassanese, S.; Capotondi, F.; Castronovo, D.; Cinquegrana, P.; Danailov, M.B.; D’Auria, G.; Demidovich, A.; De Monte, R.; et al. The FERMI free-electron lasers. J. Synchrotron Radiat. 2015, 22, 485–491. [Google Scholar] [CrossRef] [PubMed]
- Saldin, E.L.; Schneidmiller, E.A.; Yurkov, M.V. Similarity techniques in a one-dimensional theory of a FEL oscillator. Opt. Commun. 1993, 102, 360–378. [Google Scholar] [CrossRef]
- Dattoli, G.; Giannessi, L.; Ottaviani, P.L.; Renieri, A. A model for the saturation of a storage ring free electron laser. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1995, 365, 559–563. [Google Scholar] [CrossRef]
- Dattoli, G.; Ottaviani, P.L.; Pagnutti, S. Pulse propagation and nonlinear harmonic generation in free electron laser oscillators. J. Appl. Phys. 2007, 101, 024914. [Google Scholar] [CrossRef]
- Curcio, A.; Dattoli, G.; Di Palma, E.; Petralia, A. Free electron laser oscillator efficiency. Opt. Commun. 2018, 425, 29–37. [Google Scholar] [CrossRef]
- Madey, J.M.J. Stimulated emission of Bremsstrahlung in a periodic magnetic field. J. Appl. Phys. 1971, 42, 1906–1913. [Google Scholar] [CrossRef]
- Madey, J.M.J.; Schwettman, H.A.; Fairbank, W.M. A free electron laser. IEEE Trans. Nucl. Sci. 1973, 20, 980–983. [Google Scholar] [CrossRef]
- Hopf, F.A.; Meystre, P.; Scully, M.O.; Louisell, W.H. Classical theory of a free-electron laser. Phys. Rev. Lett. 1976, 37, 1215–1218. [Google Scholar] [CrossRef]
- Colson, W.B.; Richardson, J.L. Multimode theory of free-electron laser oscillators. Phys. Rev. Lett. 1983, 50, 1050–1053. [Google Scholar] [CrossRef]
- Colson, W.B.; Freedman, R.A. Synchrotron instability for long pulses in free electron laser oscillators. Opt. Commun. 1983, 46, 37–42. [Google Scholar] [CrossRef]
- McVey, B.D.; Goldstein, J.C.; Tokar, R.L.; Elliott, C.J.; Gitomer, S.J.; Schmitt, M.J.; Thode, L.E. Numerical simulations of free electron laser oscillators. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1989, 285, 186–191. [Google Scholar] [CrossRef][Green Version]
- Parazzoli, C.G. FELEXN, Boeing simulation code, version B08. In Proceedings of the X-ray FEL Theory and Simulation Codes Workshop (SLAC Report No. LCLS-TN-00-1); SLAC: Stanford, CA, USA, 1999; p. 161. [Google Scholar]
- Dattoli, G.; Ottaviani, P.L. Design considerations for X-ray free electron lasers. J. Appl. Phys. 1999, 86, 5331–5336. [Google Scholar] [CrossRef]
- Dattoli, G.; Ottaviani, P.L.; Renieri, A.; Biedron, S.G.; Freund, H.P.; Milton, S.V. A compact free electron laser device operating in the UV-soft X-ray region. Opt. Commun. 2004, 232, 319–326. [Google Scholar] [CrossRef]
- Dattoli, G.; Ottaviani, P.L.; Pagnutti, S. High gain oscillators: Pulse propagation and saturation. J. Appl. Phys. 2007, 101, 103109. [Google Scholar] [CrossRef]
- Dattoli, G.; Ottaviani, P.L.; Pagnutti, S. The PROMETEO code: A flexible tool for free electron laser study. Nuovo C. Della Soc. Ital. Fis. C 2009, 32, 283–287. [Google Scholar] [CrossRef]
- Van der Slot, P.J.M.; Freund, H.P.; Miner, W.H., Jr.; Benson, S.V.; Shinn, M.D.; Boller, K.J. Time-dependent, three-dimensional simulation of free-electron-laser oscillators. Phys. Rev. Lett. 2009, 102. [Google Scholar] [CrossRef]
- Freund, H.P.; Biedron, S.G.; Milton, S.V. Nonlinear harmonic generation in free-electron lasers. IEEE J. Quantum Electron. 2000, 36, 275–281. [Google Scholar] [CrossRef]
- Karssenberg, J.G.; van der Slot, P.J.M.; Volokhine, I.V.; Verschuur, J.W.J.; Boller, K.J. Modeling paraxial wave propagation in free-electron laser oscillators. J. Appl. Phys. 2006, 100, 093106. [Google Scholar] [CrossRef]
- Reiche, S. GENESIS 1.3: A fully 3D time-dependent FEL simulation code. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1999, 429, 243–248. [Google Scholar] [CrossRef]
- Campbell, L.T.; McNeil, B.W.J. Puffin: A three dimensional, unaveraged free electron laser simulation code. Phys. Plasmas 2012, 19, 093119. [Google Scholar] [CrossRef]
- McNeil, B.W.J.; Thompson, N.R.; Dunning, D.J.; Karssenberg, J.G.; van der Slot, P.J.M.; Boller, K.J. A design for the generation of temporally-coherent radiation pulses in the VUV and beyond by a self-seeding high-gain free electron laser amplifier. New J. Phys. 2007, 9, 239. [Google Scholar] [CrossRef]
- Pongchalee, P.; McNeil, B.W. Unaveraged simulation of a regenerative amplifier free electron laser. In Proceedings of the 39th International Free-Electron Laser Conference; JACoW Publishing: Hamburg, Germany, 2019; pp. 106–109. [Google Scholar] [CrossRef]
- Freund, H.P.; van der Slot, P.J.M.; Grimminck, D.L.A.G.; Setija, I.D.; Falgari, P. Three-dimensional, time-dependent simulation of free-electron lasers with planar, helical, and elliptical undulators. New J. Phys. 2017, 19, 023020. [Google Scholar] [CrossRef]
- Freund, H.P.; van der Slot, P.J.M. Variable polarization states in free-electron lasers. J. Phys. Commun. 2021. Submitted. [Google Scholar]
- FEL Simulation Code MINERVA. Available online: https://gitlab.utwente.nl/tnw/ap/lpno/public-projects/MINERVA (accessed on 25 May 2021).
- Sprangle, P.; Ting, A.; Tang, C.M. Analysis of radiation focusing and steering in the free-electron laser by use of a source-dependent expansion technique. Phys. Rev. A 1987, 36, 2773–2781. [Google Scholar] [CrossRef]
- Born, M.; Wolf, E. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light, 7th ed.; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Lee, J.S.; Gensch, M.; Hinrichs, K.; Seidel, W.; Schade, U. Determination of the polarization characteristics of the ELBE free electron laser. Infrared Phys. Technol. 2008, 51, 537–540. [Google Scholar] [CrossRef]
- Allaria, E.; Diviacco, B.; Callegari, C.; Finetti, P.; Mahieu, B.; Viefhaus, J.; Zangrando, M.; De Ninno, G.; Lambert, G.; Ferrari, E.; et al. Control of the polarization of a vacuum-ultraviolet, high-gain, free-electron laser. Phys. Rev. X 2014, 4, 041040. [Google Scholar] [CrossRef]
- Giannessi, L.; Alesini, D.; Antici, P.; Bacci, A.; Bellaveglia, M.; Boni, R.; Boscolo, M.; Briquez, F.; Castellano, M.; Catani, L.; et al. Self-amplified spontaneous emission for a single pass free-electron laser. Phys. Rev. Spec. Top. Accel. Beams 2011, 14, 060712. [Google Scholar] [CrossRef]
- Emma, P.; Akre, R.; Arthur, J.; Bionta, R.; Bostedt, C.; Bozek, J.; Brachmann, A.; Bucksbaum, P.; Coffee, R.; Decker, F.J.; et al. First lasing and operation of an ångstrom-wavelength free-electron laser. Nat. Photonics 2010, 4, 641–647. [Google Scholar] [CrossRef]
- Optical Propagation Code (OPC). Available online: https://gitlab.utwente.nl/tnw/ap/lpno/public-projects/Physics-OPC (accessed on 25 May 2021).
- Siegman, A.E. Lasers; University Science Books: Mill Valley, CA, USA, 1986. [Google Scholar]
- Haus, H. Waves and Fields in Optoelectronics; Prentice-Hall: Englewood Cliffs, NJ, USA, 1984. [Google Scholar]
- Goodman, J.W. Introduction to Fourier Optics; McGraw-Hill: New York, NY, USA, 1996. [Google Scholar]
- Van der Slot, P.J.M.; Karssenberg, J.G.; Boller Mesa, K.J. Modelling mirror aberrations in FEL oscillators using OPC. In Proceedings of the 29th International Free Electron Laser Conference; JACoW Publishing: Novosibirsk, Russia, 2007; pp. 207–210. [Google Scholar]
- Van der Slot, P.J.M.; Freund, H.P.; van der Meer, R.; Boller, K.J. Mirror aberrations in a low gain FEL oscillator. In Proceedings of the 30th International Free Electron Laser Conference; JACoW Publishing: Gyeongju, Korea, 2008; pp. 63–66. [Google Scholar]
- Shvyd’ko, Y.V. X-ray Optics: High-Energy Resolution Applications; Optical Sciences; Springer: Berlin, Germany, 2004; Volume 98. [Google Scholar]
- Fox, A.G.; Li, T. Resonant modes in a maser interferometer. Bell Syst. Tech. J. 1961, 40, 453–488. [Google Scholar] [CrossRef]
- Van der Slot, P.J.M.; Biedron, S.G.; Milton, S.V. Design of a resonator for the CSU THz FEL. In Proceedings of the 35th International Free-Electron Laser Conference; JACoW Publishing: New York, NY, USA, 2013; pp. 719–722. [Google Scholar]
- Benson, S.V.; Davidson, P.S.; Jain, R.; Kloeppel, P.K.; Neil, G.R.; Shinn, M.D. Optical modeling of the Jefferson laboratory IR demo FEL. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1998, 407, 401–406. [Google Scholar] [CrossRef][Green Version]
- Shinn, M.D.; Baker, G.R.; Behre, C.P.; Benson, S.V.; Bevins, M.E.; Dillon-Townes, L.; Dylla, H.F.; Feldl, E.J.; Gubeli, J.F.; Lassiter, R.D.; et al. Design of the Jefferson Lab IR Upgrade FEL optical cavity. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2003, 507, 196–199. [Google Scholar] [CrossRef]
- Nguyen, D.C.; Sheffield, R.L.; Fortgang, C.M.; Goldstein, J.C.; Kinross-Wright, J.M.; Ebrahim, N.A. First lasing of the regenerative amplifier FEL. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1999, 429, 125–130. [Google Scholar] [CrossRef]
- Madey, J.M.J. Relationship between mean radiated energy, mean squared radiated energy and spontaneous power spectrum in a power series expansion of the equations of motion in a free-electron laser. Il Nuovo C. B Ser. 11 1979, 50, 64–88. [Google Scholar] [CrossRef]
- Freund, H.P.; Nguyen, D.C.; Sprangle, P.A.; van der Slot, P.J.M. Three-dimensional, time-dependent simulation of a regenerative amplifier free-electron laser. Phys. Rev. Spec. Top. Accel. Beams 2013, 16, 010707. [Google Scholar] [CrossRef]
- Freund, H.P.; van der Slot, P.J.M.; Shvyd’ko, Y.V. An X-ray regenerative amplifier free-electron laser using diamond pinhole mirrors. New J. Phys. 2019, 21, 093028. [Google Scholar] [CrossRef]
- Xie, M. Design optimization for an X-ray free electron laser driven by SLAC linac. In Proceedings of the Particle Accelerator Conference; IEEE: Dallas, TX, USA, 1995; Volume 1, pp. 183–185. [Google Scholar] [CrossRef]
- Huang, Z.; Kim, K.J. Review of X-ray free-electron laser theory. Phys. Rev. Spec. Top. Accel. Beams 2007, 10, 034801. [Google Scholar] [CrossRef]
- Saldin, E.L.; Schneidmiller, E.A.; Yurkov, M.V. The Physics of Free Electron Lasers; Advanced Texts in Physics; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar] [CrossRef]
- Ishikawa, T.; Aoyagi, H.; Asaka, T.; Asano, Y.; Azumi, N.; Bizen, T.; Ego, H.; Fukami, K.; Fukui, T.; Furukawa, Y.; et al. A compact X-ray free-electron laser emitting in the sub-ångström region. Nat. Photonics 2012, 6, 540–544. [Google Scholar] [CrossRef]
- Milne, C.; Schietinger, T.; Aiba, M.; Alarcon, A.; Alex, J.; Anghel, A.; Arsov, V.; Beard, C.; Beaud, P.; Bettoni, S.; et al. SwissFEL: The Swiss X-ray free electron laser. Appl. Sci. 2017, 7, 720. [Google Scholar] [CrossRef]
- Kang, H.S.; Min, C.K.; Heo, H.; Kim, C.; Yang, H.; Kim, G.; Nam, I.; Baek, S.Y.; Choi, H.J.; Mun, G.; et al. Hard X-ray free-electron laser with femtosecond-scale timing jitter. Nat. Photonics 2017, 11, 708–713. [Google Scholar] [CrossRef]
- Ko, I.; Kang, H.S.; Heo, H.; Kim, C.; Kim, G.; Min, C.K.; Yang, H.; Baek, S.; Choi, H.J.; Mun, G.; et al. Construction and commissioning of PAL-XFEL facility. Appl. Sci. 2017, 7, 479. [Google Scholar] [CrossRef]
- Weise, H.; Decking, W. Commissioning and first lasing of the European XFEL. In Proceedings of the 38th International Free-Electron Laser Conference; JACoW Publishing: Santa Fe, NM, USA, 2017; pp. 9–13. [Google Scholar] [CrossRef]
- Tanaka, T. Proposal for a pulse-compression scheme in X-ray free-electron lasers to generate a multiterawatt, attosecond X-ray pulse. Phys. Rev. Lett. 2013, 110, 084801. [Google Scholar] [CrossRef]
- Prat, E.; Reiche, S. Simple method to generate terawatt-attosecond X-ray free-electron-laser pulses. Phys. Rev. Lett. 2015, 114, 244801. [Google Scholar] [CrossRef]
- Prat, E.; Löhl, F.; Reiche, S. Efficient generation of short and high-power X-ray free-electron-laser pulses based on superradiance with a transversely tilted beam. Phys. Rev. Spec. Top. Accel. Beams 2015, 18, 100701. [Google Scholar] [CrossRef]
- Emma, C.; Fang, K.; Wu, J.; Pellegrini, C. High efficiency, multiterawatt X-ray free electron lasers. Phys. Rev. Accel. Beams 2016, 19, 020705. [Google Scholar] [CrossRef]
- Freund, H.P.; van der Slot, P.J.M. Studies of a terawatt X-ray free-electron laser. New J. Phys. 2018, 20. [Google Scholar] [CrossRef]
- Shim, C.H.; Parc, Y.W.; Kumar, S.; Ko, I.S.; Kim, D.E. Isolated terawatt attosecond hard X-ray pulse generated from single current spike. Sci. Rep. 2018, 8, 7463. [Google Scholar] [CrossRef]
- Lindberg, R.R.; Kim, K.J. Mode growth and competition in the X-ray free-electron laser oscillator start-up from noise. Phys. Rev. Spec. Top. Accel. Beams 2009, 12, 070702. [Google Scholar] [CrossRef]
- Kim, K.J.; Shvyd’ko, Y.V. Tunable optical cavity for an X-ray free-electron-laser oscillator. Phys. Rev. Spec. Top. Accel. Beams 2009, 12, 030703. [Google Scholar] [CrossRef]
- Lindberg, R.R.; Kim, K.J.; Shvyd’ko, Y.V.; Fawley, W.M. Performance of the X-ray free-electron laser oscillator with crystal cavity. Phys. Rev. Spec. Top. Accel. Beams 2011, 14, 010701. [Google Scholar] [CrossRef]
- Kim, K.J.; Shvyd’ko, Y.V.; Lindberg, R.R. An X-ray free-electron laser oscillator for record high spectral purity, brightness, and stability. Synchrotron Radiat. News 2012, 25, 25–31. [Google Scholar] [CrossRef]
- Kim, K.J. A harmonic X-ray FEL oscillator. In High-Brightness Sources and Light-Driven Interactions; OSA: Washington, DC, USA, 2016; p. ES2A.2. [Google Scholar] [CrossRef]
- Qin, W.; Huang, S.; Liu, K.X.; Kim, K.J.; Lindberg, R.R.; Ding, Y.; Huang, Z.; Maxwell, T.; Bane, K.; Marcus, G. Start-to-end simulations for an X-ray FEL oscillator at the LCLS-II and LCLS-II-HE. In Proceedings of the 38th International Free-Electron Laser Conference; JACoW Publishing: Santa Fe, NM, USA, 2017; pp. 247–250. [Google Scholar] [CrossRef]
- Shvyd’ko, Y.V.; Stoupin, S.; Cunsolo, A.; Said, A.H.; Huang, X. High-reflectivity high-resolution X-ray crystal optics with diamonds. Nat. Phys. 2010, 6, 196–199. [Google Scholar] [CrossRef]
- Shvyd’ko, Y.V.; Stoupin, S.; Blank, V.; Terentyev, S. Near-100% Bragg reflectivity of X-rays. Nat. Photonics 2011, 5, 539–542. [Google Scholar] [CrossRef]
- Shvyd’ko, Y.V. Feasibility of X-ray cavities for free electron laser oscillators. Beam Dyn. News Lett. 2013, 60, 68–83. [Google Scholar]
- Kolodziej, T.; Vodnala, P.; Terentyev, S.; Blank, V.; Shvyd’ko, Y.V. Diamond drumhead crystals for X-ray optics applications. J. Appl. Crystallogr. 2016, 49, 1240–1244. [Google Scholar] [CrossRef]
- Kolodziej, T.; Shvyd’ko, Y.V.; Shu, D.; Kearney, S.; Stoupin, S.; Liu, W.; Gog, T.; Walko, D.A.; Wang, J.; Said, A.; et al. High Bragg reflectivity of diamond crystals exposed to multi-kW/mm2 X-ray beams. J. Synchrotron Radiat. 2018, 25, 1022–1029. [Google Scholar] [CrossRef]
- LCLS-II Final Design Report; SLAC Pub LCLSII-1.1-DR-0251-R0. 2014; Available online: https://portal.slac.stanford.edu/sites/ad_public/people/galayda/Shared_Documents/FDR.pdf (accessed on 27 May 2021).
- Huang, Z.; Ruth, R.D. Fully coherent X-ray pulses from a regenerative-amplifier free-electron laser. Phys. Rev. Lett. 2006, 96, 144801. [Google Scholar] [CrossRef]
- Marcus, G.; Halavanau, A.; Huang, Z.; Krzywinski, J.; MacArthur, J.; Margraf, R.; Raubenheimer, T.; Zhu, D. Refractive guide switching a regenerative amplifier free-electron laser for high peak and average power hard X-rays. Phys. Rev. Lett. 2020, 125, 254801. [Google Scholar] [CrossRef]
- Snigirev, A.; Kohn, V.; Snigireva, I.; Lengeler, B. A compound refractive lens for focusing high-energy X-rays. Nature 1996, 384, 49–51. [Google Scholar] [CrossRef]
- Lengeler, B.; Schroer, C.; Tümmler, J.; Benner, B.; Richwin, M.; Snigirev, A.; Snigireva, I.; Drakopoulos, M. Imaging by parabolic refractive lenses in the hard X-ray range. J. Synchrotron Radiat. 1999, 6, 1153–1167. [Google Scholar] [CrossRef]
- Li, H.; Jia, Q. Commissioning and first lasing of the FELiChEM: A new IR and THz FEL oscillator in China. In Proceedings of the 39th International Free-Electron Laser Conferenc; JACoW Publishing: Hamburg, Germany, 2019; pp. 15–19. [Google Scholar] [CrossRef]
- Lee, T.Y. Storage ring based X-ray FEL oscillator. In Proceedings of the AIP Conference Proceedings 2054; AIP: Taipei, Taiwan, 2019; p. 030021. [Google Scholar] [CrossRef]
- Petrillo, V.; Opromolla, M.; Bacci, A.; Broggi, F.; Drebot, I.; Ghiringhelli, G.; Puppin, E.; Rossetti Conti, M.; Rossi, A.R.; Ruijter, M.; et al. Coherent, high repetition rate tender X-ray free-electron laser seeded by an extreme ultra-violet free-electron laser oscillator. New J. Phys. 2020, 22, 073058. [Google Scholar] [CrossRef]
- Yan, J.; Hao, H.; Huang, S.; Li, J.; Litvinenko, V.N.; Liu, P.; Mikhailov, S.F.; Popov, V.G.; Swift, G.; Vinokurov, N.A.; et al. Polarization control of a free-electron laser oscillator using helical undulators of opposite helicities. Phys. Rev. Accel. Beams 2020, 23, 060702. [Google Scholar] [CrossRef]
- Paraskaki, G.; Grattoni, V.; Lang, T.; Zemella, J.; Faatz, B.; Hillert, W. Optimization and stability of a high-gain harmonic generation seeded oscillator amplifier. Phys. Rev. Accel. Beams 2021, 24, 034801. [Google Scholar] [CrossRef]
- Campbell, L.T.; Freund, H.P.; Henderson, J.R.; McNeil, B.W.J.; Traczykowski, P.; van der Slot, P.J.M. Analysis of ultra-short bunches in free-electron lasers. New J. Phys. 2020, 22, 073031. [Google Scholar] [CrossRef]

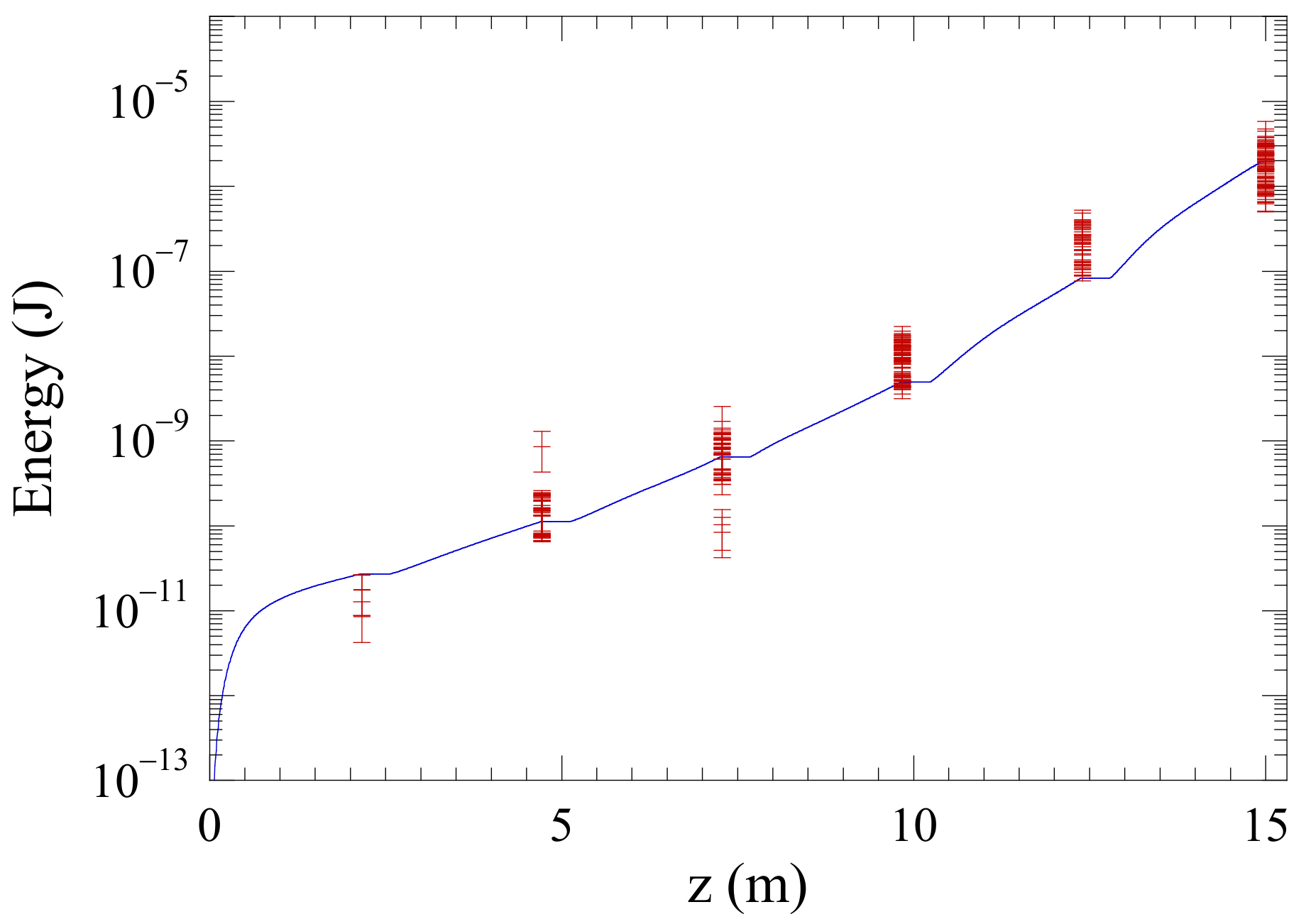
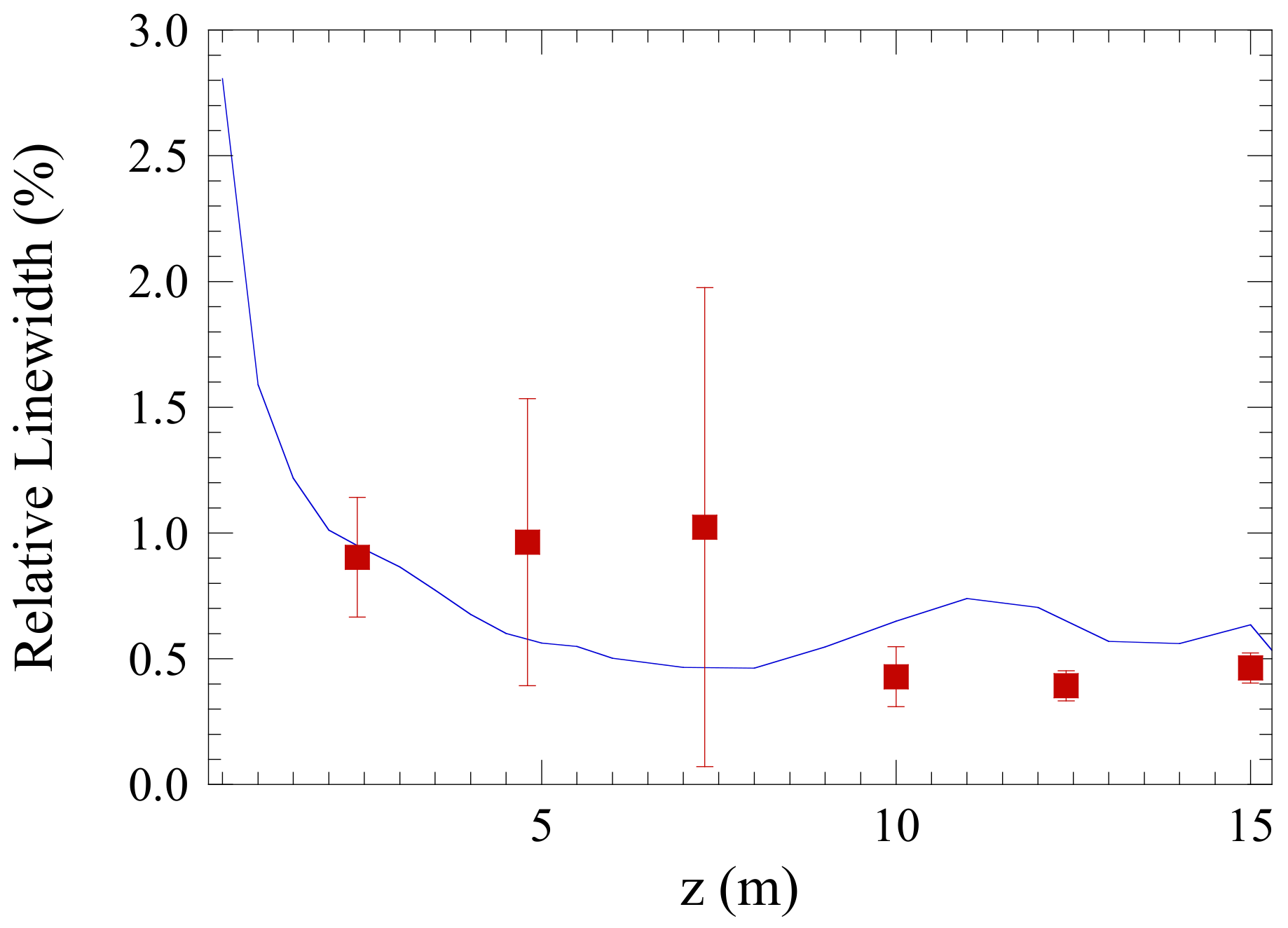
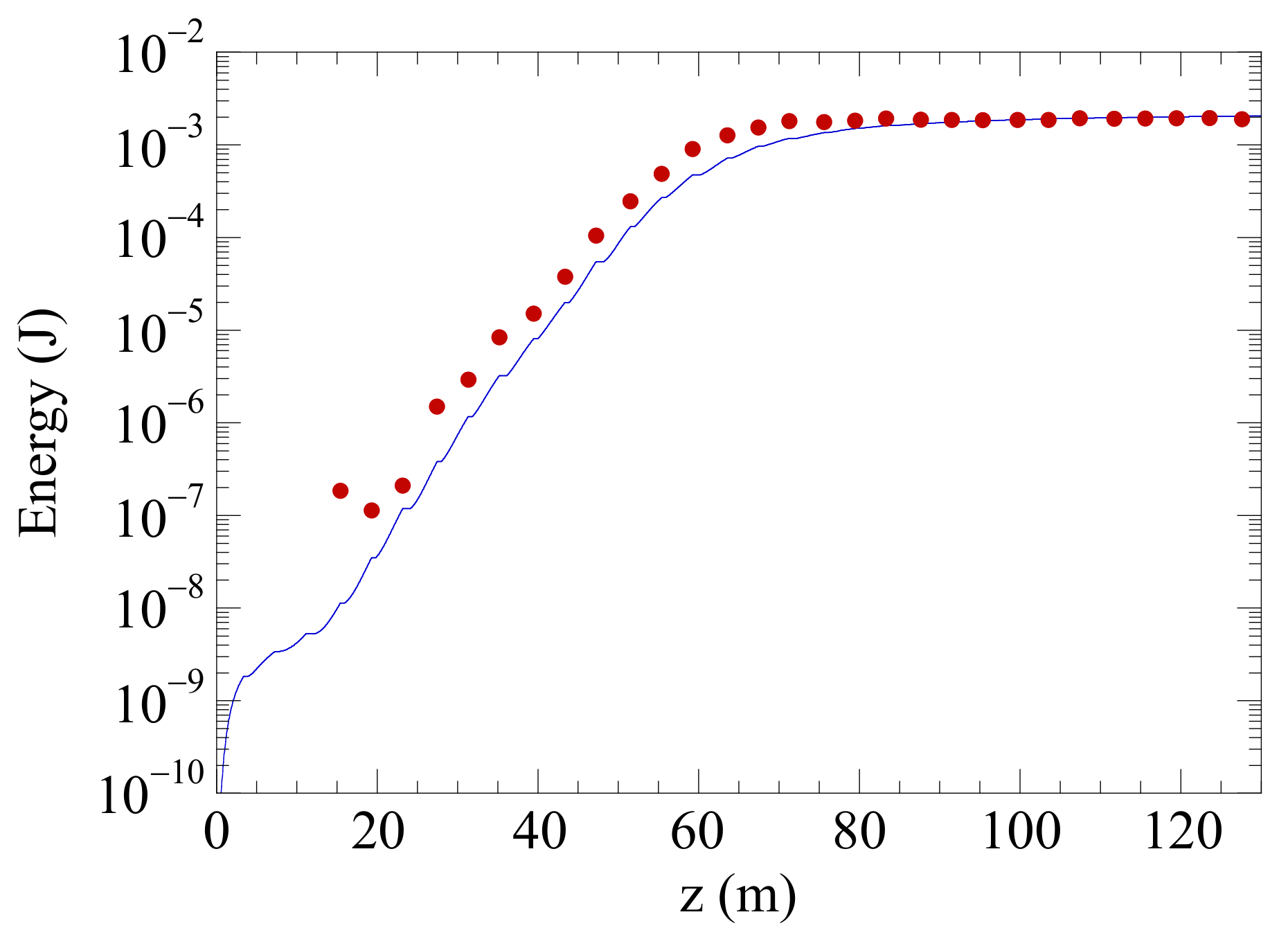
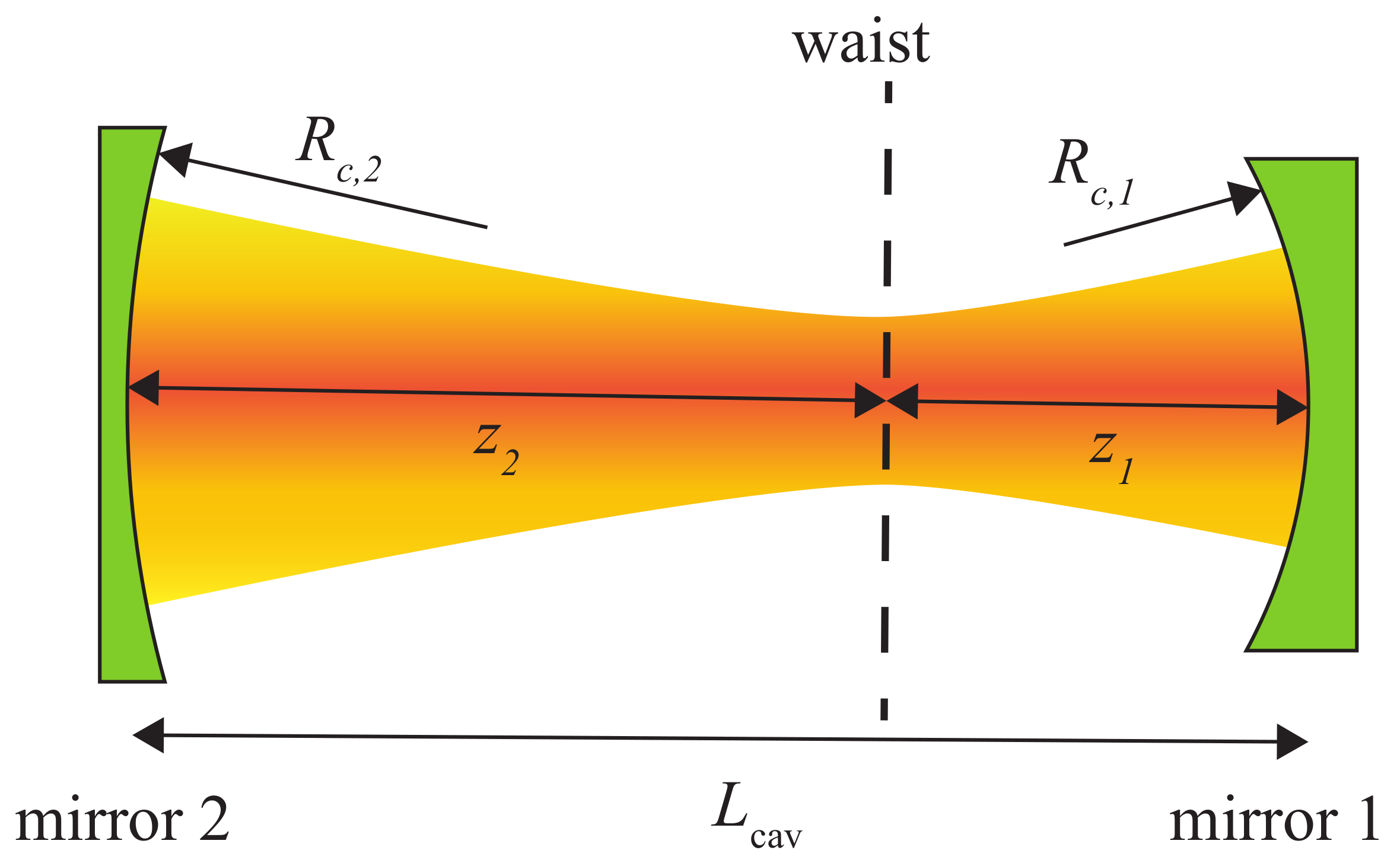
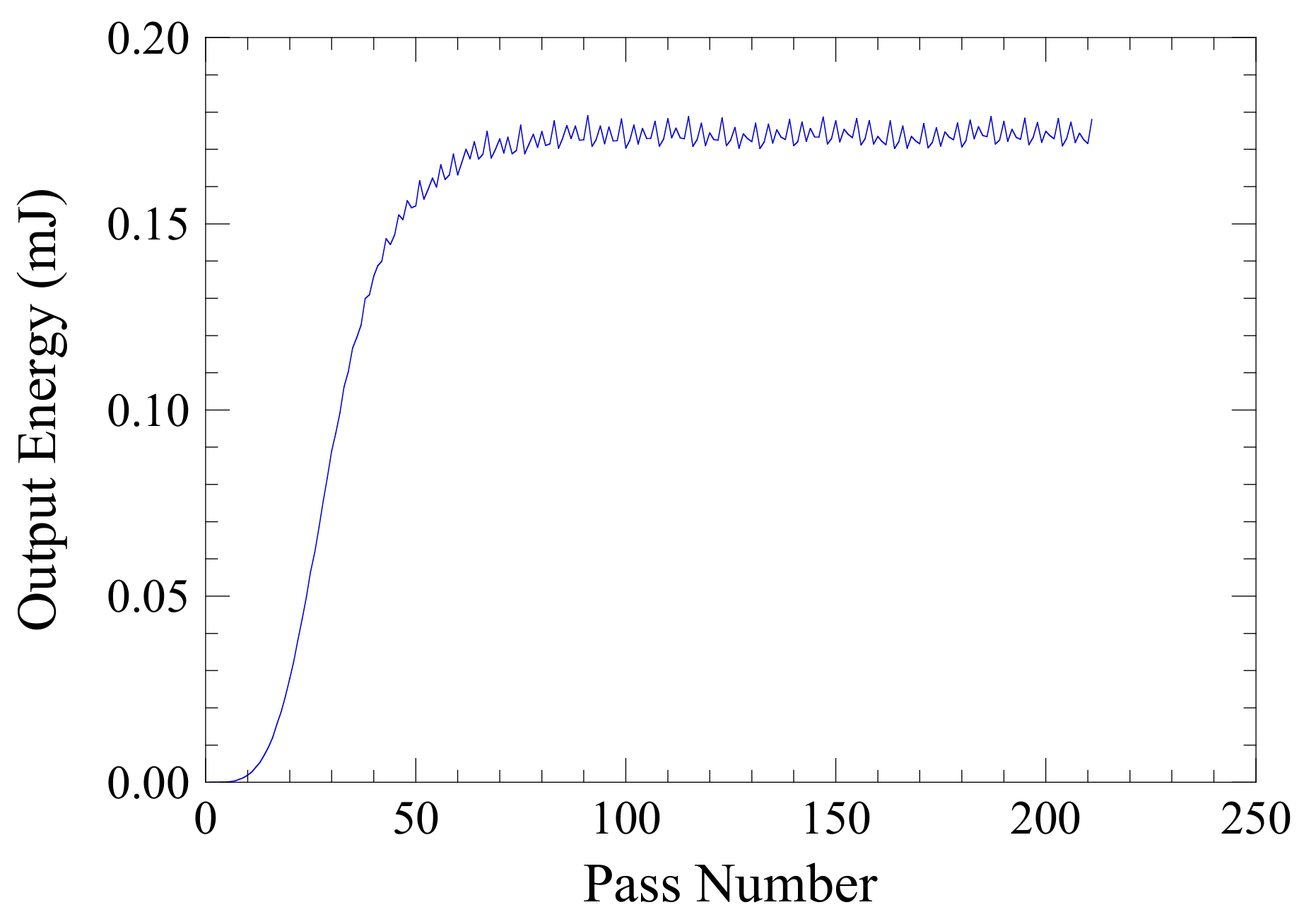
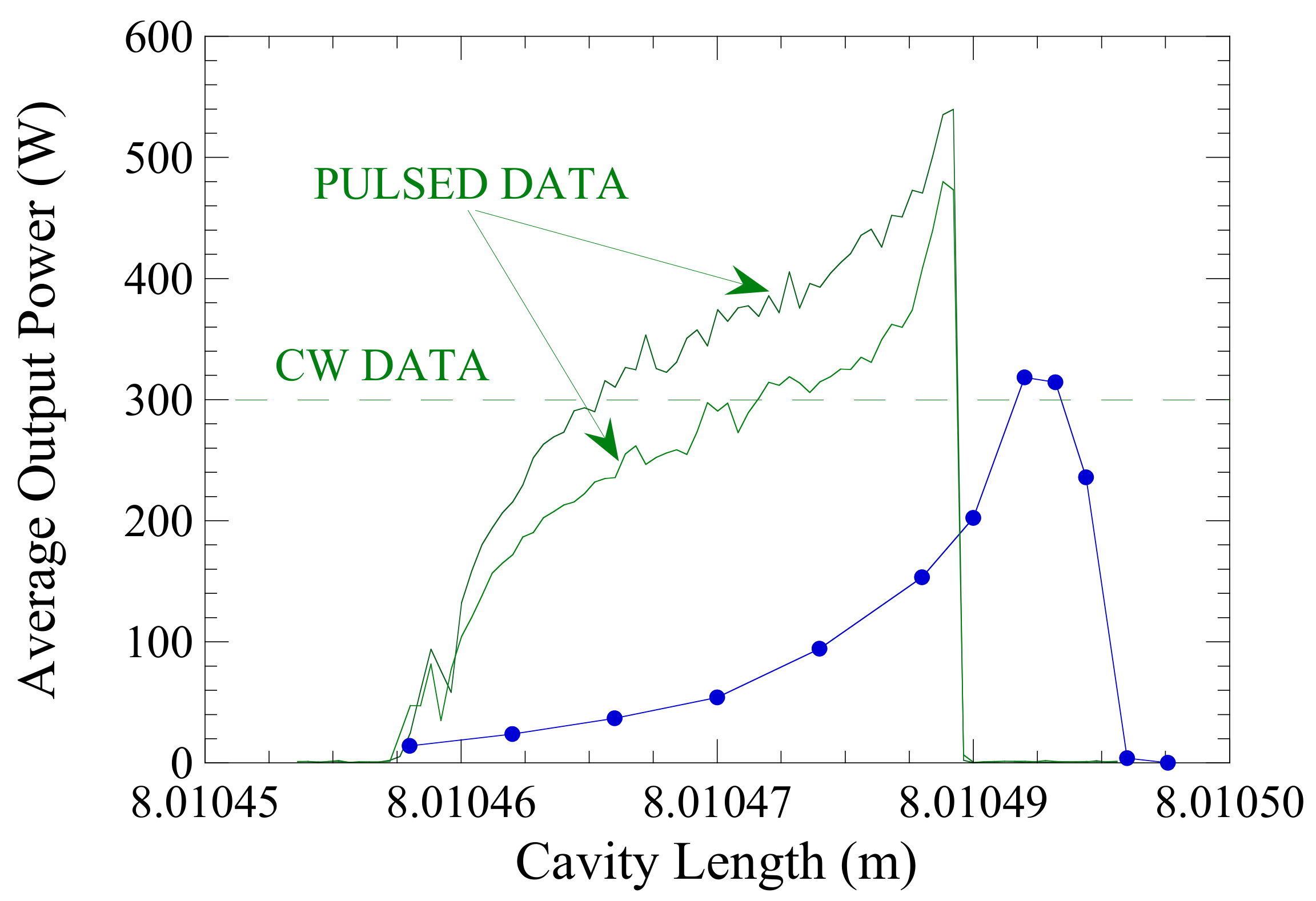
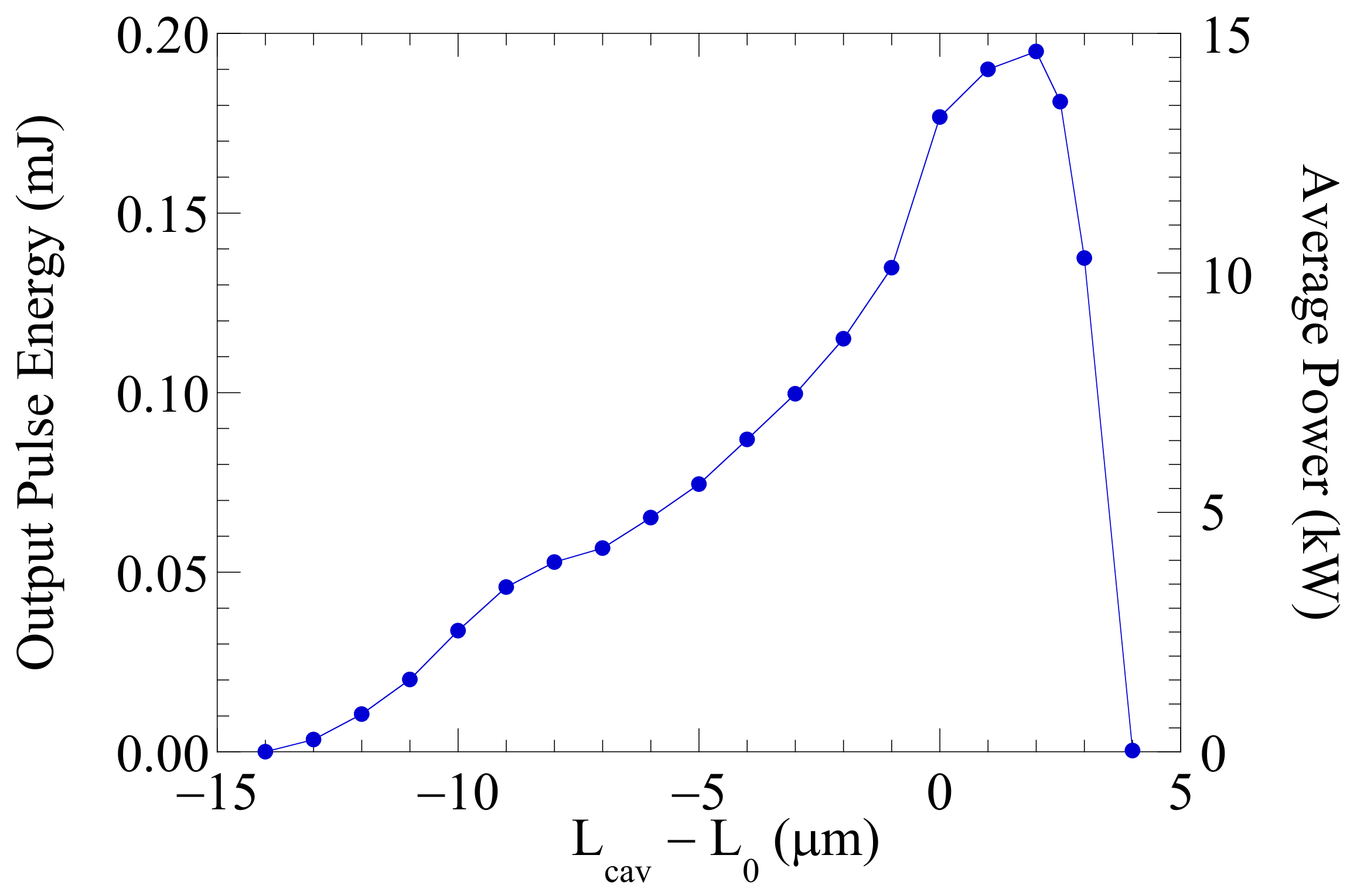
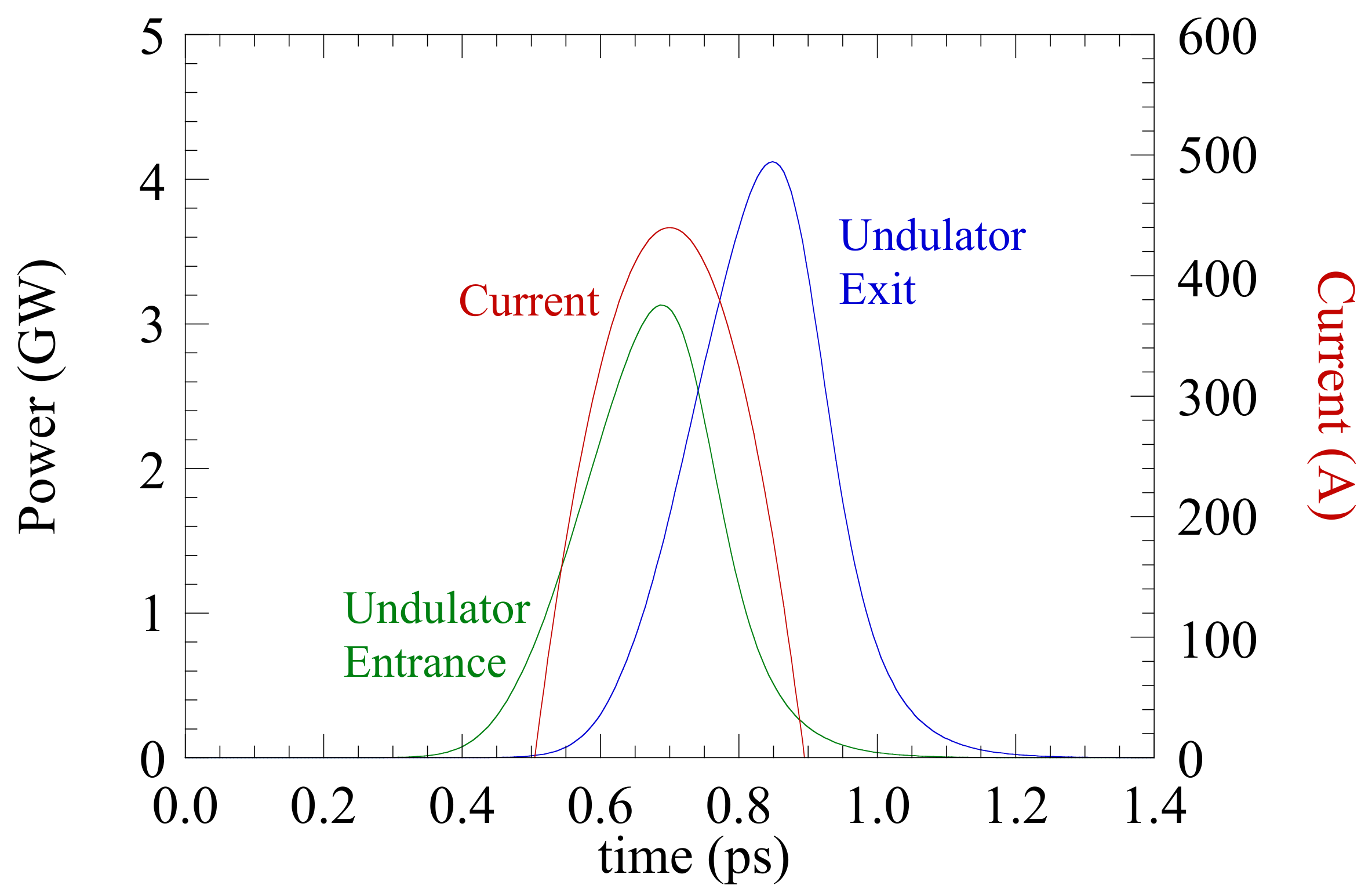
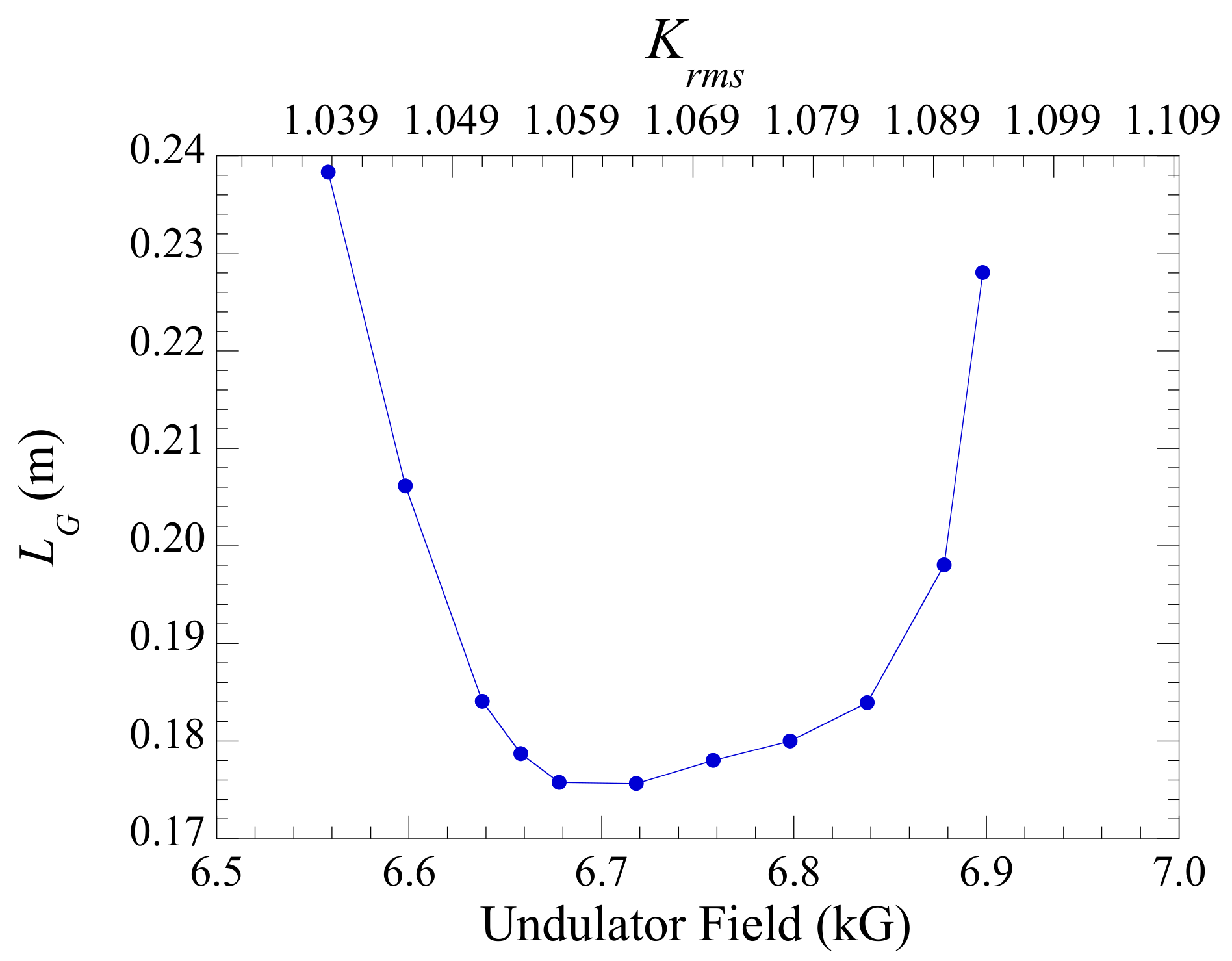
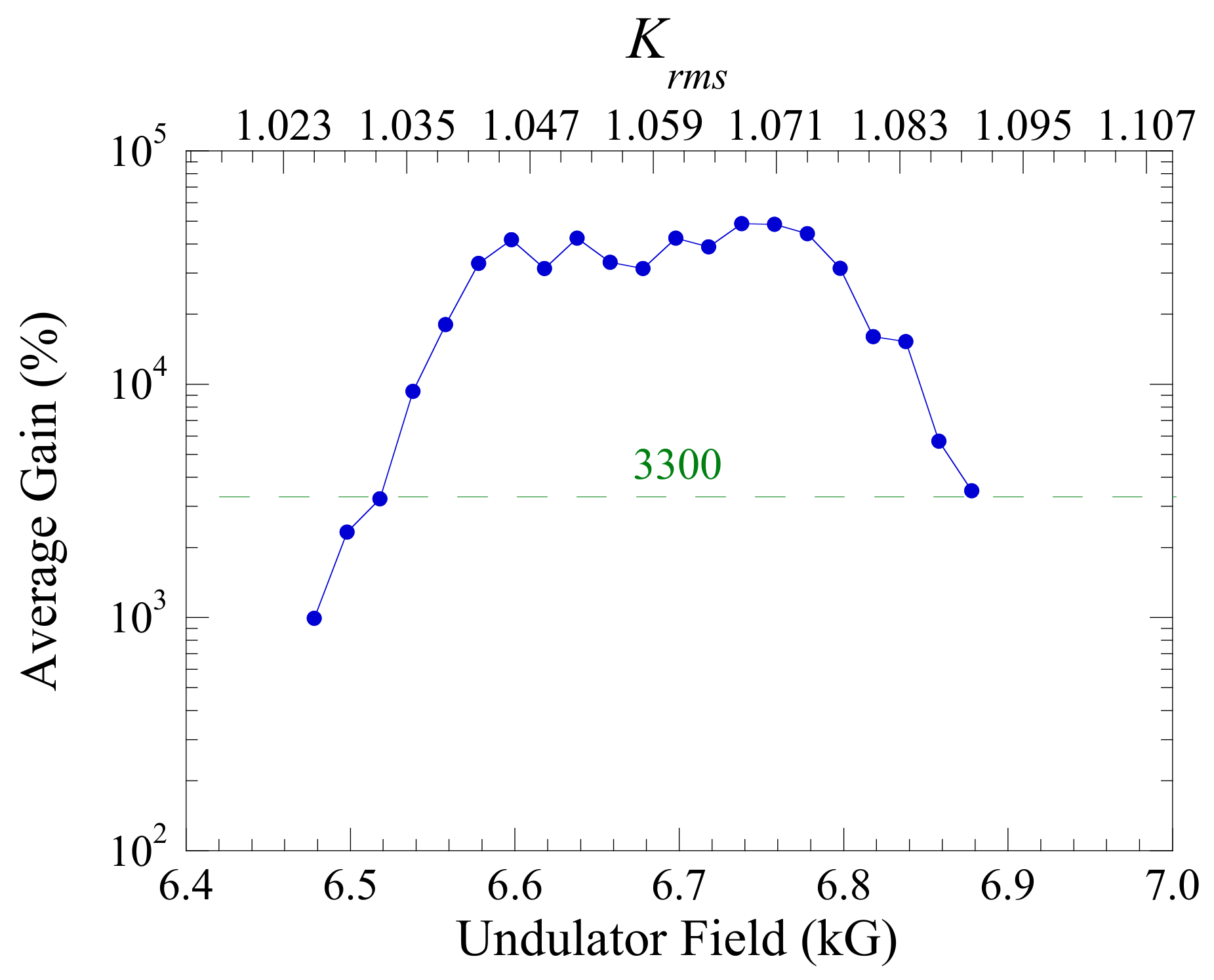
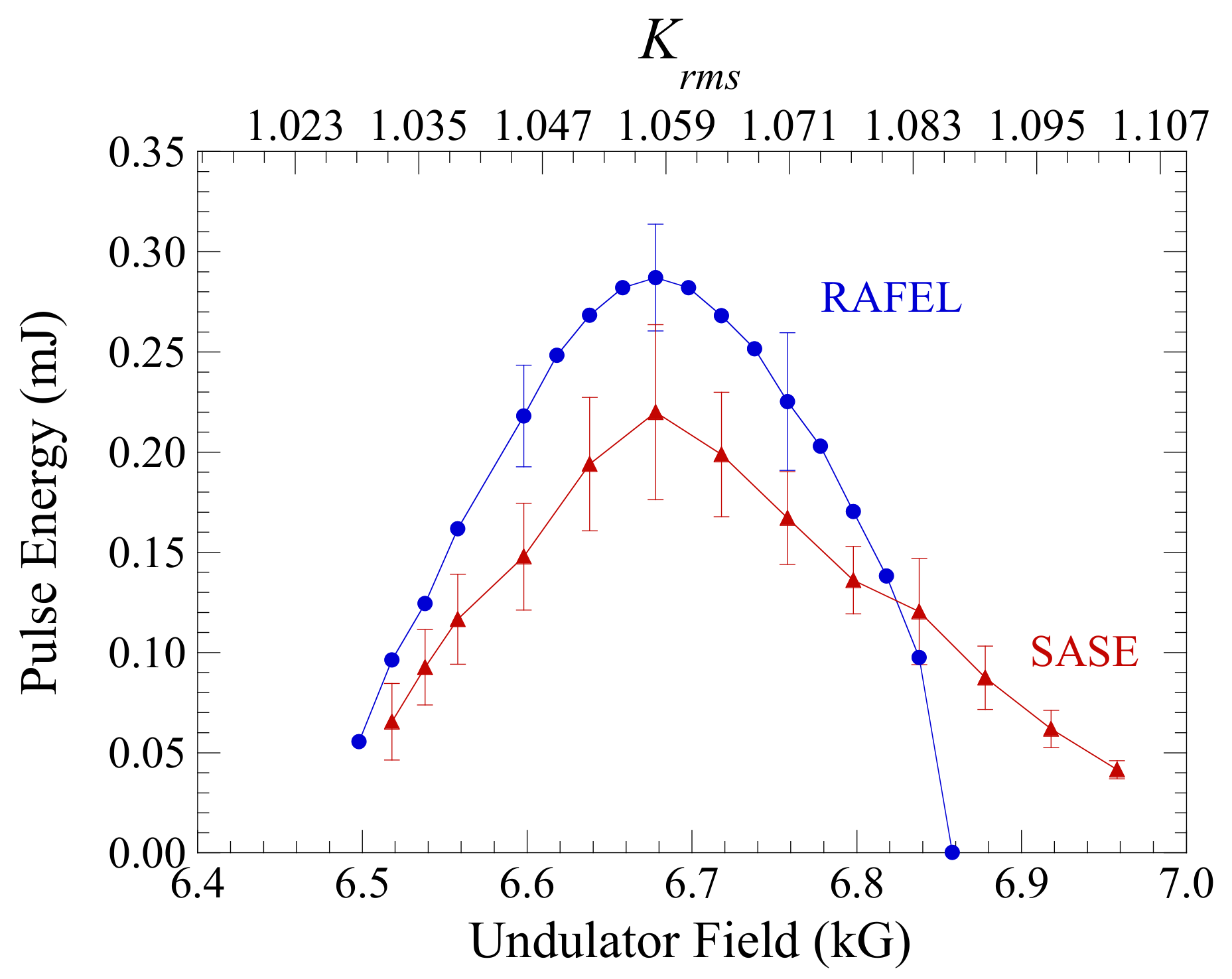
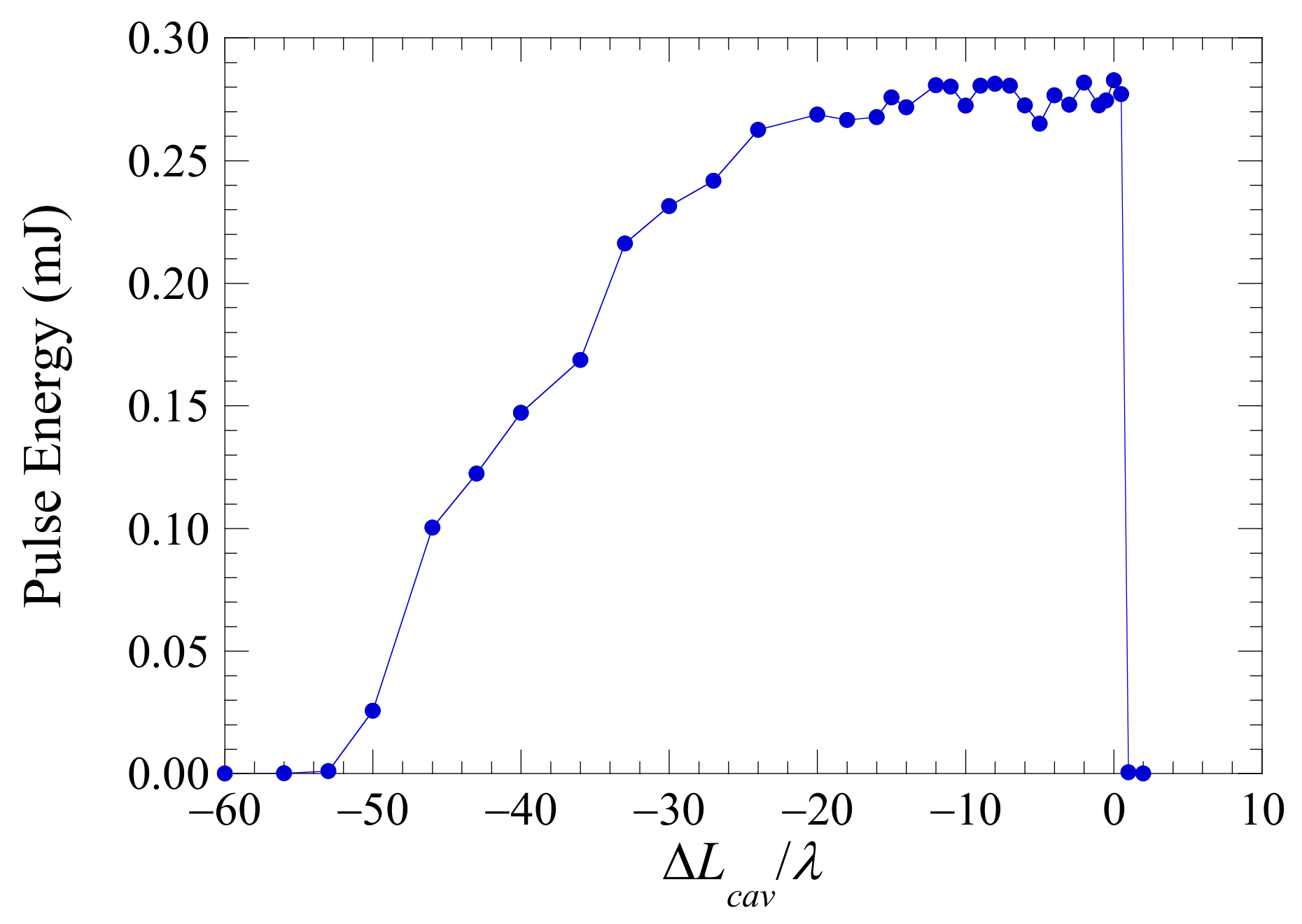
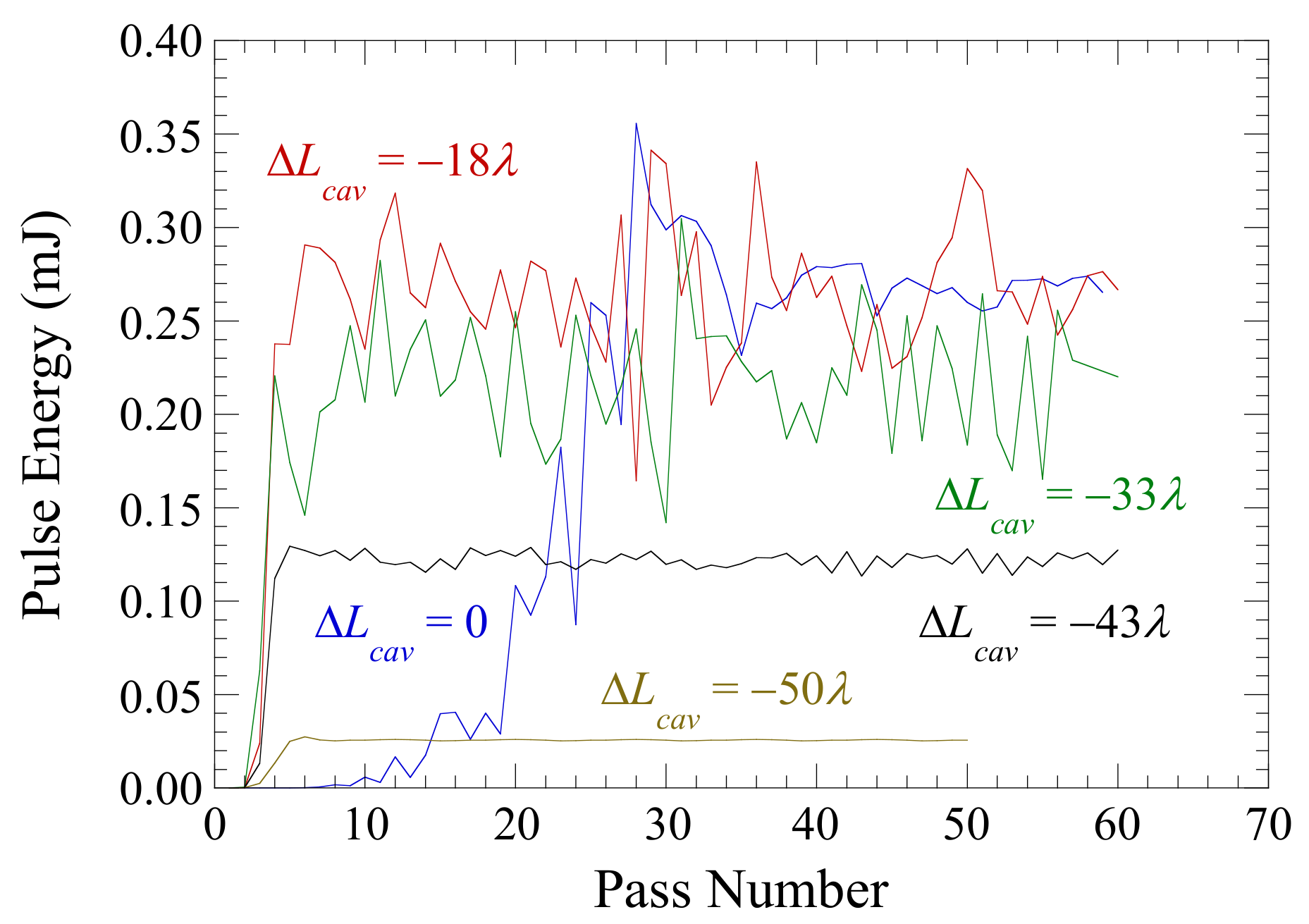
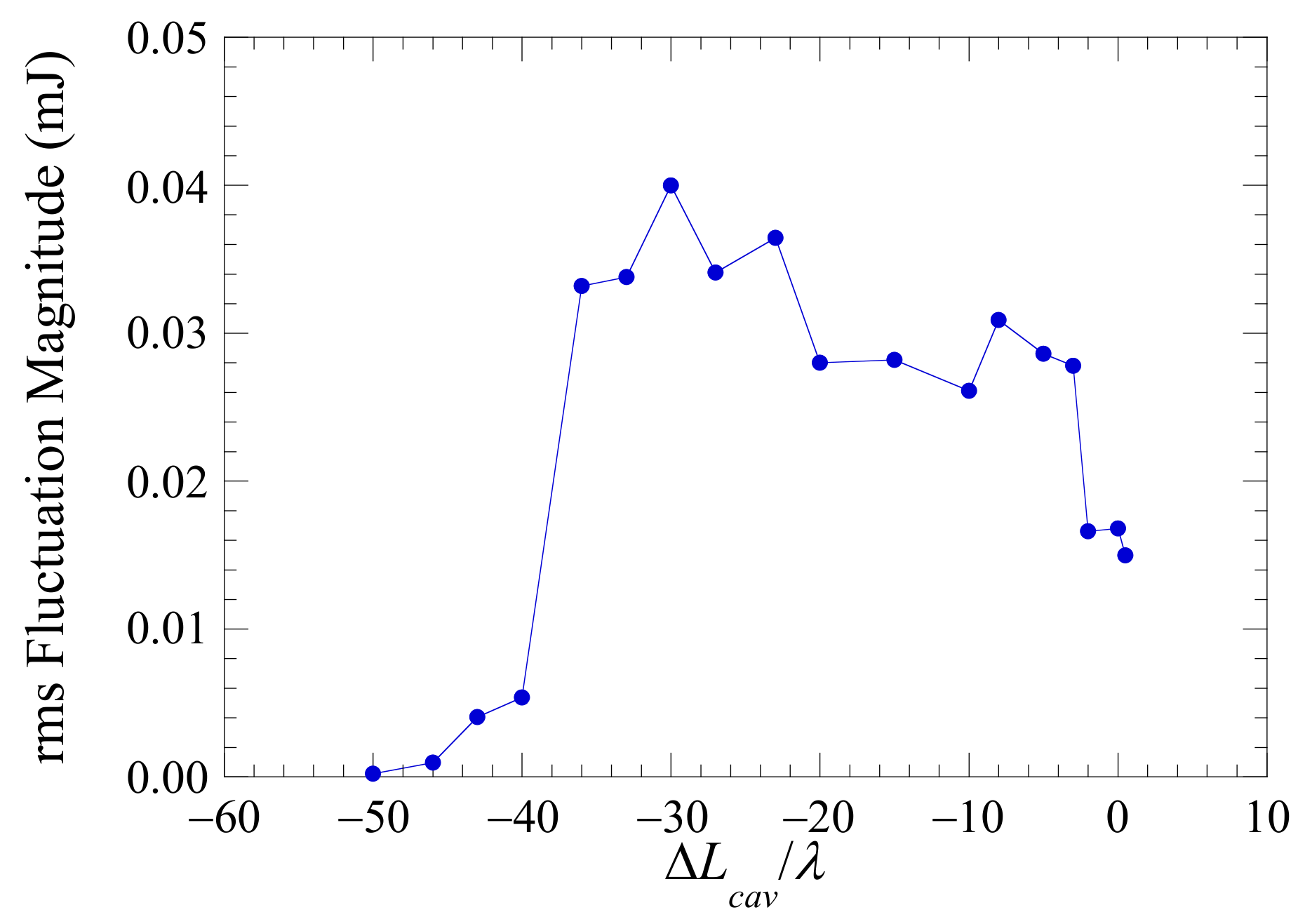
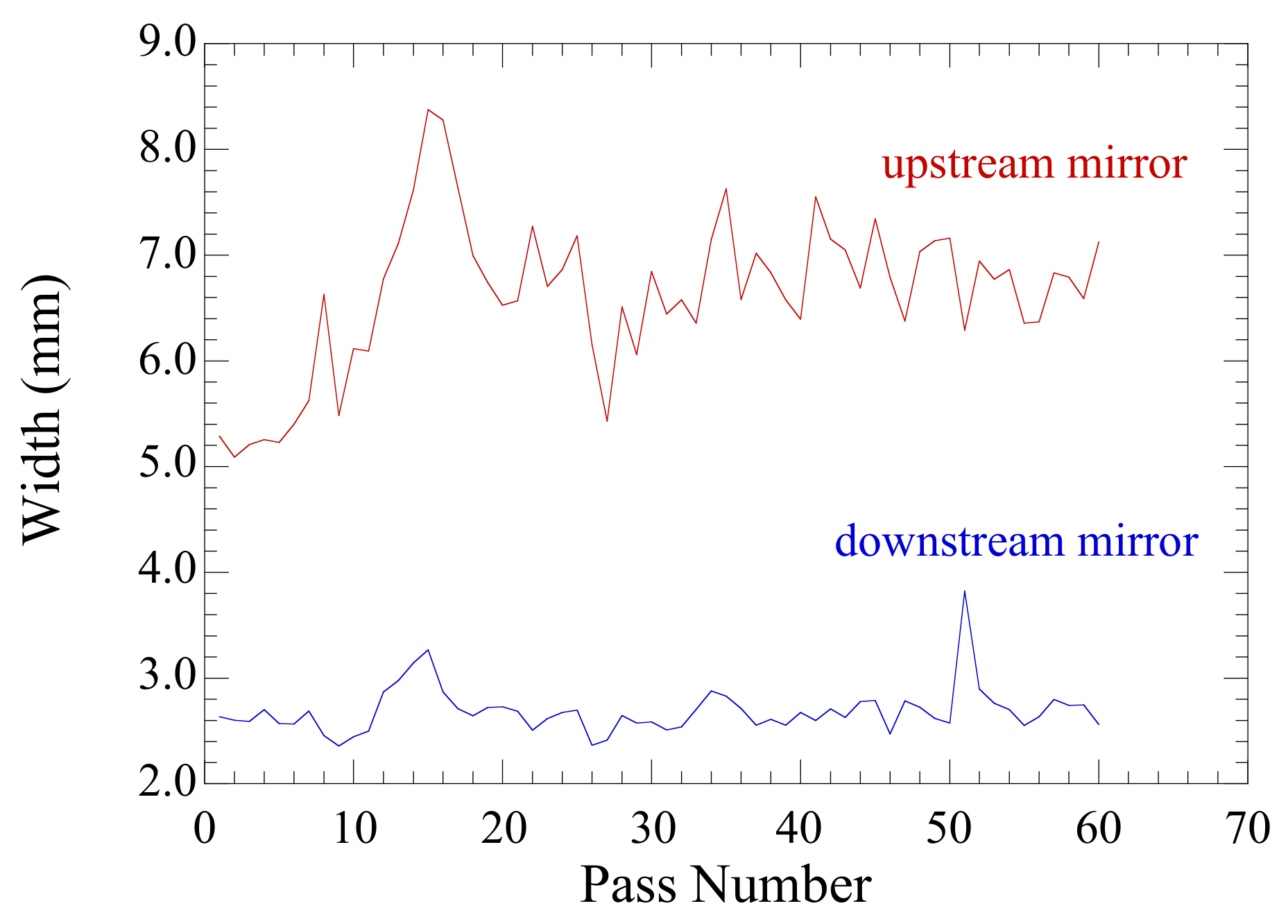
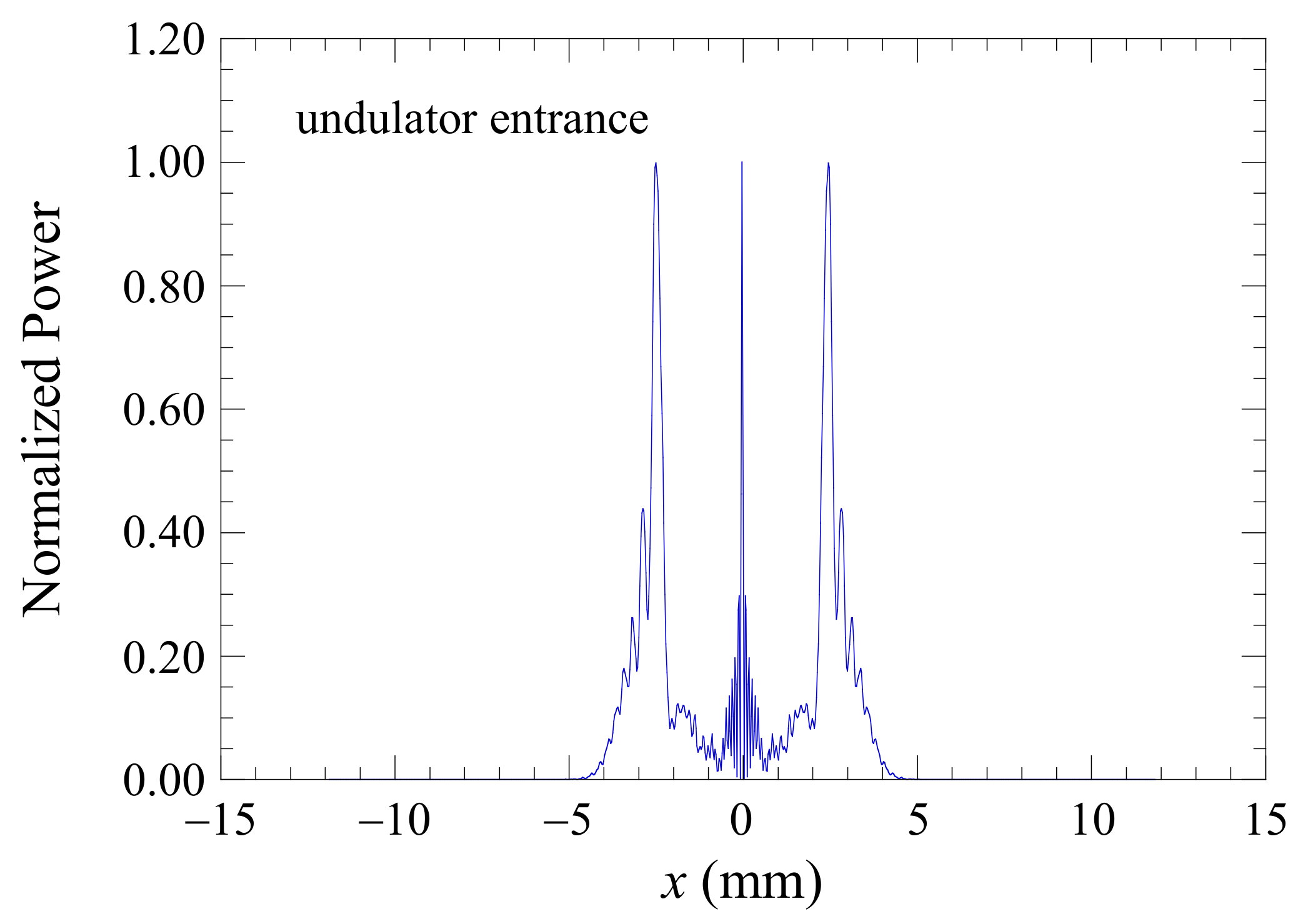

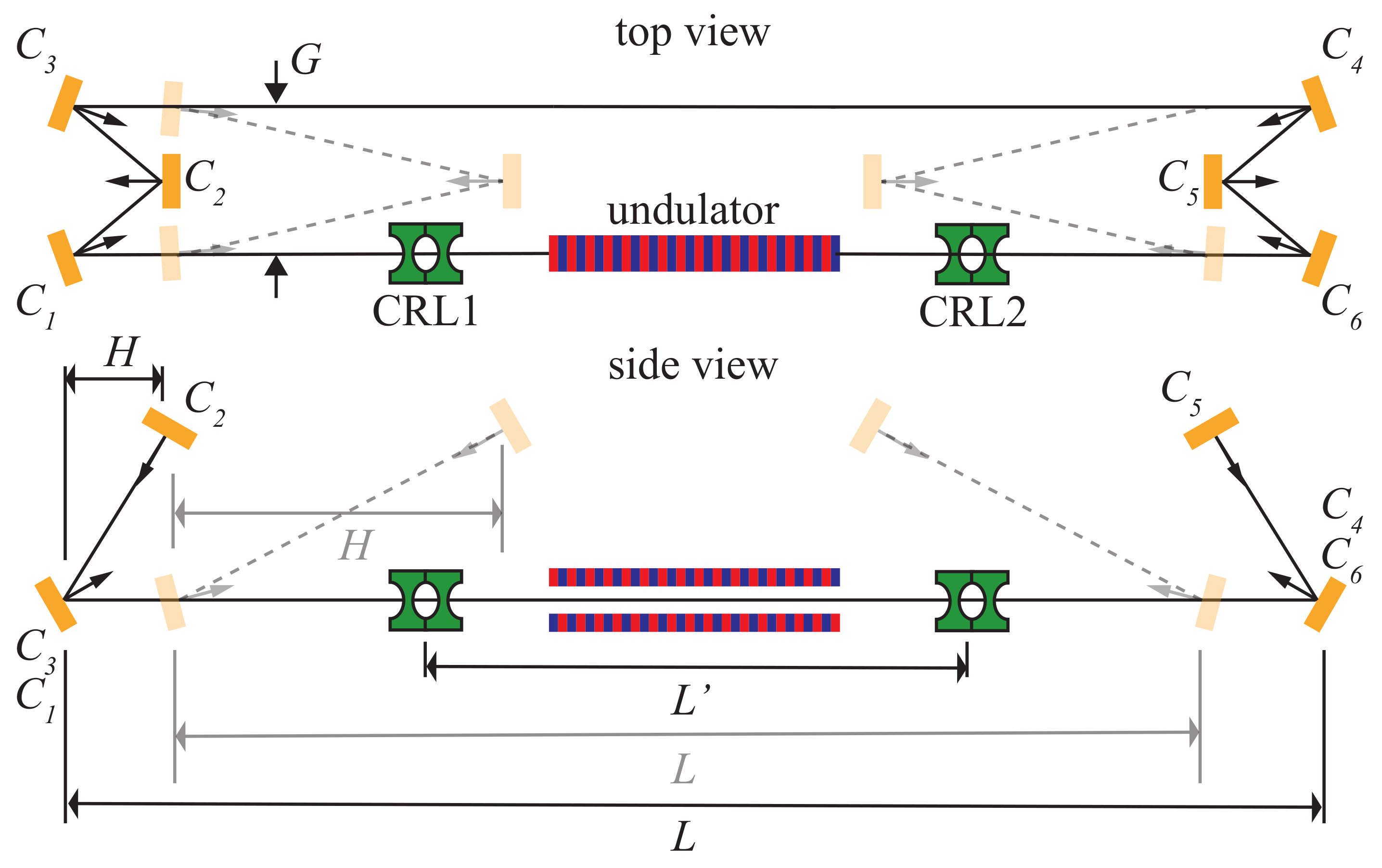


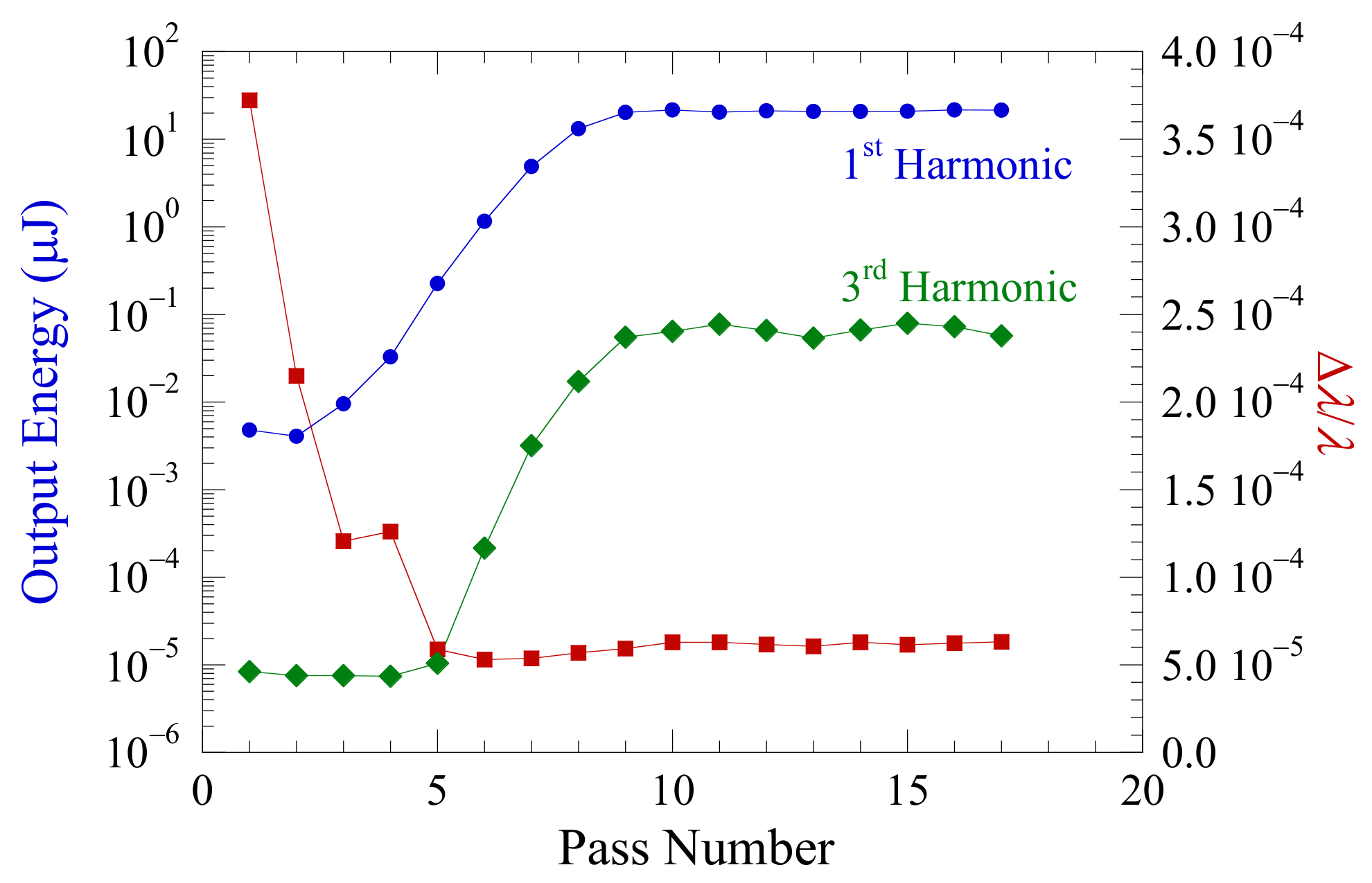
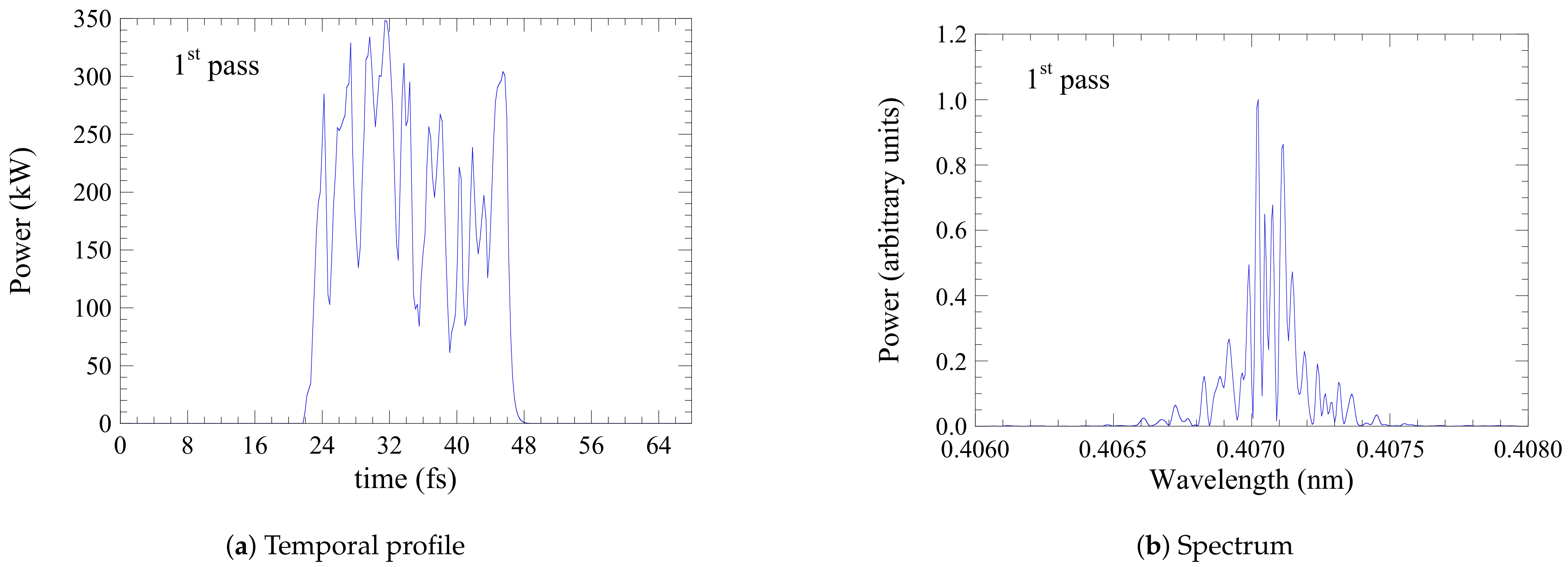
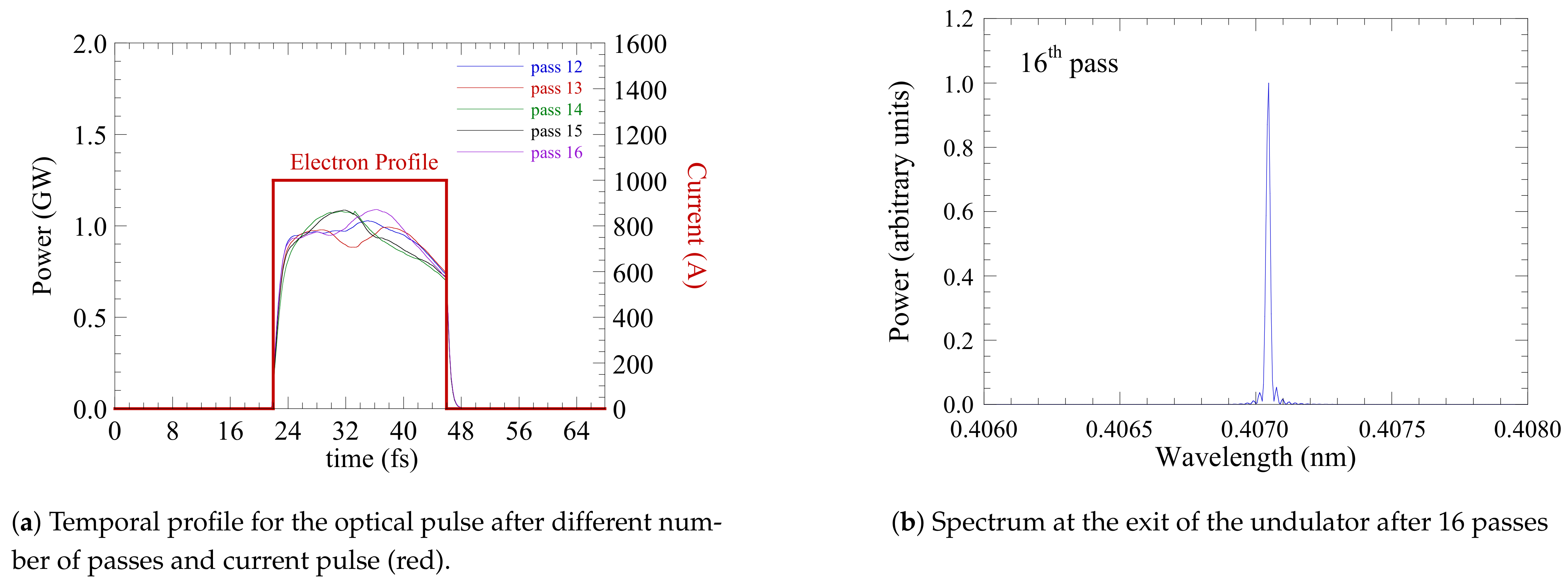
| Electron Beam | |||
| Energy | 55 | MeV | |
| Charge | 800 | pC | |
| Bunch duration | 1.2 | ps | parabolic |
| Repetition rate | 87.5 | MHz | |
| Normalized emittance | 15 | mm-mrad | |
| Energy spread | 0.25% | ||
| Matched beam radius | 392 | µm | |
| Undulator | two-plane focusing | ||
| Period | 2.4 | cm | |
| Magnitude | 6.5–7.0 | kG | |
| 1.03–1.11 | |||
| Length | 98 uniform | ||
| Resonator | Concentric | ||
| Wavelength | 2.2 | µm | |
| Length | 6.852 | m | |
| Radii of curvature | 3.5 | m | |
| Rayleigh range | 0.5 | m | |
| Hole radius | 5.0 | mm | |
| Out-coupling | 97% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
van der Slot, P.J.M.; Freund, H.P. Three-Dimensional, Time-Dependent Analysis of High- and Low-Q Free-Electron Laser Oscillators. Appl. Sci. 2021, 11, 4978. https://doi.org/10.3390/app11114978
van der Slot PJM, Freund HP. Three-Dimensional, Time-Dependent Analysis of High- and Low-Q Free-Electron Laser Oscillators. Applied Sciences. 2021; 11(11):4978. https://doi.org/10.3390/app11114978
Chicago/Turabian Stylevan der Slot, Peter J. M., and Henry P. Freund. 2021. "Three-Dimensional, Time-Dependent Analysis of High- and Low-Q Free-Electron Laser Oscillators" Applied Sciences 11, no. 11: 4978. https://doi.org/10.3390/app11114978
APA Stylevan der Slot, P. J. M., & Freund, H. P. (2021). Three-Dimensional, Time-Dependent Analysis of High- and Low-Q Free-Electron Laser Oscillators. Applied Sciences, 11(11), 4978. https://doi.org/10.3390/app11114978







