A Simplified Method for Assessing the Response of RC Frame Structures to Sudden Column Removal

Abstract

Column loss is a type of damage that can occur in frame structures subjected to explosions or impacts. The response of such structures largely depends on the capacity of the assembly of elements and on the inertia effects due to the sudden nature of the phenomenon. Frame structures are able to develop various resisting mechanisms that prevent the collapse to progress. The assessment of the robustness often requires complex and detailed numerical modelling. For the preliminary design of a robust frame, simplified methods to assess the effectiveness of the redistribution of the loads after the removal of a member are welcome. In the present paper, an approach based on the idealisation of the damaged structure into a single degree-of-freedom system with an elastic-plastic compliance law is proposed. The output of the method is the dynamic response of a target point, which can serve for assessing the residual safety of the structure. Comparing the obtained results with the outputs of a more sophisticated FE (Finite Elements) analysis, a satisfying accuracy is found.

1. Introduction

The effect of localised damage on frame structures is an open problem in structural engineering. Many studies on progressive collapse presuppose that an initial damage occurs on the structure. Various approaches can be followed to assess the damage tolerance of a structure [1,2]. Nonlinear analyses accounting for second-order effects and large displacements are usually adopted for assessing the robustness of the structure [3], which usually undergoes plastic deformations. The duration of the damage, that is, the triggering of the progressive collapse, can last from few milliseconds, in case of an explosion, to several years, say, in the case of chemical corrosion.

Sudden column loss is a dynamic removal phenomenon that can emerge right after explosions or impacts. The response of a structure to sudden column loss can be numerically simulated by adding an extra downward load, accounting for the removed element, to the remaining building [4,5,6,7]. From a dynamical point of view, it was found that column removal time is insignificant for rise time smaller than 10 ms [8,9,10], that is, it can be considered instantaneous. Similarly, it was found both that a rise time smaller than 1/10 of the vibration period of the structure does not affect its dynamic response [11,12]. Thus, the response to sudden load application represents an upper bound in terms of displacements [13]. The study of the behaviour of frame structures under such type of events may require sophisticated numerical analysis accounting for material and geometric non-linearities.

As proved by the large literature available on the topic, many issues are still open and simple rules to design a robust structure are hard to find. This paper deals with a simplified approach to obtain the maximum dynamic displacement of a reinforced concrete frame structure subjected to sudden column removal. The behaviour of such structures is non-trivial since the resisting mechanisms that arise in a damaged frame structure are various and have been recently addressed by experimental [14,15,16,17] and numerical papers [18,19,20,21]. Compressive arch action provides an additional capacity to the flexural mechanism at small deformations, while catenary effects activate for large deformation, preventing the collapse to progress. The proposed methods consists in two tools. The former refers to the possibility to create a synthetic model that simulates the behaviour of the frame subjected to the damage. The structure can be modelled through an equivalent single degree of freedom (SDOF) system [22,23] since its response to a sudden load mainly depends on its vertical vibration mode. The latter accounts for the fact that the application of a dynamic load produces a response in term of displacement, say $u_{dyn}$, that is larger than the one that can be obtained applying the same force in a quasi-static loading process, $u_{st}$ [24]. To study such effect, the dynamic amplification factor (DAF) is adopted as a metrics of the dynamic effect, that is,

$$\mathrm{D}\mathrm{A}\mathrm{F}=\frac{u_{dyn}}{u_{st}}.$$

(1)

The value of the parameter is largely dependent on the rise time [25]; in elastic systems subjected to a step load the DAF is equal to 2. On the contrary, the value can be larger in inelastic systems [26,27,28].

In the following, the basics of the modeling of column loss are presented and the synthetic SDOF system is described (Section 2. Thanks to the dimensional analysis approach, the relevant quantities that affect the response of the system to the damage are defined. The simplified approach for the analysis of the damaged frame is then detailed (Section 3). An example on a three storey-four column RC frame is proposed (Section 4) and the accuracy of the results is discussed (Section 5).

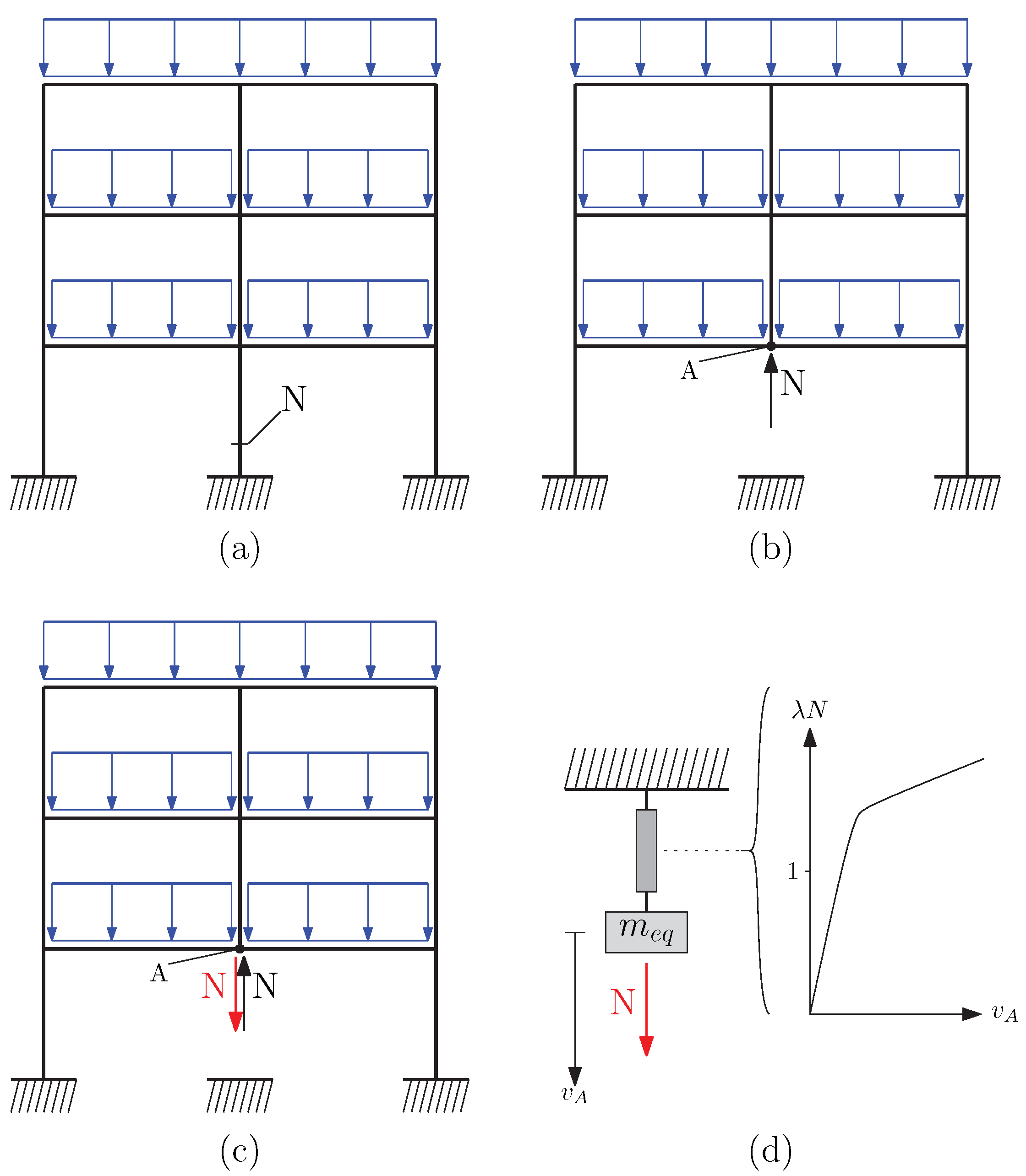
2. Modelling Sudden Column Removal on Frame structures

This section deals with the modelling of column removal. Among the various approaches proposed in the literature [12,29], a simple model consisting of the summation of reaction forces is proposed for the present study. The approach, recalled from a previous publication of the authors [1], consists in three steps as sketched in Figure 1. As soon as the removed element is identified, the internal forces within the element are evaluated through a linear analysis of the undamaged loaded structure, as it behaves elastically during the majority of its expected life. For sake of simplicity, let us suppose that only axial compression force acts in the column, thus the normal force N is evaluated, see Figure 1a. Then, the selected element is removed and a nodal force, namely a replacement force, is applied at the top end of the column, that is, at the control node A. The force is equal (but opposite) to the internal force computed the the previous step, Figure 1b. This modification does not vary the structural response of the frame since the solution can be superimposed on linear elastic systems. Finally, in the last step, a sudden downward force of magnitude equal to N, is applied at the node and the nonlinear dynamic response of the system is measured, Figure 1c. The response of the frame structure under the sudden downward force can be studied through various numerical techniques [30].

Among the possible displacements of the control node A, with the aim of simplified analysis, the vertical downward displacement is concerned, only. Thus, the behaviour of the frame structure in the last step of the analysis previously illustrated can be described by means of an equivalent single degree of freedom system, as depicted in Figure 1d. The behaviour of the connector relates to the structural behaviour of the frame along the vertical direction once subjected to a downward vertical force at the control node A. Thus, connector law is determined by performing a nonlinear static incremental analysis on the frame subjected to an increasing vertical force applied at the control node. Referring to Figure 1c, this results in an incremental analysis with a load multiplier parameter $\lambda$ applied to the red vertical downwards force N. It is important to note that, when the incremental analysis is performed, the black upwards N force is still acting on the frame.

As a result, for $\lambda =1$ the reaction force of the removed column and the applied force are equal and opposite, thus the effect of the former is null, resulting in the complete removal of the column. In the incremental analysis, all the resisting mechanisms of a statically indeterminate structure, say the alternate load path due to the redistribution of the loads across the members [31], rise. The resulting $\lambda$-v curve, Figure 1d, would highlight the presence of an initial elastic stage into which all the members are subjected to allowable stresses. For a given load multiplier ($\lambda \ge 1$) plastic hinges would form and an overall hardening-like phase would be observed on the compliance law. The analysis should extend to the maximum allowable displacement, or to the overall failure of the frame.

2.1. Maximum Dynamic Response of the System

From the previous considerations, it results that the dynamic response of the system can be studied through the synthetic system. To study the effect of the connector law, the general dynamics of a system consisting of a mass m connected to a fixed support through a device with a nonlinear behaviour (Figure 2) is briefly illustrated. The system is subjected to a sudden force f. The derivation of the solution of the dynamic equilibrium equation of each phase is reported in Appendix A. It is supposed that the damping is null since it has been proved that it does not influences the maximum response of the damaged system [32].

The nonlinear connector has an elastic-plastic behaviour. This is the simplest, but most recurrent, trend that can be observed in the incremental analysis previously described. Recalling the classical notations of structural mechanics, the following stages result in a suddenly loaded system (Figure 3):

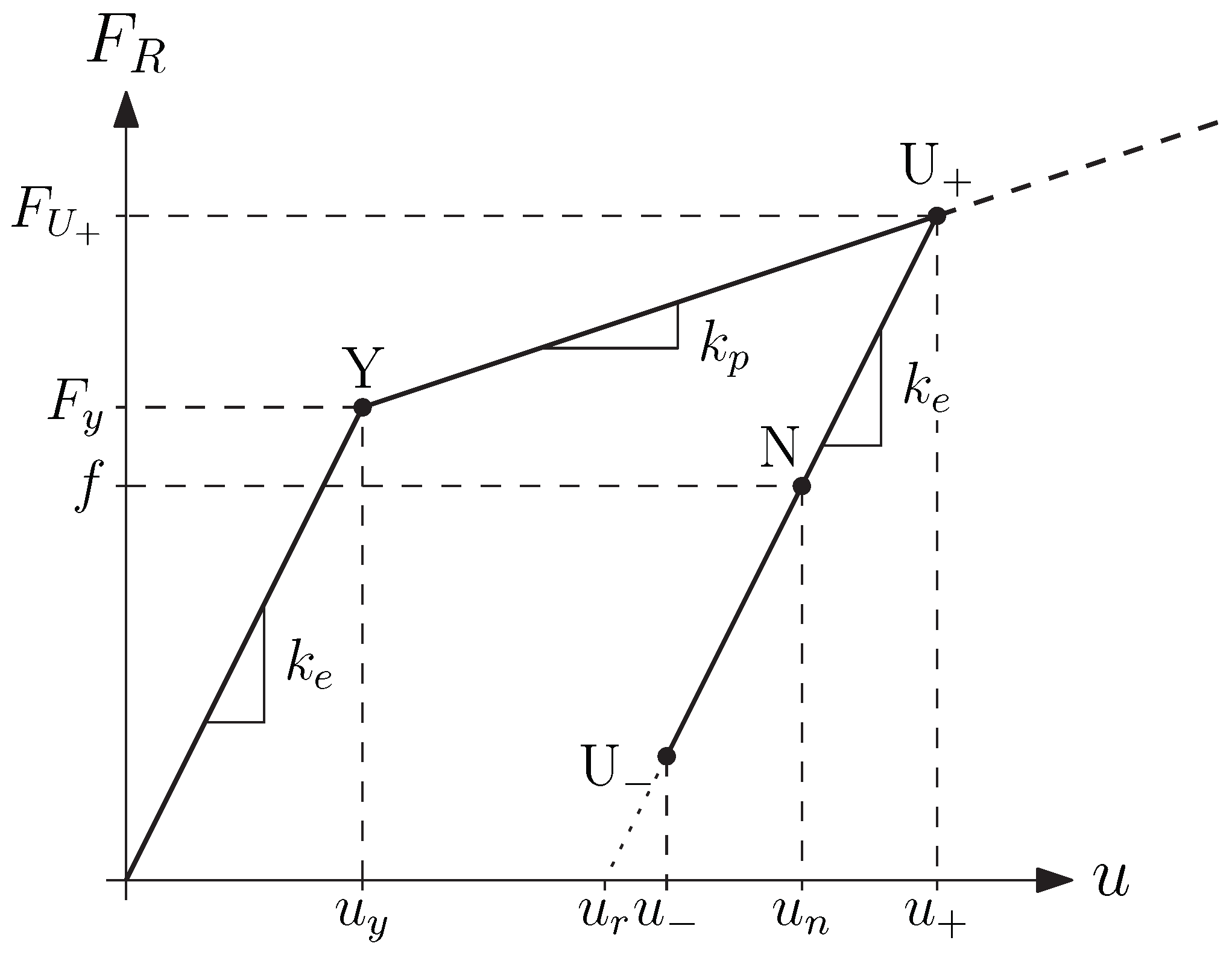
• a linear elastic phase with tangent stiffness $k_e$. This phase ends at a yielding force $F_y$, corresponding to a displacement $u_y=F_y/k_e$;
• a hardening phase with plasticity. The tangent stiffness of this phase has tangent stiffness $k_p$. The system increases its displacement up to $u_{+}$, when its velocity is null;
• the unloading follows a linear elastic law with tangent stiffness equal to $k_e$.

If undamped, the system oscillates around and equilibrium position $u_n$.

2.2. Dimensional Analysis for the Dynamic Phase of the Sudden Damage

Many quantities determine the behaviour of the previously described SDOF system. With the aim to study the effects of the connector law on the dynamic response, a general approach is required. The main variable of interest is represented by the maximum elongation of the device, that is, the maximum vertical displacement in the frame structure subjected to the sudden column removal. This quantity was previously identified as $u_{+}$ and can be considered in engineering terms as the dynamic response of the system subjected to a sudden load. For this reason, in the following, this term is recalled as $u_{dyn}=u_{+}$.

The value of $u_{dyn}$ depends on many parameters: the yielding force, $F_y$, the applied force, f, the mass, m, the tangent stiffnesses of the elastic, $k_e$, and the plastic with hardening, $k_p$, rules. In general, $u_{dyn}$ can be written as

$$u_{dyn}=\phi \left(F_y,f,m,k_e,k_p\right),$$

(2)

where $\phi \left(·\right)$ is the solution of the dynamic problem illustrated in the appendix. A dimensional analysis approach was adopted to investigate the influence of the parameters on the maximum displacement. This technique is a mathematical tool that serves for identifying the relationships that describe the physical phenomena [33]. With respect to the previous Equation (2), $u_{dyn}$ represents the dependent variable, while the remaining are the independent terms. Following the principle of dimensional homogeneity, Equation (2) can be rewritten using Buckingham’s $\mathrm{\Pi }$-theorem [34,35]. Three base dimensions, that is, the length $\left[L\right]$, the mass $\left[M\right]$ and the time $\left[T\right]$ are needed to define the six dependent and independent variables. Hence, it results $u_{dyn}\doteq \left[L\right]$, $F_y\doteq \left[M\right]\left[L\right]{\left[T\right]}^{-2}$, $f\doteq \left[M\right]\left[L\right]{\left[T\right]}^{-2}$, $m\doteq \left[M\right]$, $k_e\doteq \left[M\right]{\left[T\right]}^{-2}$, and $k_p\doteq \left[M\right]{\left[T\right]}^{-2}$. According to Buckingham’s theorem, Equation (2) can be contracted to

$${\mathrm{\Pi }}_1^{dyn}=\Phi \left({\mathrm{\Pi }}_2,{\mathrm{\Pi }}_3\right),$$

(3)

where ${\mathrm{\Pi }}_i$ ($i=1,2,3$) are dimensionless quantities, which number is equal to the number of variables appearing in Equation (2), that is, 6, minus the number of base dimensions, that is, 3. The ${\mathrm{\Pi }}_i$ terms are obtained by identifying among the six variables three repeating terms and using these to turn the remaining into dimensionless quantities. The repeating variables must have independent dimensions, that is, any product between them cannot be dimensionless. In the present approach, the mass m, the elastic stiffness $k_e$ and the yielding force $F_y$ were chosen as repeating variables. Therefore, the resulting three ${\mathrm{\Pi }}_i$ terms were ${\mathrm{\Pi }}_1^{dyn}=u_{dyn}{k}_e/F_y$, ${\mathrm{\Pi }}_2=f/F_y$, and ${\mathrm{\Pi }}_3=k_p/k_e$. Considering that the displacement at yielding is $u_y=F_y/k_e$, for a SDOF system with elastic-plastic with hardening rule, the governing equation is

$$\frac{u_{dyn}}{u_y}=\Phi \left(\frac{f}{F_y},\frac{k_p}{k_e}\right).$$

(4)

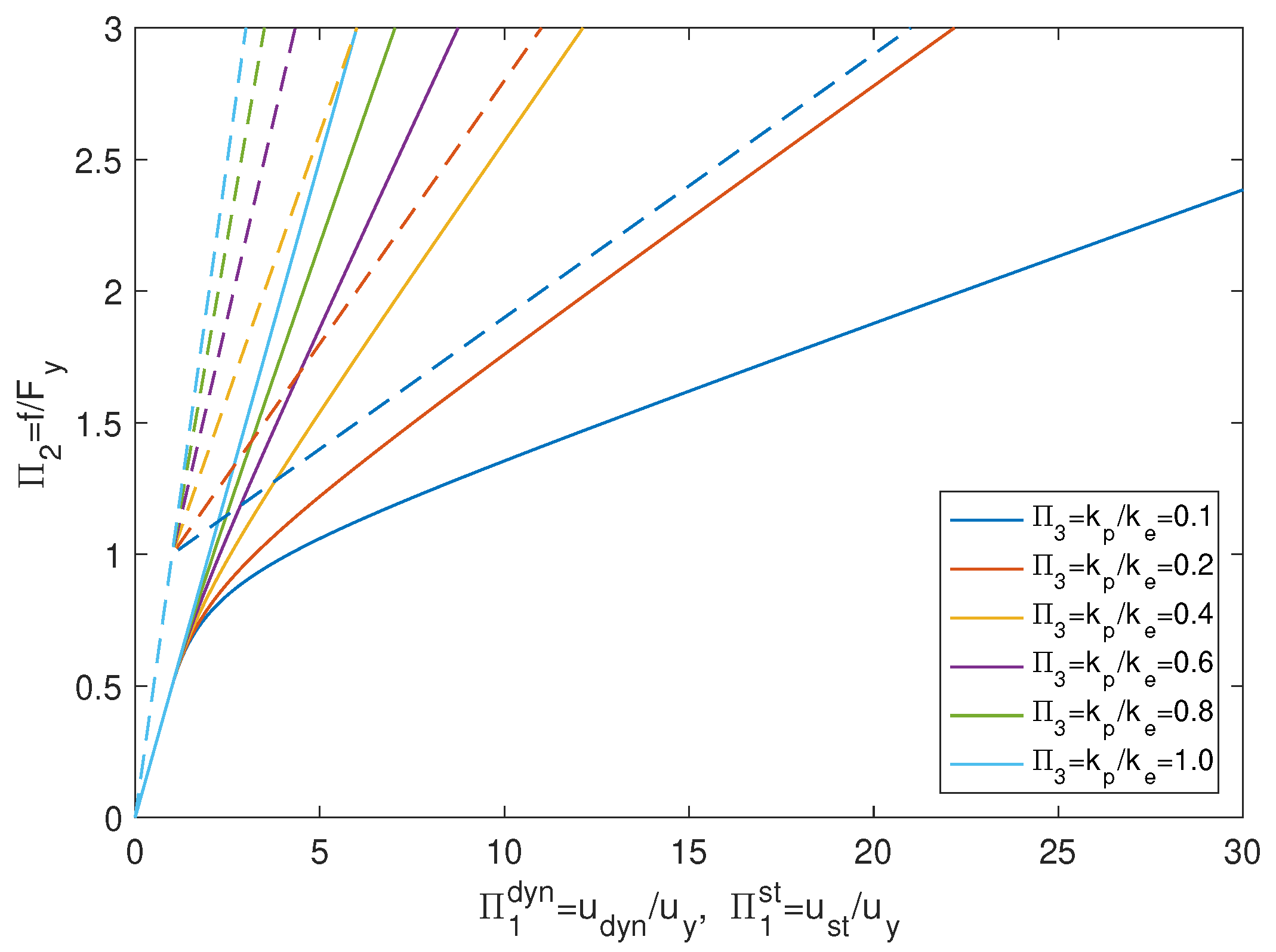
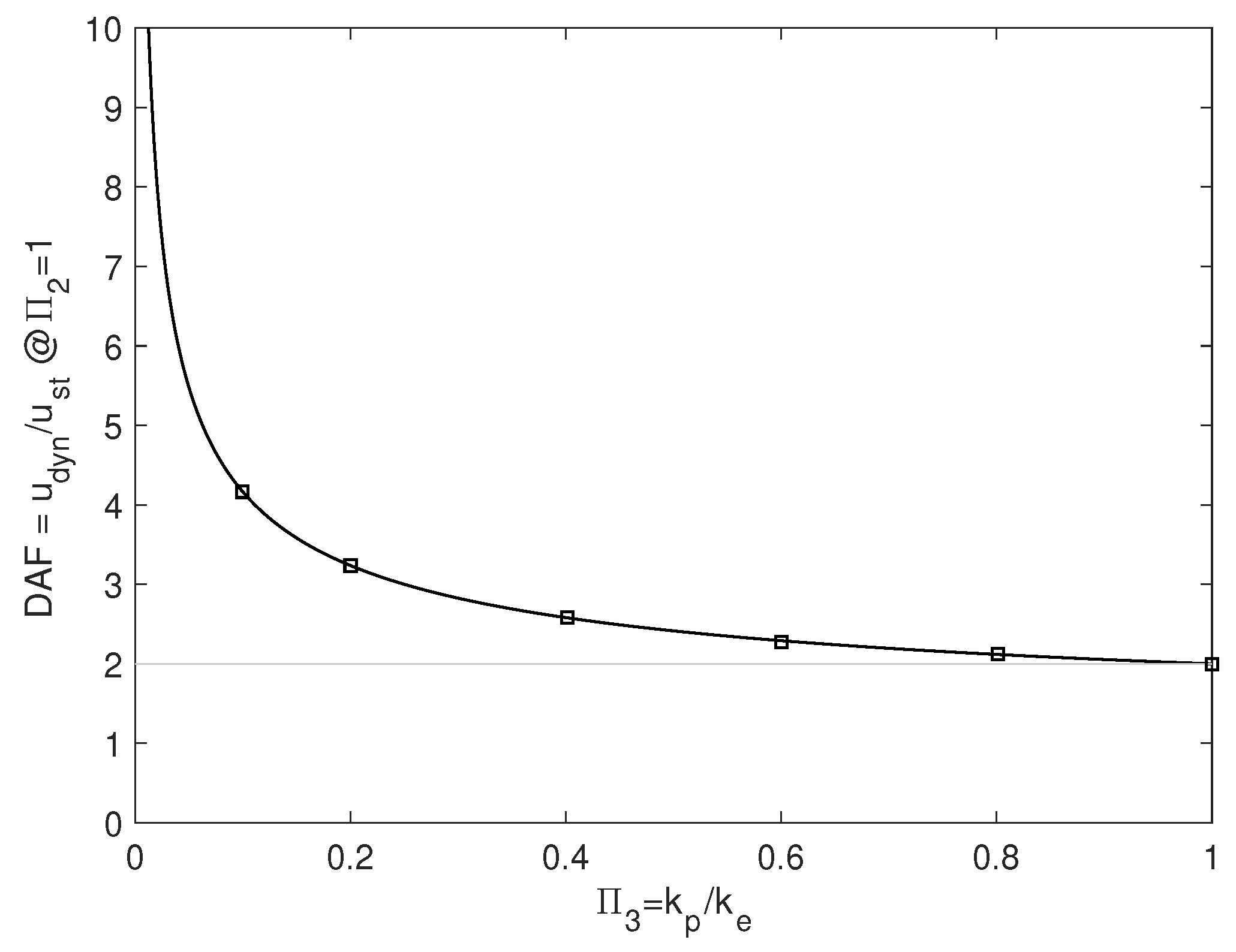
2.3. Dynamic Amplification Factor (DAF)

The maximum dynamic displacement $u_{dyn}$ of the SDOF system was computed through the expressions reported in Appendix A assigning an arbitrary value to the repeating variables, for example, $m=1$ kg, $k_e=1$ N/m and $F_y=1$ N. The solution was implemented into a Matlab script consists in applying, in the order, Equations (A3), (A4), (A9), (A10), (A12), and, finally, Equation (A8). The displacement due to quasi-static loading of the system was determined as

$$u_{st}=\left\{\begin{array}{cc}\frac{f}{k_e}\hfill & f\le F_y\hfill \\ u_y+\frac{f-F_y}{k_p}\hfill & f>F_y.\hfill \end{array}\right..$$

(5)

The dimensionless displacement was computed for both the dynamic analysis, ${\mathrm{\Pi }}_1^{dyn}$, and the quasi-static loading ${\mathrm{\Pi }}_1^{st}=u_{st}/u_y$. Figure 4 depicts the relationship between normalised displacements, forces and ratios between tangential stiffnesses. Observing the dashed curves, related to the quasi-static loading process, the elastic-plastic law of the connecting device clearly emerges. The curves as $f/F_y=1$ and diverges for larger forces depending on the hardening stiffness. On the contrary, the continuous curves accounting for the dynamics of the system show a different behaviour, diverging for $f/F_y>0.5$.

The dynamic amplification factor was computed as

$$\mathrm{D}\mathrm{A}\mathrm{F}=\frac{{\mathrm{\Pi }}_1^{dyn}}{{\mathrm{\Pi }}_1^{st}}=\frac{u_{dyn}}{u_{st}}.$$

(6)

Figure 5 reports the DAF for various dimensionless external forces ${\mathrm{\Pi }}_2$ and stiffnesses ratios ${\mathrm{\Pi }}_3$. It is shown that for systems with an elastic-plastic characteristics the $\mathrm{D}\mathrm{A}\mathrm{F}\ge 2$. In particular, the well-known value $\mathrm{D}\mathrm{A}\mathrm{F}=2$ occurs if $k_p=k_e$, that is, the system can be though as pure elastic. The dynamic amplification factor for elastic-plastic with hardening systems increases for $f>F_y/2$ and has a peak for $f=F_y$. This is due to the fact that the mass has its maximum velocity at $u_y$, when the system turns from elastic to plastic, resulting in the maximum discrepancy between the dynamic and the quasi-static maximum displacements. A decreasing trend of the DAF curves is observed for $f>F_y$. They asymptotically tend to 2 for large $f/F_y$ ratios since the plastic phase is predominant if $f\gg F_y$, that is, the restoring force in the device depends on the tangent stiffness $k_p$.

Figure 6 plots the maximum values of the dynamic amplification factor, DAF, for $f=F_y$, that is, ${\mathrm{\Pi }}_2=1$, where the peaks in Figure 5 were observed. The maxima curve has a vertical asymptote for ${\mathrm{\Pi }}_3=0$ corresponding to $k_p=0$, that is, an elastic perfectly plastic system. As observed, the maximum DAF is 2 for $k_e=k_p$.

3. Proposed Method for the Simplified Analysis

As a result of the previous sections, it results that the dynamic behaviour of the equivalent system is ruled by parameters of the compliance curve, namely, the tangent stiffnesses, the force in the removed element and the yielding force of the system. As emerges in Equation (4), the equivalent mass of the SDOF oscillator is not needed to estimate its maximum dynamic displacement $u_{dyn}$. Besides, mass information is required if the force is not applied instantaneously.

The proposed method consists in computing a compliance law and applying the dimension-less analysis to estimate the dynamic amplification factor, DAF. The analysis is performed with respect to reinforced concrete planar frame structures, for which a quick and preliminary assessment is required. The proposed approach is based on the following assumptions: the frame has regular bays geometry, that is, the widths of the bays are (at least across the considered column) equal; the concrete beams have equal capacity and ductility properties for all the floors (at least across the considered column); following column removal, the damage propagates on the frame structure through a zipper-type progressive collapse mode [36] which can be idealised with the formation of plastic hinges at both ends of the beams spanning from the considered column, as sketched in Figure 7a. The procedure consists in the following steps:

1.

the capacity and the ductility properties of the beams are assessed and a bending moment-curvature (BM-$\chi$) relationship is obtained. The bending moment at yielding, $M_y$, and the ultimate bending moment, $M_u$, and the corresponding kinematic quantities, ${\chi }_y$ and ${\chi }_u$, are considered as representative for the behaviour of the concrete cross-section;

2.

the axial force, $\mathrm{N}$, acting in the removed column is computed considering the loads applied on its tributary area, that is, half of the dead and live loads each beam plus the weight of the upper columns.

3.

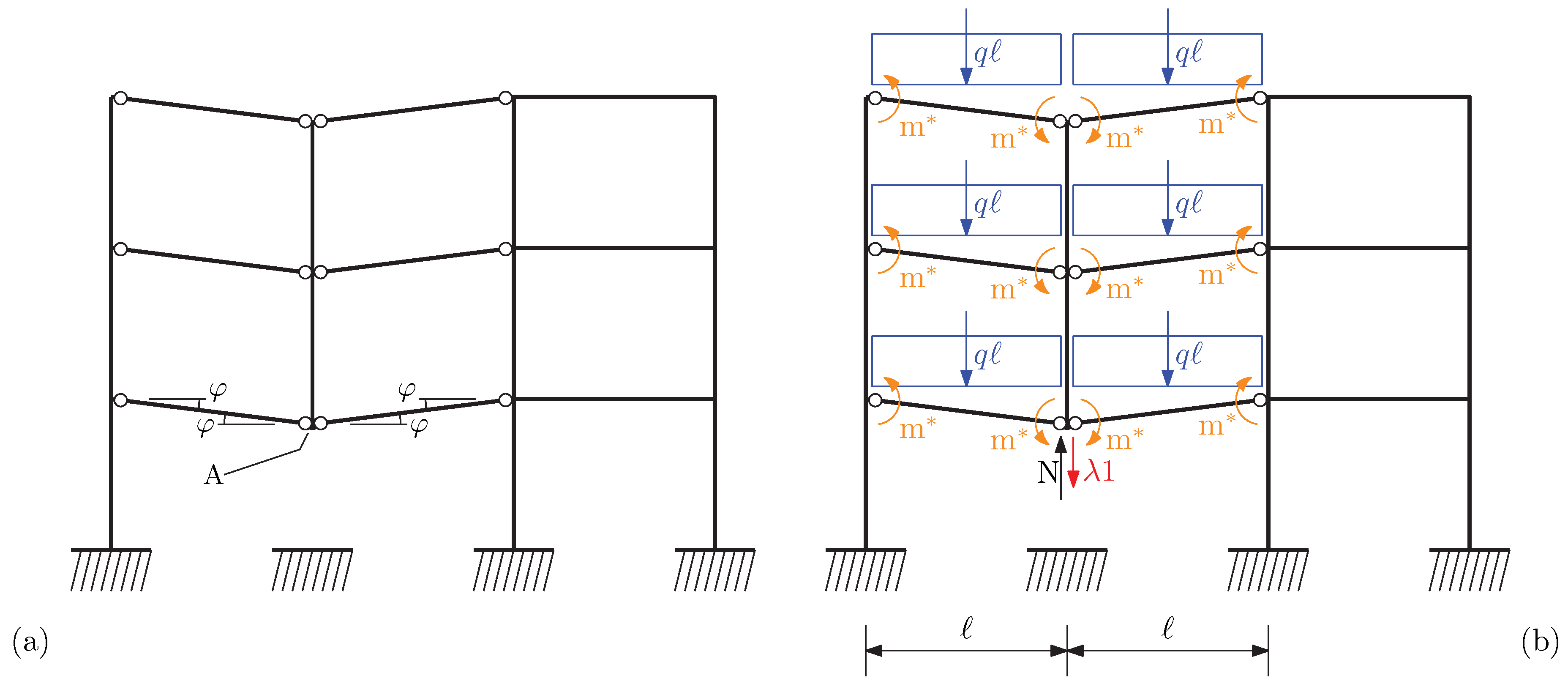
the mechanism that originates following column removal is studied and the upper bound theorem of the plastic analysis is applied. With reference to Figure 7b, the replacement axial force $\mathrm{N}$ previously computed is inserted in the mechanism as an upward force located in A; bending moments m${}^{*}$ are applied in the plastic hinges. A downward variable force, that is, column removal force, $\lambda 1$ is inserted in A. The value of $\lambda$ for which the virtual work principle (VWP) holds defines an upper bound collapse load, $\lambda \left(m^{*}\right)$ [37];

4.

the chord rotation of beams ends, ${\theta }^{*}$, is computed and an approximate downward displacement of node A is obtained as ${\delta }^{*}={\theta }^{*}\ell$;

5.

the compliance curve is built repeating points 3. and 4. considering the yielding and ultimate capacities of the beams. The yielding force, $F_y$, is computed through the load multiplier $\lambda \left(M_y\right)$ and the corresponding displacement, ${\delta }_y$, through the chord rotation at yielding, ${\theta }_y$. A similar approach is required for the ultimate point, that is, for $F_u$ and ${\delta }_u$. The tangent stiffnesses in the elastic and in the plastic with hardening part of the curve are evaluated as

$$k_e=\frac{F_y}{{\delta }_y}{k}_p=\frac{F_u-F_y}{{\delta }_u-{\delta }_y};$$

(7)

6.

the displacement due to a quasi-static column removal process is evaluated as

$$u_{st}=\frac{\mathrm{N}}{k_e}.$$

(8)

The dimensionless quantities ${\mathrm{\Pi }}_1$, ${\mathrm{\Pi }}_2$ and ${\mathrm{\Pi }}_3$ are computed and the dynamic amplification factor is evaluated following the steps reported in Appendix A;

7.

the maximum dynamic displacement is computed as $u_{dyn}=\mathrm{D}\mathrm{A}\mathrm{F}{u}_{st}$.

The approach can be adapted from middle to side sudden column removal accounting for the actions deriving from a different tributary area. The mechanisms that originates still considers that plastic hinges form in the beams, where the whole rotation is assumed to occur. Thus, the column stays vertical, and, implicitly, in the elastic stage. This simplification allows to derive the vertical displacement as ${\delta }^{*}={\theta }^{*}\ell$.

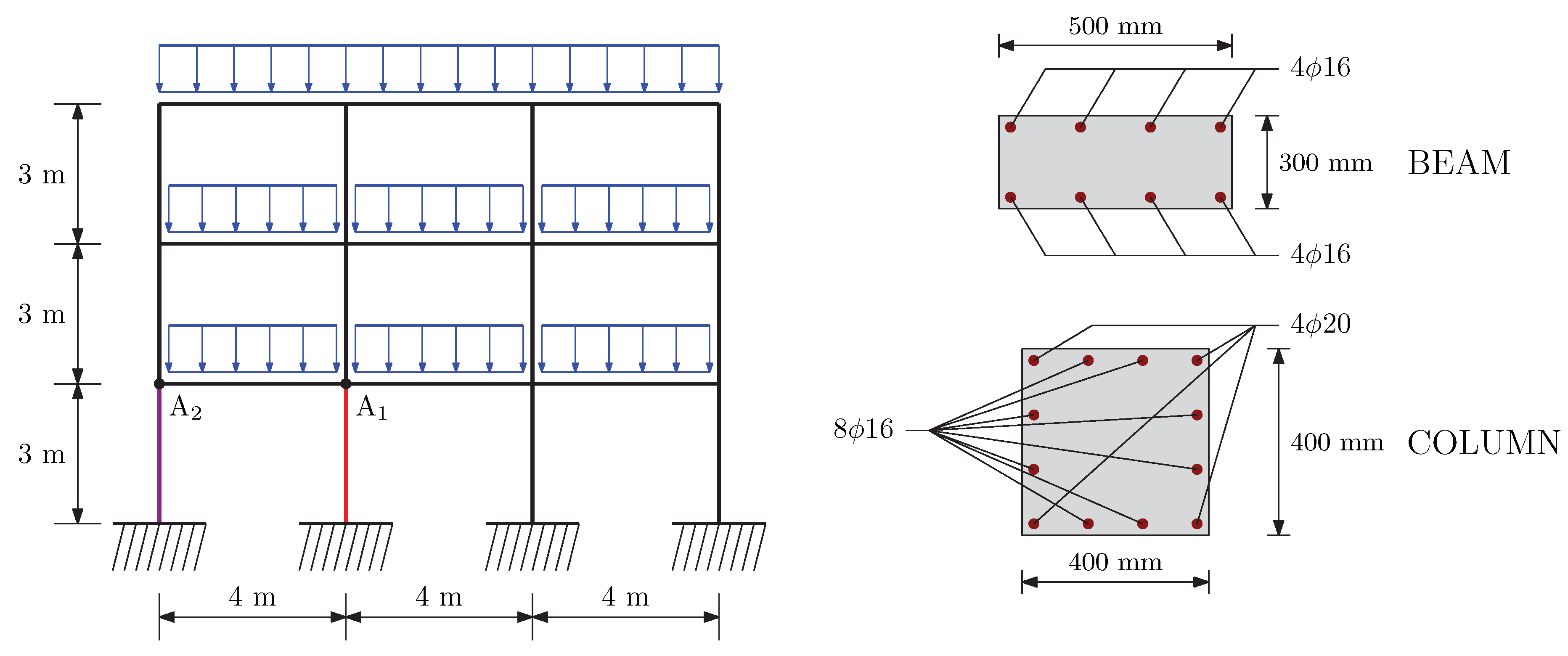
4. An Example

The proposed method was applied on a test structure consisting in a three storey-four columns frame with interstorey height equal to 3 m and beams length equal to 4 m. The 400 mm × 400 mm square columns are longitudinally reinforced with 4$\varphi$20 bars in the corners and 8$\varphi$16 bars along the sides and transversely reinforced with $\varphi$10 stirrups 100 mm-spaced. The 300 mm-deep rectangular beams are 500 mm wide and reinforced with 4+4$\varphi$16 bars and $\varphi$10 stirrups 100 mm-spaced. Yield stress and Young’s modulus of the reinforcement steel are 500 MPa and 200 GPa, respectively; the concrete is ascribed to C25/30 class according to Eurocode 2 [38]. The frame is subjected to a 10 kN/m live load; beam and column linear weights are 3.60 kN/m and 3.84 kN/m, respectively. Figure 8 sketches the frame and identifies the suddenly removed middle column at the bottom floor. The top end of the removed element is set as the control node and its vertical displacement as the control displacement. The steps of the simplified method are proposed in reference to the enumerated list reported in Section 3.

1.

The analytical model proposed by Park and Paulay [39] was adopted for the evaluation of the bending moments and the corresponding curvatures. It results a bending moment at yielding equal to $M_y=94.5$ kNm and a curvature equal to ${\chi }_y=1.18\times {10}^{-2}$ m${}^{-1}$. Referring to the ultimate capacity, it follows that at the ultimate concrete compressive strain, ${\epsilon }_{cu}=0.0035$, the compression steel is not yielding. The ultimate bending moment and curvature are $M_u=102.8$ kNm and ${\chi }_u=8.16\times {10}^{-2}$ m${}^{-1}$, respectively.

2.

The axial force in the selected column was evaluated considering the tributary area of the column, that is, half length of the beam. The force results from the following expression

$$\mathrm{N}=n_f\left(\mathrm{D}\mathrm{L}+\mathrm{L}\mathrm{L}\right)\ell +g_b\left(\ell -w_c\right)n_f+g_c\left(n_f-1\right)h,$$

(9)

where $\mathrm{D}\mathrm{L}$ and $\mathrm{L}\mathrm{L}$ are the dead and the live loads, respectively, $g_b$ and $g_c$ are the linear weights of beam and column, respectively, ℓ is the length of the beam, h is the interstorey height, $n_f$ is the number of floors and $w_c$ is the width of the column. For the present example, the axial force is $\mathrm{N}=181.9$ kN.

3.

The upper bound theorem of the plastic analysis was applied and the load multiplier that defines the collapse load $\lambda \left(m^{*}\right)$ is determined as

$$\lambda \left(m^{*}\right)=\frac{1}{\ell }\left\{4n_f{m}^{*}+N\ell -n_f\left[\left(\mathrm{D}\mathrm{L}+\mathrm{L}\mathrm{L}\right)\ell +g_b\left(\ell -w_c\right)\right]\ell -g_c\left(n_f-1\right)h\ell \right\}.$$

(10)

Substituting the values of the yielding and the ultimate bending moments it results $\lambda \left(M_y\right)=283.5$ and $\lambda \left(M_u\right)=308.5$, respectively.

4.

The chord rotation of beams end were computed through the analytical models proposed in the Italian Building Code [40,41] for an equivalent cantilever: the elastic rotation is due to an elastic curvature increasing from zero (at the free end of the cantilever) to ${\chi }_y$ (at the opposite end); the plastic curvature, that is, ${\chi }_u-{\chi }_y$, is kept constant on the plastic hinge length [42]. According to the aforementioned approach, chord rotation at yielding is ${\theta }_y=0.01112$ radians, while ultimate chord rotation is equal to ${\theta }_u=0.03117$ radians. The corresponding downward displacements are ${\delta }_y=44$ mm and ${\delta }_u=125$ mm.

5.

The bilinear compliance curve is derived from the data previously obtained. It results $F_y=283.5$ kN and $F_u=308.5$ kN. Thus, the tangent stiffnesses in the elastic and the hardening phase are computed through Equations (7), resulting in $k_e=$6,443,181 N/m and $k_p=$311,482 N/m.

6.

the displacement due to a quasi-static column removal process was computed through Equation (8) as $u_{st}=28.4$ mm. The displacement at yielding to be inserted in the dimensionless quantities computed at the following point is $u_y={\delta }_y=44$ mm.

7.

The dimensionless quantities were computed according to Section 2.2 as

$${\mathrm{\Pi }}_2=\frac{N}{F_y}=0.640{\mathrm{\Pi }}_3=\frac{k_e}{k_p}=0.049$$

(11)

from which ${\mathrm{\Pi }}_1^{dyn}=1.379$ is computed. Referring to the dimensionless static displacement, it results ${\mathrm{\Pi }}_1^{st}=0.640$.

8.

The dynamic amplification factor is

$$\mathrm{D}\mathrm{A}\mathrm{F}=\frac{1.379}{0.640}=2.155,$$

(12)

from which it results $u_{dyn}=61.3$ mm.

Special Case: Side Column Removal

The formulae proposed in the previous section refer to the removal of a middle column. With reference to the violet removed beam represented in Figure 8, a side column removal is analysed in the following. The approach is similar to the middle column removal case and the hypothesis that plastic hinges are located in the beams holds. Hence, Equation (9) can be rewritten as

$$\mathrm{N}=n_f\left(\mathrm{D}\mathrm{L}+\mathrm{L}\mathrm{L}\right)\frac{\ell }{2}+g_b\frac{\ell -w_c}{2}{n}_f+g_c\left(n_f-1\right)h.$$

(13)

Similarly, the expression of the load multiplier of Equation (10) turns into

$$\lambda \left(m^{*}\right)=\frac{1}{\ell }\left\{2n_f{m}^{*}+N\ell -n_f\left[\left(\mathrm{D}\mathrm{L}+\mathrm{L}\mathrm{L}\right)\ell +g_b\left(\ell -w_c\right)\right]\frac{\ell }{2}-g_c\left(n_f-1\right)h\ell \right\}.$$

(14)

5. Comparison with Numerical Simulations

Various numerical simulations were performed to assess the quality of the simplified methodology. SeismoStruct, a fibre-based commercial software capable of a large variety of static and dynamic analyses, was adopted [43]. The geometry of the example structure was inserted in the FE (Finite Elements) model and material and cross-section properties were assigned to the elements. The material nonlinearity derives from the fibre-based approach, for which a uniaxial stress-strain relationship is assigned to each fibre [44]. Concrete behaviour is represented through a uniaxial uniform confinement model [45] while a bilinear stress-strain model with kinematic strain hardening is assumed for the reinforcement steel bars. The sectional state of the elements is obtained through the integration across the fibres that discretize the cross section. Inelastic elements with plastic hinges according to the model proposed by Scott and Fenves [46] are adopted in the FE model. The dynamic column removal is simulated with the application of an opposite force on the node onto which the replacement force acts [1,6,30]. In the simulations that are reported in the following, the force application starts at 0.1 s and lasts 0.01 s (column removal time), that is, it can be considered as a sudden column removal. The analysis is performed with 0.001 s time integration steps adopting the integration scheme proposed by Hilber et al. [47]. Both middle and side columns removals were simulated. Three different amounts of reinforcement in the beams were adopted: 3+3$\varphi$16 and 4+4$\varphi$16 for middle column removal and 3+3$\varphi$20 for either middle or side column removal. For each configuration, the compliance curve was numerically obtained through a displacement controlled pushdown analysis, the incremental force represented by a downward force acting on the control node. It results that the vertical displacement due to a quasi-static column removal occurs when the incremental force equals in magnitude the axial force in the removed column. Figure 9 reports the compliance curves obtained in the simplified analysis and in the simulations. It is first noted that the range of vertical displacement differs: this is due to the capability of the approximate method to model the true nonlinear behaviour and resisting mechanisms that raise in such phenomenon, such as, arch resisting mechanism and catenary effects [17,21]. Meanwhile, the yielding forces and the elastic parts of the compliance laws are very close, meaning that the simplified approach approximate the real behaviour of the system well. As expected, the simplified hardening phase is limited due to the ultimate rotational capacity of the element. The previous considerations holds for middle column removal. Referring to side column removal (in violet in Figure 9), it results that the pushdown analysis shows a less rigid elastic part, but with similar yielding force.

Figure 10 depicts the results of the FE dynamic sudden column removal. After the removal, the system oscillates around the equilibrium position, which can be different from the one obtained with a quasi-static damage. Side column removal (violet curve) shows oscillations with variable amplitude due to the redistribution of the forces and across the whole frame. The X-axis is limited at 500 ms and depicts the maximum downward displacement of the control node, that is, 63.2 mm that occurs during the second oscillation. The dashed lines indicate the maximum dynamic displacements derived from the simplified analysis. It is shown that the proposed approach overestimates the downward displacement for 3+3$\varphi$20 (middle column) and 4+4$\varphi$16 cases, and underestimates it in the remaining cases.

Table 1. Comparison between numerical and simplified analysis by varying the amount of reinforcement in the beams.

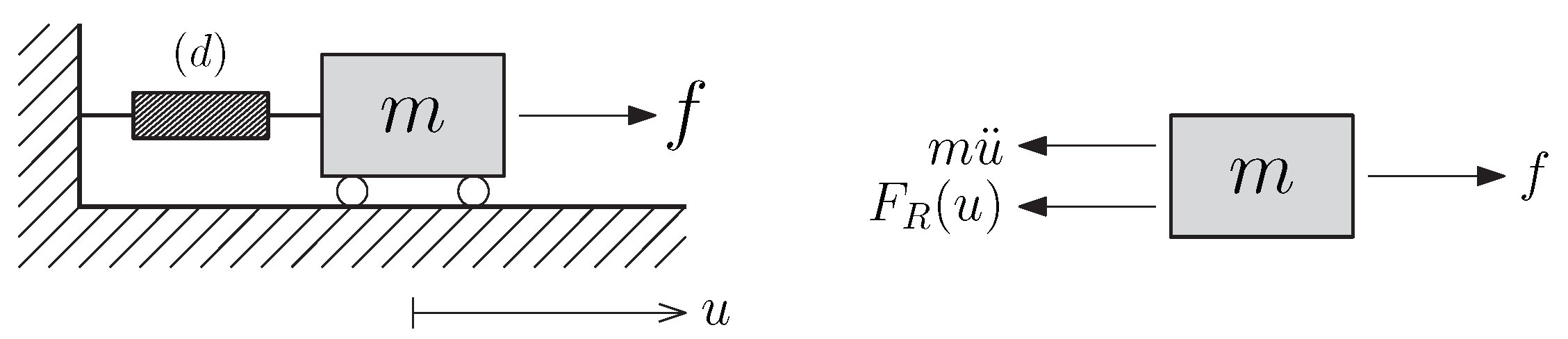
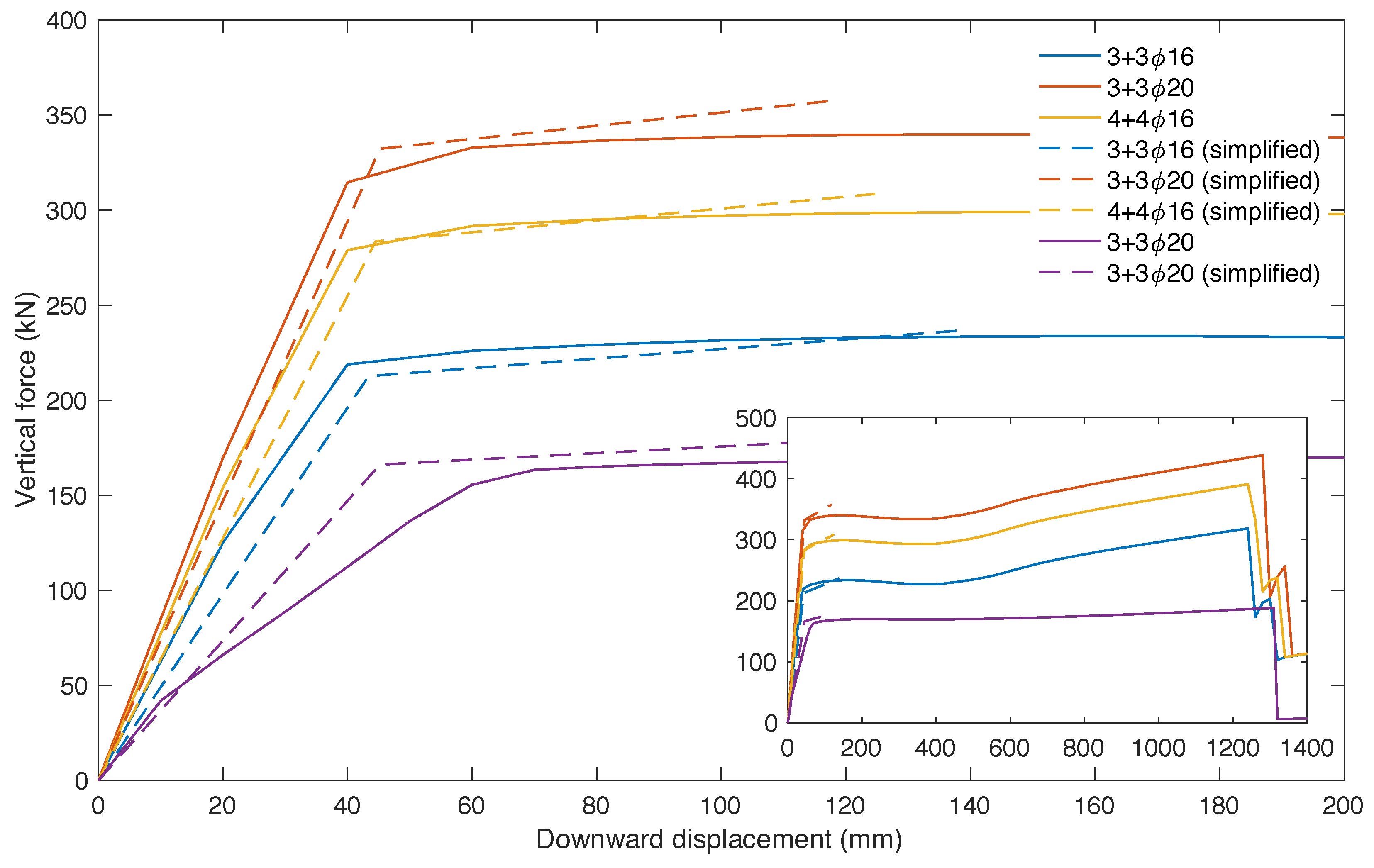
Beams	Removed	${\mathit{u}}_{\mathit{st},\mathit{num}}$	${\mathit{u}}_{\mathit{dyn},\mathit{num}}$	DAF${}_{\mathit{num}}$	${\mathit{u}}_{\mathit{dyn},\mathit{simpl}}$	Error
Reinforcement	Column	(mm)	(mm)		(mm)
3 + 3$\varphi$16	Middle	32.4	124.4	3.84	122.5	−1.5%
3 + 3$\varphi$20	Middle	23.3	47.7	2.04	49.8	+4.4%
4 + 4$\varphi$16	Middle	25.8	57.6	2.23	61.3	+6.4%
3 + 3$\varphi$20	Side	39.2	63.2	1.61	58.7	−7.7%

reports the maximum values and compares the simplified and the numerical solutions. For each numerical simulation, the static, the dynamic displacements and the corresponding dynamic amplification factor (DAF${}_{num}$) are reported. For such structures, DAFs larger that 2 are in accordance with the numerical and experimental results obtained by other scholars [5,26,27,28]. Referring to the accuracy of the simplified approach, the error is within the bound $\pm 10\%$.

6. Conclusions

This paper has presented and discussed a simplified approach for the estimation of the maximum dynamic displacement in reinforced concrete frames subjected to sudden column loss. An equivalent load application process has been adopted for exploring the effects of the damage on the structure. Despite simple, the instantaneous load application in a numerical step-by-step analysis provides an upper bound of the true displacement that can be observed if the damage progressively act. Different to the simplified procedure illustrated by Izzuddin et al. [4], following which the compliance curve is obtained applying the gravity loads on an unloaded damaged structure, the present approach considers a damage process occurring on a loaded structure.

Awareness about the phenomena that can occur in systems when subjected to forces which magnitude is large enough to engender plastic deformations is necessary for the study the effects of loading scenarios not considered during the ordinary design, such as sudden column removal or explosions on civil engineering structures. It has been proved that, despite simplified, the proposed methodology catch the dynamic behaviour of a frame structure subjected to column removal. The comparison between the results obtained with the straightforward approach herein described surprisingly has shown good agreement with the nonlinear dynamic time-history numerical analyses. Membrane actions, which provide a contribution to the capacity of the system under large displacements, have not been considered in the method. For the purposes of the simplified method, the overstrenght provided by membrane effects acts as a safety margin.

This approach is suitable in the preliminary design stage, when information about the structure is bare. The Authors implemented it on a spreadsheet into which the basic geometry of the frame, cross-section properties and acting loads are assigned. Solving the procedure, the dynamic displacement is estimated. By varying the variables, say the amount of reinforcement, the size of the elements, a preliminary design for robustness is performed. The validity of the resulting dynamic response lies in the fact that the amplification factor computed with the analytical formula overestimates the true value [13]. Obviously, the simple considerations on the dynamic response of structures to step force can be extended to other loading scenario, such as impacts due to natural phenomena [22]. In addition, this approach could be extended to other types of structures into which it is possible to identify a failure mechanism, say in steel frames or in timber structures. The possibility of including column removal time and strain rate effects into the present simplified formulation is still an open question [30] and need to be addressed in the future.