Abstract
Reliable and high-fidelity virtual ruin scenarios for collapsed buildings are essential for post-earthquake emergency search and rescue training. However, the existing research on the distribution of ruins caused by building collapse is insufficient for supporting post-earthquake rescue training. Therefore, this paper proposes a hybrid framework for simulating building collapse and ruin scenarios, using a finite element (FE) model and a physics engine. Based on this framework, the following methods are proposed: (1) geometric model conversion from the FE model to the physics engine; (2) determination of the initial moment of collapse; and (3) data mapping of the FE simulation results. In addition, a corresponding program, Finite Element Method to Rigid Body Dynamics (FEM2RBD), is developed for the hybrid framework. The proposed framework simulates the entire process of building collapse and the distribution of ruins. The accuracy of the framework is validated using a shaking table test of a three-story reinforced concrete frame. The collapse process and ruin scenario of a real-world library building is simulated as a case study. The results show that the proposed framework combines the advantages of the FE model during the small-deformation stage with the advantages of physics engines during the large-deformation stage. The proposed framework can be valuable in simulating building collapse and ruin scenarios for post-earthquake rescue training.
1. Introduction
Earthquakes can cause building collapse, and people may be buried by ruins [1,2]. Relevant statistics show that being buried is the most common cause of earthquake-related injuries [3]. Therefore, it is necessary to conduct training to improve rescue efficiency and mitigate casualties after earthquakes. To achieve this, the ability to accurately simulate ruin scenarios is required. The reliability of simulated ruins is also an essential factor for efficient training [4].
To date, several studies on the collapse simulation of buildings have been conducted using the finite element (FE) method. Such studies typically focus on the collapse resistance of structures, rather than the formation of ruins, such as the analyses of the progressive collapse resistance caused by accidental load [5,6,7,8], the simulations of seismic collapse processes, etc. [9,10,11,12,13]. Few studies that simulate the distribution of ruins induced by structural collapses have been conducted, due to the high computational workload, and the difficulty of simulating large deformations and nonlinear behaviors using the FE method [14,15].
Currently, there are two methods for performing studies on ruins induced by structural collapse:
- Shaking table testShaking table tests have been used to study the ruin distribution in many studies [16,17,18,19,20]. For example, Huang [20] analyzed the collapse process and distribution of ruins using a ¼-scale shaking table test of a three-story reinforced concrete frame. In general, the structures used in such tests are highly simplified approximations of real-world structures. Owing to the high cost and limited experimental capacity of shaking table tests, small-scale models are often required, thereby limiting the reliability of the results.
- Numerical simulation methodsThe discrete element method (DEM) [21,22], applied element method (AEM) [15,23] and physics engines are the most common numerical simulation methods for ruin simulations. A physics engine is a piece of computer software, based on Newton’s laws of dynamics, that provides an approximate simulation of complex physical behaviors, such as rigid body dynamics (including collision detection), soft body dynamics and fluid dynamics. [24]. Some physics engines have a relatively low computational demand [25]. In recent years, physics engines have been widely used to simulate structural collapse and ruin distributions [26,27,28,29,30,31]. For example, Xu et al. [28] simulated seismic damage in urban areas, based on a multi-story concentrated-mass shear model and PhysX. Bullet Constraints Builder (BCB) [29] is a building collapse simulation software, which is developed based on the open-source physics engine Bullet [32] and Blender Python script. Bullet [32] is an open-source, real-time physics engine developed by Erwin Couman in 2003, which can simulate collision detection, and soft and rigid body dynamics. The BCB can simulate the dynamic behavior of structures at the large-deformation stage, and the distribution of ruins. Furthermore, the simulation results are generally consistent with ruin scenarios in real-world earthquake events [30].
Although the physics engine-based building collapse simulation methods have advantages in simulating large structural deformations, the simulation results at the small-deformation stage are less reliable. For example, due to the difficulty of determining constraint damping in Bullet, and the oversimplification of the rebar model in BCB, the simulation results of the BCB and FE methods are quite different at the small-deformation stage. However, the process of the structural collapse is often sensitive to the initial state of the collapse. Therefore, ensuring the accuracy of collapse mode simulations using physics engine-based methods is difficult.
To address the challenges mentioned above, a hybrid framework for simulating building collapse and ruin scenarios, based on an FE model and a physics engine, is proposed. For dynamic responses during the small-deformation stage, an FE model is used because of its accuracy in such simulations. For the large-deformation stage, a physics engine-based method is used. In this work, the MSC.Marc software [33] is used to perform the FE modeling and simulations, and the BCB is used to simulate the ruin scenario. The proposed framework is also applicable to other FE software and physics engines.
In Section 2, the proposed hybrid framework is introduced. Section 3 will illustrate three key methods adopted in the proposed framework: (1) conversion of the geometric data from the FE method to the physics engine; (2) determination of the initial moment of collapse; and (3) data mapping of the FE simulation results. Section 4 will validate the feasibility and accuracy of the proposed framework using a shaking table test of a three-story reinforced concrete frame. The collapse process and ruin scenario of a real-world library building are simulated as a case study to demonstrate the high-fidelity collapse process during an earthquake. The outcome of this research contributes to the construction of virtual building collapse and ruin scenarios, and supports post-earthquake emergency rescue training.
2. Hybrid Framework Based on FE Method and Physics Engine
Figure 1 shows the proposed hybrid framework, where the software programs are in bold italics, and the detailed functions of the program are in italics. The framework consists of four modules:
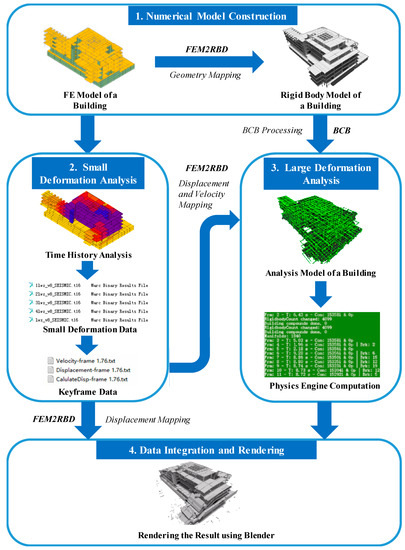
Figure 1.
Hybrid framework based on an FE model and a physics engine.
- Module 1: FE model establishment and conversionThe FE model of the target structure is established using the FE software MSC.Marc [33]. The geometric model is then converted into the rigid body model in Blender, using the geometry mapping function that is integrated into the Blender Python script “Finite Element Method to Rigid Body Dynamics (FEM2RBD)”. In the rigid body model, the elements are rigid bodies, and no internal stresses and strains are considered. The deformations of the reinforced concrete structures are considered via the constraints/springs among different rigid bodies [29].
- Module 2: Small deformation analysis and initial collapse moment determinationA nonlinear time history analysis is conducted using the FE model of the target building, to analyze the structural behavior during the small-deformation stage. Subsequently, the initial moment of collapse is determined, and the displacement and velocity data of each time step at, and before, the moment of initial collapse are extracted from the FE model. These data will be used in the large-deformation simulation based on the physics engine in Module 3 and the collapse process visualization in Module 4.
- Module 3: Data mapping and large deformation analysisBased on the mapping method of the FE results proposed in Section 3, the displacement and velocity data from the moment of initial collapse are mapped into the BCB geometric model, using the displacement and velocity mapping functions of FEM2RBD. Subsequently, this model is modified using several BCB processing functions, in the following order: (1) establish the rigid body ground; (2) remove the overlapping portions of rigid bodies; (3) map the remaining ground motion; (4) define the constraint parameters; and (5) build the constraints among rigid bodies. The analysis model used for the physics engine simulation can then be established [29]. After establishing this model, simulations are performed using the Bullet physics engine to determine the structural dynamic behavior during the large-deformation stage.
- Module 4: Data integration, rendering and visualizationAfter the large-deformation stage simulation, the render engines of Blender are used to render the data of the small and large-deformation stages. Subsequently, the rendered videos are integrated to visualize the entire structural collapse process.
3. Key Techniques
To implement the proposed framework, the following three key issues need to be addressed.
- Conversion of the geometric model from the FE method to the physics engine. The model in the physics engine-based simulation component is a rigid body spring model, the elements of which are significantly different from the elements of the FE model. Therefore, it is necessary to propose a method for converting the geometric data from the FE model to the physics engine
- Determination of the initial moment of collapse. To achieve the proposed hybrid framework, the switching moment (collapse keyframe) from the FE simulation to physics engine simulation needs to be determined based on the results of the FE simulation.
- Mapping the FE simulation data. After the FE simulation, the data computed for the small-deformation stage need to be mapped into the physics engine.
3.1. Geometric Model and Material Mapping Method
Fiber beam-column and multi-layered shell elements have been widely used to simulate beams, columns and shear walls during the nonlinear dynamic analyses of structures [10,34,35]. Compared with models that use solid elements, models that use fiber beam-column and multi-layered shell elements reduce the number of elements and the computational workload required, which makes the simulations of large-scale structures easier to conduct. In this study, soil–structure interaction (SSI) effects are neglected, assuming that that the soil underneath the foundations is infinitely rigid. It is worthwhile noting that previous studies have illustrated that SSI effects can significantly affect the lateral displacement demand and collapse capacity of building structures [36,37,38]. The classical Rayleigh damping with a damping ratio of 5% based on the initial stiffness of the building is used to model the inherent damping of the structure. Future studies should consider incorporating more accurate approaches to modeling inherent damping, as a few research works have identified drawbacks associated with the use of Rayleigh damping based on initial stiffness [39,40,41,42]. In the FE model, the geometric model of a fiber beam-column element is a line [a one-dimensional (1D) element], and the geometric model of a multi-layered shell element is a plane (a 2D element). However, the geometric model in the physics engine is a solid (a 3D object). Because the geometric models of the physics engine and FE model are different, a method is proposed to convert the FE models of the fiber beam-column and multi-layered shell elements into solid objects for the physics engine.
3.1.1. Solid Model Establishment Method in Blender
The information available from FE models consists of geometric information (including the coordinates of element nodes and sections) and material information about different elements. After data preparation, a physics engine model for large deformation analysis is established in Blender, as shown in Figure 2.
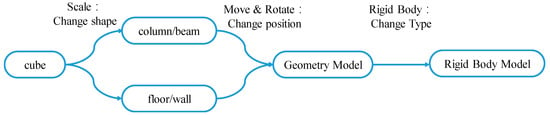
Figure 2.
Solid model establishment method in Blender.
The element establishment method in Blender is different from that in FE software. In Blender, “primitive” mesh shapes should be established first, then all the elements should be transformed from the “primitive” mesh shapes. However, as the shape and position of “primitive” mesh shapes do not coincide with the corresponding FE elements, the shape and position transformations are performed to get the target elements in FE models. Blender provides several “primitive” mesh shapes to begin modeling, including cubes, planes and cylinders [43]. Because a cube is a shape that best approximates engineering components and FE model meshes, it is selected as the basic mesh shape in Blender. The geometric model mapping is then performed in two steps.
- Step 1: Shape and position transformation (including translation and rotation).The shape and position transformations are performed on the cube mesh provided in Blender [43], to create geometric objects with the same shapes and positions as the elements in the FE model. The rotation method shown in Figure 3 is used to model inclined elements in FE models. Specifically, the rotation angle is obtained by first determining the endpoint coordinates of the longest edge of an FE element (line segment l1) and the projection of l1 in the XOY plane in the global coordinate system (line segment l2). The angle α between l2 and the X axis, and the angle β between l2 and l1, are then calculated using these endpoint coordinates. Subsequently, the shape-transformed object is rotated by angle α around the Z axis in the global coordinate system. The object is then rotated by angle β around the Y’ axis in the rotated coordinate system. The rotated coordinate system is the local coordinate system of the cube after the first rotation, where the X’O’ axis is parallel to l2.
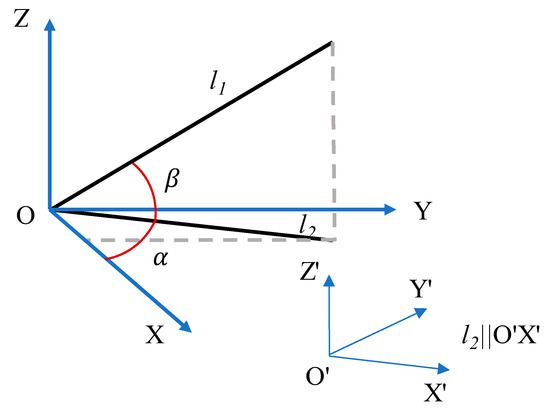 Figure 3. Rotation method for inclined elements.
Figure 3. Rotation method for inclined elements.
- Step 2: Add rigid bodies to the cubes.Convert the cubes into rigid bodies after the shape and position transformations to obtain the rigid body model for the Bullet physics engine simulation.
3.1.2. Material Mapping Method in the BCB
The BCB will group objects according to their names in Blender, and assign the same material properties to the objects in each group during the constraint building process. When establishing a geometric model in Blender, the object names need to be chosen so that objects of the same material in the FE model are mapped into the same material group by BCB. The objects in Blender are named according to the rule of “element type: material type: element number.” For example, an object derived from a beam element with material number 1 and element number 234 is named “Beam: 1: 234.” More details are available in the BCB manual [29].
3.2. Determination of the Initial Moment of Collapse
According to the proposed hybrid framework, the FE simulation is conducted before the initial moment of collapse Tc, and the physics engine simulation is conducted after Tc. Therefore, the determination of Tc is essential. Several collapse criteria have been proposed [44,45,46,47,48,49]. There are various structural collapse modes, including lateral collapse, vertical collapse, and so on. No matter which collapse mode is, the vertical displacements of structural members will exceed a specific value when the structures collapse [47,48]. Therefore, the definition of collapse depends on the moment when “the deformation of the structure is insufficient to maintain a safe use space” [47]. Besides, Zhao et al. [46] studied four collapse criteria, including the following: Criterion 1) According to Chinese seismic code [44], the earthquake-induced inter-story drift ratio of reinforced concrete frames should not be greater than 1/50; Criterion 2) Federal Emergency Management Agency (FEMA) 356 [45] recommended that the inter-story drift ratio limit for the collapse-prevention performance level of concrete structures be 4%; Criterion 3) According to Villaverde [49], when the tangent slope of the incremental dynamic analysis (IDA) curve is lower than 20% of the slope of the initial elastic stage, the structure will collapse; Criterion 4) “The vertical collapse displacement of the main structural members exceed[ing] 1 m”, is considered as Criterion 4 [46]. The work of Zhao et al. [46] shows that the conventional collapse criteria (i.e., Criteria 1–3) significantly underestimate the collapse resistance of the frames. Compared with the other three collapse criteria, Criterion 4 can better reflect the extreme nonlinear behavior of the collapse limit state. Therefore, collapse Criterion 4, proposed by Zhao et al. [46], is selected as a rule for determining Tc in this work.
3.3. FE Simulation Data Mapping Method
The published research on combining FE models and physics engines is limited [26,28]. These studies also lack applicable data mapping methods for converting FE-based numerical models that use fiber beam-column and multi-layered shell elements into physics engine models. Therefore, a method for mapping simulation data from the FE model into the Blender model is proposed.
3.3.1. Displacement Mapping Method
The keyframe method of Blender [43] is used to achieve the displacement mapping. A keyframe is a location on a timeline that marks the beginning or end of a transition. For example, the displacement keyframe defines the beginning and endpoints of the displacement. Meanwhile, a kinematic keyframe defines the information about the kinematic type. There are two kinematic types in Blender: (1) the animation system, in which the motion of the object is controlled by the displacement keyframe, and (2) the physics engine system, in which the motion of the object is controlled by the simulation results obtained using the physics engine. Displacement mapping requires only the displacement keyframe. Before the initial moment of collapse Tc, the motions of objects in Blender are controlled by the displacement keyframes derived from the FE results. This means that only Blender is used to map the FE results; the Bullet physics engine is not involved.
Specifically, the displacement mapping method is divided into three steps, as shown in Figure 4.
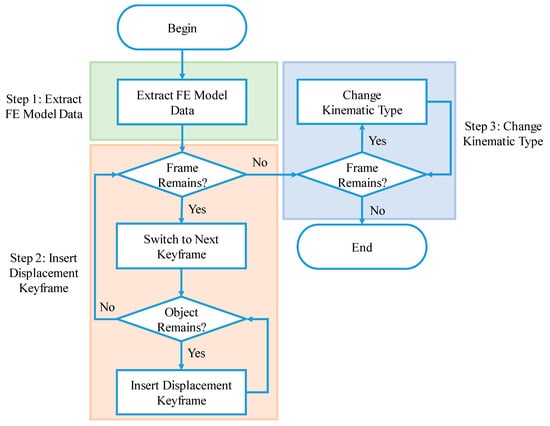
Figure 4.
Flowchart of the displacement mapping method.
- Step 1. Extract the FE model data. After the FE simulation, the displacement data of each vertex at each time step are extracted, and then the deformed coordinates of each vertex are calculated from the displacement data and the initial coordinates. The deformed centroid coordinates of each object at each time step can be calculated from the deformed vertex coordinates of each object.
- Step 2. Insert the displacement keyframe. Initially, the keyframe that corresponds to the first time step in the FE model on the Blender timeline is selected. The deformed centroid coordinates obtained from the FE results for one object are then calculated. Subsequently, the deformed centroid coordinates are inserted as the displacement keyframe. When all the objects in the structure have been processed, the simulation moves to the next time step, and the aforementioned procedure is repeated until the initial moment of collapse Tc.
- Step 3: Change the kinematic type. After Step 2, the kinematic type of each object needs to be converted to the animation system, otherwise the object motions will be controlled by the physics engine simulation, rather than by the FE result.
3.3.2. Velocity Mapping Method
When the FE simulation is converted to the Bullet physics engine simulation at the initial moment of collapse Tc, both displacement and velocity should be consistent between the two simulations. Consequently, velocity mapping is necessary. The velocity mapping method requires both the displacement and the kinematic type keyframes [43]. In Blender, the velocity of an object is defined as follows: At frame i, convert the kinematic type of an object to the animation system and insert the kinematic type as a keyframe. At frame j (where i < j), convert the kinematic type of the same object to the physics engine system, and insert the kinematic type as a keyframe again. Consequently, during frame i and frame j, the movement of the object will be controlled by the linear interpolation of the displacement at frame i and frame j, respectively. After frame j, the movement of the object will be controlled by the Bullet physics engine, and the object will gain speed at frame j, as follows:
where i and j (i < j) denote the keyframe number; dt represents the time interval between two adjacent keyframes, and in Blender, the default value is ; xi and xj represent the centroid coordinates of an object at frame i and frame j, respectively. The speed is the average velocity represented by the secant line, rather than the actual instantaneous velocity represented by the tangent line, as shown in Figure 5.
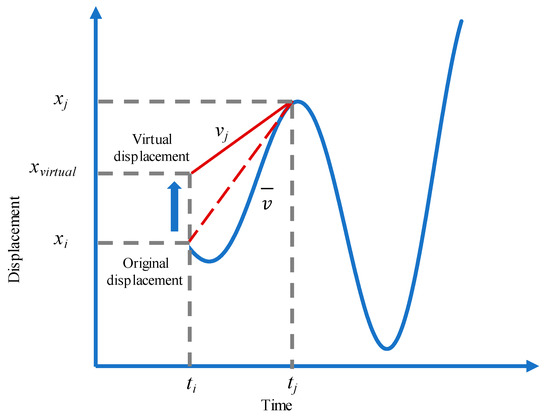
Figure 5.
Virtual displacement vector and velocity mapping method.
In Blender, the Bullet physics engine adopts the symplectic Euler algorithm to update the motion of a rigid body [50], where the position of the object in the next frame is determined by the velocity, position and force of the adjacent previous frame, as shown in Equations (2) and (3).
where Fext denotes external forces defined by the user; Fc denotes the constraint forces determined by the position and the velocity of the object in the adjacent previous frame.
If the average velocity is used instead of the instantaneous velocity vj at the initial moment of collapse Tc, an error due to approximating the velocity will be introduced. To improve the accuracy of the velocity mapping, this work proposes a velocity mapping method that uses a virtual displacement vector xvirtual. The virtual displacement is obtained using Equation (4), based on the velocity and displacement at the collapse keyframe j. The proposed mapping method is shown in Figure 5. The blue curve is the displacement curve simulated by the FE method; ti and tj are the times corresponding to the displacement keyframe insertion points; xi and xj are the displacements corresponding to the displacement keyframe insertion points; vj is the instantaneous velocity, and xvirtual is the virtual displacement vector.
Consider the virtual displacement vector:
where xj and vj represent the displacement vector of the FE model and the velocity vector of the collapse keyframe j, respectively; k is the keyframe number of , and the value of k is defined by Equation (5). After testing, the velocity cannot be mapped successfully in Blender when n is less than four. The real instantaneous velocity and displacement of the FE model are mapped in the Bullet physics engine by replacing xi with the virtual displacement vector in Equation (1).
In summary, the velocity mapping method can be divided into the following three steps, which are schematically diagrammed in Figure 6.
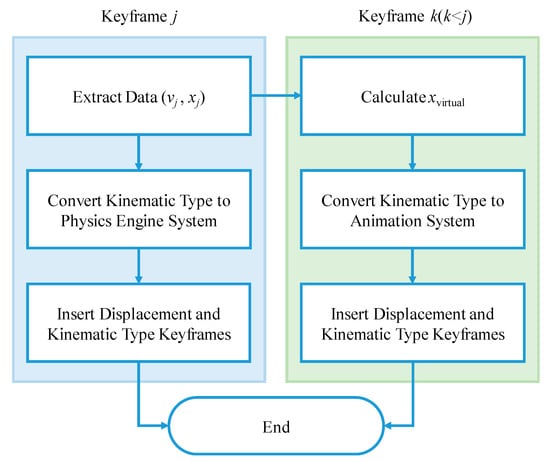
Figure 6.
Flowchart of the velocity mapping method.
- Step 1: Extract the FE results at time step tj, including velocity vj and displacement xj.
- Step 2: Obtain xvirtual using Equations (4) and (5), and set the displacement of the frame k to xvirtual.
- Step 3: At frame k, convert the kinematic type to the animation system, and then insert the displacement and kinematic type keyframes for each object. Convert the frame from frame k to frame j after the keyframe insertion at frame k. At frame j, convert the kinematic type to the physics engine system, and then insert the displacement and kinematic type keyframes for each object.
4. Validation and Case Study
4.1. Validation Using a 3D Shaking Table Test of a Three-Story Reinforced Concrete Frame
4.1.1. Basic Information
To validate the reliability of the proposed hybrid framework, a 3D shaking table test was conducted with a three-story reinforced concrete frame [20] as a case study. The collapse of the structure was simulated using three methods: (1) FE simulation, (2) BCB simulation, and (3) the proposed hybrid framework.
The details of the structure are shown in Figure 7. The concrete information is shown in Table 1, and the rebar information is shown in Table 2. The structure was subjected to the amplitude-scaled El-Centro ground motion record during the shaking table test, and the load cases are shown in Table 3. The 5%-damped pseudo-acceleration spectra of Load Case 5 are shown in Figure 8. More details can be found in [20]. The first mode is a translation with a fundamental period (elastic period) T1 = 0.316 s; the second mode is a translation with a fundamental period T2 = 0.316 s; and the third mode is the planar torsion, with a fundamental period T3 = 0.178 s.
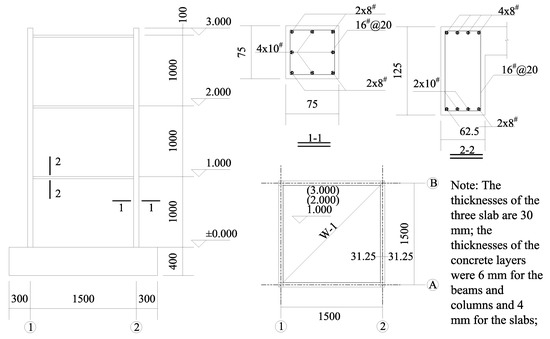
Figure 7.
Dimensions and reinforcements of the model structure (units: mm). [20] (Reproduced with permission from Huang, Q., from Study on spatial collapse responses of reinforced concrete frame structures under earthquake; published by Tongji Univerity, 2006.).

Table 1.
Concrete information.

Table 2.
Rebar information.

Table 3.
Load cases.
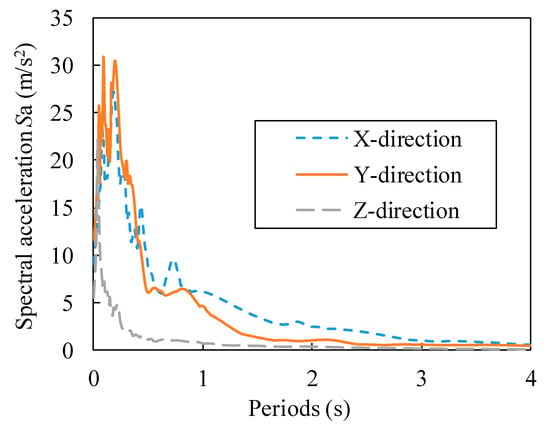
Figure 8.
Pseudo-acceleration spectra of Load Case 5.
4.1.2. Comparison of Simulation Results
Based on the information above, an FE model with fiber beam-column and multi-layered shell elements was established in MSC.Marc. Details of these element models have been reported in the published work [35]. The seismic responses of the structure under Load Cases 1–3 are used to validate the rationality of the FE model. Figure 9 shows the comparison of the maximum horizontal displacement in the X-direction between the test results and the FE simulation. The results indicate that the FE simulation agrees well with the test results.
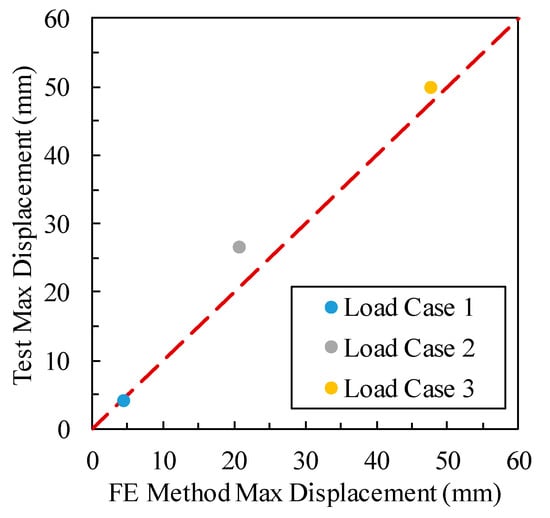
Figure 9.
Maximum horizontal displacement in the X-direction: FE method versus test.
In Load Case 5, a convergence problem occurred in the FE simulation (t = 4.16 s); therefore, the distribution of the ruins could not be obtained. The collapse process predicted by the FE simulation is shown in Figure 10. The colored contours in Figure 10 represent the longitudinal reinforcement yielding in the elements. The numerical simulation reveals that failures of the frame are initiated at both ends of the columns where the bending moment is large. Subsequent failures take place on the ground story, where the columns carry the largest lateral force. Large displacements occurred on the ground story, which leads to the collapse of the entire structure. In Figure 10c, the deformed shape of the structure at 4.16 s is shown.
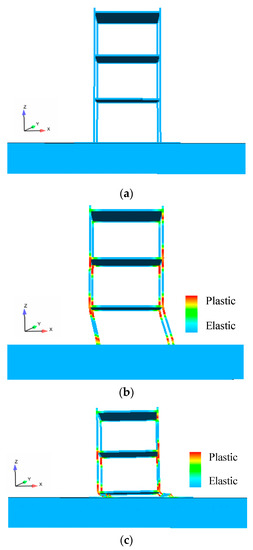
Figure 10.
Collapse process of the reinforced concrete frame subjected to the El-Centro ground motion record: (a) t = 0.00 s; (b) t = 3.88 s; (c) t = 4.16 s.
From the FE results, the initial moment of collapse is 3.88 s, using the collapse criterion in Section 3.2. A ¼-scale model is adopted; thus, the vertical collapse displacement of the collapse criterion is 0.25 m.
Subsequently, collapse simulation was performed using the proposed hybrid method. Figure 11b shows the distribution of ruins, which shows excellent agreement with the test results.

Figure 11.
Distribution of ruins: (a) test; [20] (Reproduced with permission from Huang, Q., from Study on spatial collapse responses of reinforced concrete frame structures under earthquake; published by Tongji Univerity, 2006.) (b) the proposed FE and BCB hybrid method; (c) BCB.
When BCB is used for collapse simulation, the structure collapses vertically, which agrees poorly with the test results, due to the low accuracy of the BCB simulation of the small-deformation stage. As shown in Figure 11c, the final positions of the three slabs of the three-story reinforced concrete frame almost entirely overlap.
Compared with the BCB results (Figure 11c), the distribution of the ruins obtained by the proposed hybrid method (Figure 11b) shows better agreement with the test results (Figure 11a).
The following observations are made from the comparison and analysis of the simulation methods:
- For FE models, a convergence problem occurs during the collapse simulation; therefore, the distribution of ruins cannot be easily obtained.
- The BCB simulation method is not sufficiently accurate for the small-deformation stage. Therefore, the collapse mode and the distribution of ruins differ substantially from the test results.
- The proposed hybrid method achieves the most satisfactory simulation of the structural collapse mode and the distribution of ruins.
4.2. Collapse and Ruins Simulation of a Real-World Library Building
To demonstrate the applicability of the proposed hybrid method to real-world complex structures, a case study of a multi-story reinforced concrete library building is performed. The building is a seven-story frame-shear wall structure, with a total height of 19.8 m and a building area of 15,938 m2. The total mass of the library building is 3.17 × 107 kg. All reinforcement consists of HRB400 reinforcing bars, whose strength is 400 MPa. The material properties and dimensions of the main structural members are shown in Table 4. Specifically, the library is located on a site class Ⅲ in GB50011-2010 [44], with an approximate equivalent shear wave velocity of 200 m/s for 30-m soil (VS30). The characteristic period of the site is 0.45 s. The building has an 8-degree seismic design intensity, where the peak ground acceleration is 200 cm/s2 for a design basis earthquake (DBE) with a return period of 475 years. There is no R-factor, coefficient of displacement or overstrength factor in Chinese seismic design code. However, according to Lu et al. [51] and American Society of Civil Engineers (ASCE) 7–10 [52], the design information of the building is similar to the following seismic design parameters: R factor = 4.5; overstrength factor = 2.5 and deflection amplification factor = 4.

Table 4.
The material properties and dimensions of the main structural members in the library building.
Three element types are used in this model: (a) fiber beam elements for beams and columns, (b) multilayer shell elements for shear walls, and (c) membrane elements for floor slabs. Details of these element models have been reported in the published work [35]. Figure 12a illustrates the three-dimensional FE model. The first mode of the model is a translational mode, with a fundamental period (elastic period) T1 = 0.37 s.
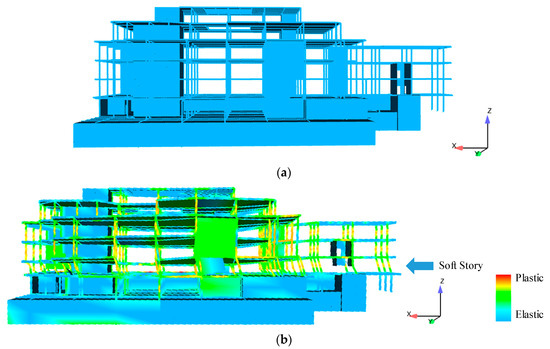
Figure 12.
FE model and simulation results of the library building: (a) FE model of the library building; (b) simulation results (t = 1.76 s).
The widely used El-Centro ground motion record, the same as that in Section 4.1, is adopted. To simulate the collapse behavior, the PGAs of the input motions along the X- and Y-directions are scaled to 4000 cm/s2. The nonlinear time history analysis results show that the maximum vertical displacement of the structural component reaches 1 m at 1.76 s, and the corresponding maximum lateral displacement is 0.97 m. The corresponding deformed shape of the structure is shown in Figure 12b. The colored contours in Figure 12 represent the longitudinal reinforcement yielding in the elements. The amount of shear walls on the third story is much lower than on the first and second stories, which results in a sudden change of stiffness. Therefore, the third story is the weak story of the building.
The geometric and material information of the FE model, and its displacement and velocity results, are mapped into Blender using the mapping methods discussed in Section 3. After pre-processing with BCB, a collapse simulation is performed using the Bullet physics engine. The collapse process of the library building is then determined, as shown in Figure 13.
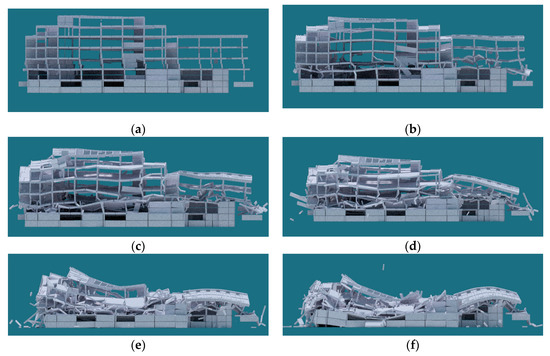

Figure 13.
Collapse process of the library building: (a) t = 2.01 s; (b) t = 3.01 s; (c) t = 3.64 s; (d) t = 4.26 s; (e) t = 5.51 s; (f) t = 6.97 s; (g) t = 14.26 s; (h) t = 18.43 s.
The damage first occurs at the soft story of the structure, as shown in Figure 12b. The structural deformation then increases substantially. Excessive deformation finally causes the collapse of the entire structure. The distribution of ruins is shown in Figure 14.

Figure 14.
Distribution of the library building ruins.
5. Conclusions
In this work, a hybrid framework for simulating building collapse and ruin scenarios using an FE method and physics engine is proposed, and the corresponding program FEM2RBD is developed. Shaking table tests of a three-story reinforced concrete frame and a real-world complex library building are performed to simulate the ruin scenarios. The following conclusions can be drawn:
- In the proposed hybrid framework, the FE method simulates structural behaviors during the small-deformation stage, and the physics engine simulates structural behaviors during the large-deformation stage. The proposed framework efficiently combines the advantages of the FE method and the physics engine.
- Using a shaking table test of a three-story reinforced concrete frame, the proposed hybrid simulation method is demonstrated to be more accurate than an approach based on the physics engine alone. The case study of a real-world complex library building shows the high-fidelity of the collapse simulation.
- The collision of structural components and the distribution of ruins after the collapse are considered in the proposed hybrid method. The proposed framework has great significance for simulating building collapse and ruin scenarios for post-earthquake rescue training.
Note that the proposed framework is also applicable to other FE software and physics engines, besides the MSC.Marc software and the Bullet physics engine that were used in this work.
Author Contributions
Conceptualization, X.L. and Z.Z.; data curation, X.L. and Z.Z.; formal analysis, Z.Z.; funding acquisition, X.L.; investigation, Y.T. and Z.Z.; methodology, Y.T. and Z.Z.; project administration, X.L.; resources, X.L.; software, Z.Z.; supervision, X.L.; validation, Z.Z.; visualization, Z.Z.; writing—original draft, Z.Z.; writing—review and editing, X.L., Y.T., Z.Y. and Z.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by BEIJING MUNICIPAL NATURAL SCIENCE FOUNDATION (grant number 8182025)
Acknowledgments
The authors would like to thank Xianglin Gu and Qinghua Huang for providing the copyright permission.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- de Bruycker, M.; Greco, D.; Annino, I.; Stazi, M.A.; de Ruggiero, N.; Triassi, M.; de Kettenis, Y.P.; Lechat, M.F. The 1980 earthquake in southern Italy: Rescue of trapped victims and mortality. Bull. World Heal. Organ. 1983, 61, 1021–1025. [Google Scholar]
- So, E.; Baker, H.; Spence, R. Casualty estimation through assessment of volume loss and external debris spread in building collapse. In Proceedings of the 16th European Conference on Earthquake Engineering, Thessaloniki, Greece, 18–21 June 2018. [Google Scholar]
- Tang, B.; Chen, Q.; Chen, X.; Glik, D.; Liu, X.; Liu, Y.; Zhang, L. Earthquake-related injuries among survivors: A systematic review and quantitative synthesis of the literature. Int. J. Disaster Risk Reduct. 2017, 21, 159–167. [Google Scholar] [CrossRef]
- Sun, X.; Liu, H.; Yang, C.; Wang, N. Virtual simulation-based scene modeling of helicopter earthquake search and rescue. In Proceedings of the AIP Conference Proceedings; AIP Publishing: New York, NY, USA, 2017; Volume 1839, p. 020140. [Google Scholar]
- Li, Y.; Lu, X.; Guan, H.; Ye, L. Progressive Collapse Resistance Demand of RC Frames under Catenary Mechanism. ACI Struct. J. 2014, 111. [Google Scholar] [CrossRef]
- Lu, X.; Lin, K.; Li, Y.; Guan, H.; Ren, P.; Zhou, Y. Experimental investigation of RC beam-slab substructures against progressive collapse subject to an edge-column-removal scenario. Eng. Struct. 2017, 149, 91–103. [Google Scholar] [CrossRef]
- Yang, T.; Han, Z.; Deng, N.; Chen, W. Collapse Responses of Concrete Frames Reinforced with BFRP Bars in Middle Column Removal Scenario. Appl. Sci. 2019, 9, 4436. [Google Scholar] [CrossRef]
- Chen, X.; Xie, W.; Xiao, Y.; Chen, Y.; Li, X. Progressive Collapse Analysis of SRC Frame-RC Core Tube Hybrid Structure. Appl. Sci. 2018, 8, 2316. [Google Scholar] [CrossRef]
- Feng, D.-C.; Kolay, C.; Ricles, J.M.; Li, J. Collapse simulation of reinforced concrete frame structures. Struct. Des. Tall Spéc. Build. 2015, 25, 578–601. [Google Scholar] [CrossRef]
- Lu, X.; Lu, X.; Guan, H.; Zhang, W.; Ye, L. Earthquake-induced collapse simulation of a super-tall mega-braced frame-core tube building. J. Constr. Steel Res. 2013, 82, 59–71. [Google Scholar] [CrossRef]
- Lu, X.; Lu, X.; Zhang, W.; Ye, L. Collapse simulation of a super high-rise building subjected to extremely strong earthquakes. Sci. China Ser. E Technol. Sci. 2011, 54, 2549–2560. [Google Scholar] [CrossRef]
- Xie, L.; Lu, X.; Guan, H.; Lu, X. Experimental Study and Numerical Model Calibration for Earthquake-Induced Collapse of RC Frames with Emphasis on Key Columns, Joints, and the Overall Structure. J. Earthq. Eng. 2015, 19, 1–25. [Google Scholar] [CrossRef]
- Lu, X.; Tian, Y.; Cen, S.; Guan, H.; Xie, L.; Wang, L. A High-Performance Quadrilateral Flat Shell Element for Seismic Collapse Simulation of Tall Buildings, and Its Implementation in OpenSees. J. Earthq. Eng. 2017, 22, 1662–1682. [Google Scholar] [CrossRef]
- Hartmann, D.; Breidt, M.; Nguyen, V.V.; Stangenberg, F.; Höhler, S.; Schweizerhof, K.; Mattern, S.; Blankenhorn, G.; Möller, B.; Liebscher, M. Structural collapse simulation under consideration of uncertainty—Fundamental concept and results. Comput. Struct. 2008, 86, 2064–2078. [Google Scholar] [CrossRef]
- Grunwald, C.; Khalil, A.; Schaufelberger, B.; Ricciardi, E.M.; Pellecchia, C.; de Iuliis, E.; Riedel, W. Reliability of collapse simulation—Comparing finite and applied element method at different levels. Eng. Struct. 2018, 176, 265–278. [Google Scholar] [CrossRef]
- Gu, X.-L.; Yu, Q.-Q.; Li, Y.; Lin, F. Collapse Process Analysis of Reinforced Concrete Super-Large Cooling Towers Induced by Failure of Columns. J. Perform. Constr. Facil. 2017, 31, 04017037. [Google Scholar] [CrossRef]
- Lignos, D.G.; Hikino, T.; Matsuoka, Y.; Nakashima, M. Collapse Assessment of Steel Moment Frames Based on E-Defense Full-Scale Shake Table Collapse Tests. J. Struct. Eng. 2013, 139, 120–132. [Google Scholar] [CrossRef]
- Wu, C.L.; Loh, C.H.; Yang, Y.S. Shake Table Tests on Gravity Load Collapse of Low-Ductility RC Frames Under near-Fault Earthquake Excitation. Adv. Exp. Struct. Eng. 2006, 725–732. Available online: http://www.cc.ntut.edu.tw/~ysyang/publications/aese2005/T087.PDF (accessed on 22 May 2020).
- Lu, Z.; Chen, X.; Lu, X.; Yang, Z. Shaking table test and numerical simulation of an RC frame-core tube structure for earthquake-induced collapse. Earthq. Eng. Struct. Dyn. 2016, 45, 1537–1556. [Google Scholar] [CrossRef]
- Huang, Q. Study on Spatial Collapse Responses of Reinforced Concrete Frame Structures under Earthquake. Ph.D. Thesis, Tongji University, Shanghai, China, 2006. [Google Scholar]
- Gu, X.; Wang, X.; Yin, X.; Lin, F.; Hou, J. Collapse simulation of reinforced concrete moment frames considering impact actions among blocks. Eng. Struct. 2014, 65, 30–41. [Google Scholar] [CrossRef]
- Lu, Z.; He, X.; Zhou, Y. Discrete element method-based collapse simulation, validation, and application to frame structures. Struct. Infrastruct. Eng. 2017, 14, 538–549. [Google Scholar] [CrossRef]
- Salem, H.; El-Fouly, A.; Tagel-Din, H. Toward an economic design of reinforced concrete structures against progressive collapse. Eng. Struct. 2011, 33, 3341–3350. [Google Scholar] [CrossRef]
- Millington, I. Game Physics Engine Development; Informa UK Limited: London, UK, 2007. [Google Scholar]
- He, H.; Zheng, J.; Sun, Q.; Li, Z. Simulation of Realistic Particles with Bullet Physics Engine. In Proceedings of the E3S Web of Conferences; EDP Sciences: Les Ulis, France, 2019; Volume 92, p. 14004. [Google Scholar]
- Xu, Z.; Lu, X.; Guan, H.; Ren, A. Physics engine-driven visualization of deactivated elements and its application in bridge collapse simulation. Autom. Constr. 2013, 35, 471–481. [Google Scholar] [CrossRef]
- Zhou, B.; Jia, Q.; Chen, Z. The Research and Development of the Earthquake Ruins Computer Aided Design System for Rescue Training. In Proceedings of the 2017 4th International Conference on Information Science and Control Engineering (ICISCE); Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2017; pp. 1303–1307. [Google Scholar]
- Xu, Z.; Lu, X.; Guan, H.; Han, B.; Ren, A. Seismic damage simulation in urban areas based on a high-fidelity structural model and a physics engine. Nat. Hazards 2013, 71, 1679–1693. [Google Scholar] [CrossRef]
- Oliver, W.; Kostack, K. Final Release of the Blender and Bullet Physics Engine Based on Fast On-Site Assessment Tool. Available online: https://inachuslaurea.files.wordpress.com/2019/07/inachus_d3.5_luas_v1.0.pdf. (accessed on 23 May 2020).
- Kostack Studio. Christchurch Earthquake Simulation & Pyne Gould Building Collapse (Inachus). Available online: https://www.youtube.com/watch?v=TCJq_2-q34k&t=24s. (accessed on 23 May 2020).
- Hamano, T.; Onosato, M.; Tanaka, F. Performance comparison of physics engines to accelerate house-collapsing simulations. In Proceedings of the 2016 IEEE International Symposium on Safety, Security, and Rescue Robotics (SSRR), Lausanne, Switzerland, 23–27 October 2016; pp. 358–363. [Google Scholar] [CrossRef]
- Boeing, A.; Bräunl, T. Evaluation of real-time physics simulation systems. In Proceedings of the 5th International Conference on Technological Ecosystems for Enhancing Multiculturality—TEEM 2017; Association for Computing Machinery (ACM): New York, NY, USA, 2007; pp. 281–288. [Google Scholar]
- MSCSoftware. Marc. Available online: https://www.mscsoftware.com/product/marc (accessed on 23 May 2020).
- Lin, X.; Kato, M.; Zhang, L.; Nakashima, M. Quantitative investigation on collapse margin of steel high-rise buildings subjected to extremely severe earthquakes. Earthq. Eng. Eng. Vib. 2018, 17, 445–457. [Google Scholar] [CrossRef]
- Lu, X.; Guan, H.; Ye, L. Collapse simulation of reinforced concrete high-rise building induced by extreme earthquakes. Earthq. Eng. Struct. Dyn. 2012, 42, 705–723. [Google Scholar] [CrossRef]
- Jeng, V.; Tzeng, W. Assessment of seismic pounding hazard for Taipei City. Eng. Struct. 2000, 22, 459–471. [Google Scholar] [CrossRef]
- Bazan, E.; Bielak, J. Earthquake Response of Nonlinear Building-Foundation Systems. Soil-Struct. Interact. 1987, 43, 13–24. [Google Scholar] [CrossRef]
- Anajafi, H.; Medina, R.A. Lessons Learned from Evaluating the Responses of Instrumented Buildings in the United States: The Effects of Supporting Building Characteristics on Floor Response Spectra. Earthq. Spectra 2019, 35, 159–191. [Google Scholar] [CrossRef]
- Léger, P.; Dussault, S. Seismic? Energy Dissipation in MDOF Structures. J. Struct. Eng. 1992, 118, 1251–1269. [Google Scholar] [CrossRef]
- Anajafi, H.; Medina, R.A.; Santini-Bell, E. Effects of the improper modeling of viscous damping on the first-mode and higher-mode dominated responses of base-isolated buildings. Earthq. Eng. Struct. Dyn. 2019, 49, 51–73. [Google Scholar] [CrossRef]
- Charney, F.A. Unintended Consequences of Modeling Damping in Structures. J. Struct. Eng. 2008, 134, 581–592. [Google Scholar] [CrossRef]
- Chopra, A.K.; McKenna, F. Modeling viscous damping in nonlinear response history analysis of buildings for earthquake excitation. Earthq. Eng. Struct. Dyn. 2015, 45, 193–211. [Google Scholar] [CrossRef]
- Blender. Blender 2.82 Manual. Available online: https://docs.blender.org/manual/en/latest/index.html (accessed on 23 May 2020).
- National Standard of the People’s Republic of China. Code for Seismic Design of Building (GB50011-2010); China Architecture and Building: Beijing, China, 2010.
- Federal Emergency Management Agency. Prestandard and Commentary for the Seismic Rehabilitation of Buildings (FEMA 356); Federal Emergency Management Agency: Washington, DC, USA, 2000.
- Zhao, P.; Yu, X.; Lu, X. Collapse capacity assessment of RC frame structures using explicit algorithm. Eng. Mech. 2020, 37, 77–87. [Google Scholar] [CrossRef]
- Lu, X.; Jiang, Q.; Miao, Z. Elasto-Plastic Analysis of Buildings Against Earthquake, 2nd ed.; China Architecture & Building Press: Beijing, China, 2015. [Google Scholar]
- Shi, W.; Ye, L.; Lu, X.; Tang, D.Y. Study on the collapse-resistant capacity of RC frames with different seismic fortification levels. Eng. Mech. 2011, 28, 41–48. [Google Scholar]
- Villaverde, R. Methods to Assess the Seismic Collapse Capacity of Building Structures: State of the Art. J. Struct. Eng. 2007, 133, 57–66. [Google Scholar] [CrossRef]
- Erwin, C. Bullet Physics Simulation Introduction to Rigid Body Dynamics and Collision Detection. Available online: https://docs.google.com/presentation/d/1-UqEzGEHdskq8blwNWqdgnmUDwZDPjlZUvg437z7XCM/edit?usp=sharing (accessed on 23 May 2020).
- Lu, X.; Li, M.; Guan, H.; Lu, X.; Ye, L. A comparative case study on seismic design of tall RC frame-core-tube structures in China and USA. Struct. Des. Tall Spéc. Build. 2015, 24, 687–702. [Google Scholar] [CrossRef]
- Asce Minimum Design Loads for Buildings and Other Structures. Minimum Design Loads for Buildings and Other Structures; American Society of Civil Engineers: Reston, VA, USA, 2013. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).