Improved Homotopy Perturbation Method for Geometrically Nonlinear Analysis of Space Trusses
Abstract
:1. Introduction
2. Geometrically Nonlinear Analysis of Trusses
2.1. Geometrically Nonlinear Analysis of Trusses
2.2. Tangent Stiffness Matrix for Members
3. Nonlinear Analysis Algorithms
3.1. Newton–Raphson Method
3.2. Improved Perturbation Method for the Nonlinear Problem
3.3. Implementation of Perturbation Method in Structural Engineering
4. Results and Computational Examples
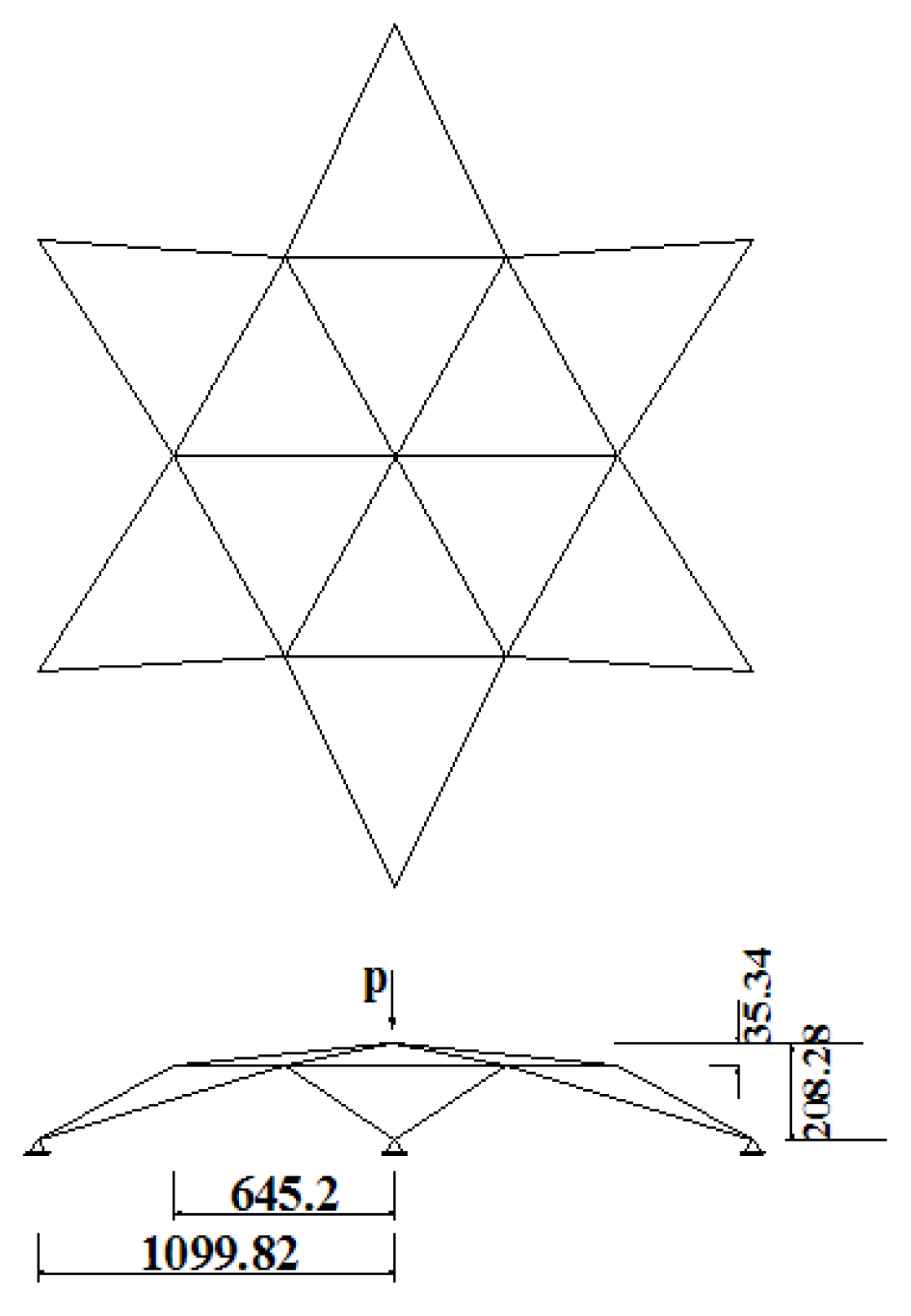
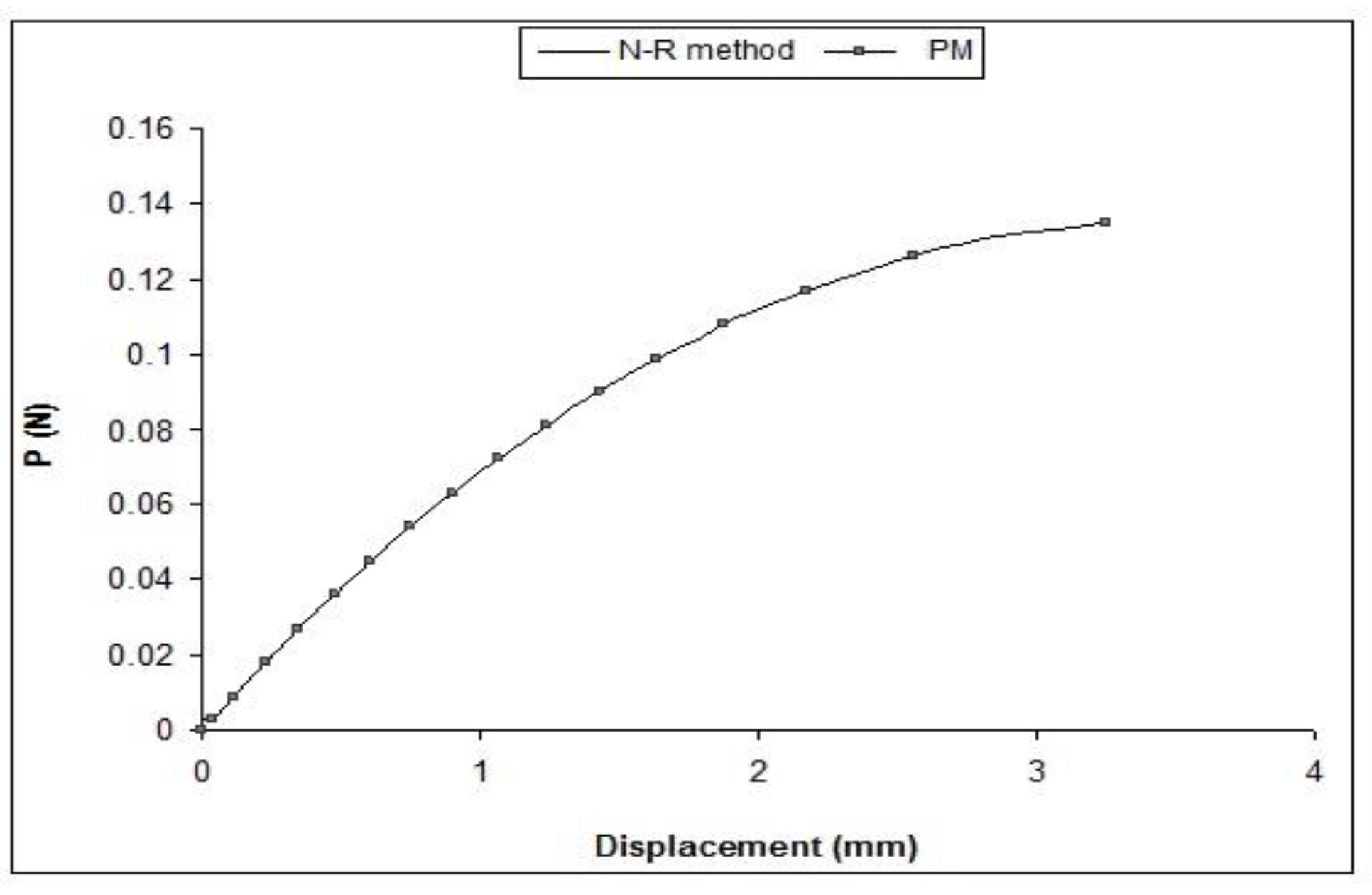
4.1. Example 1: 24-Member Space Truss
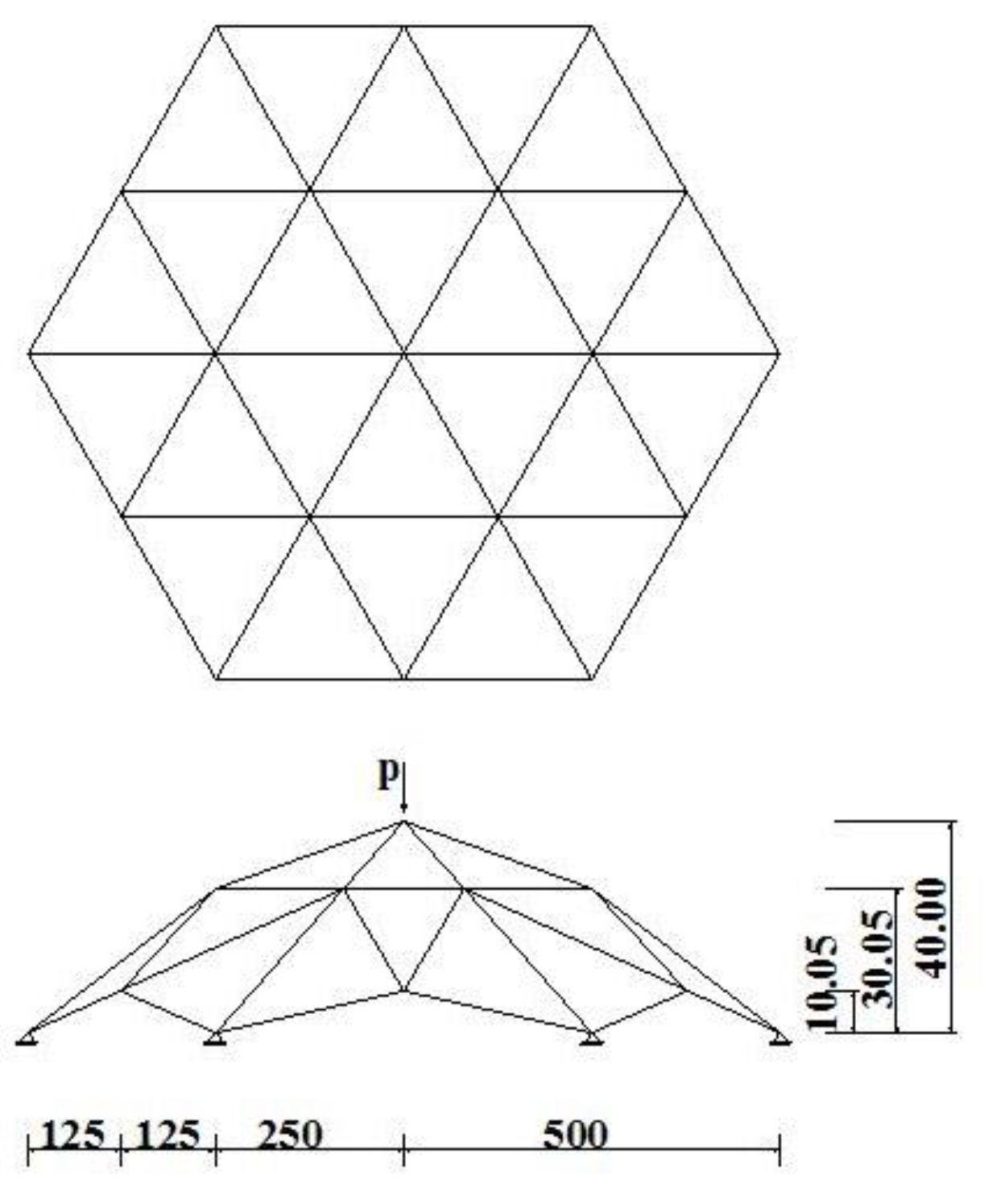
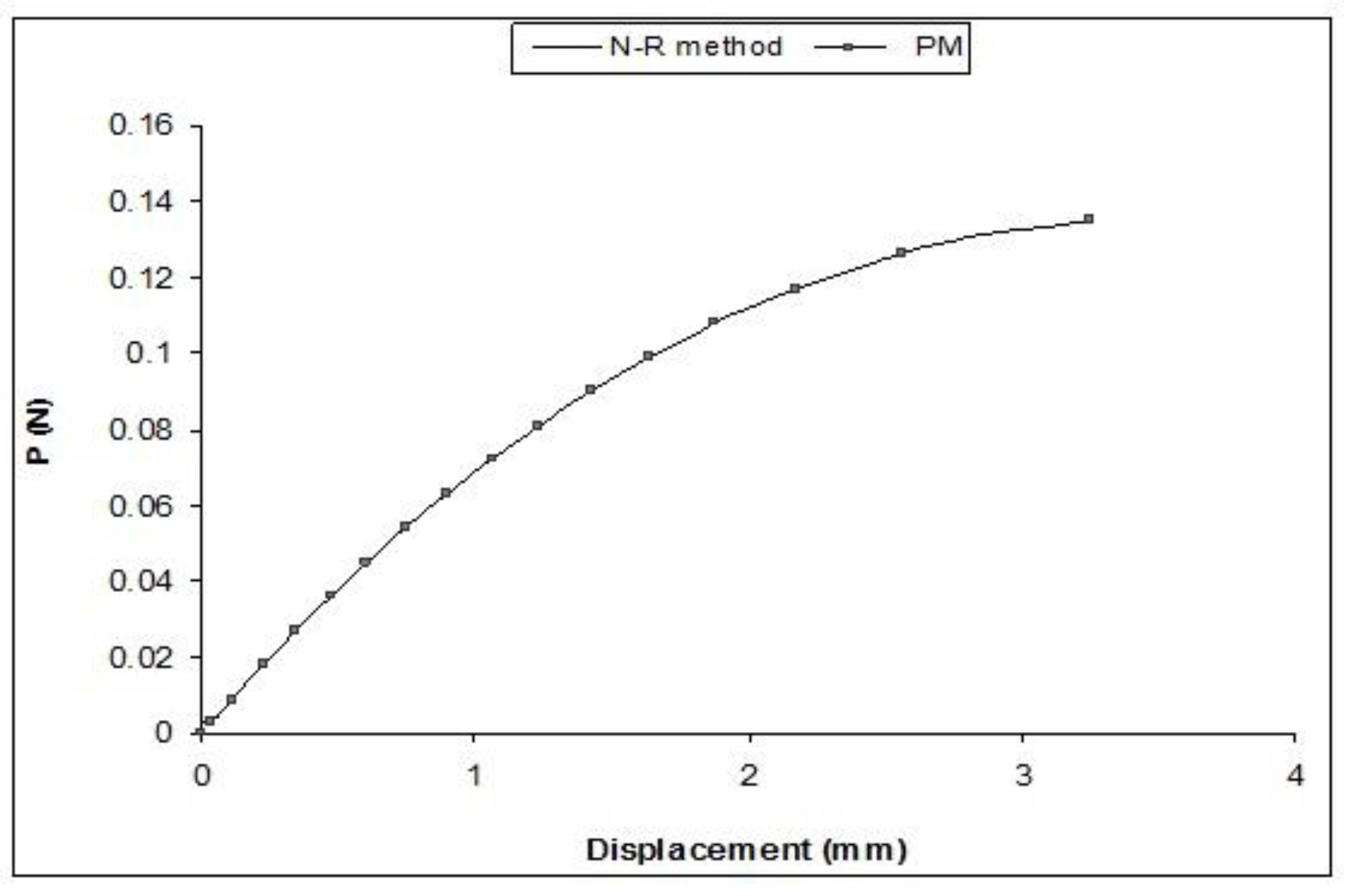
4.2. Example 2: 42-Member Space Truss
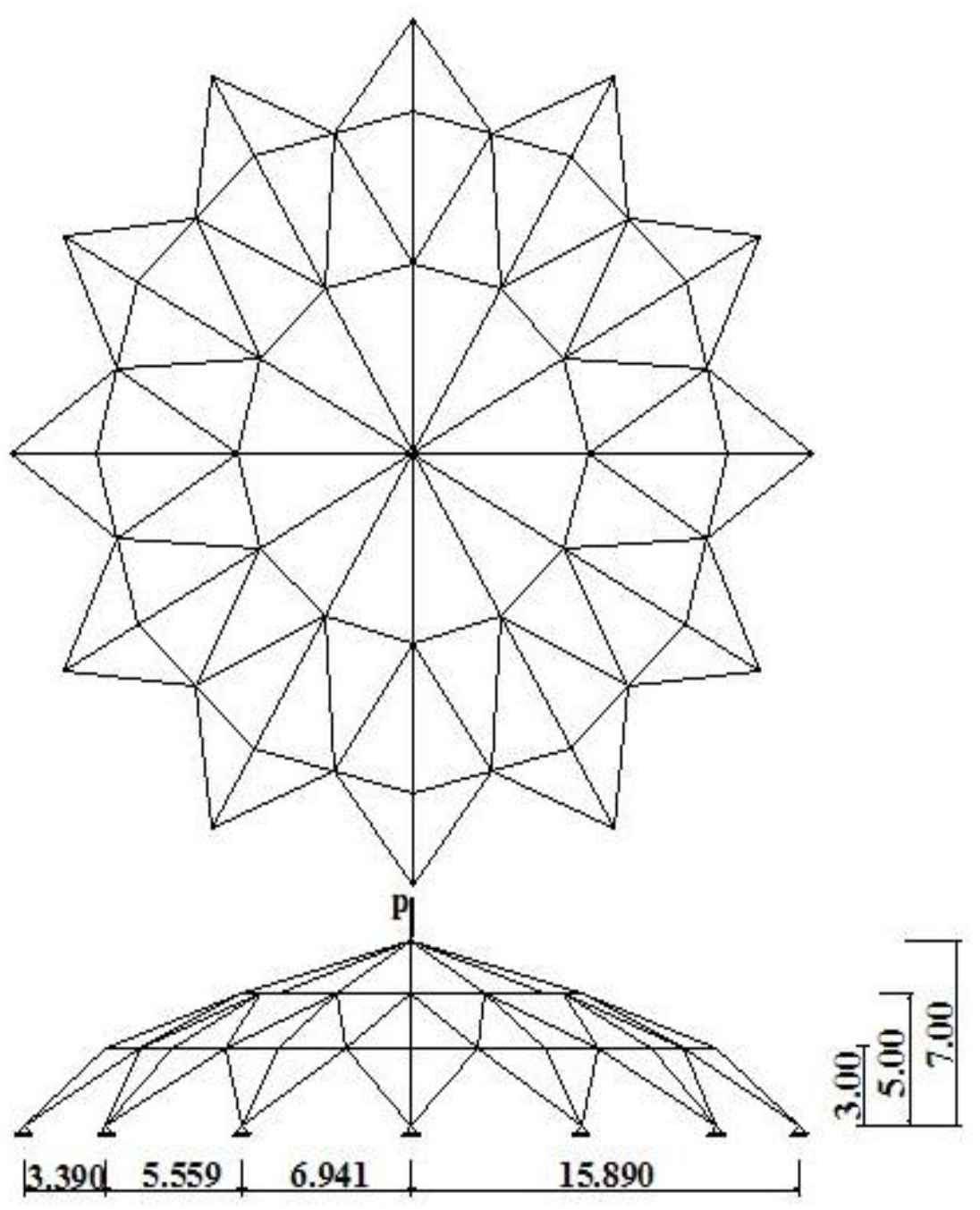
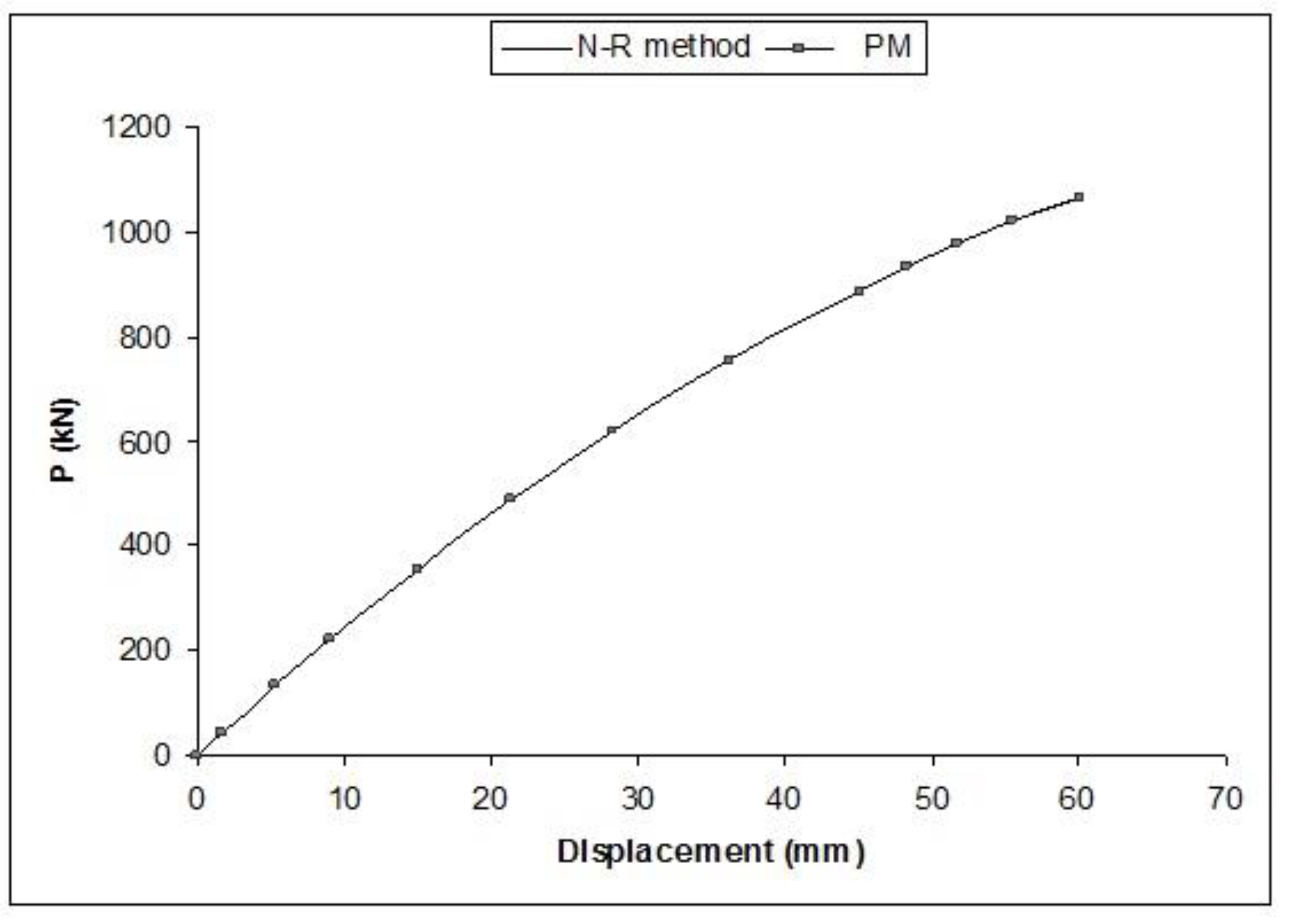
4.3. Example 3: 120-Member Space Truss
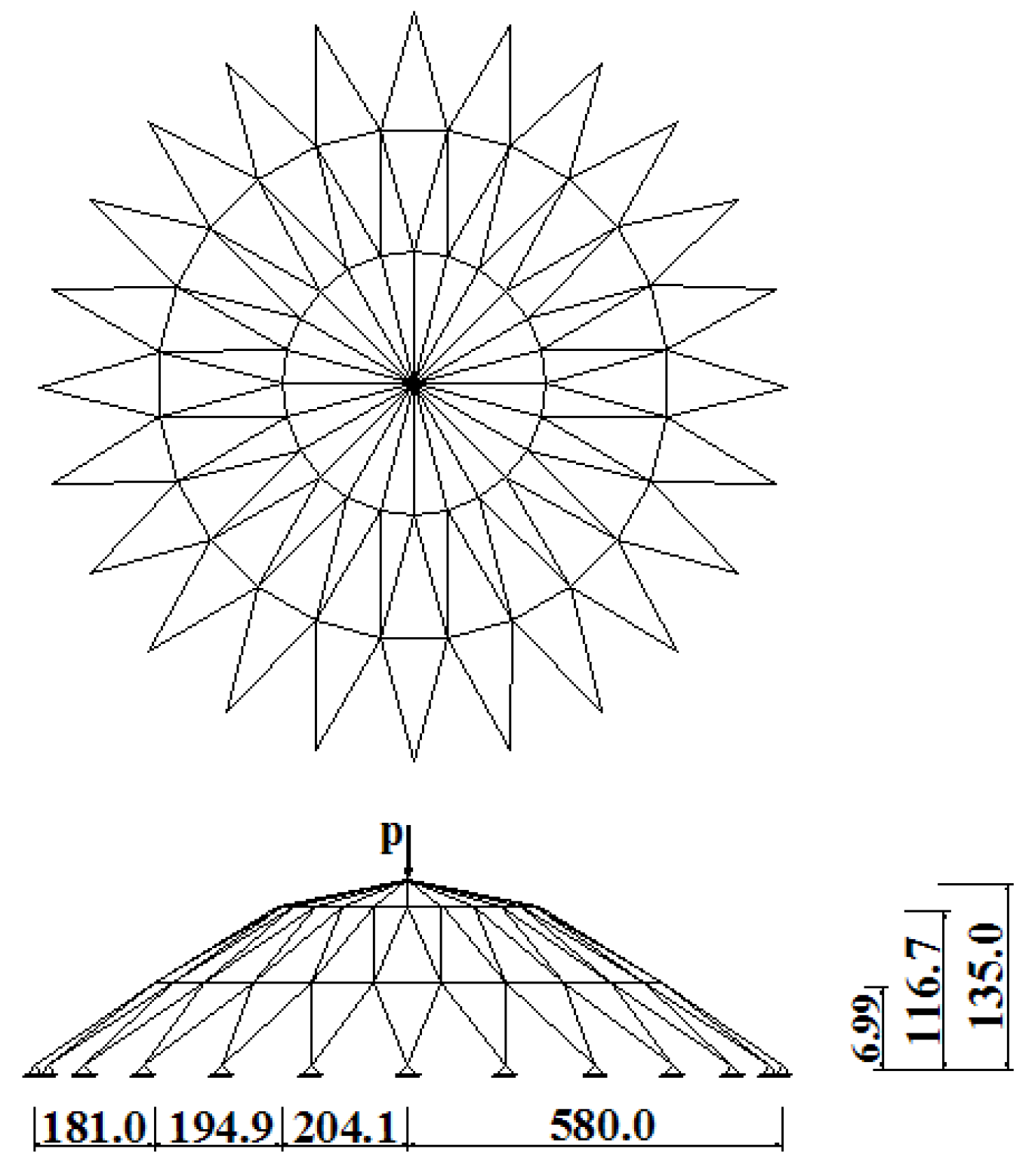
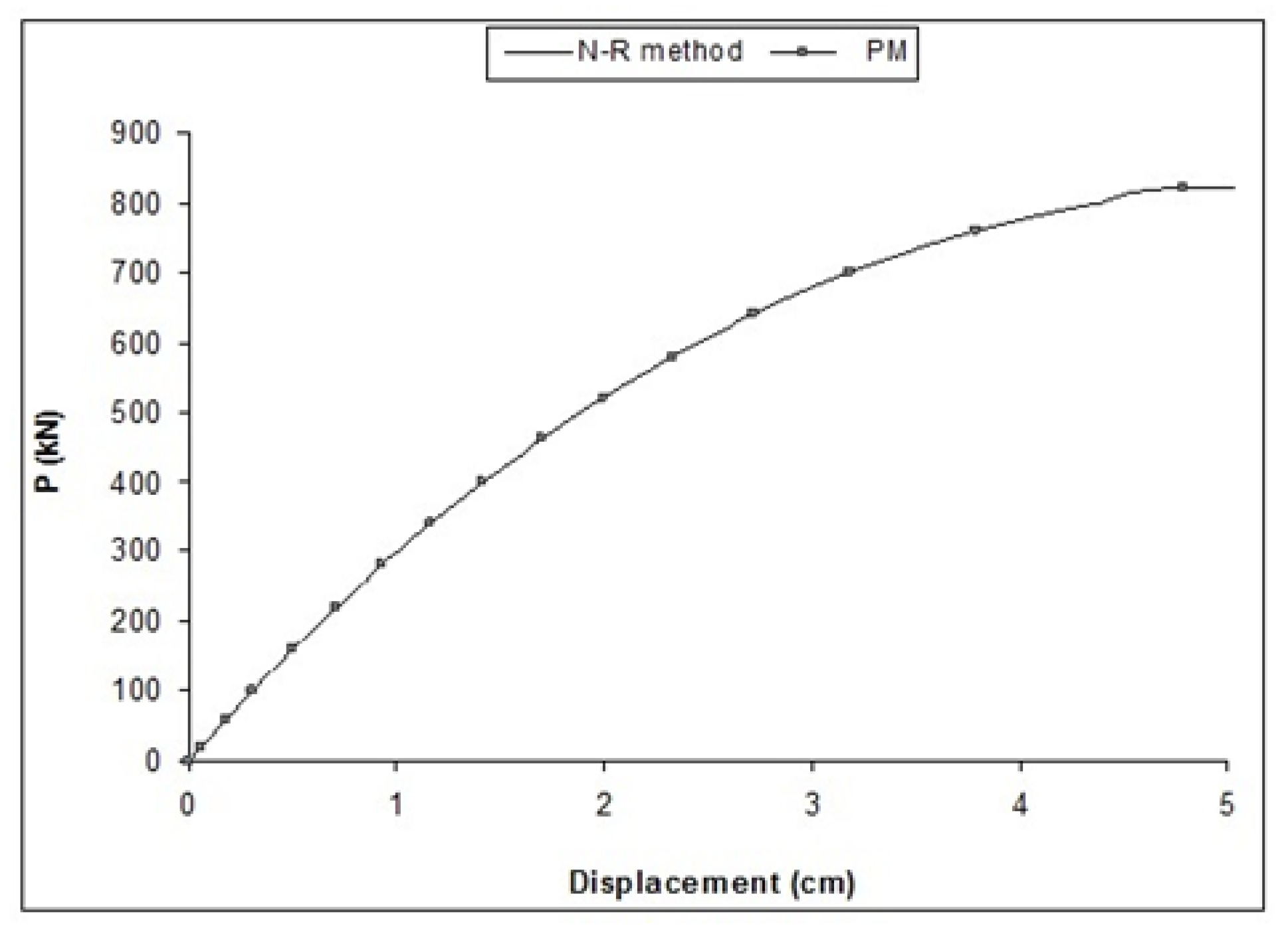
4.4. Example 4: 168-Member Space Truss
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Saffari, H.; Baghlani, A.; Mirzai, N.M.; Mansouri, I. A new approach for convergence acceleration of iterative methods in structural analysis. Int. J. Comput. Methods 2013, 10, 1350022. [Google Scholar] [CrossRef]
- Rezaiee-Pajand, M.; Naserian, R. Using residual areas for geometrically nonlinear structural analysis. Ocean Eng. 2015, 105, 327–335. [Google Scholar] [CrossRef]
- Sangeetha, P.; Senthil, R. A study on ultimate behaviour of composite space truss. KSCE J. Civ. Eng. 2017, 21, 950–954. [Google Scholar] [CrossRef]
- Zhang, D.; Li, F.; Shao, F.; Fan, C. Evaluation of Equivalent Bending Stiffness by Simplified Theoretical Solution for an FRP–aluminum Deck–truss Structure. KSCE J. Civ. Eng. 2019, 23, 367–375. [Google Scholar] [CrossRef]
- Blandford, G.E. Large deformation analysis of inelastic space truss structures. J. Struct. Eng. 1996, 122, 407–415. [Google Scholar] [CrossRef]
- Hill, C.D.; Blandford, G.E.; Wang, S.T. Post-buckling analysis of steel space trusses. J. Struct. Eng. (United States) 1991, 117, 3829–3831. [Google Scholar] [CrossRef]
- Kassimali, A.; Bidhendi, E. Stability of trusses under dynamic loads. Comput. Struct. 1988, 29, 381–392. [Google Scholar] [CrossRef]
- Mansouri, I.; Farzampour, A. Buckling assessment of imperfect cylindrical shells under axial loading using a GEP technique. E-GFOS 2018, 9, 89–100. [Google Scholar] [CrossRef]
- Papadrakakis, M.; Theoharis, A.P. Tracing post-limit-point paths with incomplete or without factorization of the stiffness matrix. Comput. Methods Appl. Mech. Eng. 1991, 88, 165–187. [Google Scholar] [CrossRef]
- Zhu, K.; Al-Bermani, F.G.A.; Kitipornchai, S. Nonlinear dynamic analysis of lattice structures. Comput. Struct. 1994, 52, 9–15. [Google Scholar] [CrossRef]
- Thai, H.T.; Kim, S.E. Large deflection inelastic analysis of space trusses using generalized displacement control method. J. Constr. Steel Res. 2009, 65, 1987–1994. [Google Scholar] [CrossRef]
- Greco, M.; Ferreira, I.P. Logarithmic strain measure applied to the nonlinear positional formulation for space truss analysis. Finite Elem. Anal. Des. 2009, 45, 632–639. [Google Scholar] [CrossRef]
- Liu, C.J.; Zheng, Z.L.; Yang, X.Y.; Guo, J.J. Geometric Nonlinear Vibration Analysis for Pretensioned Rectangular Orthotropic Membrane. Int. Appl. Mech. 2018, 54, 104–119. [Google Scholar] [CrossRef]
- Kao, R. A comparison of Newton-Raphson methods and incremental procedures for geometrically nonlinear analysis. Comput. Struct. 1974, 4, 1091–1097. [Google Scholar] [CrossRef]
- Batoz, J.-L.; Dhatt, G. Incremental displacement algorithms for nonlinear problems. Int. J. Numer. Methods Eng. 1979, 14, 1262–1267. [Google Scholar] [CrossRef]
- Lee, H.-W.; Cho, J.-R. Geometrically Non-linear Analysis of Elastic Structures by Petrov-Galerkin Natural Element Method. KSCE J. Civ. Eng. 2019, 23, 1756–1765. [Google Scholar] [CrossRef]
- Mansouri, I.; Saffari, H. An efficient nonlinear analysis of 2D frames using a Newton-like technique. Arch. Civ. Mech. Eng. 2012, 12, 485–492. [Google Scholar] [CrossRef]
- Mansouri, I.; Saffari, H. Geometrical and material nonlinear analysis of structures under static and dynamic loading based on quadratic path. Sci. Iran. 2013, 20, 1595–1604. [Google Scholar]
- Mansouri, I.; Saffari, H. A fast hybrid algorithm for nonlinear analysis of structures. Asian J. Civ. Eng. 2014, 15, 213–230. [Google Scholar]
- Saffari, H.; Mansouri, I.; Bagheripour, M.H.; Dehghani, H. Elasto-plastic analysis of steel plane frames using Homotopy Perturbation Method. J. Constr. Steel Res. 2012, 70, 350–357. [Google Scholar] [CrossRef]
- Saffari, H.; Mirzai, N.M.; Mansouri, I. An accelerated incremental algorithm to trace the nonlinear equilibrium path of structures. Lat. Am. J. Solids Struct. 2012, 9, 425–442. [Google Scholar] [CrossRef] [Green Version]
- Saffari, H.; Mirzai, N.M.; Mansouri, I.; Bagheripour, M.H. Efficient numerical method in second-order inelastic analysis of space trusses. J. Comput. Civil. Eng. 2013, 27, 129–138. [Google Scholar] [CrossRef]
- Golbabai, A.; Javidi, M. Newton-like iterative methods for solving system of non-linear equations. Appl. Math. Comput. 2007, 192, 546–551. [Google Scholar] [CrossRef]
- Lebofsky, S. Numerically Generated Tangent Stiffness Matrices for Geometrically Non-Linear Structures. Master’s Thesis, University of Washington, Washington, DC, USA, 2013. [Google Scholar]
- Crisfield, M.A. Nonlinear Finite Element Analysis of Solid and Structure; John Wiley: Hoboken, NJ, USA, 2006. [Google Scholar]
- Bhatti, M. Advanced Topics in Finite Element Analysis of Structure; John Wiley: Hoboken, NJ, USA, 2006. [Google Scholar]
- Vahidi, A.R.; Babolian, E.; Azimzadeh, Z. An Improvement to the Homotopy Perturbation Method for Solving Nonlinear Duffing’s Equations. Bull. Malays. Math. Sci. Soc. 2018, 41, 1105–1117. [Google Scholar] [CrossRef]
- Saffari, H.; Mansouri, I. Non-linear analysis of structures using two-point method. Int. J. Nonlin. Mech. 2011, 46, 834–840. [Google Scholar] [CrossRef]
- Saka, M.P.; Ulker, M. Optimum design of geometrically nonlinear space trusses. Comput. Struct. 1992, 42, 289–299. [Google Scholar] [CrossRef]

| Decrease Percentage | Present Method | Newton Method | |||
|---|---|---|---|---|---|
| Iteration no. | Time (s) | Iteration No. | Time (s) | Iteration No. | Time (s) |
| 27 | 10.93 | 79 | 0.145 | 108 | 0.1628 |
| Decrease Percentage | Present Method | Newton Method | |||
|---|---|---|---|---|---|
| Iteration no. | Time (s) | Iteration No. | Time (s) | Iteration No. | Time (s) |
| 29 | 12.89 | 107 | 0.3107 | 151 | 0.3567 |
| Decrease Percentage | Present Method | Newton Method | |||
|---|---|---|---|---|---|
| Iteration No. | Time (s) | Iteration No. | Time (s) | Iteration No. | Time (s) |
| 31 | 10.43 | 51 | 0.4894 | 74 | 0.5464 |
| Decrease Percentage | Present Method | Newton Method | |||
|---|---|---|---|---|---|
| Iteration No. | Time (s) | Iteration No. | Time (s) | Iteration No. | Time (s) |
| 29 | 8.79 | 88 | 1.224 | 124 | 1.342 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dehghani, H.; Mansouri, I.; Farzampour, A.; Hu, J.W. Improved Homotopy Perturbation Method for Geometrically Nonlinear Analysis of Space Trusses. Appl. Sci. 2020, 10, 2987. https://doi.org/10.3390/app10082987
Dehghani H, Mansouri I, Farzampour A, Hu JW. Improved Homotopy Perturbation Method for Geometrically Nonlinear Analysis of Space Trusses. Applied Sciences. 2020; 10(8):2987. https://doi.org/10.3390/app10082987
Chicago/Turabian StyleDehghani, Hamzeh, Iman Mansouri, Alireza Farzampour, and Jong Wan Hu. 2020. "Improved Homotopy Perturbation Method for Geometrically Nonlinear Analysis of Space Trusses" Applied Sciences 10, no. 8: 2987. https://doi.org/10.3390/app10082987





