A New Differential Mutation Based Adaptive Harmony Search Algorithm for Global Optimization

Abstract

The canonical harmony search (HS) algorithm generates a new solution by using random adjustment. However, the beneficial effects of harmony memory are not well considered. In order to make full use of harmony memory to generate new solutions, this paper proposes a new adaptive harmony search algorithm (aHSDE) with a differential mutation, periodic learning and linear population size reduction strategy for global optimization. Differential mutation is used for pitch adjustment, which provides a promising direction guidance to adjust the bandwidth. To balance the diversity and convergence of harmony memory, a linear reducing strategy of harmony memory is proposed with iterations. Meanwhile, periodic learning is used to adaptively modify the pitch adjusting rate and the scaling factor to improve the adaptability of the algorithm. The effects and the cooperation of the proposed strategies and the key parameters are analyzed in detail. Experimental comparison among well-known HS variants and several state-of-the-art evolutionary algorithms on CEC 2014 benchmark indicates that the aHSDE has a very competitive performance.

1. Introduction

The Harmony Search (HS) algorithm is one of the Evolutionary Algorithms (EA), taking inspiration from the music improvisation process, which was proposed by Geem et al. [1] in 2001. It is an emerging population-based metaheuristic optimization algorithm which simulates the improvisation behavior of musicians by repeatedly adjusting the instruments, eventually generating a harmony state. In HS, the harmony of musical instrument tones is regarded as a solution vector of the optimization problem. The evaluation of musical harmonies corresponds to the objective function value.

There are four main control parameters in a canonical HS algorithm [1], including the harmony memory size (HMS), harmony memory considering rate (HMCR), pitch adjusting rate (PAR) and the bandwidth (bw). However, it is well known that the optimal setting of these parameters [2] depends on the problem. Therefore, when HS is applied to real-world problems, it is necessary to adjust the control parameters to obtain the desired results. Overall, it has attracted more and more attention and a variety of HS variants have been proposed.

In order to improve its efficiency or to overcome some shortcomings, the original HS operators have been adapted and/or new operators have been introduced. Mahdavi et al. [3] proposed an improved harmony search algorithm (IHS) in which PAR is designed to increase linearly, while bw decreases exponentially with the increase of the number of iterations. Pan et al. [4] proposed a self-adaptive global-best harmony search (SGHS). It employs a new improvisation scheme and uses a parameter adjustment strategy to generate a new solution with a learning period. Combining the harmony search algorithm with particle swarm optimization (PSO) [5], Valian et al. [6] presented an intelligent global harmony search algorithm (IGHS) which has excellent performance compared with its competitors. To enhance the search efficiency and effectiveness, a self-adaptive global-best harmony search algorithm [7] is developed. The proposed algorithm takes full advantage of the valuable information hidden in the harmony memory to devise a high-performance search strategy. It also integrates a self-adaptive mechanism to develop a parameter-setting-free technique [8]. Ouyang et al. [9] proposed an improved harmony search algorithm with three key features: adaptive global pitch adjustment, opposition-based learning and competition selection mechanism. Inspired from the simulated annealing of accepted inferior solutions, a hybrid harmony search algorithm (HSA) [10] is proposed. It accepts the inferior harmonies with a probability determined by a temperature parameter. Zhu et al. [11] proposed an improved differential-based harmony search algorithm with a linear dynamic domain which utilized two main innovative strategies. Focusing on the historical development of algorithm structures, Zhang and Geem [12] reviewed various modified and hybrid HS methods, which included the adaption of the original operators, parameter adaption, hybrid methods, handling multi-objective optimization and constraint handling.

One question is naturally proposed—why does HS work on various problems from science and engineering [13]? The unique stochastic derivative [14] gives information on the probabilistic inclination to select certain discrete points based on multiple vectors stored in HM for a discrete problem. Although HS is easy to implement and has a simple structure [13], it has shown its superiority with more complex optimization algorithms, and has been applied to many practical problems [12,15,16,17]. HS has been successfully used in a wide range of applications [18,19,20,21,22,23,24,25], which has attracted a lot of research attention undertaken to further improve its performance. Combining HS and local search, a novel sensor localization approach is proposed by Manjarres et al. [26]. Minimizing energy consumption and maximizing the network lifetime of a wireless sensor network (WSN) problem using the HS algorithm was closely studied [27,28,29,30]. Degertekin [31] optimized the frame size of truss structures by harmony search algorithm. Compared with the genetic algorithm for max-cut problem [32], the harmony search algorithm has advantages of generating new vectors after considering all of the existing vectors and parameters. Boryczka and Szwarc [33] proposed a harmony search algorithm with the additional improvement of harmony memory for asymmetric traveling salesman problems, which eliminates the imperfectness revealed in the previous research. Seyedhosseini et al. [34] researched the portfolio optimization problem using a mean-semi variance approach based on harmony search and an artificial bee colony. HSA [35] was used in reservoir engineering-assisted history, matching questions of different complex degrees, which are two material balance history matches of different scales and one reservoir history matching.

However, HS and its variants usually have the following drawbacks, which are also our research motivation.

(1)

For the pitch adjustment operator of HS, a larger bandwidth is easier to jump out of the local optimum, while a smaller bandwidth biases to find a promising solution for the fining search. Therefore, a fixed step size is not an ideal choice.

(2)

It is difficult to find the optimal solution with a constant execution probability and an adaptive adjusting method is required.

(3)

Parameter HMS has an important influence on the performance of algorithms. An adaptive sizing HMS is possible to enhance the performance of the algorithm.

Therefore, an adaptive harmony search algorithm is proposed with differential evolution mutation, periodic learning and linear population size reduction (aHSDE). The main contributions of this paper are as follows.

(1)

The pitch adjustment strategy is implemented with differential mutation. Adjust the pitch adjusting rate PAR and the scaling factor F with periodic learning strategy. Linear population size reduction strategy is adopted for HMS changing scheme.

(2)

The cooperation and effects of several strategies are analyzed step by step.

The organization of this paper is as follows. Section 2 reviews the canonical HS and several improved variants. In Section 3, the composite strategies and algorithm aHSDE are proposed. In Section 4, the effects and the cooperation of the proposed strategies and parameters analysis are presented. The comprehensive performance comparison with other HS variants and other state-of-the-art EAs are presented in Section 5. Finally, Section 6 concludes the paper.

2. Harmony Search and Several Variants

2.1. Harmony Search Algorithm

The harmony search algorithm is a new population-based metaheuristic optimization algorithm [1], which is inspired by the improvisation process of music. The improvisation process is modeled as an iterative optimization method and the musicians’ musical instruments improvise to produce a better harmony [36]. The basic steps are described in detail in Algorithm 1.

Algorithm 1:	General Framework of the Harmony Search (HS).
1:	//Initialize the problem and algorithm parameters//      $f\left(x\right)$: objective function      HMS: harmony memory size      HMCR: harmony memory considering rate      PAR: pitch adjusting rate      bw: bandwidth      DIM: dimension of decision variable      $MAX\_NFE$: maximum number of function evaluations $L_i,U_i$: the lower and upper bounds of the i-th component for the decision vector
2:	//Initialize the harmony memory$\left(x^1,x^2,\cdots ,x^{HMS}\right)$// $x_i^j=L_i+rand\left(0,1\right)·\left(U_i-L_i\right)$
3:	//Improvise a new harmony$x^{new}=\left(x_1^{new},x_2^{new},\cdots ,x_{DIM}^{new}\right)$// $for each i \in \left[1, DIM\right] do$ $if \left(rand\left(0,1\right)<HMCR\right) then$ $x_i^{new}=x_i^a,where a\in \left\{1,2,\dots ,HMS\right\}$ $if\left(rand\left(0,1\right)<PAR\right) then$ $x_i^{new}=x_i^{new}+rand\left(-1,1\right)\times bw$ $endif$ $else$ $x_i^{new}=L_i+rand\cdot (U_i-L_i)$ $endif$ $endfor$
4:	//Update the harmony memory// $if\hspace{0.17em}f(x_{}^{new})<f(x_{}^{worst})=\underset{j=1,2,\mathrm{\dots },HMS}{\max }f(x^j),\hspace{1em}then\hspace{1em}{x}_{}^{worst}=x_{}^{new}.$
5:	//Check the stopping criterion// If the termination condition is met, stop and output the best individual. Otherwise, the process will repeat from Step 3.

2.2. The Improved Harmony Search Algorithm (IHS)

In the canonical harmony search algorithm, the probability of $PAR$ and $bw$ are constant. Mahdavi et al. [3] proposed an improved harmony search algorithm, called IHS, which mainly introduced the dynamic change of $PAR$ and $bw$ using the following equations.

$$PAR\left(NFE\right)=PA{R}_{min}+\frac{PA{R}_{max}-PA{R}_{min}}{MA{X}_{NFE}}\times NFE$$

(1)

$$bw\left(NFE\right)=b{w}_{max}exp\left(\frac{ln\frac{b{w}_{min}}{b{w}_{max}}}{MA{X}_{NFE}}\times NFE\right)$$

(2)

where $PA{R}_{max}$ is the maximum adjusting rate; $PA{R}_{min}$ is the minimum adjusting rate; $b{w}_{max}$ is the maximum bandwidth; $b{w}_{min}$ is the minimum bandwidth. $MA{X}_{NFE}$ is the maximum number of function evaluation and $NFE$ is the current number of function evaluation.

2.3. A Self-Adaptive Global-Best Harmony Search (SGHS)

The SGHS [4] employs a new improvisation scheme and an adaptive parameter tuning method. To modify pitch adjustment rule, $x_i^{new}$ is assigned with the corresponding decision variable $x_i^{best}$ from the best harmony vector. In addition, the concept of a learning period is introduced. Parameters HMCR and PAR are dynamically adapted to a suitable range by recording their historical values corresponding to the generated successful harmonies entering the nest harmony memory. Furthermore, bw is dynamically updated using the following equation.

$$bw\left(NFE\right)=\{\begin{array}{c}b{w}_{max}-\frac{b{w}_{max}-b{w}_{min}}{MA{X}_{NFE}}\times 2NFE, if NFE<\frac{MA{X}_{NFE}}{2}\\ b{w}_{min} , if NFE>\frac{MA{X}_{NFE}}{2}\end{array}$$

(3)

$\mathrm{where}b{w}_{\max }$ and $b{w}_{\min }$ are the maximum and minimum values of the bandwidth (bw), respectively.

2.4. An Intelligent Global Harmony Search Algorithm (IGHS)

Valian et al. [6] modified the improvisation step by imitating one dimension of the best harmony in the harmony memory to generate the new harmony and proposed algorithm IGHS. The main steps are shown in Algorithm 2.

Algorithm 2:	Main framework of the intelligent global harmony search algorithm (IGHS).
	$for each i\in \left[1, DIM\right] do$ $if \left(rand\left(0,1\right)<HMCR\right) then$ $if\left(rand\left(0,1\right)<PAR\right) then$ $x_i^{new}= x_k^{best} , where k\in \left\{1,2,\dots ,DIM\right\}$               else $x_i^R=2\times x_i^{best}- x_i^{worst}$ $if x_i^R<L_i$ $x_i^R=L_i$ $elseif x_i^R>U_i$ $x_i^R=U_i$                       $endif$                       $x_i^{new}=x_i^{worst}+rand\cdot \left(x^R-x^{worst}\right)$               $endif$ $else$               $x_i^{new}=L_i+rand\cdot (U_i-L_i)$
	$endif$
	$endfor$

3. Adaptive Harmony Search with Differential Evolution

When musicians compose music, they take full advantage of their own knowledge and experience in the improvement direction. With the continuous optimization of music composition, musicians will also reduce the available experience and accelerate the composition. Inspired by the conception, it is desired to make full use of the information in the harmony memory and dynamically adjust the harmony memory size. Thus, the differential evolution mutation is adopted into the modified algorithm to provide an effective guidance for the generation of the new solution. The linear harmony memory size reduction strategy is also introduced into the algorithm to accelerate the convergence. Meanwhile, in order to strengthen the general suitability for various problems and reduce the dependence on the parameters, the parameter’s self-adaption with the concept of a learning period is applied to the modified algorithm.

This paper presents an adaptive harmony search algorithm (aHSDE) with differential evolution mutation, periodic learning and linear population size reduction strategy. Therefore, it is desirable to balance the ability of global exploration and local exploitation for the harmony search algorithm.

3.1. Differential Evolution

As a stochastic population optimization algorithm, differential evolution (DE) is similar to other evolutionary algorithms [37]. The basic idea of DE is summarized as follows: a set of initial individuals are generated randomly in the search space, and each individual represents a solution. After this, a new individual is generated by the following three operations in sequence: mutation, crossover and selection. The core idea of DE is that it adds the differential vectors among several individual pairs to a base vector. It controls the magnitude and direction of exploration for the promising neighborhood [38].

This paper uses DE/best/2 of DE mutation as follows:

$$x_i^{new}=x_i^{best}+F[(x_i^{r_1}-x_i^{r_2})+(x_i^{r_3}-x_i^{r_4})]$$

(4)

where $r_1,r_2,r_3 and r_4$ are mutually different individual indexes which are chosen randomly. The parameter F is a scale factor controlling the mutation step size. Scaled differential vectors with respect to the possible individual pairs adapt the property of the current neighborhood landscape. It thus can provide promising mutation directions with adjustable step size and a balance between local and global search [39].

3.2. Linear Population Size Reduction

In the former search stage of HS, the algorithm tends to explore the search space with the assistance of well-population diversity. Subsequently, it can construct some fine-tuning directions in the iterative process. In the latter stage of the algorithm, the population usually focuses on the neighbor search. Therefore, exploitation better attracts most of the computing resource. Inspired by the improved Success-History based parameter Adaptation for Differential Evolution (SHADE) [40], a monotonically reducing population size strategy is utilized with respect to the function evaluation number. It is shown as follows

$$HMS=round\left(HM{S}_{\max }-\frac{HM{S}_{\max }-HM{S}_{\min }}{MA{X}_{NFE}}\times NFE\right)$$

(5)

where $HM{S}_{\max }$ and $HM{S}_{\min }$ are the maximum and minimum values of the harmony memory size (HMS), respectively. $MA{X}_{NFE}$ is the maximum number of function evaluation and $NFE$ is the current number of function evaluation.

3.3. Differential Mutation in the Pitch Adjustment Operator

The canonical harmony search algorithm operates the pitch adjustment with the constant distance bandwidth, which cannot adapt to the searching landscapes at different searching stages for different problems. It is certain that a proper bandwidth is important for the harmony search algorithm. In this paper, we present a general framework for defining the pitch adjustment operator with the differential mutation (DE/best/2) [41], which can provide a more effective direction than the constant bandwidth to the searching landscape. It is indicated as Equation (6).

$$x_i^{new}=x_i^{best}+F[(x_i^{r_1}-x_i^{r_2})+(x_i^{r_3}-x_i^{r_4})]+rand(-1,1)\times bw$$

(6)

where i is the component index from $\left\{1,2,3,\dots ,DIM\right\}$; $r_1,r_2,r_3,r_4$ are selected randomly from $\left\{1,2,3,\dots ,DIM\right\}$ and mutually exclusive; rand(−1,1) is a uniformly distributed random number between −1 and 1. $DIM$ is the dimension of decision variables. $x^{new}$ is the newly generated harmony vector and $x^{best}$ is the current best harmony vector in the harmony memory.

If the new solution is out of the bounds $\left[L_i,U_i\right]$, it will be modified as follows,

$$x_i^{new}=\{\begin{array}{c}{L}_i, if x_i^{new}<L_i \\ U_i, if x_i^{new}>U_i\end{array}$$

(7)

where $U_i$ and $L_i$ denote the upper and lower bounds of the i-th component for the decision vector.

3.4. Self-Adaptive PAR and F

Inspired by the concept of the learning period of SGHS [21] to adaptively tune parameters HMCR and PAR, this paper employs a new modified scheme for PAR and F.

In addition, the parameters HMCR and PAR are dynamically adapted to a suitable range by recording their historic values corresponding to the generated harmonies entering the harmony memory. During the evolution, the values of HMCR and PAR for the generated successful harmony are recorded to replace the worst members in the harmony memory.

First, both the means of PAR (PARm) and F (Fm) are initialized as 0.5. Second, parameters PAR and F are generated with a normal distribution. During the generations, the values of PAR and F are recorded when the generated harmony successfully replaces the worst member in the harmony memory. After Learning Period (LP), parameters PARm and Fm are recalculated with the weighted Lehmer mean formulas [42]. The weighted Lehmer mean $mea{n}_{wl}\left(S\right)$ uses the following deterministic Equations (8)–(10) to compute. The amount of fitness difference $\Delta f_k$ is used to influence the parameter adaptation.

$$mea{n}_{wl}\left(S\right)=\frac{{{\displaystyle \sum }}_{k=1}^{\left|S\right|}{w}^k·S^k{}^2}{{{\displaystyle \sum }}_{k=1}^{\left|S\right|}{w}^k·S^k}$$

(8)

$$w^k=\frac{\Delta f^k}{{{\displaystyle \sum }}_{l=1}^{\left|S\right|}\Delta f^l}$$

(9)

$$\Delta f^k=\left|f\left(x^{new}\right)-f\left(x^{worst}\right)\right|$$

(10)

where S includes either $S_{PAR}$ or $S_F$ and $mea{n}_{wl}\left(S\right)$ is the new value of PARm or Fm. $x^{new}$ is the newly generated solution in the current generation. $x^{worst}$ is the worst solution in harmony memory. $f(*)$ denotes the fitness function.

Parameters PARm or Fm use the framework in Algorithm 3 to update their values, where generation counter lp = 1. The difference between the weighted Lehmer mean and the arithmetic mean is described as follows. Arithmetic mean means all the recorded successful parameters of PARm or Fm have the same weights. On the other hand, the weighted Lehmer mean shown in Equations (8)–(10) means that all the recorded successful parameters of PARm or Fm have the self-adaptive weights based on their fitness improvements. It is very possible that the weighted Lehmer mean outperforms the arithmetic mean statistically. However, we will not analyze their difference in this paper due to paper length restrictions, and instead cite the reference [42] directly. The detailed information of weighted Lehmer mean can be found in reference [42].

Algorithm 3:	Parameters updating of the means of PAR (PARm) and F (Fm).
	$if lp>LearnPeriod$
	$PARm=mea{n}_{wl}\left(S_{PAR}\right)$
	$Fm=mea{n}_{wl}\left(S_F\right)$           lp=1; else           lp=lp+1 endif

In general, the values of PAR and F are regenerated as the following equations.

$$\{\begin{array}{c} PAR=normrnd\left(PARm,0.1\right)\\ F=normrnd\left(Fm,0.1\right)\end{array}$$

(11)

If PAR is larger than 1, it is truncated to be 1; if PAR is less than or equal to 0, it will be assigned 0.001. The same action is executed on F.

3.5. aHSDE Algorithm Framework

The aim of this paper is to provide some beneficial strategies to improve the performance of the aHSDE from the improvisational perspective. Algorithm 4 shows the procedure of the aHSDE.

Algorithm 4:	Framework of the new adaptive harmony search algorithm (aHSDE).
1:	//Initialize the problem and parameters//        $f\left(x\right)$: objective function        HMSmax: the maximum value of the harmony memory size        HMSmin: the minimum value of the harmony memory size        HMCR: harmony memory considering rate        PARm: the mean of pitch adjusting rate        Fm: the mean of the scaled factor        bw: bandwidth        LP: learning period        $MAX\_NFE$: maximum number of function evaluation        $L,U$: the lower and upper bounds of the decision vector
2:	//Initialize the harmony memory$\left(x^1,x^2,\cdots ,x^{HMS}\right)$// $x_i^j=L_i+rand\left(0,1\right)·\left(U_i-L_i\right),j=1,2,\dots ,HMS;i=1,2,\dots ,DIM$
3:	//Improvise a new harmony$x^{new}=\left(x_1^{new},x_2^{new},\cdots ,x_{DIM}^{new}\right)$// (1) Update HMS with Equation (5). If HMS decreases, the solutions are sorted in HM according to their fitness values and the worst one is deleted. (2) To generate a new solution, the process is as follows: $for each i\in \left[1, DIM\right] do$ $if \left(rand<HMCR\right) then$ $x_i^{new}=x_i^{best}$ $if\left(rand\left(0,1\right)<PAR\right) then$                                   $x_i^{new}=x_i^{best}+F[(x_i^{r_1}-x_i^{r_2})+(x_i^{r_3}-x_i^{r_4})]\pm rand\times bw$ $endif$ $else$                    $x_i^{new}=L_i+rand\cdot (U_i-L_i)$ $endif$ $endfor$
4:	//Update the harmony memory// $if\hspace{0.17em}f(x_{}^{new})<f(x_{}^{worst})=\underset{j=1,2,\mathrm{\dots },HMS}{\max }f(x^j),\hspace{1em}then\hspace{1em}{x}_{}^{worst}=x_{}^{new}.$ Record the generation of PAR, F and the fitness difference$\Delta f^k$.
5:	//Check the stopping criterion// If the termination condition is met, stop and output the best individual. Otherwise, the process will repeat from Step 3.

4. Experimental Comparison and Analysis

The proposed strategies and the parameter adaption schemes are explained and analyzed firstly by empirical research in this section. Subsequently, the proposed aHSDE is compared with the classical HS and several state-of-the-art HS variants, which include IHS [3], SGHS [4] and IGHS [6]. It is also compared with other state-of-the-art evolutionary algorithms (non harmony ones), which are Adaptive Particle Swarm Optimization (APSO) [43] and Evolution Strategy with Covariance Matrix Adaptation (CMA-ES) [44].

4.1. Parameters and Benchmark Functions

This section evaluates the performance of the aHSDE on the CEC2014 benchmark suite [45] compared with the original HS, IHS, SGHS and IGHS. The CEC2014 benchmark suite consists of 30 test functions, which include three unimodal functions, 13 multimodal functions, six hybrid functions and eight composite functions. In particular, these hybrid functions (f17–f22) are very similar to real world problems, such as transportation networks [46], circuit theory [47], image processing [48], capacitated arc routing problems [49] and flexible job–shop scheduling problems [50]. The search range for each function is [−100, 100]^DIM, where DIM is the dimension of the problem. The experiments are conducted in 10, 50 and 100 dimensions and the maximum function evaluation number is DIM × 10000. The number of multiple runs per function is 30, and the average results of these runs are recorded. When the value difference between the found best solution and the optimal solution is lower than 1 × 10⁻⁸, the error is considered as 0.

For the comparing HS variants, the parameter settings are the same as the respective literatures, which are also shown in Algorithm 5.

Algorithm 5:	Parameters.
HS [1]	$\mathrm{HMS}=5,\mathrm{HMCR}=0.9,\mathrm{PAR}=0.3,\mathrm{bw}=0.01$
HIS [3]	$\mathrm{HMS}=5,\mathrm{HMCR}=0.9,{\mathrm{PAR}}_{min}=0.01,{\mathrm{PAR}}_{max}=0.99,$ ${\mathrm{bw}}_{min}=0.0001,{\mathrm{bw}}_{max}=\frac{x^U-x^L}{20}$
SGHS [4]	$\mathrm{HMS}=5,{\mathrm{HMCR}}_m=0.98,{\mathrm{PAR}}_m=0.9,\mathrm{Lp}=100,$ ${\mathrm{bw}}_{min}=0.0005,{\mathrm{bw}}_{max}=\frac{x^U-x^L}{10}$
IGHS [6]	$\mathrm{HMS}=5,\mathrm{HMCR}=0.995,\mathrm{PAR}=0.4$
aHSDE	${\mathrm{HMS}}_{min}=5,{\mathrm{HMS}}_{max}=18\times \mathrm{DIM},HMCR=0.99,LP=100,BW=0.01$

4.2. How HMS Changes

In order to analyze the impact of the harmony memory size HMS on the aHSDE, four functions, f1, f10, f21, f28, are chosen from four categories, respectively. In the following experiments of Section 4.2, Section 4.3, Section 4.4 and Section 4.5, the dimension size of four functions is 30 and the statistical results are obtained from 30 independent runs. The minimum value of HMS is five and the maximum value ${\mathrm{HMS}}_{max}$ is a maximal integer which is no larger than rate × DIM, which is associated with the problem dimension size. Furthermore, rate is considered changing from 0.5 to 25 with an interval 0.5. Then the best results in each case are recorded and shown in Figure 1.

As can be seen from Figure 1, the fitness of the four functions decreases exponentially when the initial value of HMS gradually changes from 0.5 × DIM to 25 × DIM. This indicates that the initial value of HMS has a great impact on the performance of the aHSDE. When the initial value is small, the fitness of function decreases rapidly. The decreasing trend is no longer clear for the fitness as the initial value increases to 15 × DIM. Therefore, the initial value of HMS is set to 18 × DIM in this paper without special explanation in the following sections.

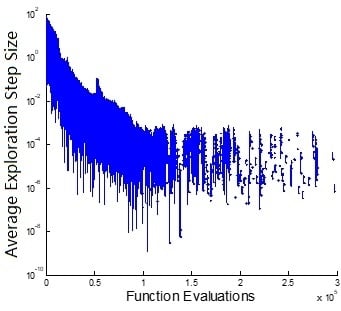
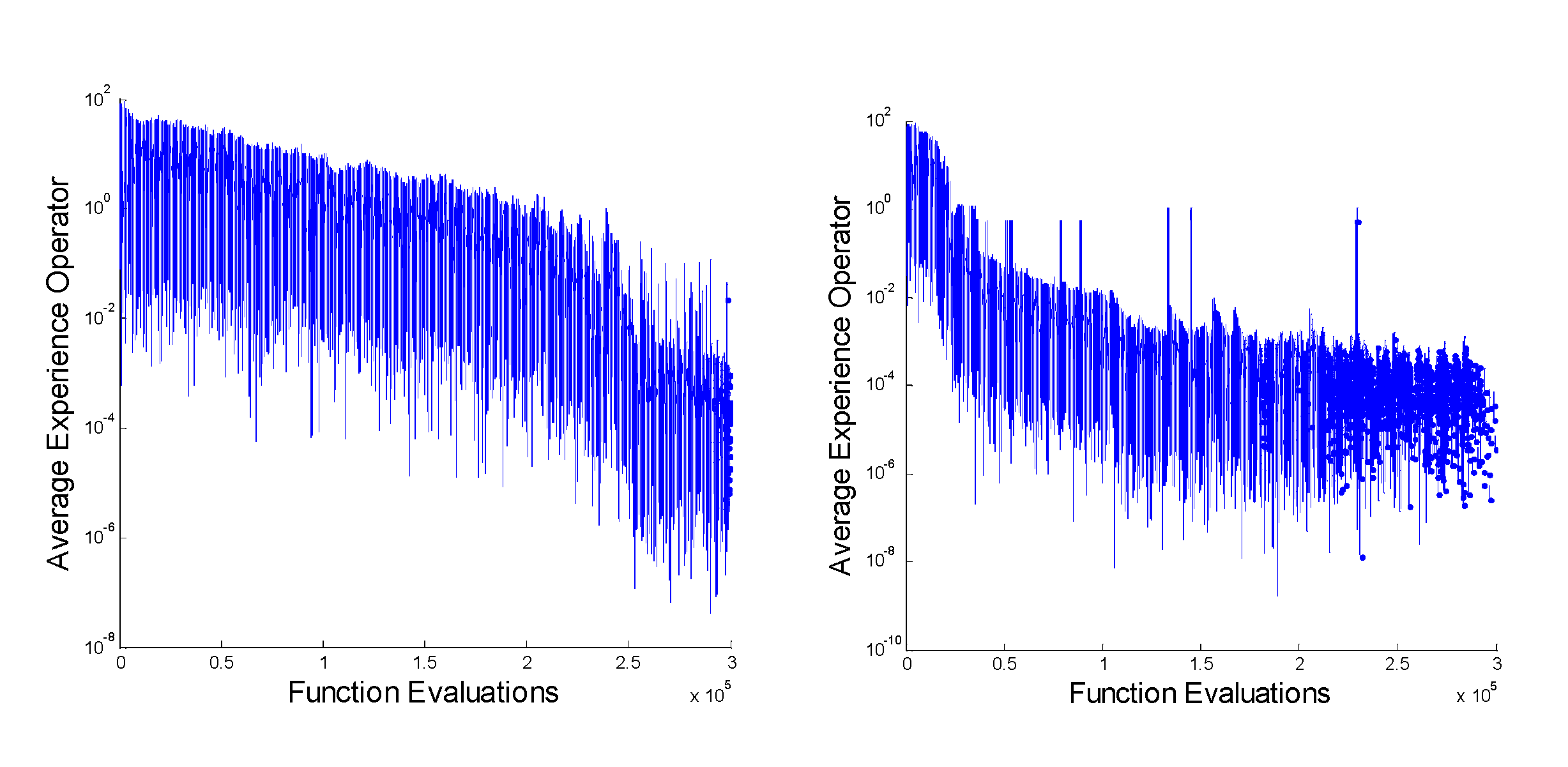
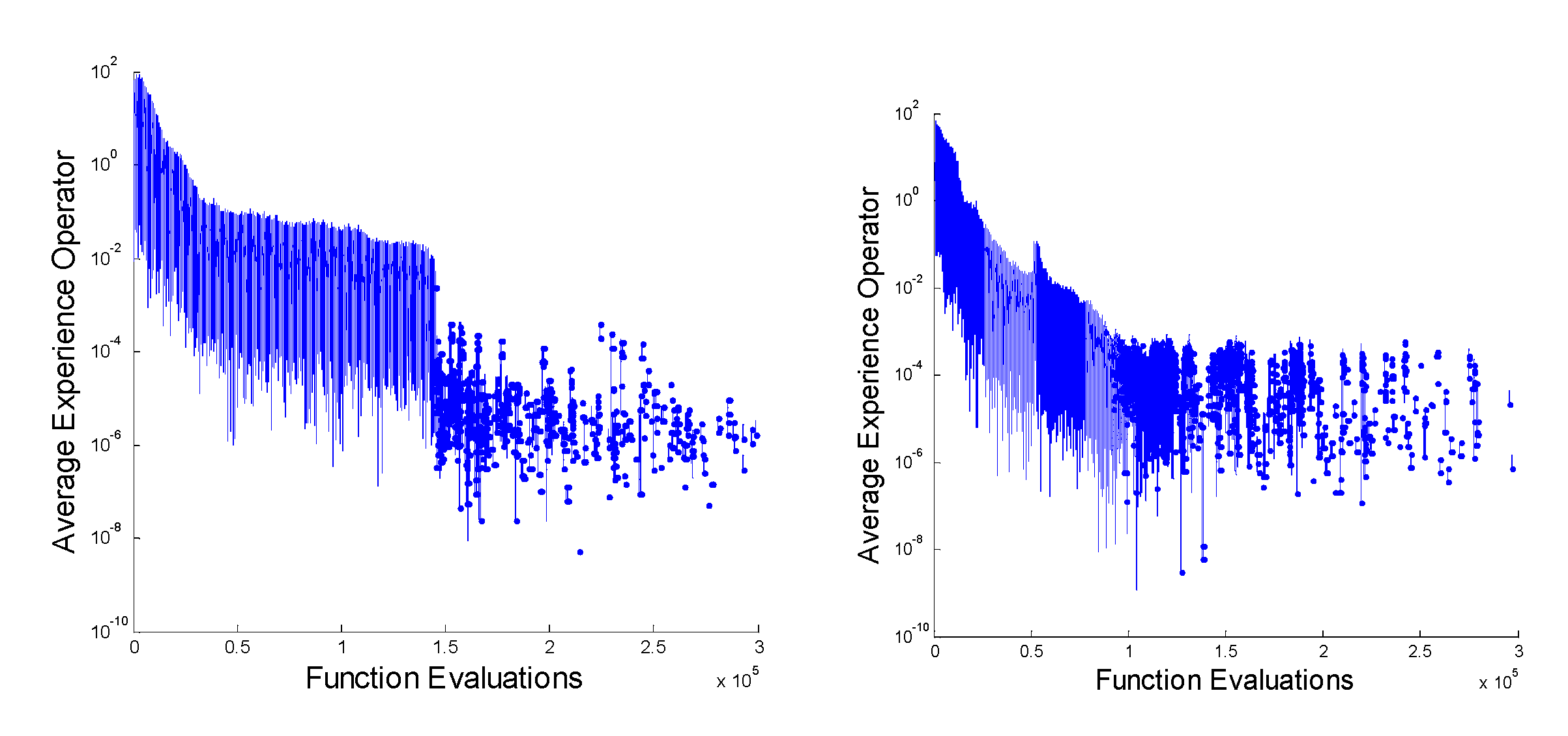
4.3. Effect of Differential Evolution Based Mutation

In this paper, mutation strategy DE/best/2 is used to adjust bandwidth to explore the landscape of the corresponding sub-stages. Therefore, $\left((x_i^{r_1}-x_i^{r_2})+(x_i^{r_3}-x_i^{r_4})\right)$, regarded as an Experience Operator (EO), is used to indicate the possible maximum searching neighborhood with the increase of generations. It can be adjusted adaptively with the change from population diverse to converging. The same analyzing functions, f1, f10, f21, f28, as detailed above, are chosen to illustrate the performance of the aHSDE algorithm with the increase of generations. Their changing trends of Eos are shown in Figure 2.

It can be seen from Figure 2 that EO is gradually convergent with the increase of generations. In the early stage of iteration, the search region of the algorithm is relatively large and EO is relatively large accordingly, which strengthens the global exploration ability. However, with the gradual convergence of HMS, the fining search of the algorithm is gradually conducted to improve the local exploitation at the latter generations. It is possible to provide a promising escape mechanism from the landscape valley with the differential mutation strategy to adjust the pitch in the aHSDE. Therefore, the aHSDE precedes over the original HS and several HS variants, which exploits the valley using a small step size.

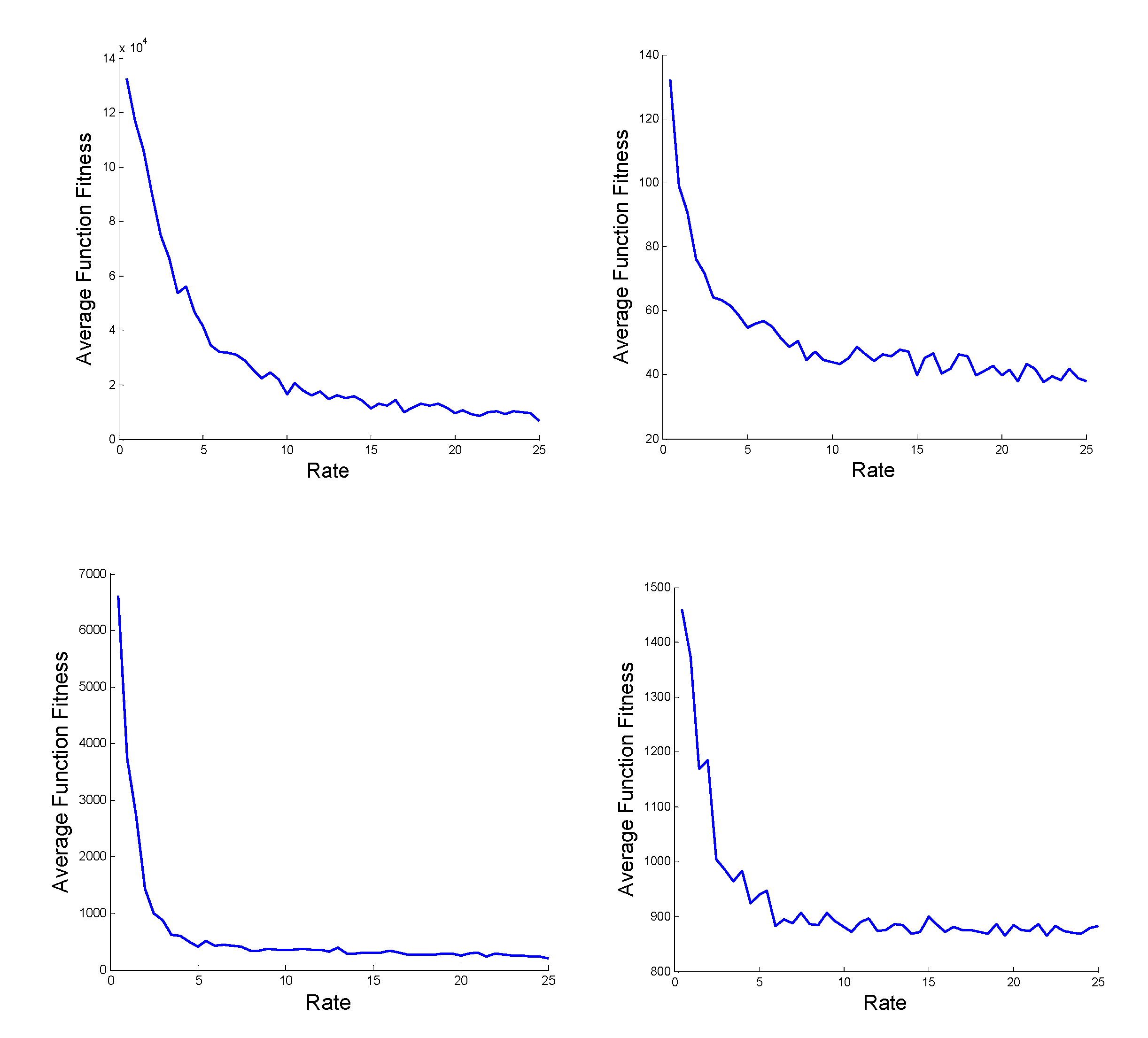
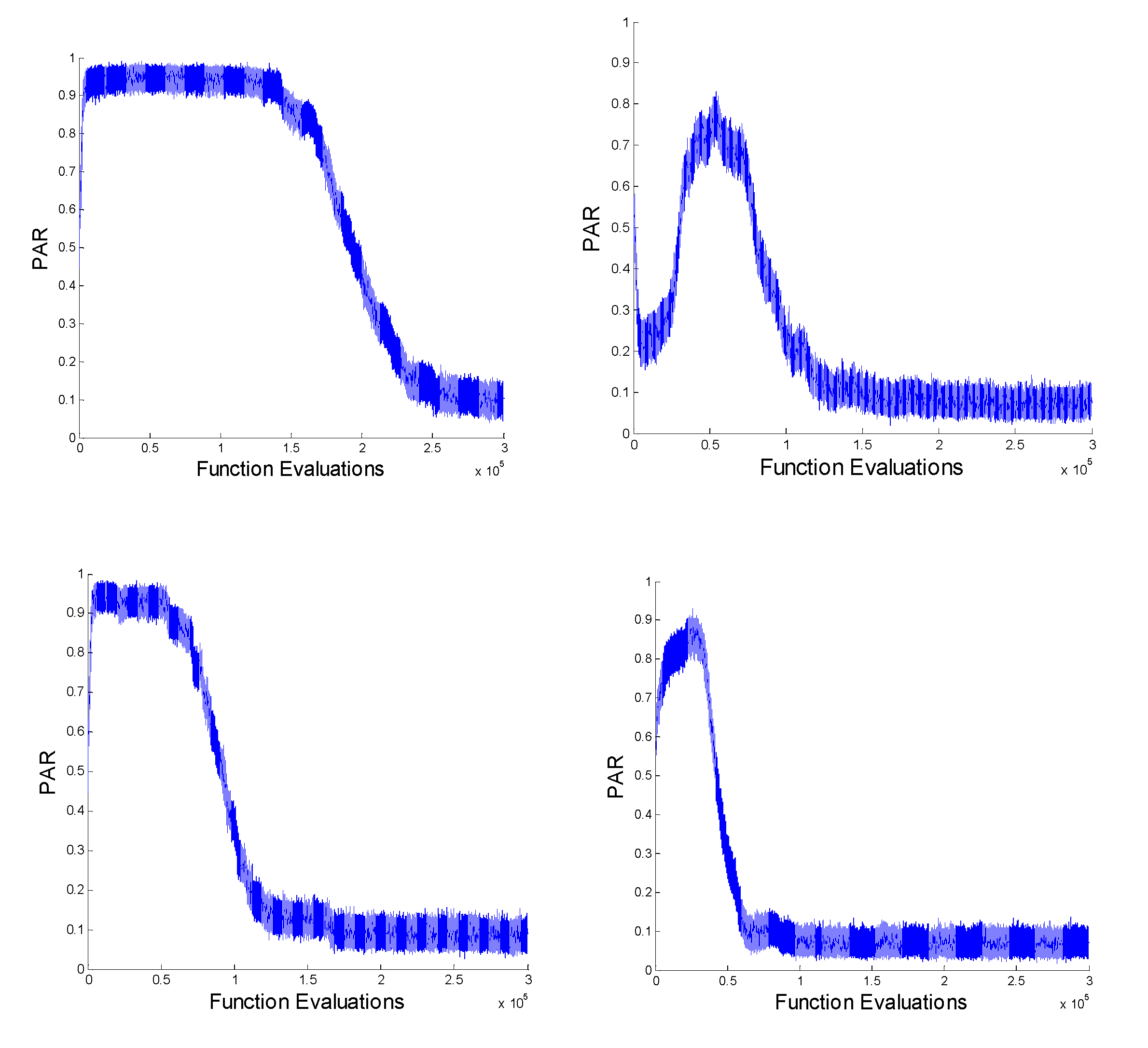
4.4. How PAR and F Change

In this paper, the concept of a learning period for PAR and F adjustment is adopted, which is computed with the weighted Lehmer mean. It aims to reduce the dependence on the parameters and enlarge the application scope of the algorithm. The results of PAR and F are recorded in 30 independent runs with the same four functions as the previous sections. Figure 3 and Figure 4 illustrate the changing trends of the adaptive adjustment strategy for PAR and F.

Observed in Figure 3, PAR probably changes between 0.7 and 0.95, which is rather large in the early generations. However, it ranges around 0.1 in the latter generations. It is necessary that the aHSDE, as one of the population-based optimization algorithms, needs a wide neighborhood-based global exploration in a high probability in the early stage. After this, a probability of pitch adjustment becomes smaller and smaller in order to improve the fine-tuning search and convergence of the algorithm in the latter generations. Thus, this adaptive modification strategy for PAR is inherently consistent with the internal variation principle of the exploring step size for population based optimization algorithms. It is possible to keep a good balance between local exploitation and global exploration.

It is observed that the overall changing trend of the scaling factor F for four functions is opposite to the parameter PAR. F is small at the beginning stage of iteration, at about 0.3. However, it becomes large at the latter iteration, probably around 0.9. It is worthy of note that the initial value of F is 0.5. Therefore, it can be roughly inferred that algorithm is not sensitive to the initial value of F. The possible reason for the four functions with similar trends is that the difference vector of the improving direction guided by DE operation is relatively large at the early generations. Therefore, a relatively small scaling factor F is suitable to the search demand for the algorithm. On the contrary, most of the solutions approximate to the optimal solution and the difference vector of improving direction is relatively small at the latter generations. Therefore, a large scaling factor F is required. In addition, although the overall changing trend of each function is similar, the adaptive adjustment behavior of F still depends on the solving problems. The curves, showing how F changes for four functions, exhibit different varying principles.

In this paper, the weighted Lehmer mean is used to adaptively tune PAR and scale the parameter F. It is a versatile and efficient automatic parameter tuner and is highly successful in tuning search and optimization algorithms [42].

4.5. Combined Adaptability Consideration for PAR and F

In order to consider the effects of parameters PAR and F, the same four functions are used to analyze the performance difference on the aHSDE with different parameter settings. The statistical results in 30 runs are shown in

Table 1. Fitness of f1 for different parameters (PAR, F).

PAR/F	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9
0.1	1.28 × 107	1.35 × 107	1.17 × 107	7.01 × 106	8.09 × 106	2.08 × 106	1.10 × 106	1.02 × 106	1.17 × 106
0.2	7.20 × 106	7.11 × 106	5.56 × 106	1.27 × 106	8.57 × 105	7.69 × 105	7.01 × 105	6.36 × 105	7.72 × 105
0.3	8.54 × 106	6.17 × 106	2.11 × 106	5.26 × 105	4.86 × 105	5.88 × 105	6.94 × 105	8.08 × 105	1.05 × 106
0.4	5.22 × 106	4.00 × 106	7.65 × 105	3.86 × 105	3.81 × 105	6.83 × 105	1.06 × 106	1.48 × 106	1.63 × 106
0.5	5.69 × 106	2.16 × 106	3.99 × 105	2.53 × 105	4.68 × 105	1.02 × 106	1.65 × 106	2.20 × 106	2.74 × 106
0.6	3.37 × 106	7.32 × 105	1.80 × 105	3.31 × 105	7.86 × 105	1.43 × 106	2.47 × 106	4.55 × 106	4.94 × 106
0.7	2.87 × 106	4.47 × 105	1.14 × 105	3.51 × 105	1.03 × 106	2.52 × 106	5.63 × 106	9.59 × 106	1.52 × 107
0.8	2.92 × 106	2.97 × 105	5.14 × 104	1.19 × 105	5.89 × 105	2.20 × 106	6.67 × 106	2.61 × 107	3.10 × 107
0.9	2.75 × 106	2.10 × 105	1.12 × 104	3.53 × 103	5.00 × 104	5.17 × 105	2.29 × 106	1.03 × 107	2.14 × 107

and Tables S1–S3. The data in the Tables S1–S3 represent the statistical results of multiple runs from different PAR and F combinations.

Table 1 shows that function f1 gets the best result when the parameter pair (PAR, F) is (0.9, 0.4). Table S1 shows that function f10 gets the best result when the parameter pair (PAR, F) is (0.1, 0.6). Table S2 shows that function f21 gets the best result when the parameter pair (PAR, F) is (0.9, 0.3). Table S3 shows that function f28 gets the best result when the parameter pair (PAR, F) is (0.7, 0.6). At the same time, it is easy to see that the performance of algorithm varies greatly with different parameter pairs. For example, the result of algorithm varies from 1.35 × 10⁷ with (PAR, F) being (0.8, 0.9) to 3.53 × 10³ with (PAR, F) being (0.9, 0.4) for Function 1. The result of the algorithm varies from 8.66 × 10⁵ with (PAR, F) being (0.1, 0.3) to 8.89 × 10 with (PAR, F) being (0.9, 0.3) for Function 2. This tells us that different functions have different sensitivities to the parameter PAR or F.

Observed from the comparison analysis of different parameter pairs on (PAR, F), the performance of the algorithm is sensitive to the parameter pair (PAR, F) to different problems. Simultaneously, it demonstrates that a certain parameter adaption scheme is necessary for problem solving. The algorithm aHSDE can obtain the best parameter pair of (PAR, F) and converge the best solution with the adaptive strategy. This scheme can reduce the dependence on the parameter for the algorithm.

Thus, it can be said that Table 1 and Tables S1–S3 fully demonstrate the effects of the adaptive strategy. In conclusion, the aHSDE is highly successful with the tuned parameter settings of PAR and F through the learning period and the weighted Lehmer mean method.

5. Experimental Comparison with HS Variants and Well-Known EAs

5.1. aHSDE vs. HS Variants

The experimental results of five algorithms (HS, IHS, SGHS, IGHS and the aHSDE) are reported and compared in Tables S4−S6 with different dimension sizes 10, 50 and 100, respectively. The items “Best”, “Mean” and “SD” represent the best and average results and the standard deviation of multiple final results, which are collected in 30 independent runs for each algorithm on each function. Meanwhile, the fitness error is assigned to zero if it was less than 1× 10⁻⁸.

It can be seen from Tables S4−S6 which can be found in the Supplementary data due to space and readability reasons) that the aHSDE has significantly competitive performance when compared with the canonical HS algorithm and several state-of-the-art HS variants. These data are the statistical results of 30 independent runs with the CEC 2014 benchmark for the 10-, 50- and 100-dimension sizes. In Tables S4−S6, the aHSDE always performs best among its competitors on f1–f3 unimodal functions. Secondly, the performance advantage of the aHSDE to its competitors increases as the dimension increases on f4–f16 multimodal functions. Let us take the concrete example as an illustration of algorithmic performance difference. For example, the mean results of Function 8 of HS, IHS, SGHS and the aHSDE. The IGHS indicates that three of four variants obtain the true optimal solution with the dimension as 10. The mean item of the aHSDE is 7.41 × 10⁻⁸, however, the best mean item of the other three algorithms is 2.52 × 10⁻² for Function 8 with the dimension as 50. The mean item of the aHSDE is 2.90 × 10⁻⁶, however, the best mean item of other three algorithms is 1.74 × 10⁻⁰ for Function 8 with the dimension as 100. This concrete example indicates that the performance advantage of the aHSDE to its competitors becomes more and more obvious with the increase of dimension size.

Moreover, the performance of the aHSDE is also all better than those of the other four HS variants on f17–f22 hybrid functions, except for Function 19, which has slightly worse performance with a dimension size of 100. Subsequently, Tables S4−S6 indicate that the performance advantage of the aHSDE is not as obvious as the previous benchmark. It performs slightly better than other competitors on the composition functions f23–f30. However, the overall statistical

Table 2. Overall statistical comparison among aHSDE and HS, improved harmony search (IHS), self-adaptive global-best harmony search (SGHS) and IGHS on CEC2014.

Groups	aHSDE vs	HS(DIM = )			IHS(DIM = )			SGHS(DIM = )			IGHS(DIM = )
		10	50	100	10	50	100	10	50	100	10	50	100
3 Unimodal Functions	+	3	3	3	3	2	3	3	2	3	3	3	3
	−	0	0	0	0	0	0	0	0	0	0	0	0
	~	0	0	0	0	1	0	0	1	0	0	0	0
13 Simple Multimodal Functions	+	6	11	12	5	11	13	8	11	10	9	13	13
	−	4	1	1	6	1	0	1	0	0	0	0	0
	~	3	1	0	2	1	0	4	2	3	4	0	0
6 Hybrid Functions	+	4	6	6	4	6	5	5	6	5	6	6	6
	−	0	0	0	1	0	0	0	0	0	0	0	0
	~	2	0	0	1	0	1	1	0	1	0	0	0
8 Composition Functions	+	4	6	6	4	5	6	6	4	6	4	6	7
	−	2	1	2	1	2	2	1	3	2	3	0	0
	~	2	1	0	3	1	0	1	1	0	1	2	1
30 All Functions	+	17	26	27	16	24	27	22	23	24	22	28	29
	−	6	2	3	8	3	2	2	3	2	3	0	0
	~	7	2	0	6	3	1	6	4	4	5	2	1

tells us that the aHSDE still has the best cases for all the composition functions f23–f30 for all the dimensional sizes. These statistical experimental comparisons and results analyses indicate that the improvement strategies of the aHSDE have significant impact on performance and its ability on global exploration and local exploitation.

5.2. Overall Statistical Comparison among HS Variants

Table 2 presents the overall statistical comparison results for the aHSDE and its competitors based on the Wilcoxon rank–sum test with the significance level $\mathsf{\alpha }$ of 0.05 for each dimension case on all the benchmark functions. The symbols “+”, “−“ and “~” mean that the aHSDE performs significantly better, significantly worse, or not significantly different compared with its competitors. Overall, it demonstrated that the performance of the aHSDE is quite competitive compared with four HS variants on the CEC2014 benchmark.

The following facts can be observed from Table 2. For three unimodal functions, the aHSDE outperforms all its competitors for 10, 50 and 100 dimensions. For thirteen multimodal functions, the aHSDE performs a little better than HS on 10 dimensions and performs much better than HS with the increase of dimension size for all competitions and all functions. For six hybrid functions, the aHSDE clearly outperforms HS, IHS, SGHS and IGHS for all the cases. These results illustrate that the aHSDE has a superior advantage to the state-of-the-art HS variants when solving various optimization problems, whose varieties may have no features. For the eight composition functions, the aHSDE significantly outperforms HS, IHS, SGHS and IGHS for 10, 50, 100 dimensions, except that the aHSDE performs comparably to SGHS for the 50-dimensional case and IGHS for the 10-dimensional case, respectively. The advantages are more obvious on higher dimensional functions. As a whole, the aHSDE performs much better than the canonical HS algorithm and HS variants in total on 10, 50, 100 dimensions on 30 benchmark functions for all dimensional cases.

5.3. Comparison with Other Well-Known EAs

In this subsection, the proposed aHSDE algorithm is compared with other state-of-the-art evolutionary algorithms (non harmony ones), including Adaptive Particle Swarm Optimization (APSO) [43] and Evolution Strategy with Covariance Matrix Adaptation (CMA-ES) [44]. The experimental results (mean best and standard deviation of multiple runs) of different algorithms are all collected with the maximum function evaluation number DIM * 10000 respectively, all of which are summarized in

Table 3. Comparison on mean best and standard deviation of multiple runs of Adaptive Particle Swarm Optimization (APSO), Evolution Strategy with Covariance Matrix Adaptation (CMA-ES) and the aHSDE based on IEEE CEC 2014 benchmarks.

Function	APSO	CMA-ES	aHSDE	Function	APSO	CMA-ES	aHSDE
f1	2.69 × 109 ± 3.28 × 108	9.42 × 104 ± 7.88 × 104	2.06 × 105 ± 9.12 × 104	f16	1.42 × 10 ± 2.37 × 10−1	1.38 × 10 ± 5.31 × 10−1	1.78 × 10 ± 1.00 × 100
f2	1.02 × 1011 ± 2.29 × 109	2.55 × 10 ± 3.85 × 109	5.77 × 103 ± 6.41 × 103	f17	2.86 × 108 ± 1.28 × 108	5.49 × 103 ± 3.62 × 103	2.66 × 103 ± 1.83 × 103
f3	1.19 × 106 ± 1.25 × 106	1.45 × 104 ± 5.66 × 103	1.25 × 100 ± 1.61 × 100	f18	8.75 × 109 ± 3.11 × 109	1.52 × 109 ± 3.93 × 108	8.88 × 10 ± 3.11 × 10
f4	2.49 × 104 ± 1.54 × 103	2.00 × 10 ± 2.63 × 10−5	4.43 × 10 ± 3.69 × 10	f19	8.45 × 102 ± 1.15 × 102	2.98 × 102 ± 4.25 × 10	1.16 × 10 ± 1.42 × 100
f5	2.13 × 10 ± 5.61 × 10−2	2.08 × 10 ± 6.69 × 10−2	2.01 × 10 ± 4.08 × 10−2	f20	1.59 × 107 ± 1.37 × 107	4.61 × 103 ± 3.88 × 103	4.07 × 10 ± 9.82 × 100
f6	4.80 × 10 ± 1.79 × 100	4.09 × 103 ± 2.13 × 100	2.02 × 10 ± 3.77 × 100	f21	1.33 × 108 ± 7.50 × 107	6.86 × 103 ± 2.76 × 103	8.35 × 102 ± 2.36 × 102
f7	1.06 × 103 ± 3.85 × 10	2.31 × 102 ± 2.83 × 10	2.14 × 10−3 ± 4.28 × 10−3	f22	1.31 × 104 ± 9.38 × 103	1.61 × 103 ± 2.92 × 102	8.30 × 102 ± 2.96 × 102
f8	5.03 × 102 ± 3.02 × 10	2.83 × 102 ± 2.21 × 10	7.41 × 10−8 ± 1.94 × 10−8	f23	2.00 × 102 ± 0.00 × 100	5.79 × 102 ± 4.94 × 10	3.44 × 102 ± 0.00 × 100
f9	4.78 × 102 ± 6.30 × 100	3.28 × 102 ± 7.65 × 10	7.89 × 10 ± 1.80 × 10	f24	2.00 × 102 ± 0.00 × 100	2.12 × 102 ± 7.49 × 100	2.69 × 102 ± 6.50 × 100
f10	9.30 × 103 ± 5.68 × 102	2.61 × 102 ± 1.06 × 102	1.94 × 10−1 ± 4.50 × 10−2	f25	2.00 × 102 ± 0.00 × 100	2.12 × 102 ± 2.97 × 100	2.07 × 102 ± 2.04 × 100
f11	9.24 × 103 ± 4.86 × 102	1.69 × 102 ± 1.98 × 102	4.71 × 103 ± 5.61 × 102	f26	1.86 × 102 ± 2.68 × 10	1.25 × 10−2 ± 5.51 × 10−1	1.00 × 102 ± 6.01 × 10−2
f12	5.91 × 100 ± 1.32× 100	3.03 × 10−1 ± 2.18 × 100	9.57 × 10−2 ± 4.16 × 10−2	f27	2.00 × 102 ± 0.00 × 100	1.07 × 103 ± 2.30 × 102	8.76 × 102 ± 1.26 × 102
f13	1.03 × 10 ± 7.53 × 10−1	5.51 × 100 ± 3.07 × 10−1	3.31 × 10−1 ± 6.32 × 10−2	f28	2.00 × 102 ± 0.00 × 100	2.79 × 103 ± 5.92 × 102	1.28 × 103 ± 8.88 × 10
f14	3.95 × 102 ± 2.22 × 10	7.53 × 10 ± 8.08 × 100	3.30 × 10−1 ± 1.12 × 10−1	f29	2.00 × 102 ± 0.00 × 100	3.52 × 104 ± 5.34 × 103	2.35 × 107 ± 1.69 × 107
f15	1.05 × 106 ± 0.00 × 100	1.02 × 104 ± 3.24 × 104	8.09 × 100 ± 2.32 × 100	f30	2.00 × 102 ± 0.00 × 100	6.48 × 105 ± 1.31 × 105	8.93 × 103 ± 6.76 × 102

. The best “mean” result for the same function is highlighted in bold.

Observed in Table 3, it can be seen that APSO, CMA-ES and the aHSDE perform best on 7, 4 and 19 benchmarks respectively from the 30 benchmark functions. It should be further noted that APSO outperforms the aHSDE on eight problems and CMA-ES outperforms the aHSDE on six functions among this IEEE CEC 2014 benchmark suite. Therefore, generally speaking, the aHSDE significantly outperforms APSO and CMA-ES on most of the benchmark functions. However, it should be especially noted that APSO outperforms CMA-ES and the aHSDE on the composition functions, which indicates that APSO is promising for the composition, or the highly complex problems. Comparatively speaking, the aHSDE has better overall performance on multiple types of problems.

6. Conclusions

Based on the analysis of HSA and the knowledge and experience of the musician, a new adaptive harmony search algorithm is proposed (aHSDE) for global optimization in this paper. It enhances the performance of HS with a differential mutation for the pitch adjustment of HS, the mechanism of decreasing HMS linearly, and the parameter adaptation of PAR and F. Firstly, the mutual influence and cooperation of three strategies and key parameters on the aHSDE are analyzed and verified in detail. After this, the performance of the aHSDE is comprehensively evaluated on IEEE CEC 2014 Benchmarks with 10-, 50- and 100-dimension sizes. The experimental results indicate that the aHSDE outperforms the canonical HS algorithm and three advanced HS variants, including IHS, SGHS and IGHS. Furthermore, other state-of-the-art metaheuristic algorithms, namely APSO and CMA-ES, are also used as competitors to evaluate the aHSDE.