Multi-Objective Optimal Reactive Power Planning under Load Demand and Wind Power Generation Uncertainties Using ε-Constraint Method
Abstract
1. Introduction
2. Uncertainty Modeling
2.1. Modeling the Load Demand Uncertainty
2.2. Modeling the Wind Power Generation Uncertainty
- Several scenarios for the load level are considered.
- The probability of each system loading scenario (level of the load) and its corresponding value using Equations (1) and (2) are calculated.
- Several scenarios for wind speed are considered.
- The probability of each wind speed scenario and its corresponding value using Equations (4) and (5) are calculated.
- The output power of the wind farm using the estimated wind speed in each scenario and Equation (6) is generated.
- The final number of combined load-wind scenarios is obtained by multiplying the number of load scenarios by the number of wind scenarios. By multiplying the probability of the load scenario by the probability of wind speed scenario, the probability of the combined load-wind scenarios () can be calculated as follows [19]:
3. Problem Formulation
3.1. Variables
3.2. Objective Functions
3.2.1. Minimization of Total VAR Investment Cost
- (1).
- The first part evaluates the expected cost of energy loss () during the generated scenarios and is expressed as follows [16,17,18,19,20,21,22,23,24,25,26]:where shows the active power losses during the scenario, represents the duration of the scenario, is a constant parameter that is related to the first part cost-based objective function and identifies the per-unit energy cost, and denotes the probability of the scenario. To calculate the total active power losses, Equation (11) can be used as follows [27,28,29,30]:where and are the sending and receiving ends voltage magnitude of the transmission line for the scenario, respectively, and are the sending and receiving ends voltage angles of the transmission line for the scenario, respectively, and is used to designate the conductance of the transmission line for the scenario.
- (2).
3.2.2. Minimization of Voltage Stability Index
3.2.3. Maximization of the Loadability Factor
3.3. Constraints
3.3.1. Equality Constraints
3.3.2. Inequality Constraints
3.4. Other Considerations in the Problem Formulation
- The transformers tap settings and output reactive power of the VAR sources are treated as continuous variables. Therefore, the whole problem is stated as a probabilistic multi-objective nonlinear problem.
- Since the matrix of power systems is dependent on the transformers tap settings and due to the fact that the transformers tap settings are defined as scenario-dependent variables, the matrix should be calculated for each scenario separately.
- The -index value varies between 0 and 1 for power systems. It should be noted that except for the defined boundaries, the -index value should be obtained without any further restriction during the optimization procedure.
4. Optimization Method
4.1. Multi-Objective Optimization Using ε-Constraint Method
- Each objective function () is optimized with the existing constraints separately and the results are saved in a table, called the payoff table.
- According to the priority of the objective functions, one objective function is selected as the main objective function. Then, the rest of the objective functions are treated as new constraints and added to the main constraints. It should be noted that except for the main objective function, if the goal is to minimize and maximize all the objective functions, then, and , respectively. Also, is a variable parameter.
- In order to assign values to , the maximum () and minimum () values of each objective function should be considered, as shown in Equation (40). It should be noted that those values can be obtained from the payoff table.
- To generate different values for , Equations (41) and (42) are used to minimize and maximize the objective function, respectively. By dividing the domain of the objective function into equal parts using Equations (41) and (42), different values are obtained for . It should be noted that denotes the number of available generated values for .
- By using the obtained values from Step 4, it can be derived that or . For different values of , a set of solutions is obtained, which forms the Pareto front of the problem.
4.2. Fuzzy Decision Maker (FDM)
5. Simulation Results and Discussions
- A.
- Deterministic multi-objective RPP without considering the loadability factor (assessing the proficiency of ε-constraint method)
- B.
- Deterministic multi-objective RPP considering the loadability factor
- C.
- Probabilistic multi-objective RPP considering the load demand uncertainty
- D.
- Probabilistic multi-objective RPP considering the wind power generation uncertainty
- E.
- Probabilistic multi-objective RPP considering load demand and wind power generation uncertainties at the same time
5.1. Case Study Descriptions and Simulation Results
5.1.1. Case A: Deterministic Multi-Objective RPP without Considering the Loadability Factor
5.1.2. Case B: Deterministic Multi-Objective RPP Considering the Loadability Factor
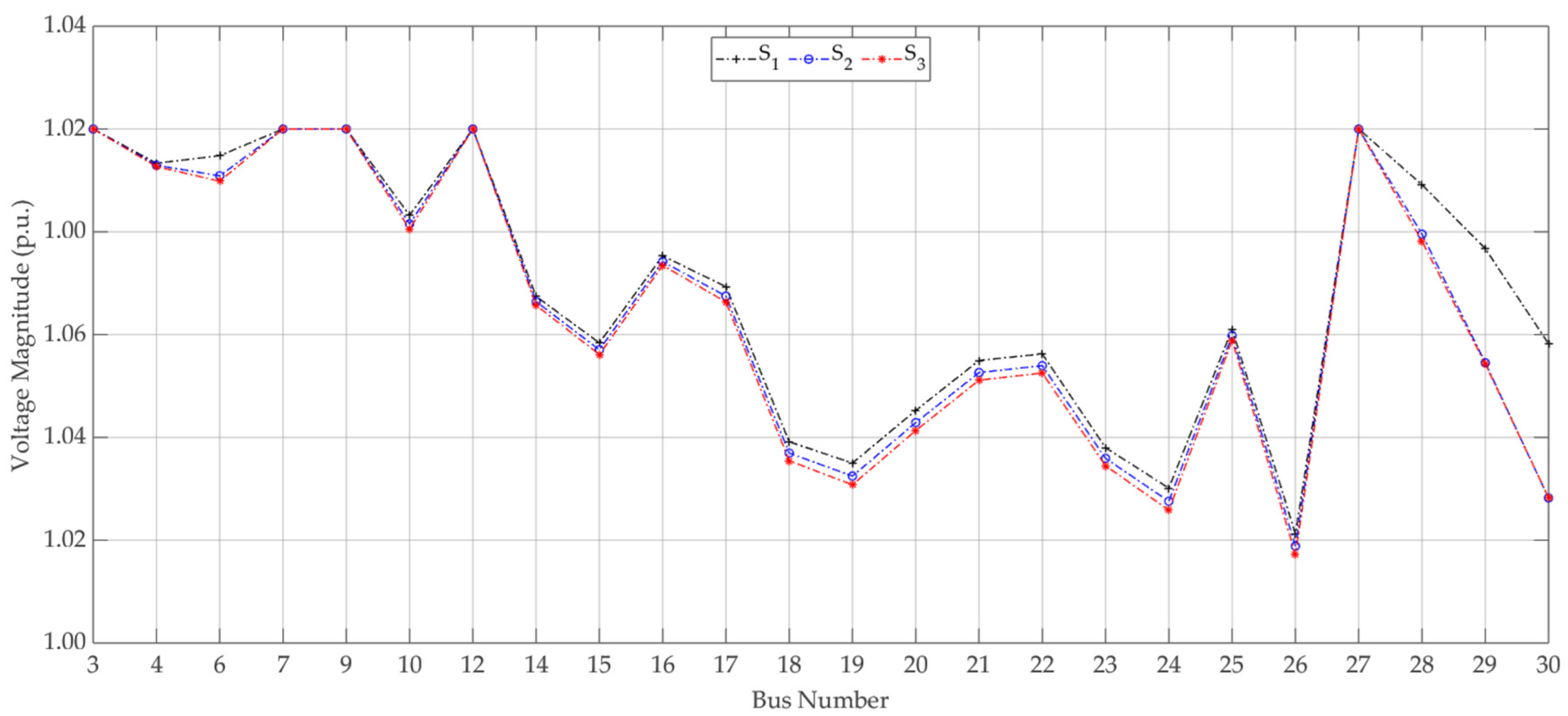
5.1.3. Case C: Probabilistic Multi-Objective RPP Considering the Load Demand Uncertainty
5.1.4. Case D: Probabilistic Multi-Objective RPP Considering the Wind Power Generation Uncertainty
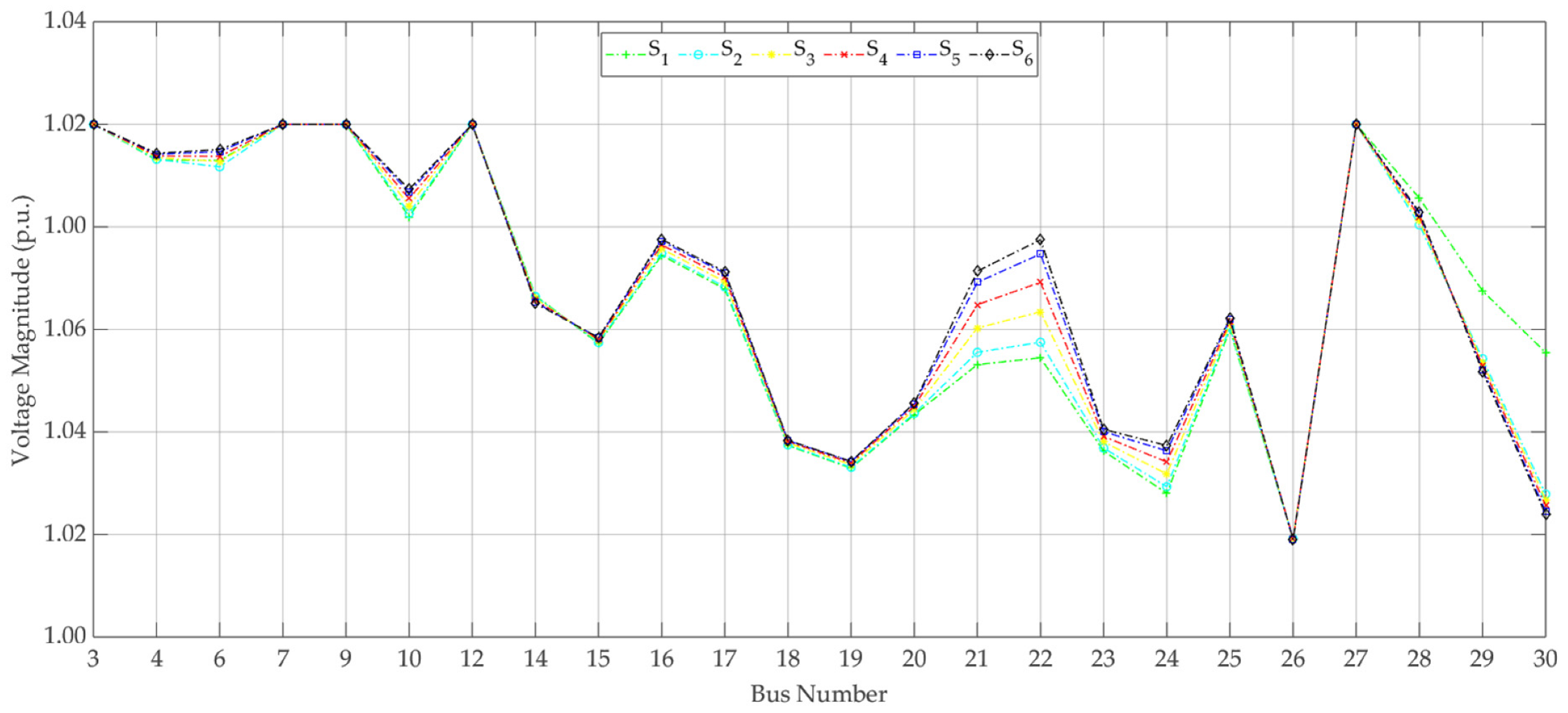
5.1.5. Case E: Probabilistic Multi-Objective RPP Considering Load Demand and Wind Power Generation Uncertainties
5.1.6. Case F: Probabilistic Multi-Objective RPP Considering Load Demand and Wind Power Generation Uncertainties Incorporating Reactive Power from Wind Farms
5.2. Discussions
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Parameter | Value |
|---|---|
| 2 | |
| 10 | |
| 3 m/s | |
| 10.28 m/s | |
| 25 m/s | |
| 40 MW |
References
- Zhang, W.; Li, F.; Tolbert, L.M. Review of Reactive Power Planning: Objectives, Constraints, and Algorithms. IEEE Trans. Power Syst. 2007, 22, 2177–2186. [Google Scholar] [CrossRef]
- Seifi, H.; Sepasian, M.S. Electric Power System Planning: Issues, Algorithms and Solutions; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Roselyn, J.P.; Devaraj, D.; Dash, S.S. Multi Objective Differential Evolution Approach for Voltage Stability Constrained Reactive Power Planning Problem. Int. J. Electr. Power Energy Syst. 2014, 59, 155–165. [Google Scholar] [CrossRef]
- Miveh, M.R.; Rahmat, M.F.; Ghadimi, A.A.; Mustafa, M.W. Control Techniques for Three-Phase Four-Leg Voltage Source Inverters in Autonomous Microgrids: A Review. Renew. Sustain. Energy Rev. 2016, 54, 1592–1610. [Google Scholar] [CrossRef]
- Miveh, M.R.; Rahmat, M.F.; Mustafa, M.W.; Ghadimi, A.A.; Rezvani, A. An Improved Control Strategy for a Four-Leg Grid-Forming Power Converter under Unbalanced Load Conditions. Adv. Power Electron. 2016, 2016. [Google Scholar] [CrossRef]
- Mohammadi, F.; Nazri, G.-A.; Saif, M. A Fast Fault Detection and Identification Approach in Power Distribution Systems. In Proceedings of the 5th International Conference on Power Generation Systems and Renewable Energy Technologies (PGSRET), Istanbul, Turkey, 26–27 August 2019. [Google Scholar]
- Han, T.; Chen, Y.; Ma, J.; Zhao, Y.; Chi, Y.-Y. Surrogate Modeling-Based Multi-Objective Dynamic VAR Planning Considering Short-Term Voltage Stability and Transient Stability. IEEE Trans. Power Syst. 2018, 33, 622–633. [Google Scholar] [CrossRef]
- Raj, S.; Bhattacharyya, B. Optimal Placement of TCSC and SVC for Reactive Power Planning Using Whale Optimization Algorithm. Swarm Evol. Comput. 2018, 40, 131–143. [Google Scholar] [CrossRef]
- Bhattacharyya, B.; Raj, S. Swarm Intelligence Based Algorithms for Reactive Power Planning with Flexible AC Transmission System Devices. Int. J. Electr. Power Energy Syst. 2016, 78, 158–164. [Google Scholar] [CrossRef]
- Alonso, M.; Amaris, H.; Alvarez-Ortega, C. A Multiobjective Approach for Reactive Power Planning in Networks with Wind Power Generation. Renew. Energy 2012, 37, 180–191. [Google Scholar] [CrossRef]
- Amaris, H.; Alonso, M. Coordinated Reactive Power Management in Power Networks with Wind Turbines and FACTS Devices. Energy Convers. Manag. 2011, 52, 2575–2586. [Google Scholar] [CrossRef]
- Fang, X.; Li, F.; Wei, Y.; Azim, R.; Xu, Y. Reactive Power Planning Under High Penetration of Wind Energy Using Benders Decomposition. IET Gener. Transm. Distrib. 2015, 9, 1835–1844. [Google Scholar] [CrossRef]
- Niu, M.; Xu, Z. Reactive Power Planning for Transmission Grids with Wind Power Penetration. In Proceedings of the IEEE PES Innovative Smart Grid Technologies, Tianjin, China, 21–24 May 2012. [Google Scholar]
- López, J.C.; Contreras, J.; Muñoz, J.I.; Mantovani, J. A Multi-Stage Stochastic Non-Linear Model for Reactive Power Planning Under Contingencies. IEEE Trans. Power Syst. 2013, 28, 1503–1514. [Google Scholar] [CrossRef]
- López, J.; Pozo, D.; Contreras, J.; Mantovani, J.R.S. A Multiobjective Minimax Regret Robust VAR Planning Model. IEEE Trans. Power Syst. 2017, 32, 1761–1771. [Google Scholar] [CrossRef]
- Yang, N.; Yu, C.; Wen, F.; Chung, C. An Investigation of Reactive Power Planning Based on Chance Constrained Programming. Int. J. Electr. Power Energy Syst. 2007, 29, 650–656. [Google Scholar] [CrossRef]
- López, J.C.; Mantovani, J.S.; Sanz, J.C.; Muñoz, J.I. Optimal Reactive Power Planning Using Two-Stage Stochastic Chance-Constrained Programming. In Proceedings of the IEEE Grenoble Conference, Grenoble, France, 16–20 June 2013. [Google Scholar]
- Aien, M.; Hajebrahimi, A.; Fotuhi-Firuzabad, M. A Comprehensive Review on Uncertainty Modeling Techniques in Power System Studies. Renew. Sustain. Energy Rev. 2016, 57, 1077–1089. [Google Scholar] [CrossRef]
- Tabatabaei, N.M.; Aghbolaghi, A.J.; Bizon, N.; Blaabjerg, F. Reactive Power Control in AC Power Systems: Fundamentals and Current Issues; Springer International Publishing: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Aien, M.; Fotuhi-Firuzabad, M.; Rashidinejad, M. Probabilistic Optimal Power Flow in Correlated Hybrid Wind–Photovoltaic Power Systems. IEEE Trans. Smart Grid 2014, 5, 130–138. [Google Scholar] [CrossRef]
- Aien, M.; Khajeh, M.G.; Rashidinejad, M.; Fotuhi-Firuzabad, M. Probabilistic Power Flow of Correlated Hybrid Wind-Photovoltaic Power Systems. IET Renew. Power Gener. 2014, 8, 649–658. [Google Scholar] [CrossRef]
- Growe-Kuska, N.; Heitsch, H.; Romisch, W. Scenario Reduction and Scenario Tree Construction for Power Management Problems. In Proceedings of the 2003 IEEE Bologna Power Tech Conference Proceedings, Bologna, Italy, 23–26 June 2003. [Google Scholar]
- Vagropoulos, S.I.; Kardakos, E.G.; Simoglou, C.K.; Bakirtzis, A.G.; Catalao, J.P. ANN-Based Scenario Generation Methodology for Stochastic Variables of Electric Power Systems. Electr. Power Syst. Res. 2016, 134, 9–18. [Google Scholar] [CrossRef]
- Mohseni-Bonab, S.M.; Rabiee, A. Optimal Reactive Power Dispatch: A Review, and A New Stochastic Voltage Stability Constrained Multi-Objective Model at the Presence of Uncertain Wind Power Generation. IET Gener. Transm. Distrib. 2017, 11, 815–829. [Google Scholar] [CrossRef]
- Mohseni-Bonab, S.M.; Rabiee, A.; Mohammadi-Ivatloo, B. Voltage Stability Constrained Multi-Objective Optimal Reactive Power Dispatch under Load and Wind Power Uncertainties: A Stochastic Approach. Renew. Energy 2016, 85, 598–609. [Google Scholar] [CrossRef]
- López, J.C.; Muñoz, J.I.; Contreras, J.; Mantovani, J. Optimal Reactive Power Dispatch Using Stochastic Chance-Constrained Programming. In Proceedings of the 2012 Sixth IEEE/PES Transmission and Distribution: Latin America Conference and Exposition (T&D-LA), Montevideo, Uruguay, 3–5 September 2012. [Google Scholar]
- Mohammadi, F.; Zheng, C. Stability Analysis of Electric Power System. In Proceedings of the 4th National Conference on Technology in Electrical and Computer Engineering, Tehran, Iran, 27 December 2018. [Google Scholar]
- Mohammadi, F.; Nazri, G.-A.; Saif, M. A Bidirectional Power Charging Control Strategy for Plug-in Hybrid Electric Vehicles. Sustainability 2019, 11, 4317. [Google Scholar] [CrossRef]
- Mohammadi, F.; Nazri, G.-A.; Saif, M. An Improved Mixed AC/DC Power Flow Algorithm in Hybrid AC/DC Grids with MT-HVDC Systems. Appl. Sci. 2020, 10, 297. [Google Scholar] [CrossRef]
- Ma, J.; Lai, L.L. Evolutionary Programming Approach to Reactive Power Planning. IEE Proc. Gener. Transm. Distrib. 1996, 143, 365–370. [Google Scholar] [CrossRef]
- Kessel, P.; Glavitsch, H. Estimating the Voltage Stability of a Power System. IEEE Trans. Power Deliv. 1986, 1, 346–354. [Google Scholar] [CrossRef]
- Singh, J.; Singh, S.; Srivastava, S. Placement of FACTS Controllers for Enhancing Power System Loadability. In Proceedings of the 2006 IEEE Power India Conference, New Delhi, India, 10–12 April 2006. [Google Scholar]
- Kalyanmoy, D. Multi-Objective Optimization using Evolutionary Algorithms; John Wiley and Sons: Hoboken, NJ, USA, 2001. [Google Scholar]
- Cohon, J.L. Multiobjective Programming and Planning; Courier Corporation: North Chelmsford, MA, USA, 2004. [Google Scholar]
- Wang, X.; Gong, Y.; Jiang, C. Regional Carbon Emission Management Based on Probabilistic Power Flow with Correlated Stochastic Variables. IEEE Trans. Power Syst. 2015, 30, 1094–1103. [Google Scholar] [CrossRef]
- Rosenthal, R.E. User’s Guide, Tutorial, GAMS; Development Corporation: Washington, DC, USA, 2010. [Google Scholar]
- Andrei, N. Nonlinear Optimization Applications Using the GAMS Technology; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Soroudi, A. Power System Optimization Modeling in GAMS; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Ferris, M.C.; Jain, R.; Dirkse, S. GDXMRW: Interfacing GAMS and MATLAB. 2010. Available online: http://www.gams.com/dd/docs/tools/gdxmrw (accessed on 15 March 2020).
- Drud, A. CONOPT Solver Manual; ARKI Consulting and Development: Bagsværd, Denmark, 1996. [Google Scholar]
- Lee, K.; Park, Y.; Ortiz, J. A United Approach to Optimal Real and Reactive Power Dispatch. IEEE Trans. Power Appar. Syst. 1985, PAS-104, 1147–1153. [Google Scholar] [CrossRef]
- Christie, R. Power Systems Test Case Archive; UW Power Systems Test Case Archive: Seattle, WA, USA, 1993. [Google Scholar]
- Nguyen, T.T.; Mohammadi, F. Optimal Placement of TCSC for Congestion Management and Power Loss Reduction Using Multi-Objective Genetic Algorithm. Sustainability 2020, 12, 2813. [Google Scholar] [CrossRef]
- Mahmoudabadi, A.; Rashidinejad, M. An Application of Hybrid Heuristic Method to Solve Concurrent Transmission Network Expansion and Reactive Power Planning. Int. J. Electr. Power Energy Syst. 2013, 45, 71–77. [Google Scholar] [CrossRef]
- Mishra, C.; Singh, S.P.; Rokadia, J. Optimal Power Flow in the Presence of Wind Power Using Modified Cuckoo Search. IET Gener. Transm. Distrib. 2015, 9, 615–626. [Google Scholar] [CrossRef]
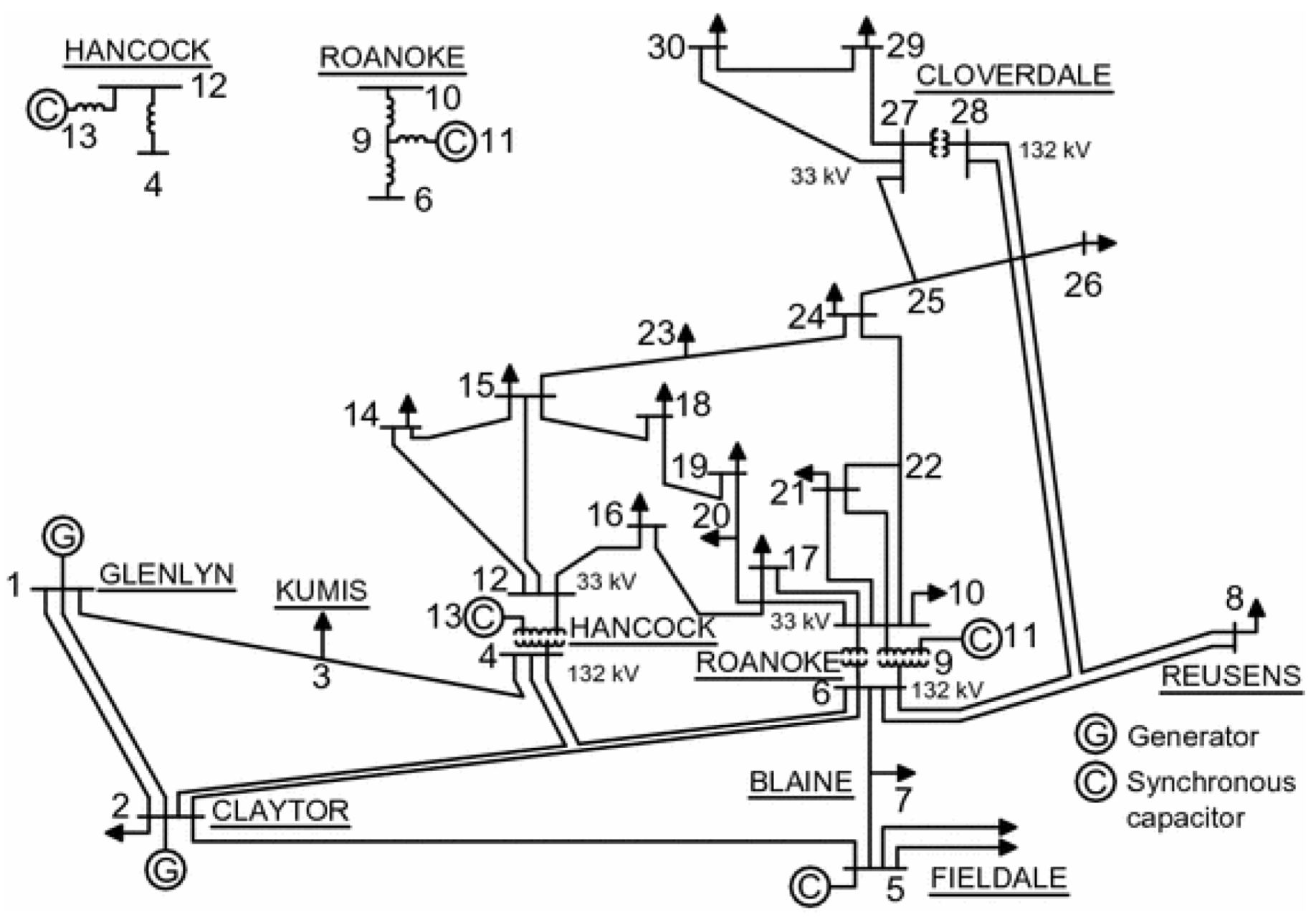

| Reference | Problem Framework | Load Demand Uncertainty | Wind Power Generation Uncertainty | Load Demand and Wind Power Generation Uncertainties | Objective Function | Solution Methodology |
|---|---|---|---|---|---|---|
| [3] | Deterministic, Multi-Objective | - | - | - | Active power losses, Total VAR cost, Voltage stability index | MOEA |
| [4] | Deterministic, Multi-Objective | - | - | - | Investment cost, Short-term voltage stability level, Transient stability level | MOEA |
| [5] | Deterministic, Single-Objective | - | - | - | Active power losses, Voltage deviations, Operating cost | WOA, DE, GWO, QODE, QOGWO |
| [6] | Deterministic, Single-Objective | - | - | - | Active power losses, Operating cost | SPSO, APSO, EPSO |
| [7] | Deterministic, Multi-Objective | - | - | - | Investment cost, Short-term voltage stability, Transient stability | MOEA |
| [8] | Deterministic, Single-objective | - | - | - | Active power losses, Voltage deviations, Operating cost | WOA, DE, GWO, QODE, QOGWO |
| [9] | Deterministic, Single-Objective | - | - | - | Active power losses, Operating cost | SPSO, APSO, EPSO |
| [10] | Deterministic, Multi-Objective | - | - | - | Loadability factor, Active power losses, VAR investment cost | GA |
| [11] | Deterministic, Single-Objective | - | - | - | Loadability factor | GA |
| [12] | Probabilistic, Single-Objective | ✓ | ✓ | ✓ | Fuel cost, VAR cost, Total cost | Mathematical Programming |
| [13] | Probabilistic, Single-Objective | - | ✓ | - | VAR investment cost | DE |
| [14] | Probabilistic, Single-Objective | ✓ | - | - | VAR investment cost | Mathematical Programming |
| [15] | Probabilistic, Multi-Objective | ✓ | - | - | Operating cost, VAR investment cost, Load shedding risk | Multi-Objective Mathematical Programming (ε-constraint method) |
| [16] | Probabilistic, Single-Objective | ✓ | - | - | Operating cost, VAR investment cost | GA |
| [17] | Probabilistic, Single- Objective | ✓ | - | - | VAR investment cost | Mathematical Programming |
| Present Paper | Probabilistic, Multi-Objective | ✓ | ✓ | ✓ | Active power losses, Total VAR cost, Voltage stability index, Loadability factor | Multi-objective Mathematical Programming (ε-constraint method) |
| Generator Voltage Magnitude | |
| (p.u.) | 1.050 |
| (p.u.) | 1.044 |
| (p.u.) | 1.023 |
| (p.u.) | 1.025 |
| (p.u.) | 1.050 |
| (p.u.) | 1.050 |
| Transformer Tap Settings | |
| (p.u.) | 0.950 |
| (p.u.) | 1.100 |
| (p.u.) | 1.025 |
| (p.u.) | 1.050 |
| VAR Compensator | |
| (MVAR) | 0.000 |
| (MVAR) | 0.000 |
| (MVAR) | 0.000 |
| (MVAR) | 0.000 |
| (MVAR) | 0.000 |
| Objective | |
| (MW) | 5.4970 |
| ($) | 2.8892 × 106 |
| 0.1635 | |
| Control Variable | Value |
|---|---|
| (p.u.) | 0.900 |
| (p.u.) | 1.100 |
| (p.u.) | 0.900 |
| (p.u.) | 1.100 |
| (MVAR) | 0.000 |
| (MVAR) | 35.00 |
| 1 | 3.0334 × 106 | 0.1241 | 0.0000 | 1.0000 | 0.0000 |
| 2 | 2.9064 × 106 | 0.1241 | 0.3033 | 0.9286 | 0.3033 |
| 3 | 2.8182 × 106 | 0.1246 | 0.5139 | 0.8571 | 0.5139 |
| 4 | 2.7532 × 106 | 0.1249 | 0.6692 | 0.7857 | 0.6692 |
| 5 | 2.7084 × 106 | 0.1252 | 0.7762 | 0.7143 | 0.7143 |
| 6 | 2.6802 × 106 | 0.1255 | 0.8437 | 0.6429 | 0.6429 |
| 7 | 2.6611 × 106 | 0.1257 | 0.8892 | 0.5714 | 0.5714 |
| 8 | 2.6496 × 106 | 0.1260 | 0.9166 | 0.5000 | 0.5000 |
| 9 | 2.6415 × 106 | 0.1263 | 0.9360 | 0.4286 | 0.4286 |
| 10 | 2.6350 × 106 | 0.1266 | 0.9516 | 0.3571 | 0.3571 |
| 11 | 2.6294 × 106 | 0.1269 | 0.9649 | 0.2857 | 0.2857 |
| 12 | 2.6247 × 106 | 0.1271 | 0.9762 | 0.2143 | 0.2143 |
| 13 | 2.6207 × 106 | 0.1274 | 0.9858 | 0.1429 | 0.1429 |
| 14 | 2.6174 × 106 | 0.1277 | 0.9936 | 0.0714 | 0.0714 |
| 15 | 2.6147 × 106 | 0.1280 | 1.0000 | 0.0000 | 0.0000 |
| Method | ||||
|---|---|---|---|---|
| ε-constraint Method | Base Case | 5.4970 | 2.8892 × 106 | 0.16350 |
| BCS | 4.9813 | 2.7084 × 106 | 0.12520 | |
| Reduction (%) | 9.3815 | 6.2578 | 23.4251 | |
| MODE Algorithm | Base Case | 4.9630 | 2.6085 × 106 | 0.19780 |
| BCS | 4.8300 | 2.5387 × 106 | 0.12040 | |
| Reduction (%) | 2.6798 | 2.6759 | 39.1304 |
| Control Variable | Optimal Value |
|---|---|
| (p.u.) | 1.06940 |
| (p.u.) | 1.06150 |
| (p.u.) | 1.04110 |
| (p.u.) | 1.04260 |
| (p.u.) | 1.10000 |
| (p.u.) | 1.05550 |
| (p.u.) | 1.03640 |
| (p.u.) | 0.92960 |
| (p.u.) | 0.97700 |
| (p.u.) | 0.99910 |
| (MVAR) | 20.9529 |
| (MVAR) | 1.84190 |
| (MVAR) | 2.34290 |
| (MVAR) | 3.28580 |
| (MVAR) | 0.00000 |
| 1 | 2.9015 × 106 | 0.1272 | 0.0000 | 1.0000 | 1.0000 | 0.0000 | 0.0000 |
| 2 | 3.1145 × 106 | 0.1309 | 0.0236 | 0.9511 | 0.9286 | 0.0724 | 0.0724 |
| 3 | 3.3885 × 106 | 0.1347 | 0.0472 | 0.8881 | 0.8571 | 0.1448 | 0.1448 |
| 4 | 3.7008 × 106 | 0.1384 | 0.0708 | 0.8164 | 0.7857 | 0.2172 | 0.2172 |
| 5 | 4.0028 × 106 | 0.1421 | 0.0944 | 0.7470 | 0.7143 | 0.2896 | 0.2896 |
| 6 | 4.3051 × 106 | 0.1459 | 0.1181 | 0.6776 | 0.6429 | 0.3620 | 0.3620 |
| 7 | 4.6107 × 106 | 0.1496 | 0.1417 | 0.6074 | 0.5714 | 0.4344 | 0.4344 |
| 8 | 4.9361 × 106 | 0.1533 | 0.1653 | 0.5326 | 0.5000 | 0.5068 | 0.5000 |
| 9 | 5.2798 × 106 | 0.1571 | 0.1889 | 0.4537 | 0.4286 | 0.5792 | 0.4286 |
| 10 | 5.6345 × 106 | 0.1608 | 0.2125 | 0.3722 | 0.3571 | 0.6515 | 0.3571 |
| 11 | 5.9691 × 106 | 0.1645 | 0.2361 | 0.2953 | 0.2857 | 0.7239 | 0.2857 |
| 12 | 6.2864 × 106 | 0.1683 | 0.2597 | 0.2224 | 0.2143 | 0.7963 | 0.2143 |
| 13 | 6.6184 × 106 | 0.1720 | 0.2833 | 0.1462 | 0.1429 | 0.8687 | 0.1429 |
| 14 | 6.9648 × 106 | 0.1757 | 0.3070 | 0.0666 | 0.0714 | 0.9411 | 0.0666 |
| 15 | 7.2547 × 106 | 0.1795 | 0.3262 | 0.0000 | 0.0000 | 1.0000 | 0.0000 |
| Control Variable | Optimal Value |
|---|---|
| (p.u.) | 1.06300 |
| (p.u.) | 1.05310 |
| (p.u.) | 1.07610 |
| (p.u.) | 1.05420 |
| (p.u.) | 1.10000 |
| (p.u.) | 1.08520 |
| (p.u.) | 1.02690 |
| (p.u.) | 0.90000 |
| (p.u.) | 1.00600 |
| (p.u.) | 0.97310 |
| (MVAR) | 0.00000 |
| (MVAR) | 0.00000 |
| (MVAR) | 0.00000 |
| (MVAR) | 3.03920 |
| (MVAR) | 2.66360 |
| Scenario | Level of the Load | Probability | Duration of the Load (h) |
|---|---|---|---|
| 0.95 | 0.1 | 2920 | |
| 1.00 | 0.8 | 4380 | |
| 1.05 | 0.1 | 1460 |
| 1 | 1.3129 × 106 | 0.1294 | 0.0000 | 1.0000 | 1.0000 | 0.0000 | 0.0000 |
| 2 | 1.4223 × 106 | 0.1339 | 0.0237 | 0.9443 | 0.9197 | 0.0722 | 0.0722 |
| 3 | 1.5418 × 106 | 0.1383 | 0.0473 | 0.8834 | 0.8395 | 0.1443 | 0.1443 |
| 4 | 1.6647 × 106 | 0.1428 | 0.0710 | 0.8207 | 0.7592 | 0.2165 | 0.2165 |
| 5 | 1.7954 × 106 | 0.1472 | 0.0946 | 0.7542 | 0.6790 | 0.2887 | 0.2887 |
| 6 | 1.9328 × 106 | 0.1517 | 0.1183 | 0.6841 | 0.5987 | 0.3609 | 0.3609 |
| 7 | 2.0774 × 106 | 0.1561 | 0.1420 | 0.6105 | 0.5185 | 0.4330 | 0.4330 |
| 8 | 2.2510 × 106 | 0.1606 | 0.1688 | 0.5220 | 0.4382 | 0.5148 | 0.4382 |
| 9 | 2.3848 × 106 | 0.1637 | 0.1893 | 0.4538 | 0.3818 | 0.5774 | 0.3818 |
| 10 | 2.5365 × 106 | 0.1673 | 0.2131 | 0.3765 | 0.3172 | 0.6501 | 0.3172 |
| 11 | 2.7000 × 106 | 0.1713 | 0.2379 | 0.2932 | 0.2447 | 0.7256 | 0.2447 |
| 12 | 2.9942 × 106 | 0.1783 | 0.2852 | 0.1433 | 0.1187 | 0.8700 | 0.1187 |
| 13 | 3.1909 × 106 | 0.1828 | 0.3143 | 0.0431 | 0.0376 | 0.9586 | 0.0376 |
| 14 | 3.2627 × 106 | 0.1844 | 0.3252 | 0.0065 | 0.0072 | 0.9919 | 0.0065 |
| 15 | 3.2754 × 106 | 0.1848 | 0.3278 | 0. 0000 | 0. 0000 | 1. 000 | 0.0000 |
| Control Variable | Expected Value | |||
|---|---|---|---|---|
| (p.u.) | 1.0621 | 1.0632 | 1.0640 | 1.0632 |
| (p.u.) | 1.0530 | 1.0532 | 1.0533 | 1.0532 |
| (p.u.) | 1.0749 | 1.0783 | 1.0794 | 1.0780 |
| (p.u.) | 1.0550 | 1.0522 | 1.0514 | 1.0524 |
| (p.u.) | 1.1000 | 1.1000 | 1.1000 | 1.1000 |
| (p.u.) | 1.0828 | 1.0903 | 1.0927 | 1.0898 |
| (p.u.) | 1.0285 | 1.0249 | 1.0234 | 1.0251 |
| (p.u.) | 0.9000 | 0.9000 | 0.9000 | 0.9000 |
| (p.u.) | 1.0036 | 1.0143 | 1.0171 | 1.0135 |
| (p.u.) | 0.9721 | 0.9500 | 0.9492 | 0.9521 |
| (MVAR) | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| (MVAR) | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| (MVAR) | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| (MVAR) | 1.8307 | 0.0000 | 0.0000 | 0.1831 |
| (MVAR) | 3.1448 | 0.0000 | 0.1993 | 0.3344 |
| Scenario | Wind Power Generation (MW) | Probability | Level of the Load | Duration of the Load (h) |
|---|---|---|---|---|
| 0.00000 | 0.0861 | 1 | 1460 | |
| 5.27050 | 0.1212 | 1 | 1460 | |
| 15.0917 | 0.1492 | 1 | 1460 | |
| 24.9726 | 0.1546 | 1 | 1460 | |
| 34.8784 | 0.1413 | 1 | 1460 | |
| 40.0000 | 0.3476 | 1 | 1460 |
| 1 | 3.7924 × 105 | 0.1222 | 0.0000 | 1.0000 | 1.0000 | 0.0000 | 0.0000 |
| 2 | 4.1835 × 105 | 0.1282 | 0.0300 | 0.9538 | 0.9096 | 0.0724 | 0.0724 |
| 3 | 4.6485 × 105 | 0.1335 | 0.0600 | 0.8988 | 0.8293 | 0.1448 | 0.1448 |
| 4 | 5.1663 × 105 | 0.1386 | 0.0900 | 0.8376 | 0.7523 | 0.2172 | 0.2172 |
| 5 | 5.7321 × 105 | 0.1442 | 0.1200 | 0.7707 | 0.6683 | 0.2896 | 0.2896 |
| 6 | 6.3071 × 105 | 0.1480 | 0.1500 | 0.7028 | 0.6093 | 0.3620 | 0.3620 |
| 7 | 6.9212 × 105 | 0.1525 | 0.1800 | 0.6302 | 0.5418 | 0.4344 | 0.4344 |
| 8 | 7.5741 × 105 | 0.1570 | 0.2100 | 0.5530 | 0.4740 | 0.5068 | 0.4740 |
| 9 | 8.2287 × 105 | 0.1615 | 0.2400 | 0.4757 | 0.4058 | 0.5792 | 0.4058 |
| 10 | 8.8964 × 105 | 0.1661 | 0.2700 | 0.3968 | 0.3355 | 0.6515 | 0.3355 |
| 11 | 9.4995 × 105 | 0.1706 | 0.3000 | 0.3255 | 0.2680 | 0.7239 | 0.2680 |
| 12 | 1.0169 × 106 | 0.1752 | 0.3300 | 0.2463 | 0.1984 | 0.7963 | 0.1984 |
| 13 | 1.0876 × 106 | 0.1798 | 0.3600 | 0.1628 | 0.1285 | 0.8687 | 0.1285 |
| 14 | 1.1621 × 106 | 0.1845 | 0.3900 | 0.0747 | 0.0583 | 0.9411 | 0.0583 |
| 15 | 1.2253 × 106 | 0.1883 | 0.4144 | 0.0000 | 0.0000 | 1.0000 | 0.0000 |
| Control Variable | Expected Value | ||||||
|---|---|---|---|---|---|---|---|
| (p.u.) | 1.0630 | 1.0627 | 1.0619 | 1.0611 | 1.0604 | 1.0599 | 1.0611 |
| (p.u.) | 1.0531 | 1.0530 | 1.0527 | 1.0523 | 1.0520 | 1.0518 | 1.0523 |
| (p.u.) | 1.0767 | 1.0778 | 1.0773 | 1.0769 | 1.0766 | 1.0765 | 1.0769 |
| (p.u.) | 1.0536 | 1.0525 | 1.0528 | 1.0531 | 1.0533 | 1.0534 | 1.0531 |
| (p.u.) | 1.1000 | 1.1000 | 1.1000 | 1.1000 | 1.1000 | 1.1000 | 1.1000 |
| (p.u.) | 1.0867 | 1.0893 | 1.0887 | 1.0883 | 1.0882 | 1.0883 | 1.0883 |
| (p.u.) | 1.0264 | 1.0266 | 1.0289 | 1.0311 | 1.0330 | 1.0338 | 1.0310 |
| (p.u.) | 0.9000 | 0.9000 | 0.9000 | 0.9000 | 0.9000 | 0.9000 | 0.9000 |
| (p.u.) | 1.0084 | 1.0121 | 1.0094 | 1.0071 | 1.0052 | 1.0043 | 1.0070 |
| (p.u.) | 0.9657 | 0.9499 | 0.9490 | 0.9480 | 0.9468 | 0.9462 | 0.9491 |
| (MVAR) | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| (MVAR) | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| (MVAR) | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| (MVAR) | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| (MVAR) | 3.8586 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.3321 |
| Scenario | Wind Power Generation (MW) | Level of the Load | Duration of the Load (h) | Probability |
|---|---|---|---|---|
| 0.00000 | 0.95 | 400 | 0.0086 | |
| 5.27050 | 0.95 | 400 | 0.0121 | |
| 15.0917 | 0.95 | 400 | 0.0149 | |
| 24.9726 | 0.95 | 400 | 0.0155 | |
| 34.8784 | 0.95 | 400 | 0.0141 | |
| 40.0000 | 0.95 | 400 | 0.0348 | |
| 0.00000 | 1.00 | 730 | 0.0689 | |
| 5.27050 | 1.00 | 730 | 0.0970 | |
| 15.0917 | 1.00 | 730 | 0.1194 | |
| 24.9726 | 1.00 | 730 | 0.1237 | |
| 34.8784 | 1.00 | 730 | 0.1130 | |
| 40.0000 | 1.00 | 730 | 0.2781 | |
| 0.00000 | 1.05 | 330 | 0.0086 | |
| 5.27050 | 1.05 | 330 | 0.0121 | |
| 15.0917 | 1.05 | 330 | 0.0149 | |
| 24.9726 | 1.05 | 330 | 0.0155 | |
| 34.8784 | 1.05 | 330 | 0.0141 | |
| 40.0000 | 1.05 | 330 | 0.0348 |
| 1 | 2.0134 × 105 | 0.1172 | 0.0011 | 1.0000 | 1.0000 | 0.0000 | 0.0000 |
| 2 | 2.1190 × 105 | 0.1224 | 0.0307 | 0.9718 | 0.9277 | 0.0717 | 0.0717 |
| 3 | 2.2563 × 105 | 0.1277 | 0.0607 | 0.9352 | 0.8555 | 0.1441 | 0.1441 |
| 4 | 2.4456 × 105 | 0.1330 | 0.0907 | 0.8847 | 0.7832 | 0.2165 | 0.2165 |
| 5 | 2.6724 × 105 | 0.1382 | 0.1207 | 0.8242 | 0.7110 | 0.2889 | 0.2889 |
| 6 | 2.9247 × 105 | 0.1435 | 0.1507 | 0.7569 | 0.6387 | 0.3614 | 0.3614 |
| 7 | 3.1866 × 105 | 0.1487 | 0.1807 | 0.6871 | 0.5667 | 0.4338 | 0.4338 |
| 8 | 3.4683 × 105 | 0.1539 | 0.2107 | 0.6119 | 0.4946 | 0.5062 | 0.4946 |
| 9 | 3.7578 × 105 | 0.1592 | 0.2407 | 0.5347 | 0.4224 | 0.5786 | 0.4224 |
| 10 | 4.0375 × 105 | 0.1644 | 0.2707 | 0.4601 | 0.3503 | 0.6511 | 0.3503 |
| 11 | 4.3143 × 105 | 0.1697 | 0.3007 | 0.3863 | 0.2782 | 0.7235 | 0.2782 |
| 12 | 4.6080 × 105 | 0.1749 | 0.3307 | 0.3079 | 0.2061 | 0.7959 | 0.2061 |
| 13 | 4.9207 × 105 | 0.1801 | 0.3607 | 0.2245 | 0.1351 | 0.8684 | 0.1351 |
| 14 | 5.2537 × 105 | 0.1850 | 0.3910 | 0.1357 | 0.0672 | 0.9414 | 0.0672 |
| 15 | 5.7623 × 105 | 0.1899 | 0.4153 | 0.0000 | 0.0000 | 1.0000 | 0.0000 |
| Control Variable | (p.u.) | (p.u.) | (p.u.) | (p.u.) | (p.u.) | (p.u.) | (p.u.) | (p.u.) | (p.u.) | (p.u.) | (MVAR) | (MVAR) | (MVAR) | (MVAR) | (MVAR) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1.0622 | 1.0530 | 1.0766 | 1.0534 | 1.1000 | 1.0868 | 1.0271 | 0.9000 | 1.0103 | 0.9522 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| 1.0618 | 1.0528 | 1.0759 | 1.0539 | 1.1000 | 1.0854 | 1.0288 | 0.9000 | 1.0072 | 0.9563 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 1.1342 | |
| 1.0610 | 1.0525 | 1.0754 | 1.0545 | 1.1000 | 1.0849 | 1.0311 | 0.9000 | 1.0047 | 0.9555 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 1.1557 | |
| 1.0602 | 1.0521 | 1.0751 | 1.0545 | 1.1000 | 1.0846 | 1.0333 | 0.9000 | 1.0026 | 0.9546 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 1.1916 | |
| 1.0594 | 1.0518 | 1.0747 | 1.0547 | 1.1000 | 1.0846 | 1.0351 | 0.9000 | 1.0007 | 0.9541 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 1.3510 | |
| 1.0594 | 1.0517 | 1.0751 | 1.0545 | 1.1000 | 1.0856 | 1.0353 | 0.9000 | 1.0008 | 0.9532 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 1.4686 | |
| 1.0631 | 1.0532 | 1.0775 | 1.0529 | 1.1000 | 1.0884 | 1.0257 | 0.9000 | 1.0114 | 0.9569 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 1.6385 | |
| 1.0627 | 1.0530 | 1.0772 | 1.0530 | 1.1000 | 1.0881 | 1.0270 | 0.9000 | 1.0100 | 0.9558 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 1.4814 | |
| 1.0619 | 1.0526 | 1.0768 | 1.0533 | 1.1000 | 1.0874 | 1.0294 | 0.9000 | 1.0073 | 0.9551 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 1.5306 | |
| 1.0611 | 1.0523 | 1.0764 | 1.0536 | 1.1000 | 1.0870 | 1.0315 | 0.9000 | 1.0050 | 0.9540 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 1.5171 | |
| 1.0603 | 1.0519 | 1.0760 | 1.0538 | 1.1000 | 1.0869 | 1.0335 | 0.9000 | 1.0029 | 0.9534 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 1.6548 | |
| 1.0599 | 1.0518 | 1.0758 | 1.0540 | 1.1000 | 1.0868 | 1.0344 | 0.9000 | 1.0018 | 0.9535 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 1.8457 | |
| 1.0639 | 1.0533 | 1.0787 | 1.0521 | 1.1000 | 1.0910 | 1.0240 | 0.9000 | 1.0141 | 0.9575 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 2.2814 | |
| 1.0635 | 1.0531 | 1.0786 | 1.0521 | 1.1000 | 1.0908 | 1.0253 | 0.9000 | 1.0130 | 0.9555 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 1.8830 | |
| 1.0628 | 1.0528 | 1.0781 | 1.0524 | 1.1000 | 1.0901 | 1.0277 | 0.9000 | 1.0102 | 0.9544 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 1.8246 | |
| 1.0620 | 1.0524 | 1.0775 | 1.0527 | 1.1000 | 1.0895 | 1.0299 | 0.9000 | 1.0076 | 0.9544 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 2.0862 | |
| 1.0610 | 1.0518 | 1.0764 | 1.0527 | 1.1000 | 1.0905 | 1.0316 | 0.9000 | 1.0075 | 0.9524 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 1.9060 | |
| 1.0606 | 1.0515 | 1.0758 | 1.0528 | 1.1000 | 1.0910 | 1.0324 | 0.9000 | 1.0074 | 0.9518 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 1.9321 | |
| Expected Value | 1.0611 | 1.0523 | 1.0764 | 1.0536 | 1.1000 | 1.0874 | 1.0314 | 0.9000 | 1.0053 | 0.9543 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 1.6427 |
| Scenario | Wind Power Generation (MVAR) |
|---|---|
| 0.0000 | |
| 1.0702 | |
| 3.0645 | |
| 5.0709 | |
| 7.0824 | |
| 8.1223 | |
| 0.0000 | |
| 1.0702 | |
| 3.0645 | |
| 5.0709 | |
| 7.0824 | |
| 8.1223 | |
| 0.0000 | |
| 1.0702 | |
| 3.0645 | |
| 5.0709 | |
| 7.0824 | |
| 8.1223 |
| 1 | 2.0015 × 105 | 0.1164 | 0.0010 | 1.0000 | 1.0000 | 0.0000 | 0.0000 |
| 2 | 2.1125 × 105 | 0.1215 | 0.0308 | 0.9706 | 0.9279 | 0.0719 | 0.0719 |
| 3 | 2.2251 × 105 | 0.1267 | 0.0608 | 0.9407 | 0.8559 | 0.1443 | 0.1443 |
| 4 | 2.4128 × 105 | 0.1319 | 0.0908 | 0.8910 | 0.7838 | 0.2167 | 0.2167 |
| 5 | 2.6295 × 105 | 0.1370 | 0.1208 | 0.8336 | 0.7118 | 0.2892 | 0.2892 |
| 6 | 2.8786 × 105 | 0.1422 | 0.1508 | 0.7676 | 0.6397 | 0.3616 | 0.3616 |
| 7 | 3.1517 × 105 | 0.1474 | 0.1808 | 0.6953 | 0.5677 | 0.4340 | 0.4340 |
| 8 | 3.4345 × 105 | 0.1525 | 0.2108 | 0.6203 | 0.4959 | 0.5064 | 0.4959 |
| 9 | 3.7331 × 105 | 0.1577 | 0.2408 | 0.5412 | 0.4240 | 0.5789 | 0.4240 |
| 10 | 4.0216 × 105 | 0.1629 | 0.2708 | 0.4648 | 0.3521 | 0.6513 | 0.3521 |
| 11 | 4.3098 × 105 | 0.1680 | 0.3008 | 0.3884 | 0.2802 | 0.7237 | 0.2802 |
| 12 | 4.6004 × 105 | 0.1732 | 0.3308 | 0.3115 | 0.2083 | 0.7961 | 0.2083 |
| 13 | 4.9099 × 105 | 0.1782 | 0.3609 | 0.2295 | 0.1377 | 0.8685 | 0.1377 |
| 14 | 5.2389 × 105 | 0.1831 | 0.3909 | 0.1423 | 0.0696 | 0.9410 | 0.0696 |
| 15 | 5.7760 × 105 | 0.1881 | 0.4153 | 0.0000 | 0.0000 | 1.0000 | 0.0000 |
| Control Variable | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1.0622 | 1.0530 | 1.0766 | 1.0534 | 1.1000 | 1.0868 | 1.0271 | 0.9000 | 1.0103 | 0.9522 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| 1.0618 | 1.0528 | 1.0757 | 1.0541 | 1.1000 | 1.0845 | 1.0301 | 0.9000 | 1.0063 | 0.9568 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 1.0974 | |
| 1.0609 | 1.0524 | 1.0748 | 1.0547 | 1.1000 | 1.0821 | 1.0350 | 0.9000 | 1.0020 | 0.9570 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 1.0878 | |
| 1.0601 | 1.0521 | 1.0739 | 1.0553 | 1.1000 | 1.0800 | 1.0397 | 0.9000 | 0.9980 | 0.9572 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 1.1175 | |
| 1.0594 | 1.0517 | 1.0732 | 1.0559 | 1.1000 | 1.0782 | 1.0441 | 0.9000 | 0.9945 | 0.9576 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 1.2400 | |
| 1.0593 | 1.0516 | 1.0732 | 1.0558 | 1.1000 | 1.0782 | 1.0458 | 0.9000 | 0.9936 | 0.9576 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 1.4022 | |
| 1.0631 | 1.0531 | 1.0773 | 1.0530 | 1.1000 | 1.0881 | 1.0258 | 0.9000 | 1.0109 | 0.9584 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 2.0174 | |
| 1.0627 | 1.0530 | 1.0770 | 1.0532 | 1.1000 | 1.0871 | 1.0284 | 0.9000 | 1.0090 | 0.9563 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 1.4457 | |
| 1.0619 | 1.0526 | 1.0761 | 1.0538 | 1.1000 | 1.0846 | 1.0333 | 0.9000 | 1.0045 | 0.9565 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 1.4365 | |
| 1.0611 | 1.0522 | 1.0753 | 1.0544 | 1.1000 | 1.0824 | 1.0380 | 0.9000 | 1.0005 | 0.9565 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 1.3856 | |
| 1.0603 | 1.0519 | 1.0744 | 1.0550 | 1.1000 | 1.0805 | 1.0425 | 0.9000 | 0.9967 | 0.9569 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 1.4942 | |
| 1.0598 | 1.0517 | 1.0740 | 1.0553 | 1.1000 | 1.0795 | 1.0447 | 0.9000 | 0.9948 | 0.9572 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 1.5764 | |
| 1.0639 | 1.0533 | 1.0787 | 1.0521 | 1.1000 | 1.0910 | 1.0240 | 0.9000 | 1.0141 | 0.9574 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 2.2599 | |
| 1.0635 | 1.0531 | 1.0783 | 1.0523 | 1.1000 | 1.0898 | 1.0266 | 0.9000 | 1.0120 | 0.9559 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 1.8262 | |
| 1.0628 | 1.0527 | 1.0774 | 1.0529 | 1.1000 | 1.0872 | 1.0315 | 0.9000 | 1.0073 | 0.9559 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 1.7669 | |
| 1.0620 | 1.0524 | 1.0766 | 1.0535 | 1.1000 | 1.0849 | 1.0363 | 0.9000 | 1.0030 | 0.9561 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 1.7580 | |
| 1.0612 | 1.0520 | 1.0758 | 1.0541 | 1.1000 | 1.0828 | 1.0408 | 0.9000 | 0.9990 | 0.9564 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 1.8356 | |
| 1.0608 | 1.0518 | 1.0754 | 1.0544 | 1.1000 | 1.0819 | 1.0431 | 0.9000 | 0.9971 | 0.9566 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 1.9071 | |
| Expected Value | 1.0610 | 1.0522 | 1.0753 | 1.0544 | 1.1000 | 1.0826 | 1.0380 | 0.9000 | 1.0006 | 0.9569 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 1.5296 |
| Case | ||||
|---|---|---|---|---|
| B | 4.9361 × 106 | 0.1533 | 0.1653 | 9.3494 |
| C | 2.2510 × 106 | 0.1606 | 0.1688 | 9.5049 |
| D | 7.5741 × 105 | 0.1570 | 0.2100 | 8.5777 |
| E | 3.4683 × 105 | 0.1539 | 0.2107 | 8.5575 |
| F | 3.4345 × 105 | 0.1525 | 0.2108 | 8.4807 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shojaei, A.H.; Ghadimi, A.A.; Miveh, M.R.; Mohammadi, F.; Jurado, F. Multi-Objective Optimal Reactive Power Planning under Load Demand and Wind Power Generation Uncertainties Using ε-Constraint Method. Appl. Sci. 2020, 10, 2859. https://doi.org/10.3390/app10082859
Shojaei AH, Ghadimi AA, Miveh MR, Mohammadi F, Jurado F. Multi-Objective Optimal Reactive Power Planning under Load Demand and Wind Power Generation Uncertainties Using ε-Constraint Method. Applied Sciences. 2020; 10(8):2859. https://doi.org/10.3390/app10082859
Chicago/Turabian StyleShojaei, Amir Hossein, Ali Asghar Ghadimi, Mohammad Reza Miveh, Fazel Mohammadi, and Francisco Jurado. 2020. "Multi-Objective Optimal Reactive Power Planning under Load Demand and Wind Power Generation Uncertainties Using ε-Constraint Method" Applied Sciences 10, no. 8: 2859. https://doi.org/10.3390/app10082859
APA StyleShojaei, A. H., Ghadimi, A. A., Miveh, M. R., Mohammadi, F., & Jurado, F. (2020). Multi-Objective Optimal Reactive Power Planning under Load Demand and Wind Power Generation Uncertainties Using ε-Constraint Method. Applied Sciences, 10(8), 2859. https://doi.org/10.3390/app10082859






