XOR Multiplexing Technique for Nanocomputers

Abstract

In emerging nanotechnologies, due to the manufacturing process, a significant percentage of components may be faulty. In order to make systems based on unreliable nano-scale components reliable, it is necessary to design fault-tolerant architectures. This paper presents a novel fault-tolerant technique for nanocomputers, namely the XOR multiplexing technique. This hardware redundancy technique is based on a numerous duplication of faulty components. We analyze the error distributions of the XOR multiplexing unit and the error distributions of multiple stages of the XOR multiplexing system, then compare them to the NAND multiplexing unit and the NAND multiplexing multiple stages system, respectively. The simulation results show that XOR multiplexing is more reliable than NAND multiplexing. Bifurcation theory is used to analyze the fault-tolerant ability of the system and the results show that XOR multiplexing technique has a high fault-tolerant ability. Similarly to the NAND multiplexing technique, this fault-tolerant technique is a potentially effective fault tolerant technique for future nanoelectronics.

1. Introduction

System reliability has always been an issue of widespread concern, and reliable systems have been widely required by various applications [1,2,3,4,5,6,7,8]. If the reliability of the system is not guaranteed, it will most likely cause serious consequences and even threaten human life. However, with silicon technology scaling, the reliability of nano-components is generally not very good. Hence, how to build reliable systems out of unreliable components is an inevitable problem. In order to solve this problem, scholars have investigated several redundant fault-tolerant techniques, such as N-tuple modular redundancy (e.g., triple modular redundancy) [9,10] and reconfiguration [11,12,13]. However, these techniques do not yield high fault tolerance for nanocomputers due to the extreme high devices’ density and the high percentage of faulty components. Since faulty components are the building blocks of the von Neumann’s multiplexing technique, faulty components are an integral part of the system. As a result, von Neumann’s multiplexing technique has received attention again [14]. A wealth of papers that reported the performance analysis of multiplexing technique have been published and, among them, the most attention was paid to NAND multiplexing [15,16,17,18] and majority multiplexing [19,20,21], first proposed by von Neumann. The multiplexing technique has been studied as an effective fault-tolerant technique for protection against the increasing transient faults in nanoelectronic circuits [22,23,24,25]. Hence, in addition to the two multiplexing techniques, scholars paid attention to other types of multiplexing technique, e.g., NOR-2multiplexing [26].

None of those multiplexing schemes mentioned how to realize the function of XOR or XNOR. In fact, they are unable to achieve it. As a universal logic gate, XOR and XNOR are widely used in integrated circuits, therefore it is necessary to study XOR multiplexing or XNOR multiplexing. In this paper, we present the XOR multiplexing technique for nanocomputers. This will make the research of multiplexing technique more comprehensive. The newly designed architecture is composed of XOR gates and NAND gates, where the XOR gates constitute the executive unit and the NAND gates constitute the restoring organs. The executive unit performs the desired logic function and the restoring organs perform the error correction function. First, we analyzed the error distributions in the XOR multiplexing unit and compared it with von Neumann’s NAND multiplexing unit. Then, the error distributions of the multiple stages system and the comparison are presented. Last, we analyzed the system performance of the architecture, i.e., its fault-tolerant ability. The system performance of the architecture is evaluated by studying its fault-tolerant ability, which can be defined by the gate error threshold and the input signal error threshold, where the gate error threshold is the maximum gate error probability in which the system can still work properly, and the input signal error threshold is the maximum input signal error probability that the system can tolerate. The experiment’s results show that the XOR multiplexing unit is more reliable than the NAND multiplexing unit and this technique has a high fault-tolerant ability and a unique feature; we name this as the critical point property, which can indicate the fault tolerant ability of the system.

The rest of paper is arranged as follows. In Section 2, we present the error distributions in the XOR executive unit and the XOR multiple stages multiplexing system, then compare them to the NAND executive unit and the NAND multiple stages multiplexing system. In Section 3, we discuss the bifurcation analysis, which is followed by Section 4: the fault-tolerant ability analysis of the XOR multiplexing system. Section 5 concludes the paper.

2. Error Distributions in the XOR Multiplexing System

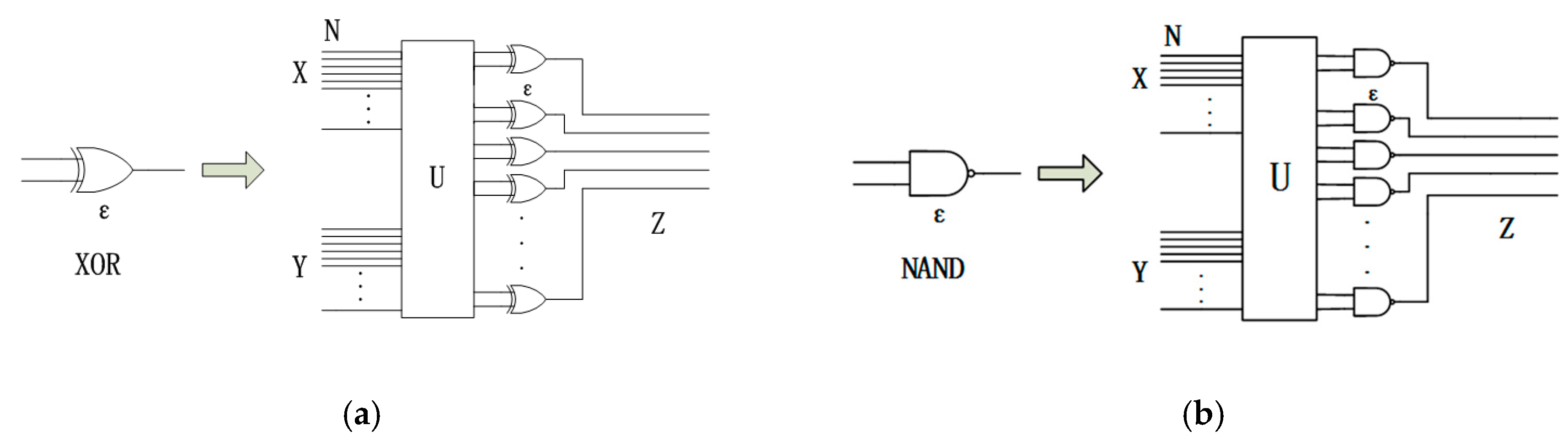
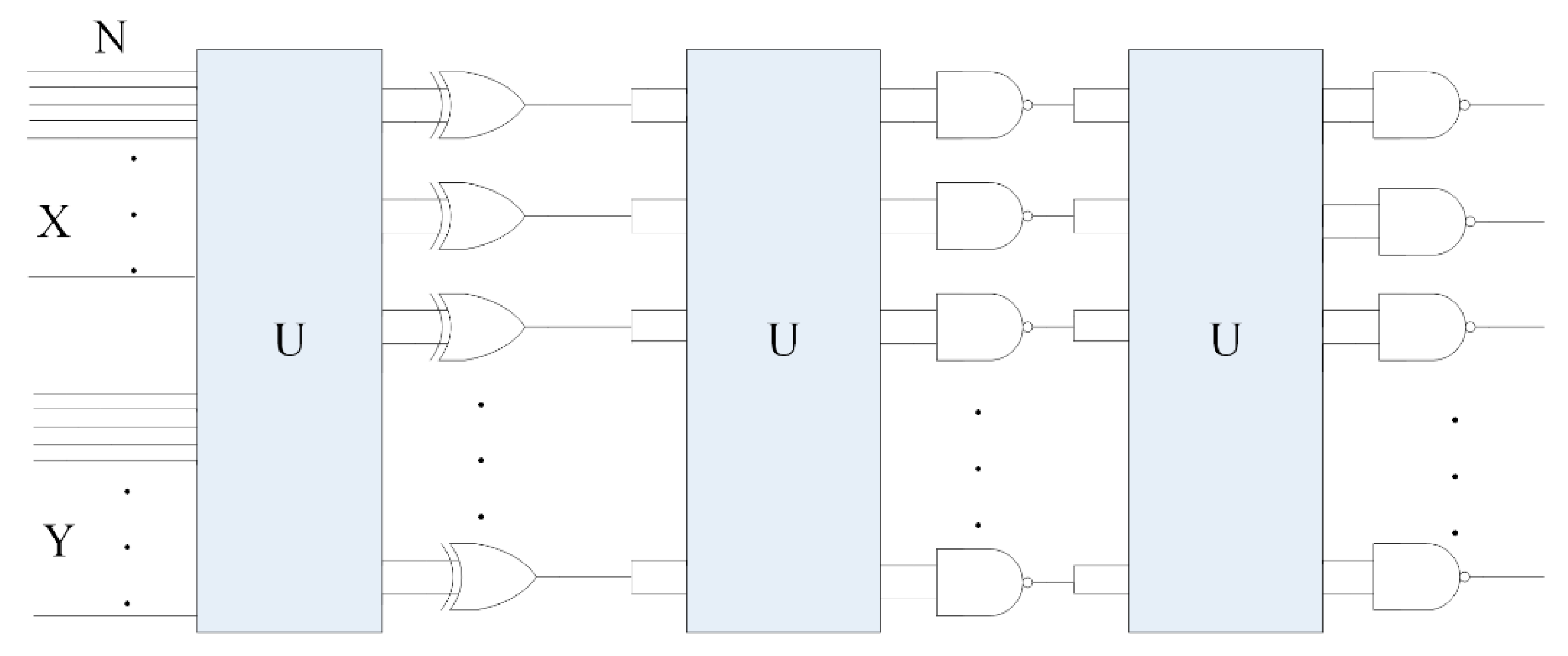
2.1. An XOR Multiplexing Unit

As shown in Figure 1, the XOR multiplexing unit has the same structure as the NAND multiplexing unit: duplicate an XOR gate N times, and replace two inputs and output of the XOR gate by a bundle of N lines [14,22], where the XOR gate has an error probability $\epsilon$.

The randomizing unit U is supposed to perform a random permutation of input signals; it has randomized interconnections, namely, each signal from the first input bundle and the second input bundle are randomly paired to connect to the next stage. Through this operation, inputs from the first bundle will be randomly paired with inputs from the second bundle to form the input pairs of the duplicated XOR gates [22]. Generally, there are three types of output error, von Neumann fault, Stuck-at-1 error and Stuck-at-0 error. However, based on the analysis results, we found that the (cumulative) probability distributions of these three types of error are quite similar; they only have a slightly different appearance. Hence, in this article, we only consider the von Neumann fault (i.e., it inverts its output).

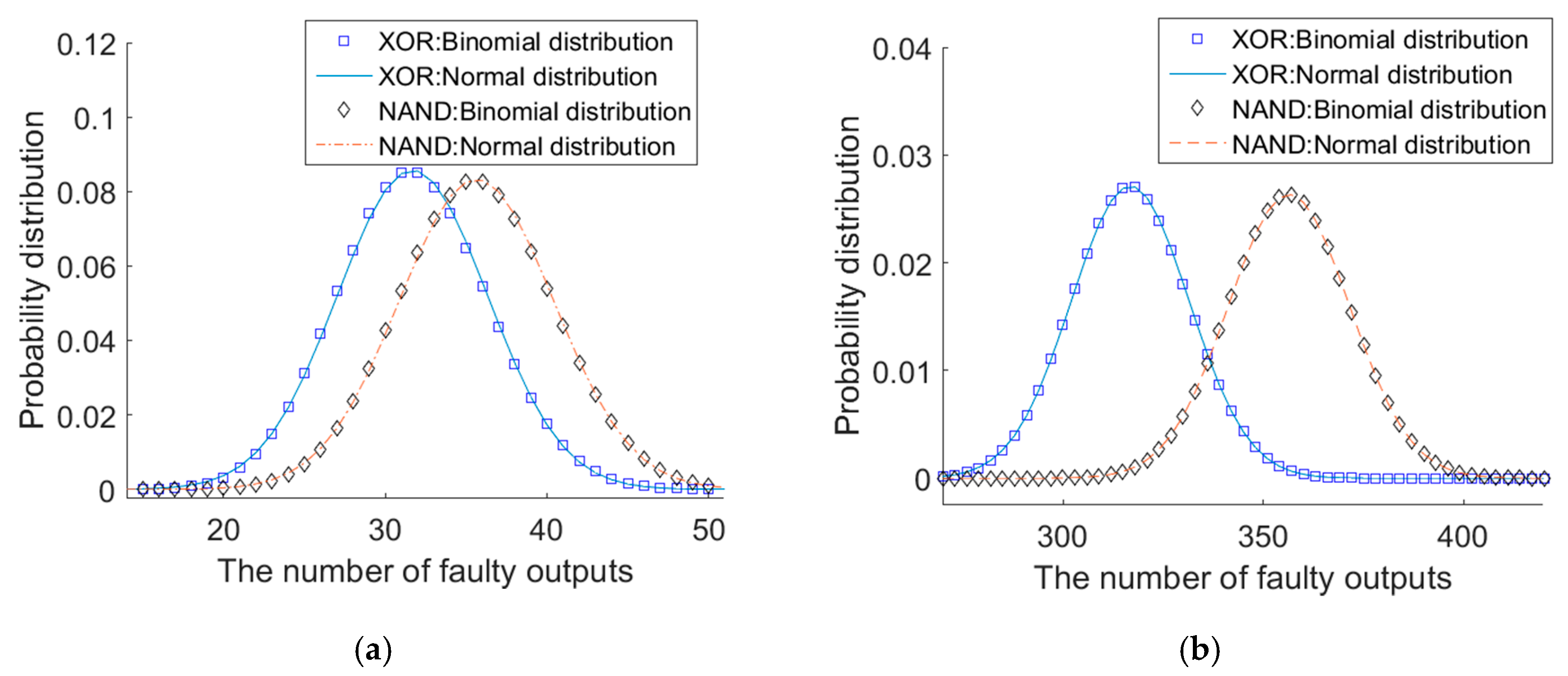
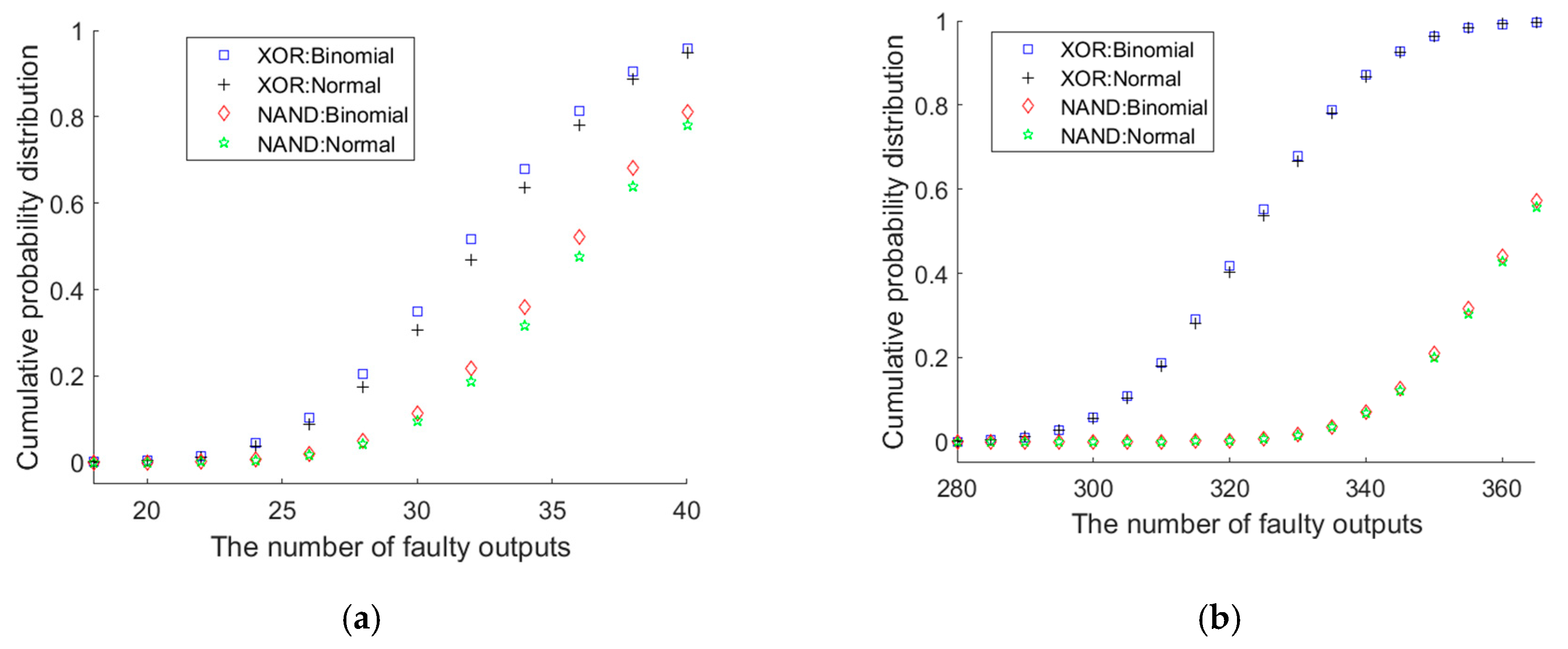
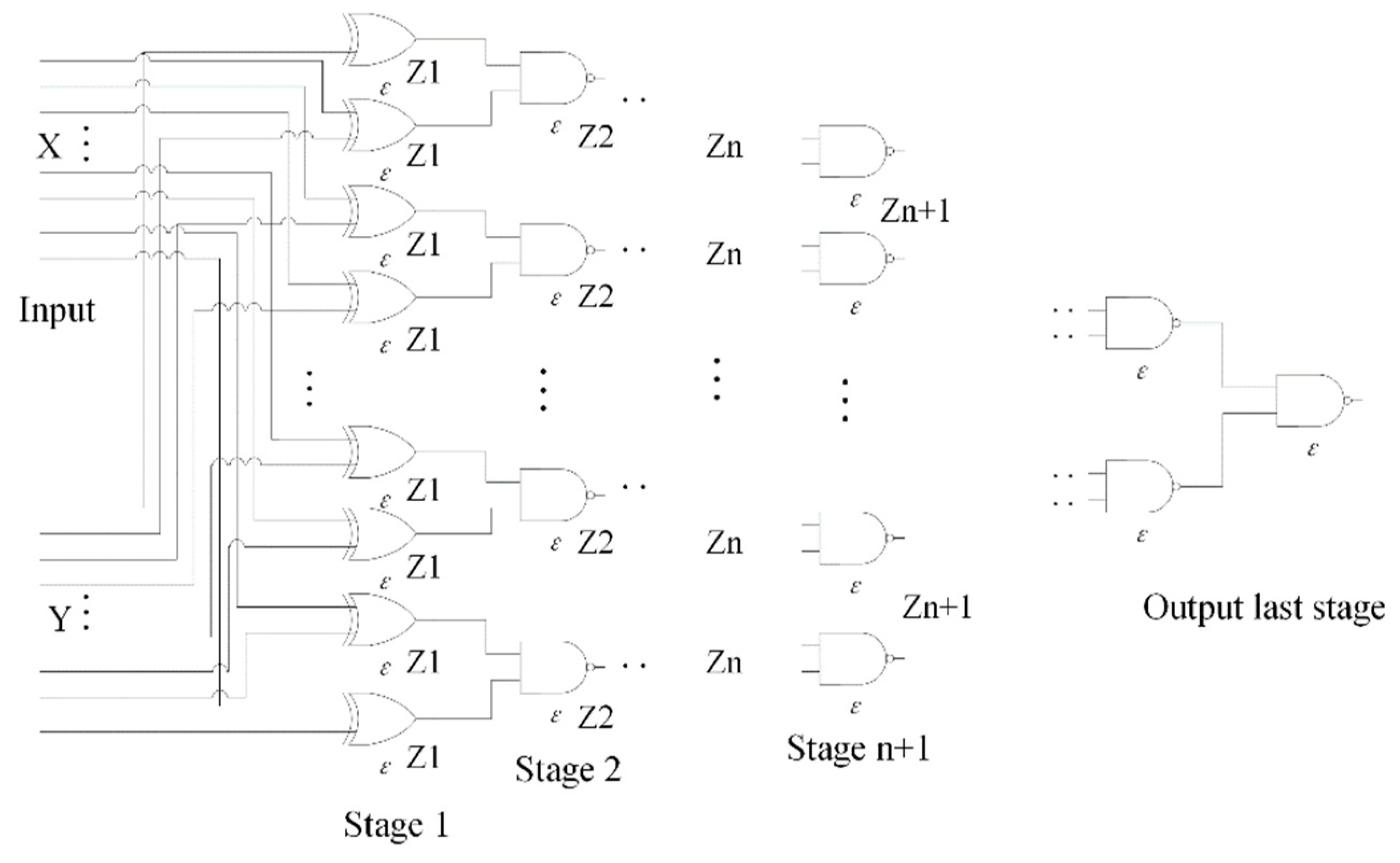
2.2. Error Distributions in the XOR Multiplexing Unit and the NAND Multiplexing Unit

The XOR multiplexing unit is shown in Figure 1. Assume that (x, y, z) are the probabilities of two input lines and output lines being stimulated, respectively. Assuming that the error probability ε of the XOR gate is zero and the error probabilities in the two input lines are independent, then the probability of the output of the XOR gate if stimulated will be z = x(1 − y) + y(1 − x) [22]. If the XOR gate is not fault-free, namely, the gate has a probability ε($\epsilon$ is not equal to zero) of making a von Neumann error, then the probability of its output being stimulated is

$$z=\left(1-\epsilon \right)\left[x\left(1-y\right)+y\left(1-x\right)\right]+\epsilon \left[xy+\left(1-x\right)\left(1-y\right)\right]$$

(1)

For the given numbers of stimulated inputs, the probability that an output is stimulated or not is actually not independent, but rather relevant to others. When N is relatively large, however, this relevance has little significant effect and can be ignored. If the N XOR gates function independently, then there is no doubt that the entire XOR multiplexing unit will constitute a Bernoulli sequence. Therefore, the distribution of the probability of stimulated outputs will be the binomial distribution. Correspondingly, the probability of exactly k outputs being stimulated is

$$P\left(k\right)=\left(\begin{array}{c}\mathrm{N}\hfill \\ k\hfill \end{array}\right)z^k{\left(1-z\right)}^{\mathrm{N}-k}$$

(2)

When N is rather large (N > 1000), the probability density of k can be obtained as [22]

$$f\left(k\right)=\frac{1}{\sqrt{2\pi }\sqrt{Nz(1-z)}}{e}^{-1/2{\left((k-Nz)/\sqrt{Nz(1-z)}\right)}^2}$$

(3)

Therefore, when N is extremely large, the probability of the number of stimulated outputs of the XOR multiplexing unit could approximately obey the normal distribution.

Since the XOR multiplexing unit and the NAND multiplexing unit have the same structure, assume the XOR gates and the NAND gates have the same error probability $\epsilon$, therefore, the probability of exactly k outputs of the NAND multiplexing unit being stimulated is [22]

$$P_N\left(k\right)=\left(\begin{array}{c}\mathrm{N}\hfill \\ k\hfill \end{array}\right){z_N}^k{\left(1-z_N\right)}^{\mathrm{N}-k}$$

(4)

where $z_N=(1-\epsilon )-(1-2\epsilon )xy$ is the probability that the output of the NAND gate is being stimulated. Similarly to the XOR multiplexing unit, the probability of the number of stimulated outputs of the NAND multiplexing unit also could be approximated to obey the normal distribution when N is extremely large. Next, the error distributions of the XOR multiplexing unit and the NAND multiplexing unit for different redundancy N and $\epsilon$ with certain value are considered. We take N = 1000 and N = 100. Specifying $x=y=0.8$ and $\epsilon =0.01$, for von Neumann error, the probability (density) of the binomial distribution and normal distribution against the number of faulty outputs is plotted in Figure 2. As the probability of possible errors below an acceptable threshold level P (k ≤ n) is an important feature to evaluate the approximation, the cumulative probability distribution P (k ≤ n) for the binomial and normal distribution is plotted in Figure 3.

As can be seen, when N is large (N = 1000), the normal distribution is in good accordance with the binomial distribution. However, for modest N (N = 100), the probability density of the normal distribution fits quite well with the binomial distribution, so the discrete binomial distribution is no longer appropriately described by the normal distribution in terms of the cumulative distribution, due to the declined bundle size N. This simulation result is consistent with the previous conclusions. As can be seen, with the same gate error probability and same input error level, when N = 1000, the error rates of the XOR multiplexing unit are distributed at the scale of approximately 270–360, while the scale of the NAND multiplexing unit is approximately at 310–400. Namely, the NAND multiplexing unit outputs more errors than the XOR multiplexing unit. We can obtain the same result for modest N (N = 100). Obviously, with the same redundancy N, same gate error probability $\epsilon$ and same input error level, the XOR multiplexing unit has a smaller mean value of error outputs, which means the XOR multiplexing unit produces fewer faulty outputs than the NAND multiplexing unit. In other words, the XOR multiplexing unit is more reliable than von Neumann’s NAND multiplexing unit.

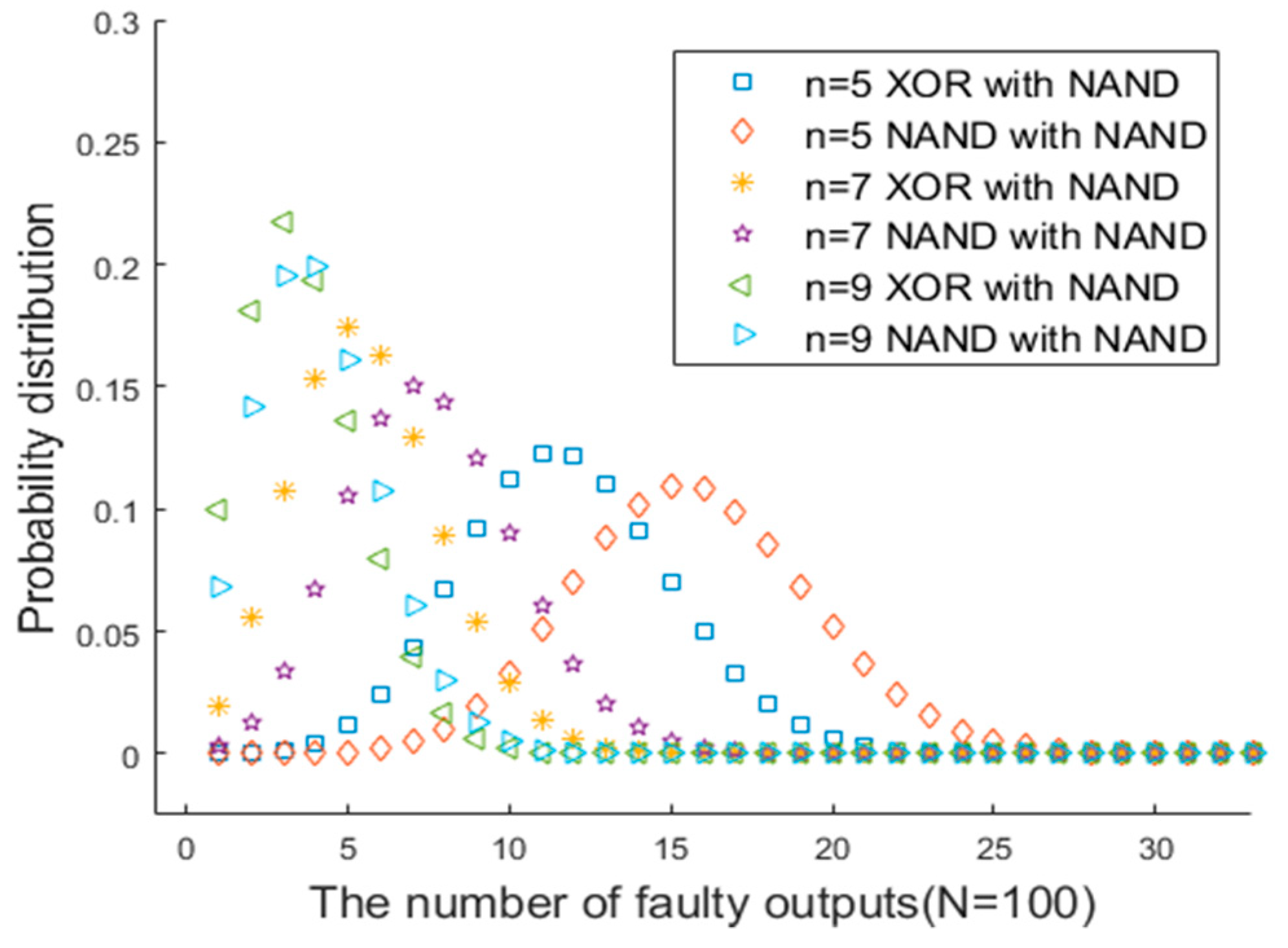
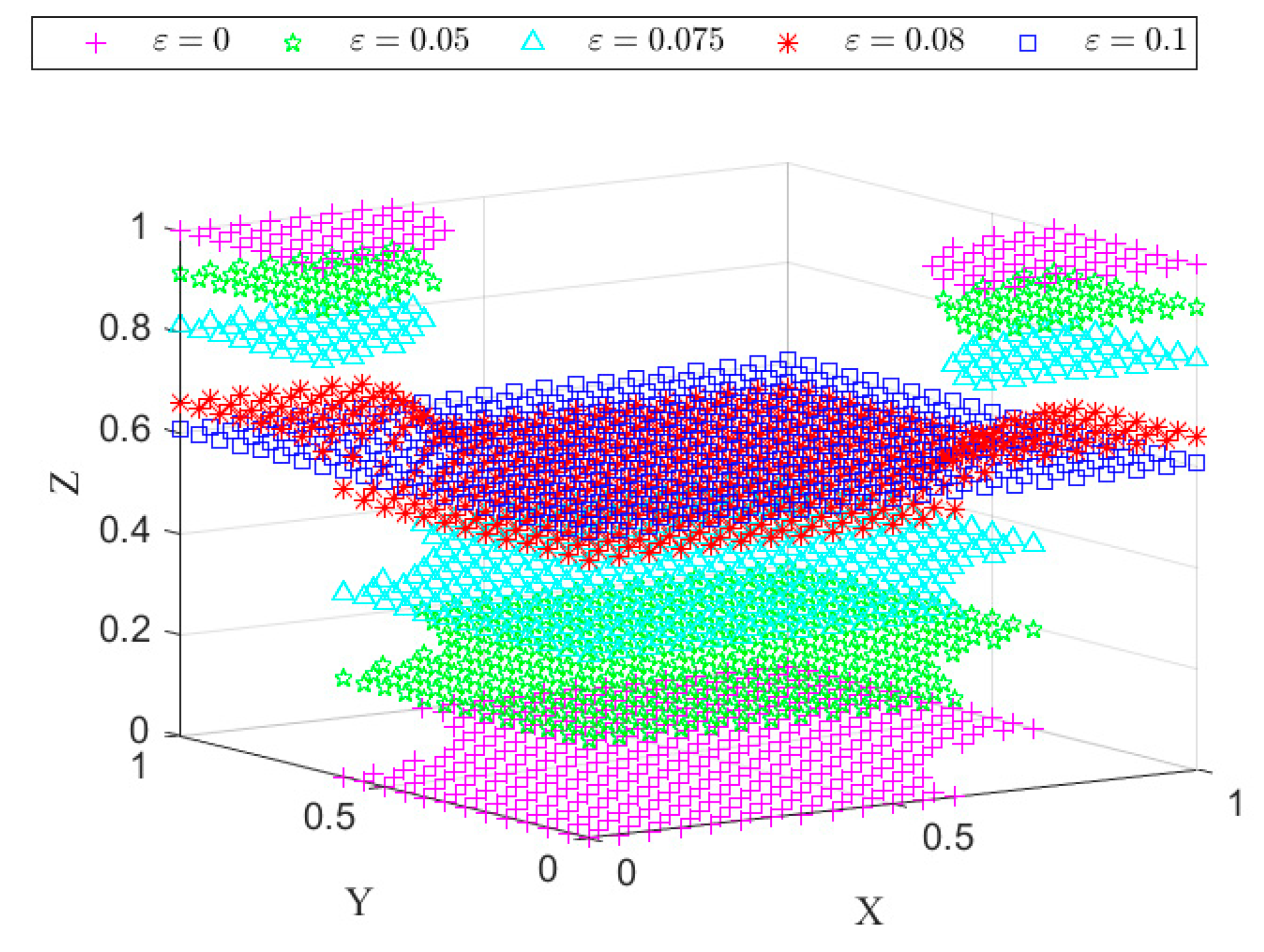
2.3. Error Distributions in the XOR Multiplexing System and the NAND Multiplexing System

Considering the multiple stages of error distribution of this XOR multiplexing and von Neumann’s NAND multiplexing with different restorative stages, i.e., n = 5, 7, 9, and specifying x = y = 0.8 (given 80% of the inputs are stimulated), N = 100 and ε = 0.01. For von Neumann error, the probability distributions against the number of fault outputs are plotted in Figure 4.

Figure 4 shows that for both XOR multiplexing and NAND multiplexing, the output error distributions move to the lower end as the number of multiplexing stages increases. Namely, the reliability can be improved by using more restorative units. When XOR multiplexing consists of seven stages, the probability that less than 10% of the output is faulty is approximately 0.9473, while 0.7739 for seven stages NAND multiplexing. Since N = 100, the probability that less than 10% of the output is faulty refers to the probability that the number of faulty outputs below 10 is a cumulative probability, which is the sum of the probability of the number of faulty outputs from 0 to 9. When the stages increase to nine stages, the probability that less than 10% of the output is faulty is approximately 0.9971 for XOR multiplexing and 0.9927 for NAND multiplexing. Based on the above analysis, Figure 4 demonstrates the conclusion that the XOR multiplexing unit is more reliable than the NAND multiplexing unit.

3. Bifurcation Analysis of the XOR Multiplexing System

Multiplexed systems contain two types of organs. The first type is the executive organ, which performs the desired basic operations on the bundles. The second type of organ is the restoring organ, which uses the redundant information available from the input bundle to provide more reliable information on the output bundle. Any logic gates, like the NAND gate, NOR gate, AND gates and OR gates, effectively alternate critical inputs (which produce critical errors) and subcritical inputs (which produce subcritical errors), thereby performing error correction. Among them, the NAND gate restoring organ is the first two-layer restoring organ with effective error correction ability. As shown in Figure 5, the XOR multiplexing system is composed of the XOR executive unit and NAND restoring organs. In order to make the system stable, multiple restoring organs would be necessary. Note that the odd stage number is necessary to keep the XOR function.

In order to derive the error threshold value for two-input XOR gates and two-input NAND gates, the circuit schematic shown in Figure 6 is involved. As can be seen, the circuit schematic is a binary tree of cascaded two-input unreliable XOR gates and NAND gates [14,23]. Assume that the XOR gates and NAND gates have the same error probability $\epsilon$ of making a von Neumann error, and their input lines and output lines function reliably. Let us denote the probabilities of the two inputs of the XOR gate being stimulated by X and Y. Since there are no feedback loops and fan-out in the circuit, the two inputs can be treated as independent. Then, the probability of the output of XOR gate being stimulated is

$$Z_1=(1-\epsilon )[X(1-Y)+Y(1-X)]+\epsilon [XY+(1-X)(1-Y)]$$

(5)

In the following analysis, we shall first assume that this circuit is a discrete time system. Then, further assume that all inputs to the XOR gates are independent and have the same probabilities, X and Y, of being stimulated. This structure not only guarantees that the inputs to all NAND gates at an arbitrary stage n are also independent but also guarantees that they have equal probabilities of being stimulated, which we denote to them by $Z_n$ [14]. Thus, for the second stage, the first stage of the NAND gates, the probability of the output being stimulated is

$$Z_2=\epsilon {Z_1}^2+(1-\epsilon )(1-{Z_1}^2)=(1-\epsilon )+(2\epsilon -1){Z_1}^2$$

(6)

For such a construction, Equation (6) reduces to a simple nonlinear map

$$Z_{n+1}=(1-\epsilon )+(2\epsilon -1){Z_n}^2$$

(7)

In order to discover the dynamic behavior of the map, bifurcation analysis is used to analyze Equation (7) [23]. For any fixed $0\le \epsilon \le 1/2$, we choose an arbitrary initial condition X, Y and then iterate Equation (7) until, after a sufficient number of iterates. it converges to an attractor. Those attractors are then plotted against each $\epsilon$ [14,23]. This leads to a nonlinear map called a bifurcation diagram and the diagram is shown in Figure 7 (∆$\epsilon$ = 0.001). This nonlinear map contains two kinds of attractors, fixed-point solution and periodic motion. The period-doubling bifurcation occurs at bifurcation point ${\epsilon }_{*}$. When ${\epsilon }_{*}\le \epsilon \le 1/2$, the system has a stable fixed-point solution; by solving the equation $z_0=(1-\epsilon )+(2\epsilon -1){z_0}^2$, we get

$$z_0=\frac{1-\sqrt{1-4(2\epsilon -1)(1-\epsilon )}}{2(2\epsilon -1)}$$

(8)

By stable, it means that for any arbitrary initial inputs condition X and Y, the output $Z_n$ will converge to $z_0$ when n is large. In other words, in this region, the system no longer functions as XOR. When $0\le \epsilon <{\epsilon }_{*}$, the system exhibits periodic motion with period 2, namely $z_0$, loses stability. We denote those two points by $Z_{+}$ and $Z_{-}$. At nth stage, when $Z_{+}$ is input, then $Z_{-}$ would be output and vice versa [14,23]. That means

$$Z_{+}=1-\epsilon +(2\epsilon -1){Z_{-}}^2$$

(9)

$$Z_{-}=1-\epsilon +(2\epsilon -1){Z_{+}}^2$$

(10)

From Equations (9) and (10), one obtains

$$Z_{\pm }=\frac{1\pm \sqrt{4(1-\epsilon )(1-2\epsilon )-3}}{2(1-2\epsilon )}$$

(11)

Clearly, when $\epsilon ={\epsilon }_{*}$, we have $Z_{+}=Z_{-}$ and it can be derived that the bifurcation point ${\epsilon }_{*}=(3-\sqrt{7})/4=0.08856\cdots$. Now, it is easy to see that the error probability interval where the system functions is $0\le \epsilon <{\epsilon }_{*}$. When $\epsilon >{\epsilon }_{*}$, the outputs converge to the stable fixed point $z_0$ regardless of what the initial inputs are. Hence, the gate error threshold is the bifurcation point ${\epsilon }_{*}=(3-\sqrt{7})/4=0.08856\cdots$.

Using fixed error probability $\epsilon$ from 0 to 0.1, and plotting the 3-D diagrams of X, Y and Z for the XOR multiplexing system, leads to Figure 8. From Figure 8, we can clearly observe the transformation of output from two distinct states to a fixed point when we fixed error probability $\epsilon$ from 0 to 0.1, with ${\epsilon }_{*}$ as the bifurcation point.

4. Fault-Tolerant Ability Analysis

In the last section, we analyzed the tolerant ability of the gate error probability (gate error threshold). Now let us analyze the tolerant ability of input signal error (input signal error threshold). In order to map each output probability to a logic state, we need a threshold $z_{*}$. According to Figure 7, it is notdifficult to find out that $z_0\left({\epsilon }_{*}\right)$ is a good choice for $z_{*}$. It is simple and effective. Substituting ${\epsilon }_{*}$ into Equation (8), then we have

$$z_0\left({\epsilon }_{*}\right)=\frac{1-\sqrt{1-4(2{\epsilon }_{*}-1)(1-{\epsilon }_{*})}}{2(2{\epsilon }_{*}-1)}=0.6076$$

(12)

Below, we shall interpret $\left[0,z_{*}\right)$ as non-stimulated state and $\left(z_{*},1\right]$ as a stimulated state. When we have fixed the input $Y=1$ and $Y=0$, then we can get 3-D diagrams, as shown in Figure 9. Clearly, the XOR multiplexing system has a higher fault-tolerant ability when inputs are both stimulated or both non-stimulated. Seen in Figure 9, the effectiveness of this threshold is obvious.

Note that for each different fixed Y, there is a different value of X (here we name it as critical point and denote it by $x_0$) that divides the output into two states when $0\le \epsilon <{\epsilon }_{*}$. Take $Y=0$ as an example, in the interval $0\le \epsilon <{\epsilon }_{*}$, when $X<x_0$, the output would be non-stimulated, and when $X>x_0$, the output would be stimulated. The calculation of the critical point can help us more intuitively understand the fault tolerant ability of the system. Since when n is large enough and $0\le \epsilon <{\epsilon }_{*}$, the output only depends on the input condition: input X and Y have the same logic state (both stimulated or both non-stimulated) or have a different logic state (one of the inputs is stimulated and the other one is non-stimulated). Let us denote the probability that two inputs X and Y have a different logic state by $P_1$, and denote the probability that two inputs X and Y have the same logic state by $P_2$. Therefore, the ratio of $P_1$ and $P_2$ will be a key parameter to determining if the final output $Z_n$ is larger than $z_{*}$ or not. X and Y are the probabilities of inputs being stimulated, and then $1-X$ and $1-Y$ are the probabilities of inputs being non-stimulated. $P_1$ and $P_2$ are shown as follows

$$P_1=X(1-Y)+Y(1-X)$$

(13)

$$P_2=XY+(1-Y)(1-X)$$

(14)

If we need the output to be stimulated, then $P_1/P_2$ must be larger than a specific value that is greater than one. Since the output logic state is associated with the output threshold $z_{*}$, the specific value will be a function of $z_{*}$ and the mathematic relation between them is shown below.

$$\frac{P_1}{P_2}=\frac{X(1-Y)+Y(1-X)}{XY+(1-X)(1-Y)}>\frac{z_{*}}{1-z_{*}}$$

(15)

Clearly, $P_1+P_2=1$, hence Equation (15) is equivalent to

$$P_1=X(1-Y)+Y(1-X)>z_{*}$$

(16)

If $P_1>z_{*}$, the final output would be larger than threshold (stimulated). When the inequality becomes

$$P_1=X(1-Y)+Y(1-X)<z_{*}$$

(17)

The final output would be smaller than threshold (non-stimulated). Hence, it is easy to obtain the critical point $x_0$ for each fixed Y by solving the following equality

$$x_0(1-Y)+Y(1-x_0)=z_{*}$$

Critical point $x_0$ is a function of Y; these critical points are then plotted against each Y (∆Y = 0.01). This leads to Figure 10, which shows that the diagram has two regions and for each different Y critical point $x_0$ has a different value and there is a parameter interval that makes the system no longer function, even though the system is fault-free, and the parameter interval is approximately 0.3924 < Y < 0.6076. If the value of one of the inputs is in this interval, then the output will always be non-stimulated for XOR multiplexing.

In order to demonstrate the tolerant ability of the input signal error probability of the system more intuitively, we extracted several fixed Y and the corresponding $x_0$ from Figure 10. These lead to

Table 1. Critical points for several fixed Y.

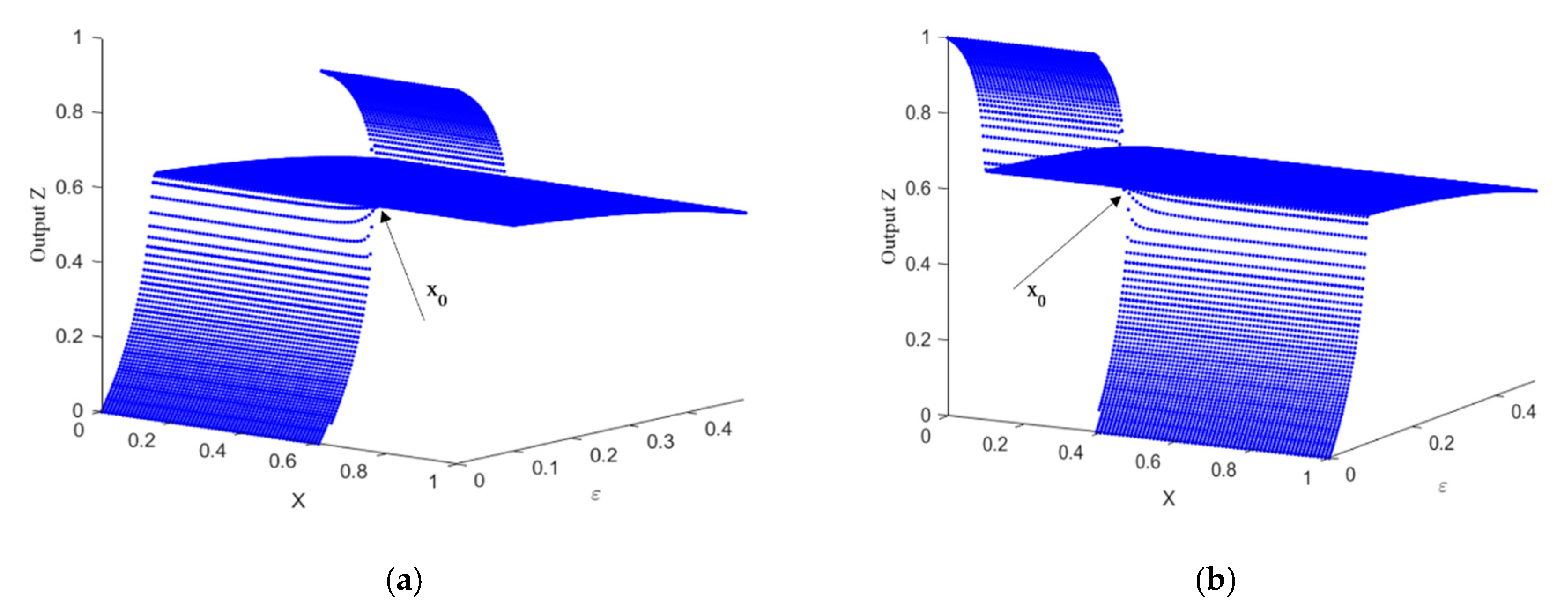
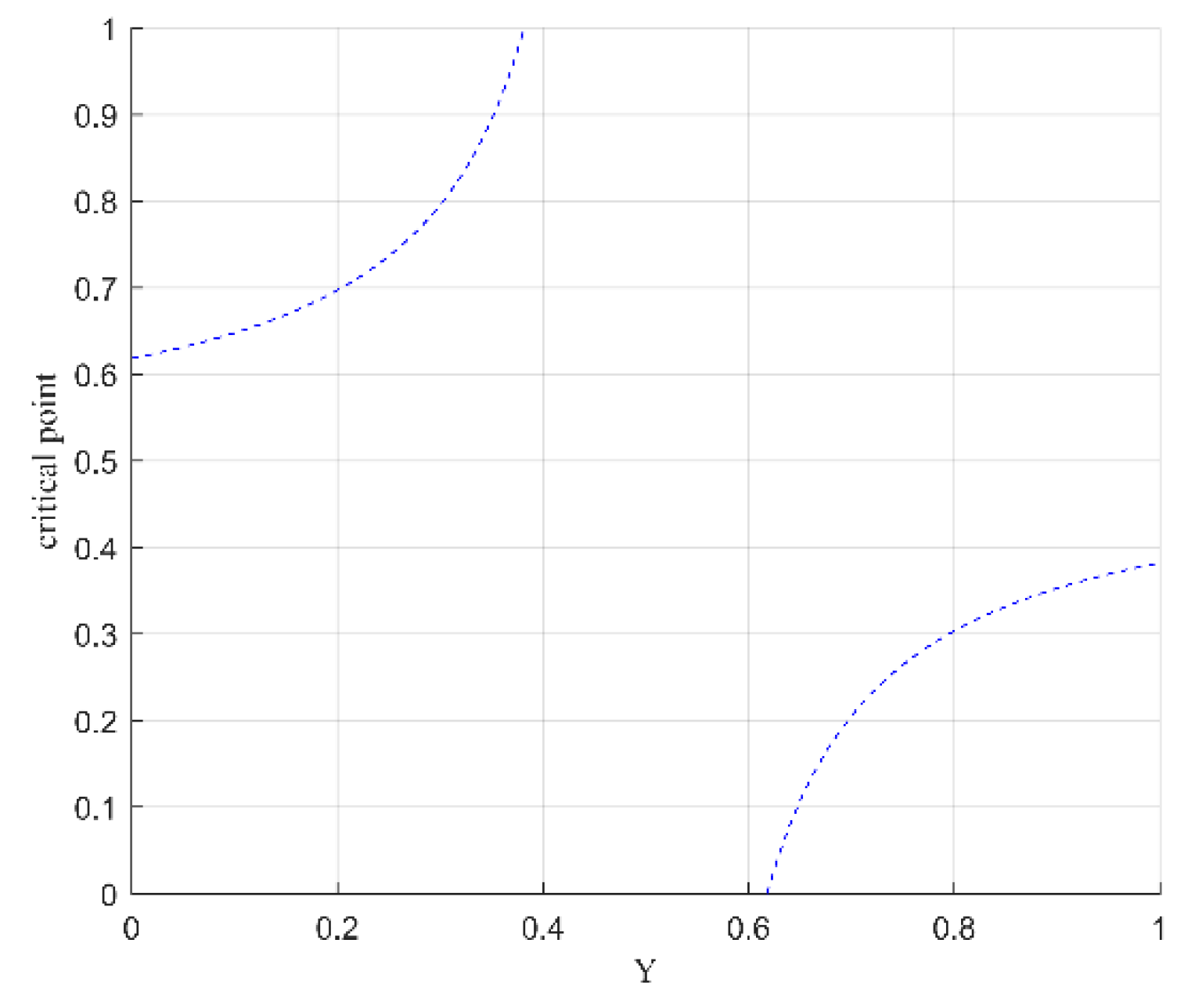
Fixed Y	Critical Points
Y = 0	0.60760
Y = 0.1	0.63450
Y = 0.2	0.67933
Y = 0.3	0.76900
Y = 0.7	0.23100
Y = 0.8	0.32067
Y = 0.9	0.36550
Y = 1	0.39240

. Let us take Y = 0.7 as an example; when input Y has a probability of 70% of being stimulated (means 30% error probability), any stimulated probability smaller than 23.1% of the other input X can be accepted. That is to say, the system can tolerate error probabilities of 30% and 23.1% for the inputs Y and X. Other situations are similar, so we omit them here. It also can be obtained that the maximum input signal error probability that the system can tolerant is 0.3924 (39.24%); namely, the input signal error threshold is 0.3924.

5. Conclusions

In order to make systems based on unreliable nanoelectronics reliable, it is necessary to design fault-tolerant architectures. This paper can be seen as a part of the endeavor devoted to this work. In this paper, we have studied a new fault-tolerant architecture for nanocomputers: XOR multiplexing. This fault-tolerant technique, based on a massive duplication of imperfect devices and randomized interconnections, was comprehensively studied. We have analyzed the error distributions of the XOR multiplexing unit and multiple stages of the XOR multiplexing system, then compared them with the NAND multiplexing technique. Analysis results have shown that the XOR multiplexing system has more stages to improve the fault tolerance. Comparison results have shown that the XOR multiplexing unit is more reliable, since it produces fewer faulty outputs than the NAND multiplexing unit. The fault tolerance ability analysis results have shown that the system has a high gate error tolerant ability and is expected to work at an acceptable reliability level when inputs have different logic states, and expected to work at a much higher reliability level when inputs have the same logic state. Although the conceived fault-tolerant architecture requires a rather large number of redundant components, which makes it inefficient for protection against permanent faults, it might be a system solution for the ultra large integration of highly unreliable nanometer-scale devices affected by dominant transient errors. Hence, this architecture is potentially effective in protection against transient faults for systems based on unreliable nanometer-scale devices. In the future, we hope to be dedicated to improving this technique so that it has a better fault-tolerant performance and a lower system redundancy.