Abstract
We consider the problem of fairly allocating indivisible tasks, focusing on a recently introduced notion of fairness called Minmax share guarantee. Minmax share (MMS) is a term of fairness guarantees that is defined to be the minimum cost that an agent can ensure for herself, if she were to partition the tasks into n bundles, and then receive the maximum cost bundle of tasks. However, the cost of tasks considered in previous work is single dimensional, and multidimensional situations have not been researched. In this work, we proposed an allocation algorithm that allocates tasks with multidimensional cost to agents under ordinal model. We prove the approximation ratio of MMS of the algorithm proposed can be guaranteed under , in addition the time complexity of the algorithm is . This proposed method is implemented and tested on datasets generated based on a real environment, and the experimental result shows that our algorithm has better performance than existing task allocation algorithms when cost of tasks is multidimensional.
1. Introduction
Multi-agent resource allocation is one of the major research topics in artificial intelligence [1], and fair allocation algorithms for items have been considered. Minmax share (MMS) fairness was proposed by the authors of [2] as a fairness concept for allocation of indivisible items. The goal is to allocate the items among the agents in a fair manner. The concept coincides with the standard proportionality fairness concept if the items to be allocated are divisible [3,4]. An agent’s MMS is the best if that agent can guarantee that they are allowed to partition the tasks, but then receives the least preferred bundle [2]. If all agents have positive utilities for the items, the items are viewed as goods. On the other hand, if all agents have negative utilities (i.e., negative utilities can be expressed as cost) for the items, the items are viewed as tasks (i.e., some form of work, task is expressed as chore). However, in all the work above, utilities of goods or the cost of tasks limited in single dimension and the situation that cost is multidimensional has not been taken into account.
In reality, we will face the task allocation problem when the cost of the task is multidimensional, such as when allocating tasks of plant protection to Unmanned Aerial Vehicles (UAV) in the agricultural environment. With the accelerated development of industrialization and urbanization, the shortage of the main rural labor force has led to a sharp rise in the cost of agricultural labor. There are approximately 2 billion hectares of arable land in the world, dozens of major pests and diseases occur all year round, and a large number of agricultural plant protection operations are needed. According to statistics from the World Health Organization (WHO) in recent years, more than 3 million cases of pesticide poisoning occur every year around the world [5]. With advancement in technologies, UAV can be useful in agricultural plant protection for crops to execute multiple tasks. To allocate tasks to UAVs in an agricultural plant protection environment, various situations need to be considered, such as reducing energy cost while minimizing overall task completion time. In order to find a method that can accomplishes fairness in allocation tasks to UAVs in the agricultural plant protection environment, evaluation of the cost of UAVs from multiple dimensions is needed. According to the authors of [6] and combined with the actual situation, the cost of UAVs by tasks usually comes from three dimensions: time cost, energy cost, and UAV service life cost. Time cost mainly includes working time and flight time of UAVs arriving at tasks. Energy cost is UAV cost of electricity and fuel during flight and working. Because of the limited life of UAVs and their assembled lithium battery, the UAV service life cost includes the life loss of UAVs and lithium battery. When allocating tasks, the cost of all dimensions needs to be considered comprehensively, not just a single dimension. The Round-Robin algorithm is a classic task allocation algorithm, its process is that the agent chooses a task according to its own preferences every round until all tasks are allocated. Although there are some variations of this algorithm, such as Greedy Round-Robin or Double Round-Robin, none of the existing algorithms can solve the task allocation problem when the cost of task is multidimensional.
In this work, we take the agricultural plant protection environment as an example to study the task allocation problem when the cost of task is multidimensional. The fairness concept we use in this work is the intensively studied and well-established MMS fairness and all tasks are set as indivisible. It needs to be emphasized that this work only uses the agricultural plant protection environment as an example to conduct research, and the conclusions obtained can be applied to all task allocation issues. The main contributions of this paper are as follows.
- Designing of a task allocation model for UAV applications in the agricultural plant protection environment.
- Defining the Minmax share when the cost of tasks is multidimensional.
- Improving the traditional Round-Robin algorithm to solve the task allocation problem when the cost of task is multidimensional.
- Prove in the form of a theorem that the Minmax share approximation can be guaranteed.
- Test and evaluate the performance of the proposed method using datasets generated based on real agricultural plant protection environment at the lab.
The remainder of the paper is structured as follows. Section 2 explains the problem and detailed model of the task allocation system in agricultural plant protection environment. Section 3 describes the key elements involved in the implementation of the algorithm we proposed and we analyze the properties of the algorithm in detail. Section 4 discusses the experiments and results of the implemented methodology. Section 5 presents the literature survey. Section 6 concludes the findings of this research and proposes future work.
2. Problem Definition
Agricultural plant protection UAV task allocation can be formalized as a multi-agent task allocation problem. In this section, we will first introduce the multi-agent task allocation problem and MMS, which is an indicator to measure the fairness of task allocation. Then, according to the background of UAV agricultural plant protection, we define the allocation problem that the cost of tasks is multidimensional. In addition, we also define the relationship between the total cost and the cost of each dimension when the cost of tasks is multidimensional.
2.1. Fair Allocation Problem
For the fair allocation problem, N is a set of n agents and M is a set of m indivisible tasks. For any and , represents the cost of task j to agent i. Next, we will illustrate the definition of preference.
Definition 1.
Preference
Imagine that agent and , then for i, if and only if
Example 1.

Assuming there are 2 agents and 2 tasks, the cost of agents by tasks can be seen in Table 1, then for agent 1, task 1 ⪯ task 2, and for agent 2, task 2 ⪯ task 1.

Table 1.
Cost of Agents by Tasks.
Different agents may have different preferences for these tasks and these preferences are generally captured by cost functions . As the goal of the problem is to fairly allocate all the tasks to these agents, the MMS fairness is defined in the following.
Definition 2.
MMS fairness:
Imagine that agent i gets the opportunity to partition all the tasks into n bundles, but she is the last to choose a bundle. Then, her best strategy is to partition the tasks such that the biggest cost of a bundle is minmized. Let denote the set of all possible n-partitionings of M. Then, the Minmax share (MMS) of agent i is defined as
where is the task bundle that agent i partitions, and represents that the cost of agent i.
Example 2.
(Continues from Example 1)
Assuming that agent 1 gets the opportunity to partition all tasks into 2 bundles and she is the last to choose, her best strategy is to partition the tasks into {task 1} and {task 2}, then the Minmax share of agent 1 is 3. Similarly, the Minmax share of agent 2 is 4.
Next, we will introduce the formal definition of MMS allocation.
Definition 3.
MMS allocation:
Let be an allocation, where and indicates if agent i gets task j under allocation x. Then, x is a MMS allocation if and only if for all
Example 3.
(Continues from Example 2) Assuming that the task 1 is allocated to agent 1 and task 2 is allocated to agent 2, then the coat of agent 1 is 2 and the coat of agent 2 is 1. All agents’ costs do not exceed their value of MMS, so this allocation is a MMS allocation.
The authors of [7] have shown that a MMS allocation does not necessarily exist, and to make it more accurate to measure the fairness of allocation, the definition of approximated MMS allocation has been proposed.
Definition 4.
approximated MMS allocation:
Let be an allocation, where and indicates if agent i gets task j under allocation x. Then, x is a approximated MMS allocation if and only if for all
In Equation (3), , because when an allocation will be called MMS-fairness, which has been shown in Definition 3. Note that a feasible allocation guarantees because a task can be assigned to only one agent when tasks are indivisible. It is assumed that all agents have underlying cardinal additive utilities over the tasks. Next, we will present the definition of the preference model that will be used in this paper.
Definition 5.
Ordinal model:
Agents are only allowed to express their preference over tasks but the cost of the tasks to agents is unknown.
We have explained the additive valuations in Section 2. Next, we will present the formal definition of the additive valuations for tasks.
Definition 6.
Additive valuations:
Let N denote the set of agents and M denote the set of indivisible tasks, agents are said to have additive valuations when, for any subset of tasks , the cost of agent i satisfies
Example 4.
(Continues from Example 1) Assuming that the task 1 and task 2 are allocated to agent 1, then according to Table 1, the cost of agent 1 is .
In the next section of this work, our research is based on an Ordinal model and additive valuations.
2.2. UAV Agricultural Plant Protection System
This section presents details of the UAV task allocation problem in agricultural plant protection environment. Compared to traditional task allocation problem, UAV task allocation in agricultural plant protection environment is a more complicated problem. UAVs considered in this work are special identical agents for agricultural plant protection, which can handle agricultural plant protection tasks. Tasks have cost to UAVs. The integral factors of the problem are defined as follows.
- Tasks are indivisible, a task is allocated to one UAV.
- Task produces 3 dimensions of cost to UAVs: time cost, energy cost, and UAV service life cost. The total cost is calculated based on these 3 costs.
- The relationship between different dimensions of cost is non-deterministic, but it is in a range (i.e., energy cost by the UAV for one hour of flight is not deterministic because the real-time environment is complex, but its lower and upper bounds can be determined).
- As the status of UAVs is different, a task has a different cost to different UAVs in a single dimension (e.g., a task may has different time cost for two UAVs because the positions of the two UAVs are different and time spent flying is counted in time cost).
- Due to the inconsistent state of UAVs, different UAVs have different weights over tasks (e.g., a UAV that is about to run out of energy has a higher weight on energy cost, and an aging UAV has a higher weight on service life cost).
- Due to the complexity of the actual situation: the cost of tasks to UAVs is unknown.
- UAVs’preference over the tasks in single dimension can be known (e.g., UAV is farther away from task 2 than task 1, then in the time cost dimension: ).
Based on these, we will formally present our problem model: the setting and meaning of the parameters can be found in Table 2, according to condition 1 the cost of a task j to UAV i can be defined as Equation (5).

Table 2.
Parameter settings.
Example 5.


Assuming that there are 2 UAVs and 2 tasks. UAV 1’s weights are (, , ), each dimension corresponds to the weight of time cost, the weight of energy cost, and the weight of UAV service life cost, respectively. Similarly, UAV 2’s weights are (, , ). The cost of agents by tasks can be seen in Table 3 and Table 4.

Table 3.
Cost of unmanned aerial vehicles (UAVs) by Task 1.

Table 4.
Cost of UAVs by Task 2.
- Then, the cost of UAV 1 by task 1 is
- The cost of UAV 1 by task 2 is
- The cost of UAV 2 by task 1 is
- The cost of UAV 2 by task 2 is
As our research focuses on additive valuations, the total cost of UAV i is calculated in Equation (6), different types of cost have a relationship, which has been explained in condition 3, and are expressed as Equations (7) and (8).
According to condition 7, UAVs’ preferences over the tasks has been reported and the cost of tasks to UAVs is unknown. As there are 3 types of cost, according to Definition 1, UAVs have a preference for tasks based on each type of cost. Formally speaking, for all , the UAV i’s preference are shown in Equations (9)–(11).
Example 6.
(Continues from Example 5) From Table 3 and Table 4, we can see that the preference of UAV 2 are as follows.
- In time cost, ;
- In energy cost, ;
- In service life cost, ;
According to above conditions, our research is to find an allocation that satisfies approximated MMS allocation. That is for all by Definition 4.
3. Problem Solution
In this section, we will propose a solution for the problem proposed in Section 2.2. To address this problem, in Section 3.1 we propose an improved Round-Robin algorithm for allocate tasks to UAVs in agricultural plant protection system to achieve Approximate MMS Fair Allocation. In Section 3.2, we analyzed that the approximation ratio of MMS of the algorithm proposed can be guaranteed under , in addition, the time complexity of the algorithm is .
3.1. Finding an Approximate Maximin Fair Allocation
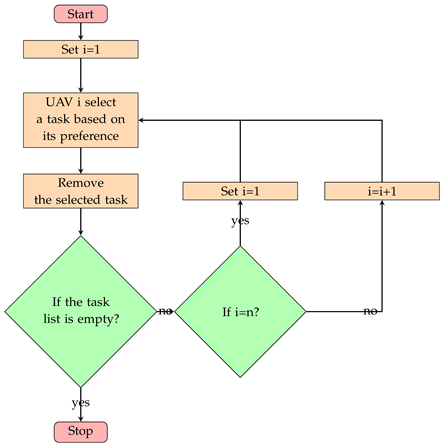
We allocate tasks to UAVs by employing an improved Round-Robin algorithm. To make the algorithm easier to understand, we briefly show some of the main steps of the algorithm through an algorithm flowchart.
The detailed process of the algorithm will be described in the following and the pseudocode of the algorithm has been shown in Algorithm 1.
- (a)
- Input and OutputIn the input phase, we enter a set N containing n UAVs and a set M containing m tasks. For each UAV, it cotains the UAV’s preference on three types of cost from tasks and the UAV’s weights for costs. In addition, the relationship between different types of cost, which have been defined in Equations (7) and (8), are also be entered. The output is allocated task set for each .
- (b)
- Importance assessmentLine 3–5 in Algorithm 1 calculated the proportion of time cost, energy cost, and service cost in total cost. Although some information is unknown, we are able to calculate the minimum proportion of each type of cost.
- (c)
- Task selectionLine 6–18 in Algorithm 1 indicate that the UAVs select a task based on their preferences. In each round, each UAV selects only one task which has minimal cost on it. Lines 19–20 indicate the loop termination when all tasks are allocated.
Example 7.
(Continues from Example 6) Here, we assume that the task set with 2 tasks to be allocated to the UAV set with 2 UAVs . It is known that each unit of time cost generates 1–2 units of energy cost and service life cost.
In first round, chooses a task. Because the weight of is (, , ), then according to the 3–5 lines of Algorithm 1, we can calculate that . As is the biggest of , selects the task according to its preferences in life cost.
Then, and .
Similarly, all UAVs in set N select a task in the manner described above cyclically until M is empty.
| Algorithm 1 Improved Round-Robin Algorithm |
| Input:n UAVs, m tasks Output: An allocation
|
3.2. Analysis of Algorithm
In Section 3.1, we have proposed an improved Round-Robin algorithm to allocate tasks to UAVs in agricultural plant protection system to achieve Approximate Maximin Fair Allocation. In this section, we will analyze the algorithm’s property.
Lemma 1.
Let be the task picked by UAV i and be the task picked by UAV . If UAV i picks before UAV picks in the Improved Round-Robin Algorithm, then we have . Here, , is cost of UAV i for task and is the maximum cost of UAV i in all tasks.
Proof.
According to Equation (5), . In the following, we assume that (same as other situations), UAV i will pick tasks in order to minimize time cost, due to UAV i pick before UAV , so , therefore .
Because and , so time cost accounts for at least of total cost. Moreover, for any , therefore . □
Lemma 2.
Let be the allocation obtained by the Improved Round-Robin Algorithm for M. Then, we have .
Proof.
The Improved Round-Robin Algorithm has exactly rounds of allocation. The task picked by UAV i ( resp.) in round k is denoted by ( resp.). Next, we will prove this lemma in five cases.
Case 1: and both UAV i and UAV have selceted the task in the last round.
In this case, UAV i will pick task before UAV in each round, then
and for round k, according to Lemma 1, . Therefore, .
Due to that , .
Case 2: and none of UAV i and UAV have selceted the task in the last round.
Similar to case 1, UAV i will pick task before UAV in each round, then
therefore .
Case 3: and UAV i have selceted the task in the last round but UAV not.
In this case, UAV i will pick task before UAV in each round but according to algorithm rules UAV i has one more task than UAV . Then,
According to Equation (12), we can get that
As , therefore .
Case 4: and UAV have selected the task in the last round but UAV i has not.
In this case, UAV i will pick a task after UAV in each round, but according to algorithm rules UAV i has one less task than UAV . Then,
According to Equation (13), we can get that
Due to the UAV i pick task in k round before UAV in round, so . Therefore .
Case 5: and both UAV i and UAV have selected the task in the last round.
In this case, UAV i will pick task after UAV in each round, then
The Equation (14) can be can be expressed as , due to the UAV i pick task in k round before UAV in round, so . Moreover, , therefore .
In summary, we can know that . □
Lemma 3.
Let be the allocation obtained by the Improved Round-Robin Algorithm for M. Then, we have
Proof.
According to lemma 2, for , so
Because , the Equation (15) divided by n can yields the result. □
Theorem 1.
The Improved Round-Robin Algorithm gives an allocation , then we have for all
Proof.
According to Definition 2, if partition P divides task set M into n bundles such that biggest cost of a bundle is minimized for UAV i, then the cost of UAV i is expressed as . Therefore, by definition of the Min-Max share guarantee and the additivity of , we obtain that
and
According to the Lemma 3, we can get that , for each agent , which proves the Theorem 1. □
Theorem 2.
The time complexity of the Improved Round-Robin Algorithm is , where m is the number of tasks in task set M.
Proof.
Here, is , in order to facilitate the expression, we will use to represent in the following.
The number of outer loop is m, inside the loop, the execution of the algorithm deos not exceed 8 steps. However, the algorithm requires finding the task with minimum cost for UAV i from the remaining task set with tasks at each round. For finding the minimum, a binary search would require at each round, thus the total time complexity is
Using Stirling’s approximation, Equation (18) can be approximately equal to , so the time complexity of the Improved Round-Robin Algorithm is . □
4. Experiment
The results in Section 3.2 give us worst case bounds on the guaranteed approximation of MMS. In this section, we present experimental results which provide a perspective on what may happen “in practice”. To examine the behavior and performance of the proposed algorithm, experiments are conducted based on multiple sets of data. As mentioned earlier, as our research is based on UAV agricultural plant protection background, so the data we use is based on UAV agricultural plant protection background as well. In Section 4.1, we detail the source and process of the data. In Section 4.2, we show our experimental results in detail. The algorithm was coded in Python and tested on a PC with an Intel Core i7 CPU.
4.1. Data Generation
In terms of data generation, we need to generate UAVs’ preferences, the cost of tasks to UAVs in all dimensions, and the relationship between different types of cost, which have been defined in Equations (7) and (8). This is because
- (1)
- the preference of the UAVs, the relationship between the different types of cost, and the cost’s weights are the input of our algorithm, and
- (2)
- in order to measure the approximation of MMS of algorithms, we need to generate the time cost, energy cost, and service life cost of tasks for UAVs.
4.1.1. Preference Generation
According to Equations (9)–(11), UAVs have different preferences for tasks in 3 dimensions. Therefore, for each UAV, we should generate 3 preferences over all tasks.
As our focus is fairness, and fairness is often hard to achieve when agents have similar valuations, we employ the Mallows model [8] and use the generator from WWW.PREFLIB.ORG in our study. Mallows models are often used in machine learning and preference handling as they allow us to easily control the correlation between the preferences of the agents; a common phenomena in preference data [8]. A Mallows model has two parameters: a Reference Order , the preference order at the center of the distribution, and a Dispersion Parameter , the variance in the distribution, which controls the level of similarity of the agent preference orders. When all agents have the same ordinal preference; when then the ordinal preferences are drawn uniformly at random from the space of all preference orders. In this work, we set .
4.1.2. Cost’s Weights and Relationship
We have defined the relationship between different types of cost in Equations (7) and (8), here we determine specific values based on the background of UAV agricultural plant protection.
We establish the relationship between different cost through the performance of UAV. The UAV data comes from the MG-1P agricultural plant protection UAV, which is a multi-rotor UAV produced by Dajiang Science and Technology [9]. According to its technical specifications, the agricultural plant protection UAV parameter settings can be seen as Table 5.

Table 5.
UAV specifications.
From Table 5 and combined with the actual situation, we know that the energy cost is Ah– Ah per minute and the UAV service life cost is – per minute. The specific parameters reflecting the relationship between cost are shown in Table 6.

Table 6.
Relationship parameters between different types of cost.
Different UAVs have different weights about cost, for example, UAVs that are about to run out of energy have a big weight in energy cost and aging UAVs have a big weight in life cost. We refer to the information in the Table 6 when setting the range of weights to ensure that it is set reasonably. The details of the parameters have been shown in Table 7. Then, we generate weights according to the uniform distribution in the range defined by the Table 7.

Table 7.
Range of weights.
4.1.3. Cost Generation
As stated in the Section 1, this research is mainly aimed at the agricultural plant protection problem in densely populated villages, where per capita agricultural land is small and agricultural land is scattered. According to previous research [6,10,11] and combined with reality, the plant protection area usually between 1 acres to 3 acres. In order to calculate the approximate range of time cost of tasks, we should first calculate the operating speed of UAVs based on its operating specifications. Table 8 shows the MG-1P model agricultural plant protection UAV’s operating specifications.

Table 8.
Operating specifications.
According to Table 8, we can calculate the time cost of the tasks in the range of 1 to 3 min, then we can generate the time cost of the tasks according to the uniform distribution in this range. From the time cost of the tasks, and according to the relationship reflected in Table 6, we can calculate the energy cost and service life cost.
Finally, when the time cost, energy cost, and service life cost are generated for UAVs, we also need to verify whether it is consistent with the preferences of the UAV generated Section 4.1.1. If they are not consistent, the data needs to be regenerated.
4.2. Result
In the this section, we provide details of the experimental performance of improved Round-Robin algorithm. As per Definition 4, we will evaluate the approximate ratio of Min-Max share of the algorithm as an indicator. Due to the real-time task allocation needed in reality, the running time of the experiment also need to be evaluated. To better illustrate the superiority of our algorithm, we compare our proposed algorithm with Random Serial Dictatorship (RSD) proposed in [8] and the SequPick algorithm proposed in [1].
First, we compare our algorithm with Random Serial Dictatorship (RSD). This comparison was made because RSD is probably the best known and most-studied mechanism in the random allocation literature. In addition, RSD guarantees the total utilitarian welfare if the utilities are normalized to sum up to one for each agent under ordinal preferences, which is similar to our model. However, the main difference is RSD targets the situation where cost comes from a single dimension, but in this work cost is multidimensional. Next, we will compare our algorithm and RSD in terms of the approximate ratio of Min-Max share and runtime.
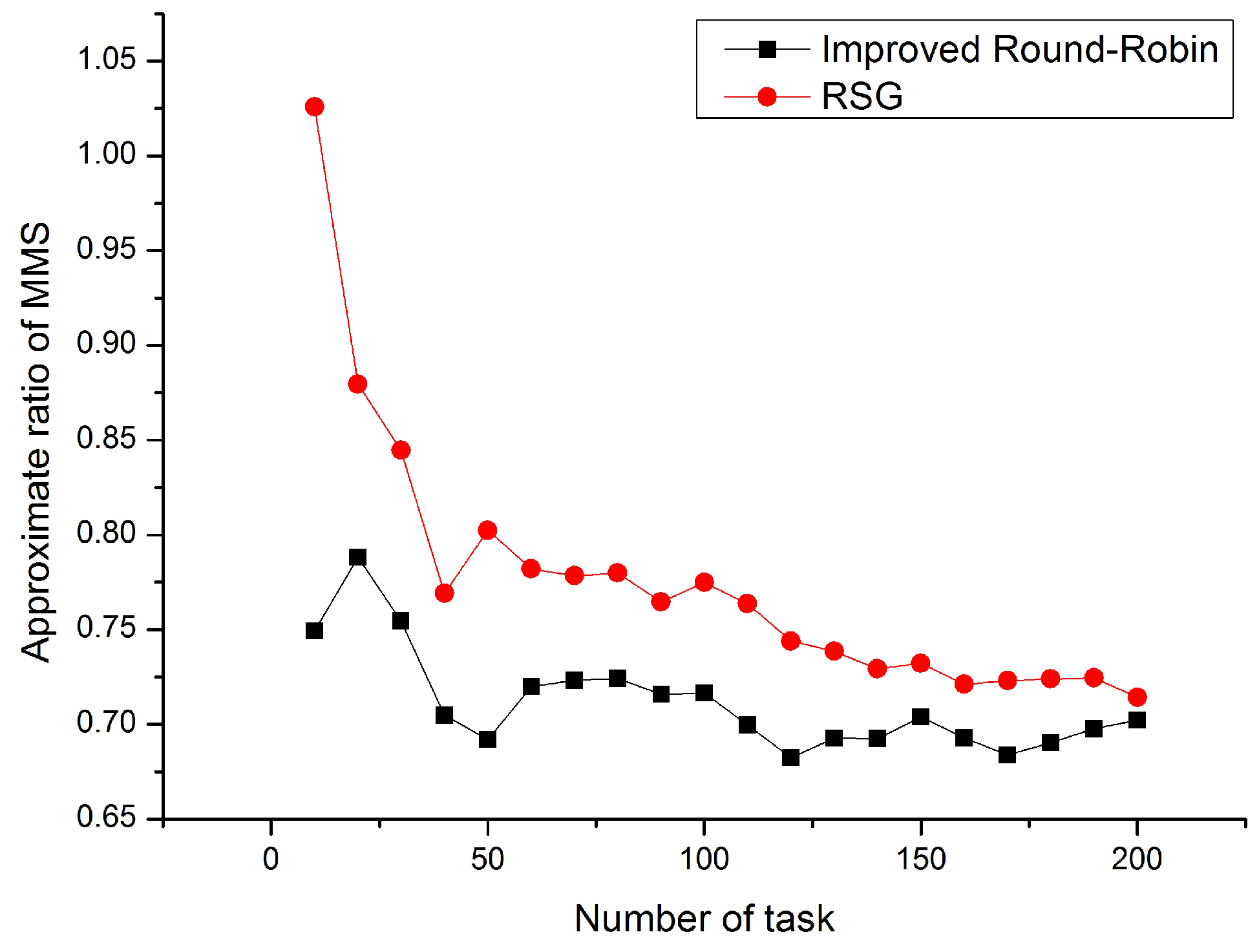
Figure 1 shows the approximate ratio of Min-Max share when the number of UAV is unchanged and the number of tasks is changed. The number of UAV is 5. From Figure 1, we can get two conclusions.
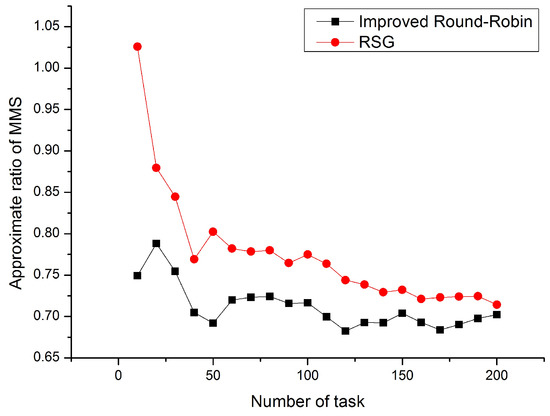
Figure 1.
Improved Round-Robin vs. RSG.
- (1)
- The algorithm proposed in Section 4 performs better than the Random Serial Dictatorship (RSD) method. By Definition 3, the allocation is Min-Max share when the approximate ratio is less than 1, so our proposed algorithm can achieve Min-Max share allocation, but the RSD can not in some cases.
- (2)
- Our proposed algorithm has a more stable performance than the RSD, because our algorithm has greater adaptability to perform well when dealing with different types of data.
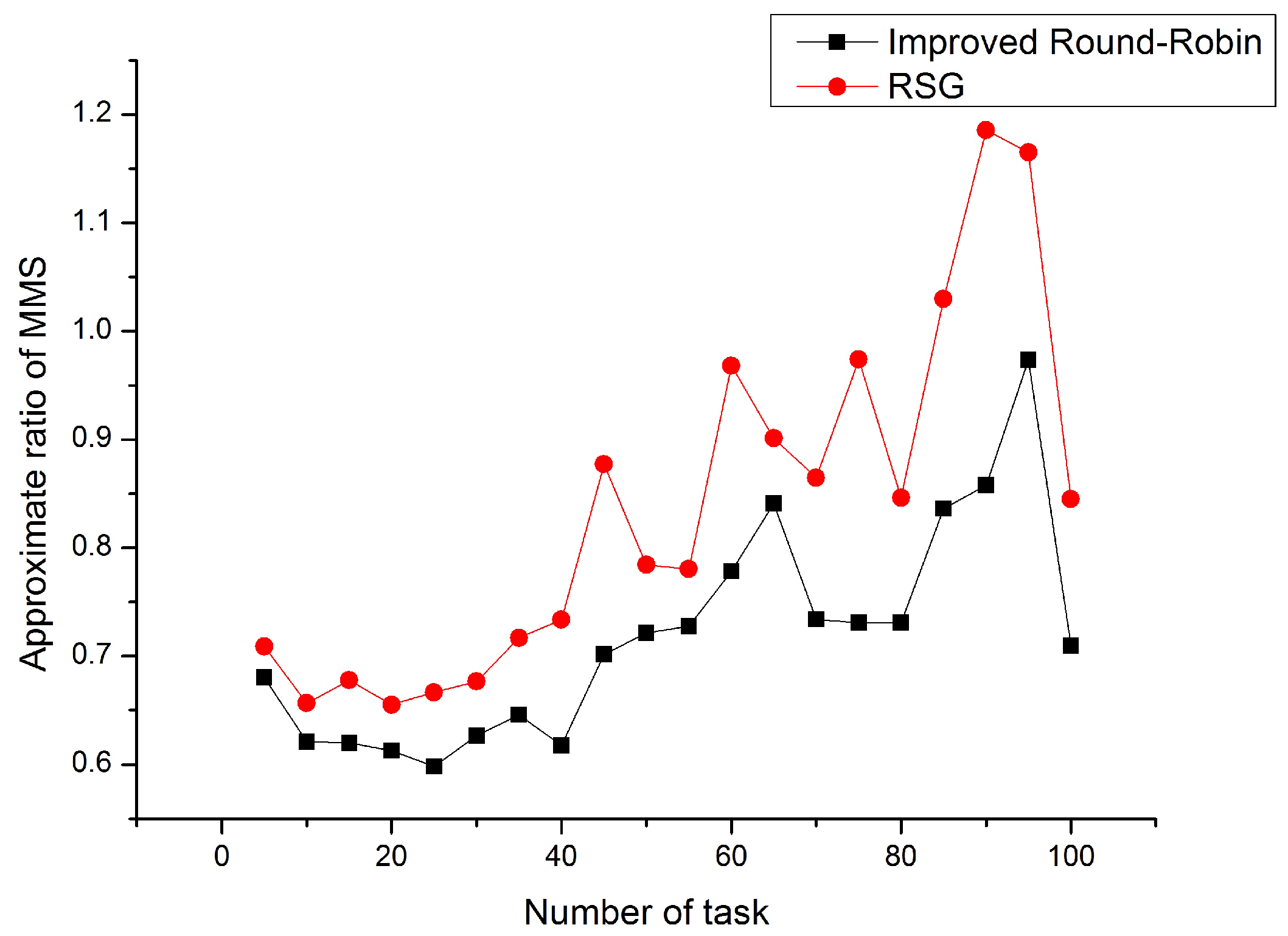
Figure 2 shows the approximate ratio of Min-Max share when the number of task is unchanged and the number of UAV is changed. The number of tasks is 200. From Figure 2, we can see that although the experimental performance varies slightly as the number of UAV changes, the overall performance is still very good. As the number of UAVs increases, the approximate ratio of Min-Max share shows fluctuation; this is because different UAVs have different weights over tasks and the approximate ratio is related to the weights, which has been proved in Theorem 1. However, from Figure 2, we can see that although the experimental performance varies slightly as the number of UAV changes, the overall performance is still very good, while the performance of the RSD is not as good as ours.
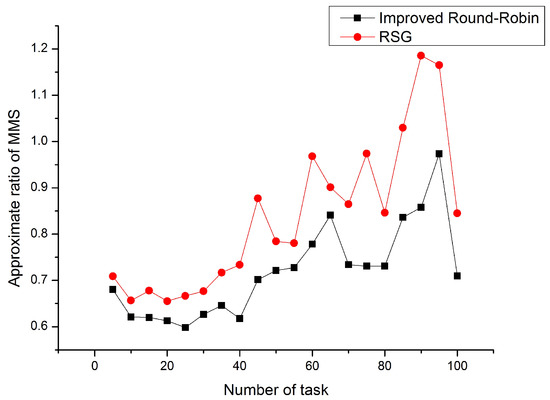
Figure 2.
Improved Round-Robin vs. RSG.
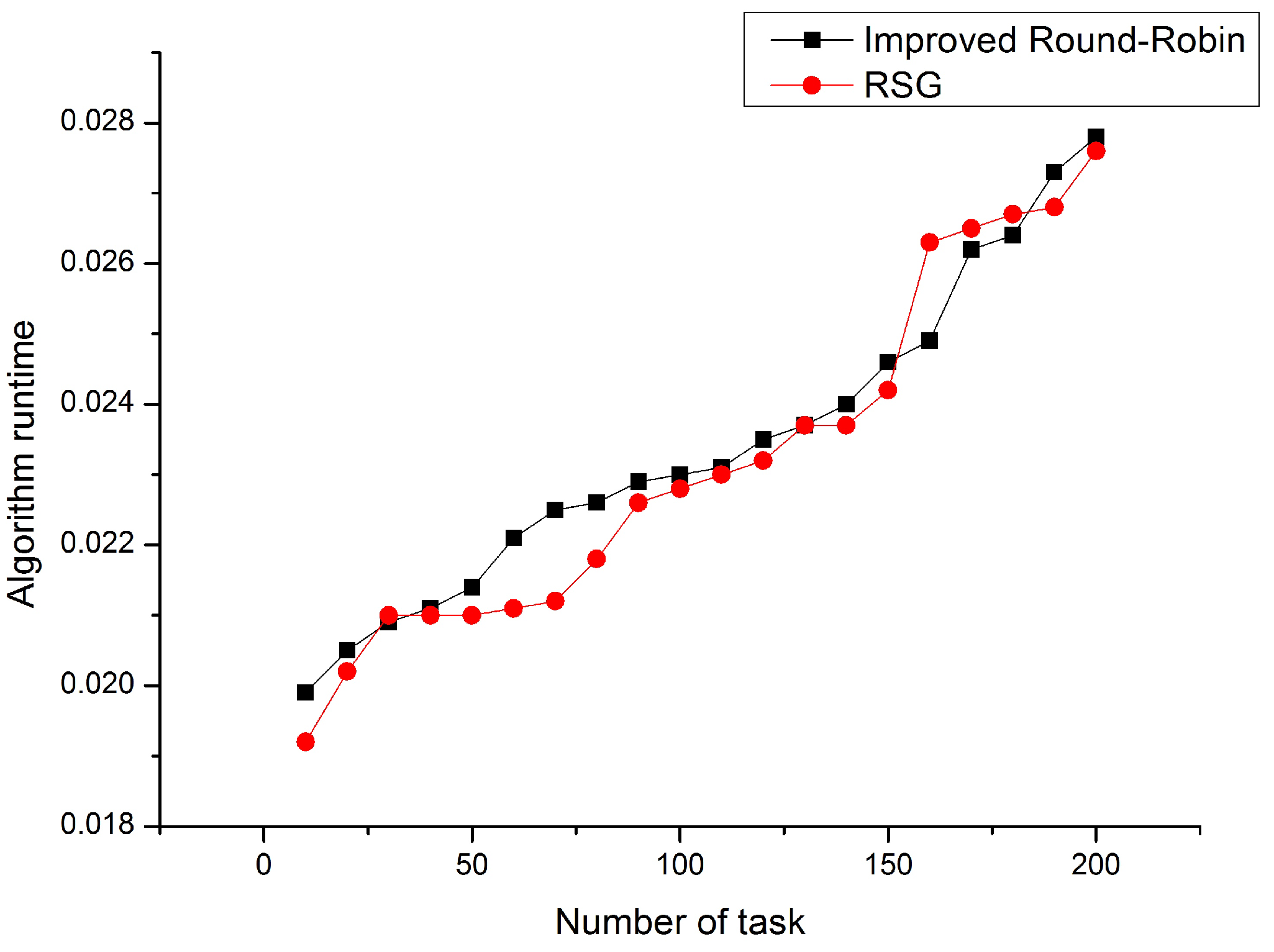
Next, we will examine the running time of the algorithm. As proved in Theorem 2, the time complexity of the Improved Round-Robin Algorithm is , which means that algorithm running time grows slowly with the number of task increases. Figure 3 shows the experimental results. From Figure 3, we draw 3 conclusions.
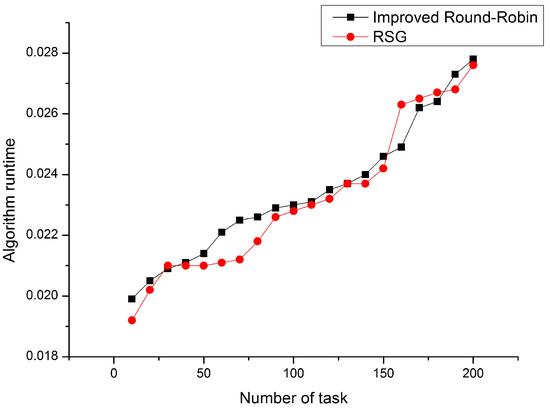
Figure 3.
Improved Round-Robin vs. RSG.
- (1)
- The running time of the two algorithms is almost the same.
- (2)
- The running time of the improved Round-Robin algorithm can meet the needs of real-time task allocation.
- (3)
- As the number of tasks increases, the algorithm runtime increases slowly, which consistent with the analysis in the Theorem 2. Moreover, it means that our proposed algorithm can handle situations with large amounts of data.
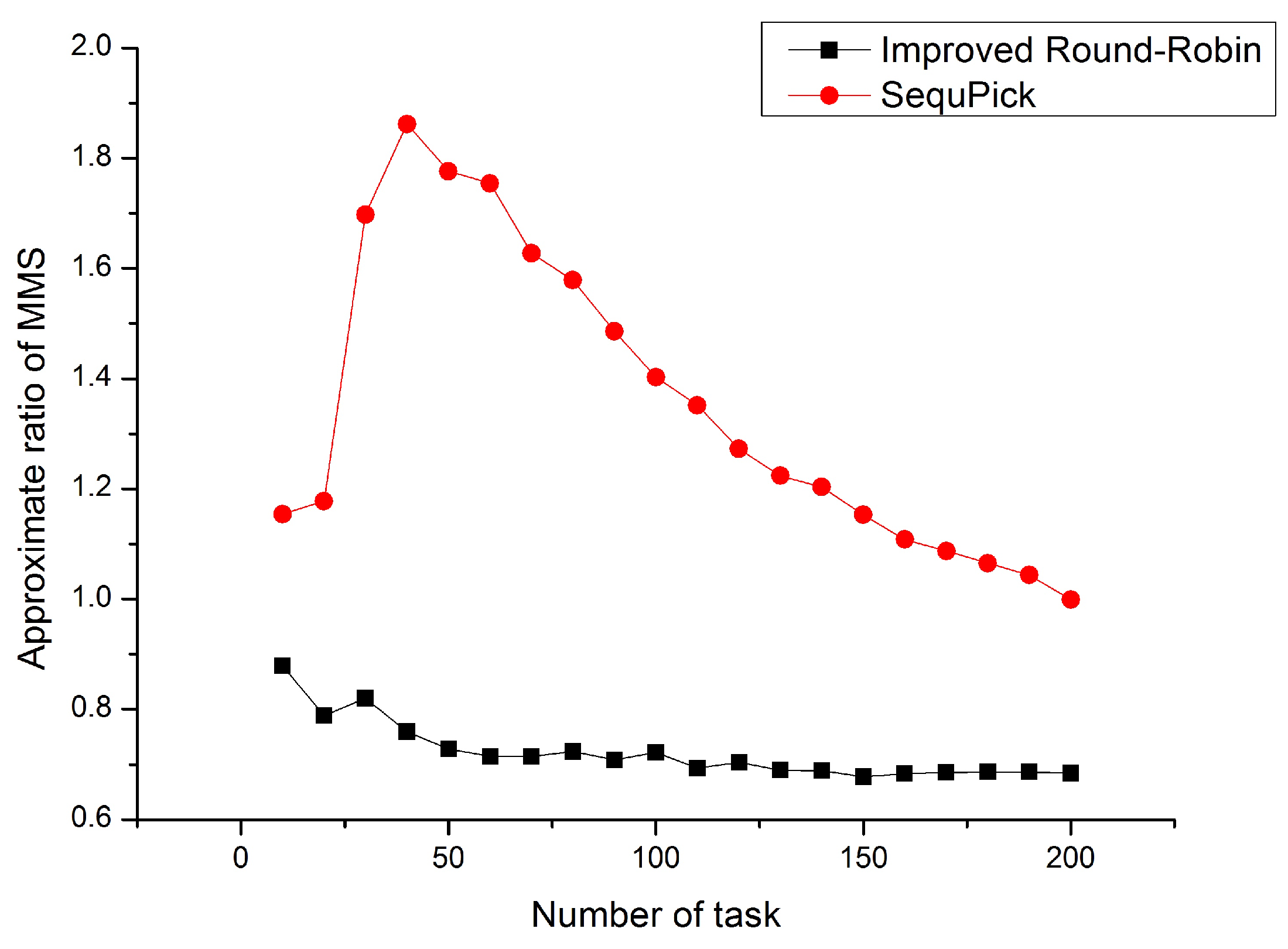
Next, we compare our work with the SequPick algorithm proposed in [1]. The SequPick algorithm requires that agents pick a certain number of tasks that have smallest cost to it in sequence. The reason compared with this method is that it guarantees the approximation ratio of MMS is no more than under ordinal preferences [1], which is the lowest approximation ratio in theory so far. In addition, SequPick algorithm has a low time complexity because all tasks only need to be allocated once. The SequPick algorithm has a good performance in single dimension, but its performance has not been verified when cost is multidimensional. Next, we will evaluate the difference between our algorithm’s performance with SequPick through experiments.
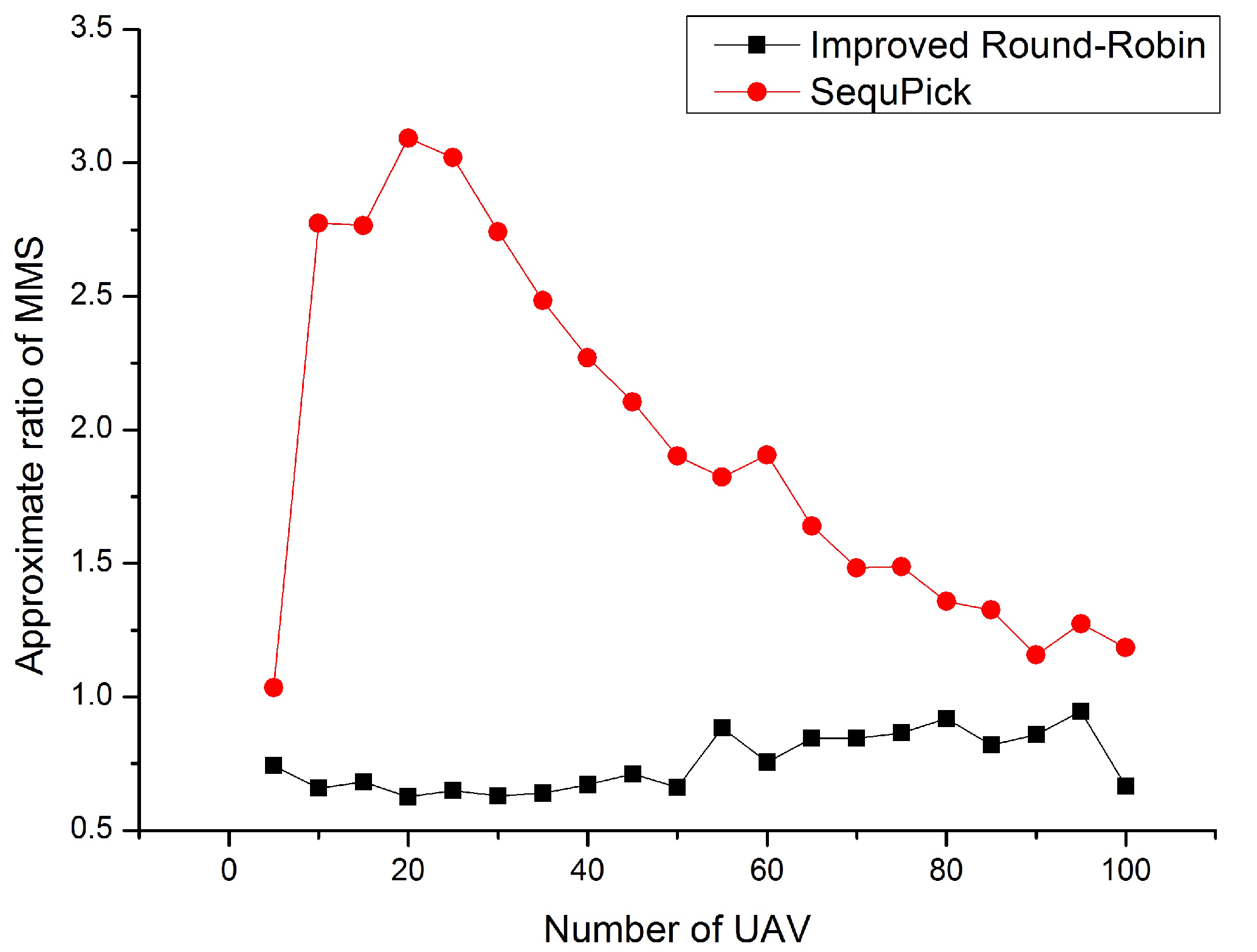
Figure 4 and Figure 5 show the comparison of the SequPick algorithm and the Improved Round-Robin algorithm. In the experiment shown in Figure 4, the number of UAVs is fixed at 5, and the number of tasks increases. In the experiment shown in Figure 5, the number of tasks is fixed at 200, and the number of UAVs increases. As we can see from the Figure 4 and Figure 5, our algorithm has better approximation rate of MMS and stability in the case that the number of tasks and the number of UAVs are different, meanwhile the SequPick algorithm performs poorly and is greatly affected by the number of tasks and UAVs.
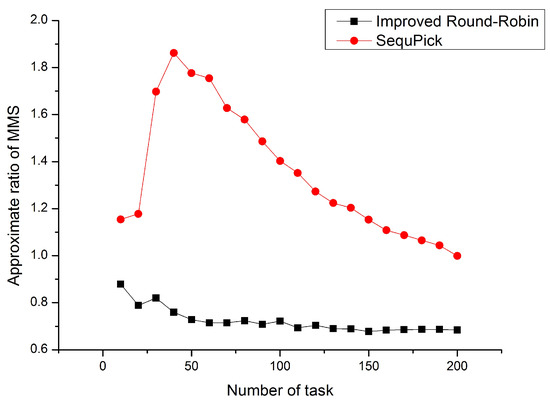
Figure 4.
Improved Round-Robin vs. SequPick.
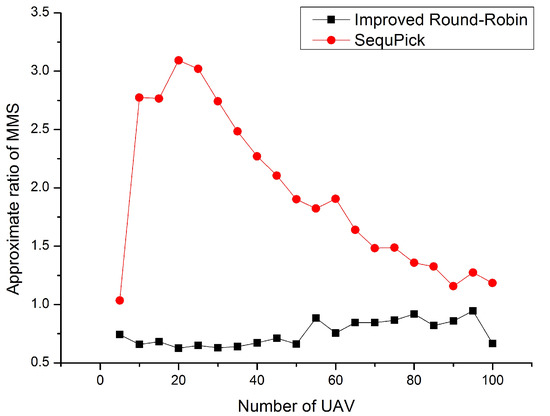
Figure 5.
Improved Round-Robin vs. SequPick.
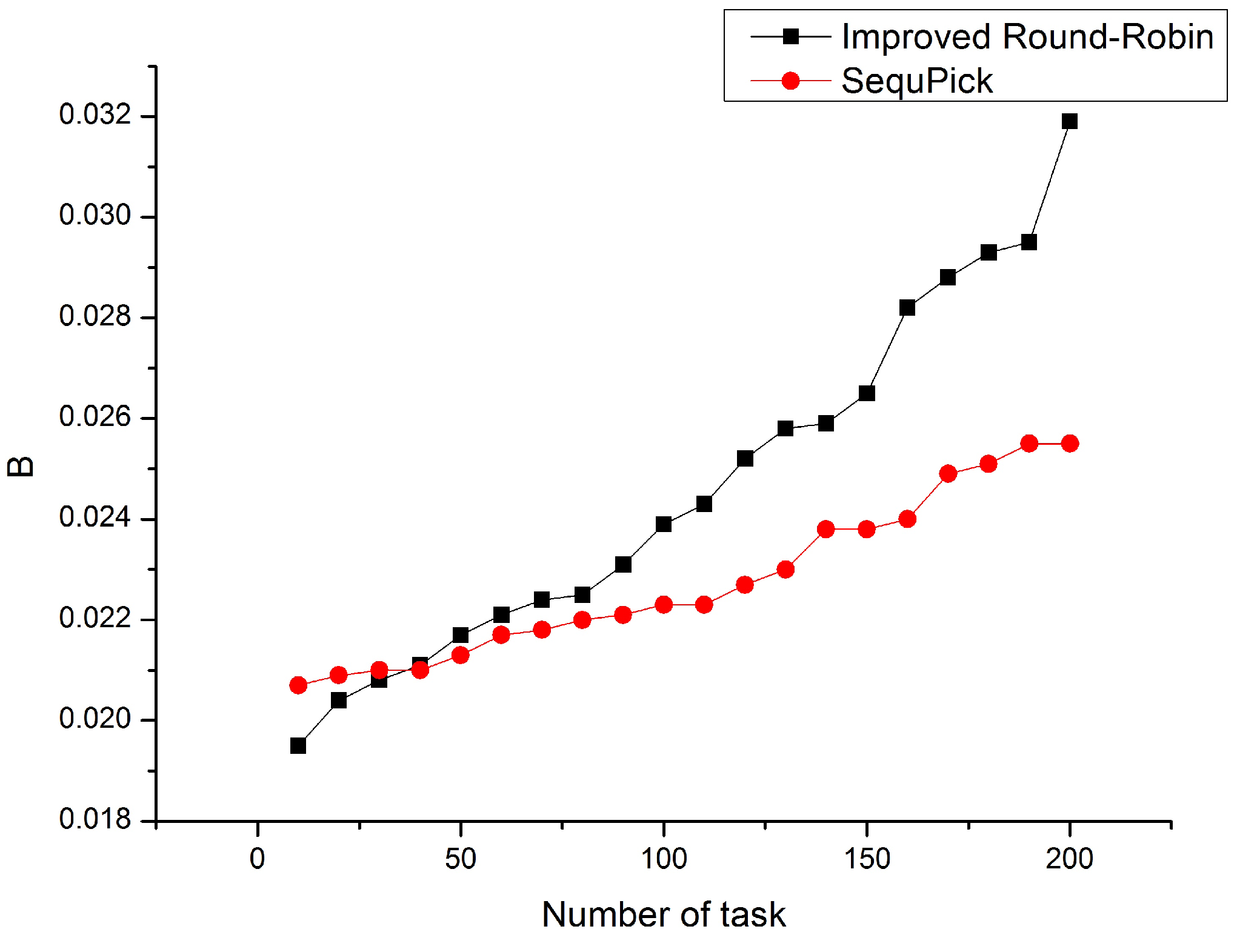
Next, we will compare the running time of the two algorithms. From Figure 6, we can see that SequPick’s running time slightly shorter than the running time of algorithm we proposed. This is because the time complexity of SequPick is , while Improved Round-Robin is , which has been proved in Theorem 2. As the number of tasks grows, the running time of algorithm we proposed increases faster than SequPick.
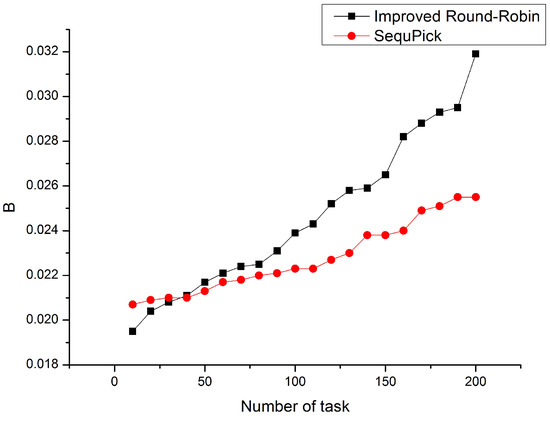
Figure 6.
Improved Round-Robin vs. SequPick.
5. Related Work
There are already some studies on the problems related to the use of UAVs in agricultural plant protection. The researchers in [10] proposed a path planning algorithm with the goal of minimizing the total energy consumption of the work, realizing the full coverage path planning of the field and the optimization of the return point location. The researchers in [11] proposed a path planning method based on Grid-GSA algorithm, which can plan a reasonable return point for the field with irregular boundaries, which makes the non-plant protection operation time the shortest. The researchers in [6] fully consider the influence of the additional flight distance caused by the change of flight height, and studied a path planning method for plant protection UAVs that can be used for three-dimensional terrain. However, these works did not take into account the differences between plant protection tasks. In this work, we will study the problem of fair allocation when there are differences in the cost of plant protection tasks.
The fair allocation of indivisible items is a central problem in multi-agent systems [3,12]. Fair allocation has been extensively studied for allocation of divisible goods, commonly known as cake cutting [13]. In order to identify fair allocations, one needs to formalize what fairness means. Multiple solution concepts, such as envy-freeness, proportionality, and equitability, have been proposed to formally capture fairness [14,15]. The authors of [16] proposed the idea of envy-freeness up to one good (EF1); it has been further popularized in [17], the researchers have shown that a natural modification of the Nash welfare maximizing rule satisfies EF1 and Pareto-optimal (PO), in addition they proposed envy freeness up to the least valued good (EFX), which is a stronger fairness concept. MMS fairness was proposed in [2] as a fairness concept for allocation of indivisible items. The concept coincides with the standard proportionality fairness concept if the items to be allocated are divisible [3,4]. An agent’s MMS is the “most preferred bundle he could guarantee himself as a divider in divide-and-choose against adversarial opponents” [2]. The authors of [2] studied the conditions under which MMS allocations would exist.
Although MMS is a highly attractive fairness concept, the authors of [3,7] have shown that an MMS allocation of items does not exist in general. This fact initiated research on approximate MMS allocations of goods in which each agents gets some fraction of her MMS guarantee [18]. There have been several works on algorithms that find an approximate MMS allocation [19,20,21,22,23]. [7] showed that although an MMS allocation of goods may not always exist, but there exists a polynomial-time algorithm that returns a -approximate MMS allocation. [21] developing a simple and efficient algorithm that achieves the same approximation guarantee. [23] proved that MMS allocations do not always exist but can be 2-approximated by a simple algorithm and also presented a PTAS for relaxation of MMS called optimal MMS.
Fair allocation of indivisible items problem can be divided into good allocation and task allocation (i.e., in some works, it is expressed as chore allocation). If all agents have positive utilities for the items, we view the items as goods. On the other hand, if all agents have negative utilities for the items, we can view the items as tasks [18]. The authors of [17] have shown that a natural modification of the Nash welfare maximizing rule satisfies EF1 and Pareto-optimal (PO) for the case of goods. Algorithms for computing approximate MMS allocations of goods are being used in practice for fair division in real-world problems [24]. The authors of [19,20,21] proposed an algorithm that can guarantee an approximate MMS allocation. The work mentioned above only focused on the case of goods. There are many settings in which agents may have negative utilities such as when tasks are allocated. The authors of [1,23] researched on fair allocation of of indivisible tasks and the authors of [21] presented an improved approximation algorithm for MMS allocation of tasks. The authors of [18,23] showed that fair allocations of goods and tasks have some fundamental connections but differences as well. The problem of combinations of goods and tasks has received attention as well [25].
Agents are said to have additive valuations when for any subset of goods , the valuation of agent i satisfies . Agents are said to have submodular valuations when for any and , the valuation of agent i satisfies . The authors of [21] have shown that under additive valuations a -approximate MMS allocation can be achieved and under submodular valuations a -approximate MMS allocation can be guaranteed. The authors of [1] consider MMS fairness in 3 preference models elicited from the agents: the cardinal model in which agents are allowed to report their utilities over the items, the ordinal model in which agents are only allowed to express their ordinal rankings over the items, and the public ranking model in which the ordinal preferences are publicly known. The authors of [1] present an MMS approximation can be guaranteed while the algorithm is strategy proof in 3 preference models. However, in all the work above, utilities of goods or the cost of tasks limited in single dimension and the situation that cost comes from multiple dimensions has not been taken into account.
There are some optimization algorithms that can be used to solve multidimensional cost problem through multi-objective optimization models. The authors of [26] used multi-objective Genetic Algorithms (GA) to solve multi-UAV mission planning. The authors of [27] proposed a methodology with heuristic based on Earliest Available Time algorithm to solve the UAV scheduling problem in an indoor environment incorporated Particle Swarm Optimization (PSO) algorithm, with an objective of minimizing the makespan. However, as the space for the solutions of our problem increases exponentially with the number of tasks and these optimizations usually requires thousands of iterations to converge to the optimal solution when dealing with NP-Hard problems. Therefore, this type of algorithm takes a long time and is not suitable for embedding into agents with low hardware facilities.
In this work, we consider a model that has costs of tasks from multiple dimensions, and in each dimension, agents are only allowed to express their ordinal rankings over tasks. In addition, the cost of tasks under additive valuations. For this model, we proposed a task allocation algorithm that guarantees low time complexity while still achieving high fairness allocation.
6. Conclusions and Future Work
In this work, to solve indivisible tasks fair allocation problem when the cost of tasks is multidimensional, a task allocation problem model using agricultural plant protection environment as an example is established. We improve the traditional Round-Robin algorithm to solve this problem and get smallest approximate ratio of Min-Max share, which is a key indicators of fairness. We have proved with a theorem that the approximate ratio of Min-Max share of our proposed algorithm is no more than and the time complexity of the algorithm is . Experiments validate our analysis; we compare our proposed method with RSD and SequPick algorithm. Compared with RSD, our proposed algorithm achieves a lower approximation ratio of MMS when the running time is similar. For the comparison with the SequPick algorithm, although the running time of the proposed algorithm is slightly longer, we have a significantly lower approximation ratio of MMS and more stable performance.
In future work, we will improve our allocation algorithm to deal with more complex problems, such as consider the impact of task allocation order on cost. This will lead to a significant increase in the time complexity of the algorithm. In order to control the time complexity of the algorithm within an acceptable range, a specific branch and bound method can be applied.
Author Contributions
Conceptualization, F.S. and X.W. and R.Z.; methodology, F.S.; software, F.S.; validation, F.S.; formal analysis, F.S.; investigation, F.S. and X.W. and R.Z.; resources, F.S. and X.W. and R.Z.; data curation, F.S. and X.W. and R.Z.; writing–original draft preparation, F.S.; writing–review and editing, F.S.; visualization, F.S.; supervision, X.W.; project administration, X.W.; funding acquisition, X.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Aziz, H.; Li, B.; Wu, X. Strategyproof and Approximately Maxmin Fair Share Allocation of Chores. arXiv 2019, arXiv:1905.08925. [Google Scholar]
- Kurokawa, D.; Procaccia, A.D.; Wang, J. When Can the Maximin Share Guarantee be Guaranteed? In Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016. [Google Scholar]
- Bouveret, S.; Lemaître, M. Characterizing conflicts in fair division of indivisible goods using a scale of criteria. Auton. Agents Multi-Agent Syst. 2016, 30, 259–290. [Google Scholar] [CrossRef]
- Budish, E. The combinatorial assignment problem: Approximate competitive equilibrium from equal incomes. J. Polit. Econ. 2011, 119, 1061–1103. [Google Scholar] [CrossRef]
- Jeyaratnam, J. Acute Pesticide Poisoning: A Major Global Health Problem. World Health Stat. Q 1990, 43, 139–144. [Google Scholar] [PubMed]
- Wang, Y.; Chen, H.; Haichuan, L.I.; University, N.A. 3D Path Planning Approach Based on Gravitational Search Algorithm for Sprayer UAV. Trans. Chin. Soc. Agric. Mach. 2018. [Google Scholar] [CrossRef]
- Procaccia, A.D.; Wang, J. Fair Enough: Guaranteeing Approximate Maximin Shares. In Proceedings of the Fifteenth ACM Conference on Economics and Computation, Palo Alto, CA, USA, 8–12 June 2014; ACM: New York, NY, USA, 2014; pp. 675–692. [Google Scholar]
- Aziz, H.; Chen, J.; Filos-Ratsikas, A.; Mackenzie, S.; Mattei, N. Egalitarianism of random assignment mechanisms. arXiv 2015, arXiv:1507.06827. [Google Scholar]
- Dajiang Science and Technology. MG-12000P Flight Battery User Guide. Available online: https://dl.djicdn.com/downloads/mg_1p/20180705/MG-12000P+Flight+Battery+User+Guide_Multi.pdf (accessed on 5 July 2018).
- Bo, X.; Liping, C.; Yu, T. Path planning Based on Minimum Enerny Consumption for plant Protection UAVs in Sorties. Trans. Chin. Soc. Agric. Mach. 2015, 46, 36–42. [Google Scholar]
- Wang, Y.; Chen, H.; Li, Y.; Li, H. Path Planning Method Based on Grid-GSA for Plant Protection UAV. Trans. Chin. Soc. Agric. Mach. 2017. [Google Scholar] [CrossRef]
- Aziz, H.; Gaspers, S.; Mackenzie, S.; Walsh, T. Fair assignment of indivisible objects under ordinal preferences. Artif. Intell. 2015, 227, 71–92. [Google Scholar] [CrossRef]
- Brams, S.J.; Taylor, A.D. Fair Division: From Cake-Cutting to Dispute Resolution. Soc. Justice Res. 1996, 12, 149–162. [Google Scholar]
- Brams, S.J.; Taylor, A.D. Fair Division: From Cake-Cutting to Dispute Resolution; Cambridge University Press: Cambridge, MA, USA, 1996. [Google Scholar]
- Moulin, H. Fair Division and Collective Welfare; MIT Press: Cambridge, MA, USA, 2004. [Google Scholar]
- Lipton, R.J.; Markakis, E.; Mossel, E.; Saberi, A. On Approximately Fair Allocations of Indivisible Goods. In Proceedings of the 5th ACM conference on Electronic Commerce, New York, NY, USA, 17–20 May 2004; ACM: New York, NY, USA, 2004; pp. 125–131. [Google Scholar]
- Caragiannis, I.; Kurokawa, D.; Moulin, H.; Procaccia, A.D.; Shah, N.; Wang, J. The unreasonable fairness of maximum Nash welfare. ACM Trans. Econ. Comput. (TEAC) 2019, 7, 12. [Google Scholar] [CrossRef]
- Aziz, H.; Rauchecker, G.; Schryen, G.; Walsh, T. Approximation algorithms for max-min share allocations of indivisible chores and goods. arXiv 2016, arXiv:1604.01435. [Google Scholar]
- Kurokawa, D.; Procaccia, A.D.; Wang, J. Fair Enough: Guaranteeing Approximate Maximin Shares; ACM: New York, NY, USA, 2018; Volume 65, p. 8. [Google Scholar]
- Amanatidis, G.; Markakis, E.; Nikzad, A.; Saberi, A. Approximation algorithms for computing maximin share allocations. ACM Trans. Algorithms (TALG) 2017, 13, 52. [Google Scholar]
- Barman, S.; Krishna Murthy, S.K. Approximation Algorithms for Maximin Fair Division. In Proceedings of the 2017 ACM Conference on Economics and Computation, Cambridge, MA, USA, 26–30 June 2017; ACM: New York, NY, USA, 2017; pp. 647–664. [Google Scholar]
- Ghodsi, M.; HajiAghayi, M.; Seddighin, M.; Seddighin, S.; Yami, H. Fair Allocation of Indivisible Goods: Improvements and Generalizations. In Proceedings of the 2018 ACM Conference on Economics and Computation, Ithaca, NY, USA, 18–22 June 2018; ACM: New York, NY, USA, 2018; pp. 539–556. [Google Scholar]
- Aziz, H.; Rauchecker, G.; Schryen, G.; Walsh, T. Algorithms for Max-Min Share Fair Allocation of Indivisible Chores. In Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017. [Google Scholar]
- Goldman, J.R.; Procaccia, A.D. Spliddit: Unleashing fair division algorithms. SIGecom Exch. 2014, 13, 41–46. [Google Scholar] [CrossRef]
- Aziz, H.; Caragiannis, I.; Igarashi, A.; Walsh, T. Fair allocation of combinations of indivisible goods and chores. arXiv 2018, arXiv:1807.10684. [Google Scholar]
- Ramirez-Atencia, C.; Bello-Orgaz, G.; R-Moreno, M.D.; Camacho, D. Solving complex multi-UAV mission planning problems using multi-objective genetic algorithms. Soft Comput. 2016, 1–18. [Google Scholar] [CrossRef]
- Khosiawan, Y.; Park, Y.; Moon, I.; Nilakantan, J.M.; Nielsen, I. Task scheduling system for UAV operations in indoor environment. Neural Comput. Appl. 2018, 1–29. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).