Mechanical Stability of Hybrid Corrugated Sandwich Plates under Fluid-Structure-Thermal Coupling for Novel Thermal Protection Systems

Abstract

Hybrid corrugated sandwich (HCS) plates have become a promising candidate for novel thermal protection systems (TPS) due to their multi-functionality of load bearing and thermal protection. For hypersonic vehicles, the novel TPS that performs some structural functions is a potential method of saving weight, which is significant in reducing expensive design/manufacture cost. Considering the novel TPS exposed to severe thermal and aerodynamic environments, the mechanical stability of the HCS plates under fluid-structure-thermal coupling is crucial for preliminary design of the TPS. In this paper, an innovative layerwise finite element model of the HCS plates is presented, and coupled fluid-structure-thermal analysis is performed with a parameter study. The proposed method is validated to be accurate and efficient against commercial software simulation. Results have shown that the mechanical instability of the HCS plates can be induced by fluid-structure coupling and further accelerated by thermal effect. The influences of geometric parameters on thermal buckling and dynamic stability present opposite tendencies, indicating a tradeoff is required for the TPS design. The present analytical model and numerical results provide design guidance in the practical application of the novel TPS.

1. Introduction

Hybrid sandwich structures refer to metallic sandwich plates filled with stochastic foam [1]. Compared to traditional lightweight structures, the hybrid sandwich structures exhibit good mechanical performances as well as enhanced multi-functionality with respect to load bearing capacity, energy absorption and thermal protection [2]. Thus, they have demonstrated a wide range of applications in shipbuilding, train manufacturing and construction industry [3,4,5,6]. Among various core topologies of the sandwich structures (e.g., pin-reinforced [7], truss [8], honeycomb [9]), corrugated cores have received major research attention because of their easy fabrication and cost-efficient maintenance [10]. In recent years, there has been growing interest in applying hybrid corrugated sandwich (HCS) plates to the novel thermal protection systems (TPS) of vehicles operating in extreme temperature environments [11,12,13]. Typical representatives are hypersonic vehicles which are exposed to severe thermal and aerodynamic loading. Due to the versatility of the HCS plates, the novel load-bearing TPS offers more weight saving than traditional TPS, leading to performance improvements of the hypersonic vehicles. A significant issue emerged is the mechanical stability of the HCS plates under thermal and aerodynamic loading, while a thorough understanding of the fluid-structure-thermal coupling effects is crucial for the novel TPS design.

Prior research has mainly focused on the mechanical properties of HCS plates. Zhang et al. discovered the limited enhancement of filling foam in compressive strength and impact resistance due to the relatively weak and low-density foam material [14]. Yan et al. [15,16] and Yu et al. [17] utilized closed-cell aluminum foam instead of polymeric foam and demonstrated that foam filler effectively improved compressive and bending strength by stabilizing effects on the corrugated members against buckling. Han et al. [18] revealed that filling foam contributed to both enhanced buckling resistance and additional mass, and subsequently assessed the structural efficiency through optimization study. Furthermore, they derived the effective thermoelastic properties of the HCS plates using a homogenization method based on the Gibbs free energy [19]. Yang et al. [20] compared modal characteristics of empty and foam-filled corrugated sandwich cylindrical panels by experiments and numerical analysis. Taghizadeh et al. [21] evaluated compressive characteristics of composite sandwich panels with different corrugated core geometries under quasi-static out-of-plane loading.

The promising application of the HCS plates to the novel TPS is an active research area, and recent studies have begun to explore the thermo-mechanical behaviors and the corresponding optimization design. Based on the solutions of 1D transient heat transfer and buckling analysis, Bapanapalli et al. [22] developed response surface approximations to implement optimization studies for a preliminary design. Gogu et al. [23] acquired the optimal dimensions and the best materials for face sheets and web corrugations from a two-stage optimization method. Martinez et al. [24,25] conducted the stress and deflection analysis using a semi-analytical equivalent model subjected to combined mechanical-thermal loads. Sharma et al. [26] developed a finite-element based homogenization procedure and predicted the equivalent stiffness and strength properties for micromechanical analysis. Xie et al. [27] carried out heat transfer and thermal-mechanical analysis to create an optimization procedure aiming at a minimum weight. Gu et al. [28] performed bending and transient dynamic analysis with temperature-dependent materials, and Gong et al. [29] employed the same equivalent model to conduct stress analysis under thermal and mechanical loads. Le et al. [13] gave the deflection and the thermal stress through thermo-mechanical analysis under simulated aerodynamic heating.

Although the thermo-mechanical analysis is a primary concern, it is not all-inclusive for the novel TPS design. When the TPS outer surfaces are exposed to high-speed airflow, the aerodynamic load generated would interact with both structural dynamics and heat transfer [30]. Therefore, the effects of the fluid-structure-thermal coupling on the novel TPS need to be verified in the design process as early and accurately as possible, which is hindered by the coupling complexity. Generally, wind tunnel tests on scaled models of the TPS have great difficulties in simulating fluid-structure-thermal coupling environments [31], while flight experiments on the TPS prototype are rather costly. Instead, most of verification work employs detailed finite element analysis using commercial software at the expense of time-consuming computation. The approaches mentioned above are not conducive to the TPS preliminary design process where combinations of different design variables are considered in order to learn parametric influence rules.

The main purposes of the present paper are (1) to establish a layerwise finite element model of the HCS plates with the fluid-structure-thermal coupling effects, and (2) to investigate the structural behaviors of the HCS plates based on the proposed model with main concerns on the mechanical stability. The paper is organized as follows. Section 2 presents the modeling procedure with key equations derived. Section 3 displays the numerical results of the coupled fluid-structure-thermal analysis. Section 4 discusses results obtained from the parametric study. Conclusions are drawn in Section 5. It is found that mechanical instabilities can be induced by fluid-structure coupling and further accelerated by thermal effects. The impacts of design variables on dynamic instability and thermal buckling instability usually show opposite tendencies, and thus a tradeoff is required in the novel TPS design to solve these two instabilities simultaneously. The present accurate and efficient model, as well as the coupled fluid-structure-thermal analysis results, are applicable to the preliminary design for the novel TPS.

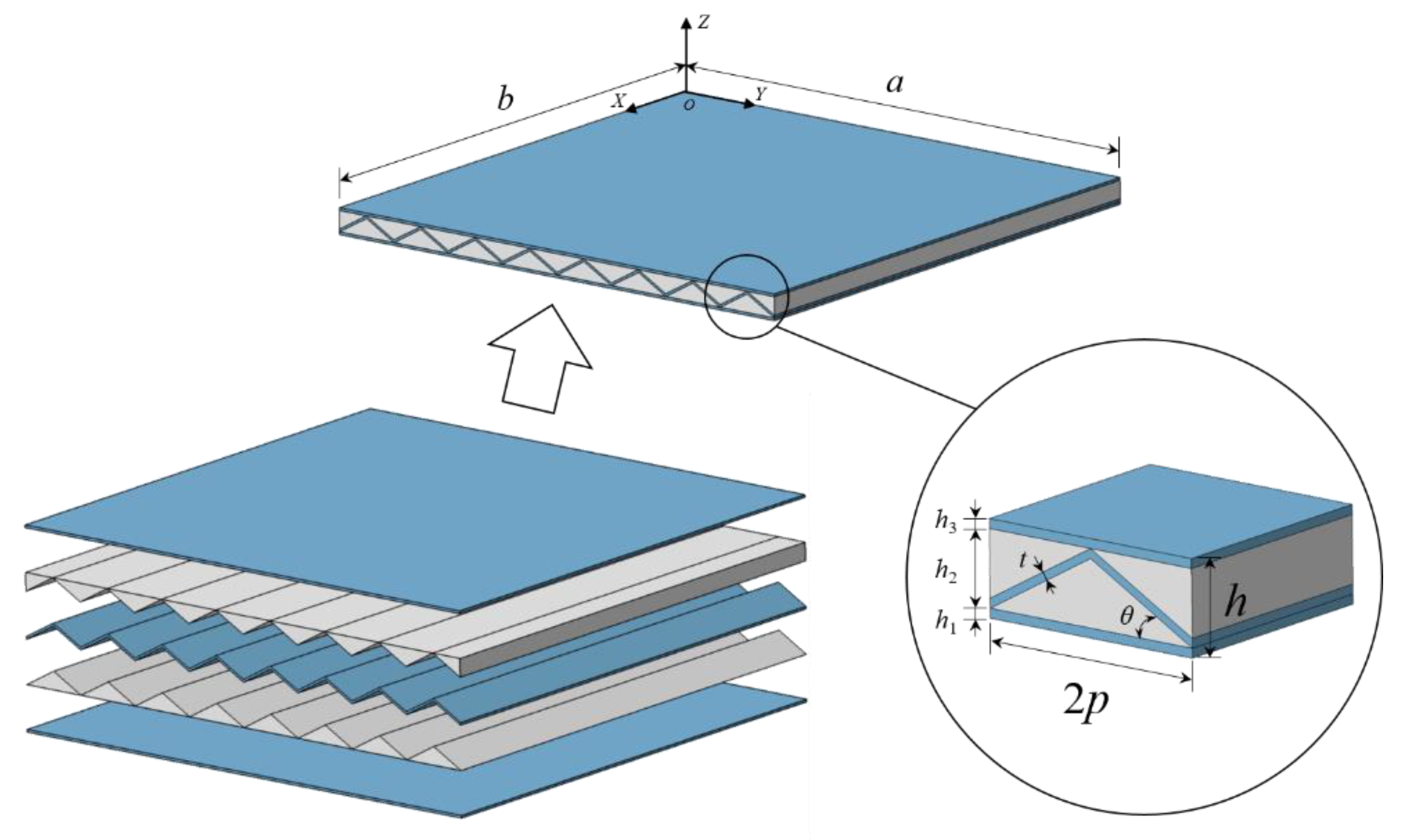
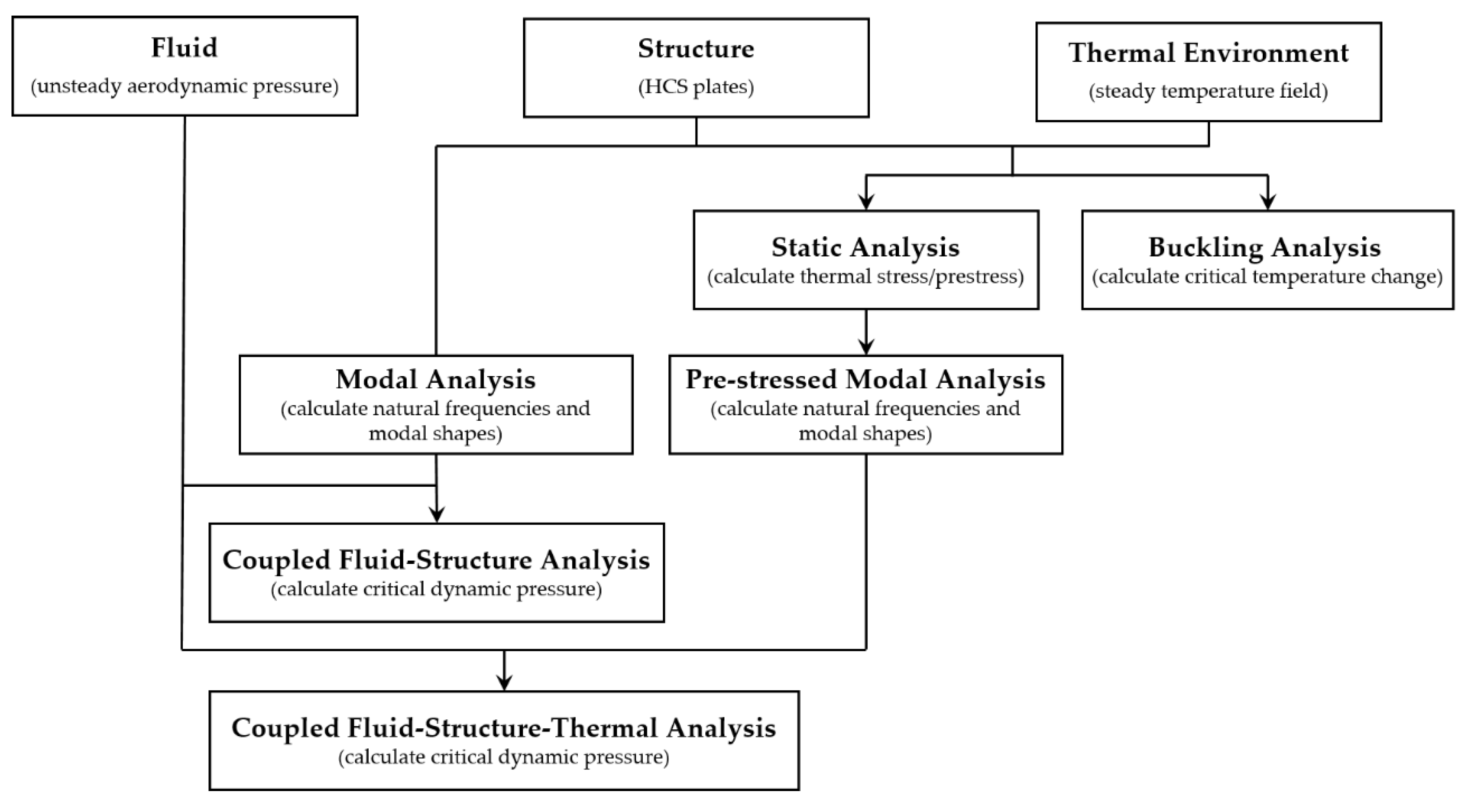
2. Methods

A HCS plate with length a, width b and total height h is depicted in Figure 1. It consists of two face sheets and a corrugated core with foam filled into the interstice of the corrugation. The bottom and top face sheets have the thicknesses of h₁ and h₃, respectively, while the height of the foam-filled corrugated core is h₂. The sandwich plate has n_c periodic and symmetric unit cells and the length of each unit cell is 2p = a/n_c. The geometric parameters of the corrugated members are the thickness t and the inclined angle θ, and the volume fraction of the corrugated members is defined as f = t/psinθ. The reference system is also shown in Figure 1, where x-axis is the machine direction (MD), y-axis the cross direction (CD) and z-axis perpendicular to the xy-plane.

2.1. Layerwise Theory

Equivalent single theories and layerwise theories are two approaches that are mostly adopted to model the displacement fields for multi-layered laminated and sandwich plates. Compared to the most commonly used equivalent single theories [32,33,34], such as classic laminate theory, first-order or higher-order shear deformation theory, layerwise theories are capable of predicting more accurate static and dynamic behavior of soft-core sandwich structures by a separate description of displacement fields for each layer [35,36,37,38].

In this paper, a layerwise theory is employed to describe displacement fields for the HCS plates with three layers. The piecewise linear in-plane displacement field is assumed through the plate thickness, maintaining displacement continuity at layer interfaces and allowing different slopes in each layer. The displacement field of the kth layer (k = 1, 2, 3) is given as

$$\begin{array}{l}{u}^{\left(k\right)}\left(x,y,{\zeta }_k\right)=U^{\left(k\right)}\left(x,y\right){\Psi }_1^{\left(k\right)}\left({\zeta }_k\right)+U^{\left(k+1\right)}\left(x,y\right){\Psi }_2^{\left(k\right)}\left({\zeta }_k\right)\\ v^{\left(k\right)}\left(x,y,{\zeta }_k\right)=V^{\left(k\right)}\left(x,y\right){\Psi }_1^{\left(k\right)}\left({\zeta }_k\right)+V^{\left(k+1\right)}\left(x,y\right){\Psi }_2^{\left(k\right)}\left({\zeta }_k\right)\\ w^{\left(k\right)}\left(x,y,{\zeta }_k\right)=w^0\left(x,y\right)\end{array}$$

(1)

where U^(k), V^(k) and U^(k+1), V^(k+1) are the in-plane displacements at lower and upper surfaces of the kth layer and w⁰ is the out-plane displacement of any point on the mid-plane of the sandwich plates. ${\Psi }_1^{\left(k\right)}$ and ${\Psi }_2^{\left(k\right)}$ are the linear interpolation functions through the thickness direction and ζ_k is the local thickness coordinate, given as

$${\Psi }_1^{\left(k\right)}=\frac{1}{2}\left(1-{\zeta }_k\right),{\Psi }_2^{\left(k\right)}=\frac{1}{2}\left(1+{\zeta }_k\right),{\zeta }^{\left(k\right)}=\frac{h_k}{2}z-\frac{z_l^{\left(k\right)}+z_u^{\left(k\right)}}{h_k}$$

(2)

where h_k is the thickness and $z_k^{\left(l\right)}$ and $z_k^{\left(u\right)}$ are the z-axis coordinates of the lower and upper surfaces.

2.2. Strain-Displacement Relations

For a three-dimensional elasticity analysis, the in-plane strain is comprised of linear and nonlinear components. The in-plane strain vector ε^(k) and transverse shear strain vector γ^(k) of the kth layer (k = 1, 2, 3) in the corrugated hybrid sandwich plates can be given as

$${\mathsf{\epsilon }}^{\left(k\right)}={\mathsf{\epsilon }}_l^{\left(k\right)}+{\mathsf{\epsilon }}_{nl}^{\left(k\right)}=\left\{\begin{array}{c}{u}_{,x}^{\left(k\right)}\\ v_{,y}^{\left(k\right)}\\ u_{,y}^{\left(k\right)}+v_{,x}^{\left(k\right)}\end{array}\right\}+\left\{\begin{array}{c}\left({\left(u_{,x}^{\left(k\right)}\right)}^2+{\left(v_{,x}^{\left(k\right)}\right)}^2+{\left(w_{,x}^{\left(k\right)}\right)}^2\right)/2\\ \left({\left(u_{,y}^{\left(k\right)}\right)}^2+{\left(v_{,y}^{\left(k\right)}\right)}^2+{\left(w_{,y}^{\left(k\right)}\right)}^2\right)/2\\ u_{,x}^{\left(k\right)}{u}_{,y}^{\left(k\right)}+v_{,x}^{\left(k\right)}{v}_{,y}^{\left(k\right)}+w_{,x}^{\left(k\right)}{w}_{,y}^{\left(k\right)}\end{array}\right\},{\mathsf{\gamma }}^{\left(k\right)}=\left\{\begin{array}{c}{\gamma }_{yzl}^{\left(k\right)}\\ {\gamma }_{xzl}^{\left(k\right)}\end{array}\right\}=\left\{\begin{array}{c}{w}_{,y}^{\left(k\right)}+v_{,z}^{\left(k\right)}\\ w_{,x}^{\left(k\right)}+u_{,z}^{\left(k\right)}\end{array}\right\}$$

(3)

The nonlinear in-plane strain vector ${\mathsf{\epsilon }}_{nl}^{\left(k\right)}$ can also take the form

$${\mathsf{\epsilon }}_{nl}^{\left(k\right)}=\frac{1}{2}{A}_G^{\left(k\right)}{g}^{\left(k\right)}$$

(4)

where

$$A_G^{\left(k\right)}=\left[\begin{array}{cccccc}{u}_{,x}^{\left(k\right)}& 0& v_{,x}^{\left(k\right)}& 0& w_{,x}^{\left(k\right)}& 0\\ 0& u_{,y}^{\left(k\right)}& 0& v_{,y}^{\left(k\right)}& 0& w_{,y}^{\left(k\right)}\\ u_{,y}^{\left(k\right)}& u_{,x}^{\left(k\right)}& v_{,y}^{\left(k\right)}& v_{,x}^{\left(k\right)}& w_{,y}^{\left(k\right)}& w_{,x}^{\left(k\right)}\end{array}\right],g^{\left(k\right)}={\left\{u_{,x}^{\left(k\right)},u_{,y}^{\left(k\right)},v_{,x}^{\left(k\right)},v_{,y}^{\left(k\right)},w_{,x}^{\left(k\right)},w_{,y}^{\left(k\right)}\right\}}^T$$

(5)

2.3. Stress-Strain Relations

For the HCS plates, the stress-strain relations of the kth layer (k = 1, 2, 3) in the thermal environment with respect to the global coordinate system are given as

$${\mathsf{\sigma }}^{\left(k\right)}=Q_{in}^{\left(k\right)}\left({\mathsf{\epsilon }}^{\left(k\right)}-{\mathsf{\epsilon }}_0^{\left(k\right)}\right),{\mathsf{\tau }}^{\left(k\right)}=Q_{tr}^{\left(k\right)}{\mathsf{\gamma }}^{\left(k\right)}$$

(6)

where $Q_{in}^{\left(k\right)}$ and $Q_{tr}^{\left(k\right)}$ are the in-plane and transverse shear stiffness matrices. ${\mathsf{\epsilon }}_0^{\left(k\right)}$ is the initial strain vector caused by thermal expansion, given as

$${\mathsf{\epsilon }}_0^{\left(k\right)}={\mathsf{\alpha }}^{\left(k\right)}\Delta T\left(z\right)$$

(7)

where α^(k) is the thermal expansion coefficient and ΔT(z) is the temperature change through the plate thickness, which could have uniform, linear or parabolic distribution.

For the bottom and top face sheets (k = 1, 3), the stiffness matrices and thermal expansion coefficient in the global coordinate system are obtained from those in the material coordinate system with transformation matrices between the global and material coordinates, which are expressed in detail in [38].

For the foam-filled corrugated core (k = 2), the effective stiffness matrices and thermal expansion coefficient are obtained from a homogenization method [19], in which the coupling effects between the corrugated structure and the filled foam are concerned. When the MD of the foam-filled corrugated core coincides with the x-direction of the global coordinate system, the plane stress-reduced and transverse shear stiffness matrices the foam-filled corrugated core are given as

$$Q_{in}^{\left(2\right)}=\left[\begin{array}{ccc}{\overline{Q}}_{11}^H& {\overline{Q}}_{12}^H& 0\\ {\overline{Q}}_{12}^H& {\overline{Q}}_{22}^H& 0\\ 0& 0& Q_{66}^H\end{array}\right],Q_{tr}^{\left(2\right)}=\left[\begin{array}{cc}{Q}_{44}^H& 0\\ 0& Q_{55}^H\end{array}\right]$$

(8)

where ${\overline{Q}}_{ij}^H=Q_{ij}^H-Q_{i3}^H{Q}_{j3}^H/Q_{33}^H\left(i,j=1,2,3\right)$ and the effective stiffnesses $Q_{ij}^H$ are comprised of contributions from the corrugated structure, the filled foam and the coupling effect between the corrugated structure and the foam, represented by $Q_{ij}^s$, $Q_{ij}^{fm}$ and $Q_{ij}^c$, respectively, and $Q_{ij}^H$ is given as

$$Q_{ij}^H=Q_{ij}^s+Q_{ij}^c+\left(1-f\right)Q_{ij}^{fm}$$

(9)

where the detailed $Q_{ij}^s$, $Q_{ij}^c$ and $Q_{ij}^{fm}$ are given in Equations (A1)–(A3) (Appendix A).

Moreover, the components of the effective thermal-stress tensor are given as

$$\begin{array}{l}{\beta }_1^H=\frac{{\alpha }_s{E}_s}{1-{\nu }_s^2}f+\left(1-f\right){\alpha }_{fm}{Q}_{11}^{fm},\\ {\beta }_2^H=\frac{{\alpha }_s{E}_s}{1-{\nu }_s^2}\cos \theta +\left(1-f\right){\alpha }_{fm}\left(Q_{22}^{fm}+2Q_{23}^{fm}\right),\\ {\beta }_3^H=\frac{{\alpha }_s{E}_s}{1-{\nu }_s^2}\frac{t}{h_2}\frac{{\sin }^2\theta }{\cos \theta }+\left(1-f\right){\alpha }_{fm}\left(Q_{33}^{fm}+2Q_{23}^{fm}\right).\end{array}$$

(10)

Therefore, the in-plane thermal expansion coefficient of the foam-filled corrugated core is obtained by

$${\mathsf{\alpha }}^{\left(2\right)}=\left\{\begin{array}{c}{\alpha }_{xx}^{\left(2\right)}\\ {\alpha }_{yy}^{\left(2\right)}\\ {\alpha }_{xy}^{\left(2\right)}\end{array}\right\}={\left(Q_{in}^{\left(2\right)}\right)}^{-1}\left\{\begin{array}{c}{\beta }_1^H\\ {\beta }_2^H\\ 0\end{array}\right\}$$

(11)

The effective density of the foam-filled corrugated core is given as

$${\rho }^{\left(2\right)}=f{\rho }_s+\left(1-f\right){\rho }_{fm}$$

(12)

2.4. Finite Element Method

In the present work, an eight-noded C⁰ isoparametric element with 9 degrees of freedom per node $\left\{U^{\left(1\right)},U^{\left(2\right)},U^{\left(3\right)},U^{\left(4\right)},V^{\left(1\right)},V^{\left(2\right)},V^{\left(3\right)},V^{\left(4\right)},w^0\right\}$ is used to develop a finite element model. For any kth layer (k = 1, 2, 3) of the HCS plates, the relationships between physical displacement vector $u^{\left(k\right)}$, linear in-plane and transverse shear strain vectors ${\mathsf{\epsilon }}_l^{\left(k\right)}$ and ${\mathsf{\gamma }}_l^{\left(k\right)}$, vector $g^{\left(k\right)}$ that is related to nonlinear strain with element nodal displacement vector δ are given as

$$u^{\left(k\right)}=S^{\left(k\right)}\mathsf{\delta }=H_D^{\left(k\right)}{N}_D^{\left(k\right)}\mathsf{\delta }$$

(13)

$${\mathsf{\epsilon }}_l^{\left(k\right)}=B_{in}^{\left(k\right)}\mathsf{\delta }=H_{in}^{\left(k\right)}{N}_{in}^{\left(k\right)}\mathsf{\delta },{\mathsf{\gamma }}_l^{\left(k\right)}=B_{tr}^{\left(k\right)}\mathsf{\delta }=H_{tr}^{\left(k\right)}{N}_{tr}^{\left(k\right)}\mathsf{\delta }$$

(14)

$$g^{\left(k\right)}=G^{\left(k\right)}\mathsf{\delta }=H_G^{\left(k\right)}{N}_G^{\left(k\right)}\mathsf{\delta }$$

(15)

where $S^{\left(k\right)}$ is the shape function matrix and $B_{in}^{\left(k\right)}$, $B_{tr}^{\left(k\right)}$, $G^{\left(k\right)}$ are the differential operator matrices of the kth layer. These matrices can be divided into matrices $H_i^{\left(k\right)}$ that are dependent on the thickness coordinate ζ_k and matrices $N_i^{\left(k\right)}$ that are independent of ζ_k, where the subscript ‘i’ donates D, in, tr or G.

2.4.1. Kinetic Energy

The element kinetic energy of the HCS plates is given as

$$T^e=\frac{1}{2}{\displaystyle \sum _{k=1}^3{\displaystyle {\int }_{V^e}{\left({\dot{u}}^{\left(k\right)}\right)}^T{\rho }^{\left(k\right)}{\dot{u}}^{\left(k\right)}dV}}=\frac{1}{2}{\displaystyle \sum _{k=1}^3{\dot{\mathsf{\delta }}}^T\left({\displaystyle {\int }_{A^e}{\left(N_D^{\left(k\right)}\right)}^T{I}^{\left(k\right)}{N}_D^{\left(k\right)}dA}\right)\dot{\mathsf{\delta }}}=\frac{1}{2}{\dot{\mathsf{\delta }}}^T{M}^e\dot{\mathsf{\delta }}$$

(16)

where I^(k) is the coefficient of the mass matrix for the kth layer and M^e is the element consistent mass matrix, given as

$$I^{\left(k\right)}=\frac{h_k}{2}{\displaystyle {\int }_{-1}^1{\left(H_D^{\left(k\right)}\right)}^T{\rho }^{\left(k\right)}{H}_D^{\left(k\right)}d{\zeta }_k},M^e={\displaystyle \sum _{k=1}^3{\displaystyle {\int }_{A^e}{\left(N_D^{\left(k\right)}\right)}^T}{I}^{\left(k\right)}{N}_D^{\left(k\right)}dA}$$

(17)

2.4.2. Potential Energy

The element potential energy of the hybrid corrugated sandwich plates is given as

$$V^e=\frac{1}{2}{\displaystyle \sum _{k=1}^3\left({\displaystyle {\int }_{V^e}{\left({\mathsf{\epsilon }}^{\left(k\right)}-{\mathsf{\epsilon }}_0^{\left(k\right)}\right)}^T{\mathsf{\sigma }}^{\left(k\right)}dV}+{\displaystyle {\int }_V{\left({\mathsf{\gamma }}^{\left(k\right)}\right)}^T{\mathsf{\tau }}^{\left(k\right)}dV}\right)}$$

(18)

Substituting Equation (14) into Equation (18), and neglecting terms with third and higher powers in displacement gradients, the total element potential energy can be expressed as

$$V^e=U_{in}^e+U_{tr}^e+V_T^e-W_T^e+C_T^e$$

(19)

$U_{in}^e$ and $U_{tr}^e$ are the element in-plane and transverse shear strain energy, given as

$$\begin{array}{l}{U}_{in}^e=\frac{1}{2}{\displaystyle \sum _{k=1}^3{\displaystyle {\int }_{V^e}{\left({\mathsf{\epsilon }}_l^{\left(k\right)}\right)}^T{Q}_{in}^{\left(k\right)}{\mathsf{\epsilon }}_l^{\left(k\right)}dV}}=\frac{1}{2}{\displaystyle \sum _{k=1}^3{\mathsf{\delta }}^T\left({\displaystyle {\int }_{A^e}{\left(N_{in}^{\left(k\right)}\right)}^T{D}_{in}^{\left(k\right)}{N}_{in}^{\left(k\right)}dA}\right)\mathsf{\delta }}=\frac{1}{2}{\mathsf{\delta }}^T{K}_{in}^e\mathsf{\delta }\\ U_{tr}^e=\frac{1}{2}{\displaystyle \sum _{k=1}^3{\displaystyle {\int }_{V^e}{\left({\mathsf{\gamma }}_l^{\left(k\right)}\right)}^T{Q}_{tr}^{\left(k\right)}{\mathsf{\gamma }}_l^{\left(k\right)}dV}}=\frac{1}{2}{\displaystyle \sum _{k=1}^3{\mathsf{\delta }}^T\left({\displaystyle {\int }_{A^e}{\left(N_{tr}^{\left(k\right)}\right)}^T{D}_{tr}^{\left(k\right)}{N}_{tr}^{\left(k\right)}dA}\right)\mathsf{\delta }}=\frac{1}{2}{\mathsf{\delta }}^T{K}_{tr}^e\mathsf{\delta }\end{array}$$

(20)

where $D_{in}^{\left(k\right)}$ and $D_{tr}^{\left(k\right)}$ are the coefficients of the structural stiffness matrices for the kth layer and $K_{in}^e$ and $K_{tr}^e$ are the element in-plane and transverse shear stiffness matrices, given as

$$\begin{array}{l}{D}_{in}^{\left(k\right)}=\frac{h_k}{2}{\displaystyle {\int }_{-1}^1{\left(H_{in}^{\left(k\right)}\right)}^T{Q}_{in}^{\left(k\right)}{H}_{in}^{\left(k\right)}d{\zeta }_k},K_{in}^e={\displaystyle \sum _{k=1}^3{\displaystyle {\int }_{A^e}{\left(N_{in}^{\left(k\right)}\right)}^T{D}_{in}^{\left(k\right)}{N}_{in}^{\left(k\right)}dA}}\\ D_{tr}^{\left(k\right)}=\frac{h_k}{2}{\displaystyle {\int }_{-1}^1{\left(H_{tr}^{\left(k\right)}\right)}^T{Q}_{tr}^{\left(k\right)}{H}_{tr}^{\left(k\right)}d{\zeta }_k},K_{tr}^e={\displaystyle \sum _{k=1}^3{\displaystyle {\int }_{A^e}{\left(N_{tr}^{\left(k\right)}\right)}^T{D}_{tr}^{\left(k\right)}{N}_{tr}^{\left(k\right)}dA}}\end{array}$$

(21)

$V_T^e$ is the element potential energy due to the nonlinear strain and the initial stress, given as

$$V_T^e=\frac{1}{2}{\displaystyle \sum _{k=1}^3{\displaystyle {\int }_{V^e}{\left({\mathsf{\epsilon }}_{nl}^{\left(k\right)}\right)}^T{\mathsf{\sigma }}_0^{\left(k\right)}dV}}=\frac{1}{2}{\displaystyle \sum _{k=1}^3{\displaystyle {\int }_{V^e}{\left(g^{\left(k\right)}\right)}^T{S}_G^{\left(k\right)}{g}^{\left(k\right)}dV}}$$

(22)

where $S_G^{\left(k\right)}$ is the initial stress matrix of the kth layer, given as

$$S_G^{\left(k\right)}=E_{3\times 3}\otimes {\left[\begin{array}{cc}{\sigma }_{xx}^0& {\tau }_{xy}^0\\ {\tau }_{xy}^0& {\sigma }_{yy}^0\end{array}\right]}^{\left(k\right)}$$

(23)

where E_3×3 denotes a 3×3 identity matrix and ⊗ denotes the Kronecker tensor product. The initial stress vector ${\mathsf{\sigma }}_0^{\left(k\right)}={\left\{{\sigma }_{xx}^0,{\sigma }_{yy}^0,{\tau }_{xy}^0\right\}}^{\left(k\right)T}$ is obtained by

$${\mathsf{\sigma }}_0^{\left(k\right)}=Q_{in}^{\left(k\right)}\left({\mathsf{\epsilon }}^{\left(k\right)}-{\mathsf{\epsilon }}_0^{\left(k\right)}\right)=Q_{in}^{\left(k\right)}{B}_{in}^{\left(k\right)}\mathsf{\delta }-Q_{in}^{\left(k\right)}{\mathsf{\alpha }}^{\left(k\right)}\Delta T$$

(24)

By using Equation (15), the element potential energy $V_T^e$ takes the form

$$V_T^e=\frac{1}{2}{\displaystyle \sum _{k=1}^3{\mathsf{\delta }}^T\left({\displaystyle {\int }_{A^e}{\left(N_G^{\left(k\right)}\right)}^T{D}_G^{\left(k\right)}{N}_G^{\left(k\right)}dA}\right)\mathsf{\delta }}=\frac{1}{2}{\mathsf{\delta }}^T{K}_G^e\mathsf{\delta }$$

(25)

where $D_G^{\left(k\right)}$ is the coefficient of the geometric stiffness matrix for the kth layer and $K_G^e$ is the element geometric stiffness matrix, given as

$$D_G^{\left(k\right)}=\frac{h_k}{2}{\displaystyle {\int }_{-1}^1{\left(H_G^{\left(k\right)}\right)}^T{S}_G^{\left(k\right)}{H}_G^{\left(k\right)}d{\zeta }_k},K_G^e={\displaystyle \sum _{k=1}^3{\displaystyle {\int }_{A^e}{\left(N_G^{\left(k\right)}\right)}^T{D}_G^{\left(k\right)}{N}_G^{\left(k\right)}dA}}$$

(26)

$W_T^e$ is the work done by the equivalent external force caused by thermal expansion, given as

$$W_T^e={\displaystyle \sum _{k=1}^3{\displaystyle {\int }_{V^e}{\left({\mathsf{\epsilon }}_l^{\left(k\right)}\right)}^T{Q}_{in}^{\left(k\right)}{\mathsf{\epsilon }}_0^{\left(k\right)}dV}}={\displaystyle \sum _{k=1}^3{\mathsf{\delta }}^T{\displaystyle {\int }_{A^e}{\left(N_{in}^{\left(k\right)}\right)}^T{P}_T^{\left(k\right)}dA}}={\mathsf{\delta }}^T{F}_T^e$$

(27)

where $P_T^{\left(k\right)}$ is the coefficient of the equivalent nodal force vector for the kth layer and $F_T^e$ is the element equivalent nodal force vector, given as

$$P_T^{\left(k\right)}=\frac{h_k}{2}{\displaystyle {\int }_{-1}^1{\left(H_{in}^{\left(k\right)}\right)}^T{Q}_{in}^{\left(k\right)}{\mathsf{\alpha }}^{\left(k\right)}\Delta Td{\zeta }_k},F_T^e={\displaystyle \sum _{k=1}^3{\displaystyle {\int }_{A^e}{\left(N_{in}^{\left(k\right)}\right)}^T{P}_T^{\left(k\right)}dA}}$$

(28)

2.4.3. Work Done by External Force

Due to their structural application as the TPS of hypersonic vehicles, the hybrid corrugated sandwich plates expose their outer surface in free airflow and withstand transverse aerodynamic pressure. Piston theory is adopted to describe the unsteady aerodynamic load, given as

$$\Delta p=-\frac{{\rho }_a{V}^2}{\sqrt{M_a^2-1}}\left(\frac{\partial w^0}{\partial x}+\frac{1}{V}\frac{M_a^2-2}{M_a^2-1}\frac{\partial w^0}{\partial t}\right)=-\lambda \frac{\partial w^0}{\partial x}-\mu \frac{\partial w^0}{\partial t}$$

(29)

where V, ρ_a, and M_a are the velocity, density and reference Mach number of free airflow, respectively. Dimensionless dynamic pressure is introduced by defining $\overline{\lambda }=\lambda /D$, where $D=E{h}^3/12\left(1-{\nu }^2\right)$. The aerodynamic load evaluated by Piston theory is not only time variable, but also dependent to the gradient of out-of-plane displacement in x-direction.

The element work of the HCS plates is given as

$$W_a^e={\displaystyle {\int }_{A^e}\left(w^0\cdot \Delta p\right)dA}={\mathsf{\delta }}^T\left(-K_a^e\mathsf{\delta }-C_a^e\dot{\mathsf{\delta }}\right)={\mathsf{\delta }}^T{F}_a^e$$

(30)

where $K_a^e$ and $C_a^e$ are the element aerodynamic stiffness and damping matrices and $F_a^e$ is the element equivalent nodal load caused by aerodynamic pressure, given as

$$K_a^e=\lambda {\displaystyle {\int }_{A^e}{N}_w^T\frac{\partial N_w}{\partial x}dA},C_a^e=\mu {\displaystyle {\int }_{A^e}{N}_w^T{N}_{w}dA},F_a^e=-K_a^e\mathsf{\delta }-C_a^e\dot{\mathsf{\delta }}$$

(31)

where $N_{wi}=\left[0,0,0,0,0,0,0,0,N_i\right],\left(i=1~8\right)$ is the shape function matrix between the out-plane displacement w⁰ and the element nodal displacement vector δ.

2.4.4. Governing Equations

By element assembling procedure, the global matrices of mass M, structural stiffness K, geometric stiffness K_G, aerodynamic stiffness K_a, aerodynamic damping C_a and the global nodal force vector F_T caused by thermal expansion are obtained according to Equations (17), (21), (26), (31) and (28). The total kinetic energy, potential energy and work done by external force are given in terms of the global nodal displacement vector d, as

$$T=\frac{1}{2}{\dot{d}}^{T}M\dot{d},V=\frac{1}{2}{d}^T\left(K+K_G\right)d,W_{ext}=W_T+W_a=d^T\left(F_T+F_a\right)$$

(32)

Hamilton’s principle is employed to formulate governing equations, given as

$${\displaystyle {\int }_{t_1}^{t_2}\left[\delta \left(T-V\right)+\delta W_{ext}\right]dt}=0$$

(33)

Substituting Equation (32) into Equation (33), the governing equation of coupled fluid-structure-thermal analysis for the HCS plates is obtained as

$$M\ddot{d}+C_a\dot{d}+\left(K+K_T+K_a\right)d=F_T$$

(34)

The solution of Equation (34) is assumed to be a sum of a time-independent solution due to static deformation and a time-dependent solution due to dynamic deformation as $d=d_s+d_d$. Therefore, the static and dynamic equilibrium equations are expressed as

$$\begin{array}{c}{K}_T{d}_s=F_T\\ M{\ddot{d}}_d+C_a{\dot{d}}_d+\left(K+K_T+K_a\right)d_d=0\end{array}$$

(35)

2.4.5. Solution Procedure

In the present work, the aforementioned layerwise theory with the equivalent model of the foam-filled corrugated cores and the finite element formulation based on this theory are adopted to investigated the effects of the thermal and aerodynamic loads on the natural frequencies and structural stabilities of the HCS plates. The solution procedure of coupled fluid-structure-thermal analysis of the HCS plates is illustrated in Figure 2. Firstly, the static stabilities subjected to thermal loads are investigated by buckling analysis and evaluated by the critical temperature change. The critical temperature change limits the maximum temperature allowed in subsequent analysis for steady-state and uniform temperature distributions. Secondly, the dynamic characteristics subjected to thermal loads are investigated by pre-stressed modal analysis in thermal environments and evaluated by the natural frequencies and mode shapes. The geometric stiffnesses induced by the initial thermal stresses are obtained from static analysis. Thirdly, the dynamic stabilities subjected aerodynamic loads are investigated by coupled fluid-structure analysis based on the natural frequencies and modal shapes from modal analysis, which is also called aeroelastic analysis, and evaluated by the critical dynamic pressure. Finally, the dynamic stabilities subjected to both thermal and aerodynamic loads are investigated by coupled fluid-structure-thermal analysis, which is also called aerothermoelastic analysis, and evaluated by the critical dynamic pressure.

The formulations for each analysis are given as

Buckling analysis:

$$K+\Delta T{K}_T=0$$

(36)

Modal analysis:

$$M{\ddot{d}}_d+K{d}_d=0$$

(37)

Pre-stressed modal analysis:

$$\{\begin{array}{l}{K}_T{d}_s=F_T\\ M{\ddot{d}}_d+\left(K+K_T\right)d_d=0\end{array}$$

(38)

Coupled fluid-structure analysis:

$$M{\ddot{d}}_d+C_a{\dot{d}}_d+\left(K+K_a\right)d_d=0$$

(39)

Coupled fluid-structure-thermal analysis:

$$\{\begin{array}{l}{K}_T{d}_s=F_T\\ M{\ddot{d}}_d+C_a{\dot{d}}_d+\left(K+K_T+K_a\right)d_d=0\end{array}$$

(40)

The critical temperature change is defined as $\overline{\Delta T_{cr}}=\Delta T_{cr}\alpha \times {10}^3$ and the dimensionless natural frequency is defined as $\overline{\omega }=\omega a^2\sqrt{\rho h/D}$. For the coupled fluid-structure-thermal analysis, a modal coordinate transformation is employed to improve the computation efficiency. A new vector of generalized modal coordinates is defined as d_d = Φq, where Φ is assembled by normal eigenvectors obtained from Equation (38). Then Equation (40) can be written as

$$\overline{M}\ddot{q}+\overline{C}\dot{q}+\overline{K}q=0$$

(41)

where $\overline{M}={\mathsf{\Phi }}^{T}M\Phi ,\overline{C}={\mathsf{\Phi }}^T{C}_a\Phi ,\overline{K}={\mathsf{\Phi }}^T\left(K+K_a+K_T\right)\mathsf{\Phi }$. The state-space form of Equation (41) is given as

$$\left\{\begin{array}{c}\dot{q}\\ \ddot{q}\end{array}\right\}=\left[\begin{array}{cc}0& I\\ -{\overline{M}}^{-1}\overline{K}& -{\overline{M}}^{-1}\overline{C}\end{array}\right]\left\{\begin{array}{c}q\\ \dot{q}\end{array}\right\}$$

(42)

The complex eigenvalue is obtained by solving Equation (42). The imaginary part of the eigenvalue is the frequencies and the real part is the damping terms. The dimensionless critical dynamic pressure $\overline{\lambda }$, corresponding to the critical airflow velocity, is determined for the HCS plates when the damping of a rth order mode changes from negative to positive or the coalescence of frequency curves of two adjacent mode occurs.

3. Numerical Examples and Results

A computer program developed by MATLAB programming language is used for coupled fluid-structure-thermal analysis of the HCS plates. A validation example is presented firstly. Then thermal buckling and pre-stressed modal analysis in thermal environments are conducted. Finally, coupled fluid-structure-thermal analysis is performed with parametric studies.

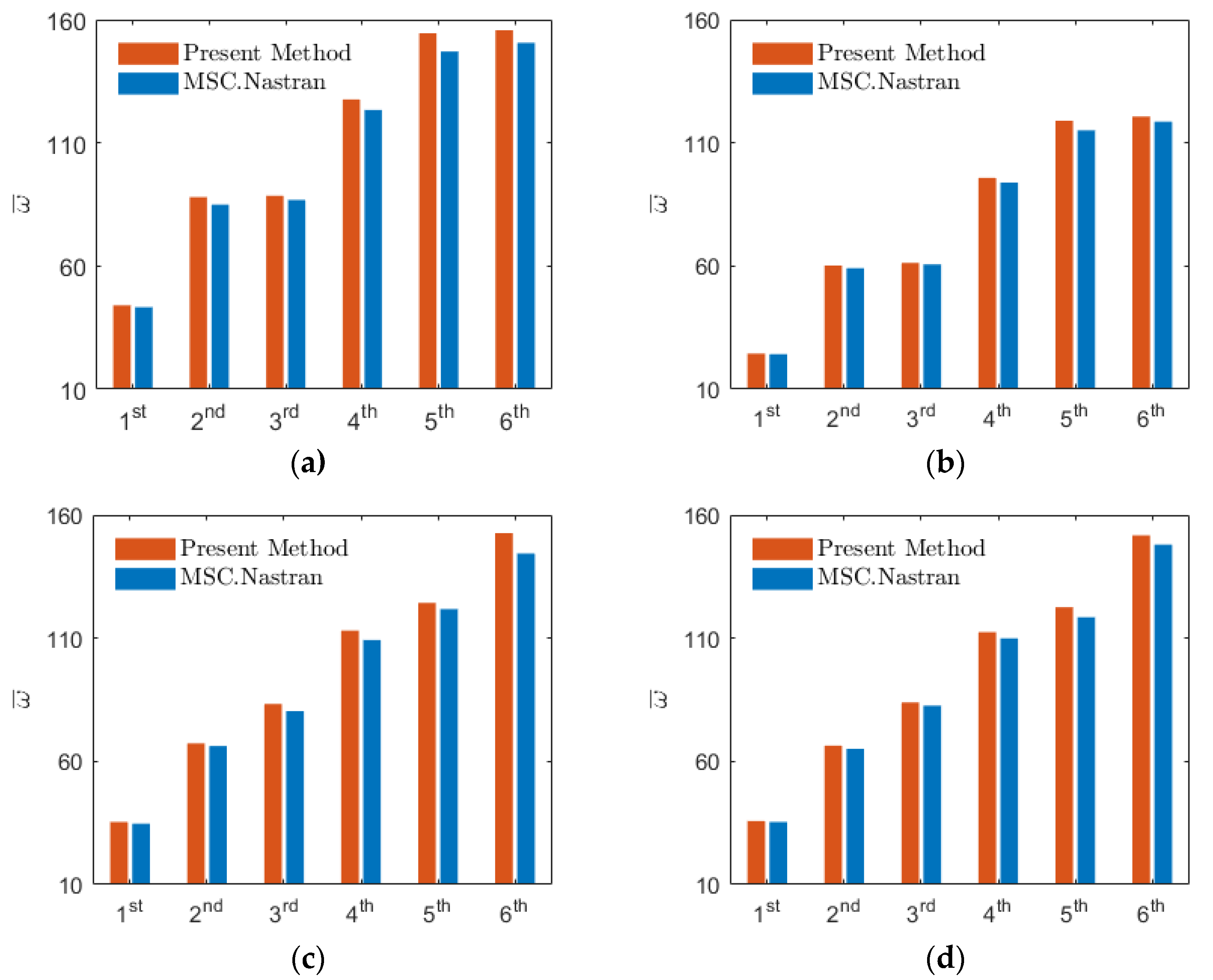
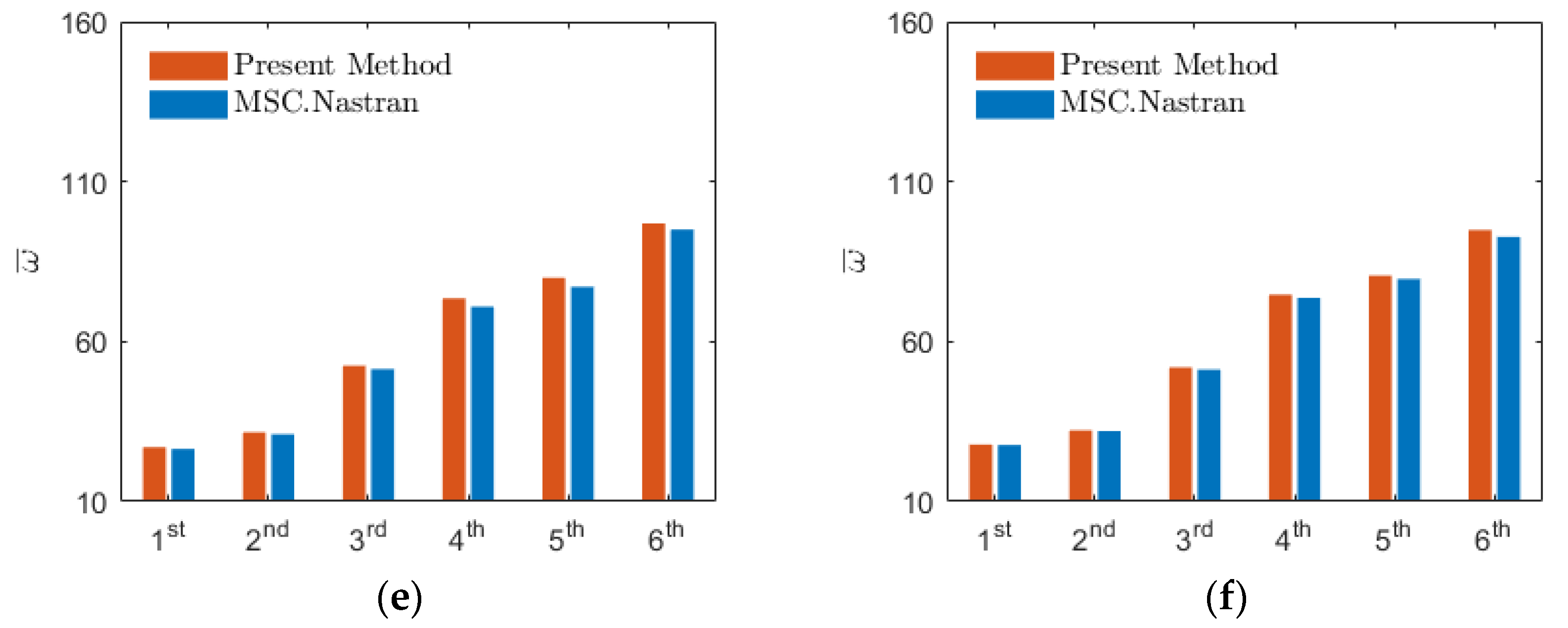
3.1. Validation Study

In order to show the accuracy of the present layerwise finite element model with a homogenization technique, a validation study is performed by comparing the dynamic characteristics of the HCS plates from the present method with those from an MSC.Nastran simulation of a detailed 3D finite element model under different boundary conditions and temperature change.

The HCS plates all made of Ti-6Al-4V with Rohacell 31 foam filled are taken into consideration. The material properties of the foam and base structures that are listed in

Table 1. Material properties of foam [19].

	Young’s Modulus (MPa)	Poisson Ratio	Density (kg/m3)	Thermal Expansion Coefficient (10−6/K)
Rohacell 31	36	0.2	31	37
Rohacell 51	70	0.3	51	33
Rohacell 71	105	0.25	75	30
Alporas	1000	0.15	230	22

and

Table 2. Material properties of base material of face sheets and corrugated members [19].

	Young’s Modulus (GPa)	Poisson Ratio	Density (kg/m3)	Thermal Expansion Coefficient (10−6/K)
Ti-6Al-4V	114	0.33	4430	8.6
304 stainless steel	210	0.3	7900	12
Aluminum 1050	69	0.25	2705	23.6

refer to the values given by Han [19]. The number of the unit cells with triangular corrugated-core shape is n_c = 25 and other dimensions are a/h = 50, b/a = 1, h₁ = h₃ = h_f = 0.1 h, t = 0.1 h. In the MSC.Nastran software, the corrugated sandwich plate and the filling foam are both simulated by CHEXA solid elements with totally 142,500 elements and 193,431 nodes as shown in Figure 3. This mesh refinement is considered to be sufficient enough that the results of the 3D finite element model can be the exact solutions.

Modal analysis of the HCS plates under different boundary conditions with no temperature change is firstly performed. The boundary conditions include: (1) simply supported at all sides (SSSS); (2) clamped at all sides (CCCC); (3) clamped in MD and simply supported in CD (CSCS); (4) simply supported in MD and clamped in CD (SCSC); (5) clamped in MD and free in CD (CFCF); (6) free in MD and clamped in CD (FCFC).

Figure 4 shows the convergence study of the presented layerwise model. The dimensionless fundamental frequency of the HCS plates under SSSS and CCCC boundary conditions with different mesh sizes is illustrated in Figure 4. It is observed that the solution converges with the mesh size of 10×10. Therefore, the following examples are calculated with 10 × 10 mesh size.

The first six dimensionless natural frequencies under different boundary conditions obtained from the present method and MSC.Nastran simulation are shown in Figure 5. It is noted that the results calculated by the present method are in good agreement with those by MSC.Nastran, and the relative error is less than 5% for all cases within the frequency range of interest.

Pre-stressed modal analysis in thermal environments of the clamped HCS plates is performed then. The first six dimensionless natural frequencies against temperature change ΔT are shown in Figure 6. It is found that for the first three modes, the results from the present method fit well with those from the MSC.Nastran simulation; meanwhile, for higher-order modes, the relative error of the dimensionless frequencies is a little larger as temperature change increases, but still within an acceptable range. Figure 7 shows the first six mode shapes of the clamped HCS plate with temperature change ΔT = 100. The mode shapes from the present method are as same as those from the MSC.Nastran simulation.

The present method not only has enough calculation accuracy but also has less computational cost compared to commercial software. All the calculations are performed using an Intel Core i7-4790K CPU with a 4GHz main frequency and a 16G memory. It takes about 240 seconds for MSC.Nastran to finish the calculation for one thermal condition; however, the average calculating time for the present method is only 1.5 seconds. Therefore, within an acceptable error range, the present method can save an enormous amount of computing time, much more efficient than MSC.Nastran simulation.

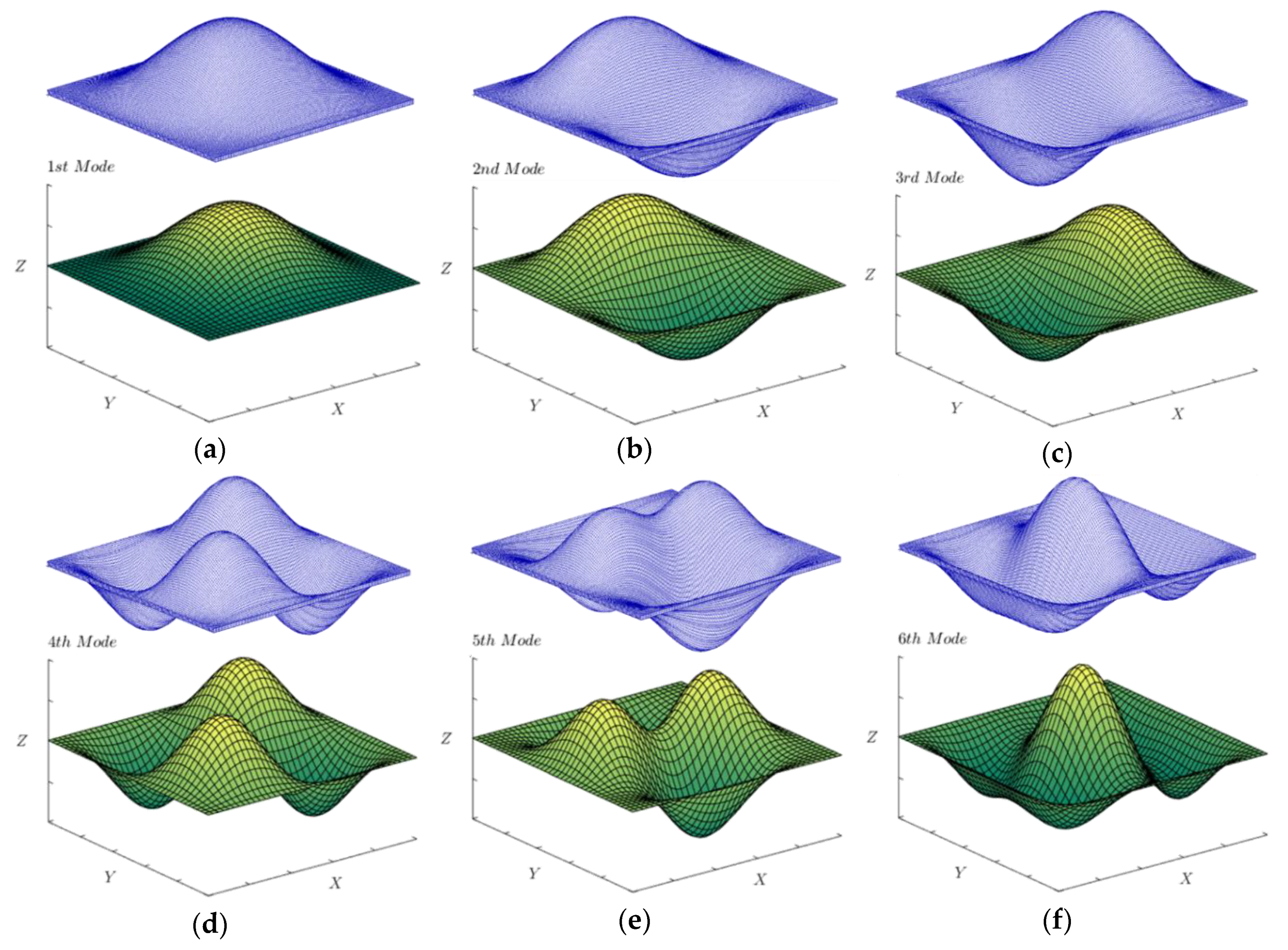
3.2. Buckling Amalysis and Pre-Stressed Modal Analysis

For the clamped HCS plates subjected to the thermal loads, the static stabilities and dynamic characteristics are evaluated by thermal buckling analysis and pre-stressed modal analysis in thermal environments. The HCS plates are made of Ti-6Al-4V and foam-filled with Rohacell 31. The reference geometric parameters are n_c = 25, a/h = 50, b/a = 1, h₁ = h₃ = h_f = 0.1h, t = 0.1h. Figure 8 shows the critical temperature and dimensionless fundamental frequency with ΔT = 100 against geometric parameters change.

The effects of the geometric parameters on the critical temperature change are discussed firstly. The number of the unit cells n_c varies from 5 to 50. With more unit cells, the critical temperature change firstly increases and then decreases with a maximum value at about n_c = 15. The inclined angle θ takes the values from 35° to 80°. The maximum critical temperature change is achieved at the minimum angle, corresponding to a triangular corrugated shape. The thickness of the face sheets h_f and the thickness of the corrugated members t both vary from 0.025h to 0.2h. The critical temperature change increases and then decreases as the facesheet thickness increases, while it decreases as the corrugation thickness increases.

The effects of geometric parameters on the dimensionless fundamental frequency with temperature change ΔT = 100 have a similar tendency as those on the critical temperature change.

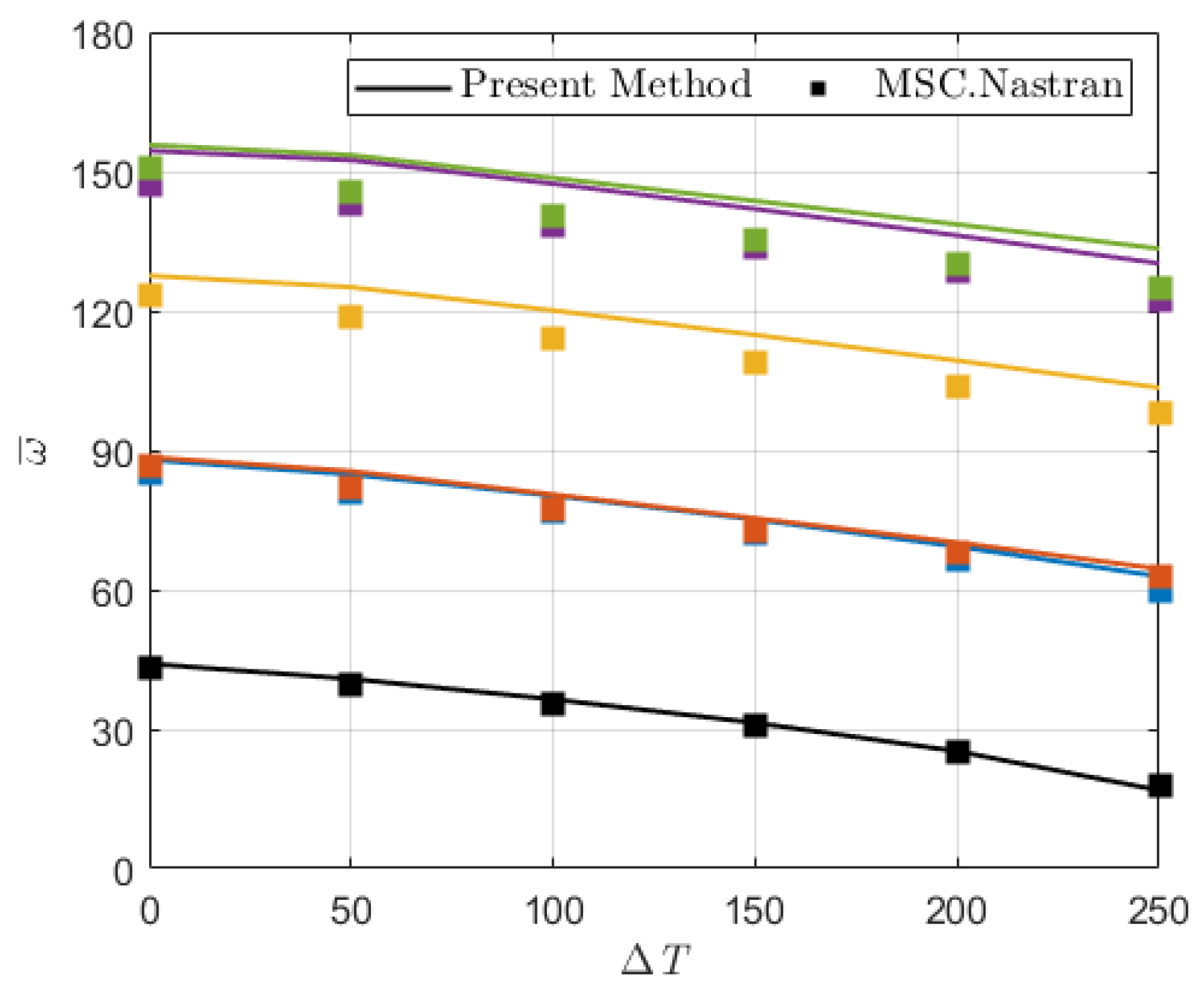
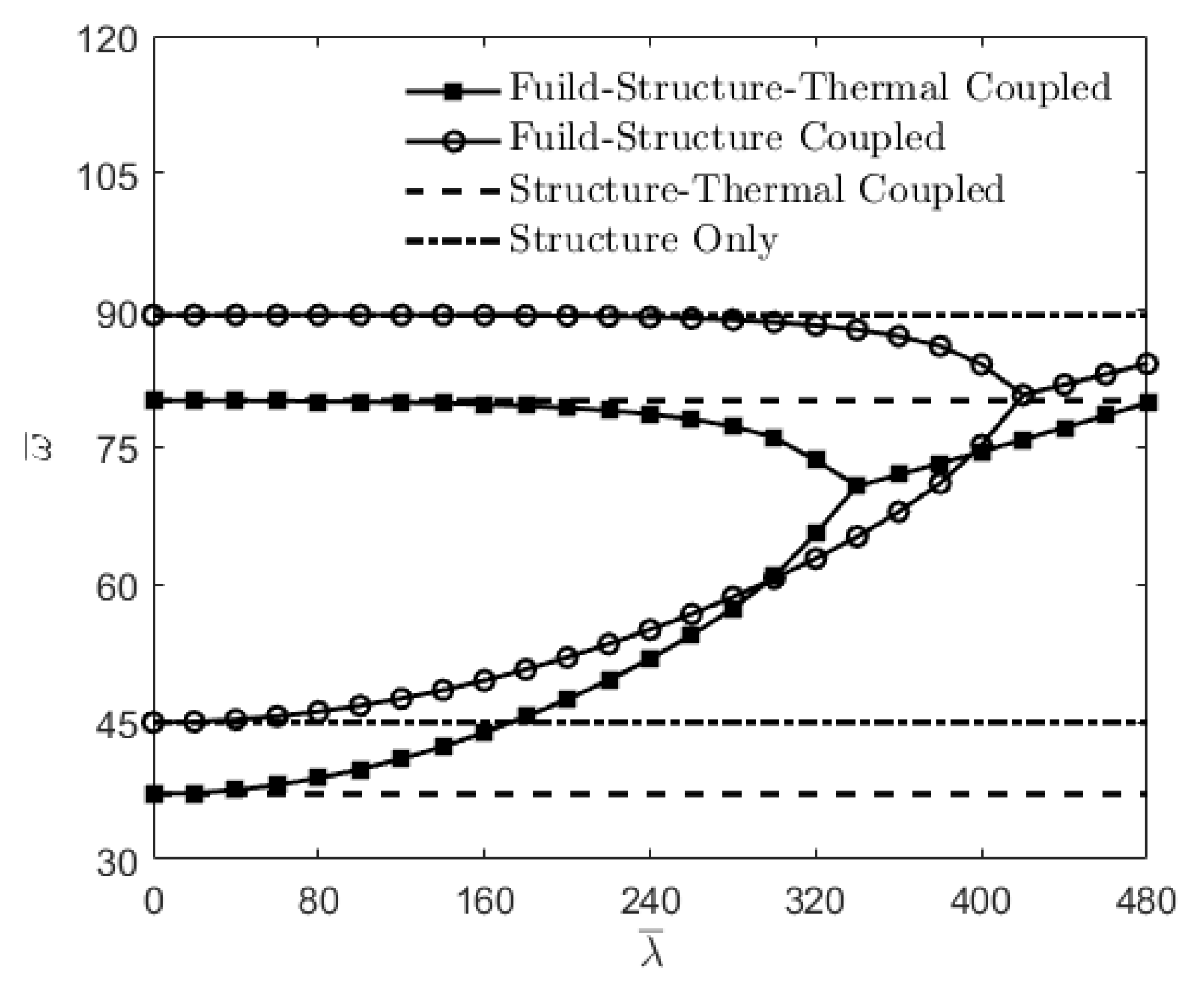
3.3. Coupled Fluid-Structure-Thermal Analysis

Coupled fluid-structure-thermal analysis is conducted for the clamped HCS plates at sea level with air density ρ_a = 1.225 kg/m³ and reference Mach number M_a = 3.0. Figure 9 illustrates the effects of temperature change (ΔT = 100) and aerodynamic pressure on the first two dimensionless natural frequencies.

For the HCS plates only subjected to thermal loads, the natural frequencies are affected only by the temperature changes. As the temperature increases, the natural frequencies decrease due to the reduced overall stiffnesses caused by the thermal-induced initial stresses. When the sandwich plates are only subjected to aerodynamic loads, the unsteady aerodynamic pressure generates the damping and stiffness that are related to the aerodynamic pressure and with the change of the dynamic pressure, the first two natural frequencies gradually approach to each other. The dynamic pressure corresponding to the coincidence of the first two consecutively varying frequencies is the critical dynamic pressure. For the HCS plate subjected to both thermal and aerodynamic loads, on the one hand, the increasing dynamic pressure causes the first two natural frequencies to coincide with each other and on the other hand, the temperature change causes the decrease in the natural frequencies, resulting in a reduction in the critical dynamic pressure.

For a given temperature field, the dynamic stabilities of the HCS plate under fluid-structure-thermal coupling mainly depend on the imposing aerodynamic pressure, which are measured by the critical dynamic pressure. It is seen from Figure 9 that the critical dynamic pressure reduces with the additional thermal effects.

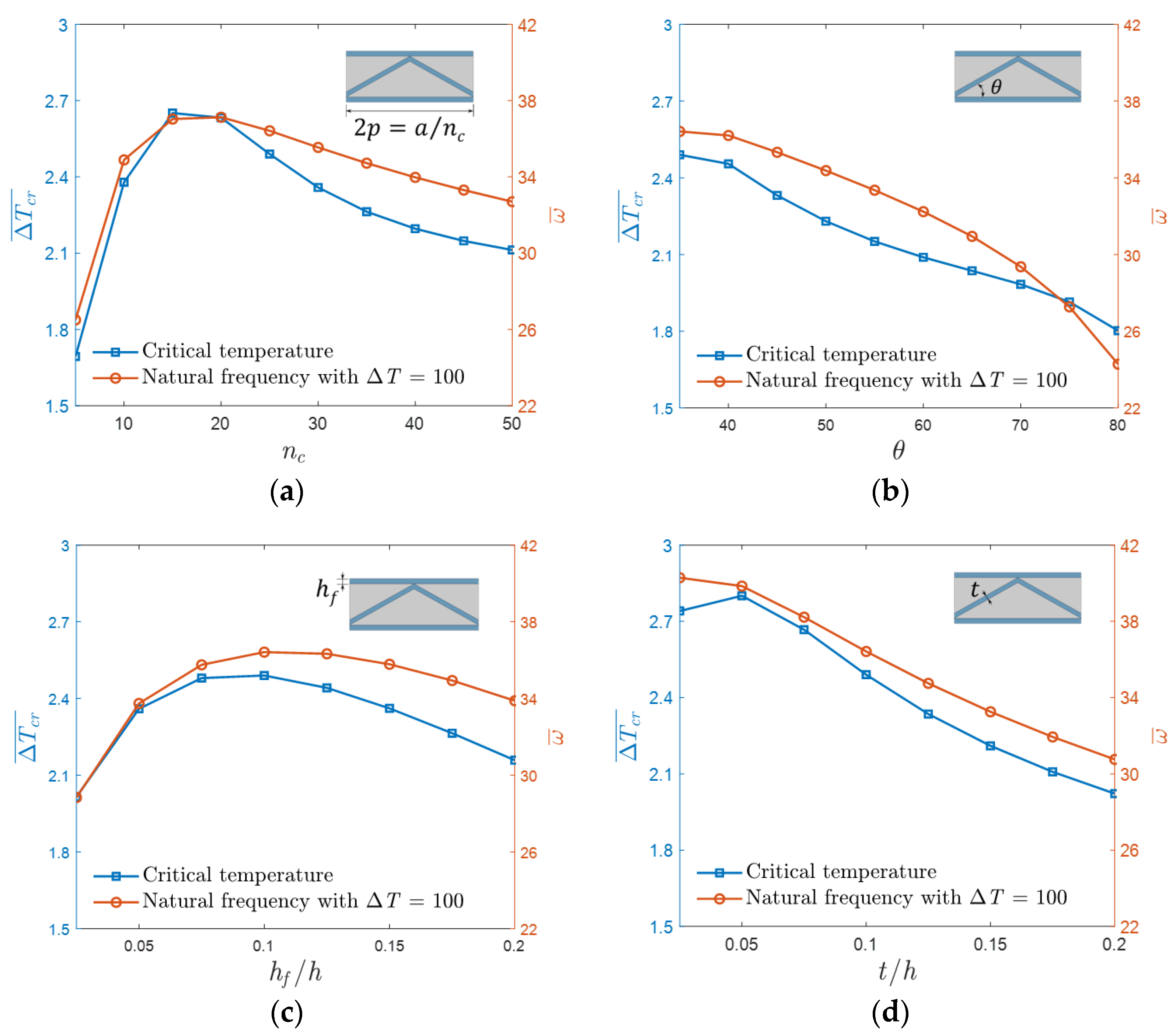
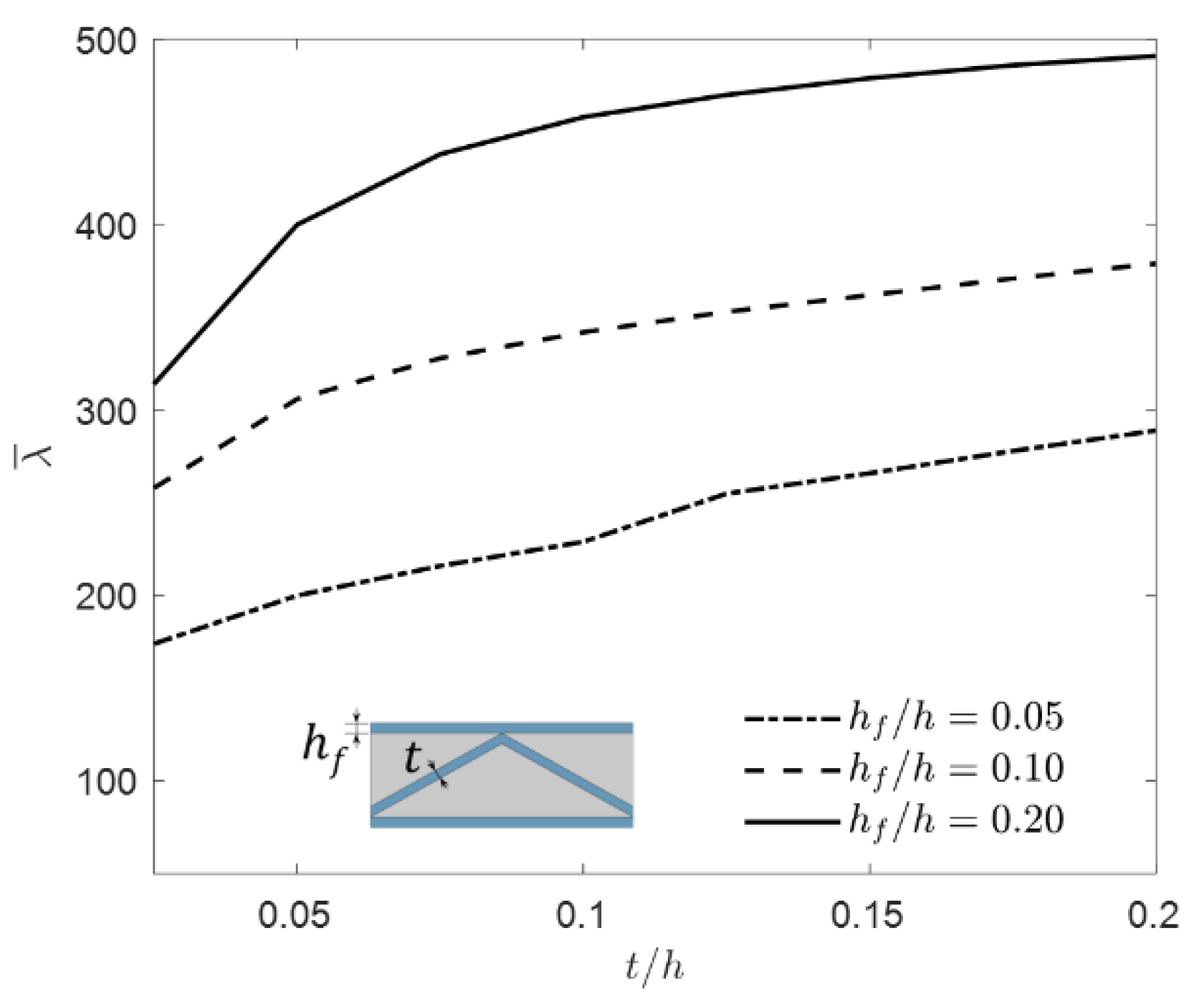
3.3.1. Parameter Study under Uniform Temperature Field

The effects of geometric and material parameters on critical dynamic pressure of the HCS plates in a uniform temperature field are investigated. The HCS plates are made of Ti-6Al-4V filled with Rohacell 31 foam. The reference geometric parameters are nc = 25, a/h = 50, b/a = 1, h₁ = h₃ = h_f = 0.1h, t = 0.1h.

1. Effects of aspect ratio and airflow direction

Figure 10 illustrates the effects of aspect ratio b/a and airflow direction on the dimensionless critical dynamic pressure. The aspect ratio takes the value of 0.5, 1.0, 1.5 and the airflow direction is parallel or perpendicular to machine direction (MD) of the corrugated plate. It is shown that with an increasing aspect ratio, the critical dynamic pressure decreases regardless of the airflow direction. Meanwhile, the streamwise has a limited influence on the critical dynamic pressure and the critical dynamic pressure is slightly higher when it is parallel to MD as opposed to perpendicular to MD.

2. Effects of number of unit cell and inclined angle

Figure 11 illustrates the effects of number of unit cells n_c and inclined angle θ on the dimensionless critical dynamic pressure. The number of unit cells varies from 15 to 45 and the inclined angle varies from 30° to 75°. The critical dynamic pressure increases with the increase in the number of unit cells or the inclined angle. Within a smaller range of temperature change, the discrepancy of the critical dynamic pressure between different numbers of unit cells or different corrugation angles is quite evident. However, for a larger temperature change, the critical dynamic pressure does not change much with these two changing parameters.

3. Effects of thickness of face sheets and corrugated members

Figure 12 illustrates the effects of the thickness of the face sheets h_f and the corrugated members t on the dimensionless critical dynamic pressure with temperature change ΔT = 100. The thickness of face sheets takes the value of 0.05, 0.10, 0.20 and the thickness of corrugated members varies from 0.02 to 0.20. It is clearly seen that increasing either the facesheet or corrugation thickness can both improve the critical dynamic pressure. Moreover, the stability enhancement for the HCS plates is more obvious when thickening the facesheet thickness as opposed to the corrugation thickness.

4. Effects of Material properties

Material properties of the foam and corrugated sandwich plates are also taken into consideration.

Table 3. Effects of material combination of foam and base structures on critical temperature change and dimensionless critical dynamic pressure with temperature change ΔT = 100.

Materials		$\overline{\mathbf{\Delta }{\mathit{T}}_{\mathit{c}\mathit{r}}}$			$\overline{\mathit{\lambda }}$
	Base	Ti	Steel	Al	Ti	Steel	Al
Foam
Empty		2.35	2.39	2.35	338	306	193
RC31		2.49	2.45	2.39	342	307	195
RC51		2.64	2.52	2.41	346	310	197
RC71		2.59	2.50	2.39	345	309	196
AC		2.43	2.45	2.33	346	310	198

shows the effects of the material combination of the foam and base structures on the critical temperature change and dimensionless critical dynamic pressure with temperature change ΔT = 100. Ti, Steel and Al denote Ti-6Al-4V, 304 stainless steel and Aluminum 1050 for the base structures, respectively. RC31, RC51, RC71, AC and empty denote the corrugated sandwich plate filled with Rohacell 31, Rohacell 51, Rohacell 71, aluminum foam (Alporas) and no filler, respectively. The material properties are given in Table 1 and Table 2.

It is shown that the base materials of the face sheets and the corrugated members have a much greater influence on the critical dynamic pressure than the foam material. The filling foam increases both the critical temperature change and dynamic pressure to a certain degree compared to the unfilled cases. The HCS plates made of Ti-6Al-4V and filled with Rohacell 51 foam have the best performance for both static and dynamic stabilities.

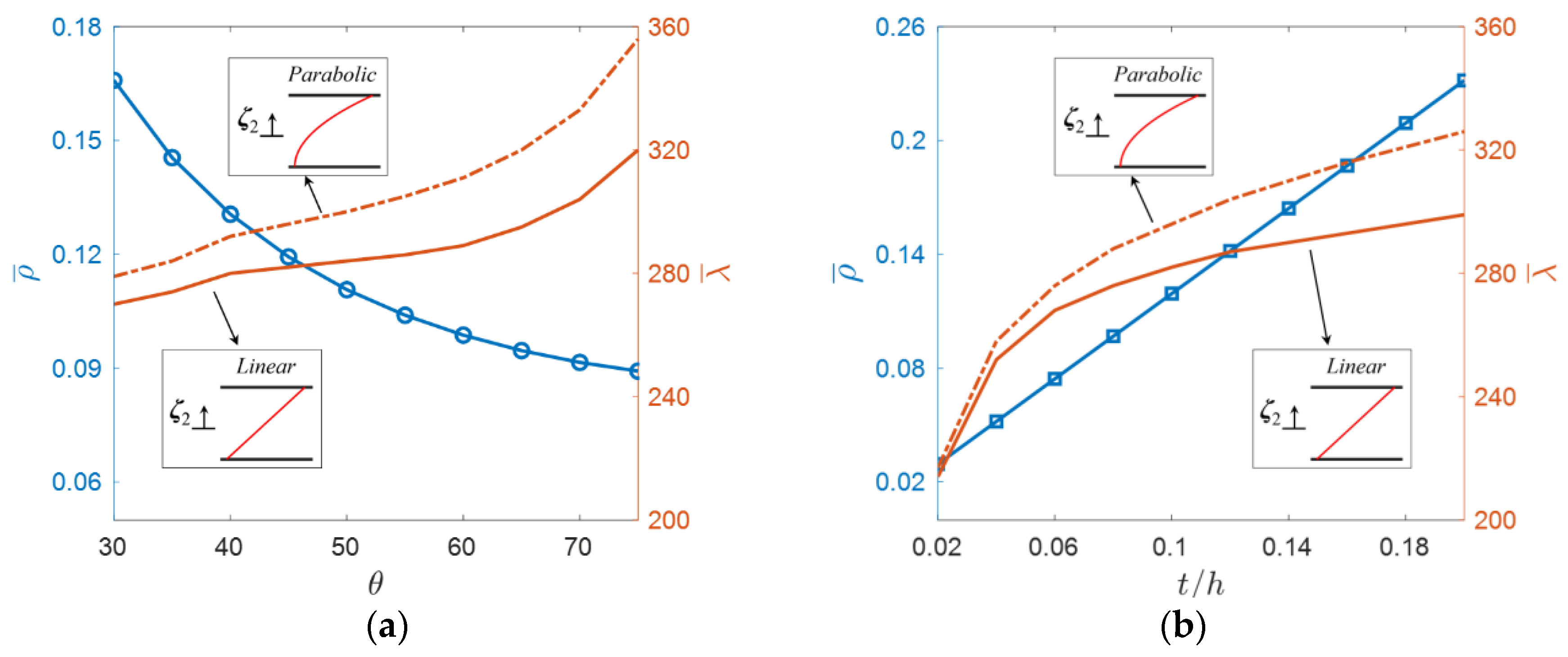
3.3.2. Parameter Study under Uneven Temperature Field

An uneven temperature field is considered for the coupled fluid-structure-thermal analysis of the HCS plates. For the bottom and top face sheets, the temperature fields are treated as uniform due to their relatively thin thickness compared with the core layer. For the foam-filled corrugated core, the temperature field can be a linear or parabolic distribution.

Therefore, the temperature field for the bottom face sheet is assumed to be ΔT₁ = 50, the temperature field for the top face sheet is assumed to be ΔT₃ = 300 and the temperature field for the foam-filled corrugated core is given.

In linear distribution:

$$\Delta T_2=\Delta T_1+\frac{\Delta T_3-\Delta T_1}{2}\left(1+{\xi }_2\right)$$

In parabolic distribution:

$$\Delta T_2=\Delta T_1+\frac{\Delta T_3-\Delta T_1}{2}\frac{1}{2}{\left(1+{\xi }_2\right)}^2$$

For the HCS plates under this uneven temperature field, the structural dynamic stabilities are mainly determined by the geometric parameters of the foam-filled corrugated core. Therefore, the effects of the inclined angle θ and the corrugation thickness t on the dimensionless critical dynamic pressure under the linear or parabolic temperature field are investigated Figure 13 shows the critical dynamic pressure and the equivalent density against the inclined angle and corrugation thickness in a linear or parabolic temperature field. With the increase in the inclined angle, the equivalent density decreases, and the critical dynamic pressure increases for both linear and parabolic temperature distributions. It seems that increasing the inclined angle is a clever way to improve structural efficiency; however, as shown in Figure 8, the corrugated sandwich plate with a larger inclined angle has a smaller critical temperature change, which is more prone to occur thermal buckling. As for the corrugation thickness, with its increasing, the critical dynamic pressure improves, accompanied by the deterioration of mass and buckling characteristics.

Meanwhile, for the given temperature field of bottom and top face sheets, the critical dynamic pressure obtained from the linear temperature distribution is smaller than that from the parabolic distribution. This means that the assumption of linear temperature distribution will lead to more conservative results for the HCS plates under aerodynamic pressure and uneven temperature fields.

4. Discussion

The validation example in Section 3.1 has proved that the present layerwise finite element model possesses the advantages of both computational accuracy and efficiency compared to MSC.Nastran simulation. This model is thus conducive to the efficient parameter studies of the HCS plates.

The frequency characteristics presented in Figure 9 demonstrate that the unsteady aerodynamic pressure causes two adjacent frequency to gradually coalesce with each other and the coalescence point indicates a critical stable state. The temperature change causes the decrease in natural frequencies which leads to an earlier occurrence of the structural instability.

The geometric and material parameters, including number of unit cells, inclined angle, facesheet thickness, corrugation thickness as well as materials of foam and base structures, have been taken into consideration in the thermal buckling, pre-stressed modal and coupled fluid-structure-thermal analysis of the HCS plates.

In general, the effects of the geometric parameters on the critical temperature change are similar to those on the natural frequency, but quite different from those on the critical dynamic pressure. As shown in Figure 8a and Figure 11a, with the increase in the number of unit cells, the critical temperature change and the fundamental frequency in thermal environments firstly go up and then down, while the critical dynamic pressure keeps growing. As shown in Figure 8b and Figure 11b, with the increase in the inclined angle, the critical temperature change and the fundamental frequency falls, and the critical dynamic rises. The improvement of the critical dynamic pressure due to the increase in inclined angle is obvious under no thermal loads or lower temperature changes. As shown in Figure 8c and Figure 12, as the facesheet thickness increases, the critical temperature change and the fundamental frequency reaches a maximum when it is equal to the corrugation thickness, while the critical dynamic presents a great improvement. As shown in Figure 8d and Figure 12, as the corrugation thickness increases, the critical temperature change and the fundamental frequency increase, while the critical dynamic decreases. It can be observed that for most cases, parameter changes improve static stabilities while deteriorates dynamic stabilities in coupled fluid-structure-thermal analysis. Due to the different influences of the geometric parameters on the critical temperature change and dynamic pressure, the final structural efficiency of the HCS plates is a trade-off between static and dynamic stabilities under fluid-structure-thermal coupling.

Table 3 displays the effects of material properties of foam and base structures. The critical temperature change is closely related to both the foam and base materials and the critical dynamic pressure is mainly determined only by the base materials. Compared to the unfilled sandwich plates, the foam filling improves the structural efficiency to a certain degree. Among the materials adopted in the analysis, the best combination is a Ti-6Al-4V-made corrugated sandwich plate fill with Rohacell 51 foam.

Furthermore, additional investigations about the effects of airflow direction and aspect ratio on the critical dynamic pressure are conducted. Figure 10 indicates that regardless of the aspect ratio, the critical dynamic pressure is always slightly higher when the fiber or machine direction of the HCS plates is parallel to the streamwise than perpendicular to the streamwise.

Finally, uneven temperature fields of linear and parabolic distributions are taken into the consideration. As can be seen in Figure 13, the critical dynamic pressure is smaller in the linear assumption than in the parabolic assumption, indicating that a linear distribution between the top and bottom face sheets brings about a conservative solution.

The future research will focus on the designing, manufacturing and testing of the HCS plates for the novel TPS. Further studies may include 1) optimization design aimed at a balanced structural efficiency; 2) introducing heat transfer into the present fluid-structure-thermal coupling analysis.

5. Conclusions

In this paper, a C⁰ layerwise finite element model with a thermo-elastic homogenization procedure is presented for the coupled fluid-structure-thermal analysis of the HCS plates under thermal and aerodynamic loading. The thermal effect is evaluated by steady temperature change and the unsteady aerodynamic pressure is calculated by the first-order Piston theory. Parameter studies are performed to evaluate the mechanical stability. The main conclusions are summarized as follows:

• The present method for the coupled fluid-structure-thermal analysis of the HCS plates possesses both computational accuracy and efficiency.
• The dynamic instability of the HCS plates can be induced by fluid-structure coupling and further accelerated by involved thermal effects.
• As for frequency characteristics of the HCS plates, unsteady aerodynamic pressure causes two adjacent frequency curves to gradually coalesce with each other, meanwhile, temperature change causes natural frequencies to decrease, resulting in an earlier occurrence of the frequency coalescence.
• The influences of design variables on dynamic instability and thermal buckling instability show opposite tendencies, and therefore a tradeoff is required for the TPS design.
• A linear assumption of temperature fields through plate thickness brings out conservative solutions compared to parabolic distribution, providing safety margins in the preliminary design.
• The present analytical model and numerical results for the HCS plates provide design guidance in terms of the practical application of the novel TPS.