Evaluating the Impact of Turbulence Closure Models on Solute Transport Simulations in Meandering Open Channels
Abstract
1. Introduction
2. Methodology
2.1. Hydrodynamic Model
2.2. Solute Tansport Model
2.3. Geometric Setups
2.4. Computational Setups
3. Results and Discussion
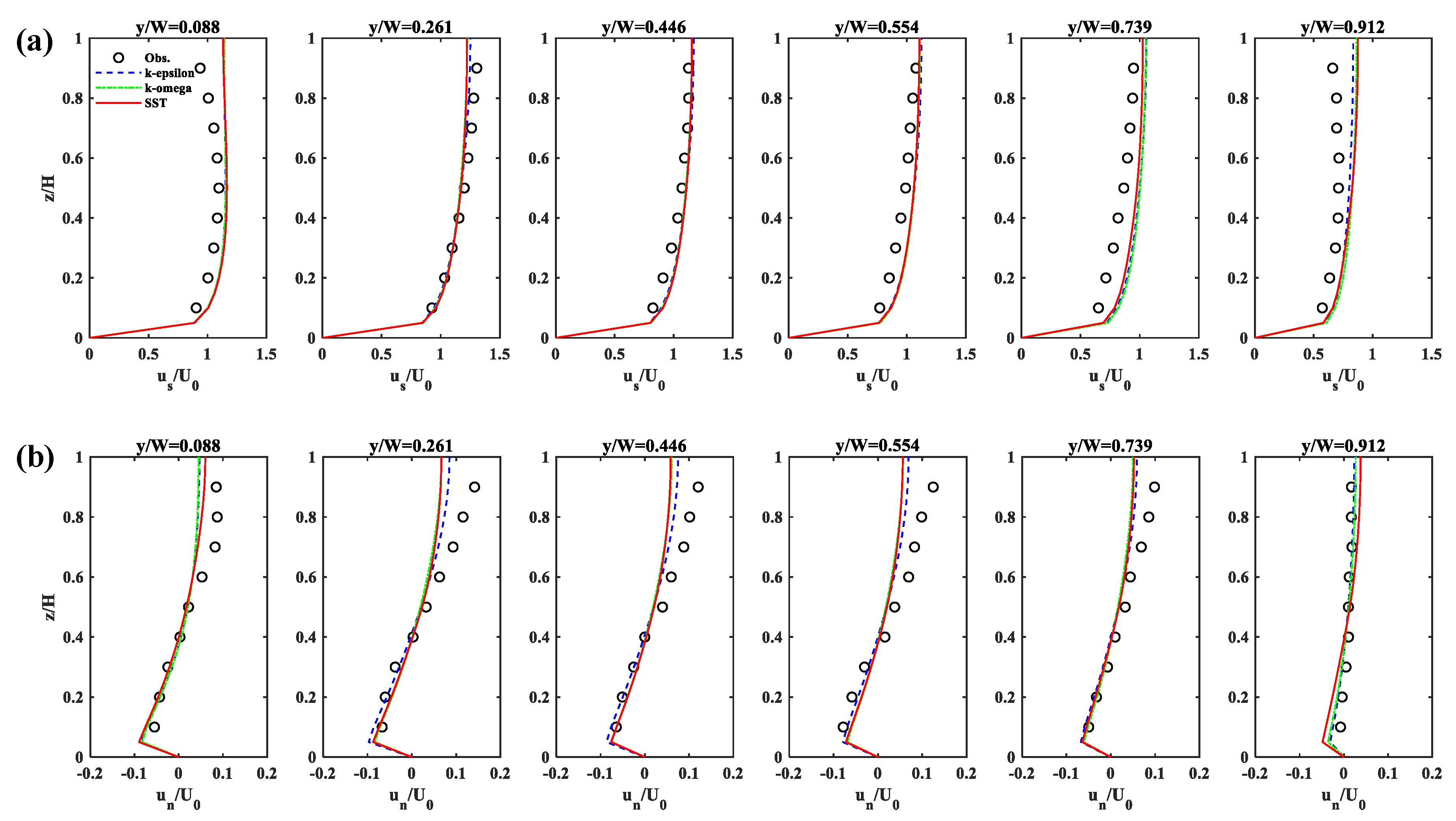
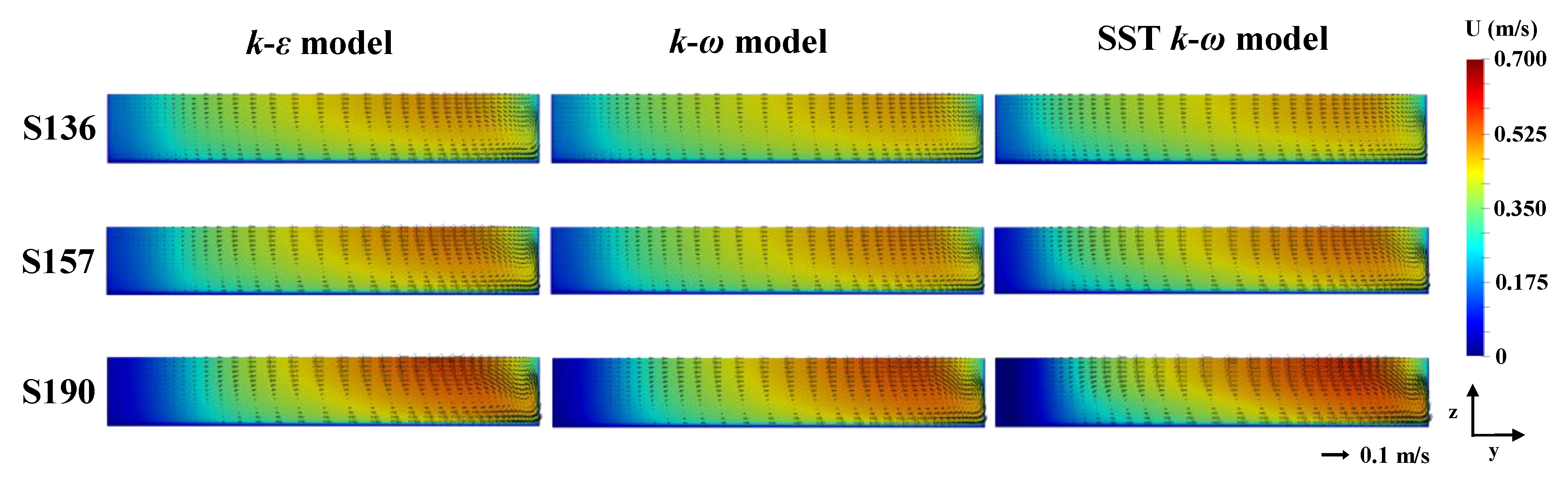
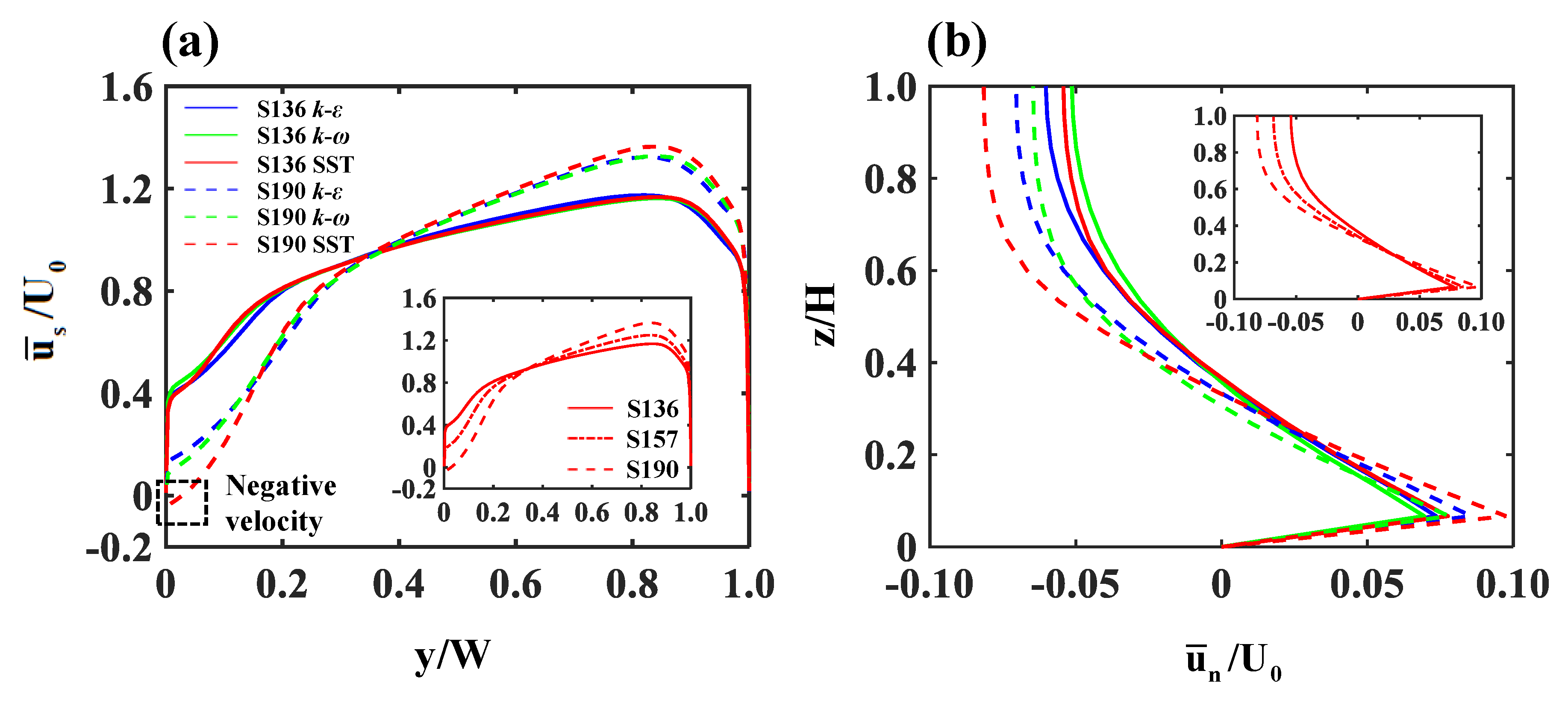
3.1. Velocity Distributions
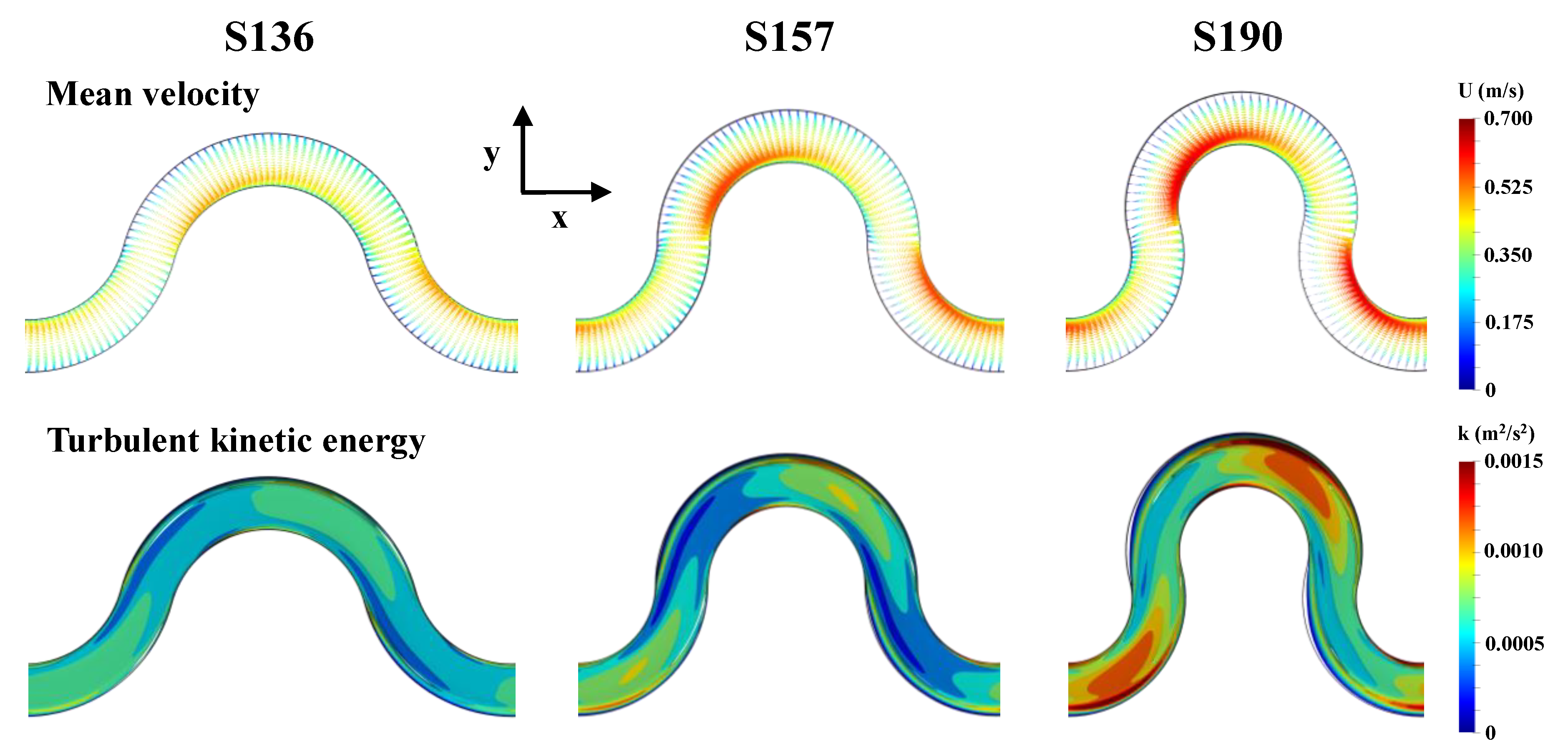
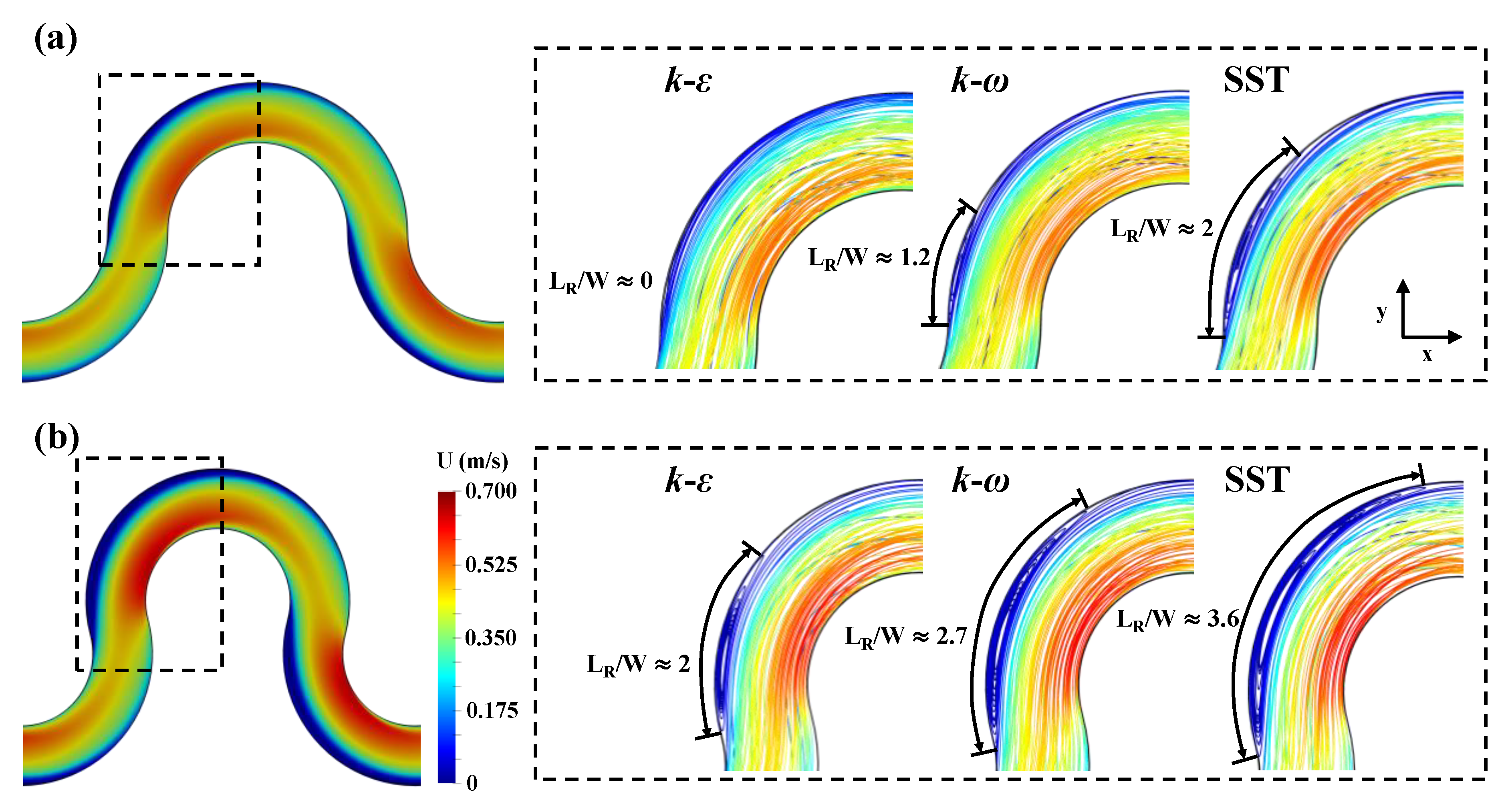
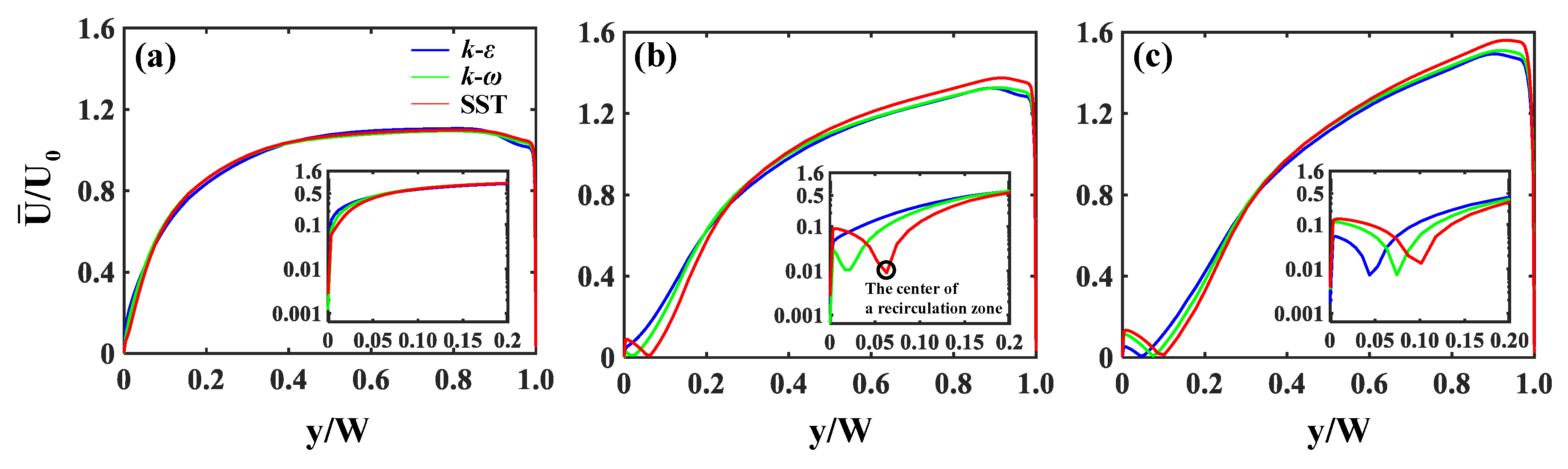
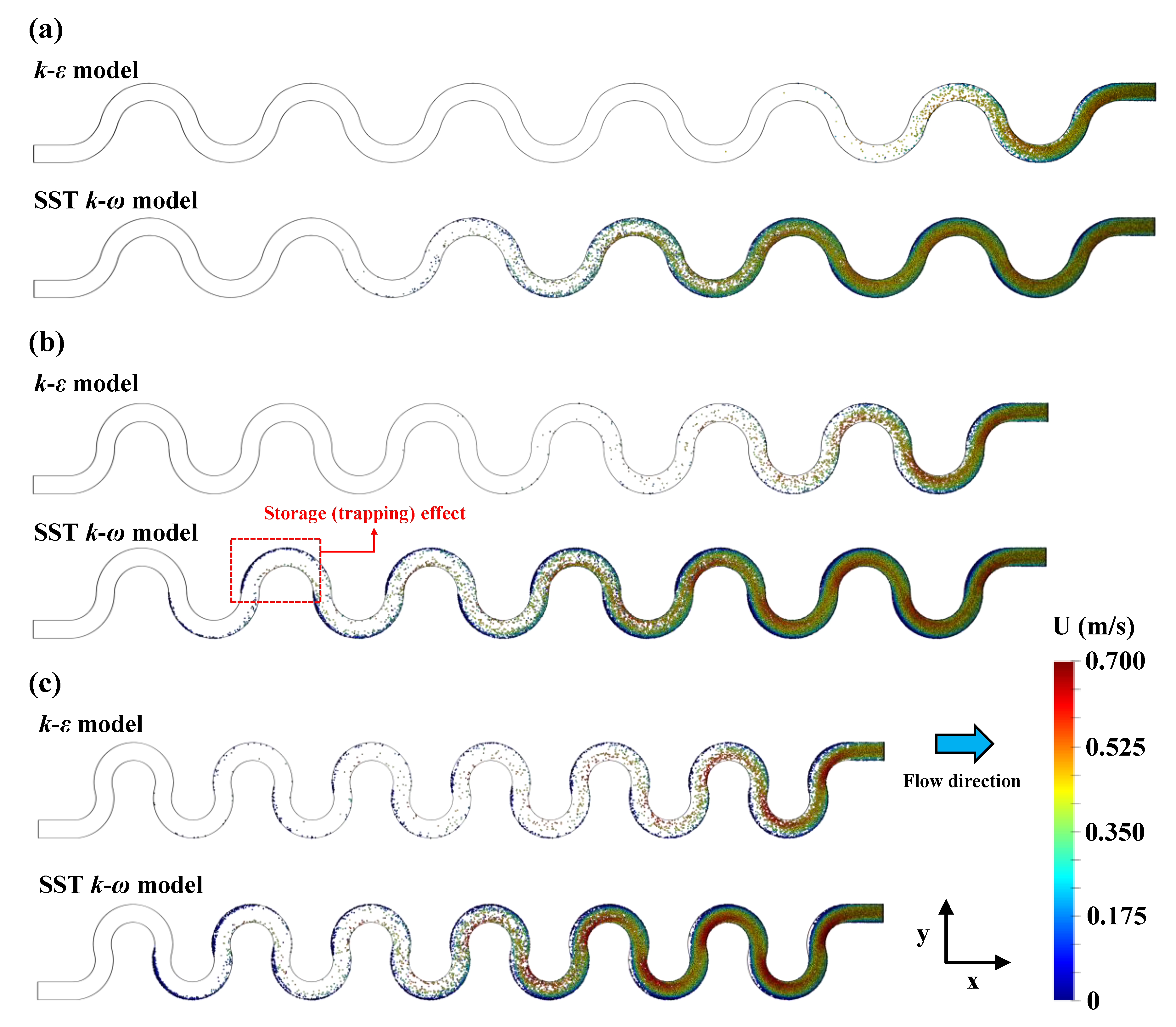
3.2. Separated Recirculating Flows
3.3. Solute Transport and Dispersion
4. Conclusions
- The strong transverse gradients of mean velocity simulated with increasing sinuosity induce the flow separation along the outer bank for channel sinuosity 1.57 and 1.90 because of the adverse pressure gradients. The size of the flow separation increases as sinuosity increases.
- The onset and size of the flow separation are significantly affected by the turbulence models. Notably, the model fails to predict the emergence of the flow separation or unpredicts its reattachment length and width by underestimating the velocity gradients.
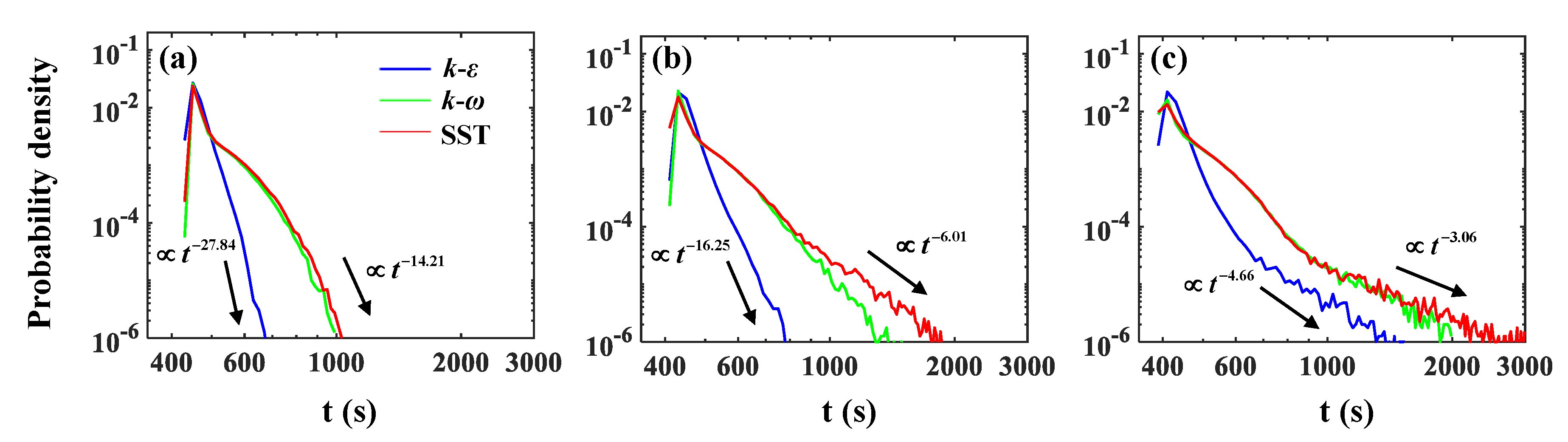
- The flow separation with vigorous recirculating flows acts as a storage (trapping) zone of solute particles, and the trapping effects increase solute residence times. Here, the model underestimates the power-law tailing of BTCs since it undervalues the effects of the separated flow recirculation compared to the other turbulence models.
- The SST model yields heavier-tailed BTCs characterized by flatter power-law slopes and larger truncation times as it reproduces larger and faster recirculating flows than the and models.
Author Contributions
Funding
Conflicts of Interest
References
- Johannesson, H.; Parker, G. Secondary flow in mildly sinuous channel. J. Hydraul. Eng. 1989, 115, 289–308. [Google Scholar] [CrossRef]
- Blanckaert, K.; de Vriend, H.J. Nonlinear modeling of mean flow redistribution in curved open channels. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Marion, A.; Zaramella, M. Effects of velocity gradients and secondary flow on the dispersion of solutes in a meandering channel. J. Hydraul. Eng. 2006, 132, 1295–1302. [Google Scholar] [CrossRef]
- Boxall, J.B.; Guymer, I. Analysis and prediction of transverse mixing coefficients in natural channels. J. Hydraul. Eng. 2003, 129, 129–139. [Google Scholar] [CrossRef]
- Baek, K.O.; Seo, I.W.; Jeong, S.J. Evaluation of dispersion coefficients in meandering channels from transient tracer tests. J. Hydraul. Eng. 2006, 132, 1021–1032. [Google Scholar] [CrossRef]
- Davis, P.M.; Atkinson, T.C.; Wigley, T.M.L. Longitudinal dispersion in natural channels: 2. The roles of shear flow dispersion and dead zones in the River Severn, UK. Hydrol. Earth Syst. Sci. 2000, 4, 355–371. [Google Scholar] [CrossRef]
- Park, I.; Seo, I.W. Modeling non-Fickian pollutant mixing in open channel flows using two-dimensional particle dispersion model. Adv. Water Resour. 2018, 111, 105–120. [Google Scholar] [CrossRef]
- Rameshwaran, P.; Nade, P.S. Three-dimensional modelling of free surface variation in a meandering channel. J. Hydraul. Res. 2004, 42, 603–615. [Google Scholar] [CrossRef]
- Wormleaton, P.R.; Ewunetu, M. Three-dimensional k-ε numerical modelling of overbank flow in a mobile bed meandering channel with floodplains of different depth, roughness and planform. J. Hydraul. Res. 2006, 44, 18–32. [Google Scholar] [CrossRef]
- Fischer-Antze, T.; Ruther, N.; Olsen, N.R.B.; Gutknecht, D. Three-dimensional (3D) modeling of non-uniform sediment transport in a channel bend with unsteady flow. J. Hydraul. Res. 2009, 47, 670–675. [Google Scholar] [CrossRef]
- Rüther, N.; Olsen, N.R.B. Three-dimensional modeling of sediment transport in a narrow 90° channel bend. J. Hydraul. Eng. 2005, 131, 917–920. [Google Scholar] [CrossRef]
- Stoesser, T.; Ruether, N.; Olsen, N.R.B. Calculation of primary and secondary flow and boundary shear stresses in a meandering channel. Adv. Water Resour. 2010, 33, 158–170. [Google Scholar] [CrossRef]
- Van Balen, W.; Blanckaert, K.; Uijttewaal, W.S.J. Analysis of the role of turbulence in curved open-channel flow at different water depths by means of experiments, LES and RANS. J. Turbul. 2010, 11, 1–34. [Google Scholar] [CrossRef]
- Farhadi, A.; Sindelar, C.; Tritthart, M.; Glas, M.; Blanckaert, K.; Habersack, H. An investigation on the outer bank cell of secondary flow in channel bends. J. Hydro-Environ. Res. 2018, 18, 1–11. [Google Scholar] [CrossRef]
- Russell, P.; Vennell, R. High resolution observations of an outer-bank cell of secondary circulation in a natural river bend. J. Hydraul. Res. 2019, 145, 04019012. [Google Scholar] [CrossRef]
- Demuren, A.O.; Rodi, W. Calculation of flow and pollutant dispersion in meandering channels. J. Fluid Mech. 1986, 172, 63–92. [Google Scholar] [CrossRef]
- Ye, J.; McCorquodale, J.A. Simulation of curved open channel flows by 3D hydrodynamic model. J. Hydraul. Eng. 1998, 124, 687–698. [Google Scholar] [CrossRef]
- Ferguson, R.I.; Parsons, D.R.; Lane, S.N.; Hardy, R.J. Flow in meander bends with recirculation at the inner bank. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Abad, J.D.; Frias, C.E.; Buscaglia, G.C.; Garcia, M.H. Modulation of the flow structure by progressive bedforms in the Kinoshita meandering channel. Earth Surf. Process. Landf. 2013, 38, 1612–1622. [Google Scholar] [CrossRef]
- Rameshwaran, P.; Naden, P.; Wilson, C.A.; Malki, R.; Shukla, D.R.; Shiono, K. Inter-comparison and validation of computational fluid dynamics codes in two-stage meandering channel flows. Appl. Math. Model. 2013, 37, 8652–8672. [Google Scholar] [CrossRef][Green Version]
- Argyropoulos, C.D.; Markatos, N.C. Recent advances on the numerical modelling of turbulent flows. Appl. Math. Model. 2015, 39, 693–732. [Google Scholar] [CrossRef]
- Wilcox, D.C. Formulation of the k-ω turbulence model revisited. AIAAJ J. 2008, 46, 2823–2838. [Google Scholar] [CrossRef]
- El-Behery, S.M.; Hamed, M.H. A comparative study of turbulence models performance for separating flow in a planar asymmetric diffuser. Comput. Fluids 2011, 44, 248–257. [Google Scholar] [CrossRef]
- Khosronejad, A.; Rennie, C.D.; Salehi Neyshabouri, S.A.A.; Townsend, R.D. 3D numerical modeling of flow and sediment transport in laboratory channel bends. J. Hydraul. Eng. 2007, 133, 1123–1134. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Sparrow, E.M.; Abraham, J.P.; Minkowycz, W.J. Flow separation in a diverging conical duct: Effect of Reynolds number and divergence angle. Int. J. Heat Mass Transf. 2009, 52, 3079–3083. [Google Scholar] [CrossRef]
- Luo, H.; Fytanidis, D.K.; Schmidt, A.R.; García, M.H. Comparative 1D and 3D numerical investigation of open-channel junction flows and energy losses. Adv. Water Resour. 2018, 117, 120–139. [Google Scholar] [CrossRef]
- Nguyen, T.H.T.; Ahn, J.; Park, S.W. Numerical and physical investigation of the performance of turbulence modeling schemes around a scour hole downstream of a fixed bed protection. Water 2018, 10, 103. [Google Scholar] [CrossRef]
- Khosronejad, A.; Hansen, A.T.; Kozarek, J.L.; Guentzel, K.; Hondzo, M.; Guala, M.; Wilcock, P.R.; Finlay, J.C. Large eddy simulation of turbulence and solute transport in a forested headwater stream. J. Geophys. Res. Earth Surf. 2016, 121, 146–167. [Google Scholar] [CrossRef]
- Kim, J.S.; Baek, D.; Seo, I.W.; Shin, J. Retrieving shallow stream bathymetry from UAV-assisted RGB imagery using a geospatial regression method. Geomorphology 2019, 341, 102–114. [Google Scholar] [CrossRef]
- Blanckaert, K. Topographic steering, flow recirculation, velocity redistribution, and bed topography in sharp meander bends. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Blanckaert, K. Hydrodynamic processes in sharp meander bends and their morphological implications. J. Geophys. Res. Earth Surf. 2011, 116. [Google Scholar] [CrossRef]
- Blanckaert, K.; Kleinhans, M.G.; McLelland, S.J.; Uijttewaal, W.S.; Murphy, B.J.; van de Kruijs, A.; Parsons, D.R.; Chen, Q. Flow separation at the inner (convex) and outer (concave) banks of constant-width and widening open-channel bends. Earth Surf. Process. Landf. 2013, 38, 696–716. [Google Scholar] [CrossRef]
- Jackson, T.R.; Haggerty, R.; Apte, S.V.; Coleman, A.; Drost, K.J. Defining and measuring the mean residence time of lateral surface transient storage zones in small streams. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Sandoval, J.; Mignot, E.; Mao, L.; Pastén, P.; Bolster, D.; Escauriaza, C. Field numerical investigation of transport mechanisms in a surface storage zone. J. Geophys. Res. Earth Surf. 2019, 124, 938–959. [Google Scholar] [CrossRef]
- Wilson, C.A.M.E.; Guymer, I.; Boxall, J.B.; Olsen, N.R.B. Three-dimensional numerical simulation of solute transport in a meandering self-formed river channel. J. Hydraul. Res. 2007, 45, 610–616. [Google Scholar] [CrossRef]
- Zhang, M.L.; Li, C.W.; Shen, Y.M. A 3D non-linear k-ε turbulent model for prediction of flow and mass transport in channel with vegetation. Appl. Math. Model. 2010, 34, 1021–1031. [Google Scholar] [CrossRef]
- Liu, X.; García, M.H. Three-dimensional numerical model with free water surface and mesh deformation for local sediment scour. J. Waterw. Port Coast. Ocean Eng. 2008, 134, 203–217. [Google Scholar] [CrossRef]
- Bayon-Barrachina, A.; Lopez-Jimenez, P.A. Numerical analysis of hydraulic jumps using OpenFOAM. J. Hydroinform. 2015, 17, 662–678. [Google Scholar] [CrossRef]
- Bayon, A.; Valero, D.; García-Bartual, R.; Vallés-Morán, F.J. Performance assessment of OpenFOAM and FLOW-3D in the numerical modeling of a low Reynolds number hydraulic jump. Environ. Model. Softw. 2016, 80, 322–335. [Google Scholar] [CrossRef]
- Hromadka, T.V., II; Rao, P. Examination of computational precision versus modeling complexity for open channel flow with hydraulic jump. J. Water Resour. Prot. 2019, 11, 1233–1244. [Google Scholar]
- Wang, Y.; Politano, M.; Laughery, R.; Weber, L. Model development in OpenFOAM to predict spillway jet regimes. J. Appl. Water Eng. Res. 2015, 3, 80–94. [Google Scholar] [CrossRef]
- Duguay, J.M.; Lacey, R.W.J.; Gaucher, J. A case study of a pool and weir fishway modeled with OpenFOAM and FLOW-3D. Ecol. Model. 2017, 103, 31–42. [Google Scholar] [CrossRef]
- Bayon, A.; Toro, J.P.; Bombardelli, F.A.; Matos, J.; López-Jiménez, P.A. Influence of VOF technique, turbulence model and discretization scheme on the numerical simulation of the non-aerated, skimming flow in stepped spillways. J. Hydro-Environ. Res. 2018, 19, 137–149. [Google Scholar] [CrossRef]
- Kim, J.S.; Kang, P.K. Anomalous transport through free-flow-porous media interface: Pore-scale simulation and predictive modeling. Adv. Water Resour. 2020, 135, 103467. [Google Scholar] [CrossRef]
- Jones, W.P.; Launder, B.E. The prediction of laminarization with a two-equation model of turbulence. Int. Heat Mass Transfer. 1972, 15, 301–314. [Google Scholar] [CrossRef]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000; pp. 373–384. [Google Scholar]
- Zeng, J.; Constantinescu, G.; Weber, L. A 3D non-hydrostatic model to predict flow and sediment transport in loose-bed channel bends. J. Hydraul. Res. 2008, 46, 56–372. [Google Scholar] [CrossRef]
- Kang, S.; Lightbody, A.; Hill, C.; Sotiropoulos, F. High-resolution numerical simulation of turbulence in natural waterways. Adv. Water Resour. 2011, 34, 98–113. [Google Scholar] [CrossRef]
- Kang, S.; Sotiropoulos, F. Numerical modeling of 3D turbulent free surface flow in natural waterways. Adv. Water Resour. 2012, 40, 23–36. [Google Scholar] [CrossRef]
- Gosman, A.D.; Loannides, E. Aspects of computer simulation of liquid-fueled combustors. J. Energy 1983, 7, 482–490. [Google Scholar] [CrossRef]
- Shams, M.; Ahmadi, G.; Smith, D.H. Computational modeling of flow and sediment transport and deposition in meandering rivers. Adv. Water Resour. 2002, 25, 689–699. [Google Scholar] [CrossRef]
- Dehbi, A. Turbulent particle dispersion in arbitrary wall-bounded geometries: A coupled CFD-Langevin-equation based approach. Int. J. Multiph. Flow 2008, 34, 819–828. [Google Scholar] [CrossRef]
- Rybalko, M.; Loth, E.; Lankford, D.A. Lagrangian particle random walk model for hybrid RANS/LES turbulent flows. Powder Technol. 2012, 221, 105–113. [Google Scholar] [CrossRef]
- Hey, R.D. Geometry of river meanders. Nature 1976, 262, 482. [Google Scholar] [CrossRef]
- Chang, Y.C. Lateral mixing in meandering channels. In River Meandering; ASCE: Reston, VA, USA, 1971; pp. 598–610. [Google Scholar]
- Hodskinson, A.; Ferguson, R.I. Numerical modelling of separated flow in river bends: Model testing and experimental investigation of geometric controls on the extent of flow separation at the concave bank. Hydrol. Process. 1998, 12, 1323–1338. [Google Scholar] [CrossRef]
- Vinuesa, R.; Schlatter, P.; Nagib, H.M. Secondary flow in turbulent ducts with increasing aspect ratio. Phys. Rev. Fluids 2018, 3, 054606. [Google Scholar] [CrossRef]
- Abad, J.D.; Garcia, M.H. Experiments in a high-amplitude Kinoshita meandering channel: 1. Implications ooi:f bend orientation on mean and turbulent flow structure. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Hickin, E.J. Mean flow structure in meanders of the Squamish River, British Columbia. Can. J. Earth Sci. 1978, 15, 1833–1849. [Google Scholar] [CrossRef]
- Aubeneau, A.F.; Hanrahan, B.; Bolster, D.; Tank, J.L. Substrate size and heterogeneity control anomalous transport in small streams. Geophys. Res. Lett. 2014, 41, 8335–8341. [Google Scholar] [CrossRef]
- Drummond, J.D.; Covino, T.P.; Aubeneau, A.F.; Leong, D.; Patil, S.; Schumer, R.; Packman, A.I. Effects of solute breakthrough curve tail truncation on residence time estimates: A synthesis of solute tracer injection studies. J. Geophys. Res. Biogeosci. 2012, 117. [Google Scholar] [CrossRef]
- Runkel, R.L.; Chapra, S.C. An efficient numerical solution of the transient storage equations for solute transport in small streams. Water Resour. Res. 1993, 29, 211–215. [Google Scholar] [CrossRef]
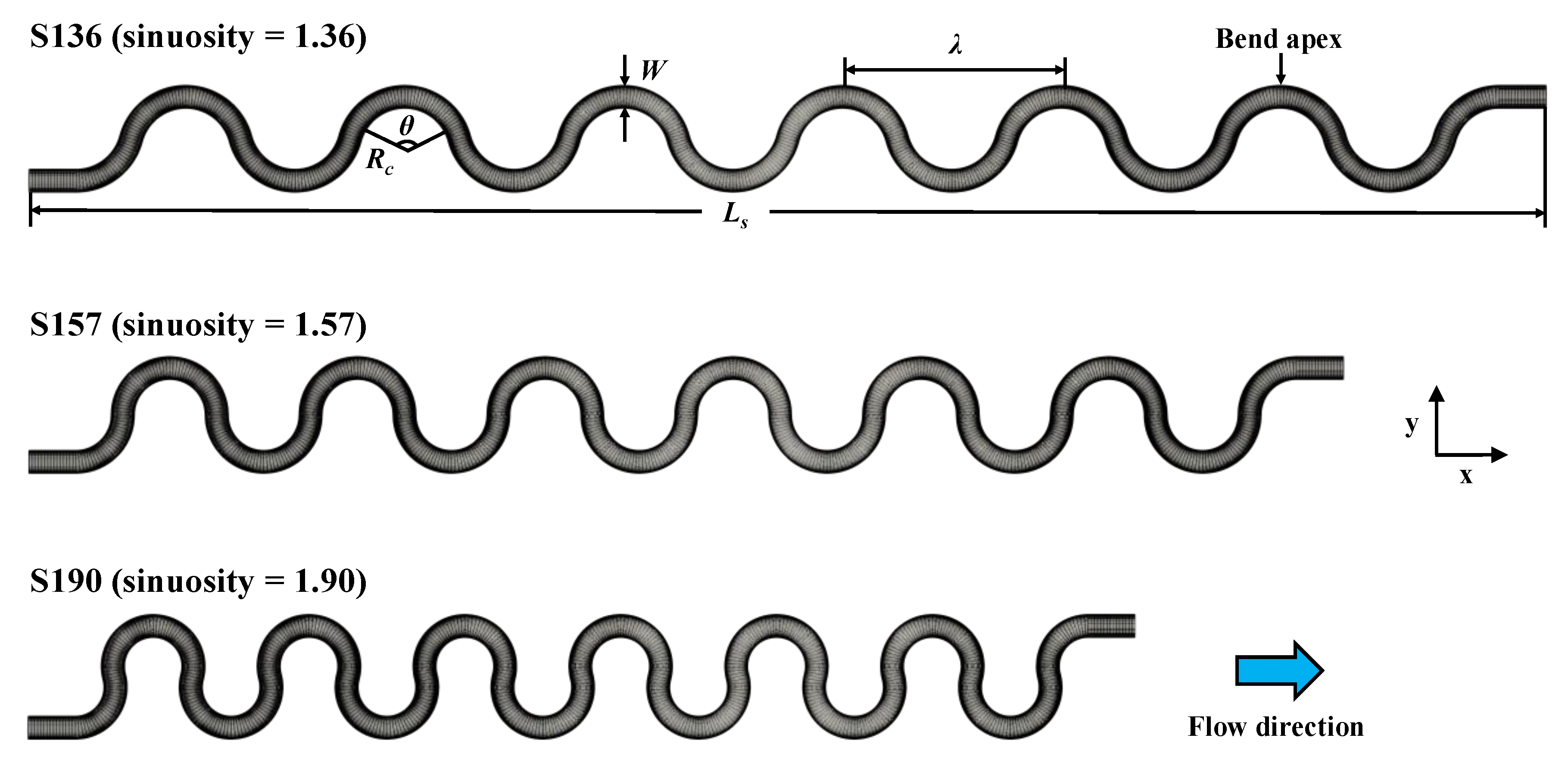

| Case | (°) | (m) | ||||
|---|---|---|---|---|---|---|
| S136 | 150 | 150 | 21.70 | 5.62 | 2.40 | 1.36 |
| S157 | 131 | 180 | 18.72 | 4.68 | 2.00 | 1.57 |
| S190 | 108 | 210 | 15.50 | 4.00 | 1.71 | 1.90 |
| Model | S136 | S157 | S190 | |||
|---|---|---|---|---|---|---|
| Tail Power-Law Slope | Truncation Time | Tail Power-Law Slope | Truncation Time | Tail Power-Law Slope | Truncation Time | |
| −27.84 | 1.49 | −16.25 | 1.81 | −4.66 | 3.54 | |
| −15.28 | 2.20 | −7.68 | 3.19 | −3.77 | 4.85 | |
| SST | −14.21 | 2.29 | −6.01 | 4.30 | −3.06 | 6.32 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, J.S.; Baek, D.; Park, I. Evaluating the Impact of Turbulence Closure Models on Solute Transport Simulations in Meandering Open Channels. Appl. Sci. 2020, 10, 2769. https://doi.org/10.3390/app10082769
Kim JS, Baek D, Park I. Evaluating the Impact of Turbulence Closure Models on Solute Transport Simulations in Meandering Open Channels. Applied Sciences. 2020; 10(8):2769. https://doi.org/10.3390/app10082769
Chicago/Turabian StyleKim, Jun Song, Donghae Baek, and Inhwan Park. 2020. "Evaluating the Impact of Turbulence Closure Models on Solute Transport Simulations in Meandering Open Channels" Applied Sciences 10, no. 8: 2769. https://doi.org/10.3390/app10082769
APA StyleKim, J. S., Baek, D., & Park, I. (2020). Evaluating the Impact of Turbulence Closure Models on Solute Transport Simulations in Meandering Open Channels. Applied Sciences, 10(8), 2769. https://doi.org/10.3390/app10082769





