DDTree: A Hybrid Deep Learning Model for Real-Time Waterway Depth Prediction and Smart Navigation
Abstract
1. Introduction
2. Related Work
3. Domain Analysis and Definition of Conceptual Model
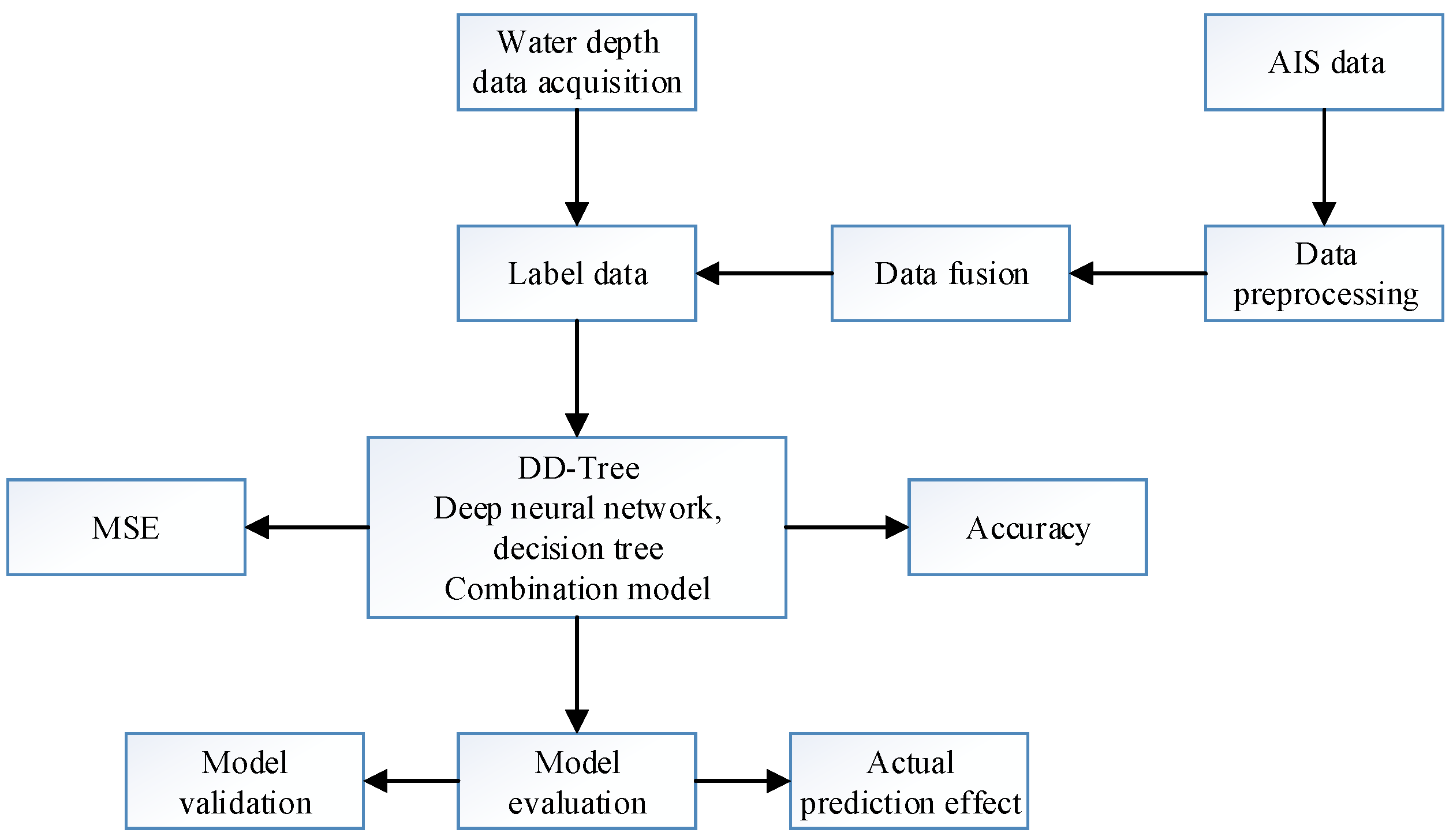
3.1. Data
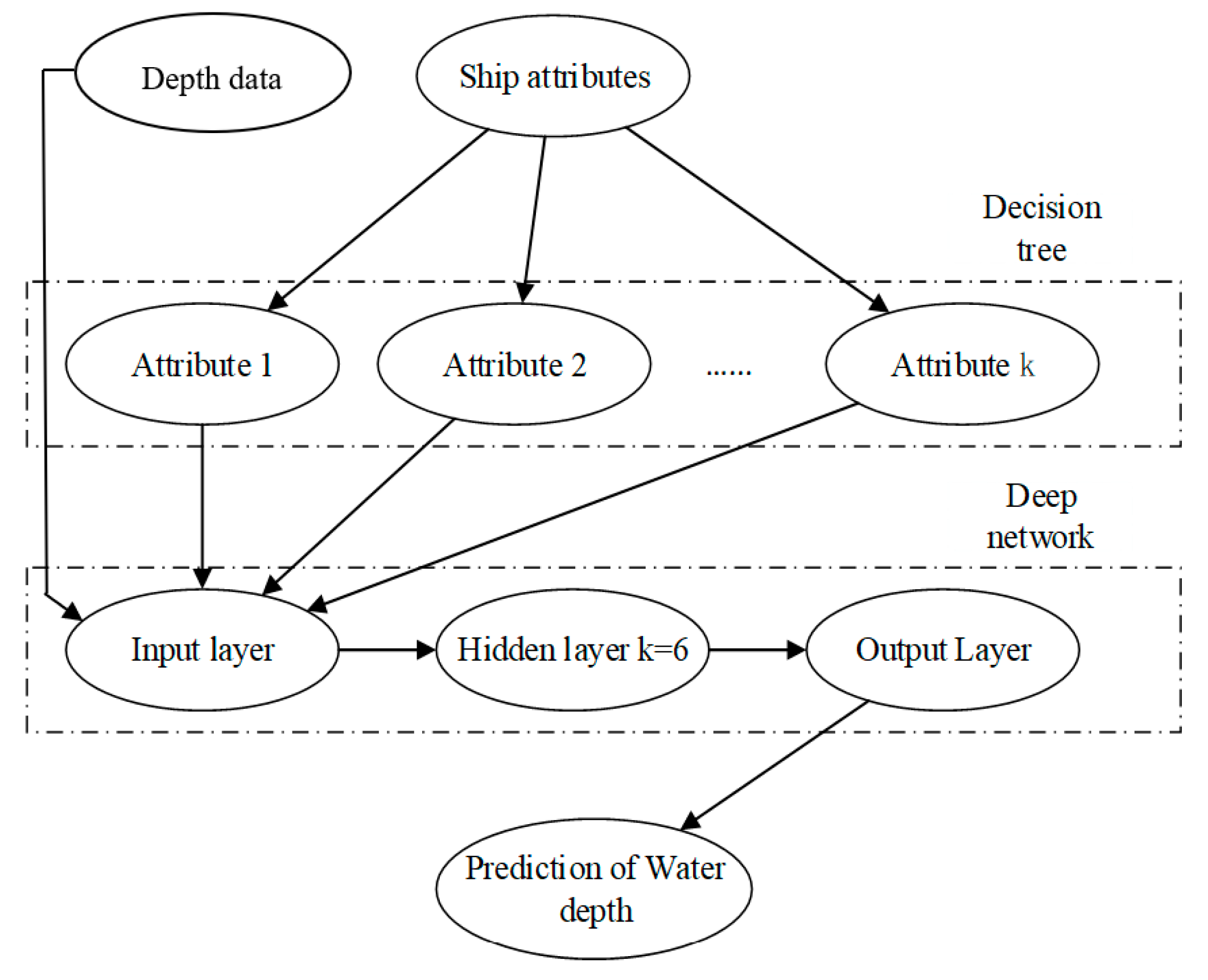
3.2. Conceptual Model
3.3. Decision Tree
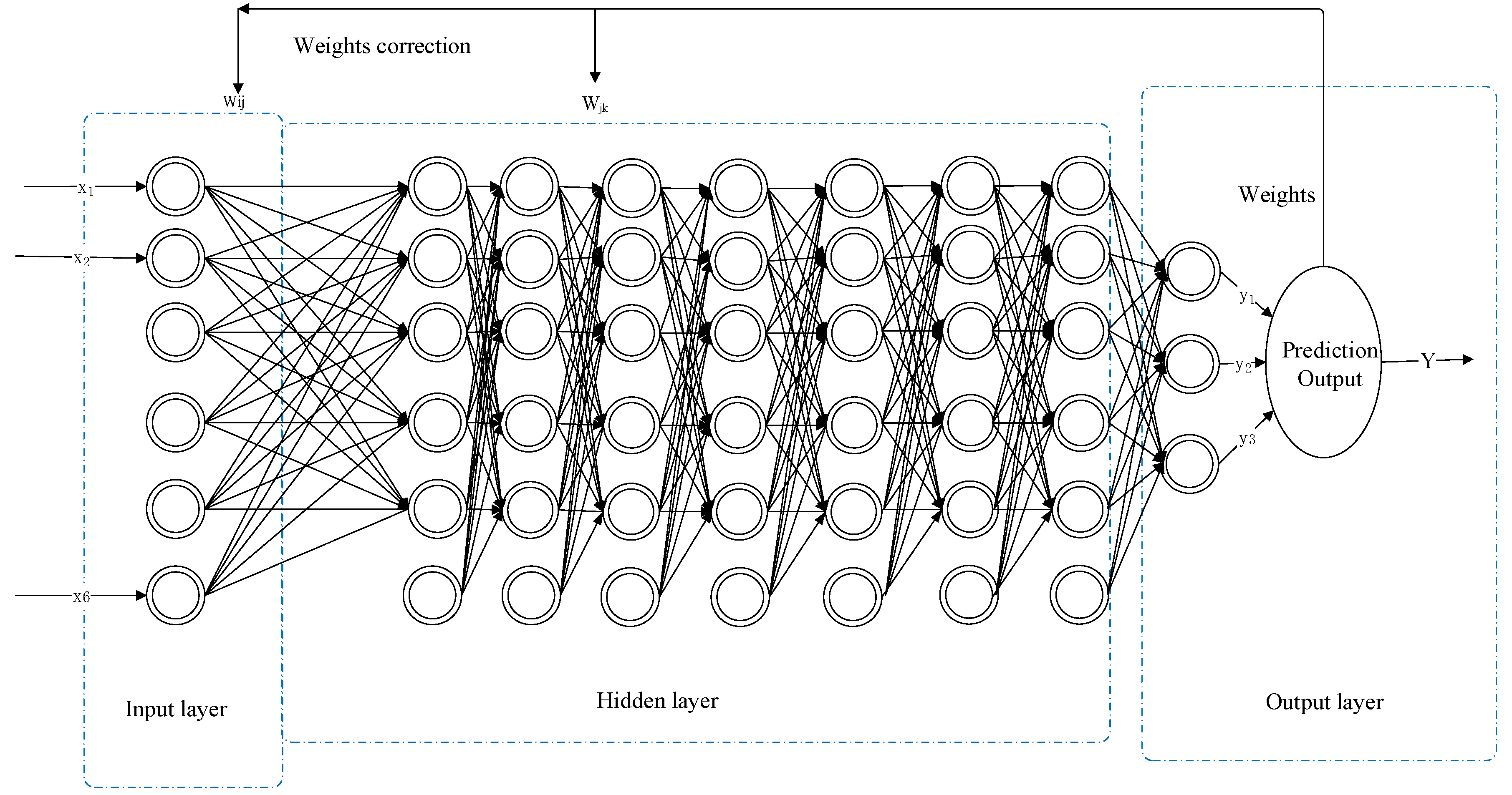
3.4. Deep Neural Network
4. Performance Analysis
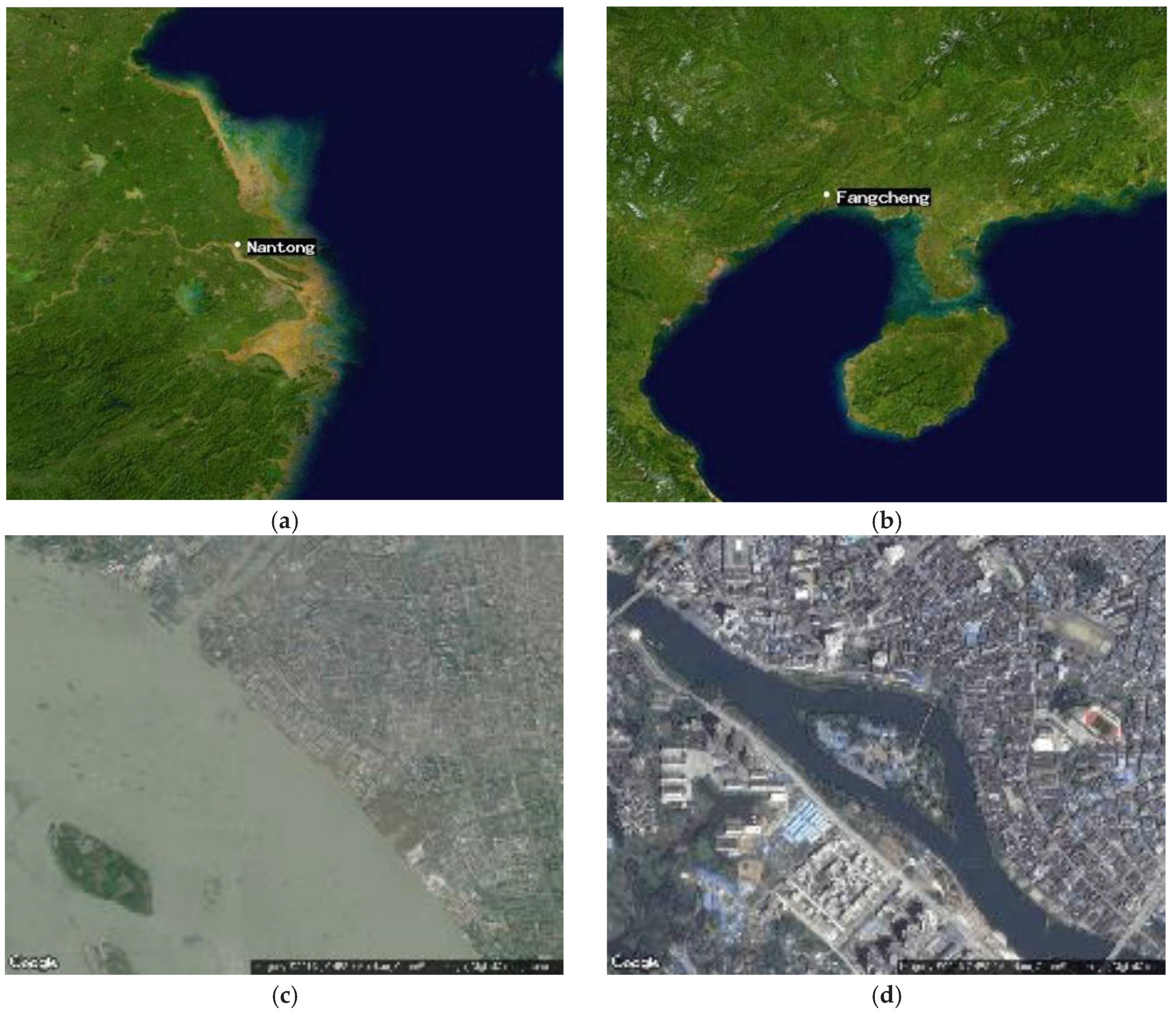
4.1. Experimental Data
4.2. Experimental Setting
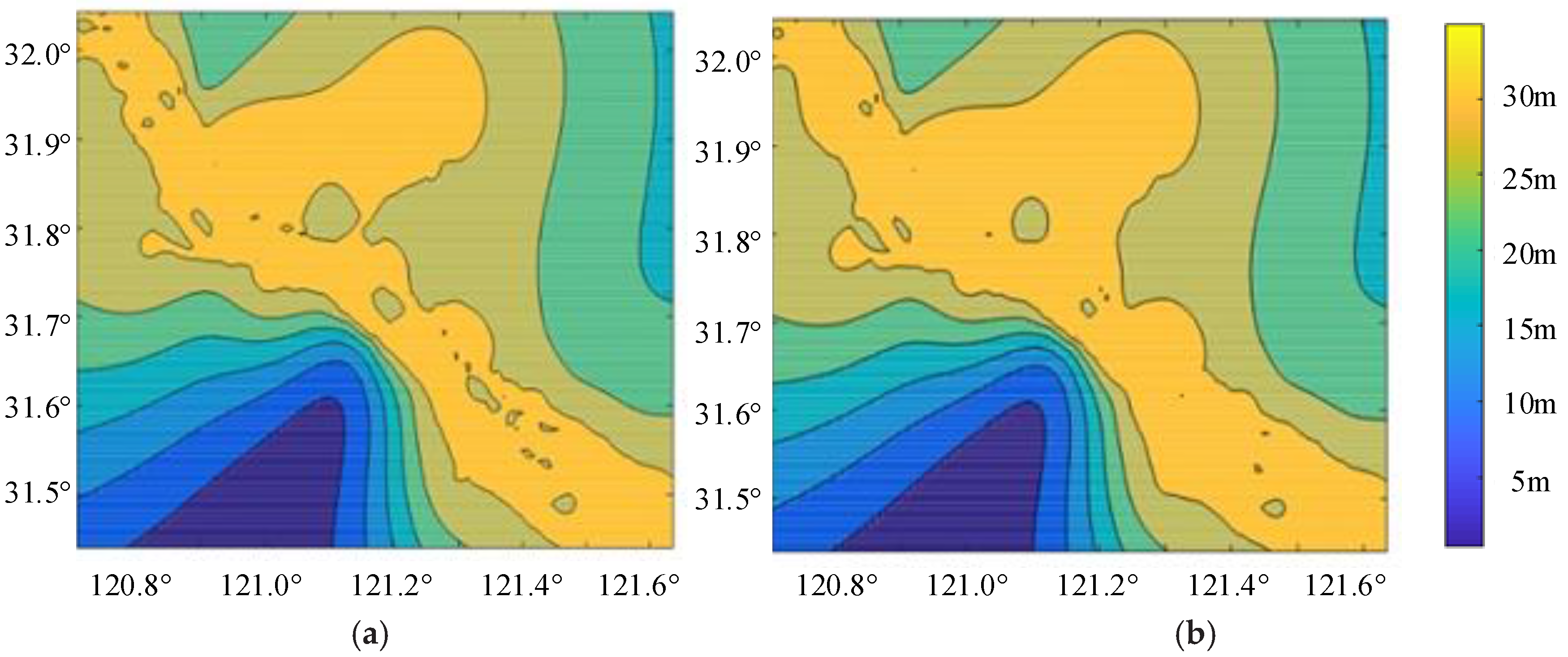
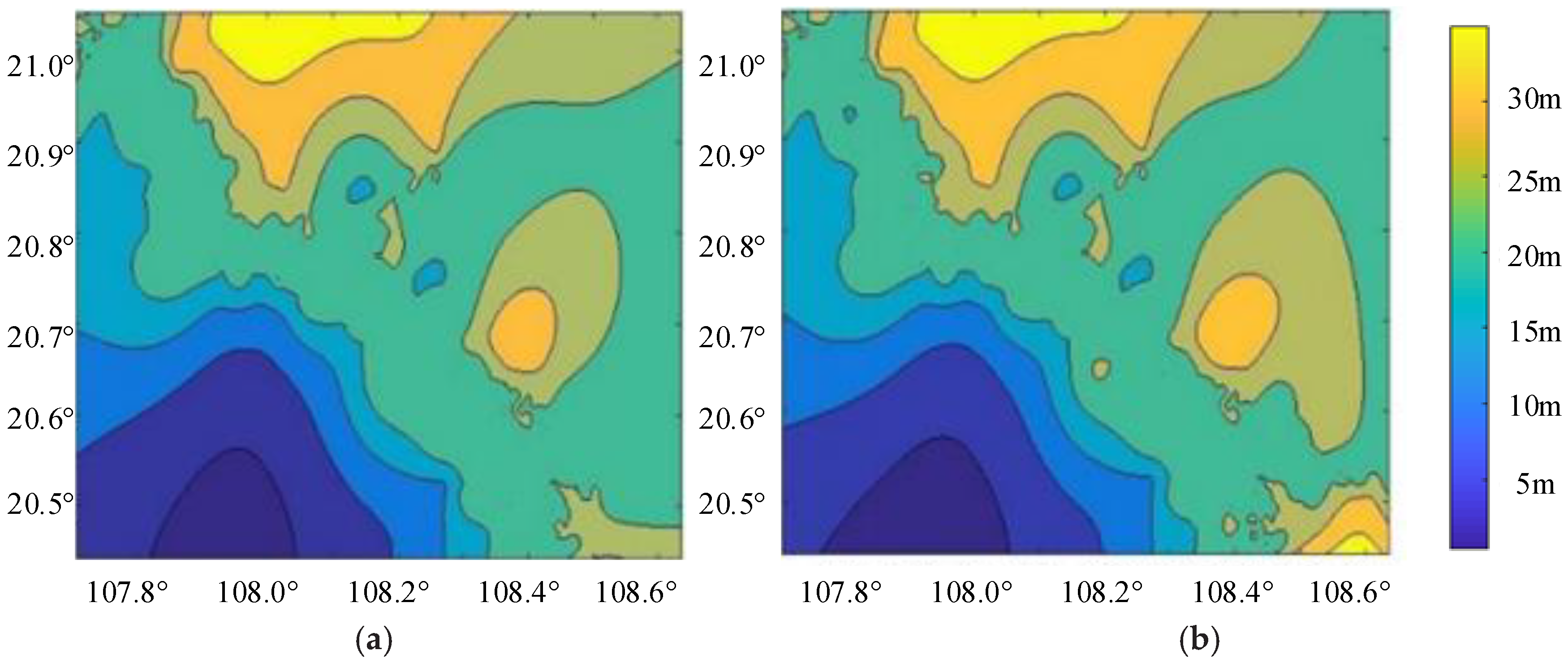
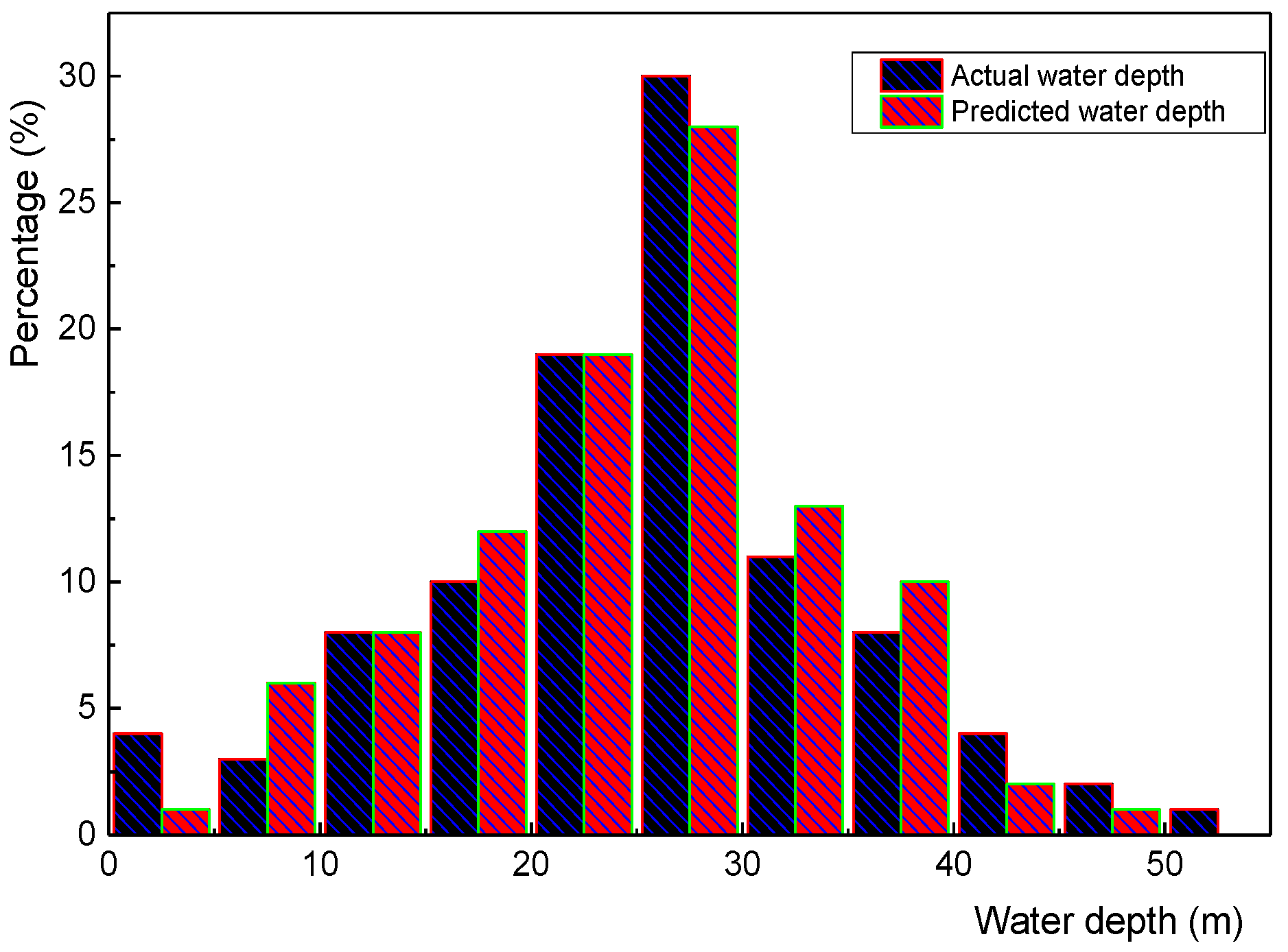
4.3. Prediction of Water Depth in Nantong Port
4.4. Predicting of Water Depth in Fangcheng Port
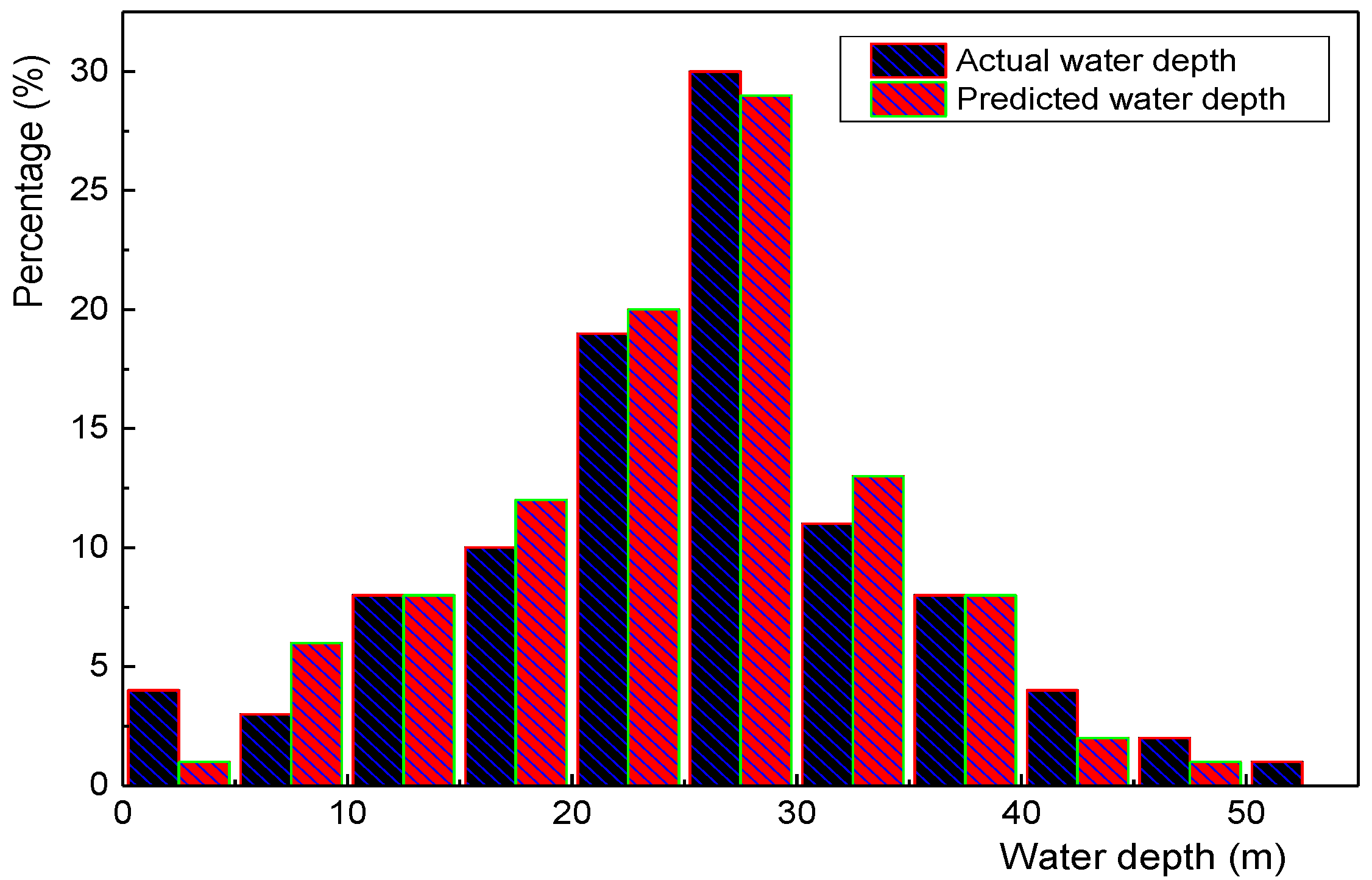
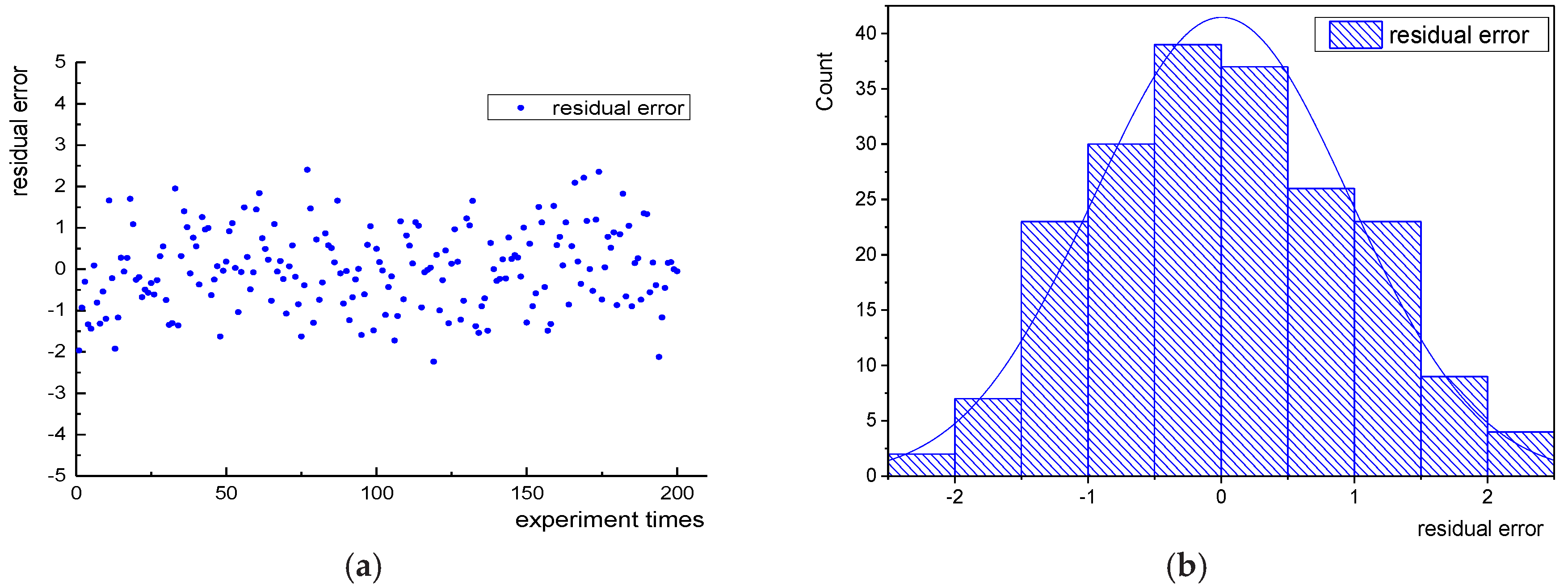
4.5. Analysis of Results Using Residual Analys
5. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- UNCTAD. Review of Maritime Transport 2018. In Technical Report UNCTAD/RMT/2018; United Nations Conference on Trade and Development: New York, NY, USA, 2019. [Google Scholar]
- Liu, C.; Mao, Q.; Chu, X.; Xie, S. An Improved A-Star Algorithm Considering Water Current, Traffic Separation and Berthing for Vessel Path Planning. Appl. Sci. 2019, 9, 1057. [Google Scholar] [CrossRef]
- Briggs, M.J.; Silver, A.L.; Kopp, P.J. Probabilistic model for predicting ship underkeel clearance: Field and laboratory validation. Coast. Eng. J. 2014, 56, 3–822. [Google Scholar] [CrossRef]
- Graziano, M.D.; Renga, A.; Moccia, A. Integration of Automatic Identification System (AIS) Data and Single-Channel Synthetic Aperture Radar (SAR) Images by SAR-Based Ship Velocity Estimation for Maritime Situational Awareness. Remote Sens. 2019, 11, 2196. [Google Scholar] [CrossRef]
- Guo, D.; Yang, Y.; Xiong, F. Statistics and Analysis of Maritime Traffic Accidents in Yangtze River and Accidents Prediction. In Proceedings of the 28th International Ocean and Polar Engineering Conference, Sapporo, Japan, 10–15 June 2018. [Google Scholar]
- Kamolov, A.; Park, S. An IoT-Based Ship Berthing Method Using a Set of Ultrasonic Sensors. Sensors 2019, 19, 5181. [Google Scholar] [CrossRef] [PubMed]
- He, W.; Li, Z.; Malekian, R.; Liu, X.; Duan, Z. An Internet of Things Approach for Extracting Featured Data Using AIS Database: An Application Based on the Viewpoint of Connected Ships. Symmetry 2017, 9, 186. [Google Scholar] [CrossRef]
- Al-Zaidi, R.; Woods, J.; Al-Khalidi, M.; Alheeti, K.M.A.; McDonald-Maier, K. Next generation marine data networks in an IoT environment. In Proceedings of the 2017 Second International Conference on Fog and Mobile Edge Computing (FMEC), Valencia, Spain, 8–11 May 2017; pp. 50–55. [Google Scholar] [CrossRef]
- Venckauskas, A.; Stuikys, V.; Damasevicius, R.; Jusas, N. Modelling of internet of things units for estimating security-energy-performance relationships for quality of service and environment awareness. Secur. Commun. Netw. 2016, 9, 3324–3339. [Google Scholar] [CrossRef]
- Capizzi, G.; Sciuto, G.L.; Woźniak, M.; Damaševičius, R. A clustering based system for automated oil spill detection by satellite remote sensing. In Proceedings of the 15th International Conference on Artificial Intelligence and Soft Computing, ICAISC 2016, Zakopane, Poland, 12–16 June 2016; pp. 613–623. [Google Scholar] [CrossRef]
- Tu, E.; Zhang, G.; Rachmawati, L.; Rajabally, E.; Huang, G.-B. Exploiting AIS data for intelligent maritime navigation: A comprehensive survey from data to methodology. IEEE Trans. Intell. Transport. Syst. 2018, 19, 1559–1582. [Google Scholar] [CrossRef]
- Su, H.; Liu, H.; Wu, Q. Prediction of Water Depth from Multispectral Satellite Imagery—The Regression Kriging Alternative. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2511–2515. [Google Scholar]
- Kang, C. A Differential Dynamic Positioning Algorithm Based on GPS/Beidou. Procedia Eng. 2016, 137, 590–598. [Google Scholar] [CrossRef]
- Maciuk, K. Advantages of combined GNSS processing involving a limited number of visible satellites. Sci. J. Sil. Univ. Technol. 2018, 98. [Google Scholar] [CrossRef]
- Chen, H. Travel-time approximation of acoustic ranging in GPS/Acoustic seafloor geodesy. Ocean Eng. 2018, 84, 133–144. [Google Scholar] [CrossRef]
- EL-Hattab, A.I. Influence of GPS antenna phase center variation on precise positioning. NRIAG J. Astron. Geophys. 2013, 2, 272–277. [Google Scholar] [CrossRef]
- Abdel-Hafez, M.F. On the GPS/IMU sensors’ noise estimation for enhanced navigation integrity, Mathematics and Computers in Simulation. Int. Assoc. Math. Comput. Simul. 2012, 86, 101–117. [Google Scholar] [CrossRef]
- Younis, B.A.; Sousa, V.; Meireles, I. Prediction of the Asymptotic Water Depth in Rough Compound Channels. J. Irrig. Drain. Eng. 2009, 135, 231–234. [Google Scholar] [CrossRef]
- Shiri, J. Wavelet and neuro-fuzzy conjunction model for predicting water table depth fluctuations. Hydrol. Res. 2012, 43, 286–300. [Google Scholar]
- Wang, Y.; Zhang, J.; Chen, X.; Chu, X.; Yan, X. A spatial–temporal forensic analysis for inland–water ship collisions using AIS data. Saf. Sci. 2013, 57, 187–202. [Google Scholar] [CrossRef]
- Vodas, M.; Pelekis, N.; Theodoridis, Y.; Ray, C.; Karkaletsis, V.; Petridis, S.; Miliou, A. Efficient AIS Data Processing for Environmentally Safe Shipping. Spoud. J. Econ. Bus. 2014, 63, 181–190. [Google Scholar]
- Li, S.; Chen, X.; Chen, L.; Chen, L.; Zhao, Y.; Sheng, T.; Bai, Y. Data Reception Analysis of the AIS on board the TianTuo-3 Satellite. J. Navig. 2017, 70, 761–774. [Google Scholar] [CrossRef]
- Mulyadi, Y.; Kobayashi, E.; Wakabayashi, N.; Pitana, T.; Wahyudi. Development of ship sinking frequency model over Subsea Pipeline for Madura Strait using AIS data. WMU J. Marit. Aff. 2014, 13, 43. [Google Scholar]
- Li, J.; Chu, X.; He, W.; Ma, F.; Malekian, R.; Li, Z. A Generalised Bayesian Inference Method for Maritime Surveillance Using Historical Data. Symmetry 2019, 11, 188. [Google Scholar] [CrossRef]
- Salmalian, K.; Soleimani, M. ANFIS and neural network for modeling and prediction of ship squat in shallow waters. Int. J. Math. Models Methods Appl. Sci. 2011, 5, 848–856. [Google Scholar]
- Niu, H.; Ozanich, E.; Gerstoft, P. Ship localization in Santa Barbara channel using machine learning classifiers. J. Acoust. Soc. Am. 2017, 142, EL455–EL460. [Google Scholar] [CrossRef] [PubMed]
- Bannari, A.; Kadhem, G. MBES-CARIS Data Validation for Bathymetric Mapping of Shallow Water in the Kingdom of Bahrain on the Arabian Gulf. Remote Sens. 2017, 9, 385. [Google Scholar] [CrossRef]
- Kim, K.; Lee, K.M. Deep Learning-Based Caution Area Traffic Prediction with Automatic Identification System Sensor Data. Sensors 2018, 18, 3172. [Google Scholar] [CrossRef]
- Jeong, M.; Lee, E.; Lee, M.; Jung, J. Multi-criteria route planning with risk contour map for smart navigation. Ocean Eng. 2019, 172, 72–85. [Google Scholar] [CrossRef]
- Rong, H.; Teixeira, A.P.; Guedes Soares, C. Data mining approach to shipping route characterization and anomaly detection based on AIS data. Ocean Eng. 2020, 198. [Google Scholar] [CrossRef]
- Xin, X.; Liu, K.; Yang, X.; Yuan, Z.; Zhang, J. A simulation model for ship navigation in the “Xiazhimen” waterway based on statistical analysis of AIS data. Ocean Eng. 2019, 180, 279–289. [Google Scholar] [CrossRef]
- Zhang, L.; Meng, Q.; Fwa, T.F. Big AIS data based spatial-temporal analyses of ship traffic in singapore port waters. Transp. Res. Part E Logist. Transp. Rev. 2019, 129, 287–304. [Google Scholar] [CrossRef]
- Yang, D.; Wu, L.; Wang, S.; Jia, H.; Li, K.X. How big data enriches maritime research–a critical review of automatic identification system (AIS) data applications. Transport. Rev. 2019, 39, 755–773. [Google Scholar] [CrossRef]
- D’Angelo, G.; Tipaldi, M.; Glielmo, L.; Rampone, S. Spacecraft autonomy modeled via Markov decision process and associative rule-based machine learning. In Proceedings of the 2017 IEEE International Workshop on Metrology for AeroSpace (MetroAeroSpace), Padua, Italy, 21–23 June 2017; pp. 324–329. [Google Scholar] [CrossRef]
- D’Angelo, G.; Pilla, R.; Tascini, C.; Rampone, S. A proposal for distinguishing between bacterial and viral meningitis using genetic programming and decision trees. Soft Comput. 2019, 23, 11775–11791. [Google Scholar] [CrossRef]
- Lee, E.; Mokashi, A.J.; Moon, S.Y.; Kim, G. The Maturity of Automatic Identification Systems (AIS) and Its Implications for Innovation. J. Mar. Sci. Eng. 2019, 7, 287. [Google Scholar] [CrossRef]
- Woźniak, M.; Połap, D. Hybrid neuro-heuristic methodology for simulation and control of dynamic systems over time interval. Neural Netw. 2017, 93, 45–56. [Google Scholar] [CrossRef] [PubMed]
- Połap, D.; Woźniak, M.; Damaševičius, R.; Maskeliūnas, R. Bio-inspired voice evaluation mechanism. Appl. Soft Comput. J. 2019, 80, 342–357. [Google Scholar] [CrossRef]
- Cagnini, H.E.L.; Barros, R.C.; Basgalupp, M.P. Estimation of distribution algorithms for decision tree induction. In Proceedings of the 2017 IEEE Congress on Evolutionary Computation, San Sebastian, Spain, 5–8 June 2017; pp. 2022–2029. [Google Scholar]
- Bottou, L. Large-scale machine learning with stochastic gradient descent. In Proceedings of the 19th International Conference on Computational Statistics COMPSTAT, Paris, France, 22–27 August 2010; pp. 177–186. [Google Scholar] [CrossRef]
- Połap, D.; Woźniak, M.; Wei, W.; Damaševičius, R. Multi-threaded learning control mechanism for neural networks. Future Gener. Comput. Syst. 2018, 87, 16–34. [Google Scholar] [CrossRef]
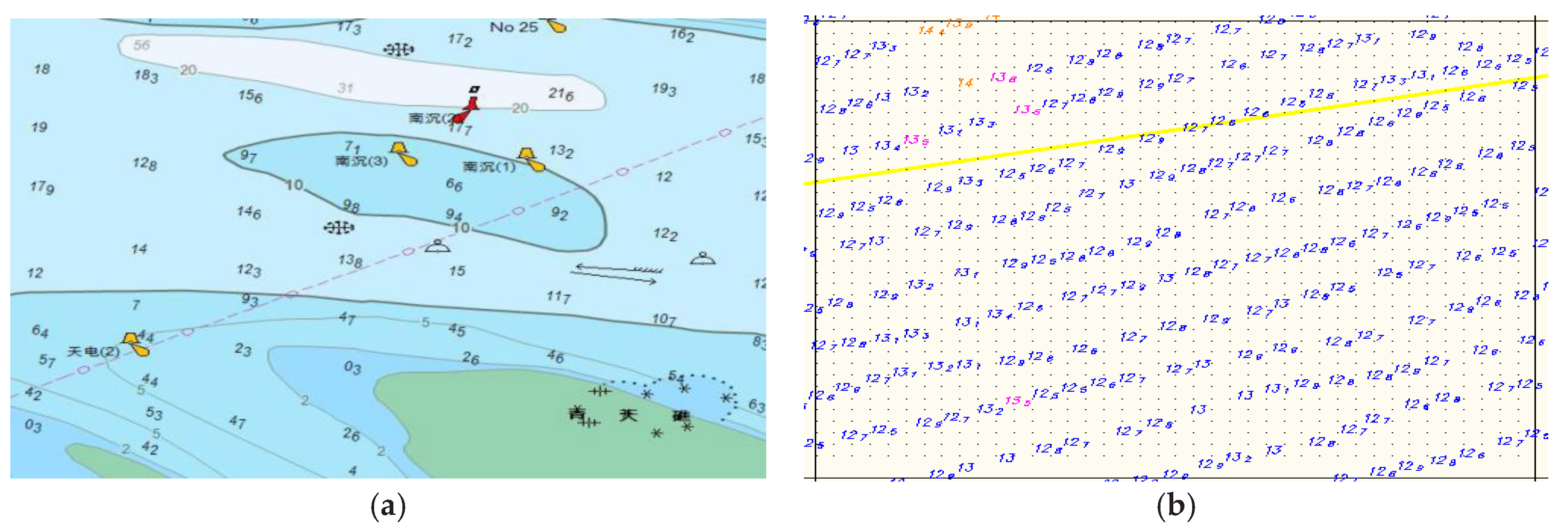

| MMSI | Longitude/(°) | Latitude/(°) | SOG/(n Mile/h) | COG/(°) | UTC |
|---|---|---|---|---|---|
| 413769173 | 114.3079 | 30.58732 | 6.0 | 33.8 | 2016/4/23 1:08 |
| 413769173 | 114.3102 | 30.59013 | 6.0 | 31.6 | 2016/4/23 1:10 |
| 413769173 | 114.3113 | 30.59168 | 6.1 | 34.0 | 2016/4/23 1:11 |
| 413769173 | 114.3124 | 30.59305 | 6.1 | 32.0 | 2016/4/23 1:12 |
| k | Depth of Decision Tree | Activation Function | Iteration Step | Epoch | Accuracy |
|---|---|---|---|---|---|
| Baseline Model | 0.7842 | ||||
| Proposed Model | |||||
| 6 | 5 | sigmoid | 100 | 400 | 0.8334 |
| 6 | 5 | relu | 200 | 600 | 0.9115 |
| 8 | 7 | sigmoid | 100 | 400 | 0.8652 |
| 8 | 7 | relu | 200 | 600 | 0.8231 |
| 10 | 9 | sigmoid | 100 | 400 | 0.8112 |
| 10 | 9 | relu | 200 | 600 | 0.7992 |
| Deep Neural Network | Hybrid DDTree Model | |
|---|---|---|
| MSE | 6.71 | 5.23 |
| 0.82 | 0.84 | |
| 0.61 | 0.85 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, F.; Qiao, Y.; Wei, W.; Wang, X.; Wan, D.; Damaševičius, R.; Woźniak, M. DDTree: A Hybrid Deep Learning Model for Real-Time Waterway Depth Prediction and Smart Navigation. Appl. Sci. 2020, 10, 2770. https://doi.org/10.3390/app10082770
Yang F, Qiao Y, Wei W, Wang X, Wan D, Damaševičius R, Woźniak M. DDTree: A Hybrid Deep Learning Model for Real-Time Waterway Depth Prediction and Smart Navigation. Applied Sciences. 2020; 10(8):2770. https://doi.org/10.3390/app10082770
Chicago/Turabian StyleYang, Fan, Yanan Qiao, Wei Wei, Xiao Wang, Difang Wan, Robertas Damaševičius, and Marcin Woźniak. 2020. "DDTree: A Hybrid Deep Learning Model for Real-Time Waterway Depth Prediction and Smart Navigation" Applied Sciences 10, no. 8: 2770. https://doi.org/10.3390/app10082770
APA StyleYang, F., Qiao, Y., Wei, W., Wang, X., Wan, D., Damaševičius, R., & Woźniak, M. (2020). DDTree: A Hybrid Deep Learning Model for Real-Time Waterway Depth Prediction and Smart Navigation. Applied Sciences, 10(8), 2770. https://doi.org/10.3390/app10082770





