Review: Mathematical Modeling of Prostate Cancer and Clinical Application
Abstract
1. Introduction
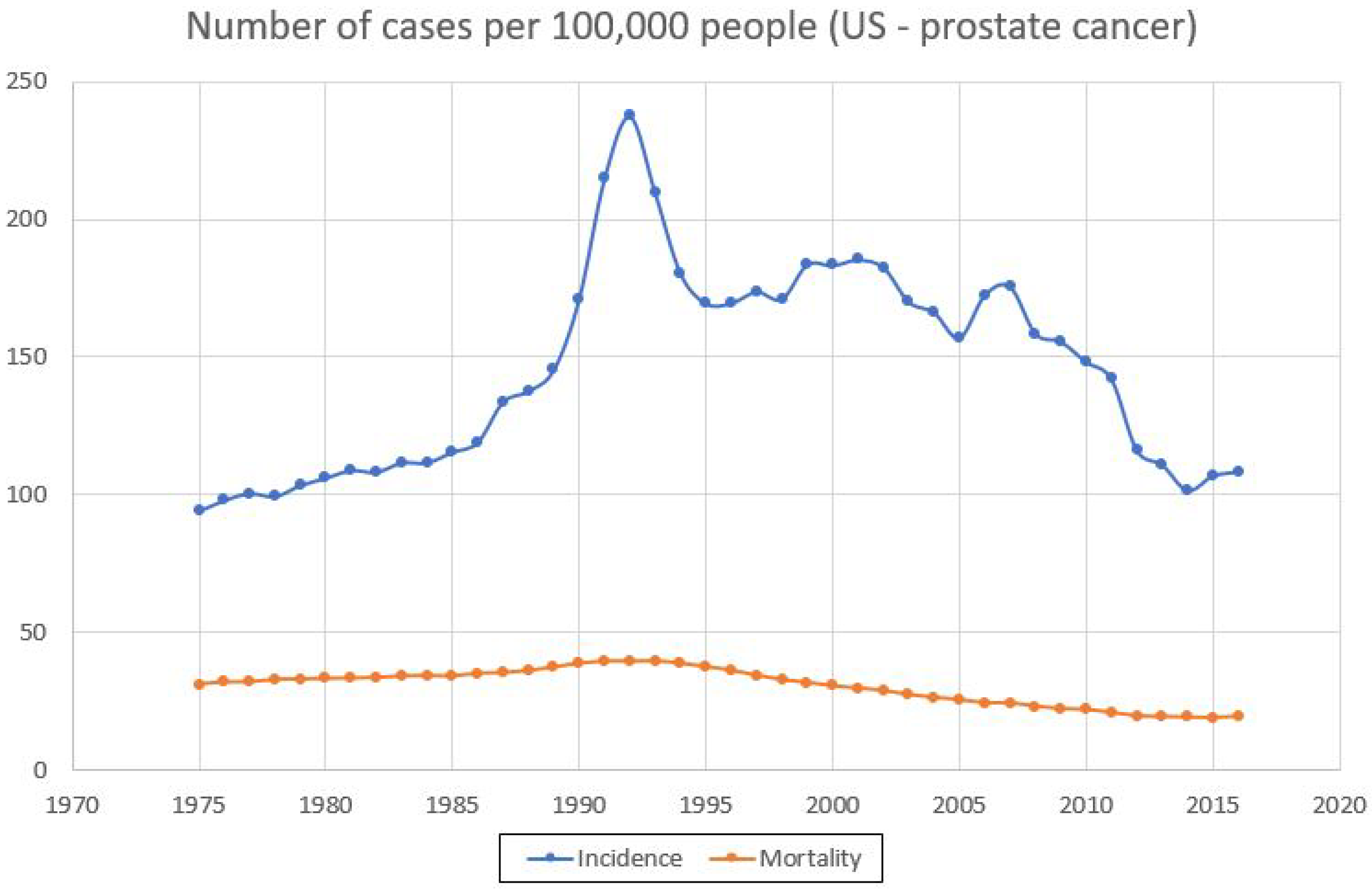
1.1. Prostate Cancer as a Public Health Problem
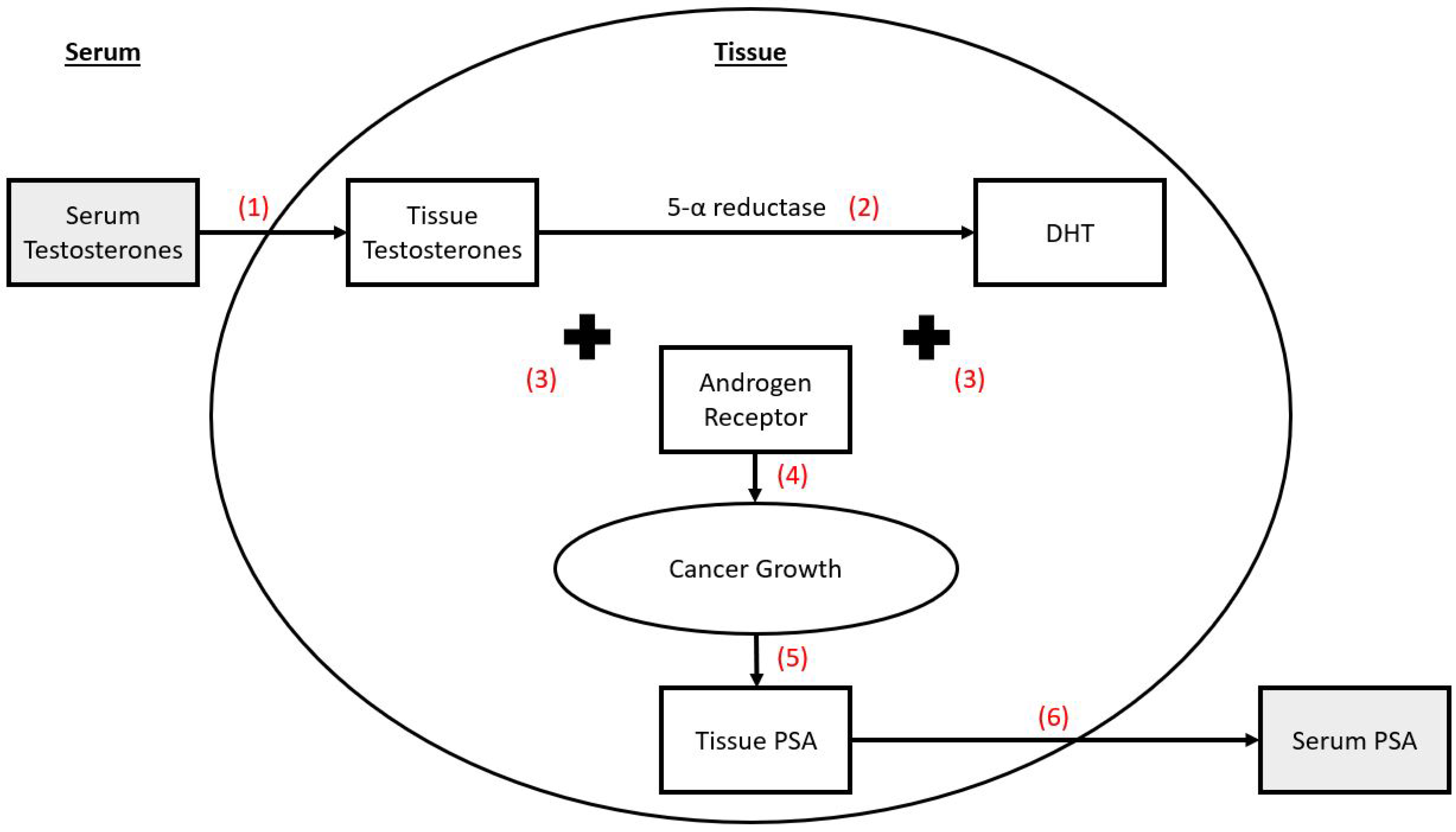
1.2. Prostate Cancer: Physiology and Treatments
1.3. Mathematical Models for Prostate Cancer
2. Elements of Mathematical Models for Clinical Applications
2.1. Population Structure and Dynamics
2.2. Applicability in Clinical Settings
3. Implications from Mathematical Models
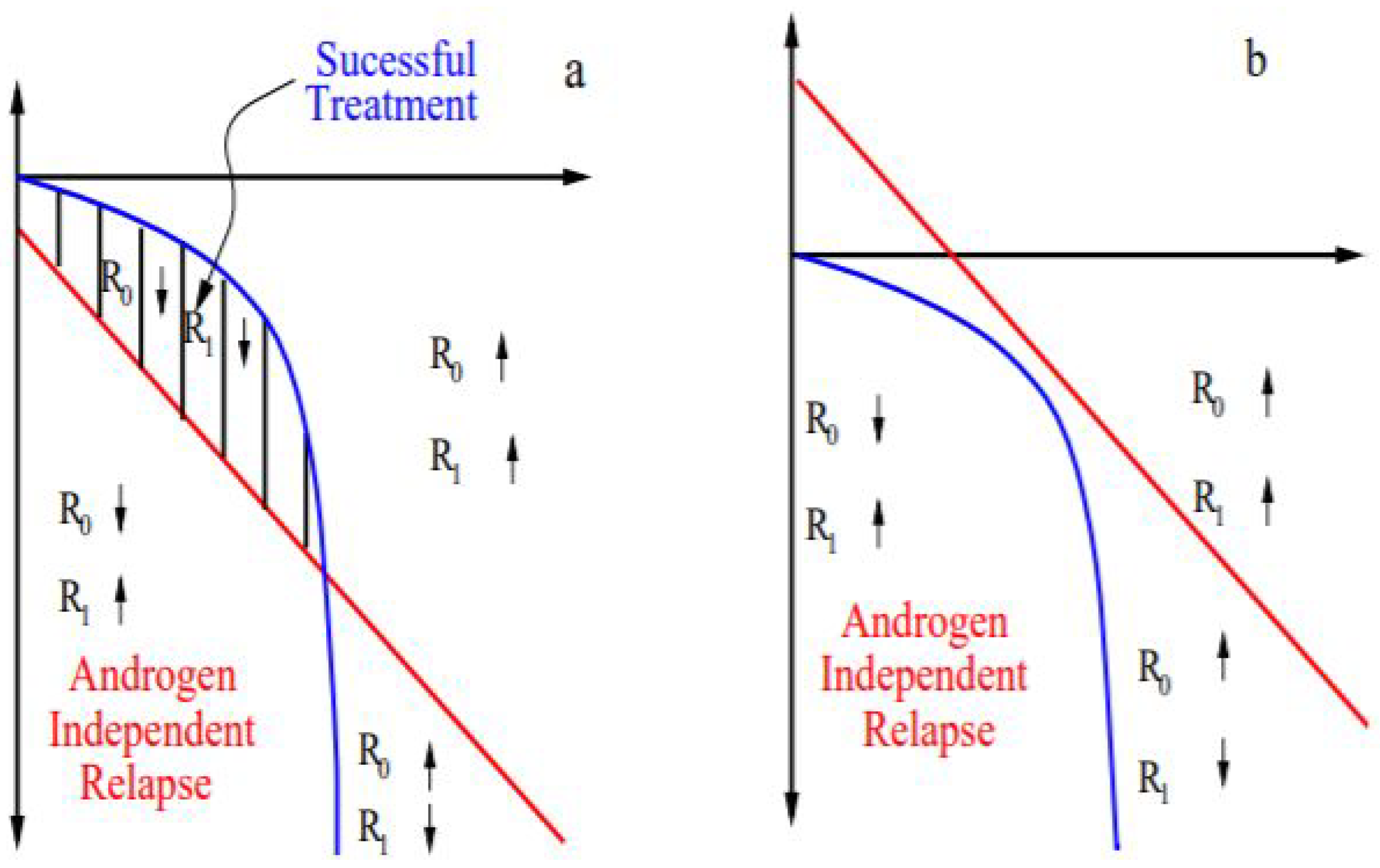
3.1. Population-Based Models of Tumor Relapse
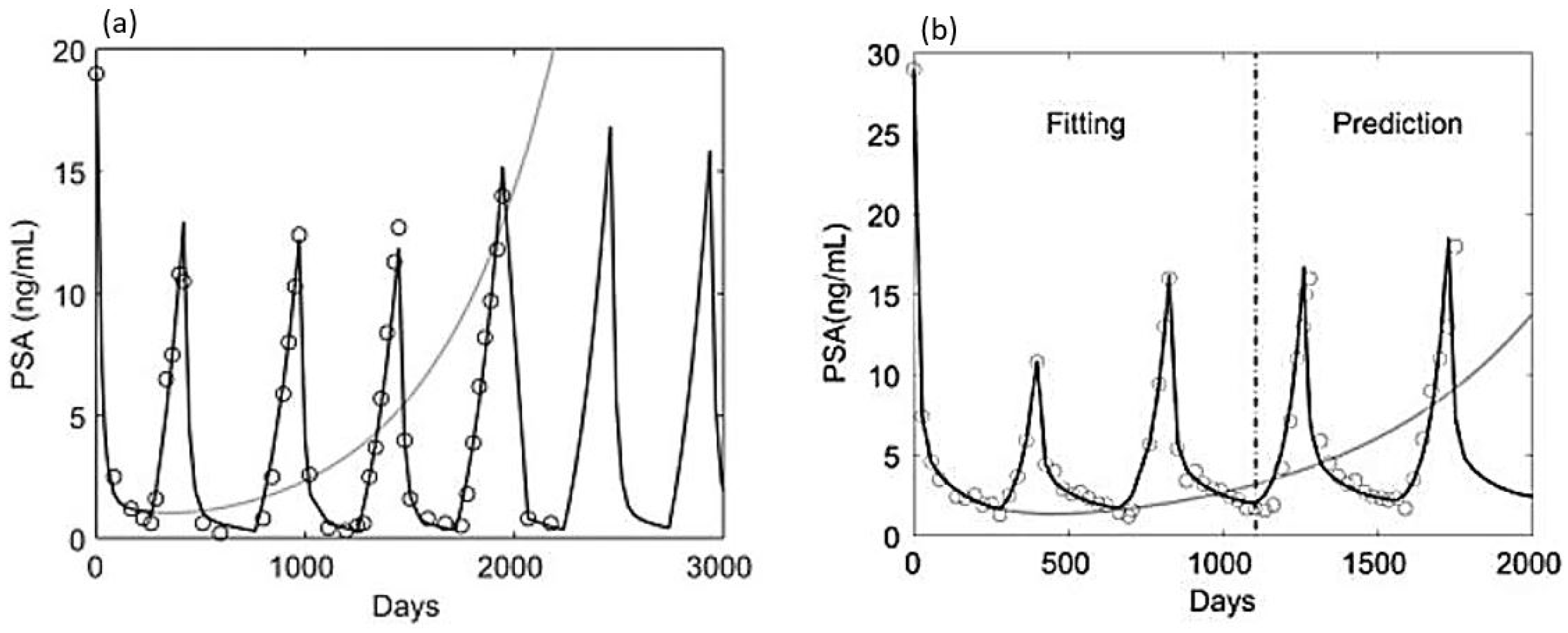
3.2. Data-Validated Models
3.3. Models of Cellular Kinetics
3.4. Models of Immunology
3.5. Limitations of Psa as a Proxy for Tumor Size
3.6. Other Approaches to Mathematical Modeling of Prostate Cancer
4. Mathematical Models in Clinical Settings
4.1. Real-Time Estimability
4.2. Uncertainty, Identifiability, and Sensitivity
4.3. Optimal Schedule and Patient Classification
5. Data, Parameter Ranges, and a Framework for Clinical Application
5.1. Data
5.2. Parameter Ranges
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| PCa | Prostate cancer |
| AR | Androgen receptors |
| ARE | Androgen Response Elements |
| DHT | 5-Dihydrotestosterone |
| PSA | Prostate-specific antigen |
| CAS | Continuous androgen suppression (therapy) |
| IAS | Intermittent androgen suppression (therapy) |
| AD | Androgen-dependent (cancer cells) |
| AI | Androgen-independent (cancer cells) |
References
- Siegel, R.L.; Miller, K.D.; Jemal, A. Cancer statistics, 2020. CA A Cancer J. Clin. 2020, 70, 7–30. [Google Scholar] [CrossRef] [PubMed]
- Blackard, C.E.; Byar, D.P.; Jordan, W.P., Jr.; Group, U.R. Orchiectomy for advanced prostatic carcinoma A reevaluation. Urology 1973, 1, 553–560. [Google Scholar] [CrossRef]
- Taitt, H.E. Global trends and prostate cancer: A review of incidence, detection, and mortality as influenced by race, ethnicity, and geographic location. Am. J. Men’s Health 2018, 12, 1807–1823. [Google Scholar] [CrossRef] [PubMed]
- Surveillance, Epidemiology, and End Results (SEER) Cancer Stat Facts: Prostate Cancer. [Online; Released April 2019, Based on the November 2018 Submission]. Available online: https://seer.cancer.gov/statfacts/html/prost.html (accessed on 15 April 2020).
- Leitzmann, M.F.; Rohrmann, S. Risk factors for the onset of prostatic cancer: Age, location, and behavioral correlates. Clin. Epidemiol. 2012, 4, 1. [Google Scholar] [CrossRef]
- Kale, H.P.; Carroll, N.V. Self-reported financial burden of cancer care and its effect on physical and mental health-related quality of life among US cancer survivors. Cancer 2016, 122, 283–289. [Google Scholar] [CrossRef]
- Ekman, P. The prostate as an endocrine organ: Androgens and estrogens. Prostate 2000, 45, 14–18. [Google Scholar] [CrossRef]
- Cherian, M.T.; Wilson, E.M.; Shapiro, D.J. A competitive inhibitor that reduces recruitment of androgen receptor to androgen-responsive genes. J. Biol. Chem. 2012, 287, 23368–23380. [Google Scholar] [CrossRef]
- Barton, H.A.; Andersen, M.E. A model for pharmacokinetics and physiological feedback among hormones of the testicular–pituitary axis in adult male rats: A framework for evaluating effects of endocrine active compounds. Toxicol. Sci. 1998, 45, 174–187. [Google Scholar]
- Stojilkovic, S.S.; Bjelobaba, I.; Zemkova, H. Ion channels of pituitary gonadotrophs and their roles in signaling and secretion. Front. Endocrinol. 2017, 8, 126. [Google Scholar] [CrossRef]
- Feldman, B.J.; Feldman, D. The development of androgen-independent prostate cancer. Nat. Rev. Cancer 2001, 1, 34–45. [Google Scholar] [CrossRef]
- Washington, T.M.; Blum, J.J.; Reed, M.C.; Conn, P.M. A mathematical model for LH release in response to continuous and pulsatile exposure of gonadotrophs to GnRH. Theor. Biol. Med. Model. 2004, 1, 9. [Google Scholar] [CrossRef] [PubMed]
- Smith, W.A.; Conn, P.M. GnRH-mediated desensitization of the pituitary gonadotrope is not calcium dependent. Endocrinology 1983, 112, 408–410. [Google Scholar] [CrossRef] [PubMed]
- Stamatiades, G.A.; Carroll, R.S.; Kaiser, U.B. GnRH—A key regulator of FSH. Endocrinology 2018, 160, 57–67. [Google Scholar] [CrossRef]
- Kuang, Y.; Nagy, J.D.; Eikenberry, S.E. Introduction to Mathematical Oncology; Chapman and Hall/CRC: Boca Raton, FL, USA, 2018. [Google Scholar]
- Jain, H.V.; Clinton, S.K.; Bhinder, A.; Friedman, A. Mathematical modeling of prostate cancer progression in response to androgen ablation therapy. Proc. Natl. Acad. Sci. USA 2011, 108, 19701–19706. [Google Scholar] [CrossRef] [PubMed]
- Litwin, M.S.; Tan, H.J. The diagnosis and treatment of prostate cancer: A review. JAMA 2017, 317, 2532–2542. [Google Scholar] [CrossRef]
- Spry, N.; Kristjanson, L.; Hooton, B.; Hayden, L.; Neerhut, G.; Gurney, H.; Corica, T.; Korbel, E.; Weinstein, S.; McCaul, K. Adverse effects to quality of life arising from treatment can recover with intermittent androgen suppression in men with prostate cancer. Eur. J. Cancer 2006, 42, 1083–1092. [Google Scholar] [CrossRef]
- Shore, N.D.; Crawford, E.D. Intermittent androgen deprivation therapy: Redefining the standard of care? Rev. Urol. 2010, 12, 1. [Google Scholar]
- Zhang, J.; Cunningham, J.J.; Brown, J.S.; Gatenby, R.A. Integrating evolutionary dynamics into treatment of metastatic castrate-resistant prostate cancer. Nat. Commun. 2017, 8, 1816. [Google Scholar] [CrossRef]
- Kantoff, P.W.; Higano, C.S.; Shore, N.D.; Berger, E.R.; Small, E.J.; Penson, D.F.; Redfern, C.H.; Ferrari, A.C.; Dreicer, R.; Sims, R.B.; et al. Sipuleucel-T immunotherapy for castration-resistant prostate cancer. N. Engl. J. Med. 2010, 363, 411–422. [Google Scholar] [CrossRef]
- Yagoda, A.; Petrylak, D. Cytotoxic chemotherapy for advanced hormone-resistant prostate cancer. Cancer 1993, 71, 1098–1109. [Google Scholar] [CrossRef]
- Hatano, T.; Hirata, Y.; Suzuki, H.; Aihara, K. Comparison between mathematical models of intermittent androgen suppression for prostate cancer. J. Theor. Biol. 2015, 366, 33–45. [Google Scholar] [CrossRef] [PubMed]
- Everett, R.; Packer, A.; Kuang, Y. Can mathematical models predict the outcomes of prostate cancer patients undergoing intermittent androgen deprivation therapy? Biophys. Rev. Lett. 2014, 9, 173–191. [Google Scholar] [CrossRef]
- Nagy, J.D. The ecology and evolutionary biology of cancer: A review of mathematical models of necrosis and tumor cell diversity. Math. Biosci. Eng. 2005, 2, 381–418. [Google Scholar] [CrossRef] [PubMed]
- Pérez-García, V.M.; Fitzpatrick, S.; Pérez-Romasanta, L.A.; Pesic, M.; Schucht, P.; Arana, E.; Sánchez-Gómez, P. Applied mathematics and nonlinear sciences in the war on cancer. Appl. Math. Nonlinear Sci. 2016, 1, 423–436. [Google Scholar] [CrossRef]
- Yorke, E.; Fuks, Z.; Norton, L.; Whitmore, W.; Ling, C. Modeling the development of metastases from primary and locally recurrent tumors: Comparison with a clinical data base for prostatic cancer. Cancer Res. 1993, 53, 2987–2993. [Google Scholar]
- Fuks, Z.; Leibel, S.A.; Wallner, K.E.; Begg, C.B.; Fair, W.R.; Anderson, L.L.; Hilaris, B.S.; Whitmore, W.F. The effect of local control on metastatic dissemination in carcinoma of the prostate: Long-term results in patients treated with 1251 implantation. Int. J. Radiat. Oncol. Biol. Phys. 1991, 21, 537–547. [Google Scholar] [CrossRef]
- Jackson, T. A mathematical model of prostate tumor growth and androgen-independent relapse. Discret. Contin. Dyn. Syst. B 2004, 4, 187–201. [Google Scholar] [CrossRef]
- Ellis, W.J.; Vessella, R.L.; Buhler, K.R.; Bladou, F.; True, L.D.; Bigler, S.A.; Curtis, D.; Lange, P.H. Characterization of a novel androgen-sensitive, prostate-specific antigen-producing prostatic carcinoma xenograft: LuCaP 23. Clin. Cancer Res. 1996, 2, 1039–1048. [Google Scholar]
- Liu, A.Y.; Corey, E.; Bladou, F.; Lange, P.H.; Vessella, R.L. Prostatic cell lineage markers: Emergence of BCL2+ cells of human prostate cancer xenograft LuCaP 23 following castration. Int. J. Cancer 1996, 65, 85–89. [Google Scholar] [CrossRef]
- Heinlein, C.A.; Chang, C. Androgen receptor in prostate cancer. Endocr. Rev. 2004, 25, 276–308. [Google Scholar] [CrossRef]
- Ideta, A.M.; Tanaka, G.; Takeuchi, T.; Aihara, K. A mathematical model of intermittent androgen suppression for prostate cancer. J. Nonlinear Sci. 2008, 18, 593. [Google Scholar] [CrossRef]
- Shimada, T.; Aihara, K. A nonlinear model with competition between prostate tumor cells and its application to intermittent androgen suppression therapy of prostate cancer. Math. Biosci. 2008, 214, 134–139. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Zhao, T.J.; Yuan, C.Q.; Xie, J.H.; Hao, F.F. A nonlinear competitive model of the prostate tumor growth under intermittent androgen suppression. J. Theor. Biol. 2016, 404, 66–72. [Google Scholar] [CrossRef]
- Guo, Q.; Tao, Y.; Aihara, K. Mathematical modeling of prostate tumor growth under intermittent androgen suppression with partial differential equations. Int. J. Bifurc. Chaos 2008, 18, 3789–3797. [Google Scholar] [CrossRef]
- Tao, Y.; Guo, Q.; Aihara, K. A mathematical model of prostate tumor growth under hormone therapy with mutation inhibitor. J. Nonlinear Sci. 2010, 20, 219–240. [Google Scholar] [CrossRef]
- Friedman, A.; Jain, H.V. A partial differential equation model of metastasized prostatic cancer. Math. Biosci. Eng. 2013, 10, 591–608. [Google Scholar]
- Lorenzo, G.; Scott, M.A.; Tew, K.; Hughes, T.J.; Zhang, Y.J.; Liu, L.; Vilanova, G.; Gomez, H. Tissue-scale, personalized modeling and simulation of prostate cancer growth. Proc. Natl. Acad. Sci. USA 2016, 113, E7663–E7671. [Google Scholar] [CrossRef]
- Hirata, Y.; Bruchovsky, N.; Aihara, K. Development of a mathematical model that predicts the outcome of hormone therapy for prostate cancer. J. Theor. Biol. 2010, 264, 517–527. [Google Scholar] [CrossRef]
- Hirata, Y.; Morino, K.; Akakura, K.; Higano, C.S.; Aihara, K. Personalizing androgen suppression for prostate cancer using mathematical modeling. Sci. Rep. 2018, 8, 2673. [Google Scholar] [CrossRef]
- Hirata, Y.; Azuma, S.i.; Aihara, K. Model predictive control for optimally scheduling intermittent androgen suppression of prostate cancer. Methods 2014, 67, 278–281. [Google Scholar] [CrossRef]
- Portz, T.; Kuang, Y.; Nagy, J.D. A clinical data validated mathematical model of prostate cancer growth under intermittent androgen suppression therapy. Aip Adv. 2012, 2, 011002. [Google Scholar] [CrossRef]
- Droop, M.R. Vitamin B 12 and marine ecology. IV. The kinetics of uptake, growth and inhibition in Monochrysis lutheri. J. Mar. Biol. Assoc. 1968, 48, 689–733. [Google Scholar] [CrossRef]
- Mizrak, O.O.; Mizrak, C.; Kashkynbayev, A.; Kuang, Y. Can fractional differentiation improve stability results and data fitting ability of a prostate cancer model under intermittent androgen suppression therapy? Chaos Solitons Fractals 2020, 131, 109529. [Google Scholar] [CrossRef]
- Akakura, K.; Bruchovsky, N.; Goldenberg, S.L.; Rennie, P.S.; Buckley, A.R.; Sullivan, L.D. Effects of intermittent androgen suppression on androgen-dependent tumors. Apoptosis and serum prostate-specific antigen. Cancer 1993, 71, 2782–2790. [Google Scholar] [CrossRef]
- Baez, J.; Kuang, Y. Mathematical models of androgen resistance in prostate cancer patients under intermittent androgen suppression therapy. Appl. Sci. 2016, 6, 352. [Google Scholar] [CrossRef]
- Phan, T.; Changhan, H.; Martinez, A.; Kuang, Y. Dynamics and implications of models for intermittent androgen suppression therapy. Math. Biosci. Eng. 2019, 16, 187–204. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.; Phan, T.; Baez, J.; Kuang, Y.; Kostelich, E.J. Predictability and identifiability assessment of models for prostate cancer under androgen suppression therapy. Math. Biosci. Eng. 2019, 16, 3512–3536. [Google Scholar] [CrossRef]
- Phan, T.; Nguyen, K.; Sharma, P.; Kuang, Y. The Impact of Intermittent Androgen Suppression Therapy in Prostate Cancer Modeling. Appl. Sci. 2019, 9, 36. [Google Scholar] [CrossRef]
- Potter, L.K.; Zager, M.G.; Barton, H.A. Mathematical model for the androgenic regulation of the prostate in intact and castrated adult male rats. Am. J. Physiol. Endocrinol. Metab. 2006, 291, E952–E964. [Google Scholar] [CrossRef]
- Reckell, T.; Nguyen, K.; Phan, T.; Crook, S.; Kostelich, E.J.; Kuang, Y. Incorporating properties of drugs in prostate cancer modeling. 2020. (Unpublished). [Google Scholar]
- Cerasuolo, M.; Maccarinelli, F.; Coltrini, D.; Mahmoud, A.M.; Marolda, V.; Ghedini, G.C.; Rezzola, S.; Giacomini, A.; Triggiani, L.; Kostrzewa, M.; et al. Modeling acquired resistance to the second-generation androgen receptor antagonist enzalutamide in the TRAMP model of prostate cancer. Cancer Res. 2020, 80, 1564–1577. [Google Scholar] [CrossRef]
- Eikenberry, S.E.; Nagy, J.D.; Kuang, Y. The evolutionary impact of androgen levels on prostate cancer in a multi-scale mathematical model. Biol. Direct 2010, 5, 24. [Google Scholar] [CrossRef]
- Thompson, I.M.; Goodman, P.J.; Tangen, C.M.; Lucia, M.S.; Miller, G.J.; Ford, L.G.; Lieber, M.M.; Cespedes, R.D.; Atkins, J.N.; Lippman, S.M.; et al. The influence of finasteride on the development of prostate cancer. N. Engl. J. Med. 2003, 349, 215–224. [Google Scholar] [CrossRef]
- Goldenberg, S.L.; Bruchovsky, N.; Gleave, M.E.; Sullivan, L.D.; Akakura, K. Intermittent androgen suppression in the treatment of prostate cancer: A preliminary report. Urology 1995, 45, 839–845. [Google Scholar] [CrossRef]
- Vardhan Jain, H.; Friedman, A. Modeling prostate cancer response to continuous versus intermittent androgen ablation therapy. Discret. Contin. Dyn. Syst. Ser. B 2013, 18, 945–967. [Google Scholar] [CrossRef]
- Hussain, M.; Tangen, C.M.; Berry, D.L.; Higano, C.S.; Crawford, E.D.; Liu, G.; Wilding, G.; Prescott, S.; Kanaga Sundaram, S.; Small, E.J.; et al. Intermittent versus continuous androgen deprivation in prostate cancer. N. Engl. J. Med. 2013, 368, 1314–1325. [Google Scholar] [CrossRef] [PubMed]
- Crook, J.M.; O’Callaghan, C.J.; Duncan, G.; Dearnaley, D.P.; Higano, C.S.; Horwitz, E.M.; Frymire, E.; Malone, S.; Chin, J.; Nabid, A.; et al. Intermittent androgen suppression for rising PSA level after radiotherapy. N. Engl. J. Med. 2012, 367, 895–903. [Google Scholar] [CrossRef]
- Gatenby, R.A.; Silva, A.S.; Gillies, R.J.; Frieden, B.R. Adaptive therapy. Cancer Res. 2009, 69, 4894–4903. [Google Scholar] [CrossRef] [PubMed]
- West, J.B.; Dinh, M.N.; Brown, J.S.; Zhang, J.; Anderson, A.R.; Gatenby, R.A. Multidrug cancer therapy in metastatic castrate-resistant prostate cancer: An evolution-based strategy. Clin. Cancer Res. 2019, 25, 4413–4421. [Google Scholar] [CrossRef]
- Sontag, E.D. For differential equations with r parameters, 2r+ 1 experiments are enough for identification. J. Nonlinear Sci. 2002, 12, 553–583. [Google Scholar] [CrossRef]
- West, J.; Ma, Y.; Newton, P.K. Capitalizing on competition: An evolutionary model of competitive release in metastatic castration resistant prostate cancer treatment. J. Theor. Biol. 2018, 455, 249–260. [Google Scholar] [CrossRef]
- Peng, H.; Zhao, W.; Tan, H.; Ji, Z.; Li, J.; Li, K.; Zhou, X. Prediction of treatment efficacy for prostate cancer using a mathematical model. Sci. Rep. 2016, 6, 21599. [Google Scholar] [CrossRef] [PubMed]
- Aragon-Ching, J.B.; Williams, K.M.; Gulley, J.L. Impact of androgen-deprivation therapy on the immune system: Implications for combination therapy of prostate cancer. Front. Biosci. 2007, 12, 71. [Google Scholar] [CrossRef] [PubMed]
- Tang, S.; Dubey, P. Opposing effects of androgen ablation on immune function in prostate cancer. Oncoimmunology 2012, 1, 1220–1221. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Portz, T.; Kuang, Y. A mathematical model for the immunotherapy of advanced prostate cancer. In BIOMAT 2012; World Scientific: Singapore, 2013; pp. 70–85. [Google Scholar]
- Kirschner, D.; Panetta, J.C. Modeling immunotherapy of the tumor–immune interaction. J. Math. Biol. 1998, 37, 235–252. [Google Scholar] [CrossRef]
- Rutter, E.M.; Kuang, Y. Global dynamics of a model of joint hormone treatment with dendritic cell vaccine for prostate cancer. Discret. Contin. Dyn. Syst. B 2017, 22, 1001. [Google Scholar] [CrossRef]
- Kronik, N.; Kogan, Y.; Elishmereni, M.; Halevi-Tobias, K.; Vuk-Pavlović, S.; Agur, Z. Predicting outcomes of prostate cancer immunotherapy by personalized mathematical models. PLoS ONE 2010, 5, e15482. [Google Scholar] [CrossRef]
- Elishmereni, M.; Kheifetz, Y.; Shukrun, I.; Bevan, G.H.; Nandy, D.; McKenzie, K.M.; Kohli, M.; Agur, Z. Predicting time to castration resistance in hormone sensitive prostate cancer by a personalization algorithm based on a mechanistic model integrating patient data. Prostate 2016, 76, 48–57. [Google Scholar] [CrossRef]
- Stura, I.; Gabriele, D.; Guiot, C. A Simple PSA-Based Computational Approach Predicts the Timing of Cancer Relapse in Prostatectomized Patients. Cancer Res. 2016, 76, 4941–4947. [Google Scholar] [CrossRef]
- Swanson, K.R.; True, L.D.; Lin, D.W.; Buhler, K.R.; Vessella, R.; Murray, J.D. A quantitative model for the dynamics of serum prostate-specific antigen as a marker for cancerous growth: An explanation for a medical anomaly. Am. J. Pathol. 2001, 158, 2195–2199. [Google Scholar] [CrossRef]
- Vollmer, R.T.; Humphrey, P.A. Tumor volume in prostate cancer and serum prostate-specific antigen: Analysis from a kinetic viewpoint. Am. J. Clin. Pathol. 2003, 119, 80–89. [Google Scholar] [CrossRef]
- Vollmer, R.T.; Egawa, S.; Kuwao, S.; Baba, S. The dynamics of prostate specific antigen during watchful waiting of prostate carcinoma: A study of 94 Japanese men. Cancer 2002, 94, 1692–1698. [Google Scholar] [CrossRef]
- McLaren, D.B.; McKenzie, M.; Duncan, G.; Pickles, T. Watchful waiting or watchful progression? Prostate specific antigen doubling times and clinical behavior in patients with early untreated prostate carcinoma. Cancer Interdiscip. Int. J. Am. Cancer Soc. 1998, 82, 342–348. [Google Scholar]
- Dimonte, G. A cell kinetics model for prostate cancer and its application to clinical data and individual patients. J. Theor. Biol. 2010, 264, 420–442. [Google Scholar] [CrossRef]
- Dimonte, G.; Bergstralh, E.; Bolander, M.; Karnes, R.J.; Tindall, D. Use of tumor dynamics to clarify the observed variability among biochemical recurrence nomograms for prostate cancer. Prostate 2012, 72, 280–290. [Google Scholar] [CrossRef]
- Singh, S.; Gill, A.A.; Nlooto, M.; Karpoormath, R. Prostate cancer biomarkers detection using nanoparticles based electrochemical biosensors. Biosens. Bioelectron. 2019, 137, 213–221. [Google Scholar] [CrossRef]
- Lorenzo, G.; Pérez-García, V.M.; Mariño, A.; Pérez-Romasanta, L.A.; Reali, A.; Gomez, H. Mechanistic modelling of prostate-specific antigen dynamics shows potential for personalized prediction of radiation therapy outcome. J. R. Soc. Interface 2019, 16, 20190195. [Google Scholar] [CrossRef]
- Farhat, A.; Jiang, D.; Cui, D.; Keller, E.; Jackson, T.L. An integrative model of prostate cancer interaction with the bone microenvironment. Math. Biosci. 2017, 294, 1–14. [Google Scholar] [CrossRef]
- Liu, B.; Kong, S.; Gao, S.; Zuliani, P.; Clarke, E.M. Towards personalized prostate cancer therapy using delta-reachability analysis. In Proceedings of the 18th International Conference on Hybrid Systems: Computation and Control, Seattle, WA, USA, 14–16 April 2015; pp. 227–232. [Google Scholar]
- Tanaka, G.; Hirata, Y.; Goldenberg, S.L.; Bruchovsky, N.; Aihara, K. Mathematical modelling of prostate cancer growth and its application to hormone therapy. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2010, 368, 5029–5044. [Google Scholar] [CrossRef]
- Zazoua, A.; Wang, W. Analysis of mathematical model of prostate cancer with androgen deprivation therapy. Commun. Nonlinear Sci. Numer. Simul. 2019, 66, 41–60. [Google Scholar] [CrossRef]
- Baez, J. Mathematical Models of Androgen Resistance in Prostate Cancer Patients under Intermittent Androgen Suppression Therapy. Ph.D. Thesis, Arizona State University, Tempe, AZ, USA, 2017. [Google Scholar]
- Hirata, Y.; Morino, K.; Suzuki, T.; Guo, Q.; Fukuhara, H.; Aihara, K. System identification and parameter estimation in mathematical medicine: Examples demonstrated for prostate cancer. Quant. Biol. 2016, 4, 13–19. [Google Scholar] [CrossRef]
- Morken, J.D.; Packer, A.; Everett, R.A.; Nagy, J.D.; Kuang, Y. Mechanisms of resistance to intermittent androgen deprivation in patients with prostate cancer identified by a novel computational method. Cancer Res. 2014, 74, 3673–3683. [Google Scholar] [CrossRef]
- Draghi, C.; Denis, F.; Tolédano, A.; Letellier, C. Parameter identification of a model for prostate cancer treated by intermittent therapy. J. Theor. Biol. 2019, 461, 117–132. [Google Scholar] [CrossRef]
- Brady, R.; Nagy, J.; Gerke, T.; Zhang, T.; Wang, A.Z.; Zhang, J.; Gatenby, R.; Enderling, H. Prostate-specific antigen dynamics predict individual responses to intermittent androgen deprivation. bioRxiv 2019, 624866. [Google Scholar] [CrossRef]
- Loladze, I. Iterative chemostat: A modelling framework linking biosynthesis to nutrient cycling on ecological and evolutionary time scales. Math. Biosci. Eng. 2019, 16, 990–1004. [Google Scholar] [CrossRef]
- Bruchovsky, N.; Klotz, L.; Crook, J.; Malone, S.; Ludgate, C.; Morris, W.J.; Gleave, M.E.; Goldenberg, S.L. Final results of the Canadian prospective phase II trial of intermittent androgen suppression for men in biochemical recurrence after radiotherapy for locally advanced prostate cancer. Cancer 2006, 107, 389–395. [Google Scholar] [CrossRef]
- Voth, A.M.; Alford, J.G.; Swim, E.W. Mathematical modeling of continuous and intermittent androgen suppression for the treatment of advanced prostate cancer. Math. Biosci. Eng. 2016, 14, 777–804. [Google Scholar] [CrossRef]
- Eisenberg, M.C.; Jain, H.V. A confidence building exercise in data and identifiability: Modeling cancer chemotherapy as a case study. J. Theor. Biol. 2017, 431, 63–78. [Google Scholar] [CrossRef]
- Suzuki, T.; Aihara, K. Nonlinear system identification for prostate cancer and optimality of intermittent androgen suppression therapy. Math. Biosci. 2013, 245, 40–48. [Google Scholar] [CrossRef]
- Cunningham, J.J.; Brown, J.S.; Gatenby, R.A.; Staňková, K. Optimal control to develop therapeutic strategies for metastatic castrate resistant prostate cancer. J. Theor. Biol. 2018, 459, 67–78. [Google Scholar] [CrossRef]
- Lenhart, S.; Workman, J.T. Optimal Control Applied to Biological Models; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Higano, C. Prospective serial measurements of bone mineral density (BMD) in prostate cancer patients without bone metastases treated with intermittent androgen suppression (IAS). In Proceedings of the 35th Annual Meeting of the American Society of Clinical Oncology (ASCO), Atlanta, GA, USA, 15–18 May 1999. [Google Scholar]
- Evan, Y.Y.; Gulati, R.; Telesca, D.; Jiang, P.; Tam, S.; Russell, K.J.; Nelson, P.S.; Etzioni, R.D.; Higano, C.S. Duration of first off-treatment interval is prognostic for time to castration resistance and death in men with biochemical relapse of prostate cancer treated on a prospective trial of intermittent androgen deprivation. J. Clin. Oncol. 2010, 28, 2668. [Google Scholar]
- Evan, Y.Y.; Kuo, K.F.; Gulati, R.; Chen, S.; Gambol, T.E.; Hall, S.P.; Jiang, P.Y.; Pitzel, P.; Higano, C.S. Long-term dynamics of bone mineral density during intermittent androgen deprivation for men with nonmetastatic, hormone-sensitive prostate cancer. J. Clin. Oncol. 2012, 30, 1864. [Google Scholar]
- Kuo, K.F.; Hunter-Merrill, R.; Gulati, R.; Hall, S.P.; Gambol, T.E.; Higano, C.S.; Evan, Y.Y. Relationships between times to testosterone and prostate-specific antigen rises during the first off-treatment interval of intermittent androgen deprivation are prognostic for castration resistance in men with nonmetastatic prostate cancer. Clin. Genitourin. Cancer 2015, 13, 10–16. [Google Scholar] [CrossRef][Green Version]
- Berges, R.R.; Vukanovic, J.; Epstein, J.I.; CarMichel, M.; Cisek, L.; Johnson, D.E.; Veltri, R.W.; Walsh, P.C.; Isaacs, J.T. Implication of cell kinetic changes during the progression of human prostatic cancer. Clin. Cancer Res. 1995, 1, 473–480. [Google Scholar]
- Vesely, S.; Knutson, T.; Damber, J.E.; Dicuio, M.; Dahlstrand, C. Relationship between age, prostate volume, prostate-specific antigen, symptom score and uroflowmetry in men with lower urinary tract symptoms. Scand. J. Urol. Nephrol. 2003, 37, 322–328. [Google Scholar] [CrossRef]
- Lotan, Y.; Roehrborn, C. Clearance rates of total prostate specific antigen (PSA) after radical prostatectomy in African-Americans and Caucasians. Prostate Cancer Prostatic Dis. 2002, 5, 111. [Google Scholar] [CrossRef][Green Version]
- Bilinsky, L.; Baer, S. Slow passage through a Hopf bifurcation in excitable nerve cables: Spatial delays and spatial memory effects. Bull. Math. Biol. 2018, 80, 130–150. [Google Scholar] [CrossRef]
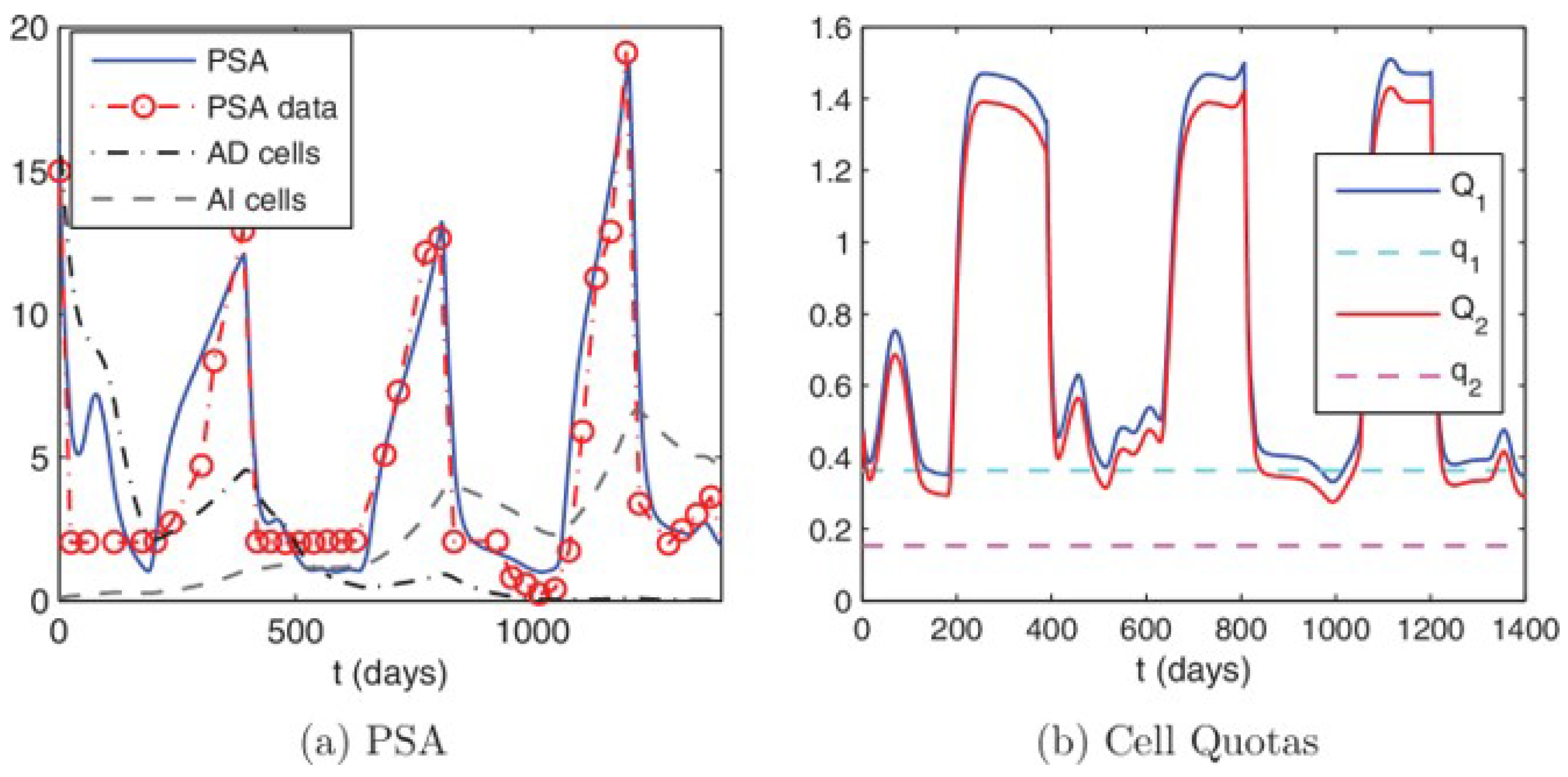
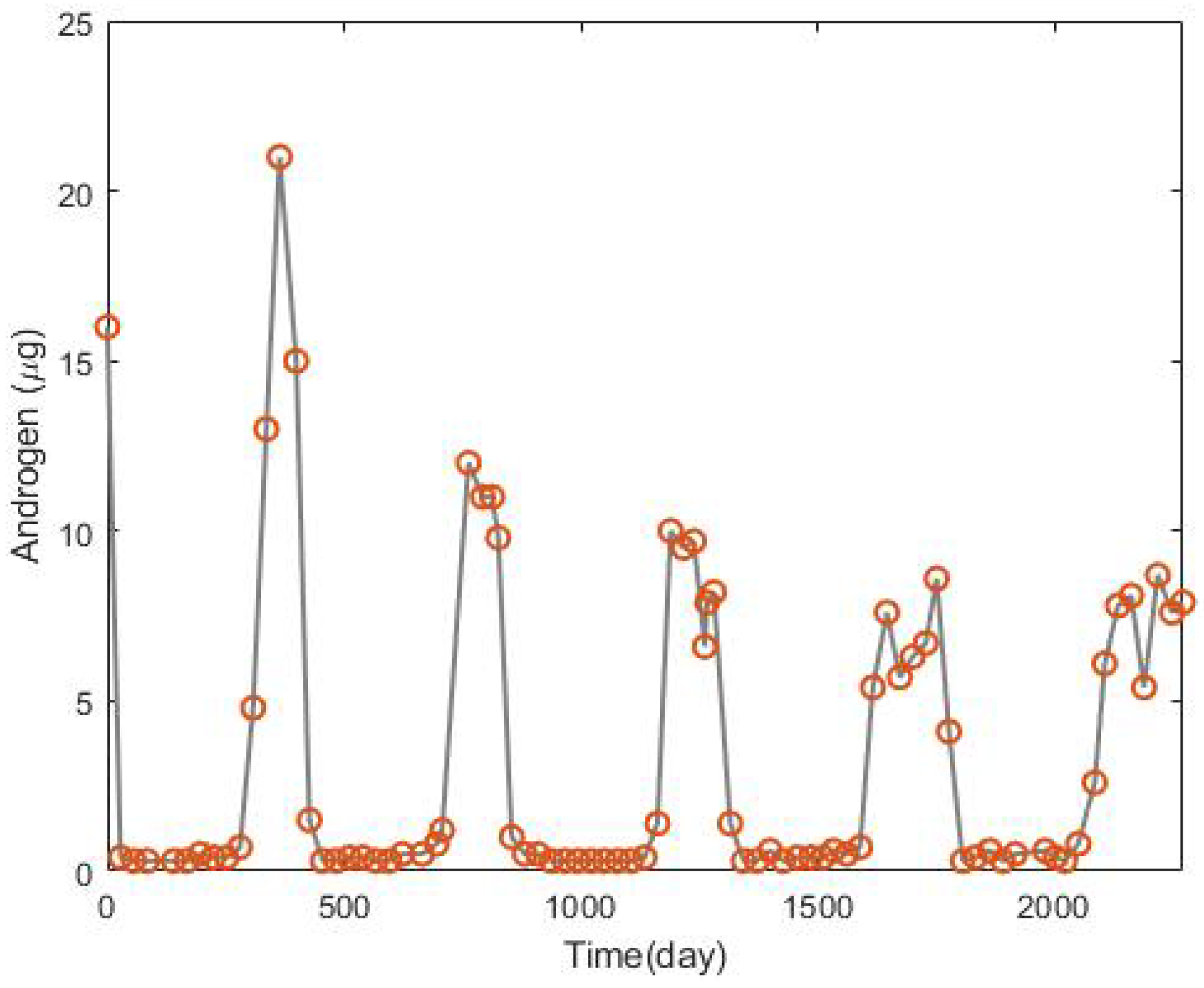
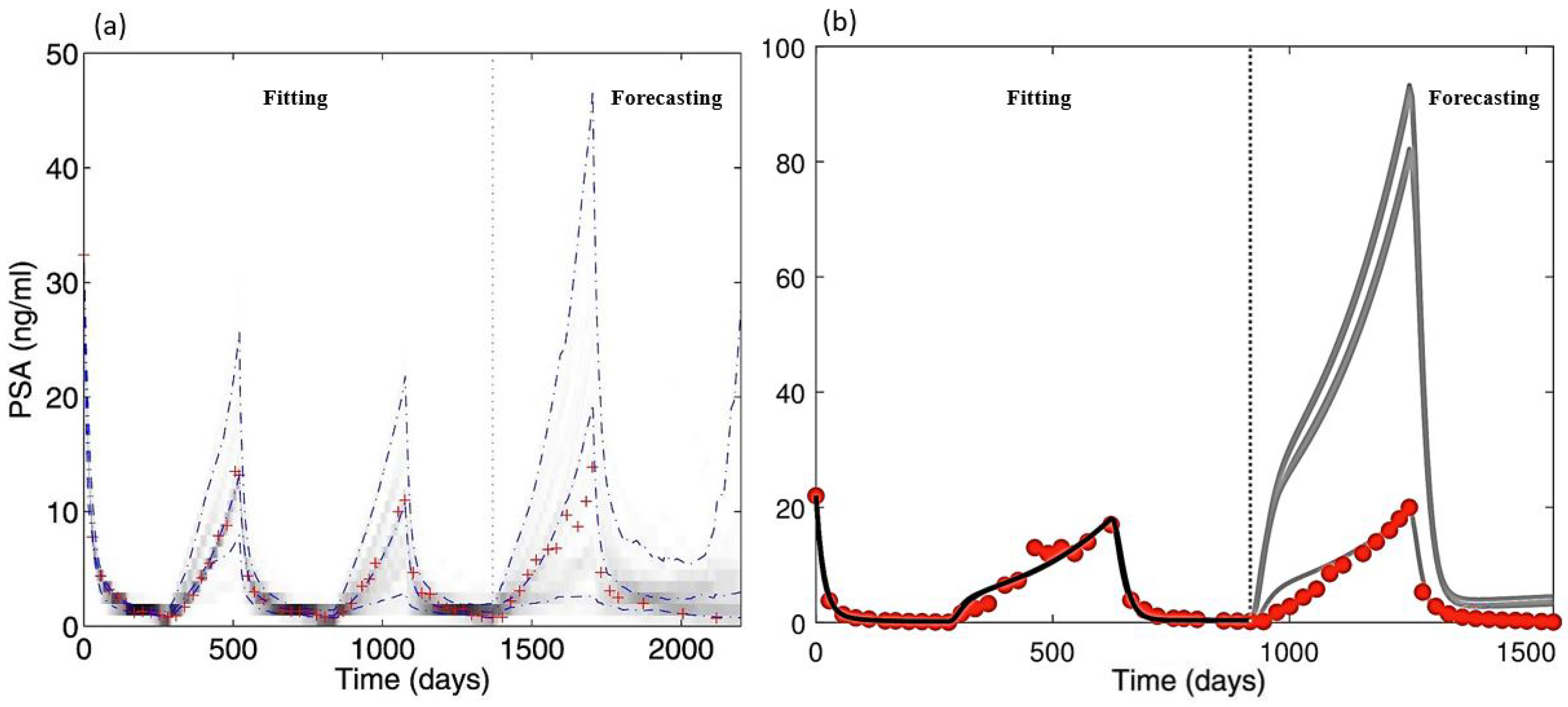
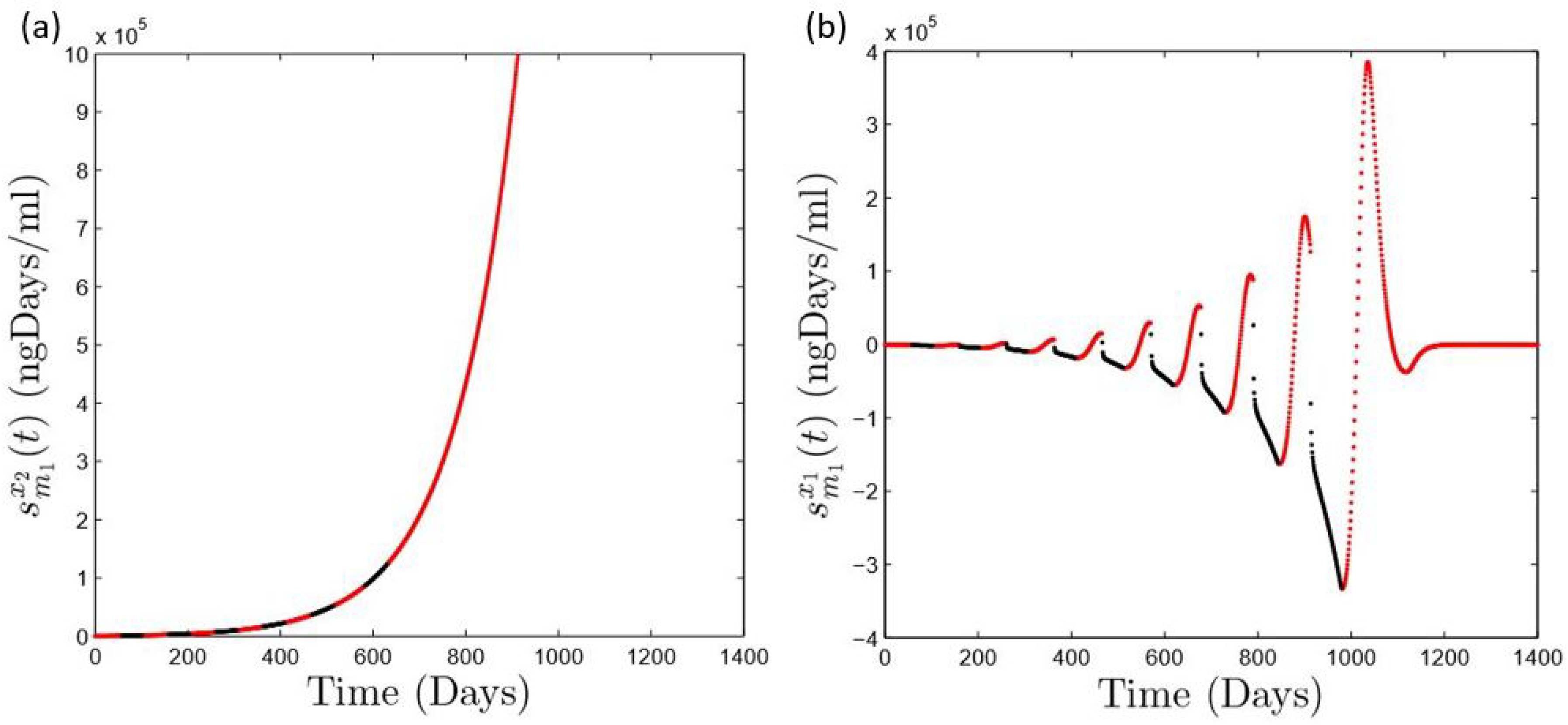
| Aspects of Mathematical Modeling | Summary of Findings | Future Exploration |
|---|---|---|
| Tumor heterogeneity and evolution Section 3.1–Section 3.4 | Treatment resistance appears to come at a competitive cost for cancer, which implies that intermittent and adaptive therapy would be superior to continuous therapy. | Quantitative measures of the evolutionary cost and when it does occur would be useful. Furthermore, the competition rates between sub-types of cancer cells should be quantified. |
| Tracking the progression of tumor Section 3.5 | The most commonly used biomarker for prostate cancer growth (PSA) is useful but can be unreliable. Instead, other measurements can be used in place or in concurrence with PSA to track tumor progression. | The accuracy of tracking the progression of tumors using multiple biomarkers needs to be examined. While accuracy is key, the availability of such biomarkers should also be taken into account. |
| Model types and dynamics Section 3.6 | Ordinary differential equations build the foundation for studying prostate cancer. However, the lack of various modes of modeling implies many aspects of prostate cancer are left unexplored. | As more data becomes available, especially imaging data, spatial, memory-based, and stochastic models will become useful in capturing spatial patterns in cancer progression and interaction, specifically, the metastatic processes. |
| Aspects of Clinical Applications | Summary of Findings | Future Exploration |
|---|---|---|
| Real-time estimability Section 4.1 | The estimation of parameters in mathematical models often require a large quantity of data. However, the nature of data collection in real-time means that reliable estimation of parameters for patients may not be possible at the early stages of treatment. | Some parameters share similar values across patients, while others are more patient-specific. This distinction should be studied in detail. Utilizing multiple data sets is another possibility to allow early estimates of parameters. Finally, parameter evolution can be accounted for to address the limitation of data availability. |
| Uncertainty, sensitivity, and identifiability Section 4.2 | Due to the large number of parameters and the heavy reliance on parameter fitting, model predictions can be unreliable. Furthermore, the issue of parameter identifiability is often ignored, which can lead to wildly different predictions for a specific patient. | Local sensitivity analysis and uncertainty quantification should be studied for each patient. Clear links between each parameter and its physical interpretation should be established, which potentially allows for laboratory estimates/bounds to resolve identifiability. |
| Optimal schedule, optimal treatment, and patient classification Section 4.3 | Studies on optimal schedule and treatment yield useful information on how intermittent, adaptive, and combination therapies should be carried out. Patient classification based on treatment effectiveness can be done using model parameters. However, both aspects are affected heavily by the estimability of the parameters and the uncertainty in the model’s forecasts. | The usefulness of optimal studies and classification hinges on how well the uncertainty in the model can be quantified, which relates to previous issues. In addition, the objective of optimal studies may be extended to include drugs’ properties, cost, and important features of each treatment. |
| Description | Range | Unit | Source |
|---|---|---|---|
| Max proliferation rate (AD) | 4.00–8.10 | [101] | |
| Max proliferation rate (AI) | 1.00–4.60 | [101] | |
| Death rate (AD) | 1.00–5.25 | [101] | |
| Death rate (AI) | 1.50–7.75 | [101] | |
| Max transformation rate | – | [24] | |
| PSA clearance rate | 1.75–4.03 | [103] | |
| PSA production rate (healthy) | – | [15] | |
| PSA production rate (cancer) | 1.72–6.97 | [73] |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Phan, T.; Crook, S.M.; Bryce, A.H.; Maley, C.C.; Kostelich, E.J.; Kuang, Y. Review: Mathematical Modeling of Prostate Cancer and Clinical Application. Appl. Sci. 2020, 10, 2721. https://doi.org/10.3390/app10082721
Phan T, Crook SM, Bryce AH, Maley CC, Kostelich EJ, Kuang Y. Review: Mathematical Modeling of Prostate Cancer and Clinical Application. Applied Sciences. 2020; 10(8):2721. https://doi.org/10.3390/app10082721
Chicago/Turabian StylePhan, Tin, Sharon M. Crook, Alan H. Bryce, Carlo C. Maley, Eric J. Kostelich, and Yang Kuang. 2020. "Review: Mathematical Modeling of Prostate Cancer and Clinical Application" Applied Sciences 10, no. 8: 2721. https://doi.org/10.3390/app10082721
APA StylePhan, T., Crook, S. M., Bryce, A. H., Maley, C. C., Kostelich, E. J., & Kuang, Y. (2020). Review: Mathematical Modeling of Prostate Cancer and Clinical Application. Applied Sciences, 10(8), 2721. https://doi.org/10.3390/app10082721







