1. Introduction
The construction sector is considered one of the main players in the generation of environmental impact. Besides cement production, which is responsible for more than 6% of all global CO
2 emissions, the total amount of construction and demolition waste (CDW) represents a third of all waste generated in the European Union. However, there are barriers to its reuse, one of the main of which lies in the lack of trust in the quality of CDW [
1].
The incorporation of recycled aggregates (RA) in concrete, by replacing a percentage of natural aggregates (NA), usually leads to poor mechanical and durability-related performances [
2,
3].
It is therefore important to understand to what extent the behavior of the RA differs from that of the NA. According to Bravo et al. [
2], the main differences between these aggregates are:
- -
Higher water absorption capacity of the RA, leading to concrete mixes with lower workability and effective water/cement ratio;
- -
Lower compactness and thus lower resistance to crushing, lower modulus of elasticity and higher short- and long-term deformability.
Chan [
4] and Bravo et al. [
2] evaluated the performance of recycled aggregate concrete (RAC), finding that the nature of RA strongly influences their binding capacity to the new cement paste, thus affecting the mechanical properties of the resulting concrete. Nevertheless, these authors also concluded that the use of these aggregates in concrete production is feasible. However, considering that their use affects the mechanical and durability-related properties of RAC, imposition of limitations and cautions on their inclusion is required.
Shotcrete is widely used in the underground mining and tunneling industry, slope stability, rehabilitation works, and in many other areas.
The tunneling industry is growing because the available space in dense urban environment tends to be used for nobler purposes than transit subways, parking lots, electric lines, water supply and sewer lines [
5].
Nowadays, the widespread use of the New Austrian Tunneling Method (NATM) has increased the use of shotcrete for linings [
6]. In recent years, several studies on the use of fibres to replace the traditional electro-welded meshes have been published [
7,
8,
9,
10].
To the authors’ knowledge, the incorporation of recycled aggregates from CDW in deep tunnels has not yet been studied in detail. This work studies the viability of using CDW in urban tunnels, because CDW is usually generated in urban environments. A technical and economic assessment of different dry-mix shotcrete compositions, incorporating coarse recycled concrete aggregates (CRCA) in substitution of coarse natural aggregates (CNA), intends to contribute to the sustainability of the construction sector.
For generalization purposes, the analysis is made for a reference case of a deep tunnel where analytical equations proposed by Carranza-Torres and Fairhurst [
11] are valid (see
Appendix A), based on the convergence-confinement method, which is broadly used to describe the ground-support interaction in design practice [
12,
13].
It is demonstrated that limited incorporation ratios of CRCA can be a valid alternative from a technical and economic perspective.
2. Experimental Program
2.1. Tests
Firstly in this experimental campaign, a detailed characterization of all aggregates used in the production of concrete was made.
The physical characterization of the aggregates involved the following tests: particle density and water absorption [
14], bulk density and volume of voids [
15], shape index [
16], Los Angeles wear [
17] and humidity content [
18].
Table 1 shows the tests performed to characterize the mechanical properties of the shotcrete mixes with RA.
It should be referred that the mechanical tests were always performed on core specimens (extracted from slabs produced with shotcrete) with a diameter of 98 mm. The ultrasound pulse velocity determination was carried out in core specimens which were then tested for compressive strength at 28 days.
2.2. Materials
In this research, limestone gravel and alluvial rolled sand were used as NA, respectively, as coarse and fine aggregates. RA from concrete were obtained by crushing a C30/37 strength class concrete with a maximum aggregate size of 14 mm. All the aggregates were added to the mixes completely dry. Type I 42.5 R cement was also used.
Table 2 shows the physical properties of the aggregates used. When compared to NA, it is confirmed (as stated in the introduction) that RA have lower density and higher water absorption capacity. This derives from the nature and porosity of the RA from concrete. For the same reason and because they possess more elongated shapes, RA present a lower bulk density than NA.
Table 2 also shows that the RA display a higher shape index than NA. This can lead to a lower workability of the concrete mix with RA compared to that of the reference concrete (RC), which has to be balanced by a higher w/c ratio.
It was also found that, due to their composition, RA show a lower resistance to fragmentation than NA.
2.3. Mixes Design
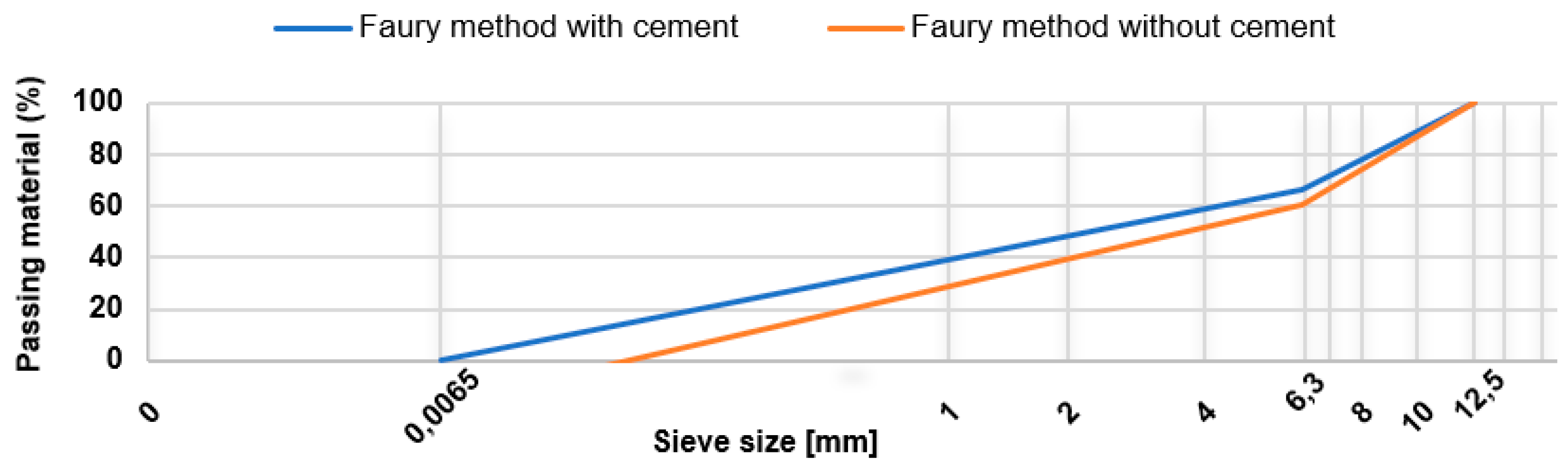
The composition of the reference concrete was determined by the Faury method for a target strength belonging to class C30/37 (
Figure 1). The maximum aggregate size used was 12.5 mm. Concrete compositions with RA were based on that of reference concrete. However, in order to keep the concrete workability constant (125 ± 25 mm slump), the w/c ratios of the concrete mixes with RA were increased.
Table 3 shows the final composition of the concrete mixes studied.
3. Mechanical Properties
Regarding the mechanical properties, as stated, the bond strength (by pull-off), compressive and splitting tensile strengths, secant modulus of elasticity, abrasion resistance and ultrasound pulse velocity were determined.
Table 4 provides a summary of the hardened state mechanical properties.
Regarding bond strength, no clear variation of this property with the incorporation of CRCA in concrete was found. As for compressive strength, it decreased as the percentage of the replacement of CNA with CRCA increased. Maximum reductions between 20% and 30% were obtained. This result is in agreement with those of several authors who analyzed cast RAC and obtained maximum reductions within this range. Even so, at seven days, the strength values of (RAC) shotcrete compared to cast RAC were lower, which supports the hypothesis that hardening is slower in the former than in the latter.
With respect to tensile strength, the incorporation of CRCA led to non-significant influence, as also reported by other authors, with maximum decreases of 15%, which are clearly lower than those in compressive strength. The reason for this is that the bond between the cement paste and CRCA is improved (compared to CNA) due to their shape and higher water absorption capacity.
The ultrasound pulse velocity decreased as the CRCA incorporation increased, which is consistent with the higher porosity of these aggregates that leads to a concrete mix with lower quality.
The modulus of elasticity was one of the properties mostly affected by the replacement of CNA with CRCA, with reductions of up to 31%. This stems from the higher deformability of the CRCA and lower strength of the bonded cement paste, the latter promoting further degradation of stress transmission capacity between the various concrete constituents. With respect to cast concrete, the reductions obtained (by the incorporation of CRCA) were more significant. The maximum aggregate size adopted also played a role, since the smaller the size the higher the porosity, and thus the higher the deformability and the lower the modulus of elasticity.
Finally, the abrasion resistance increased with the incorporation of CRCA as a result of the higher roughness and porosity of these aggregates, which yielded a better bonding to the cement paste and thus a better adhesion to concrete. Hence, the prevailing tendency was the improvement of this property with the incorporation of this type of aggregate. This result is in agreement with those of other researches, in which reductions in depth loss between 10% and 15% were obtained, showing that this property indeed improves when CRCA are incorporated in concrete.
4. Technical Viability
4.1. Case Study
Nowadays, the analysis and design of tunnels in urban environments require the use of numerical simulations to simulate with accuracy complex geometries of the tunnel and ground layering. For simplicity’s sake, the case study selected is a deep tunnel in a rock massif (hydrostatic stress field of 5 MPa), with a 3 m radius circular cross-section, where the analytical method proposed by Carranza-Torres and Fairhurst [
11] is valid and is briefly described in Annex 1. In this example, stress relief factor λ is taken equal to 85% and lining thickness, t
c, is equal to 200 mm for CNA shotcrete.
For the lining of the tunnel, shotcrete with different CRCA incorporation ratios (IR) was considered, whose mechanical properties were determined experimentally by Duarte et al. [
25].
Table 5 shows the values of the design compressive strength and modulus of elasticity obtained, including the percentage of reduction of the mechanical properties in relation to the shotcrete mix without incorporation of CRCA (IR0).
Table 5 shows that incorporating CRCA in the mix results in lower mechanical properties, ranging from about −3% for IR20 to −31% for IR100. For tunnels, the reduction of strength and stiffness in the shotcrete with recycled aggregates can be balanced by an increase of the lining’s thickness. The lining’s equivalent thickness for different CRCA incorporation ratios was computed for two criteria: (i) lining with similar stiffness and (ii) lining with similar yield stress.
4.2. Elastic Radial Stiffness Criterion, Ks
In this section, it is assumed that each shotcrete mix considered has a similar stiffness, namely the elastic radial stiffness, Ks, is equal to 636 MPa/m (tc = 200 mm for CNA shotcrete).
Table 6 quantifies the differences in yield pressure and equivalent thickness. For IR20 and IR50, the thickness increase is small (<15 mm, 3% and 7%, respectively). The thickness increase is significant (42%, 83 mm) for IR100 only.
Table 6 supports the conclusion that both IR20 and IR50 are competitive solutions from a technical point of view, with small increases of the lining’s thickness (<7%).
4.3. Maximum Pressure Criterion,
In this section, it is assumed that each shotcrete mix considered has a similar yield stress: 1.43 MPa (t
c = 200 mm for CNA shotcrete).
Table 7 quantifies the differences in stiffness and equivalent thickness. For IR20, the equivalent thickness increases 12% (24 mm), which can be considered acceptable, while IR50 and IR100 require thickness increments over 28% (more than 50 mm).
For cases where yield stress criterion is relevant, only the IR20 mix can be considered equivalent to IR0, as the other options may be compromised by an increase of the lining thickness over 50 mm.
5. Economic Viability
Adopting the equivalent thicknesses determined in
Section 3, the economic viability analysis of CRCA shotcrete is presented in this section. Based on data collected from Portuguese tunneling companies, the estimation of the current costs range to produce dry-mix shotcrete is shown in
Table 8.
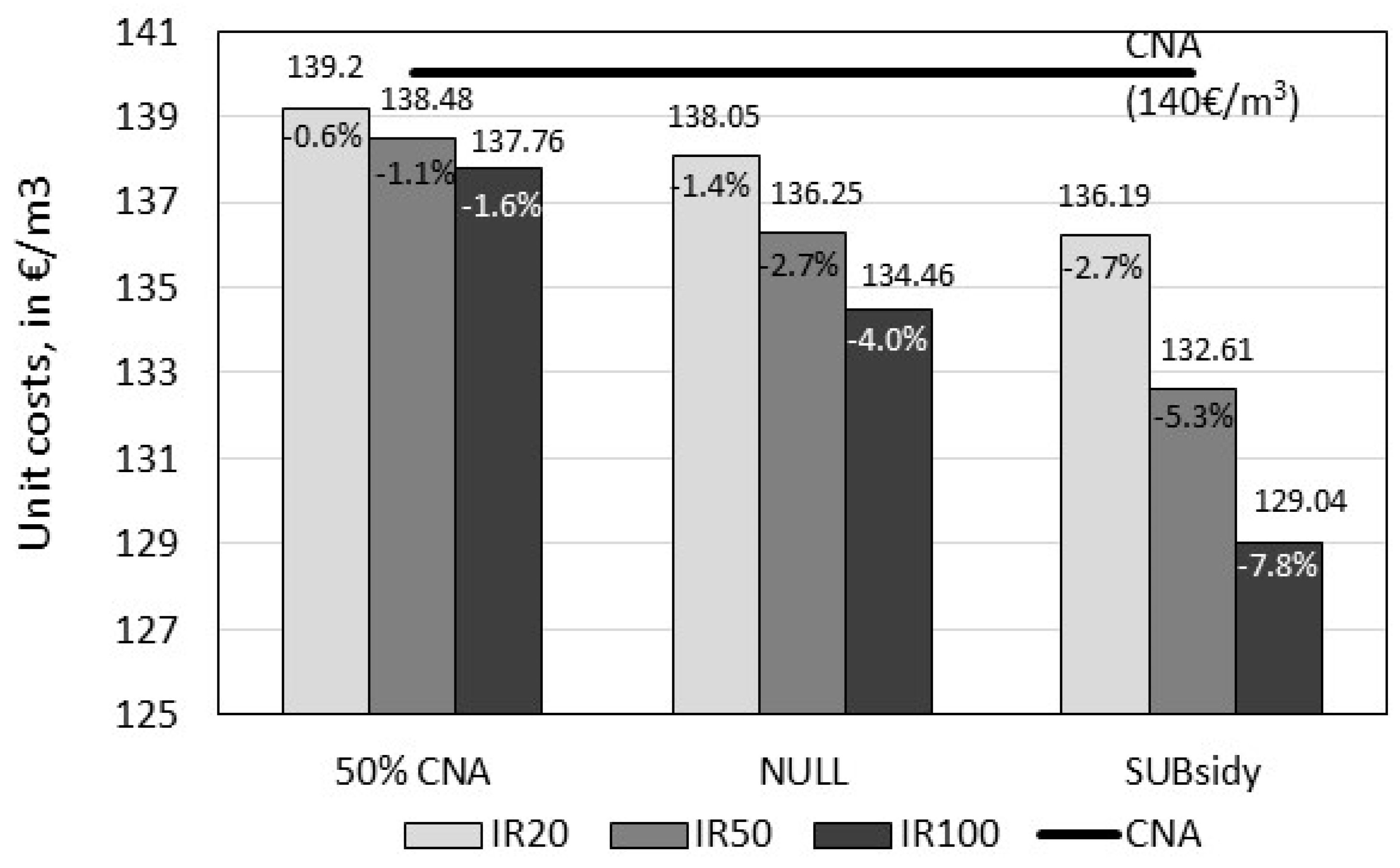
Figure 2 shows the unit costs, in €/m
3, of the different shotcrete scenarios, assuming three possible costs for CRCA to assess its impact:
Scenario 1 (50% CNA)—the recycled aggregates’ cost is taken as equal to 50% of the natural aggregates (7.5 €/m3);
Scenario 2 (NULL) —the recycled aggregates’ cost is zero (taking into account that CDW producers are ready to pay to get rid of it);
Scenario 3 (SUB) —there is a subsidy equal to 7.5 €/m3 to promote recycled aggregates’ use. Because the cost of CRCA is smaller than that of CNA, the unit cost of shotcrete with incorporation of CRCA is smaller.
Figure 2 shows that incorporating recycled aggregates in shotcrete generates small variations is cost per cubic meter (<8%), for the three scenarios analyzed.
Table 9 shows the cost of the lining per unit length of the tunnel for the two cases for which equivalent thickness was determined: similar stiffness and similar yield stress.
In all cases, for simplicity’s sake, rebound losses equal to 25% of the shotcrete’s theoretical volume were assumed.
For the case in which CRCA cost is 50% of the cost of CNA, the lining’s cost per unit length of the tunnel with CRCA is slightly higher than without CRCA for IR20 (2.3%) and IR50 (5.3%) for Case 1. For the other IR’s and cases, the increase in cost is higher than 10%.
Because the recycled aggregates’ cost represents less than 15% of the total production costs, an increase in thickness due to the lower mechanical properties leads to higher consumption of the other components, and thus costs increase.
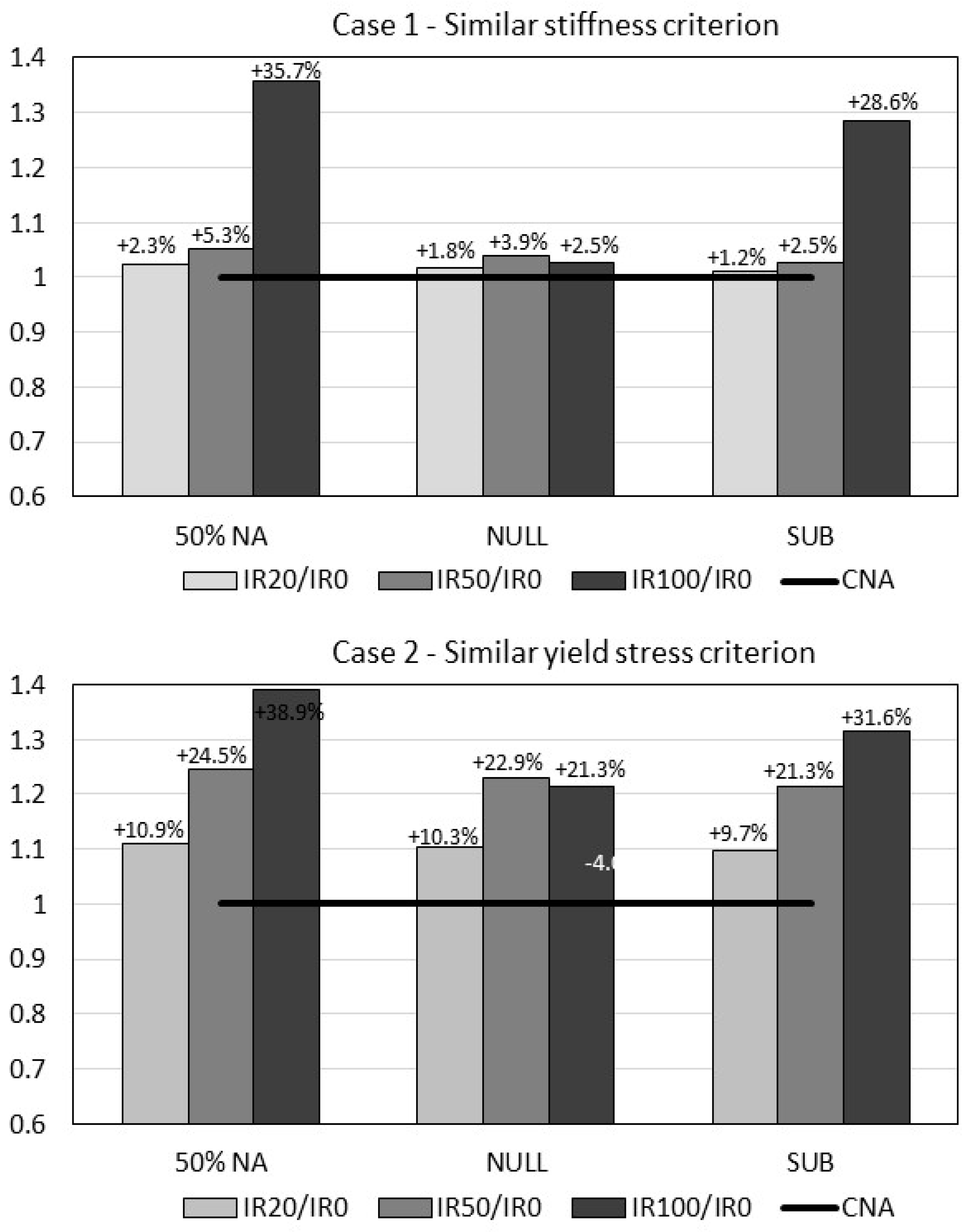
Figure 3 shows the variation of the lining’s cost per unit length of tunnel for the three hypothetical costs of CRCA.
Figure 3 shows that the lining’s cost per unit length of the tunnel is fairly insensitive to the cost of CRCA. In particular for Case 1, similar stiffness criterions-mixes IR20 and IR50 lead to marginal increases in the lining’s cost (between 1.2% and 5.3%), while the other cases studied lead to variations higher than 10%.
So, IR20 and IR50 are interesting alternatives for CRCA incorporation in dry-mix shotcrete solutions. The remaining cases require a larger increase in lining’s thickness, which is economically unattractive.
6. Conclusions
The technical economic analysis of dry-mix shotcrete incorporating CRCA was performed considering three different replacement ratios of CNA with CRCA, for two cases: similar stiffness criterion and similar yield stress criterion.
For deep tunnels, a small increase in the lining’s thickness is required to have linings of similar stiffness for the IR20 and IR50 mixes, which shows their technical viability. An economic assessment proved that both mixes can be competitive against a conventional shotcrete, with very small increases in the lining’s cost per unit length of the tunnel.
A sensitivity study to assess the impact of CRCA cost on lining’s cost per unit length shows that CRCA cost is very small, and therefore its influence on the overall costs is also small.
Based on this study, it can be concluded that using coarse recycled concrete aggregates in tunnels can be an interesting solution for the IR20 and IR50 mixes, with marginal impact on thickness and the lining’s cost per unit length of tunnel.
The viability of using CRCA in tunnel construction practice should be analyzed considering the specific data from each project, such as costs to produce dry-mix shotcrete and the strength and deformability study.
Author Contributions
Conceptualization, G.D., R.C.G., J.d.B., M.B., J.N. methodology, G.D., R.C.G, J.d.B., M.B., J.N. formal analysis, G.D., R.C.G., J.d.B. validation, J.d.B. investigation, G.D., R.C.G., J.N. data curation, G.D., R.C.G., J.N. writing—original draft, G.D., R.C.G. writing—review and editing, G.D., R.C.G., J.d.B., M.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The authors wish to thank CERIS (Civil Engineering Research and Innovation for Sustainability) research centre and FCT (Foundation for Science and Technology).
Conflicts of Interest
The authors declare no conflict of interest.
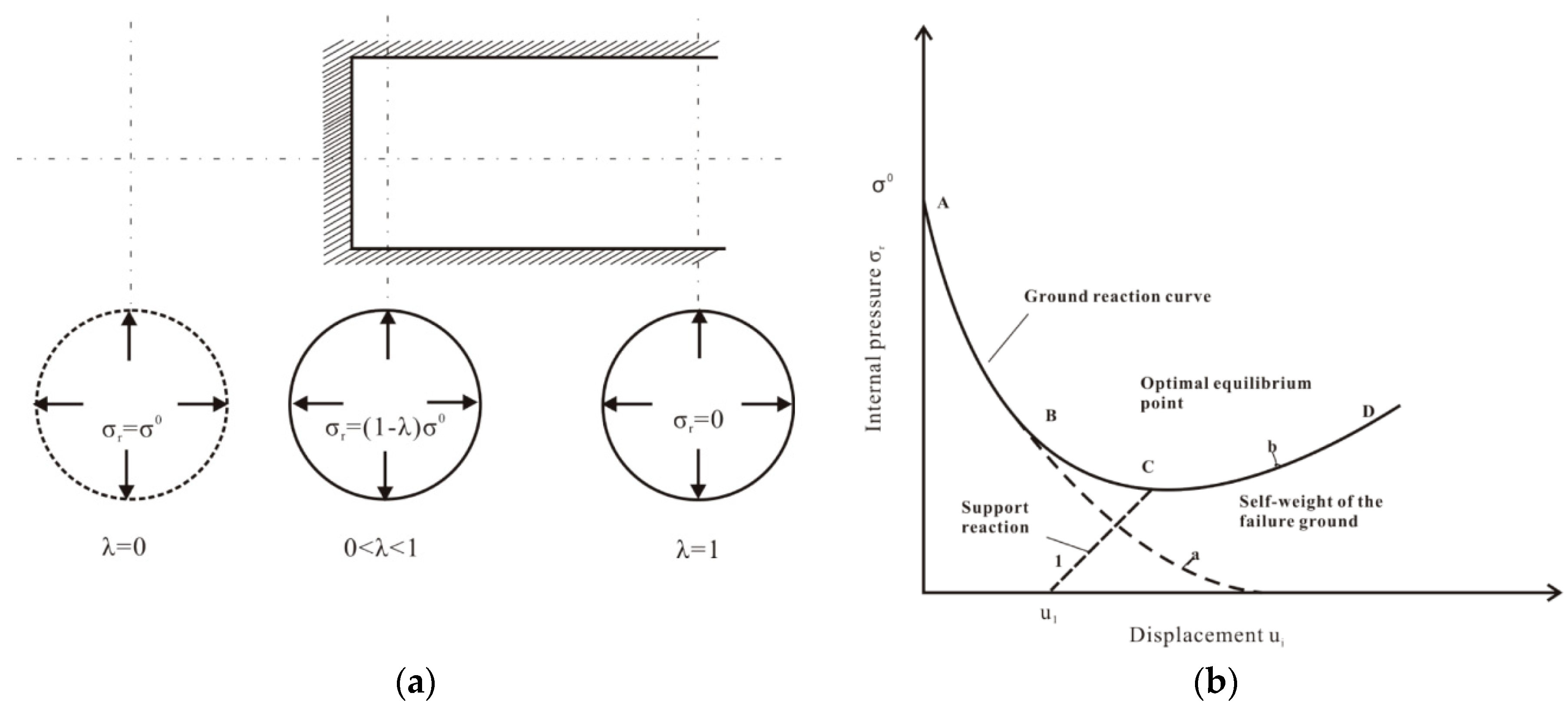
Appendix A. The Convergence-Confinement Method
The stress redistribution and three-dimensional deformation induced by tunnel excavation and lining installation during construction is a very complex three-dimensional problem. To simulate tunnel construction, the convergence-confinement method in plane strain conditions is widely used. The method relies on the ground reaction curve, which describes the response of the ground around the tunnel [
26,
27], and the support reaction curve, which describes the lining response.
The two-dimensional tunneling problem is illustrated in
Figure A1a. The tunneling process is represented by increasing the λ value from zero to one.
Figure A1b shows the main characteristics of the convergence-confinement method. The convergence curve corresponds to the internal pressure versus the tunnel radial displacement. The radial displacement of the tunnel increases as the internal pressure decreases. The tunnel can be self-stabilized without a liner (Curve [a]) in
Figure A1b) or the surrounding ground can fail which leads to an increase in the ground load acting on the tunnel lining (Curve [b] in
Figure A1). In the latter case, a liner must be installed to keep the stability of the tunnel.
Based on the convergence-confinement method, Carranza-Torres and Fairhurst [
11] proposed a set of analytical equations valid for deep circular tunnels in rock. These equations are used to ensure the technical viability of the shotcrete solutions proposed in a simplified manner, bypassing complex numerical simulations necessary for shallow tunnels and non-circular shapes, but without loss of generalization capacity of the conclusions.
Figure A1.
Convergence confinement method: (
a) evolution of tunnel convergence with face advance; (
b) ground reaction curve and support reaction curve (adapted from Orestes [
13]).
Figure A1.
Convergence confinement method: (
a) evolution of tunnel convergence with face advance; (
b) ground reaction curve and support reaction curve (adapted from Orestes [
13]).
The problem is studied as a two-dimensional plane strain case, in which the pressure, pi, and the radial displacement, ur, are constant in the tunnel walls.
The ground reaction curve is obtained from the elastoplastic solution of a circular opening subjected to a hydrostatic stress field,
σ0. Equations (A1) and (A2) present the elastic and plastic portions of the curve, respectively.
where
urel is the elastic radial displacement of the massif,
So the uniform tension around the tunnel,
pi the pressure of the walls at the tunnel, and
Grm the shear modulus of the rock massif.
where
Kψ is the dilatancy coefficient,
Picr the critical pressure, related with the transition of an elastic to plastic behavior of the tunnel walls, and
Rpl the radius of the failed region, developed when
pi <
Picr.
The shotcrete support is modeled with perfect elastoplastic behavior, with an elastic radial stiffness
ks, and maximum pressure,
ps,max. Equations (A3)–(A5) describe the support behavior [
28].
where
ps is the pressure in the support,
fcd the design compressive strength of the shotcrete,
ur the radial displacement of the support,
νc the Poisson’s coefficient of the shotcrete,
Ec the modulus of elasticity of the shotcrete,
R the radius of the shotcrete ring and
tc representing its thickness.
References
- European Commission. EU Construction & Demolition Waste Management Protocol. 2017. Available online: https://www.google.com.hk/url?sa=t&rct=j&q=&esrc=s&source=web&cd=3&ved=2ahUKEwjNvaWNjODoAhUiGaYKHfWHBWUQFjACegQIAxAB&url=https%3A%2F%2Fec.europa.eu%2Fdocsroom%2Fdocuments%2F26368%2Fattachments%2F3%2Ftranslations%2Fen%2Frenditions%2Fnative&usg=AOvVaw3cvos29Vbsj1923H9gahcM (accessed on 10 October 2019).
- Bravo, M.; de Brito, J.; Pontes, J.; Evangelista, L. Mechanical performance of concrete made with aggregates from construction and demolition waste recycling plants. J. Clean. Prod. 2015, 99, 59–74. [Google Scholar] [CrossRef]
- Bravo, M.; de Brito, J.; Pontes, J.; Evangelista, L. Durability performance of concrete with recycled aggregates from construction and demolition waste plants. Constr. Build. Mater. 2015, 77, 357–369. [Google Scholar] [CrossRef]
- Chan, C. Use of Recycled Aggregate in Shotcrete and Concrete; The University of British Columbia: Vancouver, Canada, 1998. [Google Scholar]
- Broere, W. Urban underground space: Solving the problems of today’s cities. Tunn. Undergr. Space Technol. 2016, 55, 245–248. [Google Scholar] [CrossRef]
- Kolymbas, D. Tunnelling and Tunnel Mechanics: A Rational Approach to Tunnelling; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Bentur, A.; Mindess, S. Fibre Reinforced Cementitious Composites, 2nd ed.; Taylor & Francis: Abingdon, UK, 2006. [Google Scholar]
- Jovicic, V.; Šušteršic, J.; Vukelic, Z. The application of fibre reinforced shotcrete as primary support for a tunnel in flysch. Tunn. Undergr. Space Technol. 2009, 24, 723–730. [Google Scholar] [CrossRef]
- Massone, L.; Nazar, F. Analytical and experimental evaluation of the use of fibers as partial reinforcement in shotcrete for tunnels in Chile. Tunn. Undergr. Space Technol. 2018, 77, 13–25. [Google Scholar] [CrossRef]
- Yang, J.M.; Kim, J.; Yoo, D. Performance of shotcrete containing amorphous fibers for tunnel applications. Tunn. Undergr. Space Technol. 2017, 64, 85–94. [Google Scholar] [CrossRef]
- Carranza-Torres, C.; Fairhurst, C. Application of the convergence-confinement method design to rock masses that satisfy the Hoek-Brown failure criterion. J. Tunn. Undergr. Space Technol. 2000, 15, 187–213. [Google Scholar] [CrossRef]
- Panet, M.; Guenot, A. Analysis of convergence behind the face of a tunnel: Tunnelling 82, proceedings of the 3rd international symposium, Brighton, 7–11 June 1982, P197–204. Publ London: IMM, 1982. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1983, 20, A16. [Google Scholar]
- Oreste, P. Analysis of structural interaction in tunnels using the convergence-confinement approach. J. Tunn. Undergr. Space Technol. 2003, 18, 347–363. [Google Scholar] [CrossRef]
- NP EN 1097-6. Tests for Mechanical and Physical Properties of Aggregates—Part 6: Determination of Particle Density and Water Absorption; IPQ: Lisbon, Portugal, 2003. [Google Scholar]
- NP EN 1097-3. Tests for Mechanical and Physical Properties of Aggregates—Part 3: De-termination of Loose Bulk Density and Voids; IPQ: Lisbon, Portugal, 2003. [Google Scholar]
- NP EN 933-4. Tests for Geometrical Properties of Aggregates—Part 4: Determination of Particle Shape e Shape Index; IPQ: Lisbon, Portugal, 2002. [Google Scholar]
- NP EN 1097-2. Tests for Mechanical and Physical Properties of Aggregates—Part 2: Methods for the Determination of Resistance to Fragmentation; IPQ: Lisbon, Portugal, 2002. [Google Scholar]
- NP EN 1097-5. Tests for Mechanical and Physical Properties of Aggregates—Part 5: Determination of the Water Content by Drying in a Ventilated Oven; IPQ: Lisbon, Portugal, 2002. [Google Scholar]
- EN 1542. Products and Systems for the Protection and Repair of Concrete Structures. Test Methods; Measurement of Bond Strength by Pull-Off: Brussels, Belgium, 1999. [Google Scholar]
- EN 12390-3. Testing Hardened Concrete. Compressive Strength of Test Specimens; Committee European for Normalization: Brussels, Belgium, 2003. [Google Scholar]
- EN 12390-6. Testing Hardened Concrete. Tensile Splitting Strength of Test Specimens; Committee European for Normalization: Brussels, Belgium, 2003. [Google Scholar]
- LNEC E-397. Determination of the Modulus of Elasticity in Compression (in Portuguese); National Laboratory of Civil Engineering (LNEC): Lisbon, Portugal, 1993. [Google Scholar]
- DIN 52108. Testing of Inorganic Non-metallic Materials—Wear Test Using the Grinding Wheel According to Boehme. In Deutsches Institut Fur Normung E.V; German National Standard: Berlin, Germany, 2010. [Google Scholar]
- EN 12504-4. Testing Concrete. Determination of Ultrasonic Pulse Velocity; Committee European for Normalization: Brussels, Belgium, 2004. [Google Scholar]
- Duarte, G.; Bravo, M.; de Brito, J.; Nobre, J. Mechanical performance of shotcrete produced with recycled coarse aggregates from concrete. Constr. Build. Mater. 2019, 210, 696–708. [Google Scholar] [CrossRef]
- Amberg, W.; Lombardi, G. An elasto-plastic analysis of the stress-strain state around an underground opening, Part II. In Proceedings of the 3rd Congress of ISRM, Denver, Colorado, USA, 1974; Volume 1, pp. 1049–1060. [Google Scholar]
- Panet, M. Understanding deformations in tunnels. In Comprehensive Rock Engineering; Pergamon Press: Oxford, UK, 1993; Volume 1, pp. 663–690. [Google Scholar]
- Hoek, E.; Brown, E.T. Underground Excavations in Rock; CRC Press: Boca Raton, FL, USA, 1980; 532p, ISBN 9780419160304. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).