Nanomaterials’ Influence on the Performance of Thermal Insulating Mortars—A Statistical Analysis
Abstract
1. Introduction
2. Materials and Methods
2.1. General Considerations
- The mortars had to be in the market, or a result of published research;
- A complete set of characteristics had to be available for each formulation (Table 1).
2.2. Uni and Bivariate Analysis
2.3. Principal Components and Factor Analysis
2.4. Cluster Analysis
2.5. Regression Models
3. Results and Discussion
3.1. Uni and Bivariate Analysis
3.1.1. Univariate Analysis
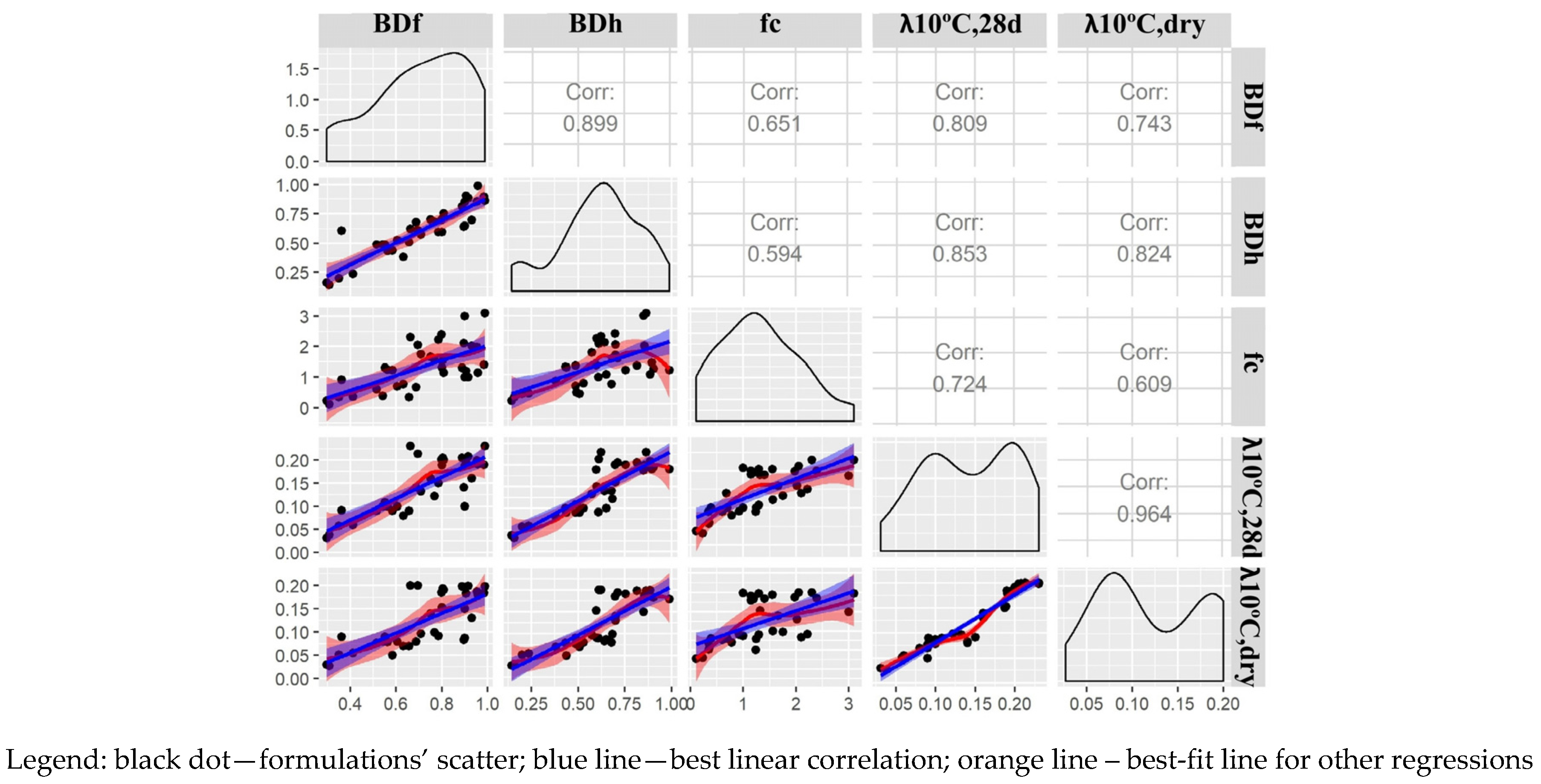
3.1.2. Bivariate Analysis
3.1.3. Discussion of the Uni and Bivariate Analysis
3.2. Principal Components and Factor Analysis
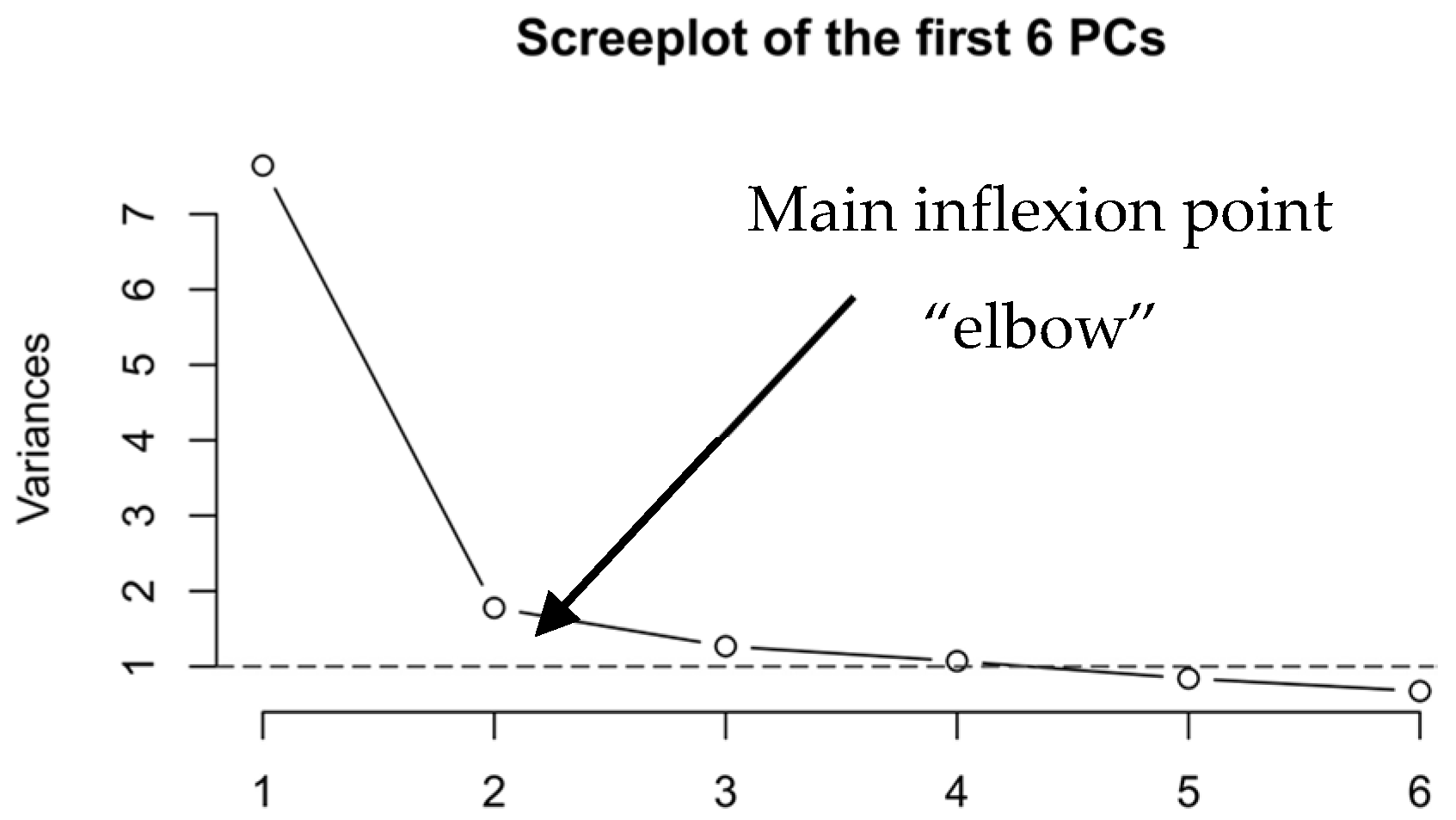
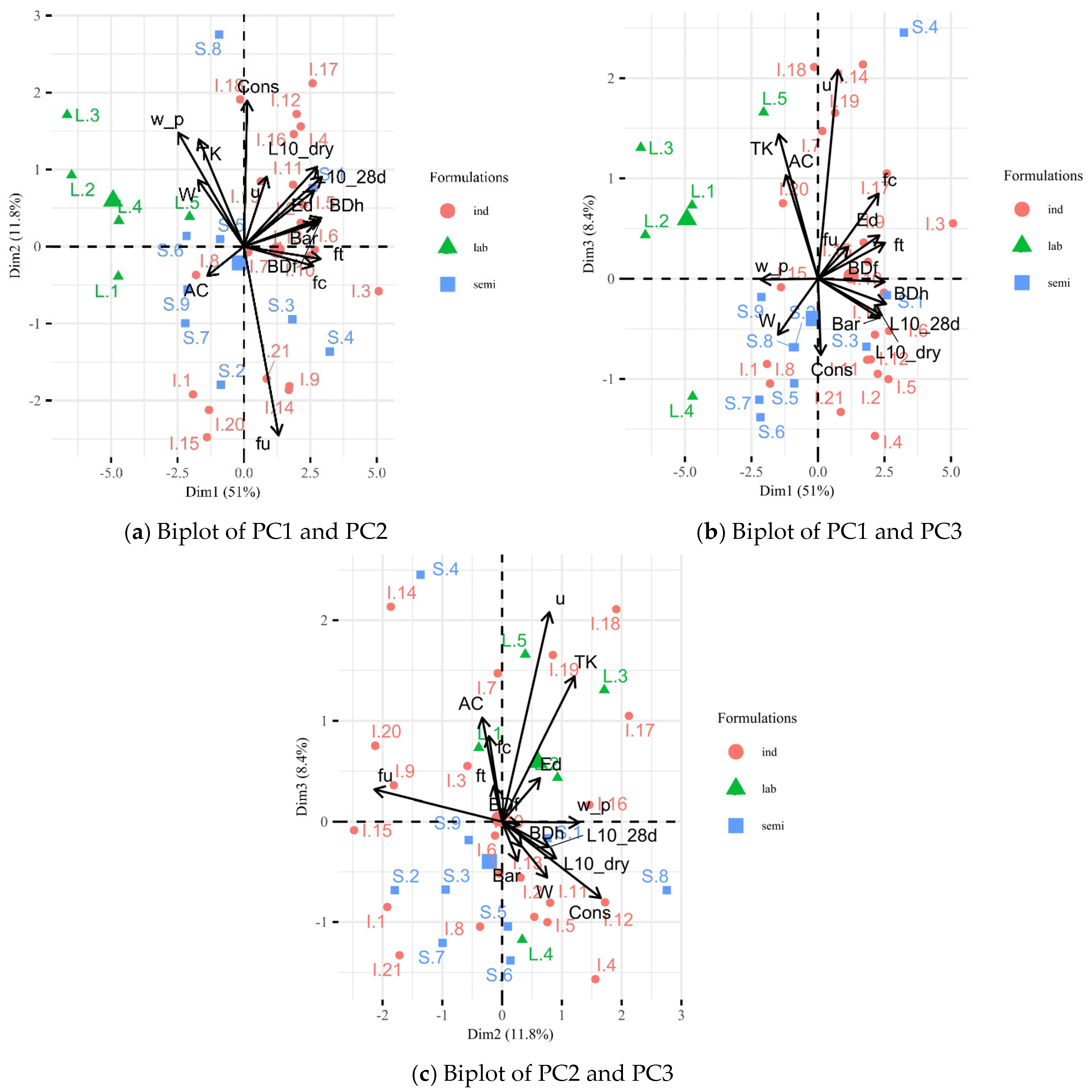
3.2.1. PCA Construction and Factor Analysis
3.2.2. Discussion of the PCA and Factor Analysis
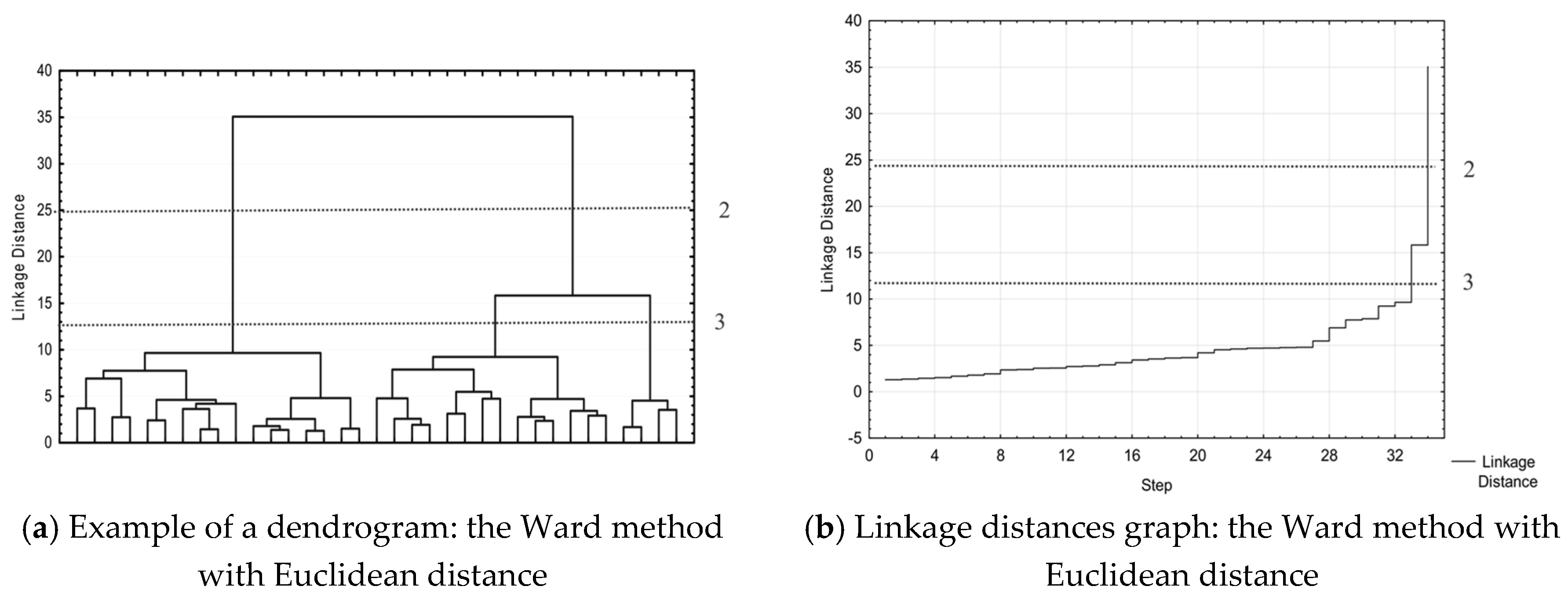
3.3. Cluster Analysis
3.3.1. Cluster Methods Results
3.3.2. Discussion of the Cluster Analysis
3.4. Regression Models
3.4.1. Regression Models Results
3.4.2. Discussion of the Regression Models
3.5. Application of the Multivariate Statistical Methods
- Due to the ease of application, the uni and bivariate analysis allow us to obtain a general overview of the sample’s characteristics, the scatter of the data, and the existence of outliers. Therefore, this analysis is so simple to apply that it is considered a good starting point before applying any other statistical technique;
- The PCA and factor analysis were revealed to be the techniques that allowed to obtain more insights that can further help to develop these products. They allowed us to find the interdependence between several characteristics and to verify the influence that the use of nanomaterials has on the performance of these formulations. These techniques can be an interesting tool to develop new formulations in the future;
- The cluster analysis, although allowing us to separate formulations into different origins, only served as a verification for the results obtained in the PCA and factor analysis, reinforcing the influence that the use of nanomaterials has on the performance. However, when considering a large amount of data, it can help the researchers to discover products that are intimately related;
- The regression models allow us to find predictive equations, when possible, for a desired dependent variable. In this case, they allowed us to predict the thermal conductivity at 10 °C and in the dry state, when knowing the thermal conductivity at 10 °C at 28 days, several days earlier.
4. Conclusions
- With the uni and bivariate analysis, it was possible to confirm: correlations between the ratio water:powder (w/p) and the remaining variables; the influence that kneading water has on the mortars’ performance; correlations between the bulk-density hardened state (BDh) and the bulk-density fresh state (BDf), and correlations between compressive strength (fc), the dynamic modulus of elasticity (Ed.), and flexural strength (ft), and other more interesting ones, such as between BDh, λ10°C,28days, and λ10°C,dry;
- PCA and factor analysis allowed us to identify three main components, the latent structure of which allowed us to classify them into the following categories: thermo-mechanical, internal cohesion, and microstructural porosity, and water permeability behaviours. Here, the most relevant finding was the achievement of a factor showing a significant impact of the use of nanomaterials as thermal insulating aggregates, where the increase in mechanical performance decreases the thermal performance. So, both the formulation and the addition of thermal insulating aggregates, like the silica aerogel, influenced their behaviour;
- With the cluster analysis, the findings of PCA were enhanced and verified. Three groups of formulations were obtained, showing the importance that nano thermal insulating aggregates, in conjunction with the base formulations (laboratory, industrial, or industrial tuned in the laboratory), have on the overall performance;
- Although simple and multiple linear regression models were studied, the simplest model was the one with the best results. Therefore, it was possible to obtain a new model that can allow researchers to save time, allowing them to predict λ10°C,dry earlier.
Notation and Acronyms
| Adhesion | fu | Flexural strength | ft |
| Air content | AC | Liquid water permeability | TK |
| Bulk-density fresh state, 20 °C | BDF | Principal Components Analysis | PCA |
| Bulk-density hardened state, 20 °C and 65%RH | BDH | Powder bulk density | Bar |
| Capillary water absorption | W | Ratio water: Powder | w/p |
| Compressive strength | fc | Thermal conductivity at 10 °C, 28 days | λ10°C,28days |
| Consistency | Cons | Thermal conductivity at 10 °C, dry state | λ10°C,dry |
| Dynamic modulus of elasticity | Ed | Water vapour permeance | Λ |
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- European Commission. Energy Performance of EU Buildings. Available online: https://ec.europa.eu/energy/en/topics/energy-efficiency/energy-performance-of-buildings (accessed on 12 December 2019).
- Belussi, L.; Barozzi, B.; Bellazzi, A.; Danza, L.; Devitofrancesco, A.; Fanciulli, C.; Ghellere, M.; Guazzi, G.; Meroni, I.; Salamone, F.; et al. A review of performance of zero energy buildings and energy efficiency solutions. J. Build. Eng. 2019, 25, 100772. [Google Scholar] [CrossRef]
- Pedroso, M.; de Brito, J.; Dinis Silvestre, J. Characterization of walls with eco-efficient acoustic insulation materials (traditional and innovative). Constr. Build. Mater. 2019, 222, 892–902. [Google Scholar] [CrossRef]
- Hipin Project. High Performance Insulation Based on Nanostructure Encapsulation of Air. Available online: http://www.hipin.eu/ (accessed on 5 January 2020).
- Koebel, M.M.; Wernery, J.; Malfait, W.J. Energy in buildings—Policy, materials and solutions. MRS Energy Sustain. 2017, 4, E12. [Google Scholar] [CrossRef]
- Ibrahim, M.; Nocentini, K.; Stipetic, M.; Dantz, S.; Caiazzo, F.G.; Sayegh, H.; Bianco, L. Multi-field and multi-scale characterization of novel super insulating panels/systems based on silica aerogels: Thermal, hydric, mechanical, acoustic, and fire performance. Build. Environ. 2019, 151, 30–42. [Google Scholar] [CrossRef]
- CEN. EN 998-1: 2016. Specification for Mortar for Masonry—Part 1: Rendering and Plastering Mortar; Comité Européen de Normalisation: Brussels, Belgium, 2016. [Google Scholar]
- Pedroso, M.; Flores-Colen, I.; Silva, L.; Sequeira, P.; Silvestre, J.D.; Gomes, M.G. Mechanical resistance characteristics of super insulating thermal mortars: State of the art. In Proceedings of the 3rd Congress on Sustainable Construction Materials, Coimbra, Portugal, 14–16 February 2018. (In Portuguese). [Google Scholar]
- Brás, A.; Leal, M.; Faria, P. Cement-cork mortars for thermal bridges correction. Comparison with cement-EPS mortars performance. Constr. Build. Mater. 2013, 49, 315–327. [Google Scholar] [CrossRef]
- Dixit, A.; Pang, S.D.; Kang, S.-H.; Moon, J. Lightweight structural cement composites with expanded polystyrene (EPS) for enhanced thermal insulation. Cem. Concr. Compos. 2019, 102, 185–197. [Google Scholar] [CrossRef]
- Brás, A.; Gonçalves, F.; Faustino, P. Cork-based mortars for thermal bridges correction in a dwelling: Thermal performance and cost evaluation. Energy Build. 2014, 72, 296–308. [Google Scholar] [CrossRef]
- Pedroso, M.; Flores-Colen, I. The influence of dimension and content of natural organic fibrous materials on the multi-performance of cement-based composites: A statistical approach. Constr. Build. Mater. 2020, 231, 117175. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, B.; Yu, F. Preparation of EPS-Based Thermal Insulation Mortar with Improved Thermal and Mechanical Properties. J. Mater. Civil. Eng. 2019, 31, 04019183. [Google Scholar] [CrossRef]
- Silvestre, J.D.; Castelo, A.M.P.; Silva, J.J.B.C.; de Brito, J.M.C.L.; Pinheiro, M.D. Retrofitting a Building’s Envelope: Sustainability Performance of ETICS with ICB or EPS. Appl. Sci. 2019, 9, 1285. [Google Scholar] [CrossRef]
- Pereira, V. Rehabilitation of ancient buildings walls, meeting the thermal requirements and maintaining the architectural façades. In Proceedings of the 9th International Masonry Conference 2014, Guimarães, Portugal, 7–9 July 2014. [Google Scholar]
- Freitas, V.P.D.; Miranda, A.M. Main Pathologies Associated with External Thermal Insulation Composite Systems (ETICS)—LFC-IC-282A-2014; APFAC: Porto, Portugal, 2014. (In Portuguese) [Google Scholar]
- Ashby, M.; Ferreira, P.J.; Schodek, D. Nanomaterials, Nanotechnologies and Design: An Introduction for Engineers and Architects, 1st ed.; Butterworth-Heinemann: Oxford, UK, 2009. [Google Scholar] [CrossRef]
- Hanus, M.J.; Harris, A.T. Nanotechnology innovations for the construction industry. Prog. Mater. Sci. 2013, 58, 1056–1102. [Google Scholar] [CrossRef]
- Jelle, B.P.; Baetens, R.; Gustavsen, A. Aerogel Insulation for Building Applications. In The Sol-Gel Handbook, 1st ed.; Levy, D., Zayat, M., Eds.; Elsevier B.V.: Amsterdam, The Netherlands, 2015; Volume 3, pp. 761–769. [Google Scholar]
- Berardi, U. Aerogel-enhanced insulation for building applications. In Nanotechnology in Eco-Efficient Construction, 2nd ed.; Pacheco-Torgal, F., Diamanti, M., Nazari, A., Granqvist, C.G., Pruna, A., Amirkhanian, S.N., Eds.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 395–416. [Google Scholar] [CrossRef]
- Reichenauer, G. Structural Characterization of Aerogels. In Aerogels Handbook: Advances in Sol-Gel Derived Materials and Technologies; Aegerter, M.A., Leventis, N., Koebel, M.M., Eds.; Springer: New York, NY, USA, 2011; pp. 449–498. [Google Scholar] [CrossRef]
- Vatjai, R. Science and Engineering of Nanomaterials. In Springer Handbook of Nanomaterials, 1st ed.; Vatjai, R., Ed.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 1–36. [Google Scholar]
- Baetens, R.; Jelle, B.P.; Gustavsen, A. Aerogel insulation for building applications: A state-of-the-art review. Energy Build. 2011, 43, 761–769. [Google Scholar] [CrossRef]
- Lu, H.; Luo, H.; Leventis, N. Mechanical Characterization of Aerogels. In Aerogels Handbook: Advances in Sol-Gel Derived Materials and Technologies; Aegerter, M.A., Leventis, N., Koebel, M.M., Eds.; Springer: New York, NY, USA, 2011; pp. 499–535. [Google Scholar] [CrossRef]
- Júlio, M.d.F.; Soares, A.; Ilharco, L.M.; Flores-Colen, I.; de Brito, J. Silica-based aerogels as aggregates for cement-based thermal renders. Cem. Concr. Compos. 2016, 72, 309–318. [Google Scholar] [CrossRef]
- Carlson, G.; Lewis, D.; McKinley, K.; Richardson, J.; Tillotson, T. Aerogel commercialization: Technology, markets and costs. J. Non-Cryst. Solids 1995, 186, 372–379. [Google Scholar] [CrossRef]
- Ebert, H. Thermal Properties of Aerogels. In Aerogels Handbook: Advances in Sol-Gel Derived Materials and Technologies, 1st ed.; Aegerter, M.A., Leventis, N., Koebel, M.M., Eds.; Springer: New York, NY, USA, 2011; pp. 537–581. [Google Scholar] [CrossRef]
- Bisson, A.; Rigacci, A.; Lecomte, D.; Achard, P. Effective thermal conductivity of divided silica xerogel beds. J. Non-Cryst. Solids 2004, 350, 379–384. [Google Scholar] [CrossRef]
- Ilharco, L.M.; Fidalgo, A.; Farinha, J.P.S.; Martinho, J.M.G.; Rosa, M.E.L. Nanostructured silica/polymer subcritical aerogels. J. Mater. Chem. 2007, 17, 2195. [Google Scholar] [CrossRef]
- Abu-Jdayil, B.; Mourad, A.-H.; Hittini, W.; Hassan, M.; Hameedi, S. Traditional, state-of-the-art and renewable thermal building insulation materials: An overview. Constr. Build. Mater. 2019, 214, 709–735. [Google Scholar] [CrossRef]
- Stahl, T.; Brunner, S.; Zimmermann, M.; Wakili, K.G.; Ghazi Wakili, K. Thermo-hygric properties of a newly developed aerogel based insulation rendering for both exterior and interior applications. Energy Build. 2012, 44, 114–117. [Google Scholar] [CrossRef]
- Westgate, P.; Paine, K.; Ball, R.J. Physical and mechanical properties of plasters incorporating aerogel granules and polypropylene monofilament fibres. Constr. Build. Mater. 2018, 158, 472–480. [Google Scholar] [CrossRef]
- Zhu, P.; Brunner, S.; Zhao, S.; Griffa, M.; Leemann, A.; Toropovs, N.; Malekos, A.; Koebel, M.M.; Lura, P. Study of physical properties and microstructure of aerogel-cement mortars for improving the fire safety of high-performance concrete linings in tunnels. Cem. Concr. Compos. 2019, 104, 103414. [Google Scholar] [CrossRef]
- Nanorender: Performance of Nanoaerogel Silica-Based Renders. Available online: http://www.florescolen.com/Documentacao/Executive_Summary(in English).pdf (accessed on 5 June 2019). (In Portuguese).
- Garrido, R.; Silvestre, J.D.; Flores-Colen, I.; Júlio, M.d.F.; Pedroso, M. Economic assessment of the production of subcritically dried silica-based aerogels. J. Non-Cryst. Solids 2019, 516, 26–34. [Google Scholar] [CrossRef]
- Ibrahim, M.; Biwole, P.H.; Achard, P.; Wurtz, E.; Ansart, G. Building envelope with a new aerogel-based insulating rendering: Experimental and numerical study, cost analysis, and thickness optimization. Appl. Energy 2015, 159, 490–501. [Google Scholar] [CrossRef]
- Fantucci, S.; Fenoglio, E.; Grosso, G.; Serra, V.; Perino, M.; Marino, V.; Dutto, M. Development of an aerogel-based thermal coating for the energy retrofit and the prevention of condensation risk in existing buildings. Sci. Technol. Built Environ. 2019, 4731, 1–10. [Google Scholar] [CrossRef]
- Pedroso, M.; Flores-Colen, I.; Silvestre, J.D.; Gomes, M.G.; Silva, L.; Ilharco, L. Physical, mechanical, and microstructural characterisation of an innovative thermal insulating render incorporating silica aerogel. Energy Build. 2020, 211, 109793. [Google Scholar] [CrossRef]
- Sousa, R.; Sousa, H.; Silva, L.; Flores-Colen, I.; Pedroso, M. Development of a wall system made with thermally optimised masonry and super insulation mortar render. Mason. Int. 2019, 32, 3–14. [Google Scholar]
- Ferreira, C.; Canhoto Neves, L.; Silva, A.; de Brito, J. Stochastic Petri net-based modelling of the durability of renderings. Autom. Constr. 2018, 87, 96–105. [Google Scholar] [CrossRef]
- Ghaffar, S.H.; Corker, J.; Fan, M. Additive manufacturing technology and its implementation in construction as an eco-innovative solution. Autom. Constr. 2018, 93, 1–11. [Google Scholar] [CrossRef]
- Granato, D.; Santos, J.S.; Escher, G.B.; Ferreira, B.L.; Maggio, R.M. Use of principal component analysis (PCA) and hierarchical cluster analysis (HCA) for multivariate association between bioactive compounds and functional properties in foods: A critical perspective. Trends Food Sci. Technol. 2018, 72, 83–90. [Google Scholar] [CrossRef]
- Moropoulou, A.; Polikreti, K.; Bakolas, A.; Michailidis, P. Correlation of physicochemical and mechanical properties of historical mortars and classification by multivariate statistics. Cem. Concr. Res. 2003, 33, 891–898. [Google Scholar] [CrossRef]
- Falchi, L.; Varin, C.; Toscano, G.; Zendri, E. Statistical analysis of the physical properties and durability of water-repellent mortars made with limestone cement, natural hydraulic lime and pozzolana-lime. Constr. Build. Mater. 2015, 78, 260–270. [Google Scholar] [CrossRef]
- Keleştemur, O.; Yildiz, S.; Gökçer, B.; Arici, E. Statistical analysis for freeze–thaw resistance of cement mortars containing marble dust and glass fiber. Mater. Des. 2014, 60, 548–555. [Google Scholar] [CrossRef]
- Sadowski, Ł.; Hoła, J.; Czarnecki, S.; Wang, D. Pull-off adhesion prediction of variable thick overlay to the substrate. Autom. Constr. 2018, 85, 10–23. [Google Scholar] [CrossRef]
- Neves, R.; Silva, A.; de Brito, J.; Silva, R.V. Statistical modelling of the resistance to chloride penetration in concrete with recycled aggregates. Constr. Build. Mater. 2018, 182, 550–560. [Google Scholar] [CrossRef]
- Potgieter-Vermaak, S.S.; Potgieter, J.H.; Worobiec, A.; van Grieken, R.; Marjanovic, L.; Moeketsi, S. Fingerprinting of South African ordinary Portland cements, cement blends and mortars for identification purposes—Discrimination with starplots and PCA. Cem. Concr. Res. 2007, 37, 834–843. [Google Scholar] [CrossRef]
- Yoon, S.; Monteiro, P.J.M.; Macphee, D.E.; Glasser, F.P.; Imbabi, M.S.E. Statistical evaluation of the mechanical properties of high-volume class F fly ash concretes. Constr. Build. Mater. 2014, 54, 432–442. [Google Scholar] [CrossRef]
- Olkin, I.; Sampson, A.R. Multivariate Analysis: Overview. In International Encyclopedia of the Social & Behavioral Sciences; Smelser, N., Baltes, P., Eds.; Pergamon: Oxford, UK, 2001; pp. 10240–10247. [Google Scholar] [CrossRef]
- Guo, S.-J.; Tucker, R.L. A generic cost-concern matrix for identifying automation needs in construction. Autom. Constr. 1996, 5, 91–104. [Google Scholar] [CrossRef]
- Pan, M.; Linner, T.; Pan, W.; Cheng, H.; Bock, T. A framework of indicators for assessing construction automation and robotics in the sustainability context. J. Clean. Prod. 2018, 182, 82–95. [Google Scholar] [CrossRef]
- Vähä, P.; Känsälä, K.; Heikkilä, R.; Kaisto, I. Use of 3-D product models in construction process automation. Autom. Constr. 1997, 6, 69–76. [Google Scholar] [CrossRef]
- CEN. EN 1745: 2012. Masonry and Masonry Products—Methods for Determining Thermal Properties; Comité Européen de Normalisation: Brussels, Belgium, 2012. [Google Scholar]
- CEN. EN 1015-2: 1998. Methods of Test for Mortar for Masonry—Part 2: Bulk Sampling of Mortars and Preparation of Test Mortars; Comité Européen de Normalisation: Brussels, Belgium, 1998. [Google Scholar]
- CEN. EN 1015-3: 1999. Methods of Test for Mortar for Masonry—Part 3: Determination of Consistence of Fresh Mortar (By Flow Table); Comité Européen de Normalisation: Brussels, Belgium, 1999. [Google Scholar]
- CEN. EN 1015-6: 1998. Methods of Test for Mortar for Masonry—Part 6: Determination of Bulk Density of Fresh Mortar; Comité Européen de Normalisation: Brussels, Belgium, 1998. [Google Scholar]
- CEN. EN 1015-7: 1999. Methods of Test for Mortar for Masonry—Part 7: Determination of Air Content of Fresh Mortar; Comité Européen de Normalisation: Brussels, Belgium, 1999. [Google Scholar]
- CEN. EN 1015-12: 2000. Methods of Test for Mortar for Masonry—Part 12: Determination of Adhesive Strength of Hardened Rendering and Plastering Mortars on Substrates; Comité Européen de Normalisation: Brussels, Belgium, 2000. [Google Scholar]
- CEN. EN 1015-11: 1999. Methods of Test for Mortar for Masonary—Part 11: Determination of Flexural and Compressive Strength of Hardened Mortar; Comité Européen de Normalisation: Brussels, Belgium, 1999. [Google Scholar]
- ASTM. ASTM E1876-15. Standard Test Method for Dynamic Young’s Modulus, Shear Modulus, and Poisson’s Ratio by Impulse Excitation of Vibration; ASTM International: West Conshohocken, PA, USA, 2015; pp. 1–15. [Google Scholar] [CrossRef]
- CEN. EN 1015-18: 2002. Methods of Test for Mortar for Masonry—Part 18: Determination of Water Absorption Coefficient Due to Capillary Action of Hardened Mortar; Comité Européen de Normalisation: Brussels, Belgium, 2002. [Google Scholar]
- LNEC. Test Sheet—LNEC FE Pa 39.1: Wall Coating. Low Pressure Water Absorption; LNEC: Lisbon, Portugal, 2002. (In Portuguese) [Google Scholar]
- CEN. EN 1015-19 1998/A1. Methods of Test for Mortar for Masonry—Part 19: Determination of Water Vapour Permeability of Hardened Rendering and Plastering Mortars; Comité Européen de Normalisation: Brussels, Belgium, 2004. [Google Scholar]
- Gomes, M.G.; Flores-Colen, I.; da Silva, F.; Pedroso, M. Thermal conductivity measurement of thermal insulating mortars with EPS and silica aerogel by steady-state and transient methods. Constr. Build. Mater. 2018, 172, 696–705. [Google Scholar] [CrossRef]
- Pedroso, M.; Flores-Colen, I.; Silva, L.; Sequeira, P.; Silvestre, J.D.; Gomes, M.G. Super insulating thermal mortars: Experimental analysis of their application in coating systems. In Proceedings of the III Simpósio de Argamassas e Soluções Térmicas de Revestimentos, Coimbra, Portugal, 11–12 October 2018. (In Portuguese). [Google Scholar]
- Pedroso, M.; Flores-Colen, I.; Silvestre, J.D.; Silva, L.; Sequeira, P.; Sousa, G. Development of super-insulating thermal renders: Preliminary studies. In Proceedings of the ICEUBI2017—International Congress on Engineering: A Vision for the Future, Covilhã, Portugal, 5–7 December 2017. (In Portuguese). [Google Scholar]
- Soares, A. Performance of Renders Incorporating Nanosilica Aerogels. Ph.D. Thesis, University of Lisbon, Lisbon, Portugal, 2018. (In Portuguese). [Google Scholar]
- Soares, A.; de Fátima Júlio, M.; Flores-Colen, I.; Ilharco, L.M.; Brito, J.D. EN 998-1 performance requirements for thermal aerogel-based renders. Constr. Build. Mater. 2018, 179, 453–460. [Google Scholar] [CrossRef]
- De Fátima Júlio, M.; Soares, A.; Ilharco, L.M.; Flores-Colen, I.; de Brito, J. Aerogel-based renders with lightweight aggregates: Correlation between molecular/pore structure and performance. Constr. Build. Mater. 2016, 124, 485–495. [Google Scholar] [CrossRef]
- Gomes, M.G.; Flores-Colen, I.; Melo, H.; Soares, A. Physical performance of industrial and EPS and cork experimental thermal insulation renders. Constr. Build. Mater. 2019, 198, 786–795. [Google Scholar] [CrossRef]
- Ng, S.; Sandberg, L.I.C.; Jelle, B.P. Insulating and Strength Properties of an Aerogel-Incorporated Mortar Based an UHPC Formulations. Key Eng. Mater. 2014, 629, 43–48. [Google Scholar] [CrossRef]
- Silva, A.; Soares, A.; Flores-Colen, I.; de Brito, J. Mechanical Characteristics of Lightweight Mortars on Small-Scale Samples. J. Test. Eval. 2016, 44, 402–413. [Google Scholar] [CrossRef]
- Diasen. Diasen Thermal Renders. Available online: https://www.diasen.com/sp/pt/isolantes-termicos-acusticos.3sp?cts=isolanti_termici_acustici (accessed on 15 July 2019).
- Secil. SECIL: Technical Sheets of Mortars and Renders. Available online: https://www.secilargamassas.pt/pt/areas/downloads/fichas-tecnicas (accessed on 18 July 2019).
- Ardex. Ardex Thermal Renders. Available online: http://www.ardex.es/es/productos/otros-productos/aislamiento-termico-y-acustico/index.html (accessed on 14 July 2019).
- Saint-Gobain. Weber Thermal Renders. Available online: https://www.pt.weber/search-content/content_type/product/area/fachadas-com-isolamento-termico-1211 (accessed on 14 July 2019).
- Chiraema. Chiraema Solutions. Available online: http://www.chiraema.it/?s=&categoria=thermo&settore=&post_type=prodotti&submit= (accessed on 13 July 2019).
- Roefix. Roefix Solutions. Available online: https://www.roefix.it/Prodotti/Risanamento-Restauro-Bioedilizia/Bioedilizia (accessed on 14 July 2019).
- Index. INDEX Solutions. Available online: https://www.indexspa.it/Indexspacom/home_en.asp# (accessed on 13 July 2019).
- Kimia. Kimia Solutions. Available online: https://www.kimia.it/it/lavorazioni (accessed on 16 July 2019).
- Heck. Technical Data Sheets: Thermal Renders. Available online: https://www.wall-systems.com/de/produkte-systeme/?no_cache=1&tx_mmdb[product]=26270 (accessed on 17 July 2019).
- EMPA. Technical Information Sheet Fixit. Available online: http://www.fixit.ch/aerogel/pdf/TIS_Fixit_222_technisches_merkblatt.pdf (accessed on 18 June 2019).
- HAGA. Technical Data Sheet: Thermal Renders. Available online: https://www.haganatur.ch/wp-content/uploads/2016/02/hagatherm_typ_aerogel.pdf (accessed on 17 June 2019).
- Montgomery, D.C.; Runger, G.C. Applied Statistics and Probability for Engineers, 6th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2014. [Google Scholar]
- Benjamin, J.R.; Cornel, C.A. Probability, Statistics and Decision for Civil Engineers, 1st ed.; McGraw Hill Companies Inc: New York, NY, USA, 2014. [Google Scholar]
- Team, R.C. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2017. [Google Scholar]
- Wickham, H. ggplot2: Elegant Graphics for Data Analysis; Springer: New York, NY, USA, 2009. [Google Scholar] [CrossRef]
- Hair, J., Jr.; Black, W.; Babin, B.; Anderson, R. Multivariate Data Analysis, 7th ed.; Pearson Education Limited: Harlow, UK, 2014. [Google Scholar]
- Meloun, M.; Militký, J. Statistical Data Analysis; Woodhead Publishing: New Delhi, India, 2011. [Google Scholar]
- Schneeweiss, H.; Mathes, H. Factor Analysis and Principal Components. J. Multivar. Anal. 1995, 55, 105–124. [Google Scholar] [CrossRef]
- Osborne, J.W.; Fitzpatrick, D.C. Replication analysis in exploratory factor analysis: What it is and what makes your analysis better. Pract. Assess. Res. Eval. 2012, 17, 1–8. [Google Scholar] [CrossRef]
- Yanai, H.; Ichikawa, M. Factor Analysis. In Handbook of Statistics; Rao, C.R., Sinharay, S., Eds.; Elsevier B. V.: Amsterdam, The Netherlands, 2006; Volume 26, pp. 257–296. [Google Scholar]
- Romesburg, H.C. Cluster Analysis for Researchers, 1st ed.; Lulu.com: Morrisville, NC, USA, 2004. [Google Scholar]
- Hennig, C.; Meila, M. Cluster Analysis: An Overview. In Handbook of Cluster Analysis, 1st ed.; Hennig, C., Meila, M., Murtagh, F., Rocci, R., Eds.; CRC Press: Boca Raton, FL, USA, 2015; pp. 1–20. [Google Scholar]
- Wilks, D.S. Cluster Analysis. Int. Geophys. 2011, 100, 603–616. [Google Scholar] [CrossRef]
- Nathans, L.L.; Oswald, F.L.; Nimon, K. Interpreting Multiple Linear Regression: A Guidebook of Variable Importance. Pract. Assess. Res. Eval. 2012, 17, 1–19. [Google Scholar]
- Galvão, J.; Duarte, R.; Flores-Colen, I.; de Brito, J.; Hawreen, A. Non-destructive mechanical and physical in-situ testing of rendered walls under natural exposure. Constr. Build. Mater. 2020, 230, 116838. [Google Scholar] [CrossRef]
- Hanif, A.; Diao, S.; Lu, Z.; Fan, T.; Li, Z. Green lightweight cementitious composite incorporating aerogels and fly ash cenospheres—Mechanical and thermal insulating properties. Constr. Build. Mater. 2016, 116, 422–430. [Google Scholar] [CrossRef]
- Singh, S.B.; Munjal, P.; Thammishetti, N. Role of water/cement ratio on strength development of cement mortar. J. Build. Eng. 2015, 4, 94–100. [Google Scholar] [CrossRef]
- Bostanci, L.; Sola, O.C. Mechanical Properties and Thermal Conductivity of Aerogel-Incorporated Alkali-Activated Slag Mortars. Adv. Civil. Eng. 2018, 2018, 1–9. [Google Scholar] [CrossRef]
- Flores-Colen, I. Performance Evaluation Methodology for Towed Façades, from the Perspective of Predictive Maintenance. Ph.D. Thesis, University of Lisbon, Lisbon, Portugal, 2009. (In Portuguese). [Google Scholar]
- Gregorova, V.; Ledererova, M.; Stefunkova, Z. Investigation of Influence of Recycled Plastics from Cable, Ethylene Vinyl Acetate and Polystyrene Waste on Lightweight Concrete Properties. Procedia Eng. 2017, 195, 127–133. [Google Scholar] [CrossRef]
- Flores-Colen, I.; Manuel Caliço Lopes de Brito, J.; Peixoto de Freitas, V. On-site performance assessment of rendering façades for predictive maintenance. Struct. Surv. 2011, 29, 133–146. [Google Scholar] [CrossRef]
- Jerman, M.; Černý, R. Effect of moisture content on heat and moisture transport and storage properties of thermal insulation materials. Energy Build. 2012, 53, 39–46. [Google Scholar] [CrossRef]
- Badache, A.; Benosman, A.S.; Senhadji, Y.; Mouli, M. Thermo-physical and mechanical characteristics of sand-based lightweight composite mortars with recycled high-density polyethylene (HDPE). Constr. Build. Mater. 2018, 163, 40–52. [Google Scholar] [CrossRef]
- Kooshkaki, A.; Eskandari-Naddaf, H. Effect of porosity on predicting compressive and flexural strength of cement mortar containing micro and nano-silica by multi-objective ANN modeling. Constr. Build. Mater. 2019, 212, 176–191. [Google Scholar] [CrossRef]
- Brandt, A.M. Cement-Based Composites: Materials, Mechanical Properties and Performance, 2nd ed.; Taylor and Francis: Abingdon, UK, 2009. [Google Scholar]
- Mehta, P.K.; Monteiro, P.J.M. Concrete: Microstructure, Properties and Materials, 3rd ed.; McGraw Hill Companies Inc.: New York, NY, USA, 2006. [Google Scholar]
- Scrivener, K.; Bazzoni, A.; Mota, B.; Rossen, J.E. Electron microscopy. In A Practical Guide to Microstructural Analysis of Cementitious Materials, 1st ed.; Scrivener, K., Snellings, R., Lothenbach, B., Eds.; CRC Press: Boca Raton, FL, USA, 2016; pp. 351–418. [Google Scholar]
- Santha Kumar, G. Influence of fluidity on mechanical and permeation performances of recycled aggregate mortar. Constr. Build. Mater. 2019, 213, 404–412. [Google Scholar] [CrossRef]
- Togkalidou, T.; Karoglou, M.; Bakolas, A.; Giakoumaki, A.; Moropoulou, A. Correlation of Water Vapor Permeability with Microstructure Characteristics of Building Materials Using Robust Chemometrics. Transp. Porous Media 2013, 99, 273–295. [Google Scholar] [CrossRef]
- Mendes, J.C.; Barreto, R.R.; de Paula, A.C.B.; Elói, F.P.D.F.; Brigolini, G.J.; Peixoto, R.A.F. On the relationship between morphology and thermal conductivity of cement-based composites. Cem. Concr. Compos. 2019, 104, 103365. [Google Scholar] [CrossRef]
- Zeng, Q.; Mao, T.; Li, H.; Peng, Y. Thermally insulating lightweight cement-based composites incorporating glass beads and nano-silica aerogels for sustainably energy-saving buildings. Energy Build. 2018, 174, 97–110. [Google Scholar] [CrossRef]
- Pedroso, M.; Flores-Colen, I.; Silvestre, J.D.; Gomes, M.G.; Silva, L.; Sequeira, P.; de Brito, J. Characterisation of a multilayer external wall thermal insulation system. Application in a Mediterranean climate. J. Build. Eng. 2020, 30, 101265. [Google Scholar] [CrossRef]
- Julious, S.A.; Mullee, M.A. Confounding and Simpson’s paradox. BMJ 1994, 309, 1480–1481. [Google Scholar] [CrossRef] [PubMed]
| State | Variable | Abbreviation | Unit | Testing Procedure |
|---|---|---|---|---|
| Fresh | Powder bulk density | Bar | g·cm−3 | EN 1015-2 [55] |
| Consistency | Cons | mm | EN 1015-3 [56] | |
| Bulk-density fresh state | BDF | g·cm−3 | EN 1015-6 [57] | |
| Ratio water: powder | w/p | - | - | |
| Air content | AC | % | EN 1015-7 [58] | |
| Hardened | Adhesion | fu | MPa | EN 1015-12 [59] |
| Bulk-density hardened state | BDH | g·cm−3 | EN 1015-11 [60] | |
| Dynamic modulus elasticity | Ed | MPa | ASTM E 1876-01 [61] | |
| Compressive strength | fc | MPa | EN 1015-11 [60] | |
| Flexural strength | ft | MPa | EN 1015-11 [60] | |
| Capillary water absorption | W | kg·m−2 | EN 1015-18 [62] | |
| Thermal conductivity at 10 °C, 28 days | λ10°C,28days | W·m−1·K−1 | EN 1745 [54] | |
| Thermal conductivity at 10 °C, dry state | λ10°C,dry | W·m−1·K−1 | EN 1745 [54] | |
| Liquid water permeability | TK | kg·m−2·min−0.5 | LNEC FE Pa39.1 [63] | |
| Water vapour permeance | Λ | kg·m−2·s−1·Pa−1 | EN 1015-19 [64] |
| Documents | Type of Formulation | Thermal Insulation Aggregates Used | References |
|---|---|---|---|
| L1 to L5 | Research works (laboratory) | Silica aerogel | [25,65,66,67,68,69,70,71,72,73] |
| S1 to S9 | Research works (semi-industrial) | Silica aerogel with others | [25,66,67,68,69] |
| I1 to I21 | Industrial product (industrial) | EPS, cork, perlite, silica aerogel | [74,75,76,77,78,79,80,81,82,83,84] |
| Reference | Bar | Cons | BDf | w/p | AC | fu | BDh | Ed | fc | ft | W | λ10°C,28days | λ10°C,dry | TK | Λ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| L1 | −1.557 | −0.160 | −1.686 | 1.561 | 1.695 | −0.736 | −1.624 | −1.390 | −1.005 | −1.432 | −0.431 | −1.446 | −0.978 | 0.754 | −0.050 |
| I6 | 1.474 | −0.298 | 1.210 | −0.450 | −0.357 | −0.736 | 1.206 | 0.643 | 0.281 | 0.960 | 0.989 | 0.971 | 1.333 | −0.637 | −0.256 |
| S7 | −0.393 | −1.475 | −0.768 | 0.390 | −1.053 | −0.973 | −0.366 | −1.208 | −0.973 | −1.432 | −0.474 | −0.727 | −0.490 | −0.615 | −0.440 |
| I21 | 0.873 | 0.878 | 0.316 | −1.621 | 0.027 | 1.516 | 0.462 | −0.226 | −0.049 | −0.030 | 0.257 | −0.353 | −0.166 | −0.464 | −1.000 |
| Method | Aggregation Method | Linking Distance |
|---|---|---|
| Hierarchical | Single linkage | Euclidean |
| Complete linkage | Euclidean | |
| Ward method | Euclidean | |
| City-block | ||
| Chebyshev | ||
| Non-hierarchical | k-means | |
| Variable | Avg. | Median | Mode | Min | Max | 25% Quart. | 75% Quart. | Variance | CV | Asymmetry |
|---|---|---|---|---|---|---|---|---|---|---|
| Bar | 0.447 | 0.450 | 0.140 | 0.135 | 0.724 | 0.298 | 0.604 | 0.032 | 40.301 | −0.253 |
| Cons | 142.314 | 143.000 | Mult. | 103.000 | 166.000 | 136.000 | 151.000 | 208.600 | 10.148 | −0.928 |
| BDf | 0.710 | 0.750 | 0.900 | 0.297 | 0.987 | 0.563 | 0.900 | 0.042 | 28.675 | −0.544 |
| w/p | 0.743 | 0.700 | Mult. | 0.300 | 1.500 | 0.550 | 0.850 | 0.075 | 36.786 | 0.969 |
| AC | 11.749 | 9.800 | 21.000 | 5.200 | 23.000 | 6.500 | 15.000 | 29.800 | 46.447 | 0.664 |
| fu | 0.159 | 0.130 | 0.100 | 0.023 | 0.300 | 0.100 | 0.210 | 0.007 | 52.668 | 0.422 |
| BDh | 0.611 | 0.622 | 0.488 | 0.144 | 0.988 | 0.488 | 0.753 | 0.046 | 35.281 | −0.509 |
| Ed | 1013.68 | 1094.80 | Mult. | 57.00 | 2395.00 | 526.50 | 1339.90 | 399185.10 | 62.33 | 0.368 |
| fc | 1.327 | 1.250 | Mult. | 0.110 | 3.100 | 0.700 | 1.980 | 0.581 | 57.441 | 0.472 |
| ft | 0.709 | 0.770 | Mult. | 0.080 | 1.250 | 0.380 | 0.992 | 0.126 | 50.101 | −0.254 |
| W | 0.479 | 0.440 | 0.600 | 0.130 | 1.000 | 0.300 | 0.640 | 0.051 | 47.013 | 0.592 |
| λ10°C,28day | 0.142 | 0.140 | 0.100 | 0.031 | 0.230 | 0.091 | 0.199 | 0.003 | 40.929 | −0.191 |
| λ10°C,dry | 0.122 | 0.097 | 0.080 | 0.027 | 0.200 | 0.079 | 0.185 | 0.003 | 47.708 | 0.122 |
| TK | 1.064 | 0.300 | 0.210 | 0.100 | 4.650 | 0.210 | 1.510 | 1.923 | 130.330 | 1.587 |
| Λ | 2.0 × 10−11 | 2.1 × 10−11 | 2.0 × 10−11 | 3.9 × 10−11 | 1.3 × 10−11 | 2.2 × 10−11 | 1.7 × 10−11 | 3.7 × 10−11 | 8.3 × 10−12 | 3.3 × 10−10 |
| Variable | Correlations in Bold are Considered Significant: p-Value < 0.05 | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bar | Cons | BDF | w/p | AC | fu | BDH | Ed | fc | ft | W | λ10°C,28days | λ10°C,dry | TK | Λ | |
| Bar | 1.00 | 0.06 | 0.91 | −0.62 | −0.31 | 0.21 | 0.85 | 0.57 | 0.52 | 0.71 | −0.28 | 0.72 | 0.68 | −0.48 | 0.22 |
| Cons | 1.00 | 0.03 | 0.15 | −0.07 | −0.25 | 0.13 | 0.10 | −0.02 | −0.06 | 0.03 | 0.18 | 0.15 | 0.06 | 0.01 | |
| BDF | 1.00 | −0.62 | −0.26 | 0.24 | 0.90 | 0.68 | 0.65 | 0.78 | −0.36 | 0.81 | 0.74 | −0.47 | 0.29 | ||
| w/p | 1.00 | 0.30 | −0.64 | −0.65 | −0.53 | −0.64 | −0.68 | 0.53 | −0.52 | −0.48 | 0.56 | −0.11 | |||
| AC | 1.00 | −0.09 | −0.27 | −0.45 | −0.30 | −0.29 | 0.20 | −0.45 | −0.44 | 0.18 | 0.09 | ||||
| fu | 1.00 | 0.24 | 0.18 | 0.50 | 0.42 | −0.35 | 0.17 | 0.07 | −0.44 | −0.00 | |||||
| BDH | 1.00 | 0.64 | 0.59 | 0.80 | −0.45 | 0.85 | 0.82 | −0.53 | 0.26 | ||||||
| Ed | 1.00 | 0.84 | 0.73 | −0.45 | 0.83 | 0.75 | −0.17 | 0.24 | |||||||
| fc | 1.00 | 0.82 | −0.44 | 0.72 | 0.61 | −0.22 | 0.26 | ||||||||
| ft | 1.00 | −0.42 | 0.80 | 0.76 | −0.39 | 0.24 | |||||||||
| W | 1.00 | −0.40 | −0.32 | 0.32 | −0.19 | ||||||||||
| λ10°C,28days | 1.00 | 0.96 | −0.41 | 0.22 | |||||||||||
| λ10°C,dry | 1.00 | −0.43 | 0.24 | ||||||||||||
| TK | 1.00 | 0.18 | |||||||||||||
| Λ | 1.00 | ||||||||||||||
| Reference | Correlation Matrix Eigenvalues | |||
|---|---|---|---|---|
| Eigenvalue | Variance (%) | Cumulative Eigenvalue | Cumulative Variance (%) | |
| 1 | 7.64 | 50.96 | 7.64 | 50.96 |
| 2 | 1.78 | 11.85 | 9.42 | 62.81 |
| 3 | 1.27 | 8.45 | 10.69 | 71.26 |
| 4 | 1.07 | 7.14 | 11.76 | 78.40 |
| 5 | 0.84 | 5.60 | 12.60 | 84.00 |
| Variable | Only > |0.60| | ||
|---|---|---|---|
| PC 1 | PC 2 | PC 3 | |
| Bar | 0.83 | ||
| Cons | 0.60 | ||
| BDF | 0.89 | ||
| w/p | 0.65 | ||
| AC | |||
| fu | −0.85 | ||
| BDH | 0.91 | ||
| Ed | 0.84 | ||
| fc | 0.73 | ||
| ft | 0.83 | ||
| W | |||
| λ10°C,28days | 0.96 | ||
| λ10°C,dry | 0.92 | ||
| TK | 0.64 | ||
| Λ | 0.79 | ||
| Total variance | 0.47 | 0.15 | 0.09 |
| Aggregation and Distance Methods | Cluster 1 | Cluster 2 | Cluster 3 |
|---|---|---|---|
| Complete linkage Euclidean | S1, S3, S4, I2, I3, I4, I5, I6, I7, I9, I10, I11, I12, I13, I14, I16, I17, I18, I19, I21 | S2, S5, S6, S7, S8, S9, I1, I8, I15, I20 | L1, L2, L3, L4, L5 |
| Ward Euclidean | S1, S3, S4, I2, I3, I4, I5, I6, I9, I10, I11, I12, I13, I14, I16, I17, I21 | S2, S5, S6, S7, S8, S9, I1, I7, I8, I15, I18, I19, I20 | L1, L2, L3, L4, L5 |
| Ward City-block | S1, S3, S4, S8, I2, I3, I4, I5, I6, I7, I9, I10, I11, I12, I13, I14, I16, I17, I18, I19, I21 | S2, S5, S6, S7, S9, I1, I8, I15, I20 | L1, L2, L3, L4, L5 |
| k-means | S1, S3, S4, I2, I3, I4, I5, I6, I9, I10, I11, I12, I13, I14, I16, I17, I19 | L1, L2, L3, L4 | S2, S5, S6, S7, S8, S9, I1, I7, I8, I15, I18, I20, I21, L5 |
| Bar | Cons | BDf | w/p | AC | fu | BDh | Ed | fc | ft | W | λ10°C,28days | TK | Λ | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R2 | 0.46 | 0.02 | 0.55 | 0.23 | 0.19 | 0.01 | 0.68 | 0.56 | 0.37 | 0.57 | 0.10 | 0.93 | 0.18 | 0.06 |
| Model | r | R2 | Adjusted R2 | F a | p-Value of F | p-Value of t < 0.05 |
|---|---|---|---|---|---|---|
| 1: λ10°C,dry = λ10°C,28days | 0.964 | 0.929 | 0.927 | 432.5 | 2.20 × 10−16 | λ10°C,28days |
| 2: λ10°C,dry = Cons+w/p+BDF+BDH+fc+ λ10°C,28days | 0.978 | 0.954 | 0.940 | 84.1 | 2.20 × 10−16 | fc, λ10°C,28days |
| 3: λ10°C,dry = Cons+w/p+BDF | 0.756 | 0.571 | 0.529 | 13.95 | 7.01 × 10−6 | BDF |
| 4: λ10°C,dry = BDH+fc+ λ10°C,28days | 0.975 | 0.950 | 0.943 | 141.2 | 2.20 × 10−16 | fc, λ10°C,28days |
| 5: λ10°C,dry = BDF+fc+ λ10°C,28days | 0.975 | 0.950 | 0.943 | 186.8 | 2.20 × 10−16 | fc, λ10°C,28days |
| 6: λ10°C,dry = fc+ λ10°C,28days | 0.992 | 0.984 | 0.983 | 877.2 | 2.20 × 10−16 | fc, λ10°C,28days |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pedroso, M.; Flores-Colen, I.; Silvestre, J.D.; Gomes, M.d.G. Nanomaterials’ Influence on the Performance of Thermal Insulating Mortars—A Statistical Analysis. Appl. Sci. 2020, 10, 2219. https://doi.org/10.3390/app10072219
Pedroso M, Flores-Colen I, Silvestre JD, Gomes MdG. Nanomaterials’ Influence on the Performance of Thermal Insulating Mortars—A Statistical Analysis. Applied Sciences. 2020; 10(7):2219. https://doi.org/10.3390/app10072219
Chicago/Turabian StylePedroso, Marco, Inês Flores-Colen, José Dinis Silvestre, and Maria da Glória Gomes. 2020. "Nanomaterials’ Influence on the Performance of Thermal Insulating Mortars—A Statistical Analysis" Applied Sciences 10, no. 7: 2219. https://doi.org/10.3390/app10072219
APA StylePedroso, M., Flores-Colen, I., Silvestre, J. D., & Gomes, M. d. G. (2020). Nanomaterials’ Influence on the Performance of Thermal Insulating Mortars—A Statistical Analysis. Applied Sciences, 10(7), 2219. https://doi.org/10.3390/app10072219








