Thermoelectricity Modeling with Cold Dipole Atoms in Aubry Phase of Optical Lattice
Abstract
1. Introduction
2. Methods
3. Results
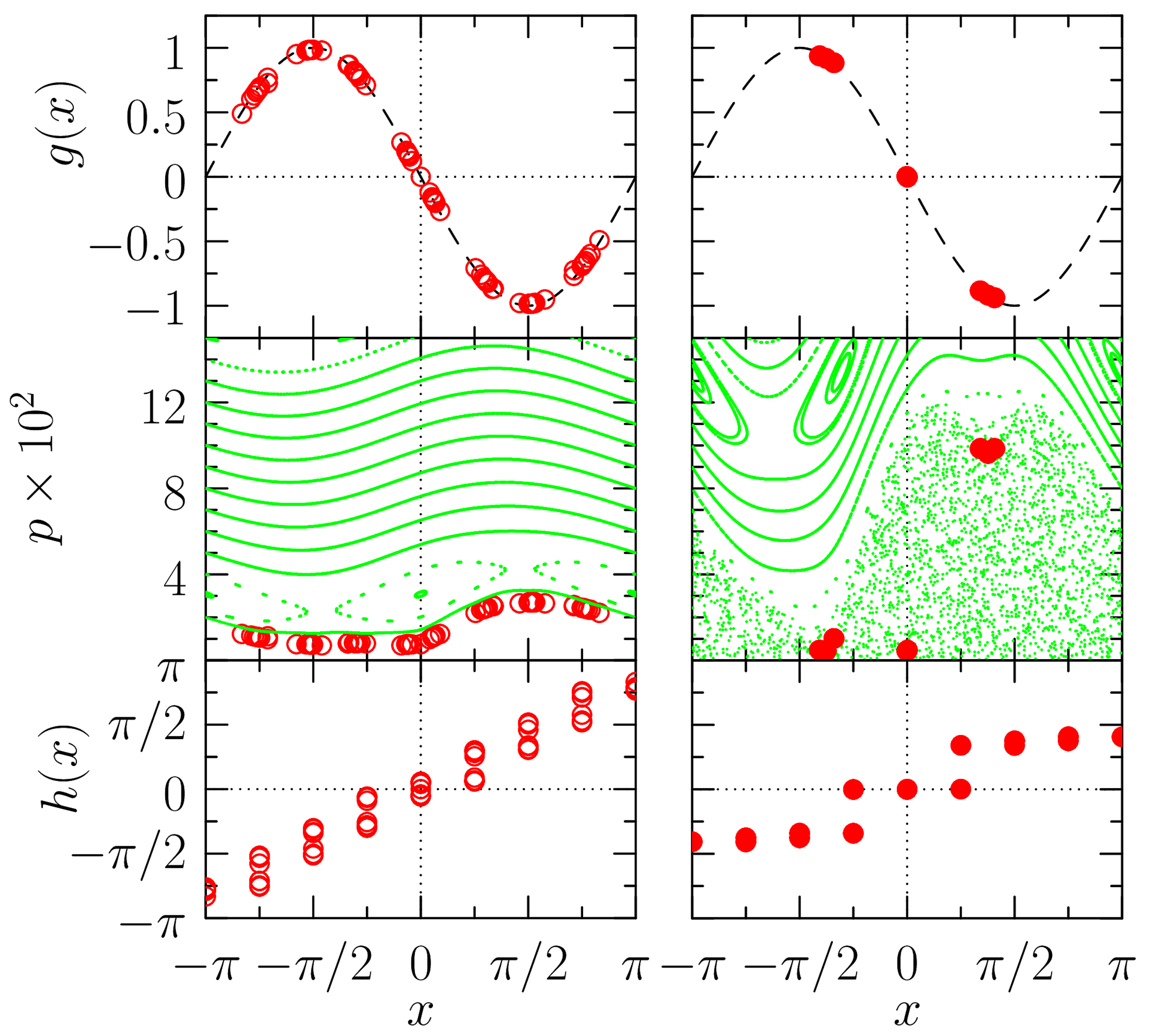
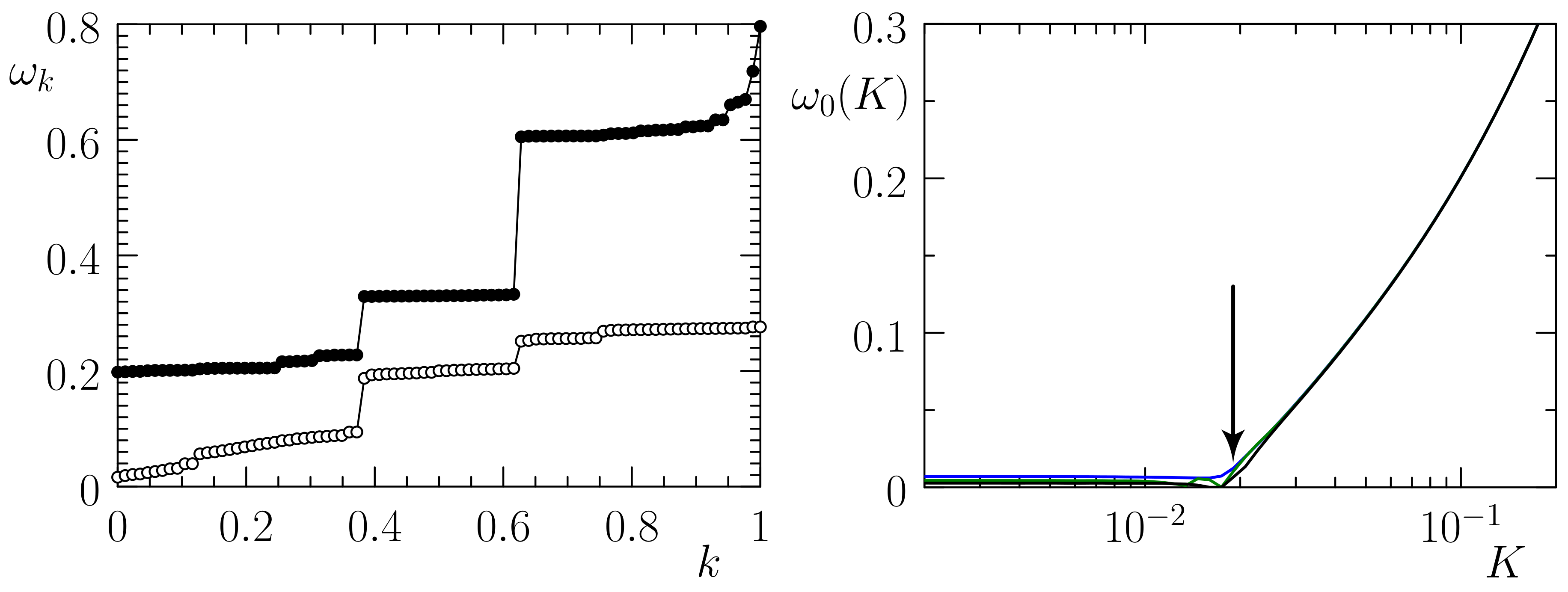
3.1. Ground State Properties
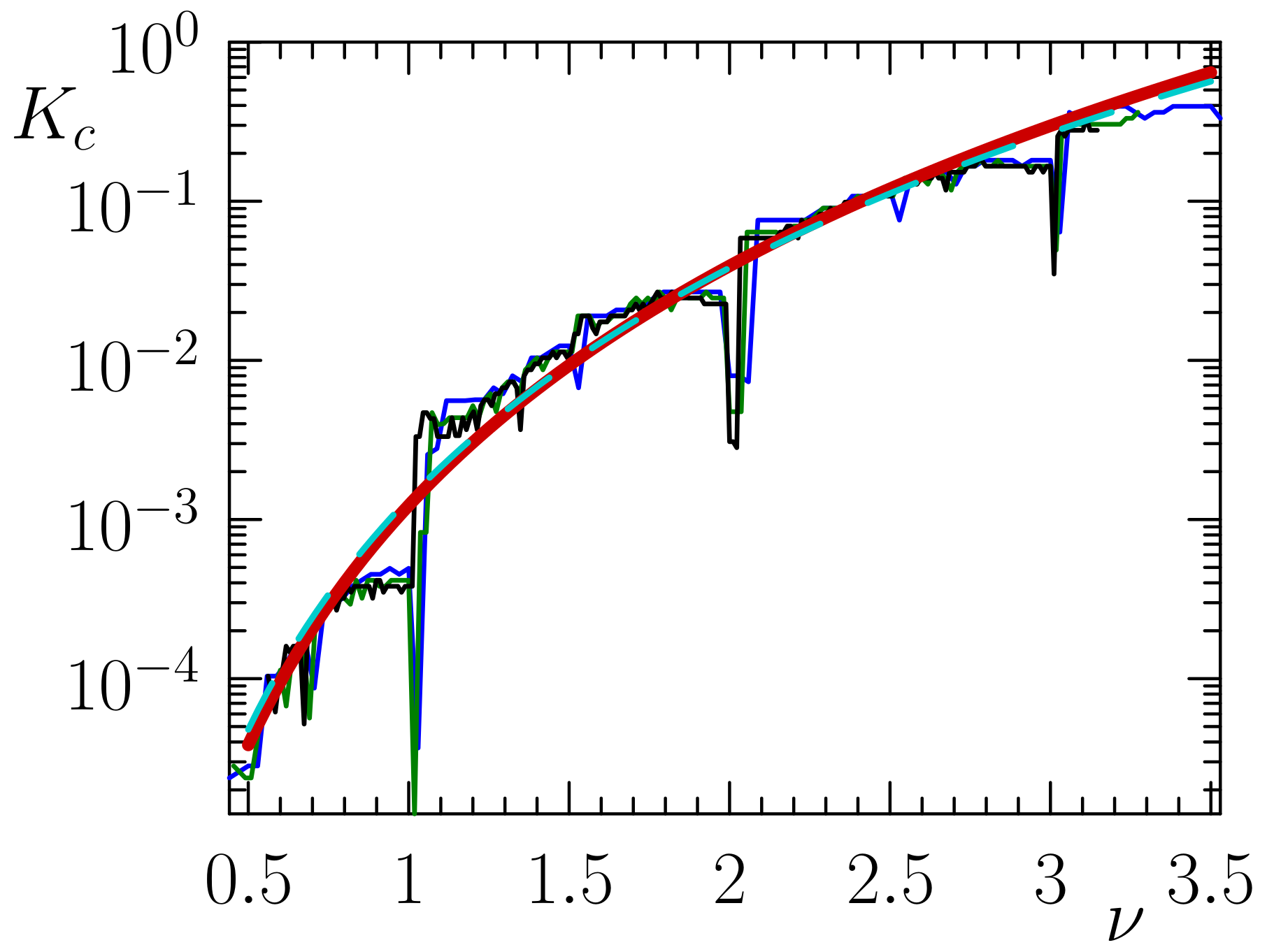
3.2. Density Dependence of Aubry Transition
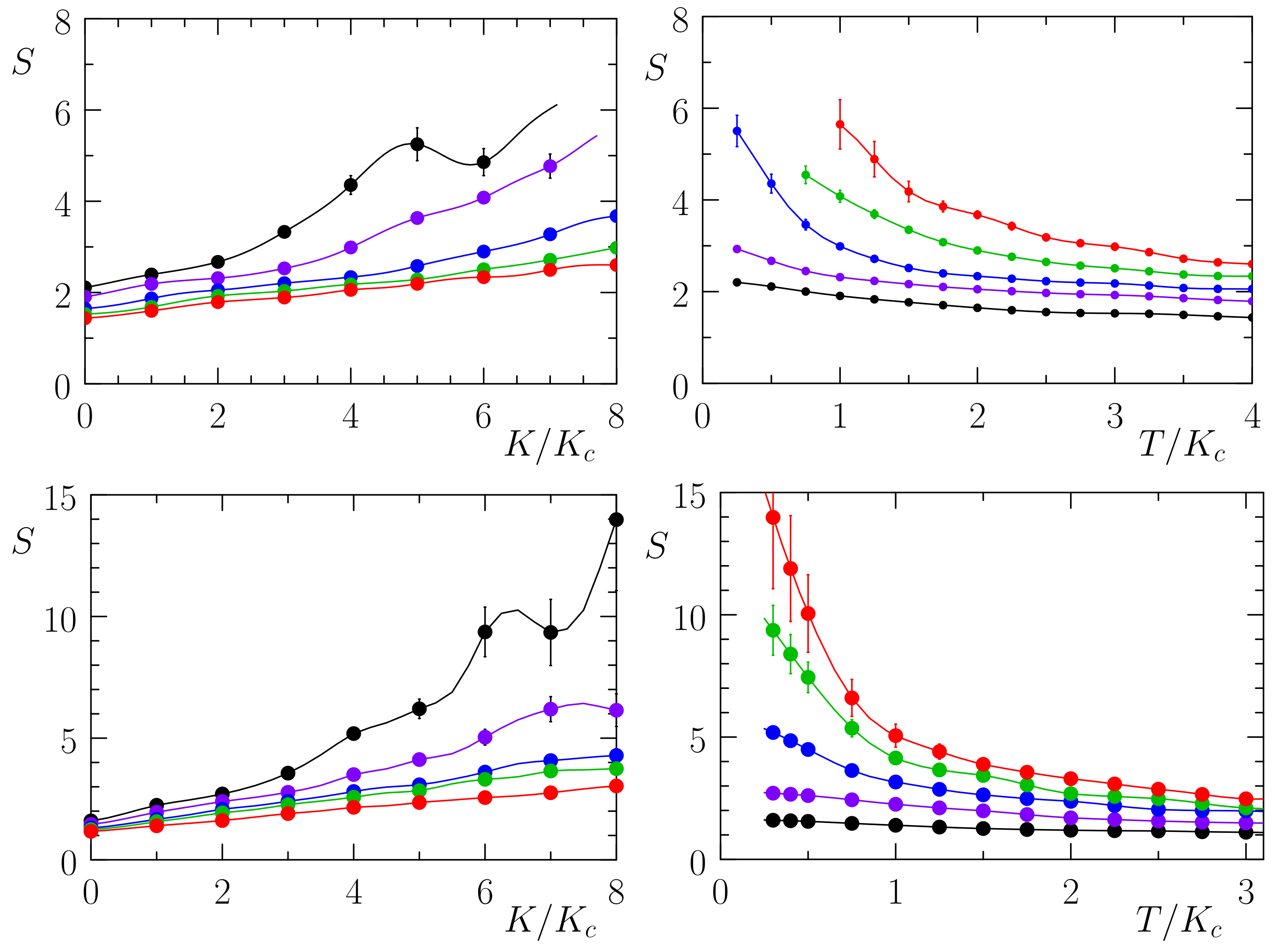
3.3. Seebeck Coefficient
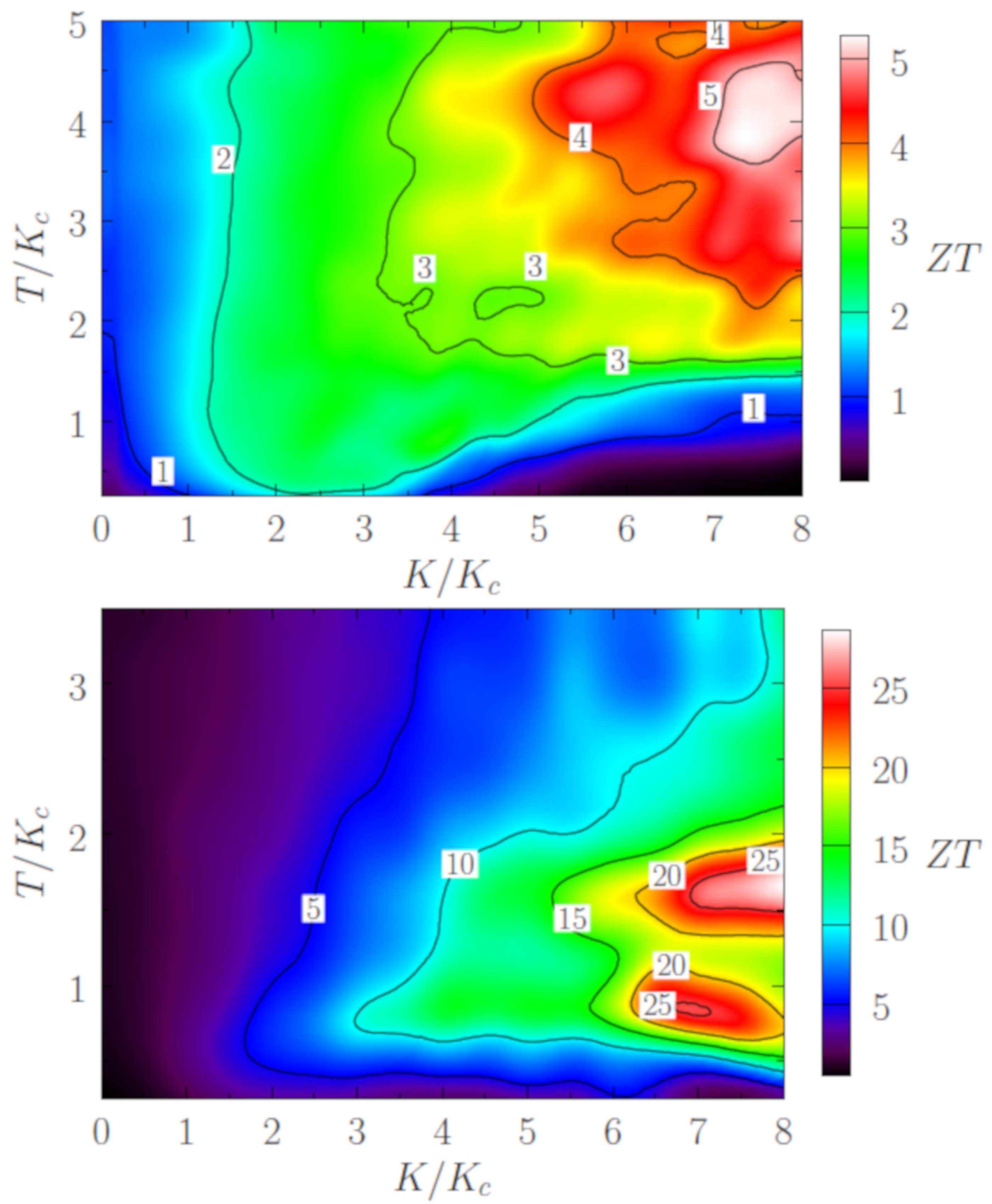
3.4. Figure of Merit
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Local Description by the Chirikov Standard Map
Appendix B. Numerical Computation of Conductivity

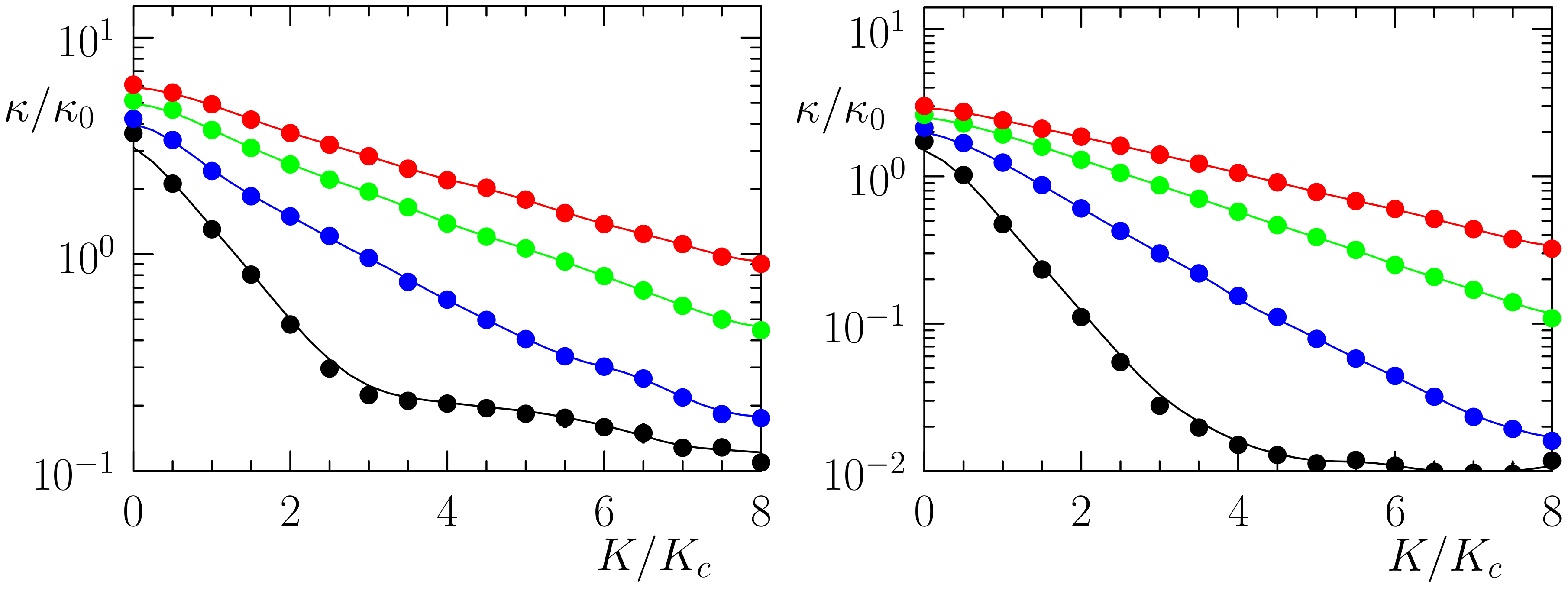
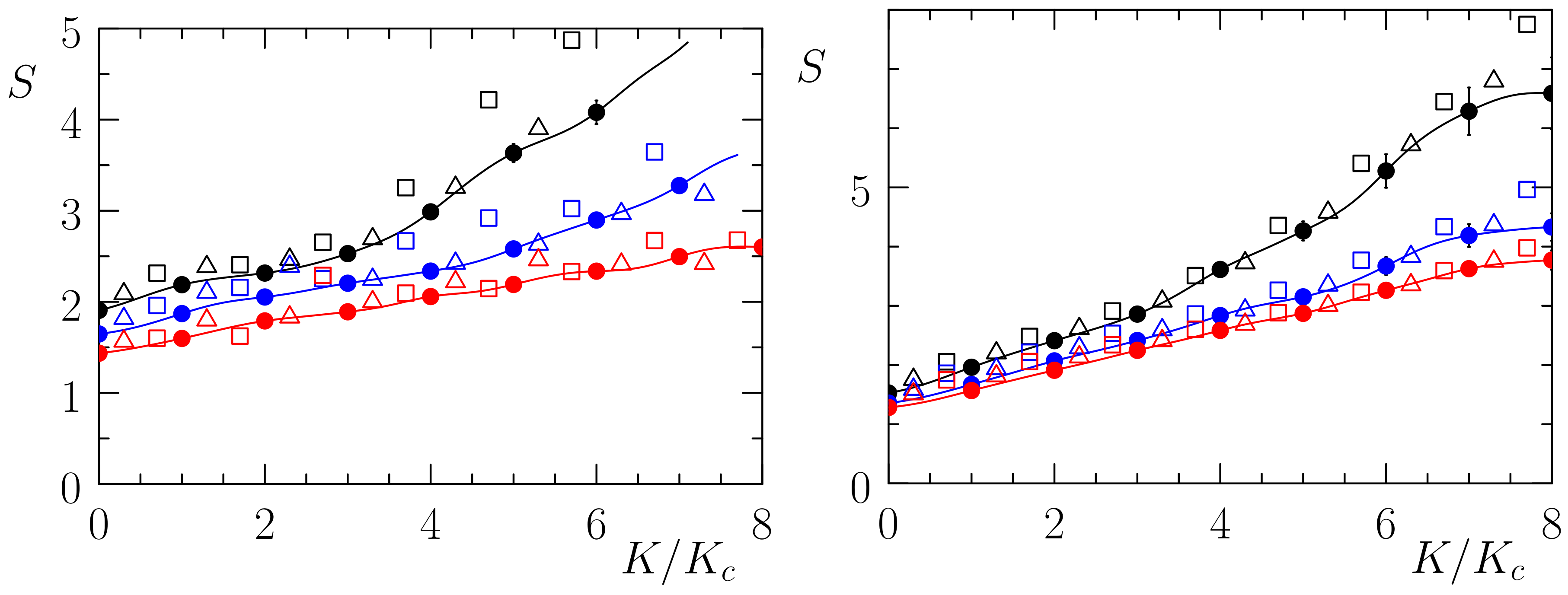
Appendix C. Independence of Chain Length
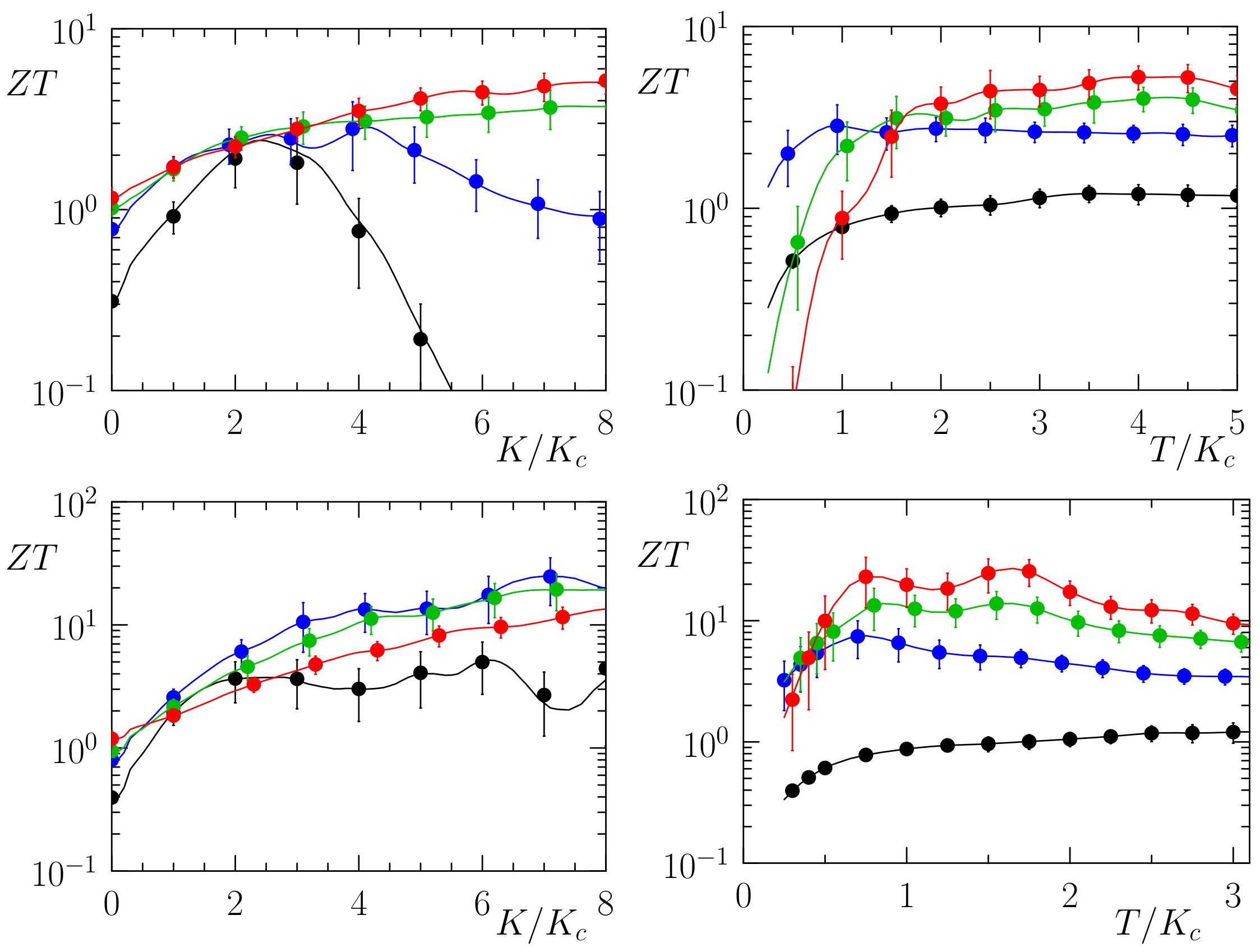
Appendix D. Additional Data for ZT
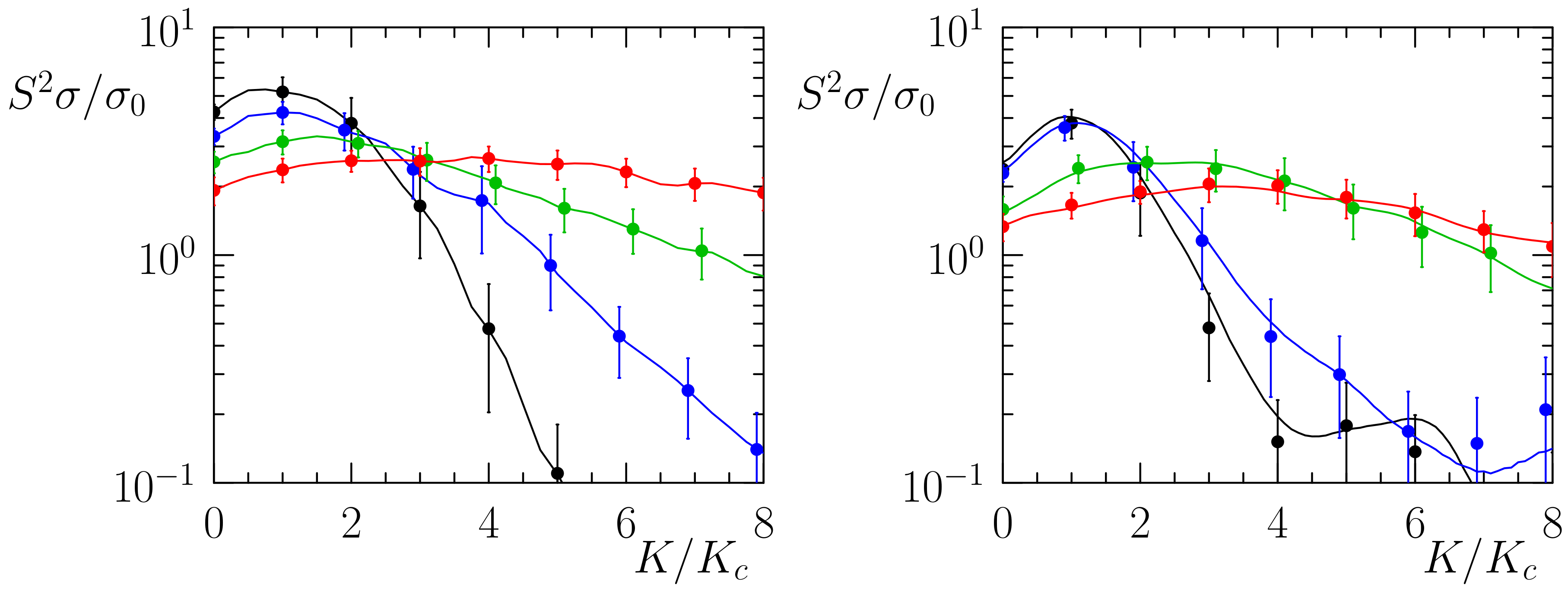
Appendix E. Additional Data for Power Factor
References
- Braun, O.M.; Kivshar, Y. The Frenkel-Kontorova Model: Concepts, Methods, and Applications; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar] [CrossRef]
- Chirikov, B.V. A universal instability of many-dimensional oscillator systems. Phys. Rep. 1979, 52, 263–379. [Google Scholar] [CrossRef]
- Lichtenberg, A.; Lieberman, M. Regular and Chaotic Dynamics; Springer: New York, NY, USA, 1992. [Google Scholar] [CrossRef]
- Meiss, J.D. Symplectic maps, variational principles, and transport. Rev. Mod. Phys. 1992, 64, 795–848. [Google Scholar] [CrossRef]
- Chirikov, B.; Shepelyansky, D. Chirikov standard map. Scholarpedia 2008, 3, 3550. [Google Scholar] [CrossRef]
- Aubry, S. The twist map, the extended Frenkel-Kontorova model and the devil’s staircase. Phys. D Nonlinear Phenom. 1983, 7, 240–258. [Google Scholar] [CrossRef]
- Pokrovsky, V.L.; Talapov, A.L. Theory of Incommensurate Crystals; Harwood Academic Publishers: New York, NY, USA, 1984. [Google Scholar]
- García-Mata, I.; Zhirov, O.V.; Shepelyansky, D.L. Frenkel-Kontorova model with cold trapped ions. Eur. Phys. J. D 2007, 41, 325–330. [Google Scholar] [CrossRef][Green Version]
- Zhirov, O.V.; Lages, J.; Shepelyansky, D.L. Thermoelectricity of cold ions in optical lattices. Eur. Phys. J. D 2019, 73, 149. [Google Scholar] [CrossRef]
- Pruttivarasin, T.; Ramm, M.; Talukdar, I.; Kreuter, A.; Häffner, H. Trapped ions in optical lattices for probing oscillator chain models. New J. Phys. 2011, 13, 075012. [Google Scholar] [CrossRef][Green Version]
- Bylinskii, A.; Gangloff, D.; Vuletić, V. Tuning friction atom-by-atom in an ion-crystal simulator. Science 2015, 348, 1115–1118. [Google Scholar] [CrossRef]
- Bylinskii, A.; Gangloff, D.; Counts, I.; Vuletić, V. Observation of Aubry-type transition in finite atom chains via friction. Nat. Mater. 2016, 15, 717–721. [Google Scholar] [CrossRef]
- Kiethe, J.; Nigmatullin, R.; Kalincev, D.; Schmirander, T.; Mehlstäubler, T.E. Probing nanofriction and Aubry-type signatures in a finite self-organized system. Nat. Commun. 2017, 8, 15364. [Google Scholar] [CrossRef]
- Lauprêtre, T.; Linnet, R.B.; Leroux, I.D.; Landa, H.; Dantan, A.; Drewsen, M. Controlling the potential landscape and normal modes of ion Coulomb crystals by a standing-wave optical potential. Phys. Rev. A 2019, 99, 031401. [Google Scholar] [CrossRef]
- Zhirov, O.V.; Shepelyansky, D.L. Thermoelectricity of Wigner crystal in a periodic potential. EPL Europhys. Lett. 2013, 103, 68008. [Google Scholar] [CrossRef]
- Ioffe, A.F. Semiconductor Thermoelements, and Thermoelectric Cooling; Infosearch Ltd.: Bangkok, Thailand, 1957. [Google Scholar]
- Joffe, A.F.; Stil’bans, L.S. Physical problems of thermoelectricity. Rep. Prog. Phys. 1959, 22, 167–203. [Google Scholar] [CrossRef]
- Majumdar, A. Thermoelectricity in Semiconductor Nanostructures. Science 2004, 303, 777–778. [Google Scholar] [CrossRef] [PubMed]
- Goldsmid, H.J. Introduction to Thermoelectricity; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar] [CrossRef]
- Li, N.; Ren, J.; Wang, L.; Zhang, G.; Hänggi, P.; Li, B. Colloquium: Phononics: Manipulating heat flow with electronic analogs and beyond. Rev. Mod. Phys. 2012, 84, 1045–1066. [Google Scholar] [CrossRef]
- Levi, B.G. Simple compound manifests record-high thermoelectric performance. Phys. Today 2014, 67, 14–16. [Google Scholar] [CrossRef]
- He, J.; Tritt, T.M. Advances in thermoelectric materials research: Looking back and moving forward. Science 2017, 357. [Google Scholar] [CrossRef]
- Bruzewicz, C.D.; Chiaverini, J.; McConnell, R.; Sage, J.M. Trapped-ion quantum computing: Progress and challenges. Appl. Phys. Rev. 2019, 6, 021314. [Google Scholar] [CrossRef]
- Schneider, C.; Porras, D.; Schaetz, T. Experimental quantum simulations of many-body physics with trapped ions. Rep. Prog. Phys. 2012, 75, 024401. [Google Scholar] [CrossRef]
- Lahaye, T.; Menotti, C.; Santos, L.; Lewenstein, M.; Pfau, T. The physics of dipolar bosonic quantum gases. Rep. Prog. Phys. 2009, 72, 126401. [Google Scholar] [CrossRef]
- Schmitt, M.; Wenzel, M.; Böttcher, F.; Ferrier-Barbut, I.; Pfau, T. Self-bound droplets of a dilute magnetic quantum liquid. Nature 2016, 539, 259–262. [Google Scholar] [CrossRef] [PubMed]
- Böttcher, F.; Schmidt, J.N.; Wenzel, M.; Hertkorn, J.; Guo, M.; Langen, T.; Pfau, T. Transient Supersolid Properties in an Array of Dipolar Quantum Droplets. Phys. Rev. X 2019, 9, 011051. [Google Scholar] [CrossRef]
- Ramm, M.; Pruttivarasin, T.; Häffner, H. Energy transport in trapped ion chains. New J. Phys. 2014, 16, 063062. [Google Scholar] [CrossRef]
- Freitas, N.; Martinez, E.A.; Paz, J.P. Heat transport through ion crystals. Phys. Scr. 2015, 91, 013007. [Google Scholar] [CrossRef]
- Lous, R.S.; Fritsche, I.; Jag, M.; Huang, B.; Grimm, R. Thermometry of a deeply degenerate Fermi gas with a Bose-Einstein condensate. Phys. Rev. A 2017, 95, 053627. [Google Scholar] [CrossRef]
- Shepelyansky, D.L. Quantum computer with cold ions in the Aubry pinned phase. Eur. Phys. J. D 2019, 73, 148. [Google Scholar] [CrossRef]
- Loye, J.; Lages, J.; Shepelyansky, D.L. Properties of phonon modes of ion trap quantum computer in the Aubry phase. arXiv 2020, arXiv:2002.03730. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhirov, O.V.; Lages, J.; Shepelyansky, D.L. Thermoelectricity Modeling with Cold Dipole Atoms in Aubry Phase of Optical Lattice. Appl. Sci. 2020, 10, 2090. https://doi.org/10.3390/app10062090
Zhirov OV, Lages J, Shepelyansky DL. Thermoelectricity Modeling with Cold Dipole Atoms in Aubry Phase of Optical Lattice. Applied Sciences. 2020; 10(6):2090. https://doi.org/10.3390/app10062090
Chicago/Turabian StyleZhirov, Oleg V., José Lages, and Dima L. Shepelyansky. 2020. "Thermoelectricity Modeling with Cold Dipole Atoms in Aubry Phase of Optical Lattice" Applied Sciences 10, no. 6: 2090. https://doi.org/10.3390/app10062090
APA StyleZhirov, O. V., Lages, J., & Shepelyansky, D. L. (2020). Thermoelectricity Modeling with Cold Dipole Atoms in Aubry Phase of Optical Lattice. Applied Sciences, 10(6), 2090. https://doi.org/10.3390/app10062090




