Multiple Current Reversals Using Superimposed Driven Lattices
Abstract
1. Introduction
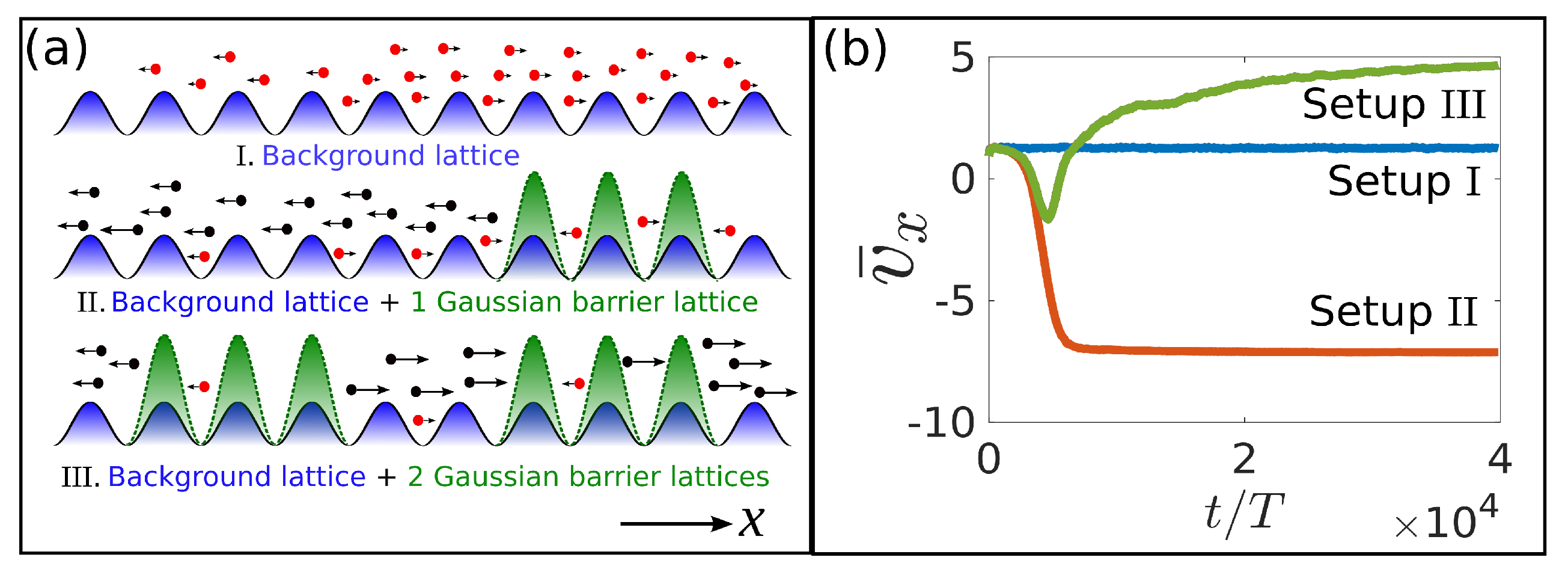
2. Setup, Equations of Motion and Symmetries
3. Results
4. Discussion
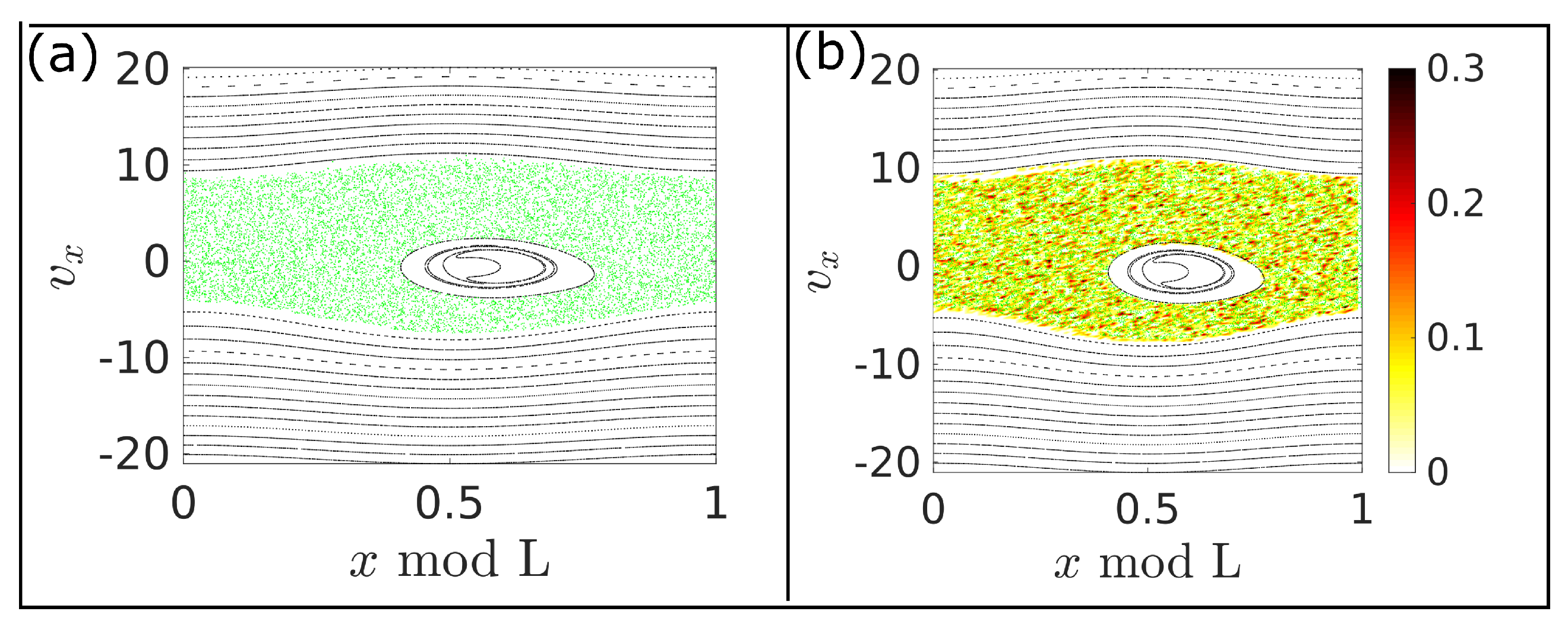
4.1. Directed Transport in Background Lattice
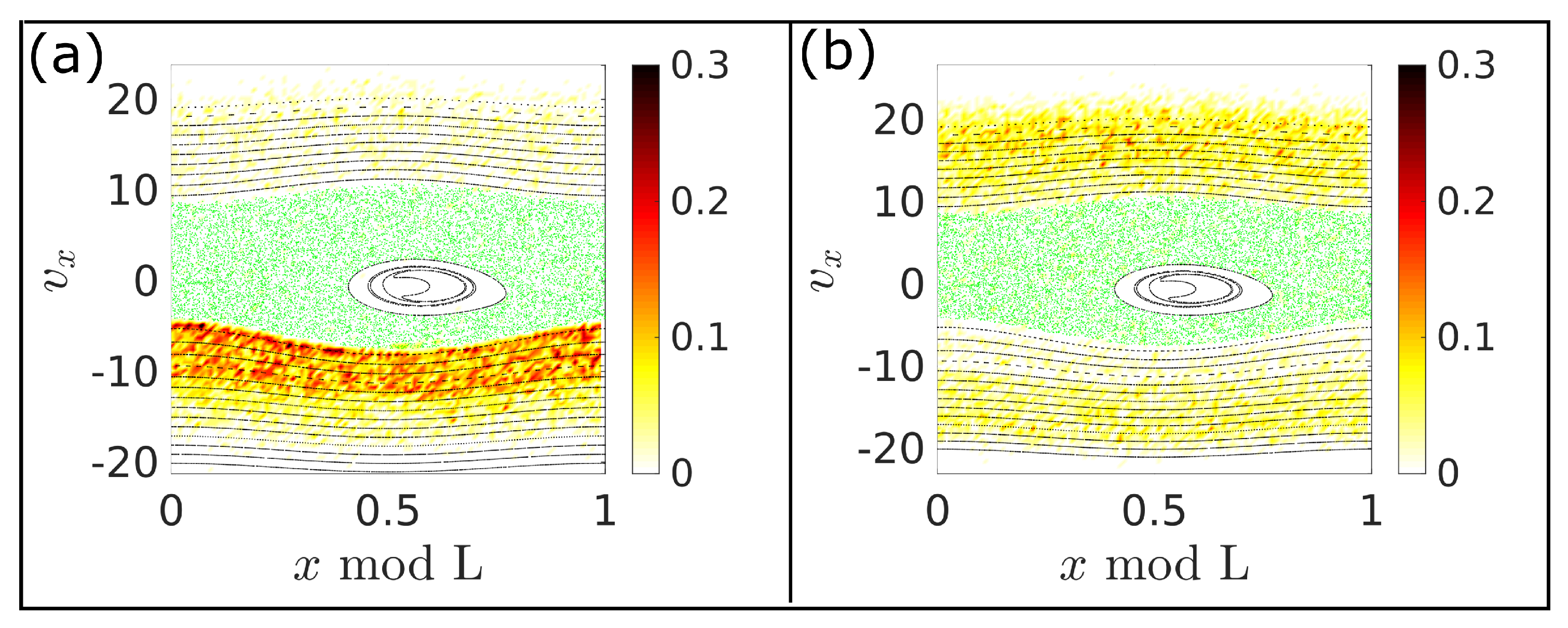
4.2. First Current Reversal
4.3. Second Current Reversal
5. Experimental Realization
6. Brief Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ait-Haddou, R.; Herzog, W. Brownian Ratchet Models of Molecular Motors. Cell Biochem. Biophys. 2003, 38, 191–214. [Google Scholar] [CrossRef]
- Astumian, R.D.; Hänggi, P. Brownian Motors. Phys. Today 2002, 55, 33. [Google Scholar] [CrossRef]
- Astumian, R.D. Thermodynamics and Kinetics of a Brownian Motor. Science 1997, 276, 917–922. [Google Scholar] [CrossRef] [PubMed]
- Jülicher, F.; Ajdari, A.; Prost, J. Modeling Molecular Motors. Rev. Mod. Phys. 1997, 69, 1269–1282. [Google Scholar] [CrossRef]
- Bartussek, R.; Hänggi, P.; Kissner, J.G. Periodically Rocked Thermal Ratchets. Europhys. Lett. 1994, 28, 459–464. [Google Scholar] [CrossRef]
- Cubero, D.; Renzoni, F. Brownian Ratchets; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar] [CrossRef]
- Denisov, S.; Flach, S.; Hänggi, P. Tunable Transport with Broken Space–Time Symmetries. Phys. Rep. 2014, 538, 77–120. [Google Scholar] [CrossRef]
- Faucheux, L.P.; Bourdieu, L.S.; Kaplan, P.D.; Libchaber, A.J. Optical Thermal Ratchet. Phys. Rev. Lett. 1995, 74, 1504–1507. [Google Scholar] [CrossRef]
- Hänggi, P.; Marchesoni, F.; Nori, F. Brownian Motors. Ann. Phys. 2005, 14, 51. [Google Scholar] [CrossRef]
- Hänggi, P.; Marchesoni, F. Artificial Brownian Motors: Controlling Transport on the Nanoscale. Rev. Mod. Phys. 2009, 81, 387–442. [Google Scholar] [CrossRef]
- Magnasco, M.O. Forced Thermal Ratchets. Phys. Rev. Lett. 1993, 71, 1477–1481. [Google Scholar] [CrossRef]
- Prost, J.; Chauwin, J.F.; Peliti, L.; Ajdari, A. Asymmetric Pumping of Particles. Phys. Rev. Lett. 1994, 72, 2652–2655. [Google Scholar] [CrossRef]
- Reichhardt, C.J.O.; Reichhardt, C. Ratchet Effects in Active Matter Systems. Annu. Rev. Condens. Matter Phys. 2017, 8, 51. [Google Scholar] [CrossRef]
- Renzoni, F. Driven Ratchets in Cold Atoms; Elsevier: Amsterdam, The Netherlands, 2009. [Google Scholar]
- Flach, S.; Yevtushenko, O.; Zolotaryuk, Y. Directed Current Due to Broken Time-Space Symmetry. Phys. Rev. Lett. 2000, 84, 2358–2361. [Google Scholar] [CrossRef]
- Schanz, H.; Dittrich, T.; Ketzmerick, R. Directed Chaotic Transport in Hamiltonian Ratchets. Phys. Rev. E 2005, 71, 026228. [Google Scholar] [CrossRef]
- Matthias, S.; Müller, F. Asymmetric Pores in a Silicon Membrane Acting as Massively Parallel Brownian Ratchets. Nature 2003, 424, 53. [Google Scholar] [CrossRef]
- Mukhopadhyay, A.K.; Liebchen, B.; Schmelcher, P. Simultaneous Control of Multispecies Particle Transport and Segregation in Driven Lattices. Phys. Rev. Lett. 2018, 120, 218002. [Google Scholar] [CrossRef]
- Wambaugh, J.F.; Reichhardt, C.; Olson, C.J. Ratchet-Induced Segregation and Transport of Nonspherical Grains. Phys. Rev. E 2002, 65, 031308. [Google Scholar] [CrossRef]
- Petri, C.; Lenz, F.; Liebchen, B.; Diakonos, F.; Schmelcher, P. Formation of Density Waves via Interface Conversion of Ballistic and Diffusive Motion. Europhys. Lett. 2011, 95, 30005. [Google Scholar] [CrossRef][Green Version]
- Wulf, T.; Petri, C.; Liebchen, B.; Schmelcher, P. Analysis of Interface Conversion Processes of Ballistic and Diffusive Motion in Driven Superlattices. Phys. Rev. E 2012, 86, 016201. [Google Scholar] [CrossRef]
- Falo, F.; Martínez, P.J.; Mazo, J.J.; Cilla, S. Ratchet Potential for Fluxons in Josephson-Junction Arrays. Europhys. Lett. 1999, 45, 700–706. [Google Scholar] [CrossRef]
- Zolotaryuk, Y. Asymmetric Ac Fluxon Depinning in a Josephson Junction Array: A Highly Discrete Limit. Phys. Rev. E 2012, 86, 026604. [Google Scholar] [CrossRef]
- Ai, B. Ratchet Transport Powered by Chiral Active Particles. Sci. Rep. 2016, 6, 18740. [Google Scholar] [CrossRef]
- Spiechowicz, J.; Łuczka, J. SQUID Ratchet: Statistics of Transitions in Dynamical Localization. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 013105. [Google Scholar] [CrossRef]
- Spiechowicz, J.; Łuczka, J. Efficiency of the SQUID Ratchet Driven by External Current. New J. Phys. 2015, 17, 023054. [Google Scholar] [CrossRef]
- Zapata, I.; Bartussek, R.; Sols, F.; Hänggi, P. Voltage Rectification by a SQUID Ratchet. Phys. Rev. Lett. 1996, 77, 2292–2295. [Google Scholar] [CrossRef]
- Faltermeier, P.; Budkin, G.V.; Unverzagt, J.; Hubmann, S.; Pfaller, A.; Bel’Kov, V.V.; Golub, L.E.; Ivchenko, E.L.; Adamus, Z.; Karczewski, G.; et al. Magnetic Quantum Ratchet Effect in (Cd,Mn)Te- and CdTe-Based Quantum Well Structures with a Lateral Asymmetric Superlattice. Phys. Rev. B 2017, 95, 155442. [Google Scholar] [CrossRef]
- Lebedev, V.; Renzoni, F. Two-Dimensional Rocking Ratchet for Cold Atoms. Phys. Rev. A 2009, 80, 023422. [Google Scholar] [CrossRef]
- Schiavoni, M.; Sanchez-Palencia, L.; Renzoni, F.; Grynberg, G. Phase Control of Directed Diffusion in a Symmetric Optical Lattice. Phys. Rev. Lett. 2003, 90, 094101. [Google Scholar] [CrossRef]
- Salger, T.; Kling, S.; Hecking, T.; Geckeler, C.; Morales-Molina, L.; Weitz, M. Directed Transport of Atoms in a Hamiltonian Quantum Ratchet. Science 2009, 326, 1241–1243. [Google Scholar] [CrossRef]
- Brown, M.; Renzoni, F. Ratchet Effect in an Optical Lattice with Biharmonic Driving: A Numerical Analysis. Phys. Rev. A 2008, 77, 033405. [Google Scholar] [CrossRef]
- Liebchen, B.; Diakonos, F.K.; Schmelcher, P. Interaction-Induced Current-Reversals in Driven Lattices. New J. Phys. 2012, 14, 103032. [Google Scholar] [CrossRef]
- Schanz, H.; Otto, M.F.; Ketzmerick, R.; Dittrich, T. Classical and Quantum Hamiltonian Ratchets. Phys. Rev. Lett. 2001, 87, 070601. [Google Scholar] [CrossRef] [PubMed]
- Cubero, D.; Renzoni, F. Control of Transport in Two-Dimensional Systems via Dynamical Decoupling of Degrees of Freedom with Quasiperiodic Driving Fields. Phys. Rev. E 2012, 86, 056201. [Google Scholar] [CrossRef] [PubMed]
- Denisov, S.; Zolotaryuk, Y.; Flach, S.; Yevtushenko, O. Vortex and Translational Currents Due to Broken Time-Space Symmetries. Phys. Rev. Lett. 2008, 100, 224102. [Google Scholar] [CrossRef]
- Arzola, A.V.; Villasante-Barahona, M.; Volke-Sepúlveda, K.; Jákl, P.; Zemánek, P. Omnidirectional Transport in Fully Reconfigurable Two Dimensional Optical Ratchets. Phys. Rev. Lett. 2017, 118, 138002. [Google Scholar] [CrossRef]
- Arzola, A.V.; Volke-Sepúlveda, K.; Mateos, J.L. Experimental Control of Transport and Current Reversals in a Deterministic Optical Rocking Ratchet. Phys. Rev. Lett. 2011, 106, 168104. [Google Scholar] [CrossRef]
- Dandogbessi, B.; Akin-Ojo, O.; Kenfack, A. Controlling Current Reversals in Chaotic Ratchet Transport. Phys. Scr. 2015, 90, 055206. [Google Scholar] [CrossRef]
- Schreier, M.; Reimann, P.; Hänggi, P.; Pollak, E. Giant Enhancement of Diffusion and Particle Selection in Rocked Periodic Potentials. Europhys. Lett. 1998, 44, 416–422. [Google Scholar] [CrossRef]
- Wickenbrock, A.; Cubero, D.; Wahab, N.A.A.; Phoonthong, P.; Renzoni, F. Current Reversals in a Rocking Ratchet: The Frequency Domain. Phys. Rev. E 2011, 84, 021127. [Google Scholar] [CrossRef]
- Dinis, L.; Quintero, N.R. Nonsinusoidal Current and Current Reversals in a Gating Ratchet. Phys. Rev. E 2015, 91, 032920. [Google Scholar] [CrossRef]
- Zeng, C.; Wang, H.; Nie, L. Multiple Current Reversals and Diffusion Enhancement in a Symmetrical Periodic Potential. Chaos Interdiscip. J. Nonlinear Sci. 2012, 22, 033125. [Google Scholar] [CrossRef]
- Kostur, M.; Łuczka, J. Multiple Current Reversal in Brownian Ratchets. Phys. Rev. E 2001, 63, 021101. [Google Scholar] [CrossRef]
- Chen, R.; Zhang, G.; Wang, C.; Nie, L.; Chen, C. Current Reversal in a Symmetric Periodic Potential. Chaos Solitons Fractals 2017, 98, 205–209. [Google Scholar] [CrossRef]
- Rana, S.; Goswami, S.; Chatterjee, S.; Pradhan, P. Current Reversal in Interacting Colloids under Time-Periodic Drive. Phys. Rev. E 2018, 98, 052142. [Google Scholar] [CrossRef]
- Da Silva, R.M.; Manchein, C.; Beims, M.W. Optimal Ratchet Current for Elastically Interacting Particles. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 111101. [Google Scholar] [CrossRef]
- De Souza Silva, C.C.; Van de Vondel, J.; Morelle, M.; Moshchalkov, V.V. Controlled Multiple Reversals of a Ratchet Effect. Nature 2006, 440, 651–654. [Google Scholar] [CrossRef]
- Marconi, V.I. Rocking Ratchets in Two-Dimensional Josephson Networks: Collective Effects and Current Reversal. Phys. Rev. Lett. 2007, 98, 047006. [Google Scholar] [CrossRef]
- Mateos, J.L. Chaotic Transport and Current Reversal in Deterministic Ratchets. Phys. Rev. Lett. 2000, 84, 258–261. [Google Scholar] [CrossRef]
- Mukhopadhyay, A.K.; Xie, T.; Liebchen, B.; Schmelcher, P. Dimensional Coupling-Induced Current Reversal in Two-Dimensional Driven Lattices. Phys. Rev. E 2018, 97, 050202. [Google Scholar] [CrossRef]
- Mukhopadhyay, A.K.; Liebchen, B.; Wulf, T.; Schmelcher, P. Freezing, Accelerating, and Slowing Directed Currents in Real Time with Superimposed Driven Lattices. Phys. Rev. E 2016, 93, 052219. [Google Scholar] [CrossRef]
- Dormand, J.R.; Prince, P.J. A Family of Embedded Runge-Kutta Formulae. J. Comput. Appl. Math. 1980, 6, 19. [Google Scholar] [CrossRef]
- Barredo, D.; de Léséleuc, S.; Lienhard, V.; Lahaye, T.; Browaeys, A. An Atom-by-Atom Assembler of Defect-Free Arbitrary Two-Dimensional Atomic Arrays. Science 2016, 354, 1021–1023. [Google Scholar] [CrossRef]
- Kim, H.; Lee, W.; Lee, H.G.; Jo, H.; Song, Y.; Ahn, J. In Situ Single-Atom Array Synthesis Using Dynamic Holographic Optical Tweezers. Nat. Commun. 2016, 7, 13317. [Google Scholar] [CrossRef]
- Nogrette, F.; Labuhn, H.; Ravets, S.; Barredo, D.; Béguin, L.; Vernier, A.; Lahaye, T.; Browaeys, A. Single-Atom Trapping in Holographic 2D Arrays of Microtraps with Arbitrary Geometries. Phys. Rev. X 2014, 4, 021034. [Google Scholar] [CrossRef]
- Stuart, D.; Kuhn, A. Single-Atom Trapping and Transport in DMD-Controlled Optical Tweezers. New J. Phys. 2018, 20, 023013. [Google Scholar] [CrossRef]
- Cubero, D.; Lebedev, V.; Renzoni, F. Current Reversals in a Rocking Ratchet: Dynamical versus Symmetry-Breaking Mechanisms. Phys. Rev. E 2010, 82, 041116. [Google Scholar] [CrossRef]
- Liebchen, B.; Schmelcher, P. Interaction Induced Directed Transport in Ac-Driven Periodic Potentials. New J. Phys. 2015, 17, 083011. [Google Scholar] [CrossRef][Green Version]
- Wulf, T.; Liebchen, B.; Schmelcher, P. Disorder Induced Regular Dynamics in Oscillating Lattices. Phys. Rev. Lett. 2014, 112, 034101. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mukhopadhyay, A.K.; Schmelcher, P. Multiple Current Reversals Using Superimposed Driven Lattices. Appl. Sci. 2020, 10, 1357. https://doi.org/10.3390/app10041357
Mukhopadhyay AK, Schmelcher P. Multiple Current Reversals Using Superimposed Driven Lattices. Applied Sciences. 2020; 10(4):1357. https://doi.org/10.3390/app10041357
Chicago/Turabian StyleMukhopadhyay, Aritra K., and Peter Schmelcher. 2020. "Multiple Current Reversals Using Superimposed Driven Lattices" Applied Sciences 10, no. 4: 1357. https://doi.org/10.3390/app10041357
APA StyleMukhopadhyay, A. K., & Schmelcher, P. (2020). Multiple Current Reversals Using Superimposed Driven Lattices. Applied Sciences, 10(4), 1357. https://doi.org/10.3390/app10041357




