A Construction Schedule Robustness Measure Based on Improved Prospect Theory and the Copula-CRITIC Method

Featured Application

The proposed criterion and methods can measure the construction schedule robustness with consideration of bounded rationality of subjective weights and the inherent importance and nonlinear intercriteria correlations of objective weights. It is applicable to the fields of robust scheduling, decision-making, evaluation, and so on. Further research can be conducted to combine with machine-learning technology to achieve the dynamic robustness measure of the construction schedule.

Abstract

A robustness measure is an effective tool to evaluate the anti-interference capacity of the construction schedule. However, most research focuses on solution robustness or quality robustness, and few consider a composite robustness criterion, neglecting the bounded rationality of subjective weights and inherent importance and nonlinear intercriteria correlations of objective weights. Therefore, a construction schedule robustness measure based on improved prospect theory and the Copula-criteria importance through intercriteria correlation (CRITIC) method is proposed. Firstly, a composite robustness criterion is established, including start time deviation r_s and structural deviation r_p for measuring solution robustness from project execution and completion probability r_c for measuring quality robustness from the project result. Secondly, bounded rationality is considered, using prospect theory to calculate subjective weights, which is improved by the interval distance formula. Thirdly, the Copula-CRITIC method is proposed to determine objective weights incorporating both inherent importance and nonlinear intercriteria correlations. Finally, an information-entropy-based evidence reasoning method is applied to combine subjective and objective weights together while identifying their validity. An underground power station in China is used for a case study, whose robustness is measured using the proposed methods, single robustness criterion, and composite robustness criterion using traditional weighting methods. The comparison results verify the consistency, representativeness, and advantage of the proposed criterion and methods.

1. Introduction

As the basis of quantitative research on schedule robustness, robustness measures are an effective tool to measure the anti-interference ability of schedules [1]. There are two aspects of construction schedule robustness, namely, solution robustness and quality robustness, in measuring a schedule’s robustness. In detail, solution robustness refers to the deviation between the planned and the actual schedule, which measures the robustness from the perspective of project execution. Quality robustness refers to the deviation between the planned and the actual construction duration, which measures the robustness from the perspective of the project result. However, current research mostly focuses on a single robustness criterion, and few consider a composite robustness criterion, neglecting the bounded rationality of subjective weights and the inherent importance and nonlinear intercriteria correlations of objective weights. Therefore, it is of great importance to measure the schedule robustness comprehensively, which considers both solution robustness from project execution and quality robustness from project execution, in addition to the bounded rationality of subjective weights and the inherent importance and nonlinear intercriteria correlations of objective weights.

Studies of the robustness measure are mainly related to job shops, while a few studies on construction schedule robustness measures have been made. While current methods measuring robustness focus on using a single criterion of solution robustness, which is lacking the quality robustness criteria. Lambrechts [2] measured the solution robustness using activity durations for project scheduling. Akkan [3] used start time deviation to measure the solution robustness and the objective optimization function of job shop production. Sundström [4] measured robustness by a solution robustness criterion, which calculates the average deviation of start time between the planned schedule and the actual schedule. Ansari [5] took covariance as a solution robustness criterion and measured the robustness of the schedule obtained by simulations and the critical chain method. Liu [6] established a robustness criterion using a time slack-based technique to deal with schedules with mechanical malfunction and new job arrivals. Xiao [7] took the expected relative deviation between the planned and actual schedule as a solution robustness criterion and used the criterion to analyze the robustness of the stochastic job shop scheduling problem. Rahmani [8] measured the schedule robustness of job shop production concerning mechanical malfunction through a solution robustness criterion. Pang [9] proposed a start time deviation as the solution robustness criterion and used it as the optimization objective for robust project scheduling. Zhong [10] carried out a construction schedule robustness measure of underground power stations by adopting a solution robustness criterion named ‘start time deviation’. Zhang [11] proposed activity delay as the solution robustness criterion to deal with the materials ordering problem. Chang [12] proposed the worst-case expected total flow time as the solution robustness criterion for the robust scheduling of a flowshop. Hu [13] took the travel time as the solution robustness criterion in scheduling vehicle routing.

Studies on the quality robustness criterion are fewer than that on solution robustness criterion and concentrate on the robustness measure of air transport schedules. Liang [14] presented the net present value as a quality criterion to investigate the robust resource-constrained project problem with stochastic activity durations. Novianingsih [15] built a simulation model of the flight and the quotient of the number of iterations to find an optimal crew pairing, and the total number of iterations was taken as its criterion measuring quality robustness. Hussain [16] generated various flight candidate schedules randomly, and their respective robustness was measured by taking quality robustness criteria into consideration, which included timeliness of delivery, amount of cargo moved, and cost. Detti [17] took the quality robustness criterion of total completion times as the optimization objective and adopted a heuristic algorithm to solve the robust scheduling problem of a job shop. Additionally, some researchers proposed criteria concerning both solution robustness and quality robustness, while these criteria were not adopted comprehensively in measuring robustness. Lu [18] proposed two criteria to measure the robustness of job shop production management—the expectation value of makespan as the quality robustness criterion and the expectation value of the total start time delay of all procedures as the solution robustness criterion. Shen [19] defined the efficiency emphasized measurement as a solution robustness criterion and a cumulative distribution function inspired measurement as a quality robustness criterion, which were respectively applied in the optimization model. Lamas [20] established a proactive management schedule in resource-restricted projects, where the start time deviation was adopted to measure the solution robustness, and the completion probability was considered as the criterion for quality robustness. Zhao [21] and Cui [22] proposed a linearly composite criterion of both solution robustness and quality robustness in job shop management concerning random malfunctions, but its weight was assigned as a subject to decision-makers’ preferences.

In summary, current research concerning robustness measures only focuses on solution robustness or quality robustness, which cannot measure the schedule robustness from both the project execution and the project result. Some criteria include both solution and quality robustness criteria, but their weights neglect the bounded rationality of subjective weights and the inherent importance and nonlinear intercriteria correlations of objective weights.

In this paper, the composite robustness criterion containing both solution robustness and quality robustness is proposed from both the project execution and the project result, considering the bounded rationality of subjective weights and the inherent importance and nonlinear intercriteria correlations of objective weights.

The remainder of this paper is organized as follows: Section 1 provides an overview of the related work on weighting methods. Section 2 describes the framework for this paper. Section 3 describes the methodology of the construction schedule robustness measure. In Section 4, a case study of an underground power station in China is presented to verify the consistency, representativeness, and the advantage of the proposed criterion and methods. The conclusion of this paper is highlighted at the end of the paper.

2. Related Work

Subjective weights are in good accordance with the basic cognition of experts to robustness criteria; however, the information contained in the robustness criteria cannot be considered by the experts when they are giving the subjective weights. Objective weights have strong data theoretical basis; however, they cannot take the experts’ experience and judgment into account. Therefore, the combination of subjective and objective weights can take advantage of and overcome the disadvantage of both weighting methods. In this section, the related work on subjective weighting methods, objective weighting methods, and methods of combining subjective and objective weights is reviewed and discussed.

Subjective weighting methods mainly include the analytic hierarchy process (AHP) [23], the Delphi method [24], and the expert-evaluation-based method [25]. These methods are effective in reflecting the importance of different criteria because experts are well-experienced in this field, and they can make reasonable judgments according to actual situations. However, individual preferences are inevitably involved in subjective weighting. Thus, in the above methods, the experts are regarded as rational humans, and the evaluation curve is regarded as an expected utility curve. However, a large number of psychological experiments have demonstrated that the actual behaviors of humans do not correspond to the expected utility curve. Due to the bounded rationality of humans, there tends to be risk aversion when the profit probability is relatively high and risk-seeking when there is a rather high loss probability. At the same time, there tends to be risk-seeking when the profit probability is relatively low, and risk aversion when there is a relatively small chance to suffer losses [26]. It can be concluded that human judgments have individual preferences. Prospect theory has established a successful model to simulate the psychological and behavioral characteristics of human beings, which has been widely applied in the field of engineering [27,28,29], economics [30,31,32], computer science [33,34,35], and so on. This provides a convincing explanation of the fact that the results of subjective empowerment do not conform to reality. So, prospect theory is useful to modify the preliminary results obtained by subjective weighting so as to make the evaluation results become “rational” ones out of the “boundedly rational” ones.

By using objective weighting methods, including entropy weight method [36], principal component analysis method [37] as well as standard deviation method [38], the weights of different criteria are calculated according to the amount of information they contain. The three robustness criteria proposed, namely, start time deviation, structural deviation, and completion probability, which can comprehensively evaluate the schedule robustness, are interrelated to some extent. Therefore, it is unreasonable to assign their respective weights without considering their intercriteria correlation. Criteria importance through intercriteria correlation (CRITIC) is an objective weighting method that measures a criterion by considering both the importance itself and the conflict caused by intercriteria correlations [39]. In summary, in the traditional CRITIC method, the intercriteria correlation is determined by the Pearson correlation coefficient function, which reflects the linear correlation. The Copula function is very useful for the analysis of the correlation between variables when it cannot determine whether the correlation between variables is linear or nonlinear. Thus, it can effectively deal with the difficult intercriteria correlation among the three robustness criteria. Therefore, the CRITIC method is improved by introducing the Copula function to replace the Pearson correlation coefficient, and the objective weights that could incorporate both inherent importance and nonlinear intercriteria correlations can be obtained using the Copula-CRITIC method.

Methods of combining subjective and objective weights, including additive integration [22], multiplicative integration [40], and the eclectic method [41], can balance the subjectivity of preferences with the objectivity of information. However, using these methods will cause an incomplete expression of subjective and objective weights. To solve this problem, Dempster and Shafer [42] proposed the evidence reasoning theory and its corresponding method [43] to combine multisource information without information loss. Liu [44] calculated the combined weight of classifiers by adopting the evidence reasoning method, thus promoting the accuracy of data classification. Bao [28] obtained the expectation values of different alternatives by using the evidence reasoning method, preventing the loss of decision-making information. Zhou [45] carried out a multi-attribute decision-making process in which the subjective weights derived from experts and the objective weights obtained from the attributes were combined via the evidence reasoning method. In fact, the evidence reasoning method generates false information by replacing true information with the complement of true information sources, which is just one of the sources of false information. However, combining subjective and objective information based on this assumption will reduce the combination credibility of the results. Therefore, an information-entropy-based effective probability validation mechanism is introduced into the evidence reasoning method to improve the combination accuracy and the effectiveness of the results in this paper. By calculating the change in entropy when synthesizing the reliability function, the validity of the subjective and objective information is judged, and the invalid information is eliminated during their combination so that the validity of the schedule robustness measure results is guaranteed.

Aiming at the above problems, a construction schedule robustness measure based on improved prospect theory and the Copula-CRITIC method is proposed. Firstly, a composite measure criterion, including start time deviation r_s, structural deviation r_p, and completion probability r_c, is proposed, so that both solution and quality robustness can be considered for measuring. Secondly, the subjective weights are assigned using improved prospect theory, which is improved by introducing an interval distance formula into it to overcome the shortcoming that prospect theory cannot deal with complete expert evaluation information, and the weights given by experts are transformed into a prospect value function so that bounded rationality can be considered. Thirdly, the Copula-CRITIC method, in which a Copula function is adopted to replace the original correlation method of the Pearson correlation coefficient for dealing with the difficult intercriteria correlation among the three robustness criteria, is proposed to determine the objective weights which could incorporate both inherent importance and intercriteria correlations. Finally, the subjective and objective weights are combined using the information-entropy-based evidence reasoning method in order to identify the validity of the weights during combination.

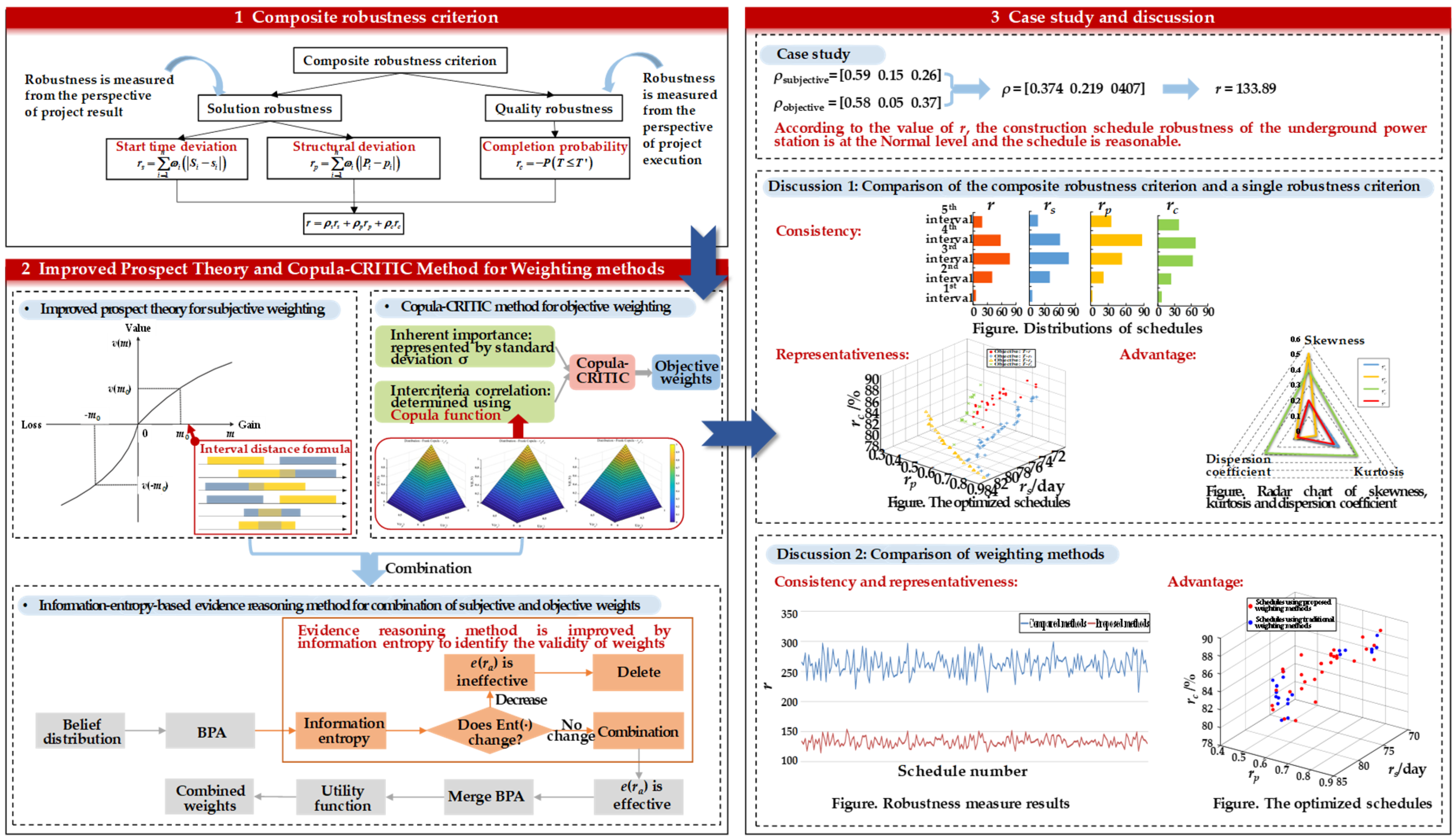
3. Research Framework

The research framework is shown in Figure 1. The composite robustness criterion with start time deviation r_s, structural deviation r_p, and completion probability r_c is established so as to measure the schedule robustness of both solution and quality robustness. The improved prospect theory is adopted to determine the subjective weights, the Copula-CRITIC method is adopted to determine objective weights, and the information-entropy-based evidence reasoning method is adopted to combine the subjective and objective weights so that the bounded rationality of subjective weights and the inherent importance and nonlinear intercriteria correlations of objective weights can be considered. Then, an underground power station in China is used for a case study, and the advantages of the proposed criterion and methods are discussed and verified.

4. Methodology of Construction Schedule Robustness Measure

4.1. Composite Robustness Criterion

For real-life construction settings, activities and logic relationships among activities are two key components of a schedule, and construction duration is an important objective value of a schedule. Thus, it is meaningful to establish the robustness criterion from those three perspectives. Therefore, the composite robustness criterion includes start time deviation r_s for measuring the schedule solution robustness via deviation between the actual start time and planned start time of each activity, structural deviation r_p for measuring the schedule solution robustness via deviation between the actual construction order and planned construction order of each activity, and completion probability r_c for measuring the schedule quality robustness via deviation of the construction duration, as shown in Equation (1):

$$r={\rho }_s{r}_s+{\rho }_p{r}_p+{\rho }_c{r}_c$$

(1)

where r_s is the absolute value of the weighted summation of the deviations between the activity’s actual start time and planned start time, i.e.,

$$r_s={\displaystyle \sum _{i=1}^n{\omega }_i}\left(\left|S_i-s_i\right|\right)$$

(2)

where i ∈ N+ is the number of activities, ${\omega }_i$ denotes the weight of activity i and is the normalized value of the additional cost corresponding to the activity i, S_i represents the actual start time of activity i and s_i represents the planned start time of activity i, the unit of which is days.

In Equation (1), r_p is the absolute value of the weighted summation of the deviations between the activity’s actual construction order and planned construction order, i.e.,

$$r_p={\displaystyle \sum _{i=1}^n{\omega }_i}\left(\left|P_i-p_i\right|\right)$$

(3)

where P_i and p_i are the actual and planned order of activity i respectively, which are dimensionless. P_i is determined by discrete event simulation [1], p_i is determined according to the design of the construction manager.

In Equation (1), r_c is the contrary number of a schedule’s completion probability, i.e.,

$$r_c=-P\left(T\le T\prime \right)$$

(4)

where T and T’ are the actual and planned construction duration, the unit of which is days. P represents probability. A schedule’s completion probability is determined as P(T ≤ T’) [10]. A bigger completion probability indicates better quality robustness of a construction schedule. Nevertheless, smaller r_s and r_p indicate better solution robustness of a construction schedule. Since it is necessary to keep the monotonicity of the r_s, r_p, and r_c consistent, r_c should be the contrary number of P(T ≤ T’), as shown in Equation (4).

In Equation (1), ${\rho }_s$, ${\rho }_p$ and ${\rho }_c$ are the weights of r_s, r_p, and r_c, whose detailed calculation methods are illustrated in Section 4.2, Section 4.3 and Section 4.4.

4.2. Improved Prospect Theory for Subjective Weighting

Improved prospect theory is proposed to determine the subjective weights. To overcome the shortcoming that the subjective weights given by experts are rationally bounded because of the experts’ individual preferences, the experts’ individual preferences are calculated and eliminated by prospect theory. In this way, the subjective weights of the bounded rationality can be transformed into subjective weights of rationality. Meanwhile, the interval distance formula is introduced into the prospect theory to overcome the shortcoming that prospect theory cannot deal with complete expert evaluation information. The procedure of subjective weighing is as follows:

• Obtain the interval-valued weights of r_s, r_p and r_c given by n experts (as shown in

  Table 1. Subjective weights given by experts.

  	Criterion	rs	rp	rc
  Expert
  E1		${\rho }_{s1}^{\mathrm{sub}}=\left[{\rho }_{s1}^{\mathrm{sub}-},{\rho }_{s1}^{\mathrm{sub}+}\right]$	${\rho }_{p1}^{\mathrm{sub}}=\left[{\rho }_{p1}^{\mathrm{sub}-},{\rho }_{p1}^{\mathrm{sub}+}\right]$	${\rho }_{c1}^{\mathrm{sub}}=\left[{\rho }_{c1}^{\mathrm{sub}-},{\rho }_{c1}^{\mathrm{sub}+}\right]$
  E2		${\rho }_{s2}^{\mathrm{sub}}=\left[{\rho }_{s2}^{\mathrm{sub}-},{\rho }_{s2}^{\mathrm{sub}+}\right]$	${\rho }_{p2}^{\mathrm{sub}}=\left[{\rho }_{p2}^{\mathrm{sub}-},{\rho }_{p2}^{\mathrm{sub}+}\right]$	${\rho }_{c2}^{\mathrm{sub}}=\left[{\rho }_{c2}^{\mathrm{sub}-},{\rho }_{c2}^{\mathrm{sub}+}\right]$
  ……		……	……	……
  En		${\rho }_{sn}^{\mathrm{sub}}=\left[{\rho }_{sn}^{\mathrm{sub}-},{\rho }_{sn}^{\mathrm{sub}+}\right]$	${\rho }_{pn}^{\mathrm{sub}}=\left[{\rho }_{pn}^{\mathrm{sub}-},{\rho }_{pn}^{\mathrm{sub}+}\right]$	${\rho }_{cn}^{\mathrm{sub}}=\left[{\rho }_{cn}^{\mathrm{sub}-},{\rho }_{cn}^{\mathrm{sub}+}\right]$

  ).
• Determine the reference intervals of the three robustness criteria by the arithmetic mean method:

  $$\begin{gathered} v{p}_s=f\left({\rho }_{s1}^{\mathrm{sub}},{\rho }_{s2}^{\mathrm{sub}},\dots ,{\rho }_{sn}^{\mathrm{sub}}\right) \\ v{p}_p=f\left({\rho }_{p1}^{\mathrm{sub}},{\rho }_{p2}^{\mathrm{sub}},\dots ,{\rho }_{pn}^{\mathrm{sub}}\right) \\ v{p}_c=f\left({\rho }_{c1}^{\mathrm{sub}},{\rho }_{c2}^{\mathrm{sub}},\dots ,{\rho }_{cn}^{\mathrm{sub}}\right) \end{gathered}$$

  (5)

  where, vp_s, vp_p and vp_c represent the reference intervals. $f(·)$ is the arithmetic mean function.
• Establish the matrix of reference intervals VP:

  VP = [vp_s, vp_p, vp_c]

  (6)
• Obtain the gain/loss matrix M, which is the matrix reflecting experts’ individual preference. Gain implies that the subjective weight given by the expert is larger than RP. Loss implies that the subjective weight given by the expert is smaller than RP. M is computed using interval distance formula, i.e.,

  $$\begin{array}{ll}M& =m\left(v{p}_a,{\rho }_{an}^{\mathrm{sub}}\right)\\ & ={{\displaystyle \int }}_0^1\left|\left[v{p}_a^{-}+x\left(v{p}_a^{+}-v{p}_a^{-}\right)\right]-\left[{\rho }_{an}^{\mathrm{sub}-}+x\left({\rho }_{an}^{\mathrm{sub}+}-{\rho }_{an}^{\mathrm{sub}-}\right)\right]\right|dx\\ & ={{\displaystyle \int }}_0^1\left|\left(v{p}_a^{-}-{\rho }_{an}^{\mathrm{sub}-}\right)+\left(-v{p}_a^{-}+v{p}_a^{+}+{\rho }_{an}^{\mathrm{sub}-}-{\rho }_{an}^{\mathrm{sub}+}\right)x\right|dx\end{array}$$

  (7)

  where $a=s,p,c$ represents the three robustness criteria, ${\rho }_{an}^{\mathrm{sub}}$ is the subjective weights given by experts, $m\left(v{p}_a,{\rho }_{an}^{\mathrm{sub}}\right)$ is the distance between vp_a and ${\rho }_{an}^{\mathrm{sub}}$. $m\left(v{p}_a,{\rho }_{an}^{\mathrm{sub}}\right)$ is calculated as follows: take the weighted absolute value of the left and right endpoint values of two intervals, then the value is traversed in [0, 1] and the combined result is the distance between the intervals.
  There are six kinds of positional relationships between $v{p}_a$ and ${\rho }_{an}^{\mathrm{sub}}$. The positional relationships and the corresponding distance formulas derived from Equation (7) are shown in Figure 2.
• Calculate the value function through M = m(vp_a, ${\rho }_{an}^{\mathrm{sub}}$). The value function is the function reflecting the value of weights given by experts, with the gain/loss as an independent variable and the value of weights given by experts as a dependent variable. It is calculated as

  $$v\left(m\right)=\{\begin{array}{ll}{m}^{\alpha }& m\ge 0\\ -\lambda {\left(-m\right)}^{\beta }& m<0\end{array}$$

  (8)

  where $v(·)$ is the value function, $\alpha$ is the positive risk attitude coefficient, while $\beta$ is the negative risk attitude coefficient, and $0\le \alpha , \beta \le 1$. $\lambda$ is the loss avoidance coefficient. It is suggested that $\alpha =0.89$, $\beta =0.92$ and $\lambda =2.25$ [46].
• Calculate the comprehensive prospect value:

  $$V={\displaystyle \sum }\pi \left(VP\right)·v\left(m\right)$$

  (9)

  where $\pi \left(VP\right)$ is the weight function and weights of different experts are assigned identically.
• Finally, the subjective weights, considering bounded rationality can be calculated:

  $${\rho }_{\mathrm{subjective}\text{-}a}=\frac{v\left(m\right)}{V}.$$

  (10)

4.3. Copula-CRITIC Method for Objective Weighting

The Copula-CRITIC method is proposed to determine the objective weights. To overcome the shortcoming that the Pearson correlation coefficient function in the CRITIC method cannot effectively deal with, i.e., the difficulty in the intercriteria correlation among the three robustness criteria, the Copula function is introduced into the CRITIC method to replace the Pearson correlation coefficient function. In this way, the nonlinear correlation among r_s, r_p, and r_c can be obtained, and the objective weights incorporating both inherent importance and nonlinear intercriteria correlations can be obtained (as shown in Figure 3).

The procedure of objective weighing is as follows:

• By using the Copula-CRITIC method, the objective weights are determined according to the inherent importance and nonlinear intercriteria correlation of three robustness criteria. Set C_a as the information contained in r_a (a = s, p, c), C_a is

  $$C_a={\sigma }_a{\displaystyle \sum }_{i=s}^c\left(1-l_{i-a}\right)$$

  (11)

  where $C_a$ represents the criterion’s information, ${\sigma }_a$ is the standard deviation to represent its inherent importance, and $l_{i-a}$ is the correlation coefficient and is computed using the Copula function.
• Compute $l_{i-a}$ using the Copula function: Five classical Copula functions [47] are applied to the distribution fitting of the robustness criteria. The unknown parameters in the five Copula functions are determined by semi-parameter estimations. Then, the best Copula function is chosen according to the squared Euclidean distance d² between the fitting Copula function and the empirical Copula function. The smaller d² is, the better the fitting degree is. The d² is calculated as follows:

  $$d^2={{\displaystyle \sum _{a=s}^c\left|\stackrel{\wedge }{C}\left(r_s,r_p,r_c\right)-C\left(r_s,r_p,r_c\right)\right|}}^2$$

  (12)

  where $\stackrel{\wedge }{C}\left(r_s,r_p,r_c\right)$ represents the empirical Copula function, and $C\left(r_s,r_p,r_c\right)$ represents the fitting Copula function.
• Calculate the objective weights ρ_objective: Considering the standard deviations ${\sigma }_a$ and the correlation coefficients $l_{i-a}$, the objective weights of each criterion can be calculated:

  $${\rho }_{\mathrm{objective}\text{-}a}=C_a/{\displaystyle \sum _{a=s}^a\left(C_a\right)}(a=s,p,c).$$

  (13)

4.4. Information-Entropy-Based Evidence Reasoning Method for the Combination of Subjective and Objective Weights

In order to exclude invalid information from the weight combination process, the evidence reasoning method is improved by introducing the information-entropy-based effectiveness validation mechanism in the initial weight assignment stage in this paper, making the robustness measure a better reflection of bounded rational of subjective weights, inherent importance and interrelationships of objective weights [48]. The procedure of combination of subjective and objective weights is as follows:

• Define H. H is the acceptance degree of ${\rho }_{\mathrm{subjective}}$ and ${\rho }_{\mathrm{objective}}$. It has five classifications {SN, N, A, Y, SY}, which correspond to {Strongly no, No, Accept, Yes, Strongly yes}. Their utility values are U(SN) = −1, U(N) = −0.5, U(A) = 0, U(Y) = 0.5, U(SY) = 1. The belief distribution of the robustness criterion r_a to weight ${\rho }_b\left(b=\mathrm{subjective},\mathrm{objective}\right)$ is:

  $$S\left({\rho }_b\left(r_a\right)\right)=\left\{\left(H_x,{\theta }_{x,b}\left(r_a\right)\right),x\in H;\left(H,{\theta }_{H,b}\left(r_a\right)\right)\right\}.$$

  (14)
• Compute BPA. Basic probability assignment (BPA) e represents the accepted probability of ${\rho }_b$ with H. The belief distribution $S\left({\rho }_b\left(r_a\right)\right)$ is transformed to BPA by Equations (15)–(18).

  $$e_{x,b}=e_b\left(H_x\right)=0.5{\theta }_{x,b}\left(r_a\right)$$

  (15)

  $$e_{H,b}=e_b\left(H\right)=1-{\displaystyle \sum _{x=SN}^{SY}{e}_{H,b}}=1-0.5{\displaystyle \sum _{x=SN}^{SY}{\theta }_{x,b}\left(r_a\right)}$$

  (16)

  $${\overline{e}}_{H,b}={\overline{e}}_b\left(H\right)=1-0.5=0.5$$

  (17)

  $${\stackrel{\sim }{e}}_{H,b}={\stackrel{\sim }{e}}_b\left(H\right)=0.5\left(1-{\displaystyle \sum _{x=SN}^{SY}{e}_{H,b}}\right)$$

  (18)

  where $e_{x,b}$ is the BPA of the total weight to ${\rho }_b$ with the acceptation degree of $H_x$, e_{H, b} is the BPA of the total weight to ${\rho }_b$ with all acceptation degrees. $e_{H,b}={\overline{e}}_{H,b}+{\stackrel{\sim }{e}}_{H,b}$. ${\overline{e}}_{H,b}$ appeared as the result of other weights, and ${\stackrel{\sim }{e}}_{H,b}$ appeared as the result of the unascertained acceptance degrees.
• Merge the basic probabilities of subjective and objective weights:

  $$e(r_a)=\left(e_1\oplus \dots \oplus e_5\right)(r_a)=\frac{{\displaystyle \sum _{e\in r_a}^{}{\displaystyle \prod _{b=\mathrm{subjective}}^{\mathrm{objective}}{e}_x(r_a)}}}{K}$$

  (19)

  where K is the orthogonalized constant, representing the combination degree of different probabilities, which is calculated as

  $$K={\displaystyle \sum _{e\in \varnothing }{\displaystyle \prod _{b=\mathrm{subjective}}^{\mathrm{objective}}{e}_x(r_a)}}.$$

  (20)
• Validate the effectiveness of weights. The effectiveness is validated by calculating the change in entropy during step 3 (as shown in Equation (21)). A decrease in entropy suggests that the merged weights are valid; otherwise, the weight is invalid and should be deleted during step 3.

  $$Ent\left(r_a\right)=\frac{e\left(r_a\right)}{-{\log }_2\left(r_a\right)}$$

  (21)
• Calculate the probabilities that ${\rho }_b$ is accepted with $H_x$ and H are calculated:

  $${\theta }_x=\frac{e_x}{1-{\overline{e}}_H},$$

  (22)

  $${\theta }_H=\frac{{\stackrel{\sim }{e}}_H}{1-{\overline{e}}_H}.$$

  (23)
• Calculate the utility of the robustness criterion. The utility function is shown in Equation (24). Thus, the minimum utility $U_{\min }$, maximum utility $U_{\max }$, and average utility $U_{\mathrm{avg}}$ can be obtained:

  $$U={\theta }_{x}U\left(H_x\right)$$

  (24)

  $$U_{\max }=\left({\theta }_1\left(r_a\right)+{\theta }_H\left(r_a\right)\right)U\left(H_1\right)+{\displaystyle \sum _{x=2}^5\left({\theta }_x\left(r_a\right)U\left(H_x\right)\right)}$$

  (25)

  $$U_{\min }=\left({\theta }_N\left(r_a\right)+{\theta }_H\left(r_a\right)\right)U\left(H_N\right)+{\displaystyle \sum _{x=1}^4\left({\theta }_x\left(r_a\right)U\left(H_N\right)\right)}$$

  (26)

  $$U_{\mathrm{avg}}=\frac{U_{\max }+U_{\min }}{2}.$$

  (27)
• The total weight of robustness criterion can be obtained:

  $${\rho }_a=U_{\mathrm{avg},a}/{\displaystyle \sum _{a=s}^a\left(U_{\mathrm{avg},a}\right)}.$$

  (28)

5. Case Study

An underground power station in China is used for a case study. Its construction schedule robustness is measured using the composite robustness criterion and weighting methods proposed in this paper. The criterion’s subjective, objective, and combined weights are calculated, and r_s, r_p, r_c of the project are determined. Then, the composite robustness criterion of the underground power station’s construction schedule is obtained.

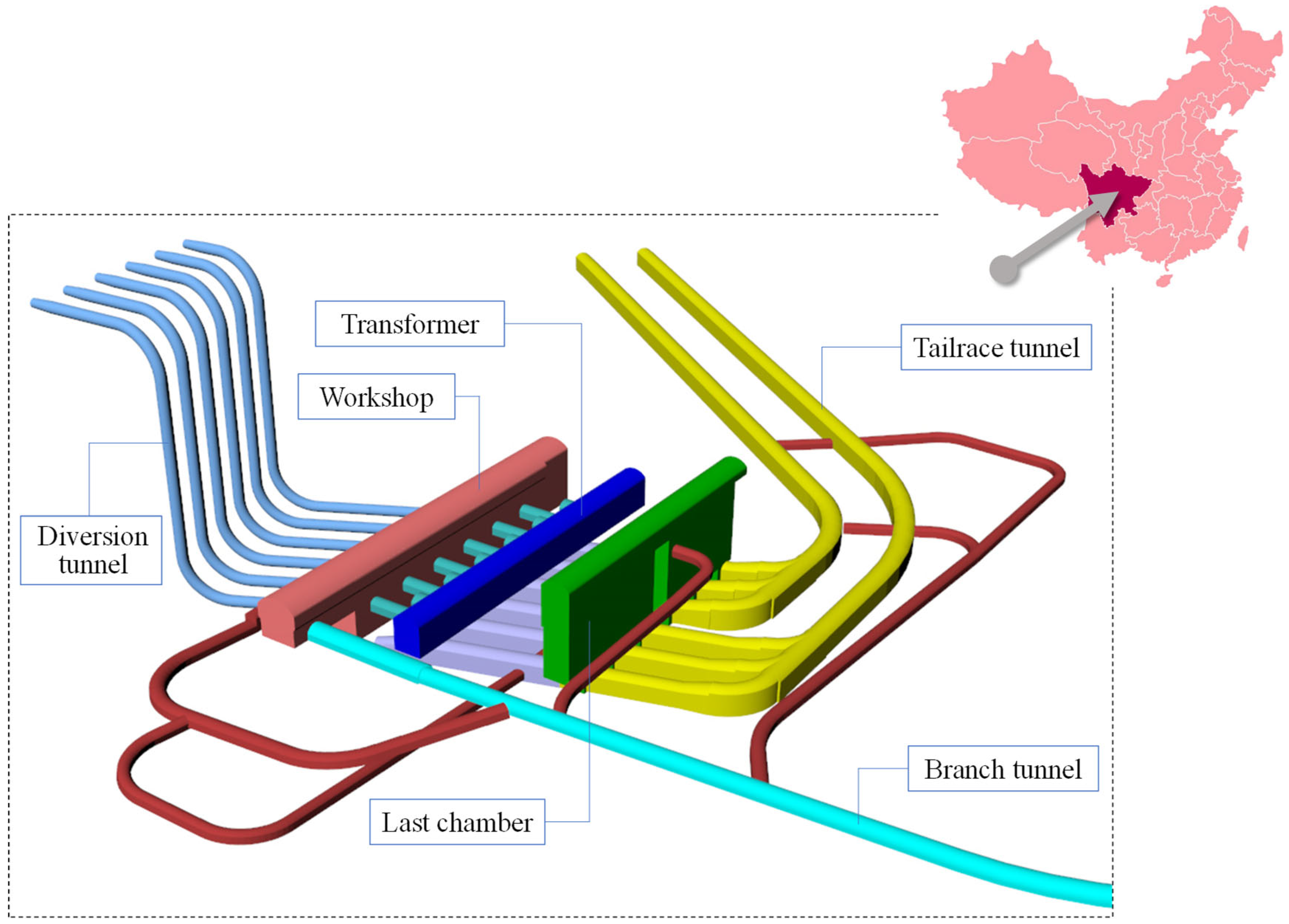
5.1. Project Overview

The underground power station used as a case study is in Southwest China. As shown in Figure 4, it is composed of the main workshop, main transformer, last chamber, and several branch tunnels.

5.2. Weighting of Robustness Criteria

5.2.1. Subjective Weighting

The subjective weights are determined. Taking underground power stations as an example, experts’ judgments on the mechanical malfunction probability of different machines are not identical to the expected utility curve. Although hand drills often fail, the malfunction rate given by experts is lower than the actual statistical results due to their low price. On the contrary, though three-arm trolleys have low failure frequency, their failure rate provided by experts is higher than the actual statistical results because of their high costs [49]. Thus, prospect theory is adopted and improved to calculate the subjective weights.

The evaluation results given by ten experts are shown in

Table 2. Evaluation results given by experts.

	Criterion	rs	rp	rc
Expert
E1		[0.2,0.5]	[0.3,0.4]	[0.4,0.5]
E2		[0.3,0.5]	[0.2,0.3]	[0.3,0.4]
E3		[0.5,0.6]	[0.1,0.2]	[0.2,0.4]
E4		[0.4,0.6]	[0.1,0.3]	[0.3,0.5]
E5		[0.3,0.4]	[0.1,0.3]	[0.4,0.6]
E6		[0.4,0.6]	[0.2,0.4]	[0.3,0.6]
E7		[0.5,0.7]	[0.1,0.2]	[0.3,0.5]
E8		[0.2,0.6]	[0.2,0.4]	[0.5,0.7]
E9		[0.3,0.6]	[0.3,0.4]	[0.3,0.5]
E10		[0.4,0.5]	[0.1,0.2]	[0.2,0.4]
RP		[0.35,0.56]	[0.17,0.31]	[0.32,0.51]

, where RPs are calculated. It can be known that the subjective weighting method adapted with improved prospect theory is capable of handling interval-valued weights.

The gain/loss matrix M and value function matrix are obtained:

$$\begin{gathered} M=\left[\begin{array}{rrr}\hfill 0.1100& \hfill -0.1050& \hfill 0.0350\\ \hfill 0.0125& \hfill -0.0550& \hfill 0.0694\\ \hfill -0.0900& \hfill 0.0950& \hfill -0.1150\\ \hfill -0.0400& \hfill 0.0450& \hfill -0.0150\\ \hfill -0.0400& \hfill -0.1050& \hfill 0.0850\\ \hfill 0.0600& \hfill 0.0450& \hfill 0.0386\\ \hfill -0.0900& \hfill 0.1450& \hfill -0.0150\\ \hfill 0.0600& \hfill 0.0634& \hfill 0.1850\\ \hfill 0.1100& \hfill 0.0228& \hfill -0.0150\\ \hfill -0.0900& \hfill 0.0277& \hfill -0.1150\end{array}\right], \\ v=\left[\begin{array}{rrr}\hfill 0.1402& \hfill -0.2829& \hfill 0.0506\\ \hfill 0.0202& \hfill -0.1561& \hfill 0.0931\\ \hfill -0.2455& \hfill 0.1231& \hfill -0.3076\\ \hfill -0.1164& \hfill 0.0633& \hfill -0.0472\\ \hfill -0.1164& \hfill -0.2829& \hfill 0.1115\\ \hfill 0.0818& \hfill 0.0633& \hfill 0.0553\\ \hfill -0.2455& \hfill 0.1793& \hfill -0.0472\\ \hfill 0.0818& \hfill 0.0859& \hfill 0.2227\\ \hfill 0.1402& \hfill 0.0345& \hfill -0.0472\\ \hfill -0.2455& \hfill 0.0411& \hfill -0.3076\end{array}\right] \end{gathered}$$

Based on the value function matrix above, the comprehensive prospect value is obtained:

$$V={\left[\begin{array}{r}\hfill 1\\ \hfill 1\\ \hfill 1\\ \hfill 1\\ \hfill 1\\ \hfill 1\\ \hfill 1\\ \hfill 1\\ \hfill 1\\ \hfill 1\end{array}\right]}^T\times \left[\begin{array}{rrr}\hfill 0.1402& \hfill -0.2829& \hfill 0.0506\\ \hfill 0.0202& \hfill -0.1561& \hfill 0.0931\\ \hfill -0.2455& \hfill 0.1231& \hfill -0.3076\\ \hfill -0.1164& \hfill 0.0633& \hfill -0.0472\\ \hfill -0.1164& \hfill -0.2829& \hfill 0.1115\\ \hfill 0.0818& \hfill 0.0633& \hfill 0.0553\\ \hfill -0.2455& \hfill 0.1793& \hfill -0.0472\\ \hfill 0.0818& \hfill 0.0859& \hfill 0.2227\\ \hfill 0.1402& \hfill 0.0345& \hfill -0.0472\\ \hfill -0.2455& \hfill 0.0411& \hfill -0.3076\end{array}\right]=\left[\begin{array}{ccc}-0.5052& -0.1314& -0.2237\end{array}\right]$$

Here the subjective weights of each criterion, considering bounded rationality, can be gained according to the value function and the comprehensive prospect value:

$${\rho }_{\mathrm{subjective}}=\left[\begin{array}{ccc}0.59& 0.15& 0.26\end{array}\right]$$

5.2.2. Objective Weighting

The objective weights are determined. Nonlinear intercriteria correlations among r_s, r_p, and r_c, are calculated using the Copula function. A total of 200 schedules are generated, and their r_s, r_p, and r_c are calculated. Their frequency distributions, including skewness and kurtosis, are shown in Figure 5.

Figure 5 indicates that the frequency distribution curves of the three robustness criteria do not obey normal, Poisson, and other basic distributions. Thus, the distribution function of the three criteria is fitted, which are shown in Figure 6.

Then, the results above are applied to the five Copula functions to estimate the unknown parameters of each function by using the maximum likelihood method. The results are shown in

Table 3. Parameter estimation of the Copula function.

rs, rp	Function	Normal Copula	t-Copula	Gumbel Copula	Clayton Copula	Frank Copula
	Estimated value	0.998	0.9983	24.8429	28.0823	130.1466
rs, rc	Function	Normal Copula	t-Copula	Gumbel Copula	Clayton Copula	Frank Copula
	Estimated value	0.9969	0.9977	20.4307	24.5123	121.3891
rprc	Function	Normal Copula	t-Copula	Gumbel Copula	Clayton Copula	Frank Copula
	Estimated value	0.9982	0.9986	27.0803	32.3490	121.1006

.

The squared Euclidean distances d² between the empirical Copula function and the five classical Copula functions are calculated, as shown in

Table 4. Squared Euclidean distances d².

rs, rp	Function	Normal Copula	t-Copula	Gumbel Copula	Clayton Copula	Frank Copula
	d2	0.0118	0.0098	0.0115	0.0348	0.0056
rs, rc	Function	Normal Copula	t-Copula	Gumbel Copula	Clayton Copula	Frank Copula
	d2	0.0180	0.0128	0.0170	0.0447	0.0064
rprc	Function	Normal Copula	t-Copula	Gumbel Copula	Clayton Copula	Frank Copula
	d2	0.0108	0.0082	0.0097	0.0267	0.0064

.

It can be seen from Table 4 that the d² between the empirical Copula function and the Frank Copula function is the smallest, which suggests that the Frank Copula function fits best. Thus, the Frank Copula function was adopted to calculate the nonlinear intercriteria correlations among robustness criteria. Figure 7 illustrates the Frank Copula functions and their comparisons with the empirical Copula function.

The parameter estimation results in Table 3 are applied to the Frank Copula function, and the rank correlation coefficients can be obtained: l_s-p = 0.9697, l_s-c = 0.9675, l_p-c = 0.9674. In addition, the standard variance reflecting the self-strength of the different criteria are ${\sigma }_s=28.61$, ${\sigma }_p=2.02$, ${\sigma }_c=17.80$.

Here the objective weights of each criterion, which could incorporate both inherent importance and nonlinear intercriteria correlations, can be gained:

$${\rho }_{\mathrm{objective}}=\left[\begin{array}{ccc}0.58& 0.05& 0.37\end{array}\right]$$

5.2.3. Combination of Subjective and Objective Weights

Thirdly, the subjective and objective weights are combined. The belief distribution of the subjective and objective weights of r_s, r_p, and r_c is shown in

Table 5. Belief distribution of the subjective and objective weights.

	rs	rp	rc
${\rho }_{\mathrm{subjective}}$ (0.5)	$\left\{\begin{array}{l}\left(N,0.01\right),\left(A,0.3\right),\\ \left(Y,0.58\right),\left(SY,0.1\right)\end{array}\right\}$	$\left\{\begin{array}{l}\left(N,0.1\right),\left(A,0.4\right),\\ \left(Y,0.15\right),\left(SY,0.15\right),\\ \left(H,0.2\right)\end{array}\right\}$	$\left\{\begin{array}{l}\left(N,0.03\right),\left(A,0.3\right),\\ \left(Y,0.26\right),\left(SY,0.3\right)\end{array}\right\}$
${\rho }_{\mathrm{objective}}$ (0.5)	$\left\{\begin{array}{l}\left(N,0.02\right),\left(A,0.3\right),\\ \left(Y,0.58\right),\left(SY,0.1\right)\end{array}\right\}$	$\left\{\begin{array}{l}\left(N,0.1\right),\left(A,0.4\right),\\ \left(Y,0.05\right),\left(SY,0.2\right),\\ \left(H,0.25\right)\end{array}\right\}$	$\left\{\begin{array}{l}\left(N,0.03\right),\left(A,0.3\right),\\ \left(Y,0.37\right),\left(SY,0.3\right)\end{array}\right\}$

.

The contents of Table 5 are then transformed to BPA, as shown in

Table 6. Basic probability assignment (BPA).

rs	rp	rc
$\left\{\begin{array}{l}\left(e_{N,\mathrm{subjective}},0.005\right),\left(e_{A,\mathrm{subjective}},0.15\right),\\ \left(e_{Y,\mathrm{subjective}},0.295\right),\left(e_{SY,\mathrm{subjective}},0.05\right),\\ \left({\overline{e}}_{H,\mathrm{subjective}},0.5\right)\end{array}\right\}$	$\left\{\begin{array}{l}\left(e_{N,\mathrm{subjective}},0.05\right),\left(e_{A,\mathrm{subjective}},0.2\right),\\ \left(e_{Y,\mathrm{subjective}},0.075\right),\left(e_{SY,\mathrm{subjective}},0.075\right),\\ \left({\overline{e}}_{H,\mathrm{subjective}},0.5\right)\end{array}\right\}$	$\left\{\begin{array}{l}\left(e_{N,\mathrm{subjective}},0.015\right),\left(e_{A,\mathrm{subjective}},0.15\right),\\ \left(e_{Y,\mathrm{subjective}},0.13\right),\left(e_{SY,\mathrm{subjective}},0.15\right),\\ \left({\tilde{e}}_{H,\mathrm{subjective}},0.055\right),\left({\overline{e}}_{H,\mathrm{subjective}},0.5\right)\end{array}\right\}$
$\left\{\begin{array}{l}\left(e_{N,\mathrm{objective}},0.01\right),\left(e_{A,\mathrm{objective}},0.15\right),\\ \left(e_{Y,\mathrm{objective}},0.29\right),\left(e_{SY,\mathrm{objective}},0.05\right),\\ \left({\overline{e}}_{H,\mathrm{objective}},0.5\right)\end{array}\right\}$	$\left\{\begin{array}{l}\left(e_{N,\mathrm{objective}},0.05\right),\left(e_{A,\mathrm{objective}},0.2\right),\\ \left(e_{Y,\mathrm{objective}},0.025\right),\left(e_{SY,\mathrm{objective}},0.1\right),\\ \left({\overline{e}}_{H,\mathrm{objective}},0.5\right)\end{array}\right\}$	$\left\{\begin{array}{l}\left(e_{N,\mathrm{objective}},0.015\right),\left(e_{A,\mathrm{objective}},0.15\right),\\ \left(e_{Y,\mathrm{objective}},0.185\right),\left(e_{SY,\mathrm{objective}},0.15\right),\\ \left({\overline{e}}_{H,\mathrm{objective}},0.5\right)\end{array}\right\}$

.

The BPAs are merged and the weight distributions are calculated, as shown in

Table 7. Weight distributions.

	SN	N	A	Y	SY	H
rs	0	0.0150	0.3000	0.5850	0.1000	0
rp	0	0.1290	0.5161	0.1290	0.2258	0
rc	0	0.0284	0.2843	0.2958	0.2843	0.1043

.

At last, the combined weights are obtained:

$$\rho =\left[\begin{array}{ccc}0.374& 0.219& 0.407\end{array}\right]$$

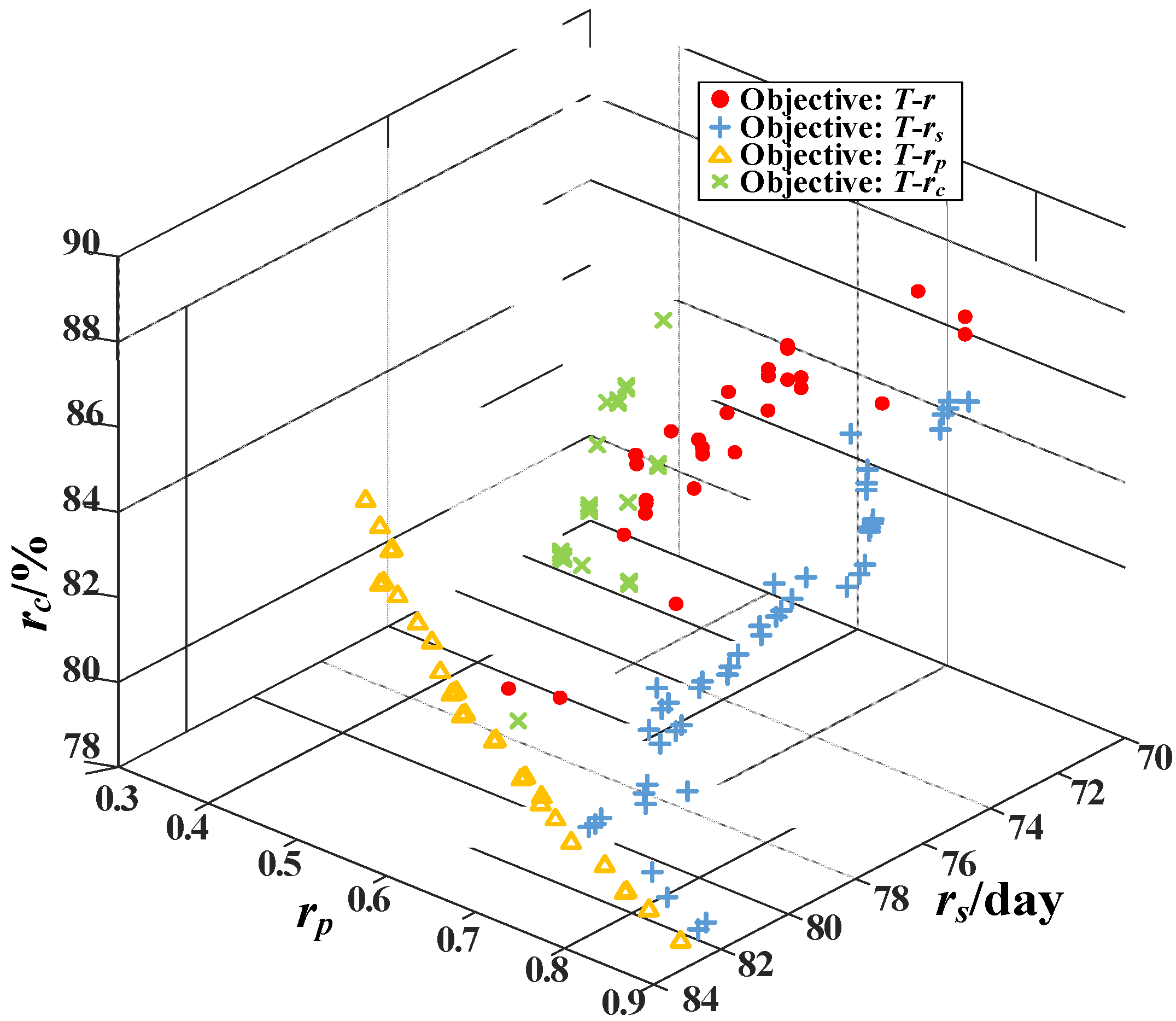
5.3. Measure Results

According to Section 4.2, the composite robustness criterion of the construction schedule can be obtained as: $r=0.374r_s+0.219r_p+0.407r_c$. Meanwhile, the three robustness criteria of this project can, respectively, be calculated as follows:

$$\begin{array}{lllll}{r}_s& ={\displaystyle \sum _{i=1}^n{\omega }_i}\left(\left|S_i-s_i\right|\right)& & & \\ & =0.0173\times \left|121-138\right|+& 0.0173\times \left|179-183\right|+& 0.0119\times \left|237-243\right|+& \dots =419.31\\ & \hspace{1em}\; \hspace{1em}\; \hspace{1em}\; \uparrow & \hspace{1em}\; \hspace{1em}\; \hspace{1em}\; \uparrow & \hspace{1em}\; \hspace{1em}\; \hspace{1em}\; \uparrow & \\ & \mathrm{main}\mathrm{transformer}& \mathrm{main}\mathrm{transformer}& \mathrm{main}\mathrm{transformer}& \dots \\ & \mathrm{hall}\mathrm{layer}\#2\text{-}1& \mathrm{hall}\mathrm{layer}\#2\text{-}2& \mathrm{hall}\mathrm{layer}\#3& \end{array}$$

$$\begin{array}{lllll}{r}_p& ={\displaystyle \sum _{i=1}^n{\omega }_i}\left(\left|P_i-p_i\right|\right)& & & \\ & =0.0173\times \left|7-7\right|+& 0.0173\times \left|11-12\right|+& 0.0119\times \left|12-15\right|+& \dots =21.64\\ & \hspace{1em}\; \hspace{1em}\; \hspace{1em}\; \uparrow & \hspace{1em}\; \hspace{1em}\; \hspace{1em}\; \uparrow & \hspace{1em}\; \hspace{1em}\; \hspace{1em}\; \uparrow & \\ & \mathrm{main}\mathrm{transformer}& \mathrm{main}\mathrm{transformer}& \mathrm{main}\mathrm{transformer}& \dots \\ & \mathrm{hall}\mathrm{layer}\#2\text{-}1& \mathrm{hall}\mathrm{layer}\#2\text{-}2& \mathrm{hall}\mathrm{layer}\#3& \end{array}$$

$$\begin{array}{ll}{r}_c& =-P\left(T\le T\prime \right)\\ & =-P\left(T\le 2043\right)=-67.98\end{array}$$

So, the composite robustness criterion of this project is r = 133.89. The range of r is [0, 275] and the schedule robustness is divided into five levels according to the contribution of criterion r change to schedule robustness: the schedule robustness is Very good when 0 ≤ r < 55, the schedule robustness is Good when 55 ≤ r < 110, the schedule robustness is Normal when 110 ≤ r < 165, the schedule robustness is Bad when 165 ≤ r < 220, and the schedule robustness is Very bad when 220 ≤ r < 275. Thus, r = 133.89 means the schedule robustness of the underground power station is at the Normal level and the schedule is reasonable.

6. Discussion

The measured results of the proposed criterion and methods are compared with the results using either the solution robustness or the quality solution, and the results using the composite criterion based on traditional weighting methods including AHP for subjective weighting [23], entropy weighting method for objective weighting [36] and geometric mean method for combining weights [40]. Thus, the consistency, representativeness, and advantage of the proposed criterion and methods are verified.

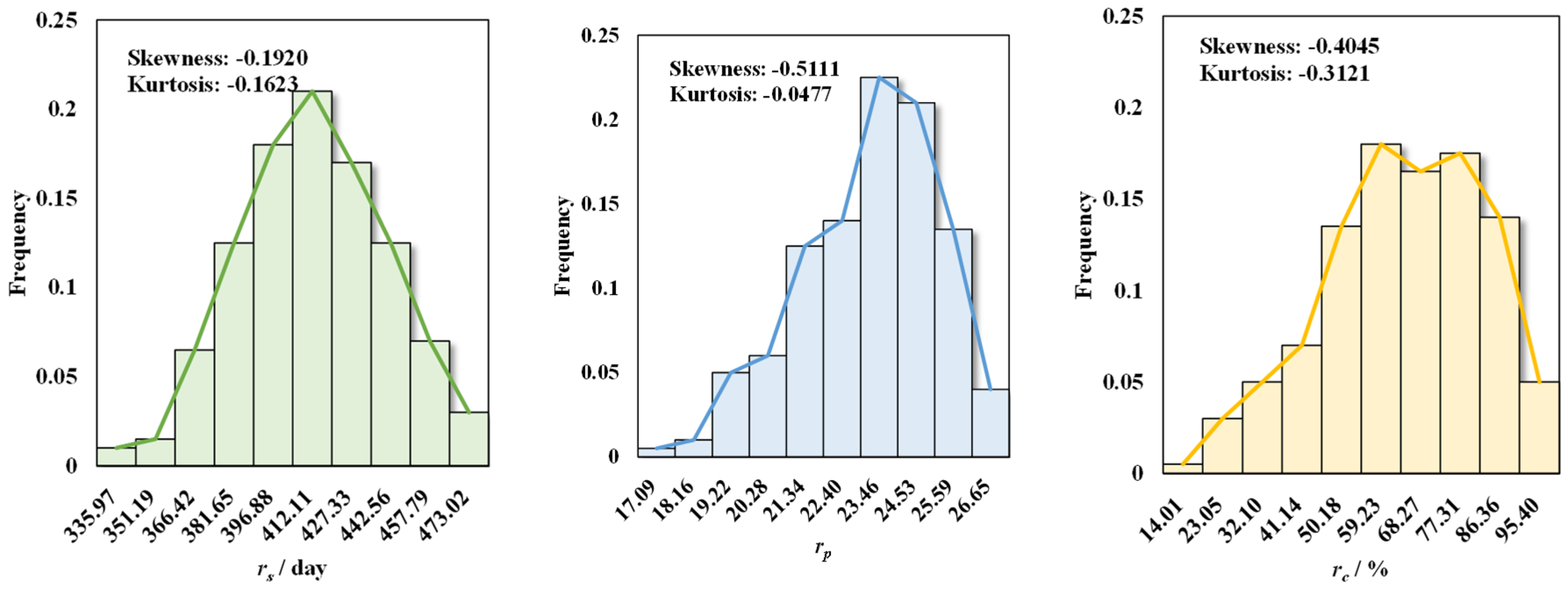
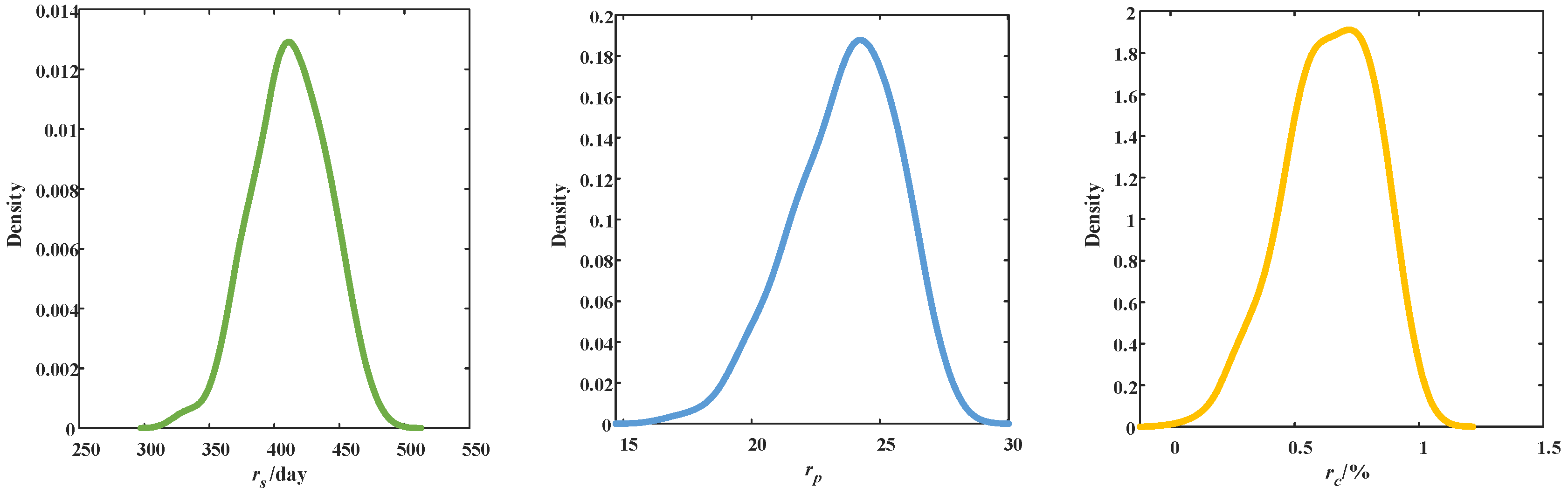
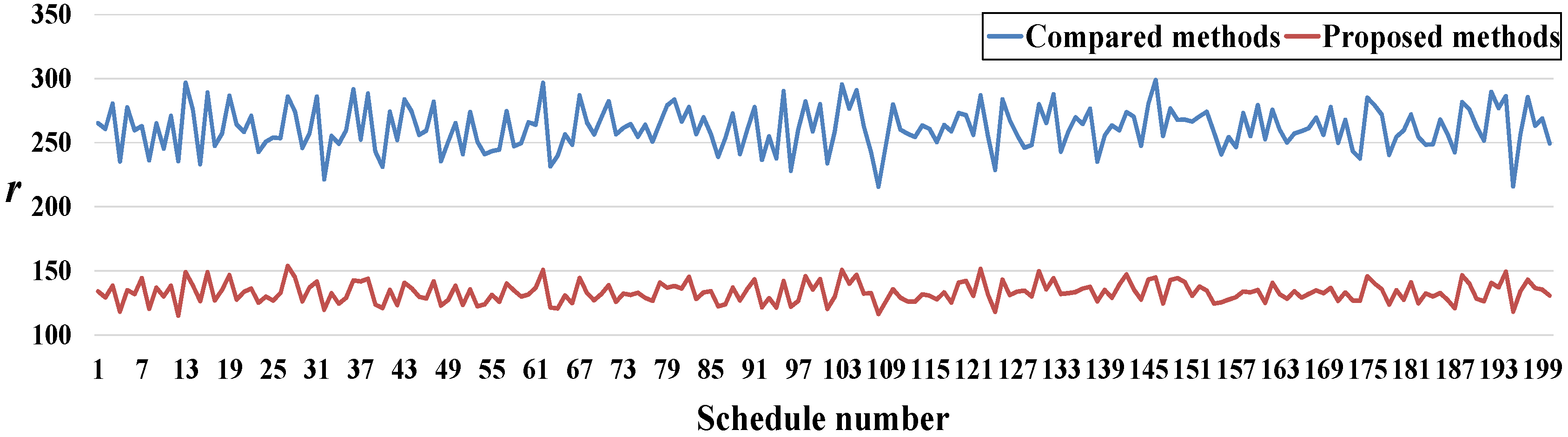
6.1. Comparison of the Composite Robustness Criterion and a Single Robustness Criterion

A total of 200 schedules meeting the logical relationship and resource restrictions of this project are generated randomly and their composite robustness criterion r and three single robustness criteria r_s, r_p, and r_c are calculated.

The measured results are divided into five intervals on average. The quantity of schedules that belongs to each interval is shown in Figure 8. The robustness of these schedules measured via r are mainly within the third and fourth intervals, and a few ones are in the second and fifth intervals, and the schedules in the first interval are the least. This phenomenon complies with the circumstances of the measured results of r_s, r_p, and r_c. Therefore, the robustness measured result of r is consistent with the results of existing single criteria.

In order to analyze the representativeness of the proposed composite robustness criterion, which is embodied by the symmetry, concentration, and even dispersion of r as well as r_s, r_p, and r_c, the skewness, kurtosis and dispersion coefficient of the measured results are calculated. As shown in Figure 9, the kurtosis of r_s and r_c is rather high, which suggests a strong concentration, and thus extreme and invalid evaluations in measuring robustness. The skewness of r_p is very high, which suggests an obvious negative skewness, and its accuracy would be low when measuring the schedule robustness whose fluctuation in structural robustness and quality robustness is small. The dispersion coefficient of r_c is rather large, which suggests poor criterion representativeness, and it would be useless when used individually. From the comparison, it can be drawn that the composite robustness criterion r has desirable symmetry, concentration, and uniform dispersion, which balances the three single criteria and is representative in robustness measure of the construction schedule.

To verify the advantage of the proposed composite robustness criterion, the optimization of construction duration and schedule robustness is conducted. Construction duration T and schedule robustness, which is measured using r, r_s, r_p, and r_c, respectively, are the two optimization objectives. A hybrid grey wolf optimizer with a sine-cosine algorithm is adopted to solve the optimization model [50]. The iteration number is set as 1000. The optimization results in Figure 10 show that when the optimization environment is the same, and optimized duration level is equal, the optimized schedules with the objectives of T-r_s (or T-r_p, T-r_c) only have good solution robustness or good quality robustness, but do not have robustness in both aspects. The optimized schedules with the objectives of T-r have both good solution robustness and good quality robustness, which ensures the schedules’ anti-interference ability from the perspectives of both project execution and project result. Therefore, the composite robustness criterion r proposed in this paper has the advantages of comprehensively measuring the robustness, in terms of both project execution and project result.

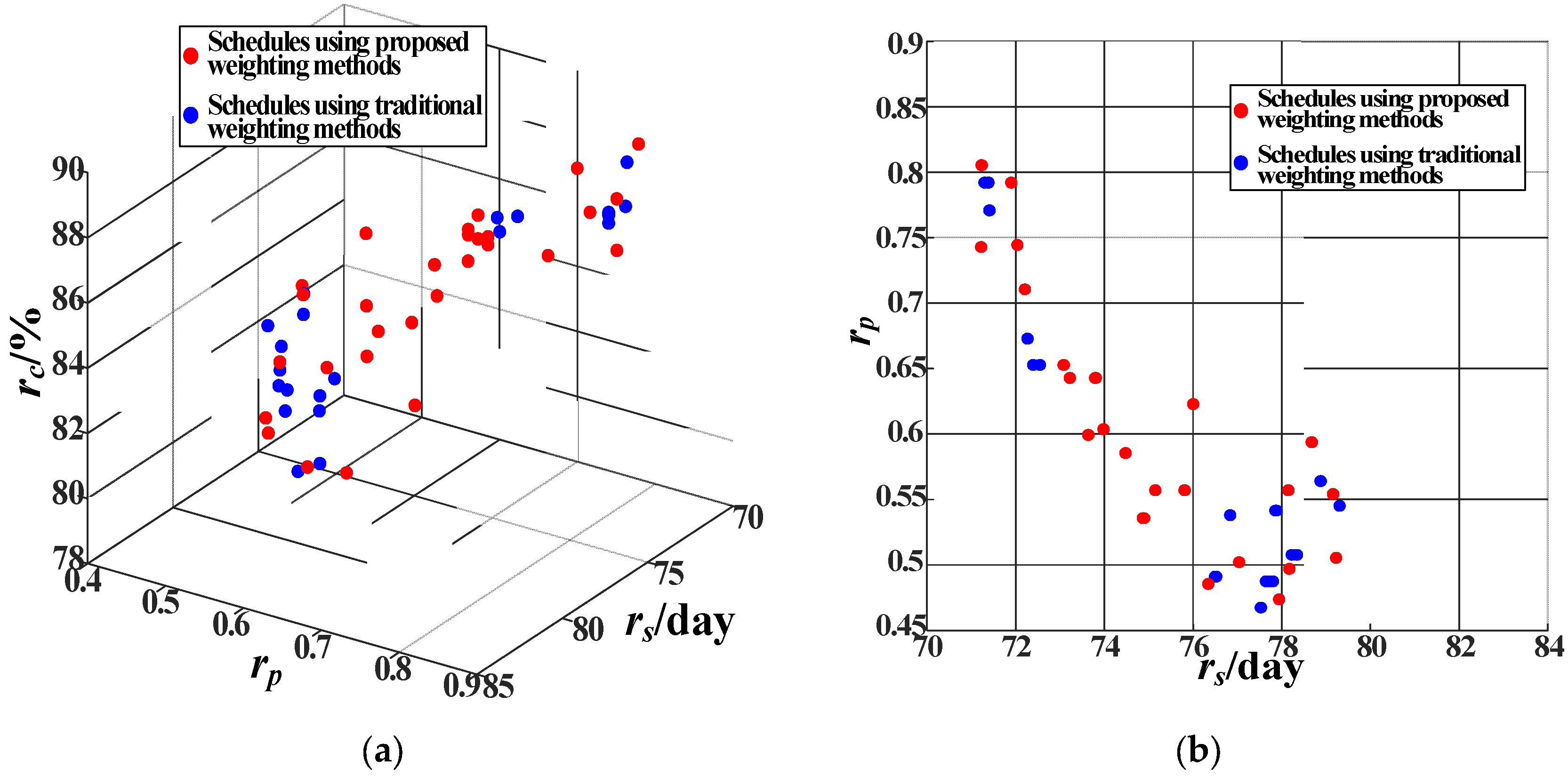
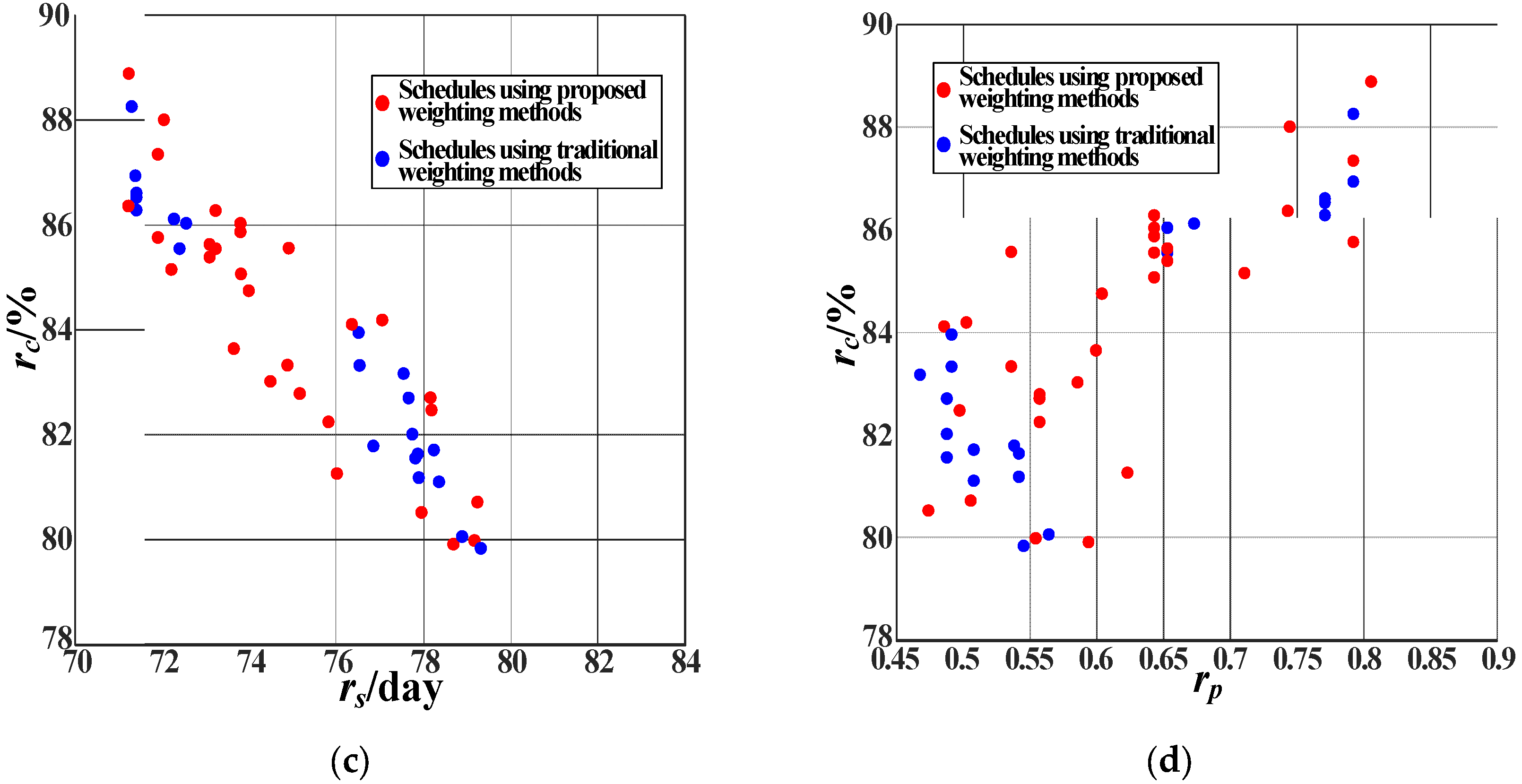
6.2. Comparison of Weighting Methods

The robustness measure of the current project can be $r=0.669r_s+0.080r_p+0.251r_c$, where the subjective weights are determined by AHP, the objective weights are calculated by entropy weighting method, and the two weights are combined by the geometric mean method. The methods proposed as well, as the traditional methods mentioned above, were respectively applied to measure the robustness of the 200 schedules. The results are shown in Figure 11. Line chart trends of the two sets of methods are obviously consistent, thus suggesting the consistency of the proposed weighting methods in measuring robustness.

In addition, the standard deviation of r with the proposed weighting methods is 7.89, while using the traditional weighting methods is 16.49. Thus, the robustness measure results using the proposed weighting methods have lower dispersion degree, suggesting their representativeness.

Then, the optimization of construction duration and schedule robustness is conducted to verify the advantage of the proposed weighting methods. Construction duration T and schedule robustness, which is measured using the composite robustness criterion using the weighting methods proposed in this paper and the traditional weighting methods, respectively, are the two optimization objectives. A hybrid grey wolf optimizer with a sine-cosine algorithm is adopted to solve the optimization model [50]. The iteration number is set as 1000. The optimization results in Figure 12 show that the optimized schedules with the objectives of T and r obtained using the proposed weighting methods are evenly distributed on the whole Pareto front, while the optimized schedules with the objectives of T and r obtained using the traditional weighting methods are distributed at the two ends of the Pareto front, lacking schedules with good start time deviation, good structural deviation, and good completion probability at the same time. Thus, the proposed weighting methods have the advantage of letting the robustness information of the composite criterion be completely expressed.

7. Conclusions

The robustness measure of a construction schedule is an effective and indispensable tool to evaluate the capability of robust scheduling. However, current research mainly pays pay to a single robustness criterion. Few studies consider both the solution robustness and quality robustness while neglecting the bounded rationality of subjective weights and the inherent importance and nonlinear intercriteria correlations of objective weights in the composite criterion. In view of these limitations, a construction schedule robustness measure based on improved prospect theory and the Copula-CRITIC method is proposed in this paper. An underground power station in China was used as a case study to verify its advantages. The main contributions of this paper are listed as follows:

• With the establishment of a composite robustness criterion containing solution robustness criteria of start time deviation and structural deviation, and quality robustness criterion of completion probability, construction schedule robustness can be measured in terms of both project execution and project result.
• The subjective weights considering bounded rationality are assigned using prospect theory improved by an interval distance formula, the objective weights taking both inherent importance and nonlinear intercriteria correlations into account are assigned using the Copula-CRITIC method, and the subjective and objective weights are combined using an information-entropy-based evidence reasoning method.
• A real underground power station was used as a case study. The results of the proposed criterion and methods, one with a single robustness criterion of either solution robustness or quality robustness, and one with a composite robustness criterion using a traditional weighting method were compared to verify the consistency, representativeness, and advantages of the proposed composite robust criterion and weighting methods.