Imaging System Based on Silicon Photomultipliers and Light Emitting Diodes for Functional Near-Infrared Spectroscopy

Featured Application

System suitable for human brain imaging (fNIRS, DOT).

Abstract

We built a fiber-less prototype of an optical system with 156 channels each one consisting of an optode made of a silicon photomultiplier (SiPM) and a pair of light emitting diodes (LEDs) operating at 700 nm and 830 nm. The system uses functional near-infrared spectroscopy (fNIRS) and diffuse optical tomography (DOT) imaging of the cortical activity of the human brain at frequencies above 1 Hz. In this paper, we discuss testing and system optimization performed through measurements on a multi-layered optical phantom with mechanically movable parts that simulate near-infrared light scattering inhomogeneities. The baseline optical characteristics of the phantom are carefully characterized and compared to those of human tissues. Here we discuss several technical aspects of the system development, such as LED light output drift and its possible compensation, SiPM linearity, corrections of channel signal differences, and signal-to-noise ratio (SNR). We implement an imaging algorithm that investigates large phantom regions. Thanks to the use of SiPMs, very large source-to-detector distances are acquired with a high SNR and 2 Hz time resolution. The overall results demonstrate the high potentialities of a system based on SiPMs for fNIRS/DOT human brain imaging applications.

1. Introduction

Functional near-infrared spectroscopy (fNIRS) is a non-invasive technique that uses light in the near-infrared spectral range to measure the optical properties of biological tissues. The technique relies on the diffusive properties of the tissue under study; thus, it works at its best on soft tissues such as the human breast and brain. In medicine, this technique is used to report blood-oxygen-level-dependent (BOLD) signals [1] via measurements of scattered light attenuation induced by hemoglobin oscillations within the cortical layers, performed non-invasively from the scalp [2]. By monitoring spatial-temporal variations in the light absorption and scattering properties of tissue, local variations in chromophores such as oxy- and deoxy-hemoglobin concentrations can be imaged and spatial maps of tissue properties such as total hemoglobin concentration and blood oxygen saturation can be obtained. With particular focus on the human brain, optical methods can be used to assess or monitor several neurological diseases manifesting as blood oxygenation related functional or metabolic alterations in the brain, including Alzheimer’s disease [3], autism spectrum disorder [4], stroke [5], and multiple sclerosis [6]. Traditionally, brain function is imaged with positron emission tomography (PET) or with functional magnetic resonance imaging (fMRI). However, PET uses ionizing radiation, which is risky for health, while fMRI involves exposure to strong magnetic fields and induced electric fields, making it a contraindication in patients with implanted electronic devices (e.g., deep brain stimulators, pacemakers, and cochlear implants). Moreover, both the techniques are quite uncomfortable for the patient who is forced to lay within a small space. Optical imaging is an alternative human brain mapping technique when both fMRI and PET are not indicated. Optical systems have, in principle, a much simpler hardware, therefore, they may be suitable for a more widespread use in medical care. One of the most popular optical techniques for brain imaging is continuous wave (CW) fNIRS. CW-fNIRS evaluates light attenuation by executing cyclic measurements of diffused light from the brain cortex at multiple source-detector couples, using at least two wavelengths in the 700–950 nm range, generally at an overall measurement rate ranging from 1 to 100 Hz [7]. In each cycle, each optode (detector, dual optical source pair) performs a measurement of the oxy- and deoxy-hemoglobin concentrations in a specific region of the brain cortex defined by the optode position on the scalp and the relative distance between the detector and the light source (source detector separation or SDS), the last providing an estimation of the investigation depth. As SDS increases, the banana-shaped probabilistic path of the detected light grows and extends deeper into the brain [8].

Traditional CW-fNIRS imaging instruments provide sparse arrangements of optodes with significantly lower spatial resolution than fMRI [2]. Sparse layouts of source-detectors are suitable to obtain functional traces rather than maps or images. However, recent developments in high-density diffuse optical tomography (HD-DOT) have broadened this perspective by providing a dramatically upgraded spatial resolution [9,10,11,12]. However, high-density arrays, particularly when covering a large portion of the head, present significant challenges in high-channel-count instrumentation, illumination interferences (separating signals detected from multiple sources), fiber-optic–scalp coupling, and lateral torqueing of the fibers. Some recently developed systems focus on solving these challenges through scalp-located semiconductor technology. However, the use of avalanche photodiodes (APDs) limits the SNR and the sensitivity at large SDSs [13] and single photon avalanche diodes (SPADs), have a very small detection area, limiting photons harvesting from the scalp. Therefore, SPADs are better indicated for time domain systems [14] employing time-correlated single photon counting that needs particularly complex hardware.

It was recently demonstrated that silicon photomultipliers (SiPMs), which constitute an array of SPADs read in parallel, are very promising to further advance fNIRS for human brain cortex monitoring [15,16,17,18]. The advantages of SiPMs arise from the combination of having a high gain, of the order of 10⁶–10⁷ electrons per detected photon, like a conventional vacuum photomultiplier, coupled with a large detection area, low operation voltage, small size, high robustness and reliability, low cost, and high SNR [19]. Thanks to the SiPM high gain, it is possible to design systems with different and large SDSs, allowing overlapping measurements and producing significant improvement in localization accuracy in optical brain imaging systems both in time domain [20,21] and continuous wave [22]. However, SiPMs have a relatively modest linearity region if compared to most of the other semiconductor photodetectors. In fact, a SiPM is an array of SPADs with resistors or active quenching circuits in series. Since the quenching time, though short, is finite, the maximum photon flux in the linear regime that can impinge on the SiPM can be estimated as N_pixel/(EQE · T_quench), where T_quench is the average avalanche quenching time for each pixel, of the order of nanoseconds; EQE is the external quantum efficiency i.e. the ratio of the number of charge carriers to the number of incident photons, and N_pixel is the number of SiPM pixels, ranging from hundreds to thousands, in commercial devices. Vice versa, the minimum limit of detectable photon flux is 3 dB above the level of the dark current related to the dark count, equal to N_pixel/t_dark where 1/t_dark is the dark count rate of a single pixel of the device [23]. The time scales of these phenomena (avalanche quenching and dark count) are relatively close, and therefore substantially limit the useful range of impinging optical power for the linear SiPM operation. This should be carefully considered when designing a brain imaging system based on SiPMs.

In this paper, by using SiPMs in their linear regime, we demonstrate the feasibility of a SiPMs and light emitting diodes (LEDs) based optical imaging system able to perform a large number of overlapping measurements by exploiting SDSs from 2 to 10 cm, in a phantom with near-infrared light scattering and absorption characteristics close to human head tissues. The apparatus is a continuous wave (CW) system suitable for fNIRS and DOT equipped with 12 dual wavelength light sources and 13 SiPM detectors arranged in a square 8 cm × 8 cm grid array. No optical fibers are used, since LEDs and SiPMs, opportunely encapsulated, are placed directly on the surface of the tissue to be analyzed, avoiding fiber-scalp coupling or fiber lateral torqueing issues. We tested the instrument on a multilayered phantom made of a highly scattered polymeric medium, with mechanically movable parts. We performed multiple measurements on the phantom and propose a suitable calibration procedure to optimize the SNR. We discuss various critical aspects, such as SiPM signal drift, SiPM linearity, corrections to channel signal differences, and the SNR. Finally, we show an example of the imaging methodology. The results clearly demonstrate the high capabilities of SiPMs for the development of human brain cortex functional imaging systems.

2. Materials and Methods

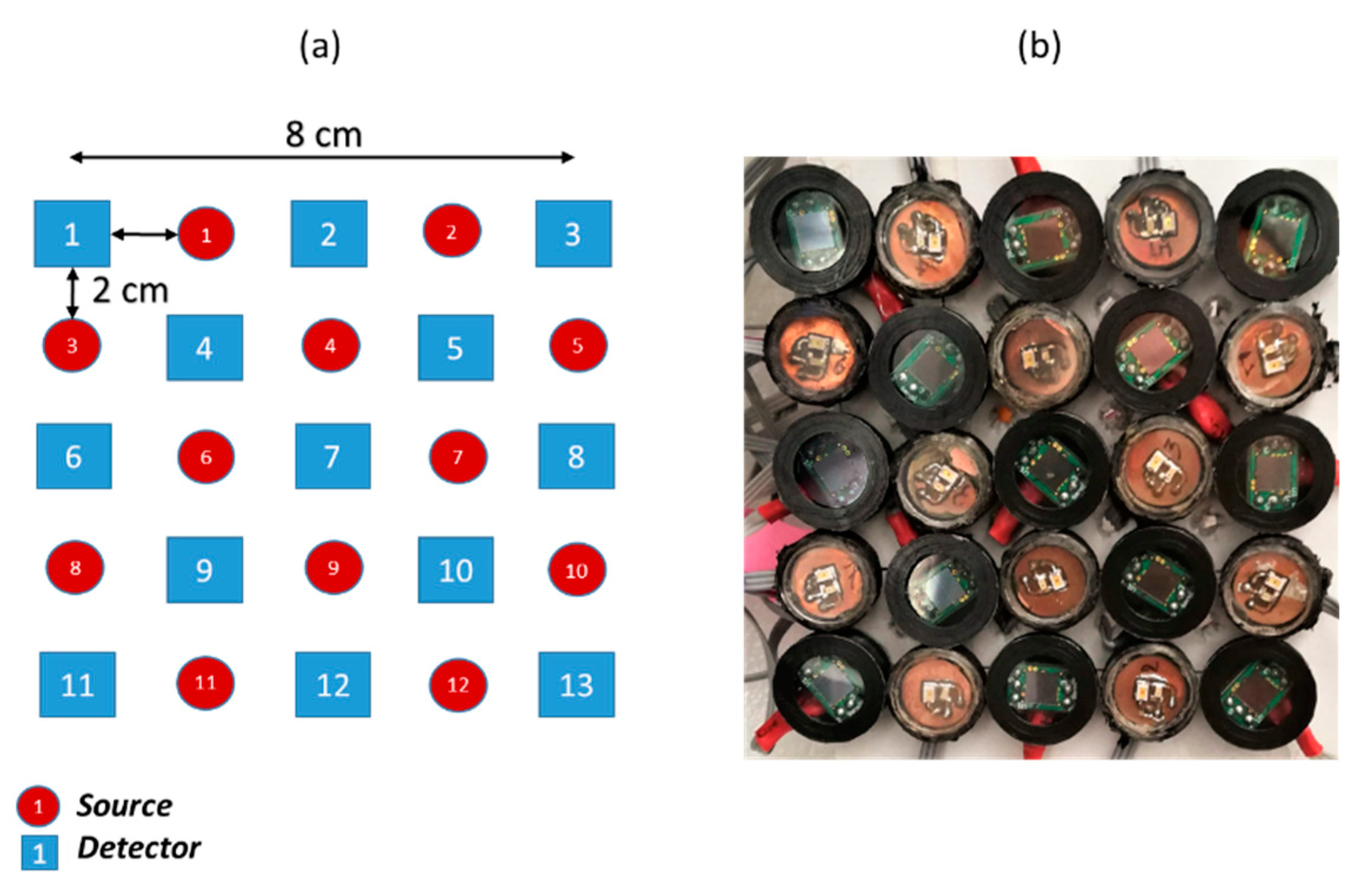
2.1. System Architecture

We built a CW system equipped with 24 LED sources (12 at 700 nm and 12 at 830 nm, arranged in couples, with each 700 nm/830 nm LED couple mounted with an inter-LED distance of 2 mm) and 13 SiPM detectors, alternatively arranged in a checkerboard of 8 cm × 8 cm area and first nearest neighbor SiPM-double LED distance of 2 cm (Figure 1a). Since the system is intended to detect oxy- and deoxy-hemoglobin concentrations, the two wavelengths were chosen to straddle the isosbestic point of the two molecular species absorption spectrums located at ~800 nm [24]. The system can acquire 325 independent time averaged measurements, that is: 13 measurements of 13 SiPMs dark currents, plus the signals under light, which are 13 SiPMs, multiplied by 24 LEDs (12 LEDs for each of the two wavelengths). In each cycle, each dark current is subtracted from the relative SiPM photocurrents measured at the two wavelengths. The overall measurement refresh rate of the complete system is about 2.1 Hz. By using the equipment in fNIRS mode, it is possible to acquire 156 optical channels (LED pair source; SiPM detector couple). In Figure 1a, the red circles represent the LED holders and the blue squares represent the SiPM holders. The 700 nm/830 nm LED pairs and each SiPM are mounted on a board and encapsulated in a holder of about 2 cm in diameter. A transparent filter (polycarbonate) is mounted on the top on the holders so that SiPMs and LEDs are optically well coupled and electrically insulated as seen in Figure 1b. The geometry of this arrangement is characterized by SDS distances of 2 cm, 4.47 cm, 6 cm, 7.21 cm, 8.24 cm, and 10 cm. Through the chosen placement of LEDs and SiPMs, it is possible to obtain various overlapping measurements at different SDSs in numerous points.

It has been shown that in fNIRS of the human brain cortex, as SDS increases, the photodetector signal becomes more sensitive to the tissues located at a larger depth and in the middle region between the source and the detector, with SDS values lower than 6 cm. Above such a value, the SNR and the exponential decrease in sensitivity at large inter-optode distances give rise to important limitations [8]. The system described here takes into consideration quite large values of SDS, up to 10 cm. As shown in the following, such values are possible because of the combination of two factors: first, the better SNR achievable thanks to the use of the SiPM as a photodetector; second, the lower scattering of the phantom material compared to the human head tissues (about 28%).

To test the proposed system, we built a multilayered phantom made of a medium providing high light scattering. The medium is expanded polyethylene (EPE). Starting from the base at the bottom (Figure 2), the phantom is constituted by a 50 cm × 40 cm × 3 cm EPE layer and a 3 cm thick layer of air in which a Newport Step Motor moves a 1 mm diameter/20 cm long metal bar. On the top, we placed a second 3 cm thick EPE layer on which the black patch with sensors and LEDs is positioned.

The stepper motor rotates 100 degrees in about 200 s (0.5 deg/s), so that the end of the bar travels a linear distance of about 10 cm in 30 s. Thanks to the motion driven by the stepper motor, the phantom is dynamic and constitutes a tool to test our system with good reproducibility.

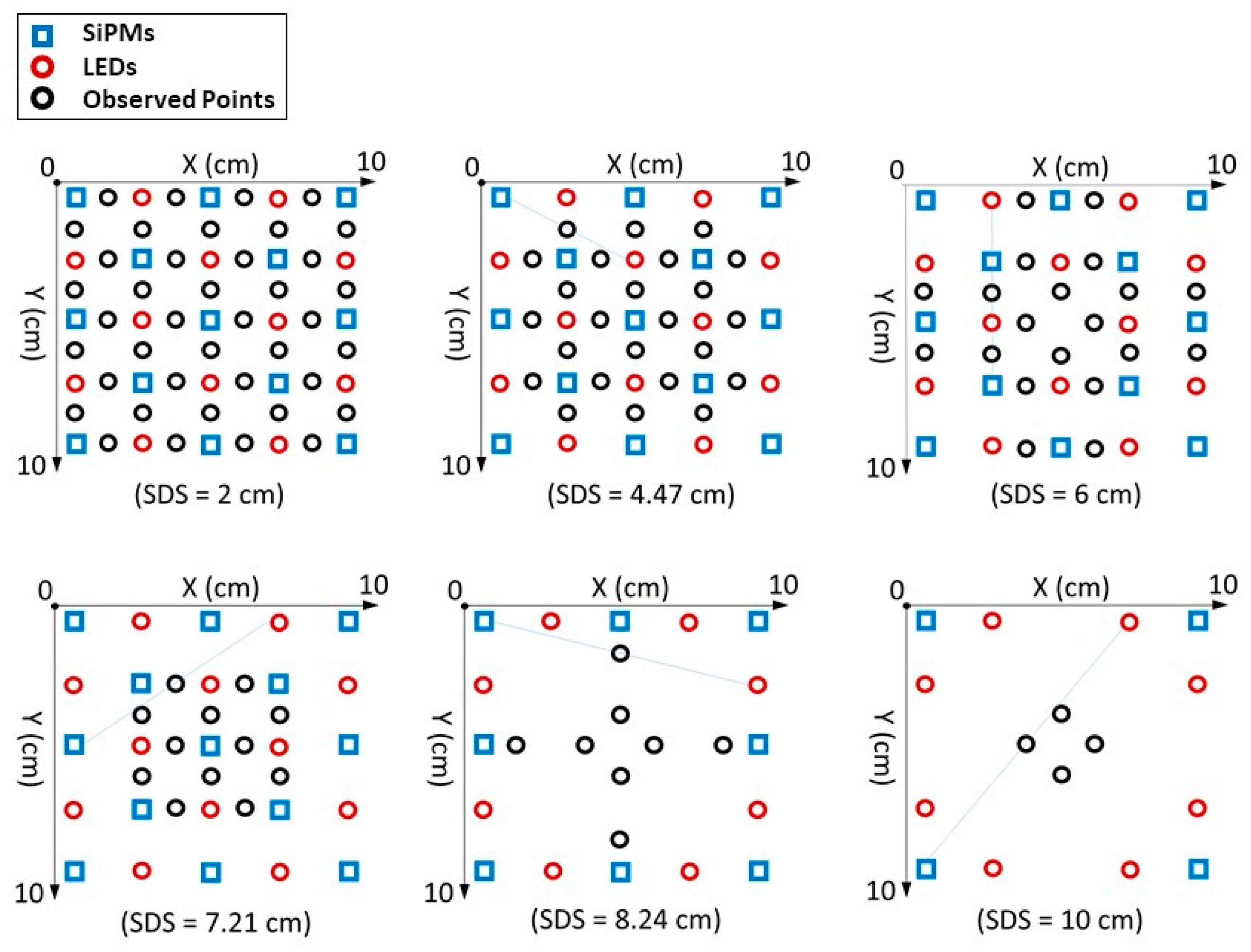
2.2. Phantom Optical Characterization

The optical characteristics of the EPE layers are relatively close to those of human brain tissues. To investigate such an aspect, we performed reflectivity measurements of the phantom by varying the SDS. Such measurements provide a quantitative evaluation of the parameter $\sqrt{{\mu }_a·{\mu }_s^{\prime }}$, where ${\mu }_a$ is the absorption coefficient and ${\mu }_s^{\prime }$ is the reduced scattering coefficient. In the brain cortex tissues ${\mu }_a$ and ${\mu }_s^{\prime }$ are of the order of 0.1 cm⁻¹ and 10 cm⁻¹, respectively [25], so that $\sqrt{{\mu }_a·{\mu }_s^{\prime }}$ is approximatively 1 cm⁻¹. In back-scattering measurements, on which the CW-fNIRS principle of operation is based, the light diffusion transport is modeled by using the modified Lambert–Beer law:

$$I\left(\lambda \right)=I_0\left(\lambda \right)\exp \left[-{\mu }_{\alpha }\left(\lambda \right)·SDS·DPF\left(\lambda \right)+G\left(\lambda \right)\right]$$

(1)

where $I\left(\lambda \right)$ is the measured wavelength-dependent diffused reflected light intensity, I₀(λ) is the incident light intensity, µ_α(λ) is the absorption coefficient, DPF(λ) is the differential path length factor, and G(λ) is a wavelength-, medium-, and geometry-dependent constant. DPF(λ) is a scaling factor shown to be approximately equal to $\frac{1}{2}\sqrt{3{\mu }_s^{\prime }/{\mu }_a}$ [26]. Hence, $I\left(\lambda \right)$ can be rewritten as

$$I\left(\lambda \right)=k·\exp \left[-\sqrt{3·{\mu }_a\left(\lambda \right)·{\mu }_s^{\prime }\left(\lambda \right)}·\frac{SDS}{2}\right]$$

(2)

a decreasing exponential function of SDS.

Figure 3 reports the photocurrents measured on the phantom at different SDSs under 700 nm and 830 nm illumination. From the data reported in Figure 3, we directly measure the effective attenuation coefficient using the photocurrent slope [27]. Therefore, we estimate that the EPE layer $\sqrt{{\mu }_a·{\mu }_s^{\prime }}$ is approximately 0.53 cm⁻¹, relatively close to the human brain cortex tissues for which the $\sqrt{{\mu }_a·{\mu }_s^{\prime }}$ values are about 1 cm⁻¹ in the near-infrared (NIR) range.

Hence, though the effective attenuation coefficient of the EPE medium is close to the human tissues one, the phantom is relatively more “transparent” in the NIR range. Our phantom is characterized by an air gap, so we evaluate the weight of such an air gap on the light back diffusion.

Figure 3 reports the comparison of near-infrared light back diffusion for two types of phantom: phantom 1 is a 50 cm × 40 cm × 6 cm EPE slab with no air gap while phantom 2 is the multilayer phantom used in this work, made of an EPE slab of 50 cm × 40 cm × 3 cm, on a 3 cm air gap, and on a second EPE slab of 50 cm × 40 cm × 3 cm.

The measurements were taken by a voltage drop across a 50 Ω resistor in series to a single SiPM detector illuminated alternatively by two LEDs (700 nm and 830 nm wavelengths) both biased at a fixed current of 1.40 µA and mounted on a board with an inter-LED distance of 2 mm. The comparison of the measurements taken at different SDSs on phantom 1 and phantom 2 shown in Figure 3 confirms that the air gap gives a small contribution: the CW photocurrents in phantom 2 are only slightly lower. Moreover, the measured $\sqrt{{\mu }_a·{\mu }_s^{\prime }}$ values are quite similar at the two used wavelengths, 700 nm and 830 nm. The coupling of the data in Figure 3 to measurements of time-of-flight (TOF) in phantom 1 allows for evaluating both µ_a and µ_s’ for the used EPE material. For this purpose, we collected TOF data at nine different SDS values measured on phantom 1. For the TOF measurements, we used a MICRORB-10035 SiPM by ON Semiconductor, mounted on a printed circuit board (MICRORB−SMA). We connected the fast output pin of the RB10035 to a time-correlated single photon counting (TCSPC) module (SPC-130, Becker & Hickl). A 760 nm pulsed laser by PicoQuant with <90 ps pulse full width at half maximum (FWHM) was used as the light source.

Arridge et al. [28] showed that for a point source and point detector separated by a distance d in a semi-infinite homogeneous diffusing medium (where d ≫ 1∕μ_s’ and μ_s’ ≫ μ_a), the average flight time of photons <t> is given as

$$<t>=\frac{d^2}{2\left({\gamma }^2+d\gamma \sqrt{c{\mu }_a}\right)}$$

(3)

where c is the velocity of light in the medium and γ is given as:

$${\gamma }^2=\frac{c}{3\left({\mu }_a+{\mu }_s^{\prime }\right)}$$

(4)

Figure 4 reports the <t> vs. d data measured on phantom 1 (black connected points). In the same graph, we also report theoretical <t> vs. d curves evaluated by Equations (3) and (4) for µ_a values varying from 0.01 cm⁻¹ to 10 cm⁻¹ at a step of 0.01 cm⁻¹, and by imposing that $\sqrt{{\mu }_a·{\mu }_s^{\prime }}$ = 0.53 cm⁻¹, as required by the data of Figure 3 (colored continuous lines). The best fit of the model to the data occurs for µ_a ≈ 0.1 cm⁻¹ and µ_s’ ≈ 2.8 cm⁻¹. Therefore, compared to the parameter values of human head tissues, the EPE phantom has a similar µ_a and an µ_s’ about one quarter lower.

2.3. System Functioning and Components

The system control works as follows: during operation, time division measurements of all the SiPMs outputs are performed on the active input channels of a National Instruments USB-6255 multifunction data acquisition board at 1.25 MHz sampling frequency. The system starts performing a measurement of the dark current of all SiPMs when all the LEDs are in off state. Then the 700 nm LED of the first LED couple is turned on and the system reads all the channels and calculates each point as the average of 250 measurements on the SiPM output. Then when the 700 nm turns off and the 830 nm LED of the couple turns on, the system acquires all the SiPMs currents and repeats this operation for all the LED couples. Then, the cycle restarts from the beginning. This procedure prevents illumination interferences and ensures the correct definition of the channels. As far as the time resolution is concerned, the photocurrent signals are acquired on a 13-channel, 1.25 MHz frequency Analog to Digital Converter (ADC), that is, each photocurrent is monitored for 1/1.25 × 10⁶ s (=0.8 µs) on every 13/1.25 × 10⁶ (=10.4 µs). We perform 250 acquisitions, corresponding to a total measure time on all SiPM channels with only one LED on of 2.6 ms. Such operation is repeated for all LEDs, plus one dark phase. Hence, one complete measurement cycle may be performed in principle in 25 × 2.6 ms = 65 ms. However, we need to avoid all the transients due to LED switch on and off and to SiPM thermal transients [19]. For such reason we used a much larger time window, with a minimum cycle time of 476 ms and an overall frequency of about 2.1 Hz. Considering the optodes configuration reported in Figure 1a, Figure 5 reports the x–y geometrical positions of the mid-points between the sources and the detectors involved in the measurements classified by the SDSs.

As shown in a study by Strangman, Li, and Zhang [8], for a given source-detector pair the maximum sensitivity region is located for the x and y coordinates at the midpoint, and deeper and deeper as the SDS increases. Hence, in Figure 5 we report the resulting two-dimensional matrices classified by the SDSs by using such assumptions. Some of the source-detector paths identify the same point in the medium, to a total of 108 different observed points. In each map the observed points (black circles), sources (red circles), and detectors (blue squares) involved in the definition of the channels are represented for each SDS.

Large area p-on-n MICROFJ-60035 SiPM detectors manufactured by ON Semiconductors were used for the measurements presented here [29]. The SiPM structure is formed by planar p+/n microcells with a total area of 6.07 × 6.07 mm², 22,292 square microcells, a geometrical fill factor of 75%, packaged in a surface mount housing (Surface Mounting Device, SMD), sealed by transparent glass with a refractive index of about 1.53 at 436 nm. The SiPM devices have a breakdown voltage of about 24.5 V at room temperature, and a photon detection efficiency (PDE) of about 10% measured at 700 nm and 6 V overvoltage (voltage above the breakdown, OV). Roithner LaserTechnik SMC700 and SMC830 AlGaAs LEDs in SMD ceramic packages emitting respectively at 700 nm and 830 nm wavelengths, were used as optical light sources. The LEDs have an area of 2 × 2 mm², viewing angle of ±55°, and average spectral bandwidth of 20 nm and 35 nm at 700 nm and 830 nm emission wavelengths, respectively.

SiPMs were biased by using a 30 V stabilized power supply; their output currents were measured by the voltage drop across a 1 kΩ resistor mounted on the same board of the SiPM holder. All 13 SiPMs boards were connected to the analog inputs of the NI USB-6255 Multifunction device. The LEDs were connected to the 24 Transistor-Transistor Logic CMOS (TTL/CMOS) digital input/output (I/O) lines of the NI-6255 through 0–5 kΩ resistive trimmers mounted on an auxiliary board.

The operative range of the SiPMs is evaluated by measuring the photocurrent as a function of the optical intensity incident on the photodetector (Figure 6). The lower limit of the data points in Figure 6 for the incident optical power is approximately in correspondence with a SiPM photocurrent about equal to the dark current. Therefore, this is the lower limit of usable incident optical power. As far as the upper limit is concerned, taking as reference the case of 30 V SiPM bias, as shown in Figure 6, a saturation of the SiPM photocurrent at about 1 mA is evident. Therefore, the corresponding optical power, of the order of 10⁻⁷ W/cm², represents the incident power upper limit. It should be noted, however, that such onset for the sub-linearity regime is not due to the above-mentioned SiPM avalanche pile-up effect, which takes place at a higher optical power for the used devices, but it is rather due to the use of the 1 kΩ resistor put in series in our system scheme. That is, the used resistor causes a reduction of the linear range compared to the native linear range of the detectors. In fact, if both the value of the resistance and the value of the photocurrent are high, the voltage drop on the resistor causes a shift of the SiPM working point during illumination, and consequently non-linearity is generated. For example, under about 5 × 10⁻⁷ W/cm² illumination, the 1 mA output current of the SiPM on 1 kΩ resistor causes a reduction of the overvoltage of 1 V.

Based on the data of Figure 6, all the trimmers in series with the LEDs are regulated to get each SiPM output close to the upper limit of the linear range (i.e., ≈1 mA), considering the nearest neighbor SDS of the checkerboard, to obtain high sensitivity for all the source-detector separations and to avoid non-linearity effects to the measurements. In such a way, for each LED, the photocurrent value falls within the linear range of the SiPM. In fact, in our experiment, when the rod moves in the phantom, the SiPMs only undergo a decrease of the photocurrent, as shown in the next section.

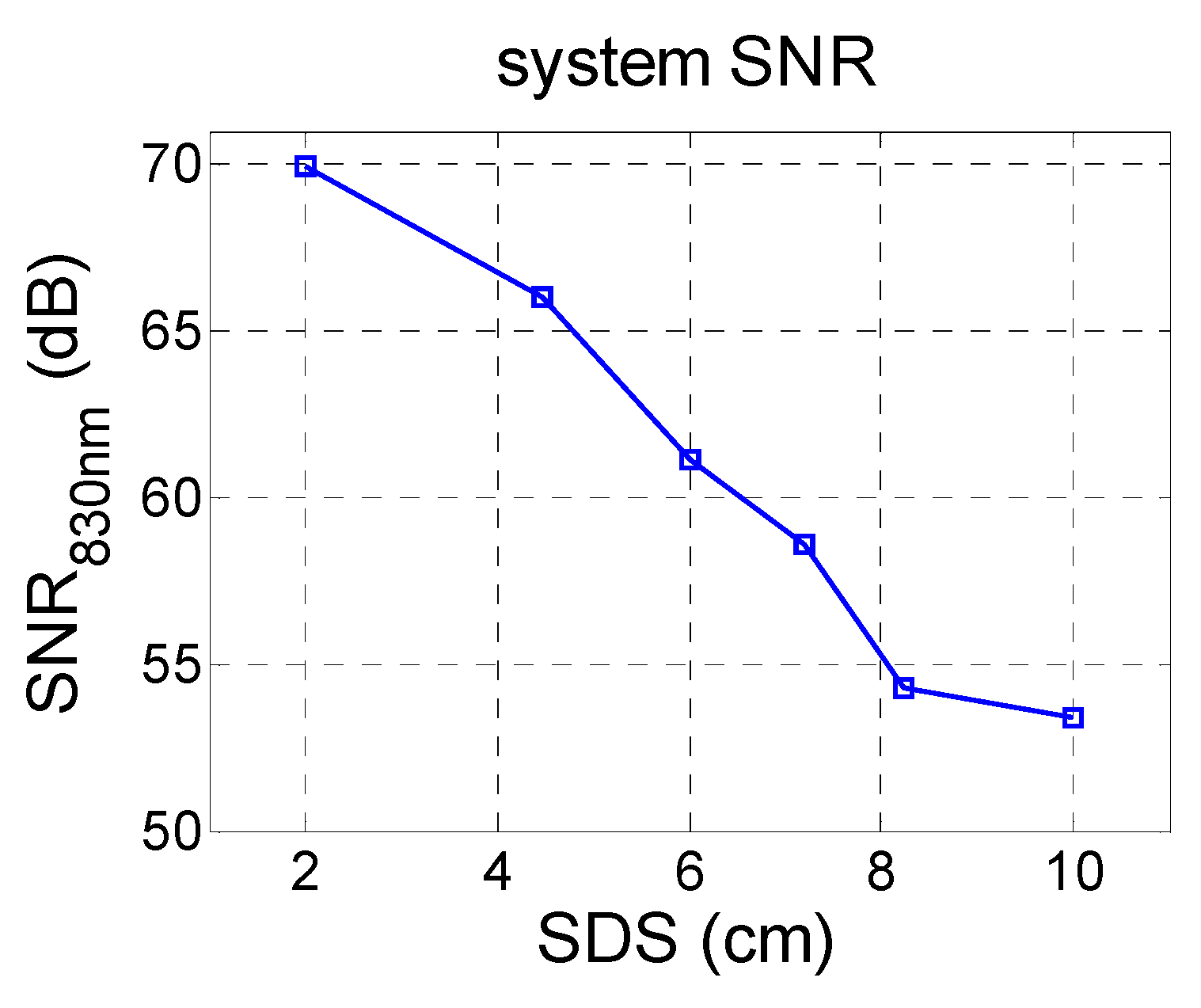
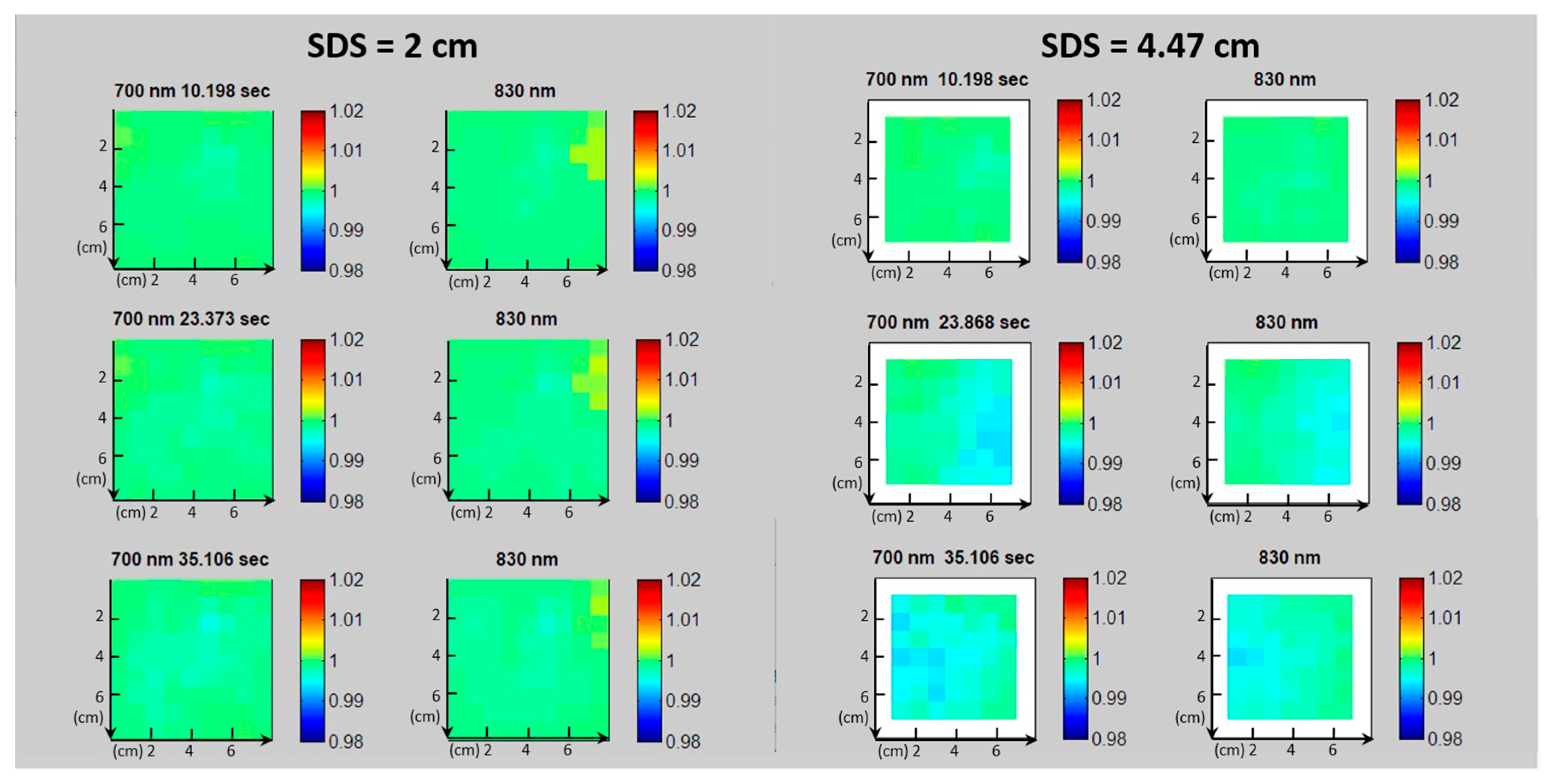
3. Results and Discussion

3.1. Data Correction

The system SNR measured in dB is defined as $20lo{g}_{10}\left(m_S/{\sigma }_S\right)$, where σ_S is the standard deviation of a data set S with average m_S, collected by the system on the static phantom in 20 s. For a total effective acquisition time of 65 ms on 13 SiPMs, 24 LEDs, and 1 dark phase for all the photodetectors, as above described, the SNR values, reported in Figure 7, are quite remarkable. At 830 nm illumination wavelength, the SNR at 2 cm SDS results in about 70 dB and remains quite high, resulting in 53.4 dB at SDS equal to 10 cm.

Though the SNR values are quite promising, the photocurrent signals still show instability and inhomogeneity effects. In Figure 8a, the photocurrents (12 time traces for 830 nm light and 12 time traces for 700 nm light) related to the fourth nearest-neighbor source-detector distance (SDS = 7.21 cm) are reported. Figure 8b reports, in detail, one of the photocurrent time traces related to 830 nm light.

It is possible to observe two types of phenomena affecting the measurement:

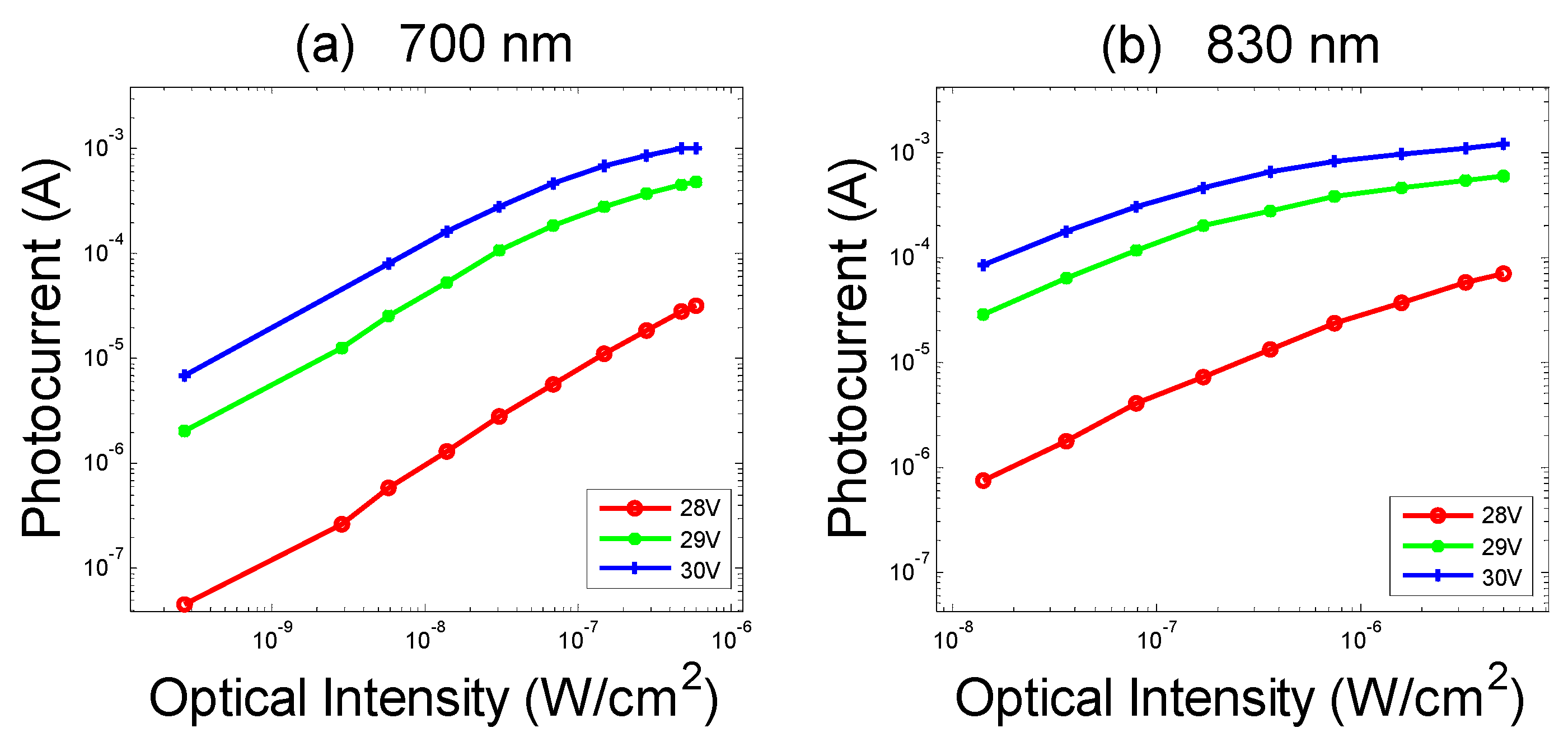
• Differences on the value of the photocurrents related to channels with the same SDS, as shown in Figure 8a. They are due to little displacements of the LEDs or of the SiPMs, small differences in the EQE of the different SiPMs involved, or differences among LEDs’ brightness.
• Drifts over time of the photocurrents, as shown in Figure 8b. To explain the decrease over time of the photocurrents recorded on the static phantom, it is important to consider that we subtract the dark current to determine the SiPM signal. In general, at a constant bias voltage, as SiPM temperature increases, both the photocurrent and the dark current in a SiPM increase while the gain slightly decreases. Moreover, the light output of an LED at a constant current also decreases with the increase of its junction temperature [30]. All this instability effects the sum up giving rise to the overall slow drift effects shown in Figure 8.

To correct such issues, we performed a calibration procedure directly on the phantom before starting the metal bar motion experiment. First, considering the 2 cm SDS, each resistive trimmer on the LEDs is regulated to guarantee the output current of the SiPMs being at the upper limit of their linear range (Figure 6), as described above. Second, the photocurrent levels at both wavelengths for each channel are recorded after a stabilization phase, lasting five minutes, with the system in the on state. Such data are then used for the actual data calibration, as explained in the following. After the calibration, the test phase starts. The mobile bar of the phantom starts its motion at constant velocity with the step motor rotating 100 degrees in about 200 s (0.5 deg/s), so that the bar’s end travels a linear distance of about 10 cm in 30 s. During the movement, all the SiPMs outputs are recorded while the LEDs are singularly turned on and then turned off sequentially, as explained in the previous section. Off-line, each photocurrent vs. time data is filtered with a moving average method. Then, for each channel, the photocurrent vs. time data recorded in the test conditions are divided by the photocurrents’ values measured after the five minutes of stabilization in the calibration phase. That is, the actual signals used for further data processing are the normalized to baseline photocurrents for each channel at different SDS. Such a procedure compensates all the thermal drifts and differences between channels with the same SDS.

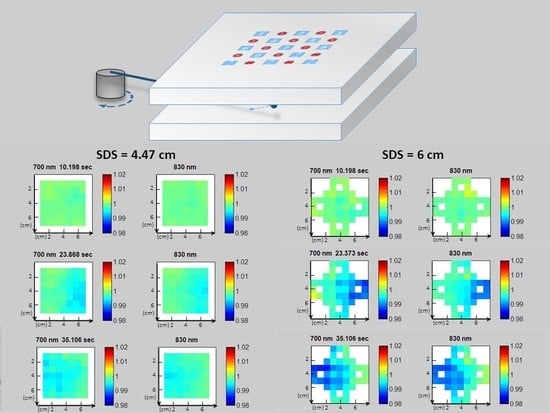
3.2. Image Reconstruction

As previously described, each optical channel is characterized by the corresponding SiPM/LED pair position and SDS and its sensitivity is a continuous function of space (banana shape). Hence it is possible to estimate the central position of the region monitored by each channel. Such positions, given the banana-shape light diffusion paths described above, can be approximately located in the middle point in between the particular SiPM/LED pair, at a depth about equal to SDS/2. In fact, for an accurate image reconstruction from the photocurrent data, a rigorous treatment of the near-infrared light transport from the source to the detector and a quite complex data processing are necessary and have to be combined [31,32,33,34,35]. However, here we want to concentrate on the signals deriving from the hardware, focusing on the achievable SNR and on the elimination of SiPM/LED dishomogeneities and time drifts in realistic conditions. Therefore, we chose to simply and directly investigate the normalized photocurrent signals by considering the geometric arrangement of the SiPM/LED pairs. A software developed in MATLAB® provides an arrangement of the collected photocurrents data at the two wavelengths and after the normalization. The data are displayed as a color change of pixels placed on planes classified by the SiPM/LED distances, and taking into account the geometrical positions of sources and detectors, as described in Section 2.3 and in Figure 5, following a back-projection approach [36]. Figure 9, Figure 10 and Figure 11 report examples of such images at three different time instants to give an idea of the temporal evolution of the images. The pixels represent the measured phantom regions, arranged in a two-dimensional (2D) map, and the pixel color represents the photocurrent normalized to the baseline; the green color represents the baseline, whose value is 1. The value of the color in each pixel at any time is the signal at that time divided by the baseline. Each plane is related to a particular SDS. Clearly, for the lowest SDS, since all the LED/SiPM pairs are involved, the highest number of channels and image pixels is obtained. It should be noted that on each plane some of the pixels do not actually correspond to measurements. For such pixels we attributed a color by performing a linear interpolation (i.e., by assigning them a color given by the average of the closest pixels). This is done only for the pixels with nearest neighbors actually measured. During the bar motion in the phantom, the photocurrents change and, as a consequence, the pixel colors change too. The time sequence of the images of a plane can be visualized as a movie which provides the time evolution of the particular image plane. This can be repeated for each SDS and corresponding plane. Figure 9, Figure 10 and Figure 11 are, in fact, frames of such movies. From the figures it is evident that the movies of each plane clearly show the localization of the metal bar, whose shape and position are smeared by the light diffusion and its movement.

For the planes defined by the SDS = 2 cm, no relevant variation is visible since the rod is moving in the phantom at a depth which is not reached by the banana-shaped photons’ path. On the contrary, at SDS = 4.47 cm, the sequence starts to show the passage of a shadow in spatial correspondence with the bar, moving from the right to the left side of the plane. Starting from the 6 cm SDS, the sequence clearly shows the bar passage taking place in the air gap at a depth between 3 cm and 6 cm, below the first EPE layer. Moreover, since at larger SDS values the banana-shaped path of the detected light grows and becomes wider, the moving shadow of the metal bar grows in size as the SDS increases. The signal due to the metal bar motion evidenced in Figure 9, Figure 10 and Figure 11, of the order of 1% of the baseline (i.e., $20lo{g}_{10}\left(0.01\right)$ = 40 dB or somewhat higher), is clearly well detected, although the bar is quite small.

In fact, it corresponds to a volume change of the order of 2 × 10⁻⁴ (i.e., 0.02%), estimated as the ratio of the metal bar volume divided by the total volume under test. The large ability to detect such a small volumetric change is due to the high system SNR values and the very effective calibration, coherent with the data reported in Figure 7.

4. Conclusions

We fabricated a fiber-less CW imaging system prototype suitable for fNIRS/DOT imaging equipped with 13 SiPMs and 24 LED sources capable of managing 156 double wavelength channels at six different SDSs, ranging from 2 cm to 10 cm. We discussed the SiPM signal drift and its compensation, the SiPM linearity, the corrections to channel signal differences, and the SNR ratio. The proposed system allows to reconstruct images at a refresh rate in the 2–5 Hz range, and to perform fNIRS analysis with a SNR between 53 dB and 70 dB within the considered SDSs.