1. Introduction
During the last two decades the development of energy management systems (EMSs) has been of interest by the energy research community. This interest is due to the continued and improved development of renewable energy systems (RE), and the EMS optimization techniques with advanced energy storage systems [
1].
The efficient use of energy in any field has become paramount due to environmental, economic and operational aspects, therefore, the study of energy management in a microgrid is vital [
2]. Microgrid can be classified according to their operation in autonomous and non-autonomous, the use of an autonomous microgrid can be seen in rural areas and in the use of equipment that needs energy autonomy for their operation as space vehicles or other sea vehicles where it cannot connect to the power distribution grid [
3]. The non-autonomous grid can be seen in the residential, industrial grid and currently it is also connected to a general energy distribution grid either to export or import energy for many different applications [
4]. However, the efficient use of the microgrid is difficult due to the presence of distributed energy resources, which can be controllable (or dispatchable), such as gas turbines or diesel engines, but also not controllable (or non-dispatchable), such as wind turbines or photovoltaic (PV) generators. Tidal generators whose production depends largely on weather conditions, which in turn can be predicted for long periods of time with some uncertainty [
4]. Microgrids contribute to the preservation of the environment and energy sustainability as they reduce losses in the distribution lines and also mitigate the expansion of the main network and can be used to provide electricity to rural areas, space vehicles and autonomous sea vehicles and many other applications [
5].
Wang et al. [
6] conducted a comparative study of the different energy management strategies and examined the operation modes via simulation studies.
Zia et al. [
7] presents a comparative and critical analysis on decision making strategies and their solution methods for microgrid energy management systems. To manage the volatility and intermittency of renewable energy resources and load demand, various uncertainty quantification methods are summarized. A comparative analysis on communication technologies is also discussed for cost-effective implementation of microgrid energy management systems. Finally, insights into future directions and real-world applications are provided. An overview of the DC microgrid system and the estimation of the energy savings of the DC microgrid over conventional AC systems are described in [
8]. The study examined the system performance in locations across the United States for several commercial building types and operating profiles. It is found that the DC microgrid uses generated PV energy 6%–8% more efficiently than traditional AC systems.
Zafar et al. [
9] presents a comparative study of different optimization techniques, the genetic algorithm, the pattern search method and the interior point algorithm are used to optimally schedule the energy required from the thermal power generators to meet the load demand by taking into account the power from the renewable energy resource, a comparison of the optimal cost values that each optimization method obtained is made, the emission comparison is also performed and finally the time i uses to converge each method. In [
10] the author illustrates the utilization of the particle swarm optimization (PSO) method for cost-efficient energy management in multi-source renewable energy microgrids. PSO algorithm is used to find out optimal energy mixing rates that can minimize daily energy cost of a renewable microgrids under energy balance and ant islanding constraints. The optimal energy mixing rates can be used by multi-pulse width modulation (M-PWM) energy mixer units, the methodology analyzed is TRM-PWM that is a pulse wide modulated switching method that can mix energy flow from various energy sources by allocating pulse wide duration at different time rates for several sources [
11]. Askarzadeh et al. [
12] proposes a memory-based genetic algorithm (MGA) that optimally shares the power generation task among a number of Distributed Energy Resources (DERs). The MGA is utilized for minimization of the energy production cost in the smart grid framework. It shares optimally the power generation in a microgrid including wind plants, photovoltaic plants and a combined heat and power system. In order to evaluate the performance of the proposed approach, the results obtained by the MGA are compared with the results found by a genetic algorithm and two variants of particle swarm optimization. Simulation results accentuate the superiority of the proposed MGA technique.
This paper presents a unified model of EMS for microgrids, which considers basic models of the elements of the photovoltaic panels, batteries for the energy storage system, as well as the geometric model of solar radiation. The model is solved by means of the hybrid internal point method and genetic algorithm (IP-GA) and particle swarm optimization (PSO) method provided by the MATLAB
® optimization toolbox [
13]. The solution of this model then allows us to evaluate the optimal management of energy storage devices. In addition to the geometric model of solar radiation, it is possible to evaluate the impact of the solar resource on energy management in that of storage systems. The analysis of optimal use of the storage system is illustrated by means of a numerical example, which considers a microgrid of four nodes.
The main novelty of this work is that the difference of the works presented in the introduction paragraph where only one optimization method is presented in this document presents two different optimization methods for EMS that has results obtained for energy optimization, also in this work, as it is proposed under the concept of day ahead, it uses the power balance and inequality constraint equations to maintain the power and voltage levels of all the elements of the microgrid obtaining adequate operational results of the affected variables.
The paper is organized as follows:
Section 2 presents the models mathematical of the different components of the microgrid, this section describes the model mathematical of the photovoltaic system, the storage system (battery), the electric load and the geometric model of global radiation on an arbitrarily inclined surface.
Section 3 describes the general and specific optimization model, in this section the models of the microgrid components are unified into a single model. In addition, the EMS algorithm for the microgrid is based on the equations of the unified microgrid model.
Section 4 shows the results obtained from the simulation of the unified microgrid model, where the power levels generated by the microgrid sources are shown, the voltage levels in the nodes, the comparison of fitness value and computation time are observed of the optimization methods.
Section 5 presents the conclusions of the paper.
3. DC Microgrid Model
The general model of the microgrid is posed as a problem of optimization. The optimization model [
20] is given by Equations (13)–(16). It should be noted that, in this model, it is considered that the period of time T is composed of a set of time stages tz (∀= 1,…, end), such that T= (t1,…, tend).
The terms of the optimization model are as follows: the objective function
to be optimized in stage i of the time interval
T,
represents the set of equality constrains that are raised as the power balance equations in all the connection nodes of the microgrid, as well as other operating conditions that must be fulfilled unconditionally,
is a set of constraints of inequalities that represent the maximum and minimum values that can be physically taken by the different renewable energy sources that form the microgrid, x is the set of variables to optimize for energy management composed of subsets
,
and
such x = [
,
,
]. Where,
,
and
represent batteries variables, microgrid and photovoltaic modules, respectively. These decision variables are specified for each element of the microgrid in the final part of the specific model of the DC microgrid section. The upper and lower limits,
and
, of these variables are formulated through the inequality constraints, see in Equation (16). The physical values of the limits of these variables are specified in
Appendix A and
Table A1.
3.1. Specific Model of the DC Microgrid
The specific model of the DC microgrid is explicitly formulated in this section for an autonomous DC microgrid. For this purpose, the objective function is expressed in extended form in the Equation (17).
Note that Equation (17) denotes that the objective is to minimize the cost of the total energy photovoltaic system during the period of time T to supply the demand curves predicted .
The set of equality constraints
n(
x) is expressed in Equation (14) and correspond to the equations of the active power balance of the nodes of the DC microgrid
, these constraints are written in the first block of Equation (18) where the lower limit ∀
j∈
m means each element
j is connected to the node m. For example, in this block we have the sum of the charge
and discharge powers
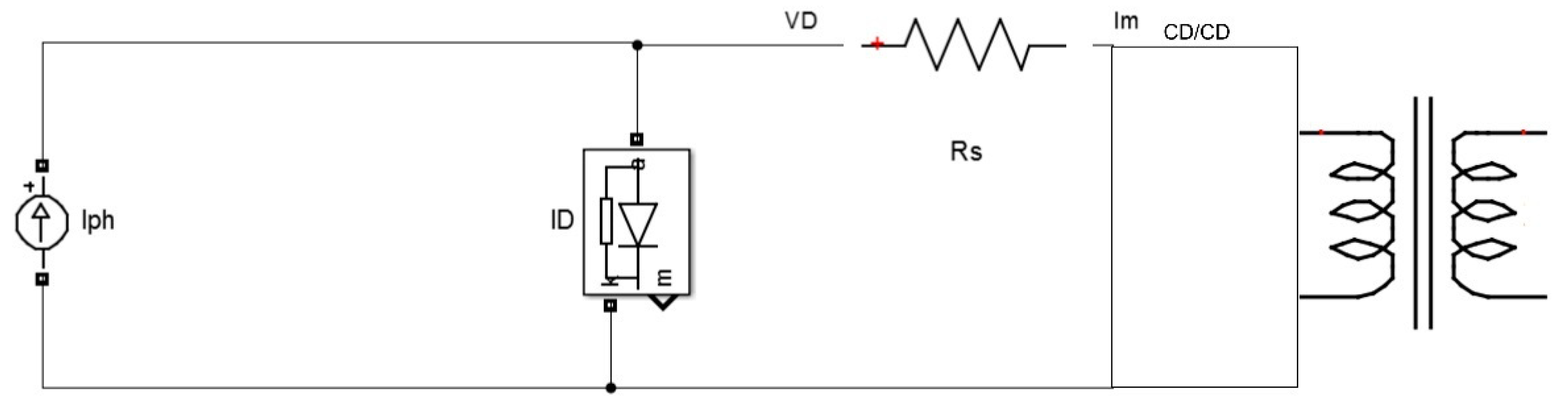
of the storage system, the sum of the power of the photovoltaic panel
and the powers injected
into the nodes of the microgrid. In the third block of Equation (18) is expressed the equations of active power balance in node of photovoltaic panel
[
9].
The only inequality constraints function
z(
x) introduced in the optimization problem are those due to the storage system, because the batteries have finite charge and discharge capacity that can vary between a minimum of 20% and a maximum of 100% depending on the battery material. Therefore, the SOC is modulated over the period
T through Equation (19) [
21].
The inequality constraints variable
x is set up of the set decision variables that must have admissible values for the operation of the microgrid. The decision variables must be limited to appropriate values throughout the time interval
T, the inequality constraints variable is expressed in Equation (20).
The microgrid has a set of decision variables associated with each node, which are the magnitude of the voltage as well as the powers exchanged with the different energy sources, such as ; , whereas the decision variables batteries are Finally, the photovoltaic modules decision variables are ; .
3.2. Algorithms
The algorithms described in this paper are composed of the genetic algorithm and interior point methods and PSO method. The first algorithm is applied through of the ga function, which belongs to the MATLAB
® ‘Direct Search and Genetic Algorithm Toolbox’ and is especially useful for the optimization of global non-linear problems with or without constraints. Furthermore, it provides a better flexibility since it contains multiple parameters of configuration [
13,
22].
The ga function suggested specifies the values of the arguments of the set of inputs IA and outputs OA that are established and regulated for its execution. The general form of this function is shown in Equation (21).
The second algorithm is applied through the PSO function, which belongs to the MATLAB
® ‘Particle Swarm Toolbox’ and is especially useful for the optimization of global non-linear problems with or without constraints. Furthermore, it provides a better flexibility since it contains multiple parameters of configuration [
13].
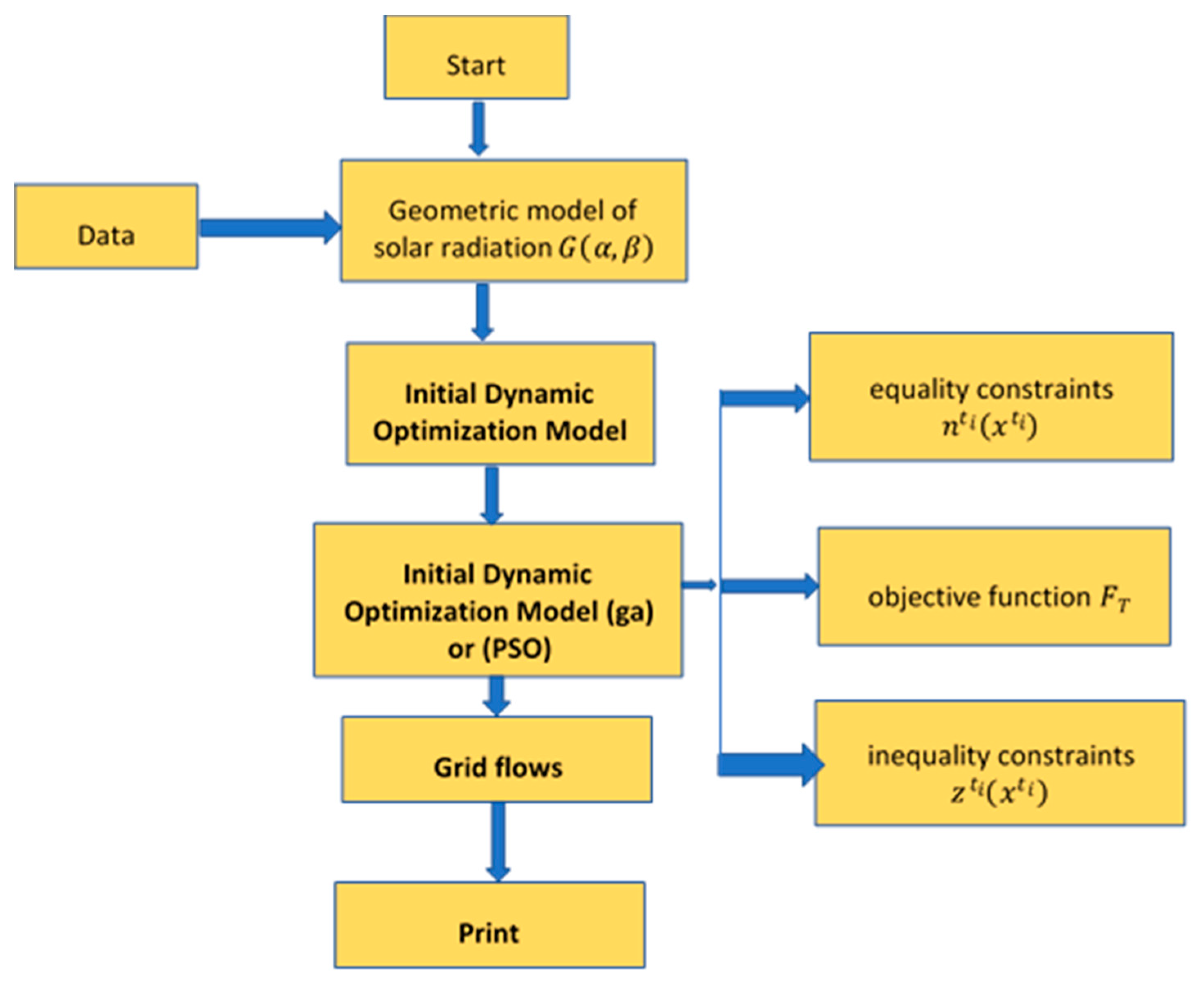
The description of the implementation of the algorithms is summarized by means of the represented algorithm in
Figure 3.
4. Results
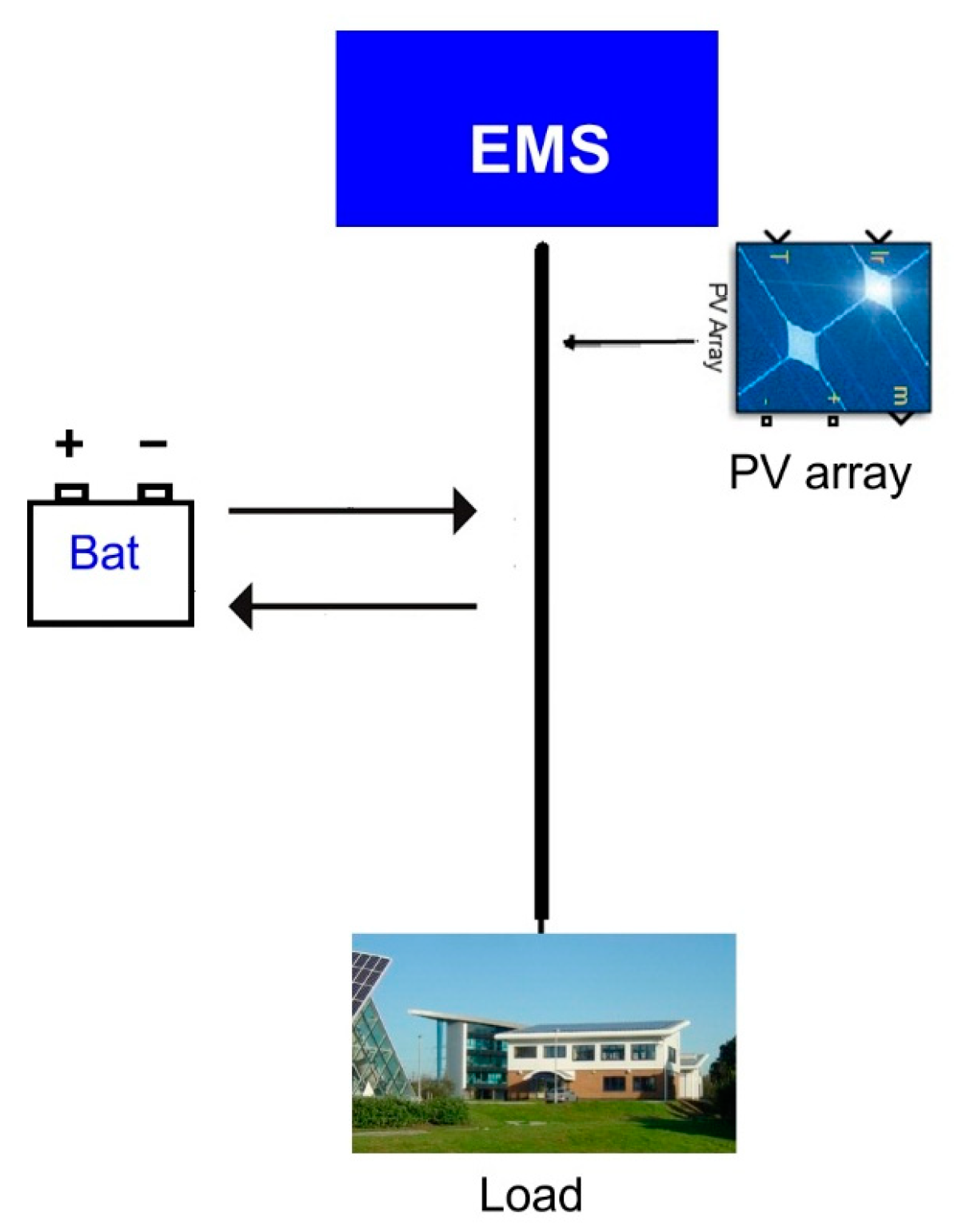
The results obtained numerically through a simulation carried out with a test microgrid, which is integrated by a photovoltaic system (PV), storage system (S) and the load (L). The data that were used for the test microgrid are real and also with these data the global irradiance on an arbitrarily oriented and inclined surface was calculated, a global irradiance profile of Cancun city (Mexico) and Baglan (Wales, UK) to make the comparison of the energy generation of the photovoltaic solar system for two different places in the world. The load profile used is the real data obtained from the Baglan Energy Park, Port Talbot, United Kingdom.
The results present the numerical values of the geometric model of solar radiation from the two cities mentioned above. It also presents the results of the behavior of the photovoltaic solar system and the storage system within the microgrid resolved through hybrid IP-GA method and PSO method, the methods to solve the optimization problem is determined in a PC DELL, with 8 GB RAM and an Intel i5-4210U CPU@ 2.40 GHz processor. The characteristics of the computer directly influence the speed in which the optimization algorithm can be solved.
In this work, solar radiation data from two different places in the world are compared to verify the behavior of the EMS considering the solar resource of each place evaluated. The load profile is based on a relatively small (64 m2) two store office block, which in fact forms part of a facility called the Hydrogen Center (University of Glamorgan at Baglan Energy Park, Port Talbot, United Kingdom).
The microgrid test is shown in
Figure 4. The values of the parameters of the different models of the microgrid are presented in
Appendix A.
Comparative load and irradiation profile for a clear day (summer) for both cities are observed in
Figure 5. The power and voltage bases were selected in 10 kW and 24 V, respectively.
The limits of the magnitudes of the microgrid are per unit. The SOC limits on the battery are , whilst the initial condition of the battery charge is .
The EMS was developed with the genetic algorithm method with interior point hybrid (
IP-GA) provided by the ga-fmincon function developed by MATLAB
®.
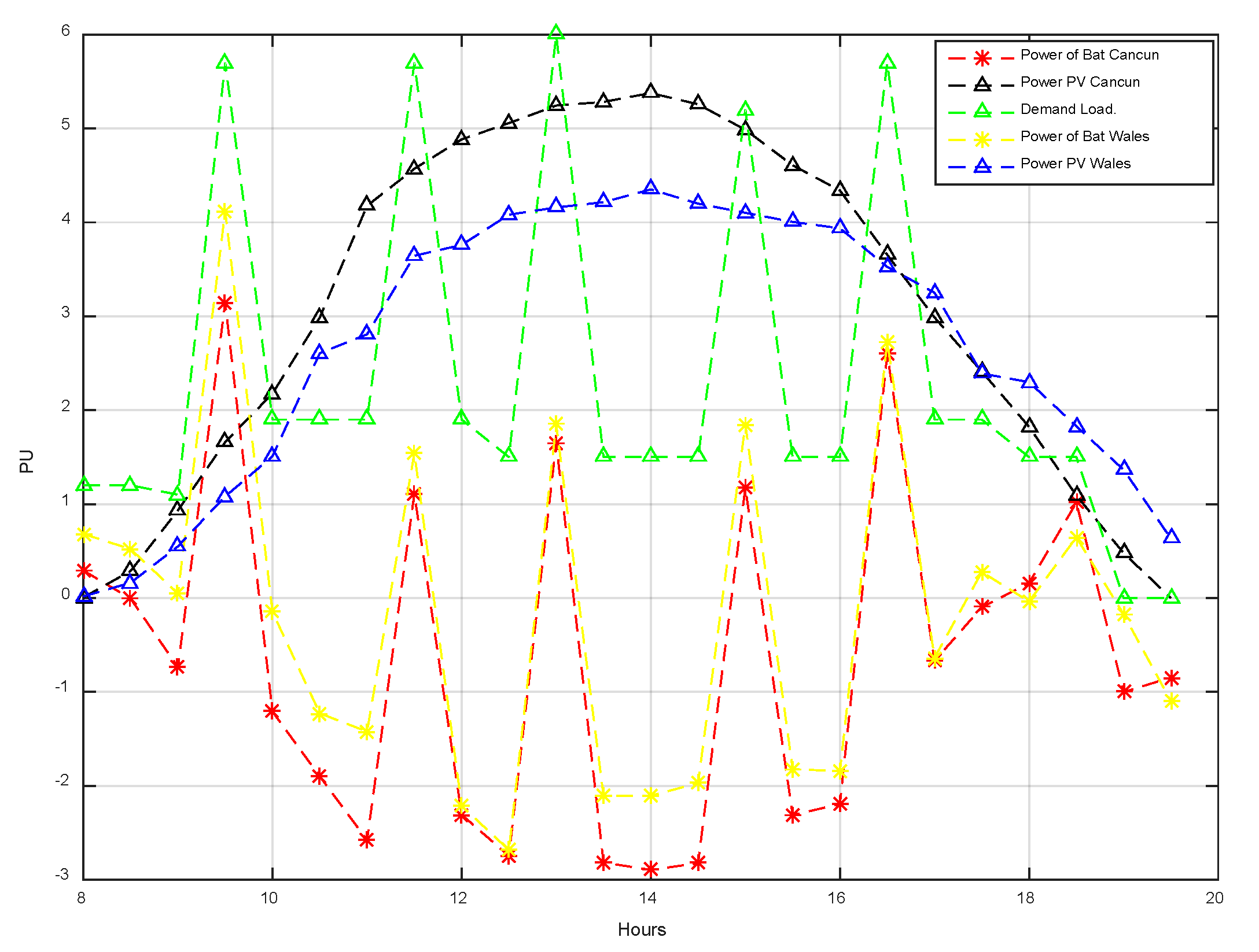
Figure 6 shows the comparison of the active power supplied by the photovoltaic panel and the battery for the two solar radiation conditions of a clean summer day in Cancun and Baglan. This figure shows that between the stages 8–20 h a demand profile is presented in the office block. In the demand that ranges between 1 and 6 KW, it is observed that the demand peaks occur at 9:30, 11:30, 13, 15 and 17 h.
The power supplies by the photovoltaic panel are not enough to supply the load demand, making it necessary to use the energy stored in the batteries to satisfy the load demand and avoid problems within the microgrid.
It can be observed, that the batteries take advantage of charging at times where the demand for the charge is minimal, such as in 9, 11, 12:30, 14, 15:45 and 17 h. This way it is possible to verify that the EMS algorithm works correctly. Furthermore, it was also observed from the two generation curves of the photovoltaic panel where the generation curve for the Cancun city shows a greater amount of energy than the Baglan city curve, due to the geographical position of each city.
Figure 6 indicates the active power supplied by the batteries. It is important to understand that the energy supplied by the batteries in the region of Cancun is less than that supplied in Baglan and it can also be seen that the batteries are charged with more energy in the city of Cancun since in this city the photovoltaic panel produces more energy for the largest amount of solar resources in the region.
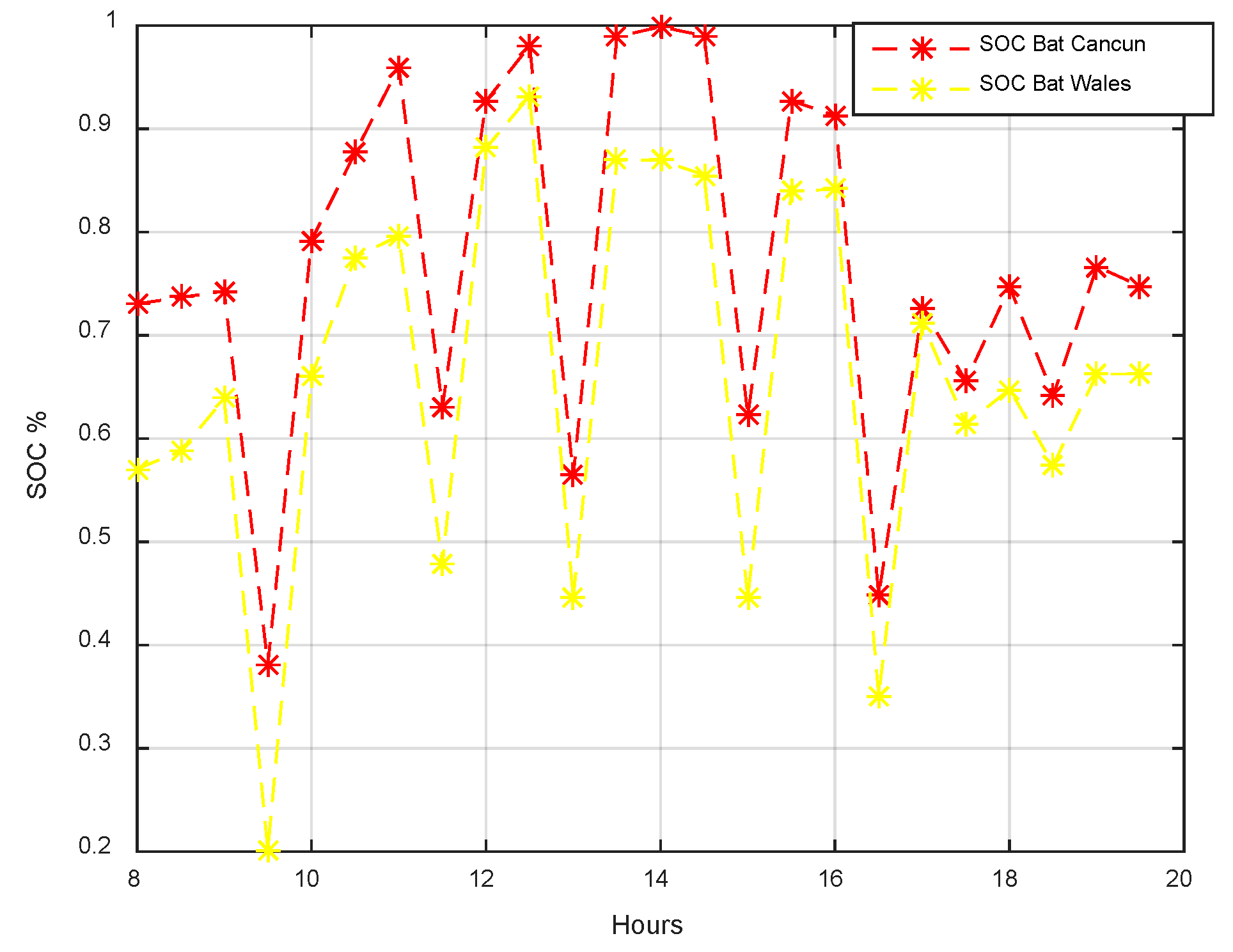
Figure 7 shows the SOC of the battery in yellow for the city of Baglan and in red the behavior in the city of Cancun. The results show that the SOC of the battery is consistent with the behavior of the battery charge and discharge graph of
Figure 6. We could observe that at all hours of time the SOC of the battery in Cancun was higher due to the production of PV power in this city being greater due to the available solar radiation and therefore there was an opportunity to charge the battery more. For example, from 8:00 a.m. to 10:00 a.m. the battery in Cancun has a higher SOC the behavior was very similar from 10:00 a.m. to 4:00 p.m. at 5:00 p.m. the battery in Baglan managed to have an SOC similar to the battery of Cancun since at this time the production of PV in Baglan was greater. For the discharge we observed that at 9:30 a.m. the battery in Baglan is discharged to the maximum possible 20% while in Cancun the battery is discharged at 40%, this behavior is similar at 11:30, 13:00, 15:00 and 16:30.
This comparison shows us that having a greater availability of solar radiation the battery in an isolated micro network has less wear due to the lower number of use cycles.
In
Figure 8 shows the behavior of the nodal voltages within the microgrid. It is observed that the voltage levels were maintained in the minimum and maximum permissible values of 95%–105%, in this way it was verified that the inequality constraints to variable were preserved.
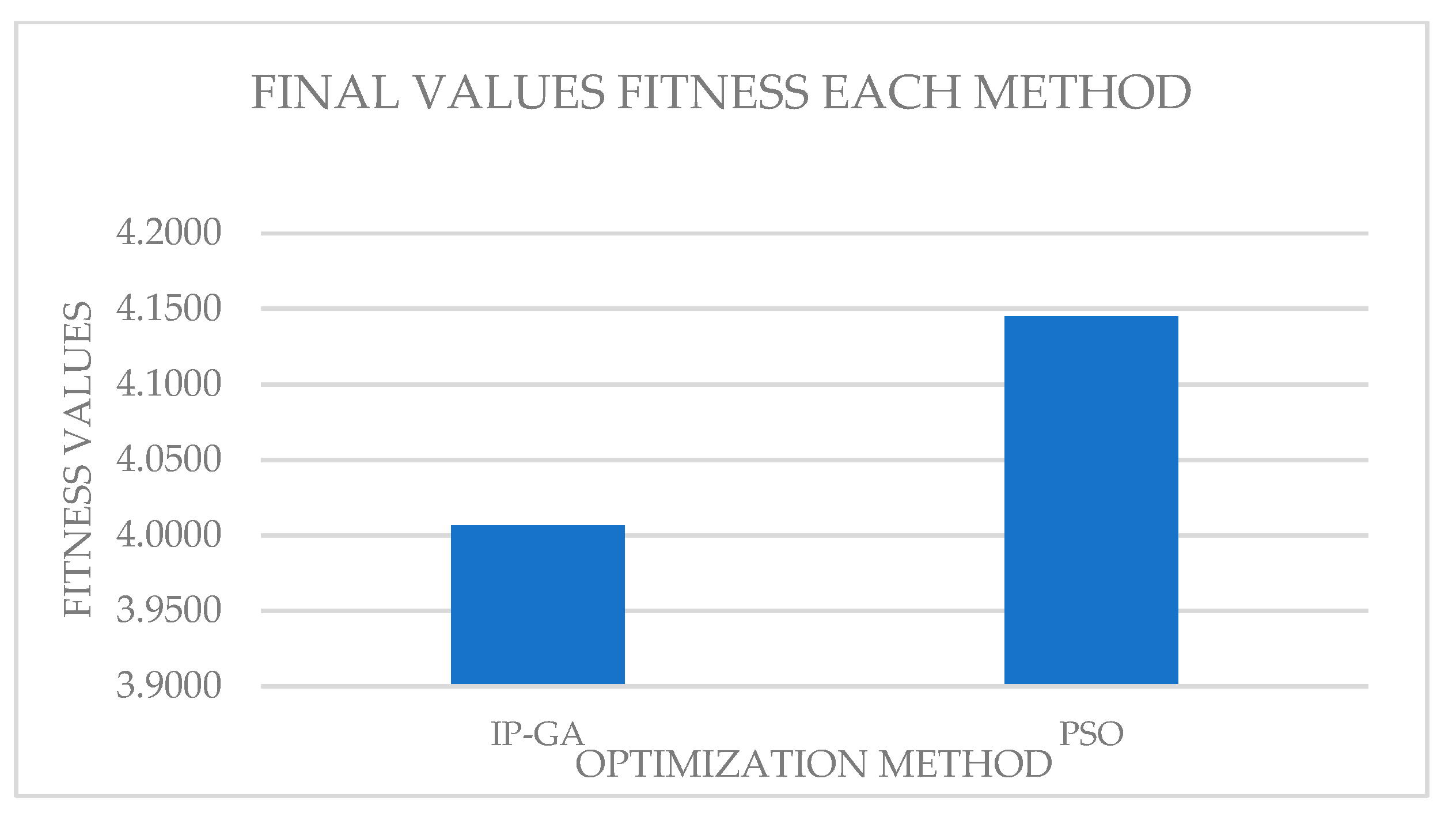
Figure 9 shows that the two methods IP-GA and PSO, the IP-GA method gave a better fitness value than the PSO method. The IP-GA was faster than PSO, reducing the computing time about 300 seg. as the
Figure 10 shows.
Although the GA-IP was faster, the two methods used to solve the optimization problem in the microgrid could be considered like an effective method to solve the optimization problem and worked like a tertiary control within the microgrid. This is possible due the energy cost from the battery for the optimization methods being the most expensive for all times.