Theoretical Analysis of Fractional Viscoelastic Flow in Circular Pipes: General Solutions
Abstract
1. Introduction
2. Problem Formulation
2.1. Domain Definition
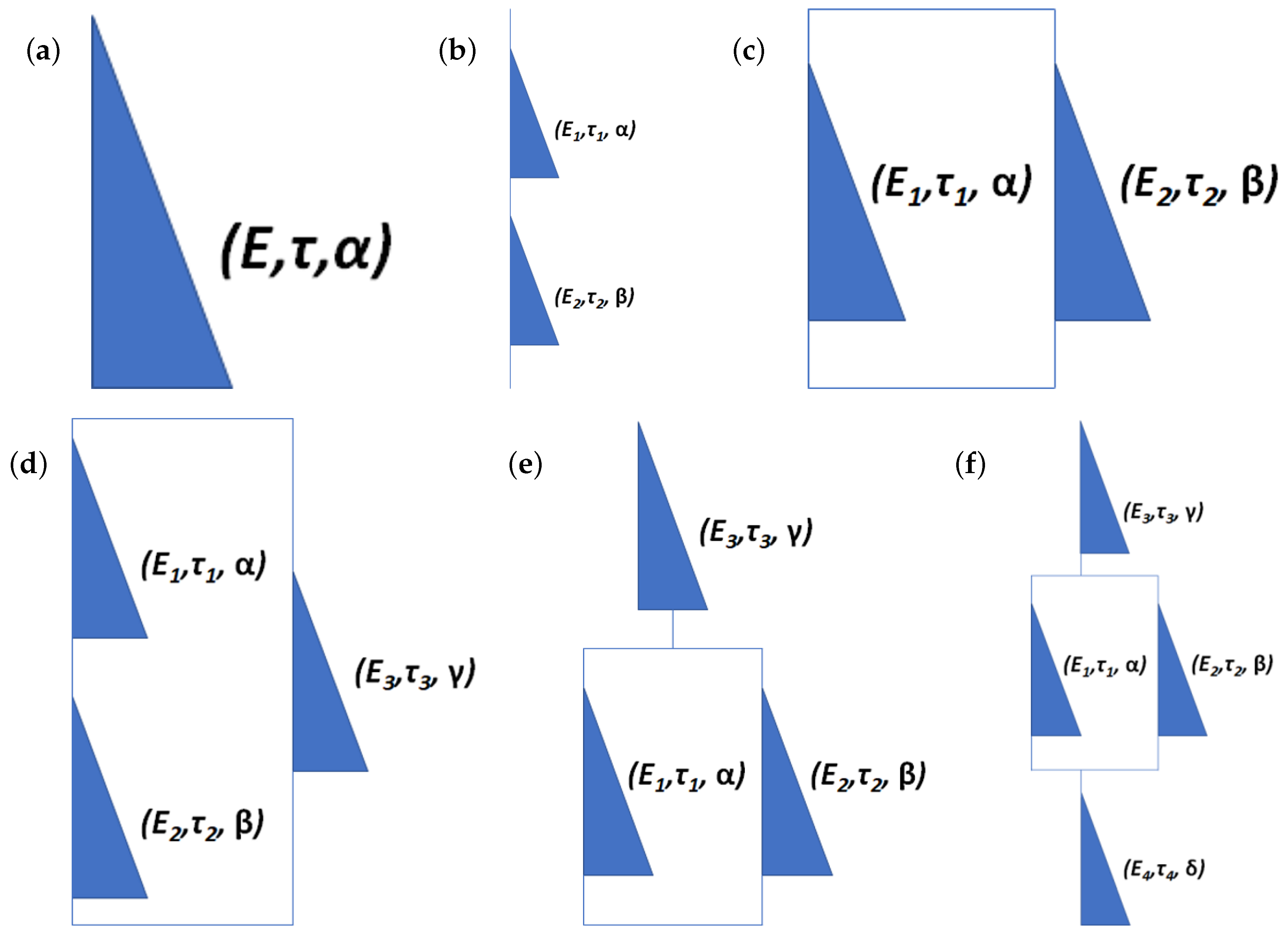
2.2. Fractional Element
2.3. Fractional Maxwell Model
2.4. Fractional Kelvin–Voigt Model
2.5. Fractional Zener Model
2.6. Fractional Poynting–Thomson Model
2.7. Fractional Burgers Model
3. Results and Discussion
3.1. General Solution
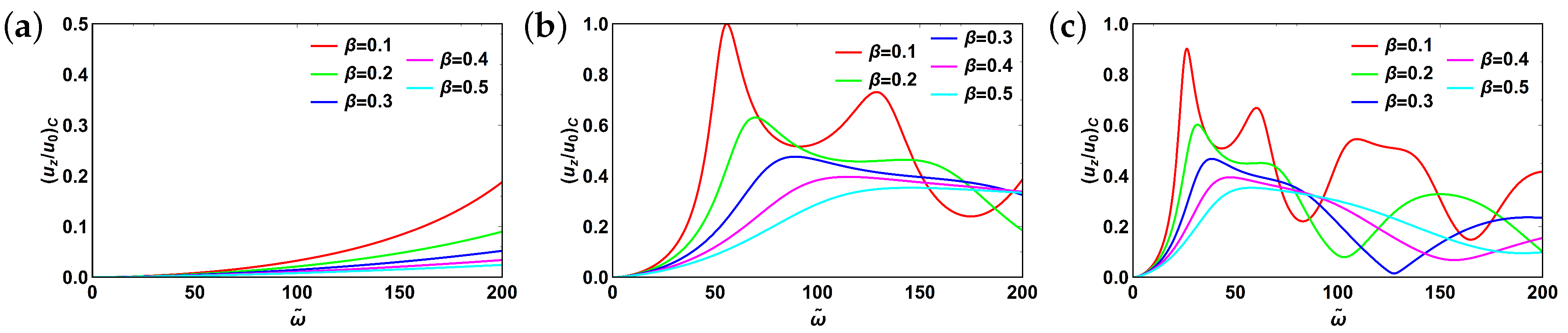
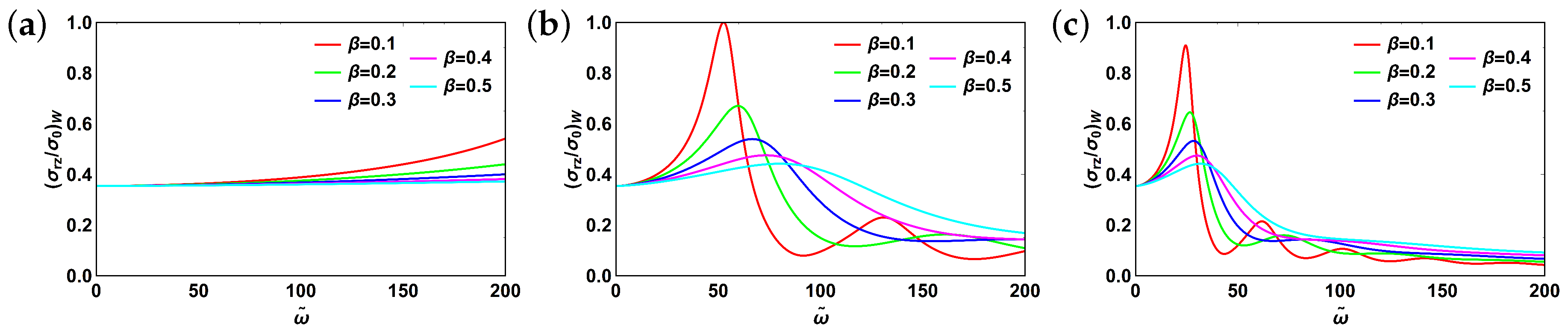
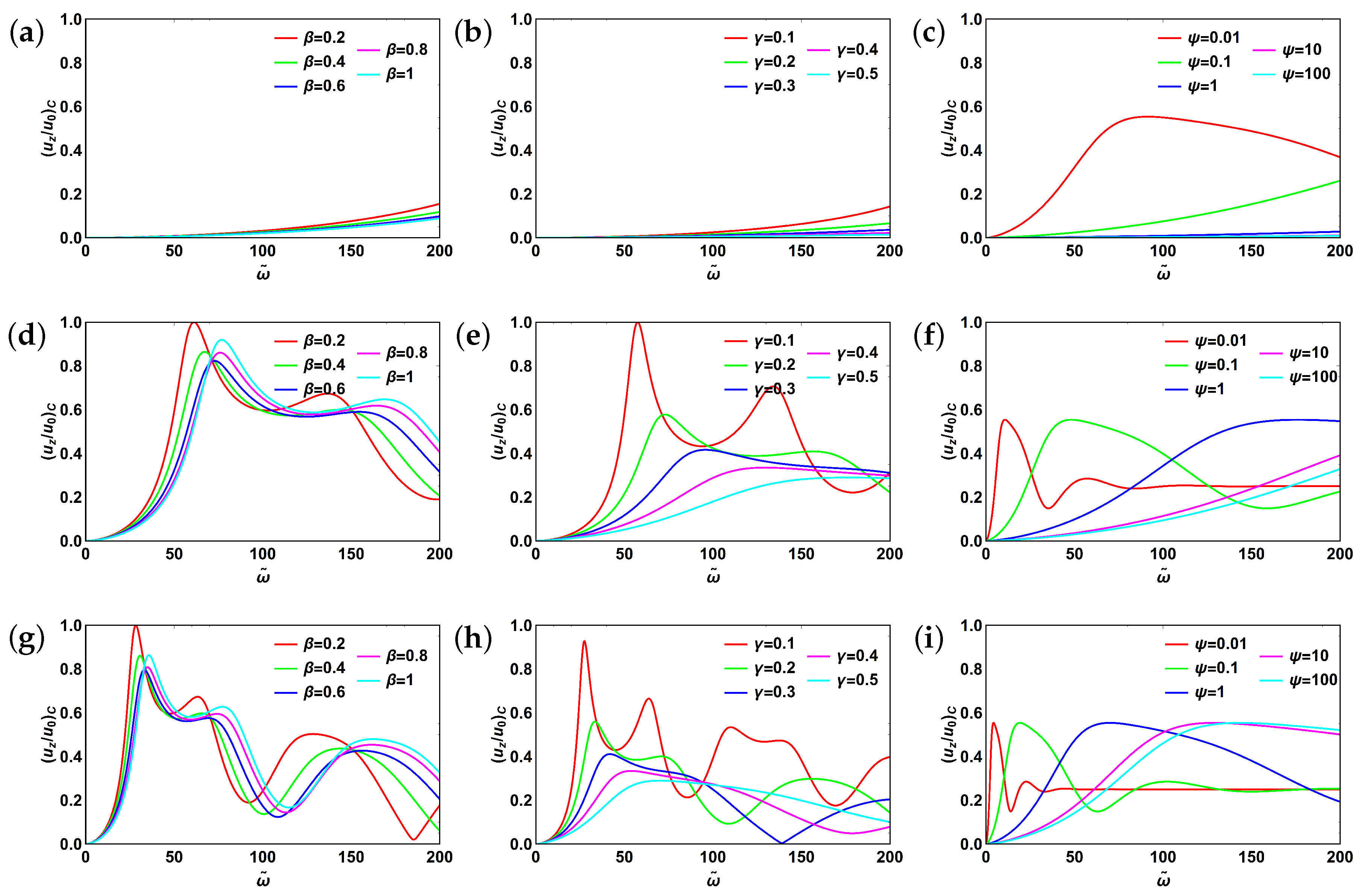
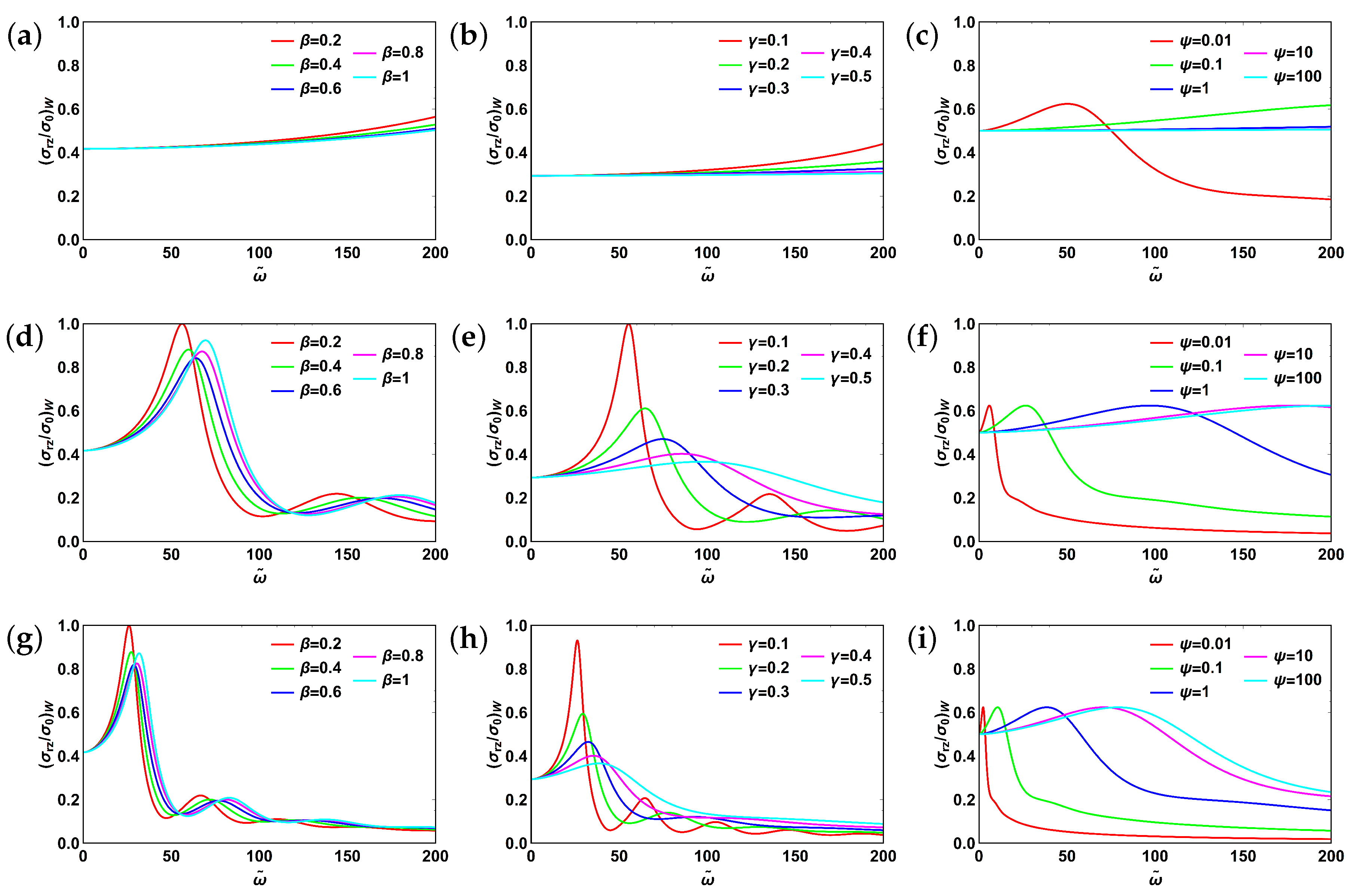
3.2. Fractional Maxwell Model
3.3. Fractional Kelvin–Voigt Model
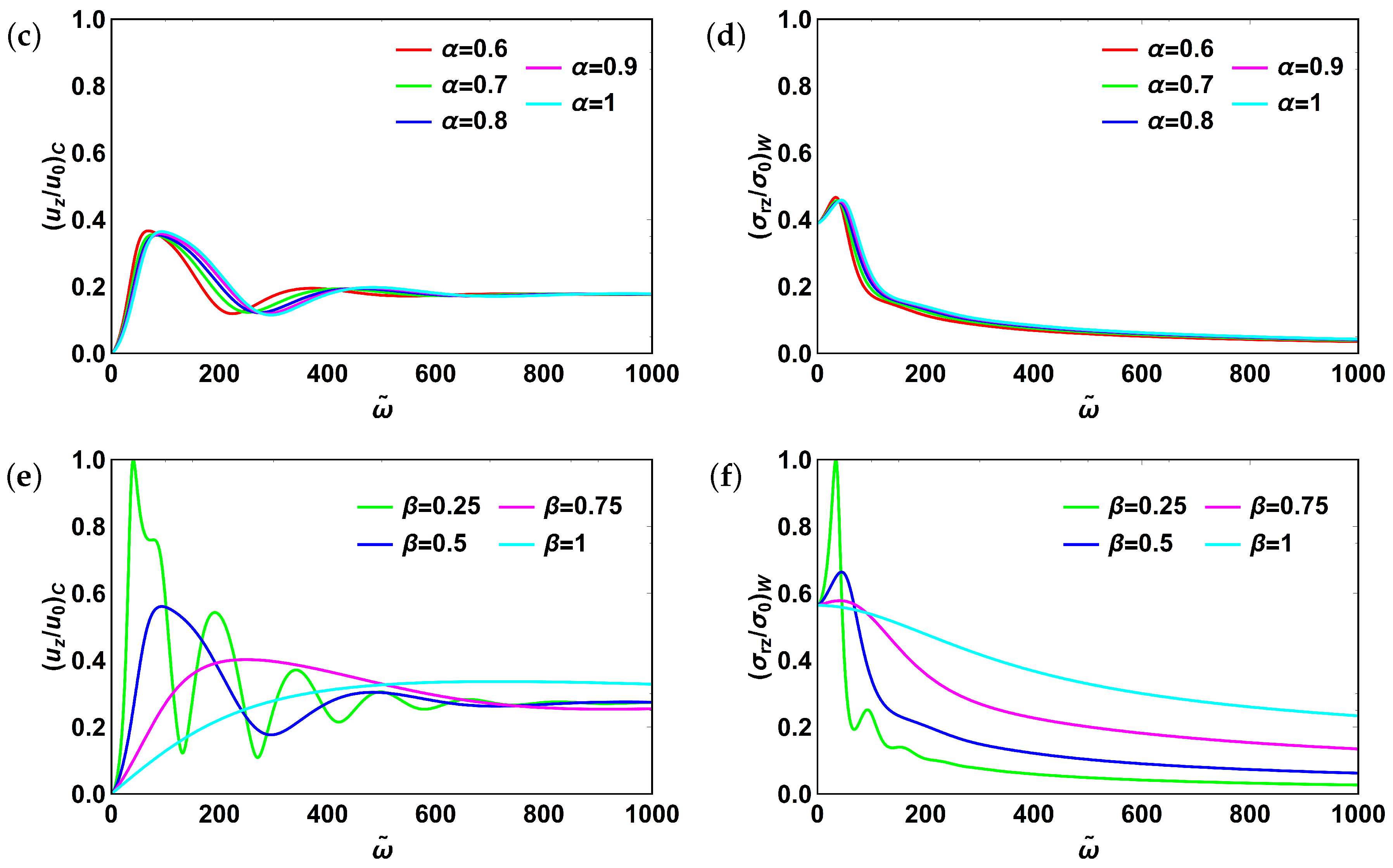
3.4. Fractional Zener Model
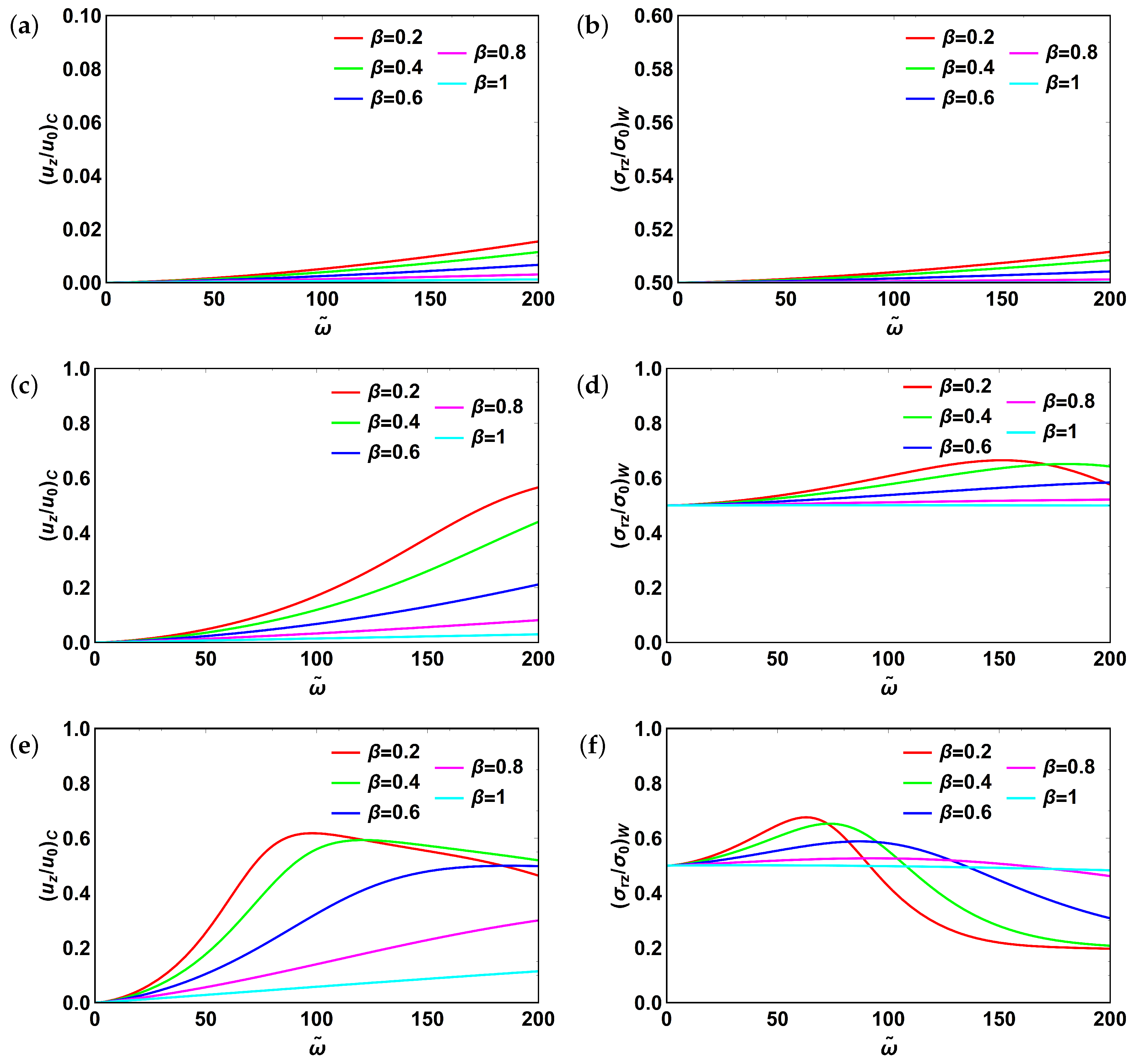
3.5. Fractional Poynting–Thomson Model
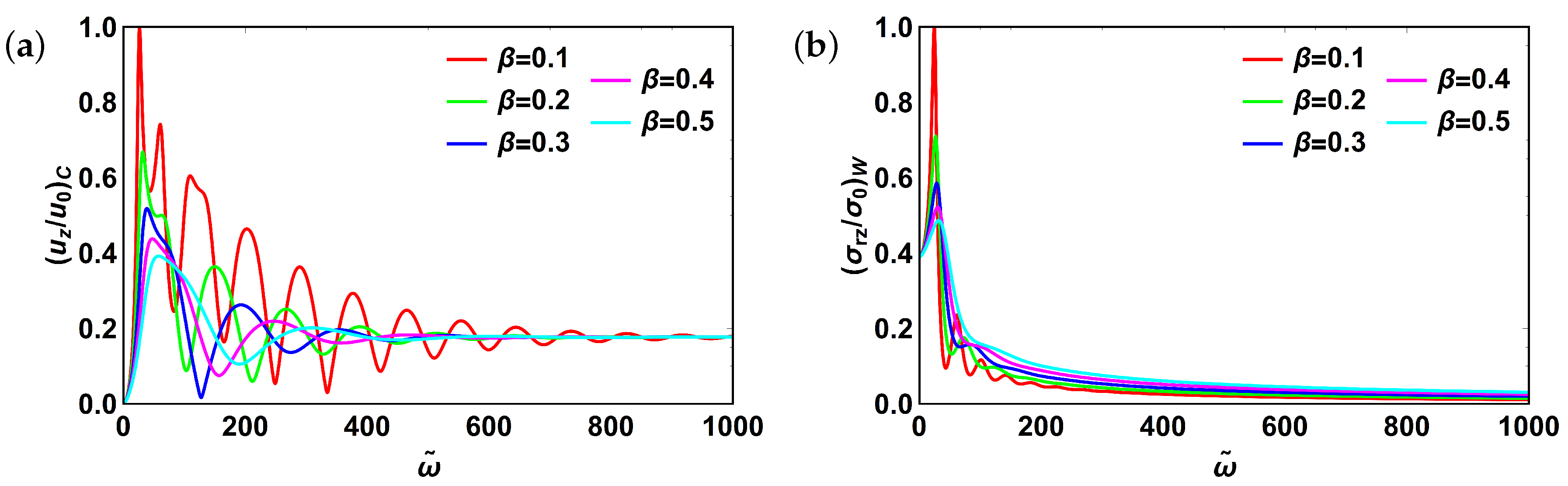
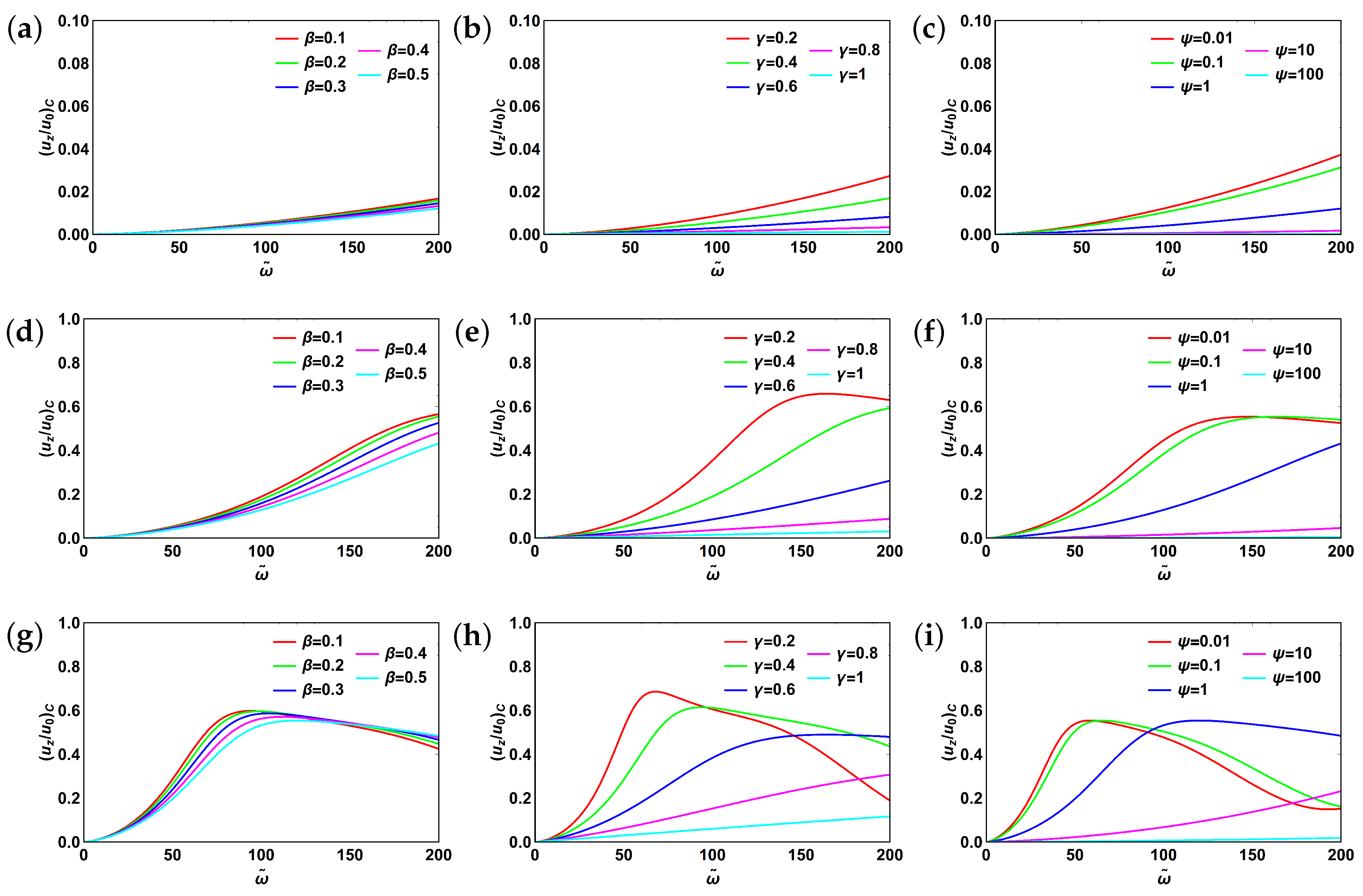
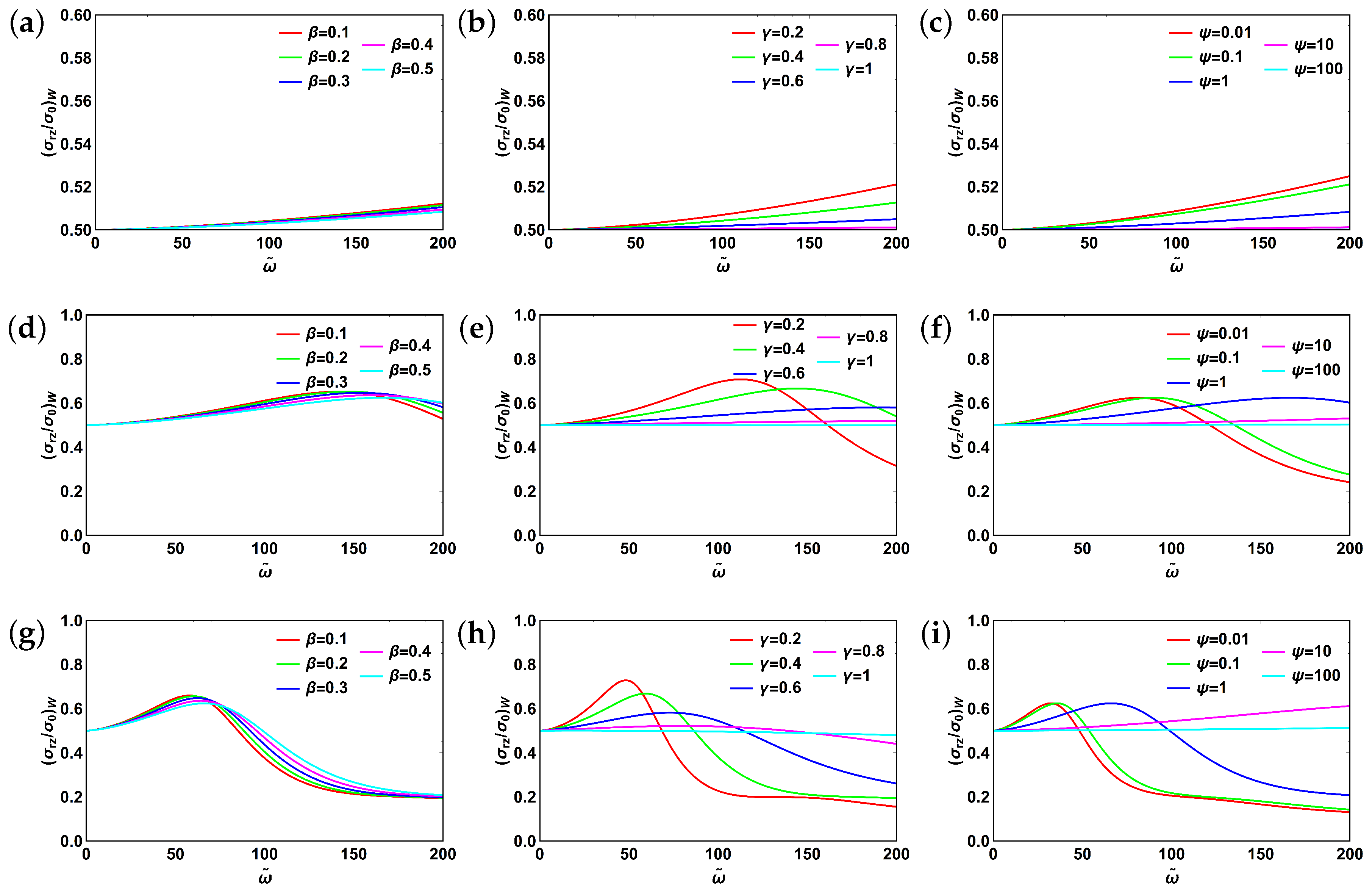
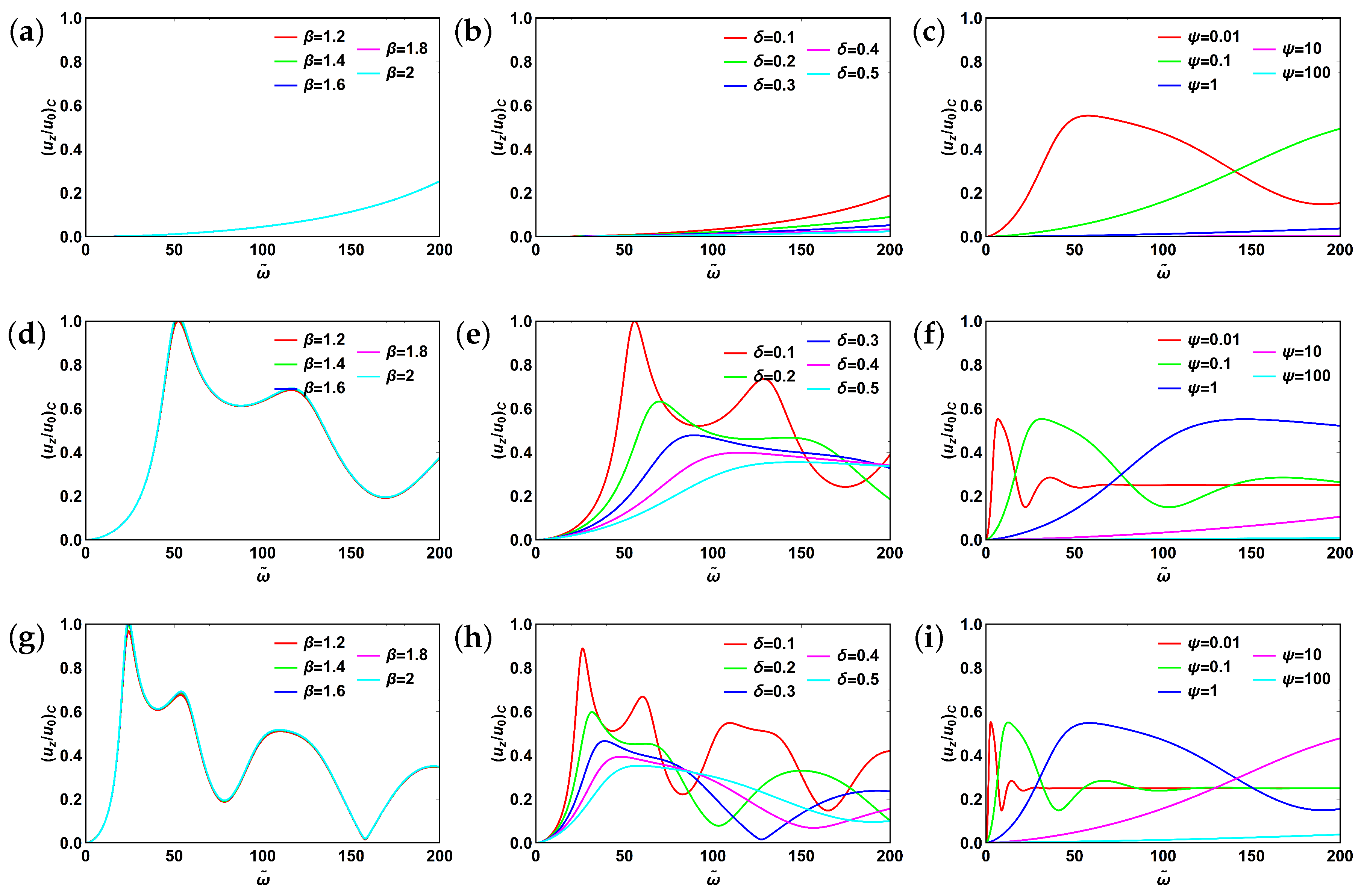
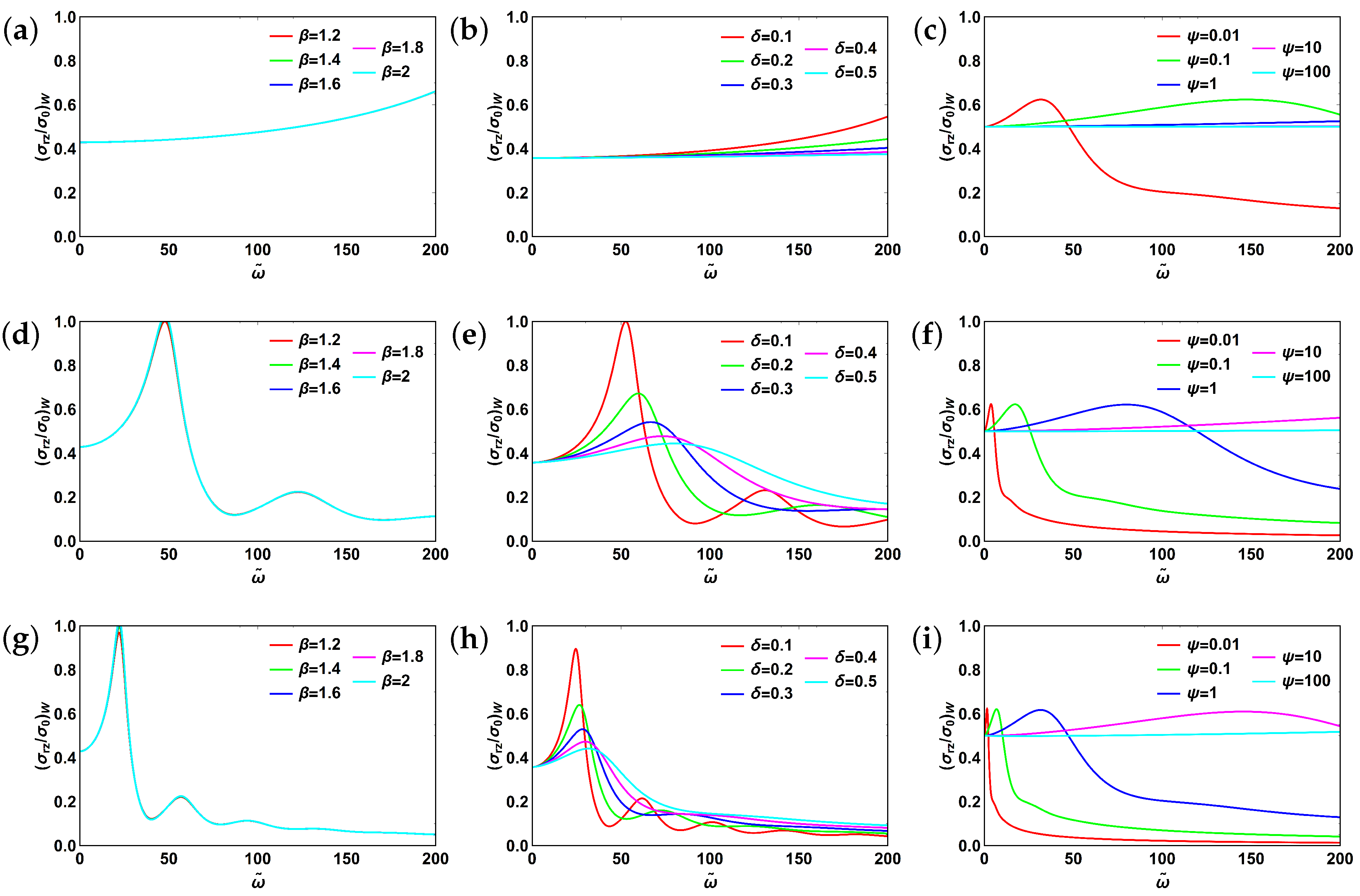
3.6. Fractional Burgers Model
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Leibniz, G. Letter from Hanover, Germany, to GFA L’Hopital, September 30; 1695. Math. Schriften 1849, 2, 301–302. [Google Scholar]
- Ross, B. The development of fractional calculus 1695–1900. Hist. Math. 1977, 4, 75–89. [Google Scholar] [CrossRef]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley: Hoboken, NJ, USA, 1993. [Google Scholar]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of their Solution and Some of their Applications; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Mainardi, F. Fractional Calculus: Theory and Applications; MDPI: Basel, Switzerland, 2018. [Google Scholar]
- Hilfer, R. (Ed.) Applications of Fractional Calculus in Physics; World Scientific: Singapore, 2000; Volume 35. [Google Scholar]
- Herrmann, R. Fractional Calculus: An Introduction for Physicists; World Scientific: Singapore, 2014. [Google Scholar]
- Tarasov, V. Handbook of Fractional Calculus with Applications, Volume 4: Applications in Physics, Part A; De Gruyter: Berlin, Germany, 2019. [Google Scholar]
- Tarasov, V. Handbook of Fractional Calculus with Applications, Volume 5: Applications in Physics, Part B; De Gruyter: Berlin, Germany, 2019. [Google Scholar]
- Baleanu, D.; Lopes, A.M. Handbook of Fractional Calculus with Applications, Volume 7: Applications in Engineering, Life and Social Sciences, Part A; De Gruyter: Berlin, Germany, 2019. [Google Scholar]
- Baleanu, D.; Lopes, A.M. Handbook of Fractional Calculus with Applications, Volume 8: Applications in Engineering, Life and Social Sciences, Part B; De Gruyter: Berlin, Germany, 2019. [Google Scholar]
- Atanacković, T.M.; Janev, M.; Pilipović, S. On the thermodynamical restrictions in isothermal deformations of fractional Burgers model. Philos. Transact. R. Soc. A 2020, 378, 20190278. [Google Scholar] [CrossRef]
- Chen, R.; Wei, X.; Liu, F.; Anh, V.V. Multi-term time fractional diffusion equations and novel parameter estimation techniques for chloride ions sub-diffusion in reinforced concrete. Philos. Transact. R. Soc. A 2020, 378, 20190538. [Google Scholar] [CrossRef] [PubMed]
- Li, S.N.; Cao, B.Y. Fractional-order heat conduction models from generalized Boltzmann transport equation. Philos. Transact. R. Soc. A 2020, 378, 20190280. [Google Scholar] [CrossRef] [PubMed]
- Bologna, E.; Di Paola, M.; Dayal, K.; Deseri, L.; Zingales, M. Fractional-order nonlinear hereditariness of tendons and ligaments of the human knee. Philos. Transact. R. Soc. A 2020, 378, 20190294. [Google Scholar] [CrossRef] [PubMed]
- Chugunov, V.; Fomin, S. Effect of adsorption, radioactive decay and fractal structure of matrix on solute transport in fracture. Philos. Transact. R. Soc. A 2020, 378, 20190283. [Google Scholar] [CrossRef] [PubMed]
- Failla, G.; Zingales, M. Advanced materials modelling via fractional calculus: Challenges and perspectives. Philos. Transact. R. Soc. A 2020, 378, 20200050. [Google Scholar] [CrossRef]
- Fang, C.; Shen, X.; He, K.; Yin, C.; Li, S.; Chen, X.; Sun, H. Application of fractional calculus methods to viscoelastic behaviours of solid propellants. Philos. Transact. R. Soc. A 2020, 378, 20190291. [Google Scholar] [CrossRef]
- Ionescu, C.M.; Birs, I.R.; Copot, D.; Muresan, C.; Caponetto, R. Mathematical modelling with experimental validation of viscoelastic properties in non-Newtonian fluids. Philos. Transact. R. Soc. A 2020, 378, 20190284. [Google Scholar] [CrossRef]
- Li, J.; Ostoja-Starzewski, M. Thermo-poromechanics of fractal media. Philos. Transact. R. Soc. A 2020, 378, 20190288. [Google Scholar] [CrossRef] [PubMed]
- Tenreiro Machado, J.; Lopes, A.M.; de Camposinhos, R. Fractional-order modelling of epoxy resin. Philos. Transact. R. Soc. A 2020, 378, 20190292. [Google Scholar] [CrossRef] [PubMed]
- Di Paola, M.; Alotta, G.; Burlon, A.; Failla, G. A novel approach to nonlinear variable-order fractional viscoelasticity. Philos. Transact. R. Soc. A 2020, 378, 20190296. [Google Scholar] [CrossRef]
- Patnaik, S.; Hollkamp, J.P.; Semperlotti, F. Applications of variable-order fractional operators: A review. Proc. R. Soc. A 2020, 476, 20190498. [Google Scholar] [CrossRef]
- Patnaik, S.; Semperlotti, F. Variable-order particle dynamics: Formulation and application to the simulation of edge dislocations. Philos. Transact. R. Soc. A 2020, 378, 20190290. [Google Scholar] [CrossRef]
- Povstenko, Y.; Kyrylych, T. Fractional thermoelasticity problem for an infinite solid with a penny-shaped crack under prescribed heat flux across its surfaces. Philos. Transact. R. Soc. A 2020, 378, 20190289. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Ostoja-Starzewski, M. Impact force and moment problems on random mass density fields with fractal and Hurst effects. Philos. Transact. R. Soc. A 2020, 378, 20190591. [Google Scholar] [CrossRef] [PubMed]
- Zorica, D.; Oparnica, L. Energy dissipation for hereditary and energy conservation for non-local fractional wave equations. Philos. Transact. R. Soc. A 2020, 378, 20190295. [Google Scholar] [CrossRef] [PubMed]
- Blair, G.S. The role of psychophysics in rheology. J. Coll. Sci. 1947, 2, 21–32. [Google Scholar] [CrossRef]
- Bagley, R.L.; Torvik, P. A theoretical basis for the application of fractional calculus to viscoelasticity. J. Rheol. 1983, 27, 201–210. [Google Scholar] [CrossRef]
- Gloeckle, W.G.; Nonnenmacher, T.F. Fractional integral operators and Fox functions in the theory of viscoelasticity. Macromolecules 1991, 24, 6426–6434. [Google Scholar] [CrossRef]
- Metzler, R.; Schick, W.; Kilian, H.G.; Nonnenmacher, T.F. Relaxation in filled polymers: A fractional calculus approach. J. Chem. Phys. 1995, 103, 7180–7186. [Google Scholar] [CrossRef]
- Friedrich, C.; Braun, H. Generalized Cole-Cole behavior and its rheological relevance. Rheol. Acta 1992, 31, 309–322. [Google Scholar] [CrossRef]
- Friedrich, C. Relaxation and retardation functions of the Maxwell model with fractional derivatives. Rheol. Acta 1991, 30, 151–158. [Google Scholar] [CrossRef]
- Nonnenmacher, T.; Glöckle, W. A fractional model for mechanical stress relaxation. Philos. Mag. Lett. 1991, 64, 89–93. [Google Scholar] [CrossRef]
- Schiessel, H.; Blumen, A. Mesoscopic pictures of the sol-gel transition: Ladder models and fractal networks. Macromolecules 1995, 28, 4013–4019. [Google Scholar] [CrossRef]
- Schiessel, H.; Blumen, A. Hierarchical analogues to fractional relaxation equations. J. Phys. A Math. Gen. 1993, 26, 5057. [Google Scholar] [CrossRef]
- Schiessel, H.; Blumen, A.; Alemany, P. Dynamics in disordered systems. In Transitions in Oligomer and Polymer Systems; Springer: Berlin, Germany, 1994; pp. 16–21. [Google Scholar]
- Heymans, N.; Bauwens, J.C. Fractal rheological models and fractional differential equations for viscoelastic behavior. Rheol. Acta 1994, 33, 210–219. [Google Scholar] [CrossRef]
- Schiessel, H.; Metzler, R.; Blumen, A.; Nonnenmacher, T. Generalized viscoelastic models: Their fractional equations with solutions. J. Phys. A Math. Gen. 1995, 28, 6567. [Google Scholar] [CrossRef]
- Friedrich, C.; Schiessel, H.; Blumen, A. Constitutive behavior modeling and fractional derivatives. In Rheology Series; Elsevier: Amsterdam, The Netherlands, 1999; Volume 8, pp. 429–466. [Google Scholar]
- Hernández-Jiménez, A.; Hernández-Santiago, J.; Macias-Garcıa, A.; Sánchez-González, J. Relaxation modulus in PMMA and PTFE fitting by fractional Maxwell model. Polym. Test. 2002, 21, 325–331. [Google Scholar] [CrossRef]
- Makris, N.; Constantinou, M. Spring-viscous damper systems for combined seismic and vibration isolation. Earthq. Eng. Struct. Dyn. 1992, 21, 649–664. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, S.; Zhang, Q.; Zhou, Y. Experimental and theoretical research on the stress-relaxation behaviors of PTFE coated fabrics under different temperatures. Adv. Mater. Sci. Eng. 2015, 2015, 319473. [Google Scholar] [CrossRef] [PubMed]
- Khajehsaeid, H. Application of fractional time derivatives in modeling the finite deformation viscoelastic behavior of carbon-black filled NR and SBR. Polym. Test. 2018, 68, 110–115. [Google Scholar] [CrossRef]
- Khajehsaeid, H. A Comparison Between Fractional-Order and Integer-Order Differential Finite Deformation Viscoelastic Models: Effects of Filler Content and Loading Rate on Material Parameters. Int. J. Appl. Mech. 2018, 10, 1850099. [Google Scholar] [CrossRef]
- Yin, B.; Hu, X.; Song, K. Evaluation of classic and fractional models as constitutive relations for carbon black–filled rubber. J. Elastom. Plast. 2018, 50, 463–477. [Google Scholar] [CrossRef]
- Xu, H.; Jiang, X. Creep constitutive models for viscoelastic materials based on fractional derivatives. Comp. Math. Appl. 2017, 73, 1377–1384. [Google Scholar] [CrossRef]
- Stankiewicz, A. Fractional Maxwell model of viscoelastic biological materials. In BIO Web of Conferences; EDP Sciences: Les Ulis, France, 2018; Volume 10, p. 02032. [Google Scholar]
- Farno, E.; Baudez, J.C.; Eshtiaghi, N. Comparison between classical Kelvin-Voigt and fractional derivative Kelvin-Voigt models in prediction of linear viscoelastic behaviour of waste activated sludge. Sci. Total Environ. 2018, 613, 1031–1036. [Google Scholar] [CrossRef]
- Grace, S. XCIV. Oscillatory motion of a viscous liquid in a long straight tube. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1928, 5, 933–939. [Google Scholar] [CrossRef]
- Sexl, T. Uber den von EG Richardson entdeckten “Annulareffekt”. Z. Phys. 1930, 61, 349–362. [Google Scholar] [CrossRef]
- Womersley, J.R. Method for the calculation of velocity, rate of flow and viscous drag in arteries when the pressure gradient is known. J. Physiol. 1955, 127, 553. [Google Scholar] [CrossRef]
- Womersley, J.R. XXIV, Oscillatory motion of a viscous liquid in a thin-walled elastic tube—I: The linear approximation for long waves. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1955, 46, 199–221. [Google Scholar] [CrossRef]
- Uchida, S. The pulsating viscous flow superposed on the steady laminar motion of incompressible fluid in a circular pipe. Z. Angew. Math. Phys. ZAMP 1956, 7, 403–422. [Google Scholar] [CrossRef]
- Taylor, M. An approach to an analysis of the arterial pulse wave II. Fluid oscillations in an elastic pipe. Phys. Med. Biol. 1957, 1, 321. [Google Scholar] [CrossRef] [PubMed]
- Sergeev, S. Fluid oscillations in pipes at moderate Reynolds numbers. Fluid Dyn. 1966, 1, 121–122. [Google Scholar] [CrossRef]
- Ramaprian, B.; Tu, S.W. An experimental study of oscillatory pipe flow at transitional Reynolds numbers. J. Fluid Mech. 1980, 100, 513–544. [Google Scholar] [CrossRef]
- Harris, J.; Maheshwari, R. Oscillatory pipe flow: A comparison between predicted and observed displacement profiles. Rheol. Acta 1975, 14, 162–168. [Google Scholar] [CrossRef]
- Hino, M.; Sawamoto, M.; Takasu, S. Experiments on transition to turbulence in an oscillatory pipe flow. J. Fluid Mech. 1976, 75, 193–207. [Google Scholar] [CrossRef]
- Wood, W. Transient viscoelastic helical flows in pipes of circular and annular cross-section. J. Non Newton. Fluid Mech. 2001, 100, 115–126. [Google Scholar] [CrossRef]
- Yin, Y.; Zhu, K.Q. Oscillating flow of a viscoelastic fluid in a pipe with the fractional Maxwell model. Appl. Math. Comp. 2006, 173, 231–242. [Google Scholar] [CrossRef]
- Yang, D.; Zhu, K.Q. Start-up flow of a viscoelastic fluid in a pipe with a fractional Maxwell’s model. Comp. Math. Appl. 2010, 60, 2231–2238. [Google Scholar] [CrossRef]
- Shah, S.H.A.M.; Qi, H. Starting solutions for a viscoelastic fluid with fractional Burgers’ model in an annular pipe. Nonlinear Anal. Real World Appl. 2010, 11, 547–554. [Google Scholar] [CrossRef]
- Nazar, M.; Fetecau, C.; Awan, A. A note on the unsteady flow of a generalized second-grade fluid through a circular cylinder subject to a time dependent shear stress. Nonlinear Anal. Real World Appl. 2010, 11, 2207–2214. [Google Scholar] [CrossRef]
- Qi, H.; Liu, J. Some duct flows of a fractional Maxwell fluid. Eur. Phys. J. Spec. Top. 2011, 193, 71–79. [Google Scholar] [CrossRef]
- Khandelwal, K.; Mathur, V. Exact solutions for an unsteady flow of viscoelastic fluid in cylindrical domains using the fractional Maxwell model. Int. J. Appl. Comput. Math. 2015, 1, 143–156. [Google Scholar] [CrossRef][Green Version]
- Mathur, V.; Khandelwal, K. Exact Solutions for the Flow of Fractional Maxwell Fluid in Pipe-Like Domains. Adv. Appl. Math. Mech. 2016, 8, 784–794. [Google Scholar] [CrossRef]
- Maqbool, K.; Mann, A.; Siddiqui, A.M.; Shaheen, S. Fractional generalized Burgers’ fluid flow due to metachronal waves of cilia in an inclined tube. Adv. Mech. Eng. 2017, 9, 1687814017715565. [Google Scholar] [CrossRef]
- Tang, Y.; Zhen, Y.; Fang, B. Nonlinear vibration analysis of a fractional dynamic model for the viscoelastic pipe conveying fluid. Appl. Math. Model. 2018, 56, 123–136. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, Y. Dynamic Analysis of the Viscoelastic Pipeline Conveying Fluid with an Improved Variable Fractional Order Model Based on Shifted Legendre Polynomials. Fractal Fract. 2019, 3, 52. [Google Scholar] [CrossRef]
- Javadi, M.; Noorian, M.; Irani, S. Stability analysis of pipes conveying fluid with fractional viscoelastic model. Meccanica 2019, 54, 399–410. [Google Scholar] [CrossRef]
- Sun, H.; Zhang, Y.; Baleanu, D.; Chen, W.; Chen, Y. A new collection of real world applications of fractional calculus in science and engineering. Commun. Nonlinear Sci. Num. Simulat. 2018, 64, 213–231. [Google Scholar] [CrossRef]
- Crandall, I.B. Theory of Vibrating Systems and Sound; D. Van Nostrand Company: New York, NY, USA, 1926. [Google Scholar]
- Urbanowicz, K.; Duan, H.F.; Bergant, A.; Urbanowicz, K.; Bergant, H.F.D.A. Transient Liquid Flow in Plastic Pipes. STROJNISKI VESTNIK J. Mech. Eng. 2020, 66, 77–90. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gritsenko, D.; Paoli, R. Theoretical Analysis of Fractional Viscoelastic Flow in Circular Pipes: General Solutions. Appl. Sci. 2020, 10, 9093. https://doi.org/10.3390/app10249093
Gritsenko D, Paoli R. Theoretical Analysis of Fractional Viscoelastic Flow in Circular Pipes: General Solutions. Applied Sciences. 2020; 10(24):9093. https://doi.org/10.3390/app10249093
Chicago/Turabian StyleGritsenko, Dmitry, and Roberto Paoli. 2020. "Theoretical Analysis of Fractional Viscoelastic Flow in Circular Pipes: General Solutions" Applied Sciences 10, no. 24: 9093. https://doi.org/10.3390/app10249093
APA StyleGritsenko, D., & Paoli, R. (2020). Theoretical Analysis of Fractional Viscoelastic Flow in Circular Pipes: General Solutions. Applied Sciences, 10(24), 9093. https://doi.org/10.3390/app10249093





