Development of Post Processing for Wave Propagation Problem: Response Filtering Method
Abstract
1. Introduction
2. Finite Element Analysis for the Transient Stress Response
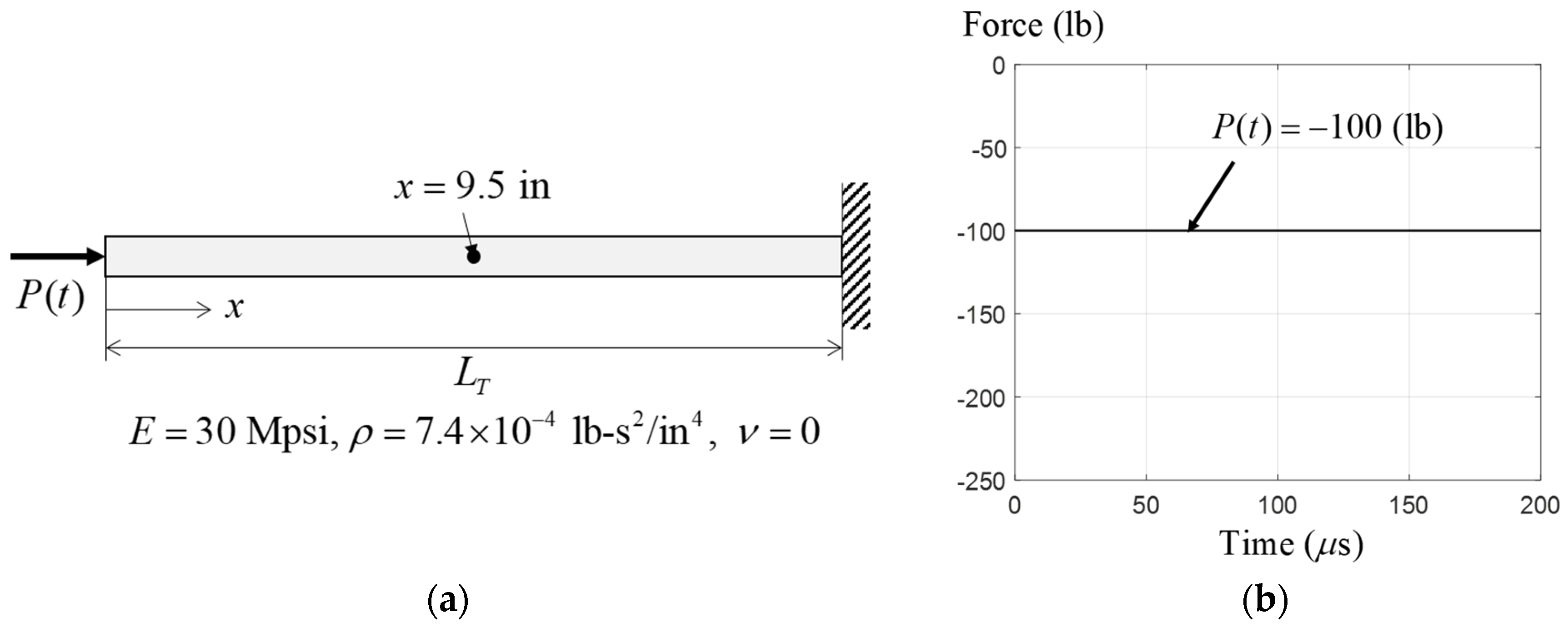
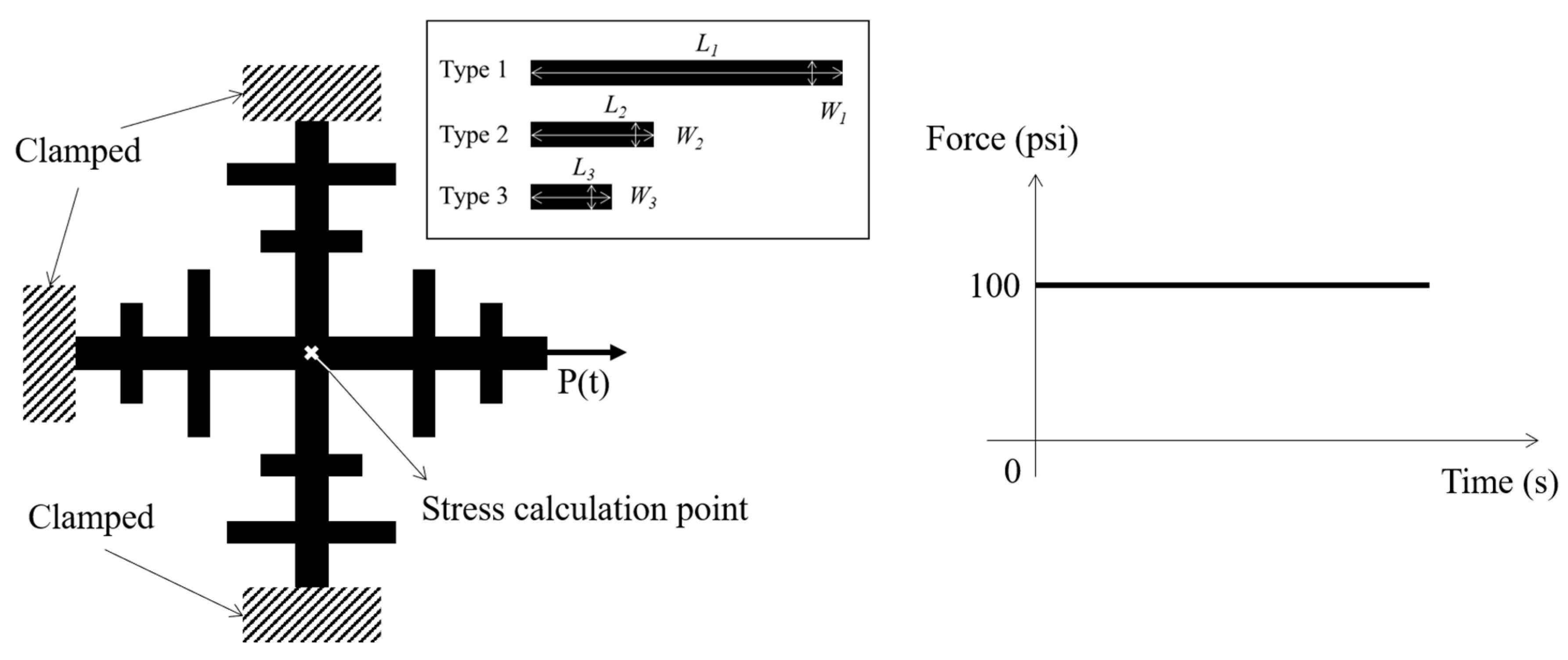
2.1. Transient Finite Element Simulation
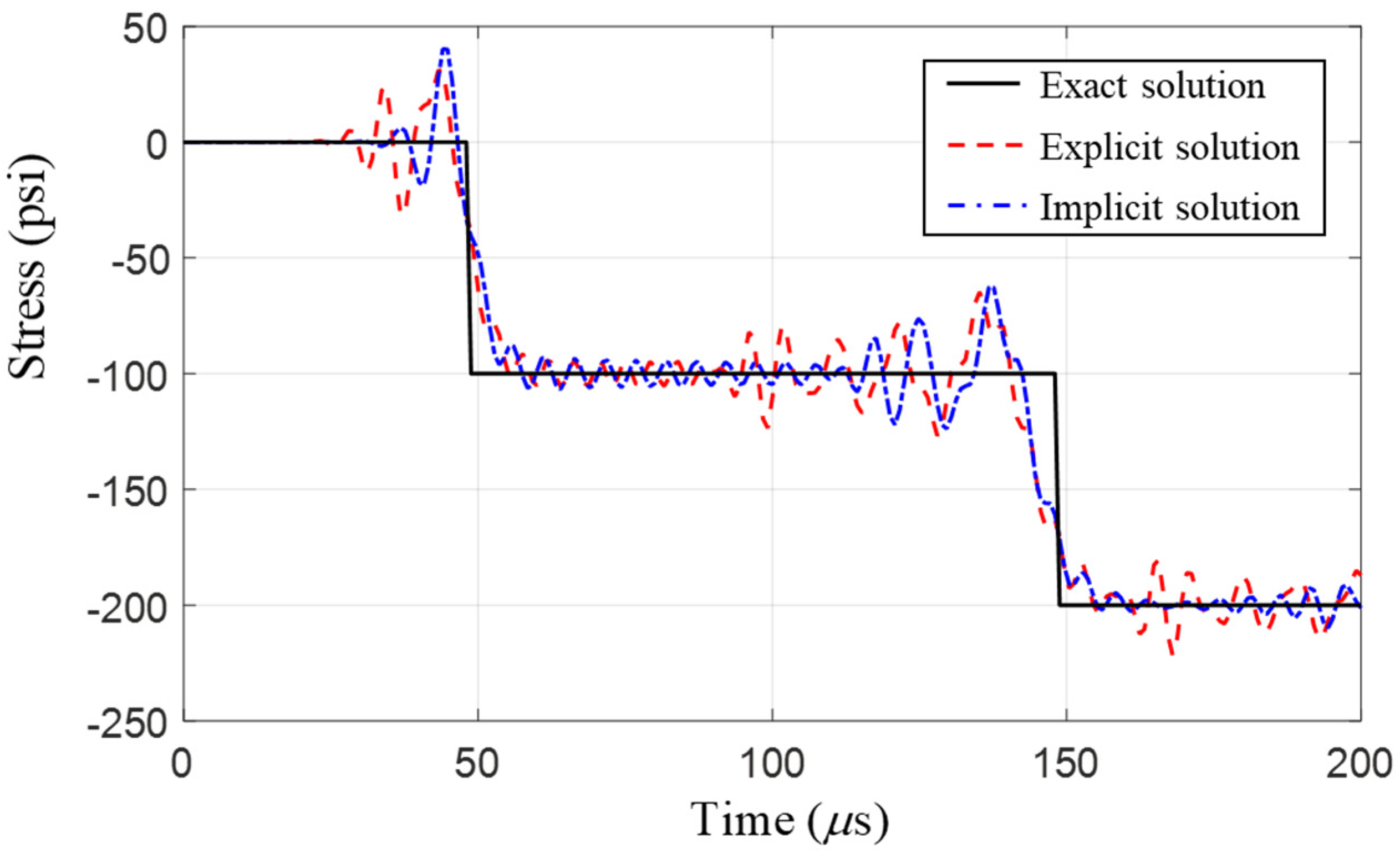
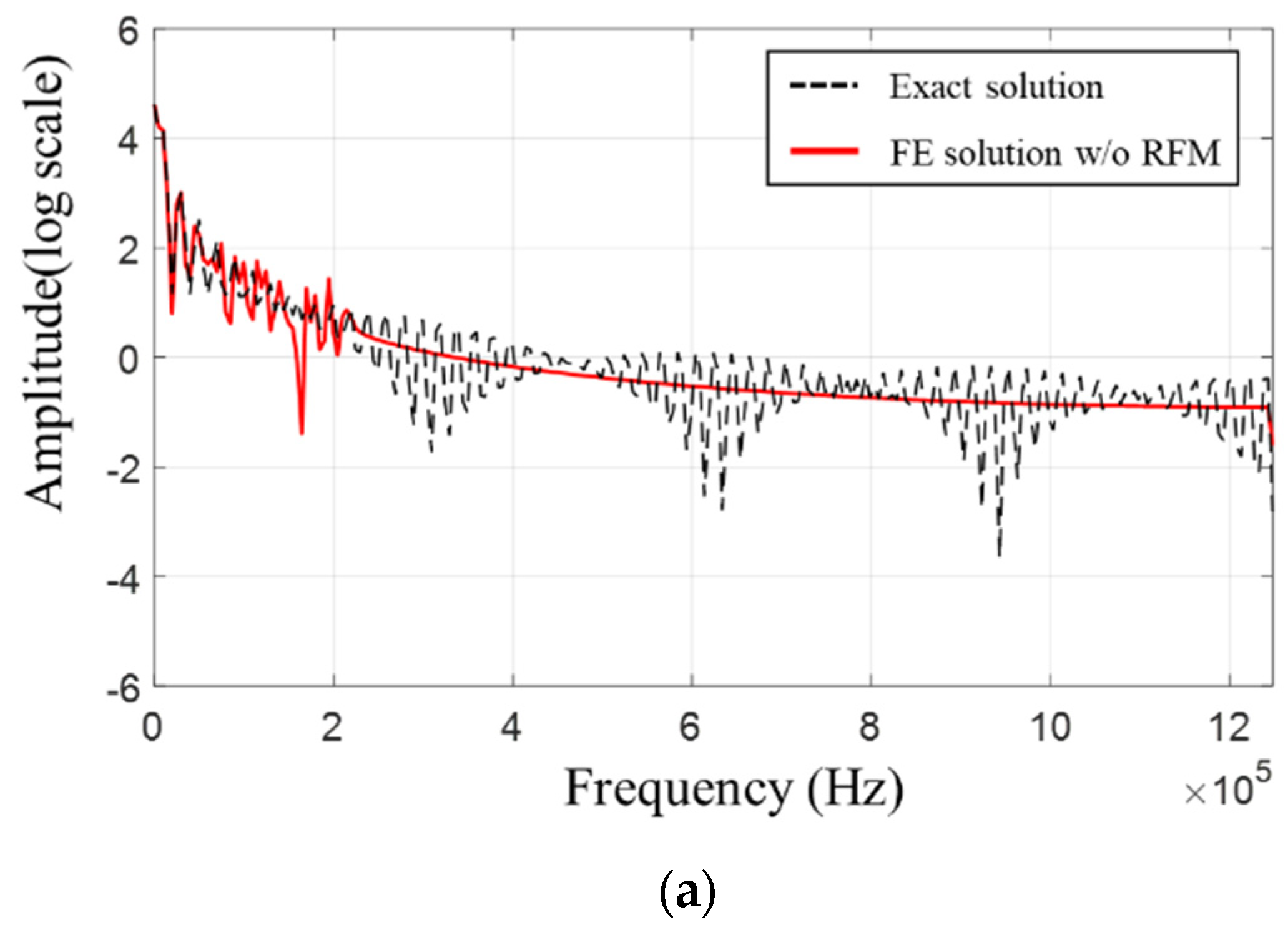
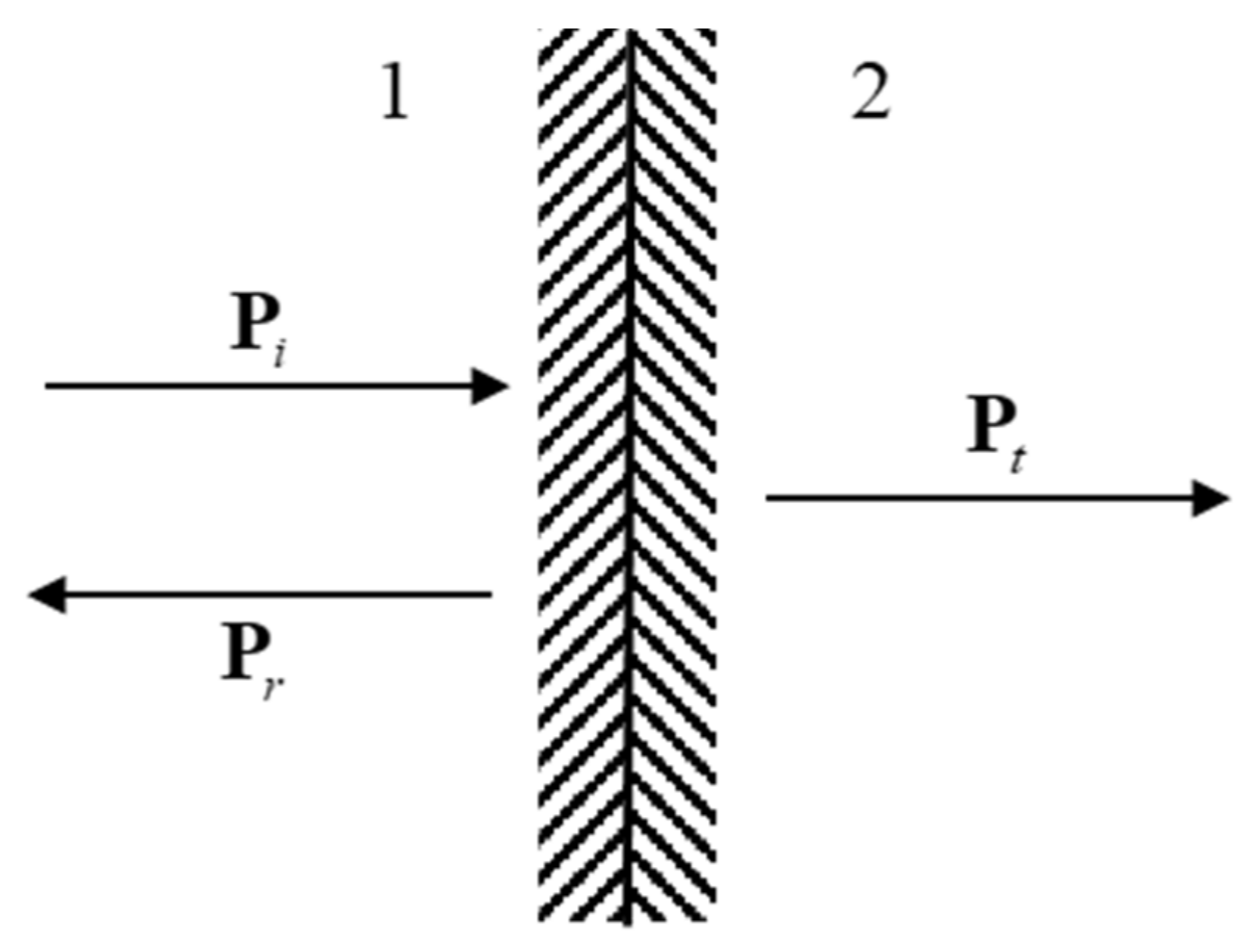
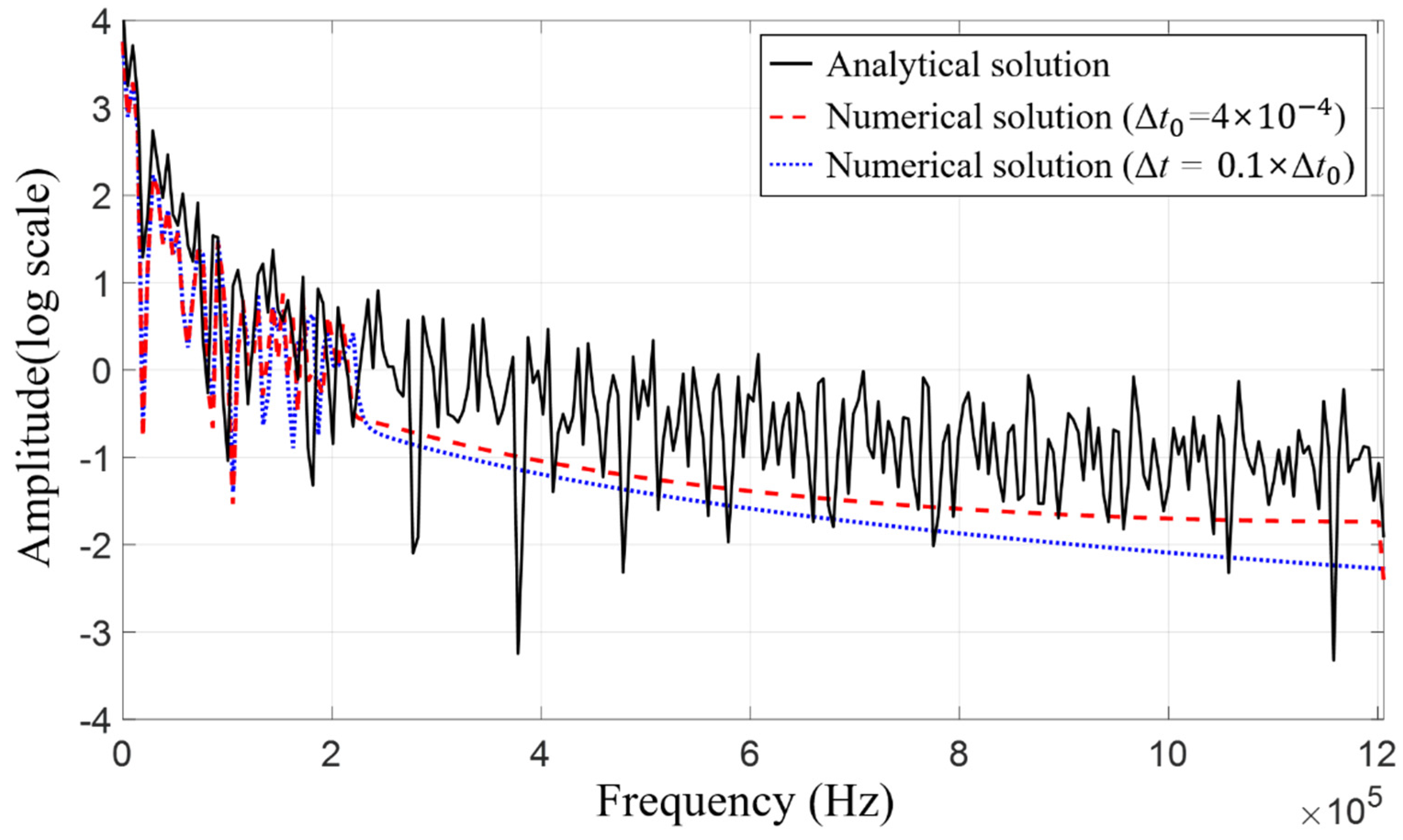
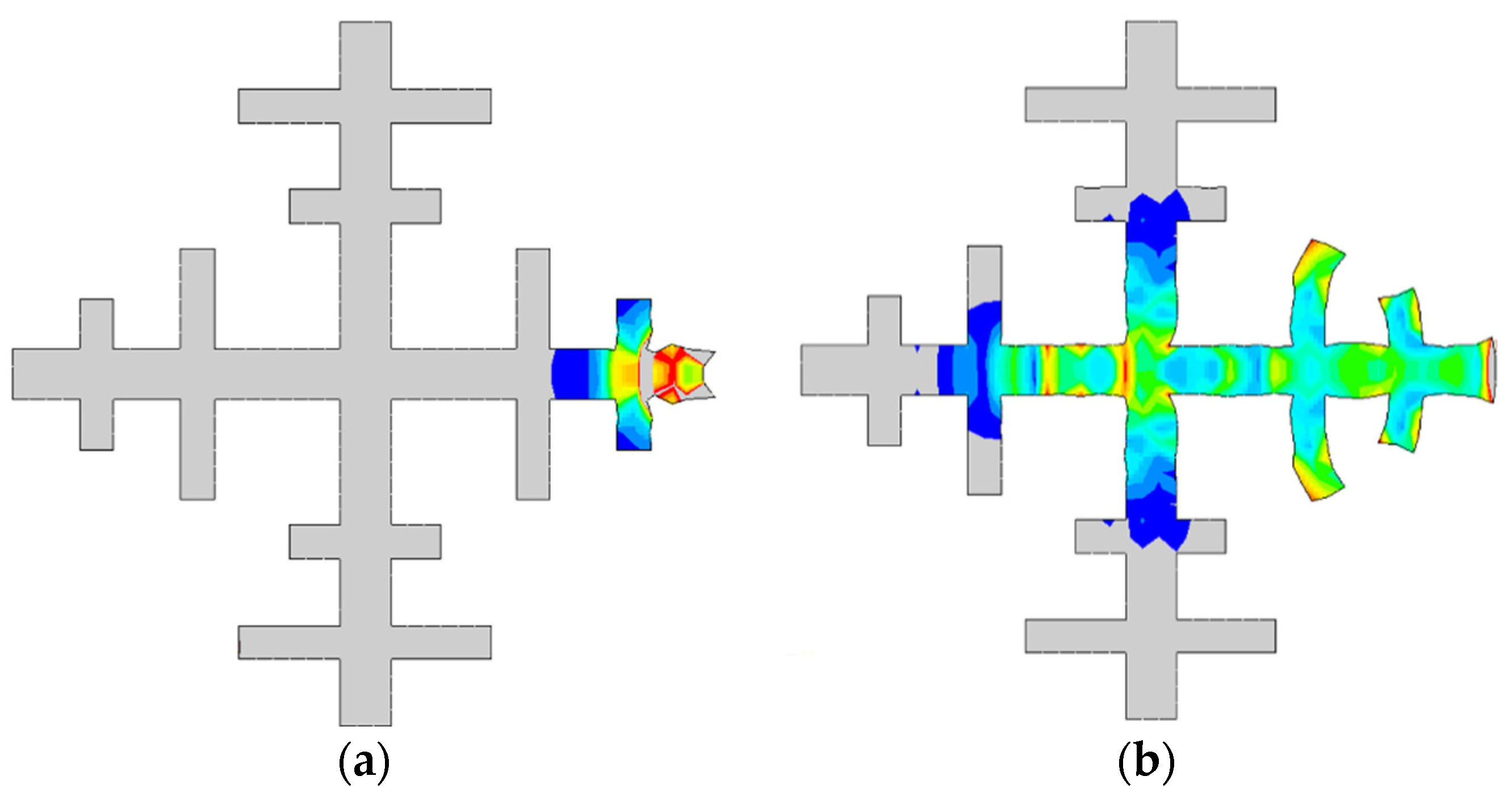
2.2. Wave Propagation Analysis and Gibb’s Phenomenon
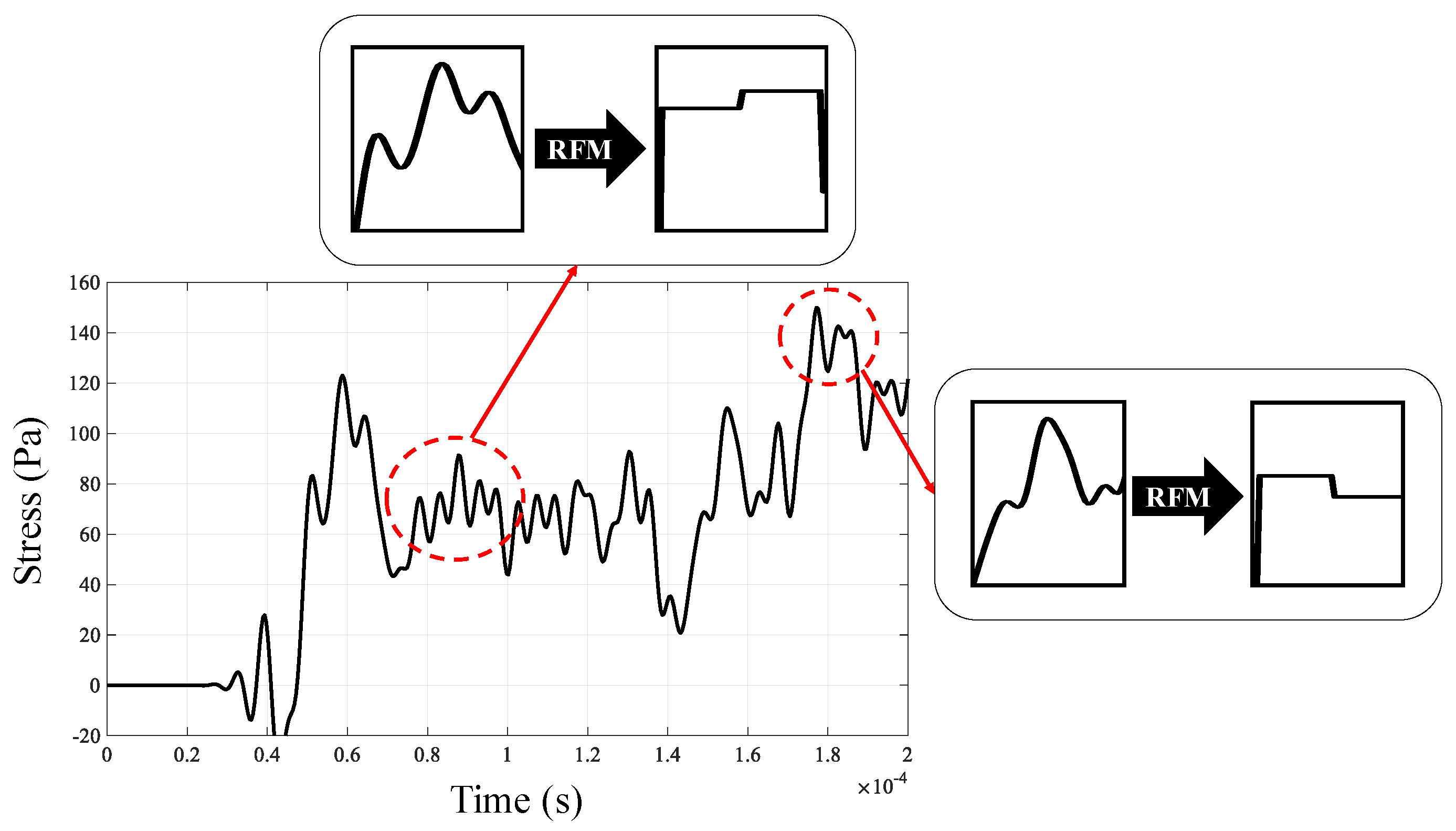
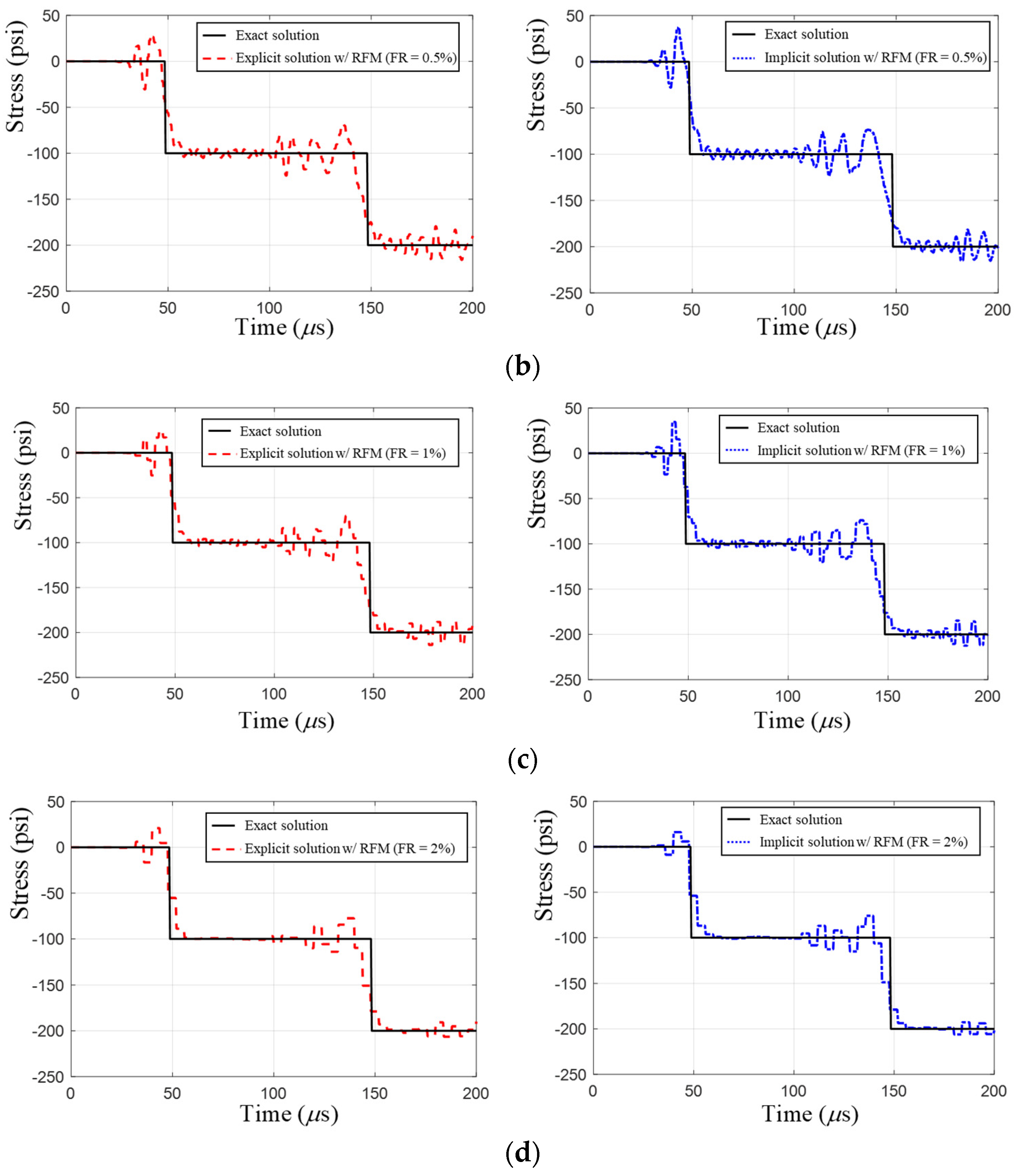
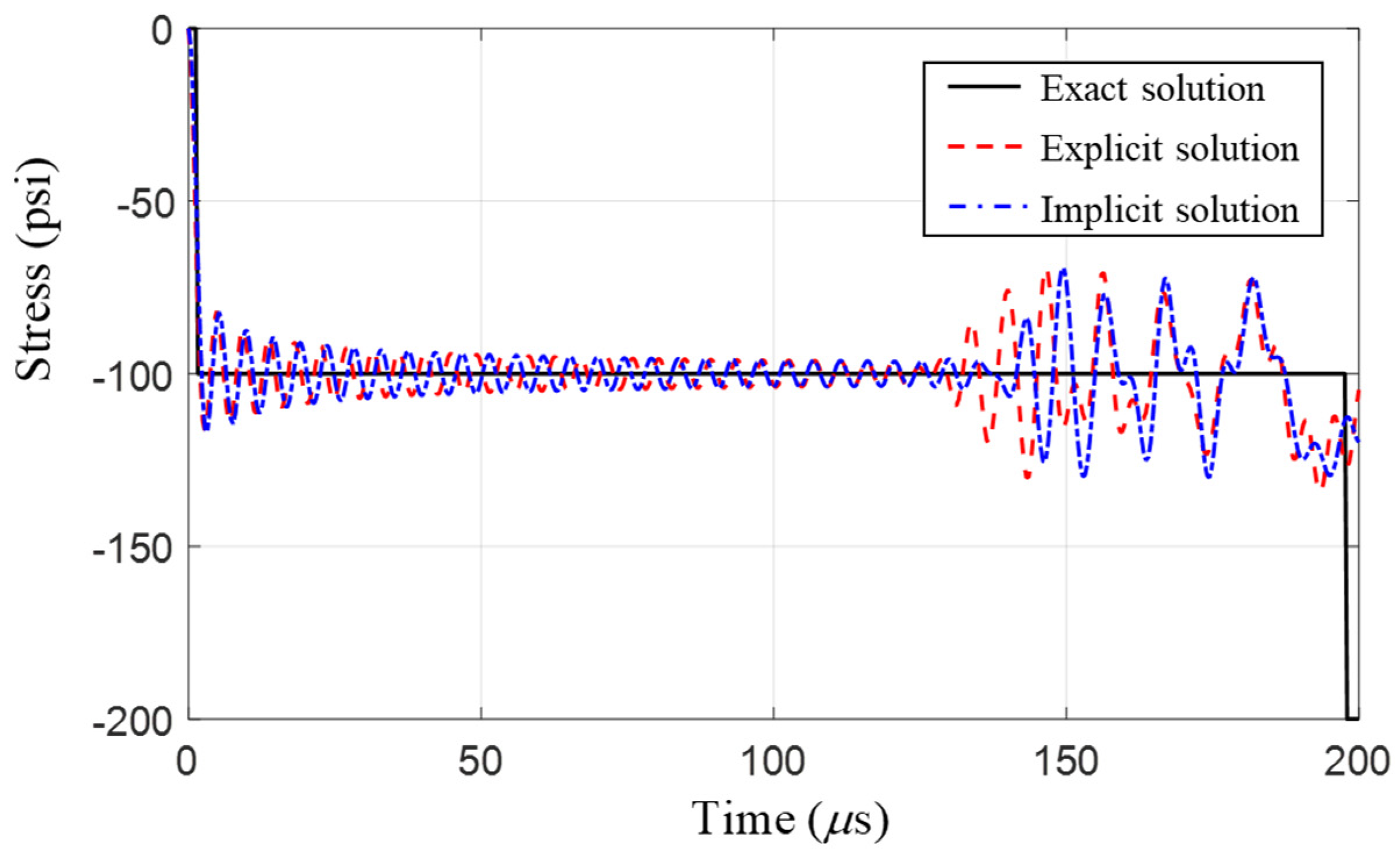
3. Response Filtering Method for Improved Transient Stress
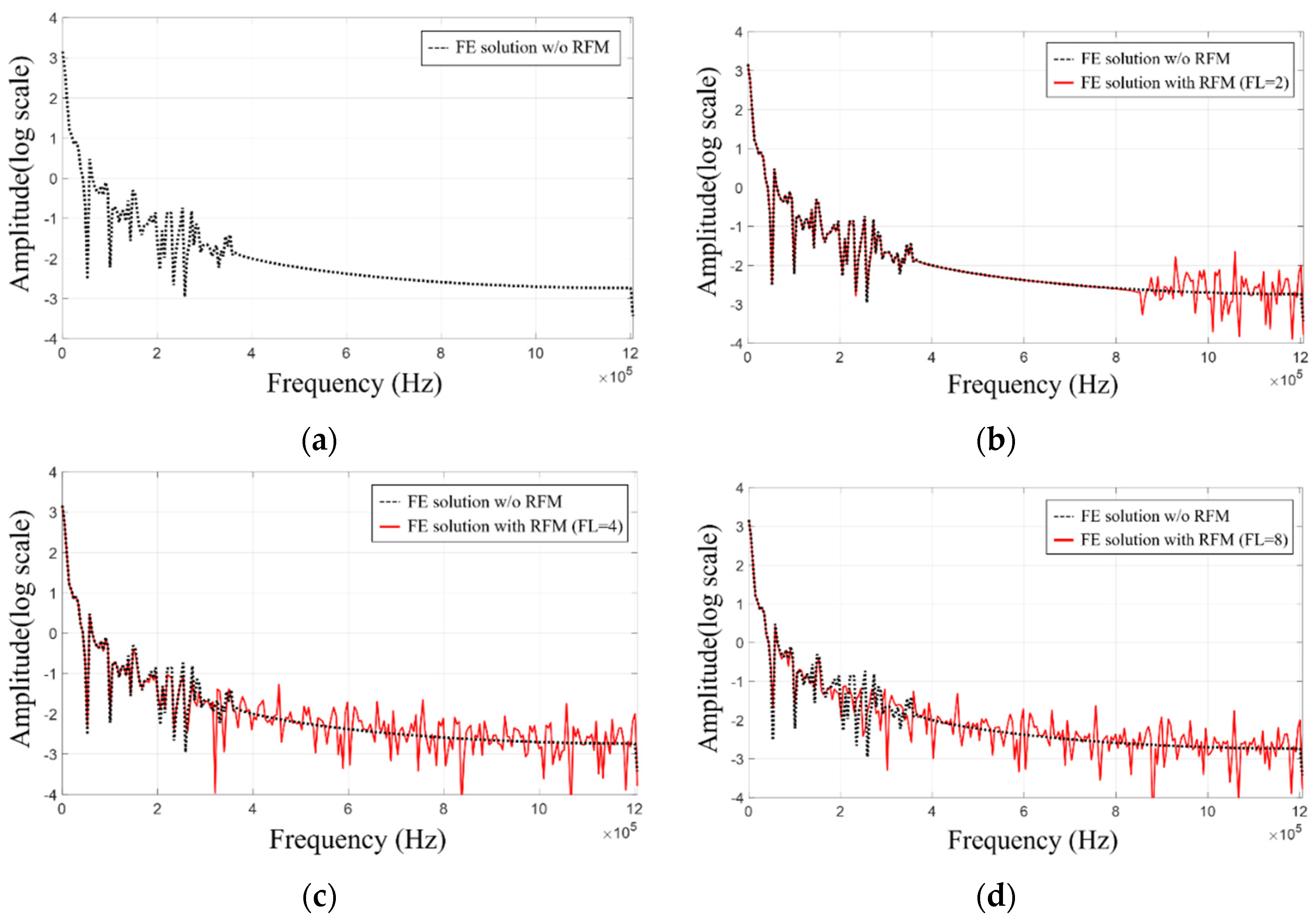
3.1. Response Filtering Method
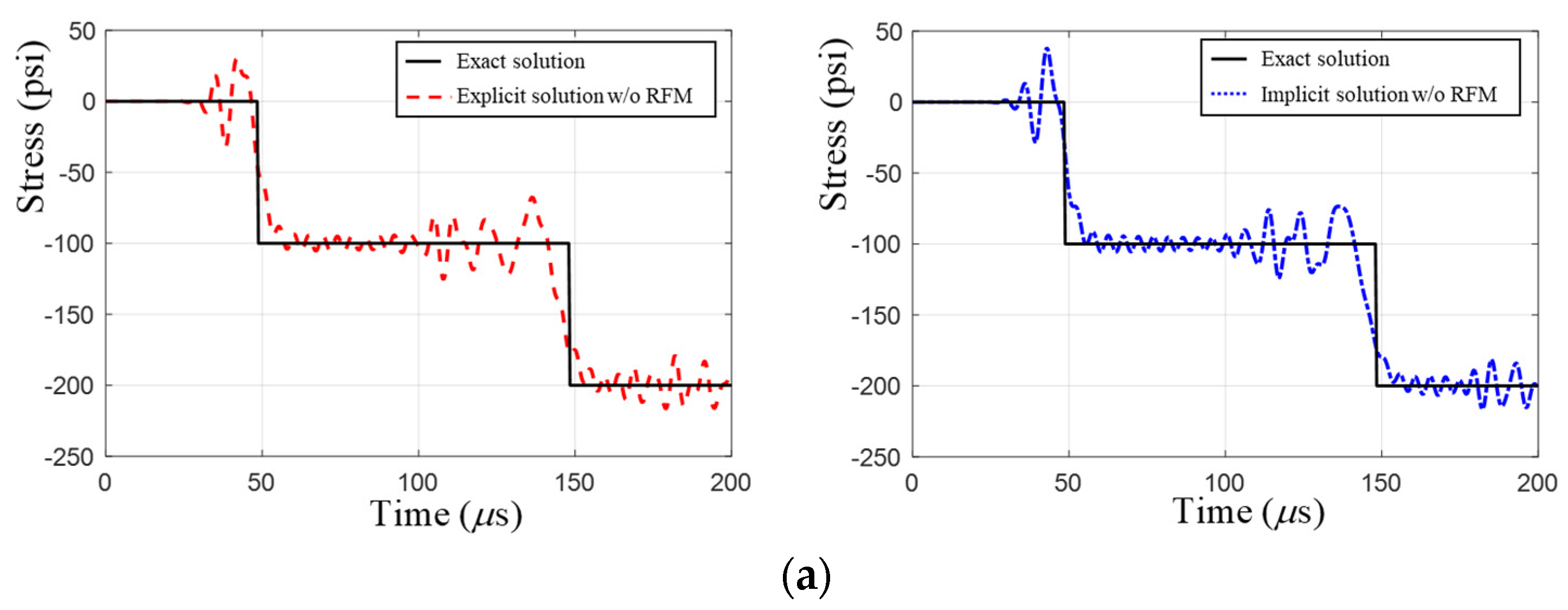
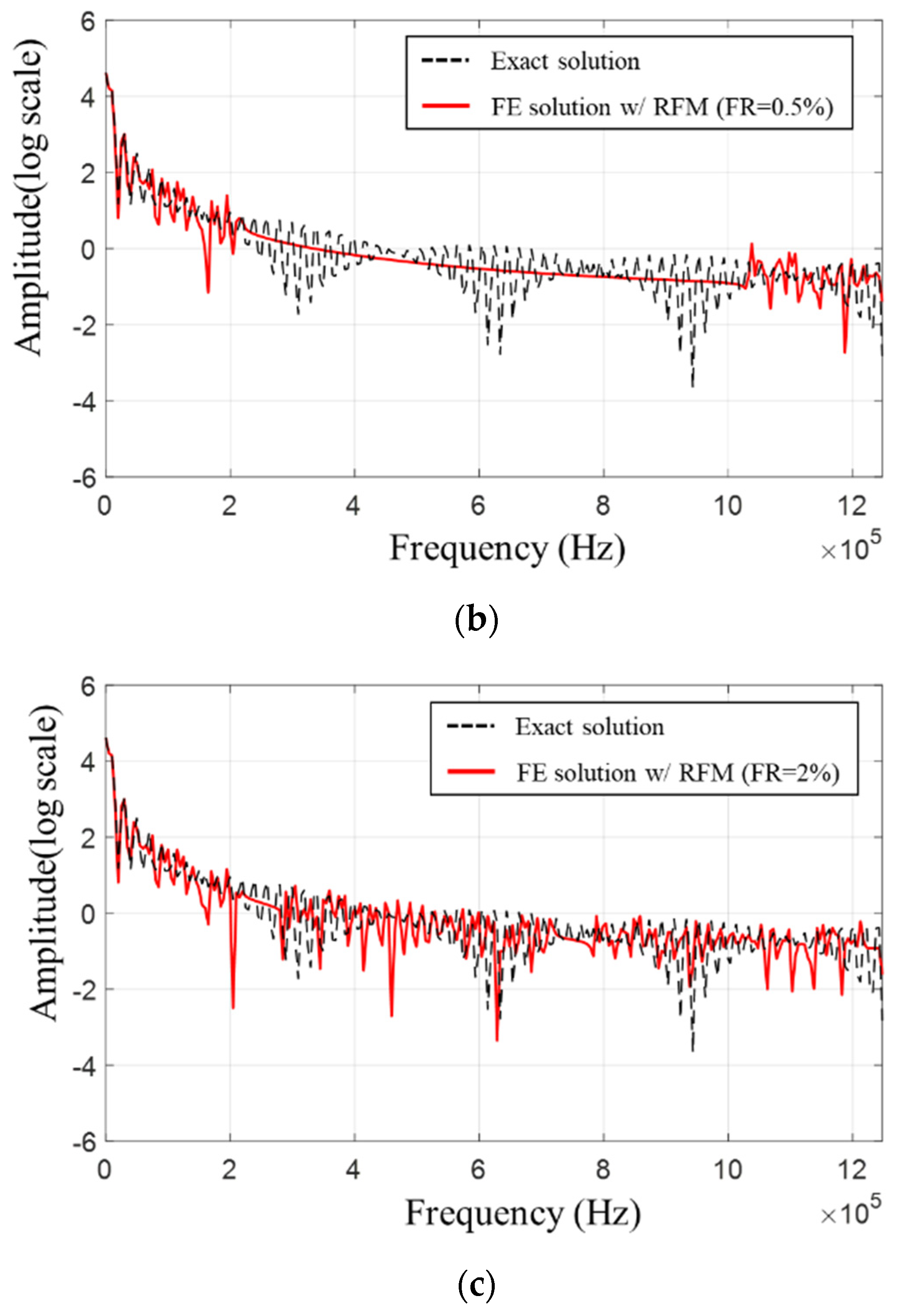
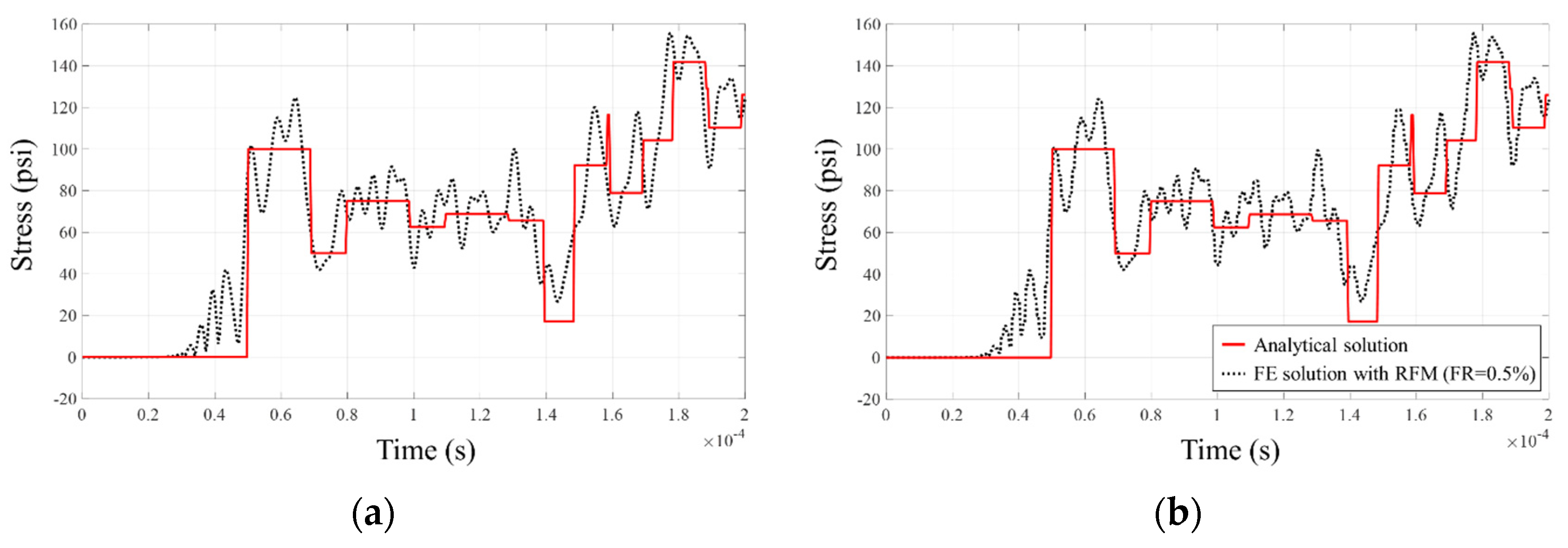
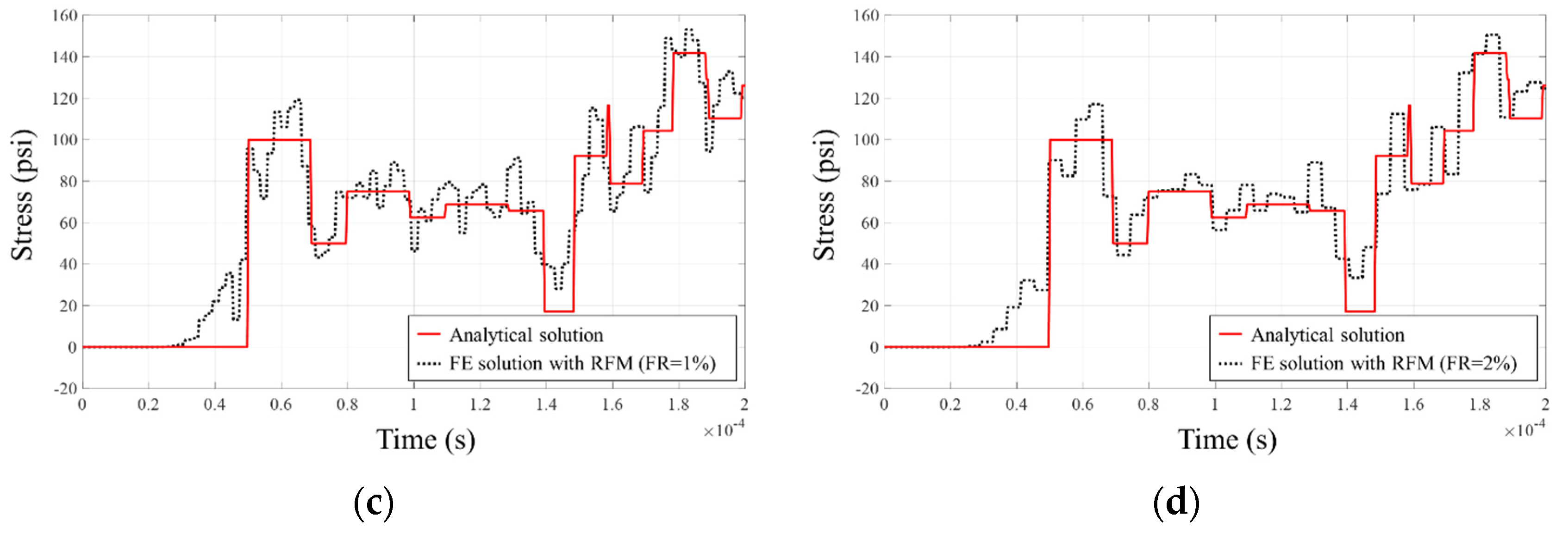
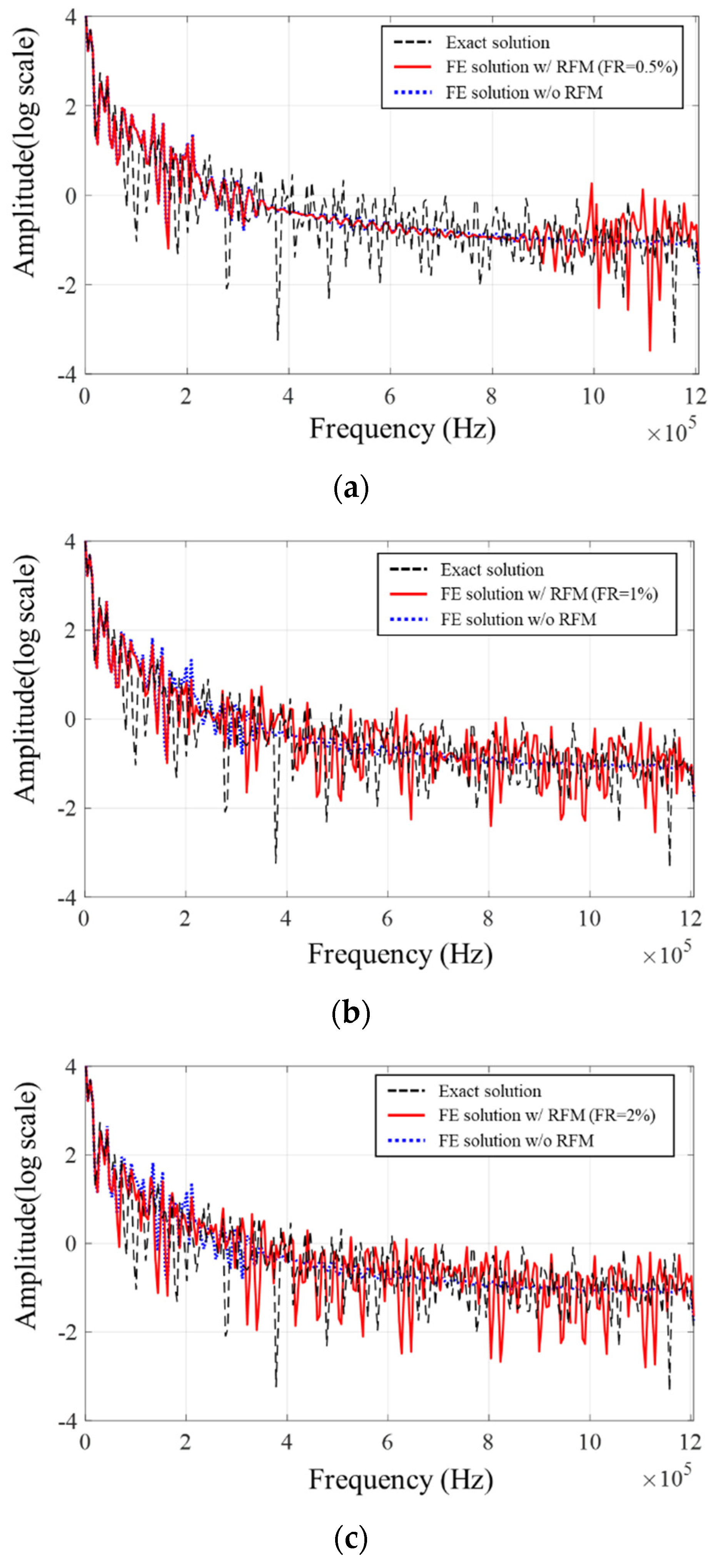
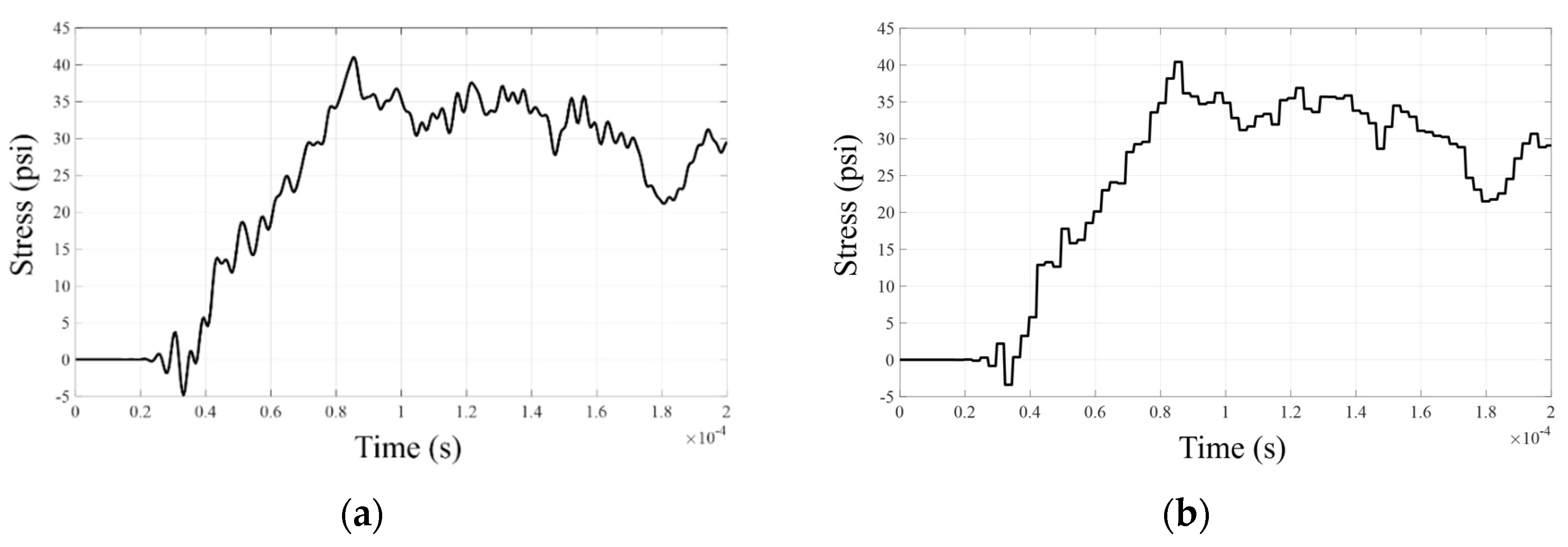
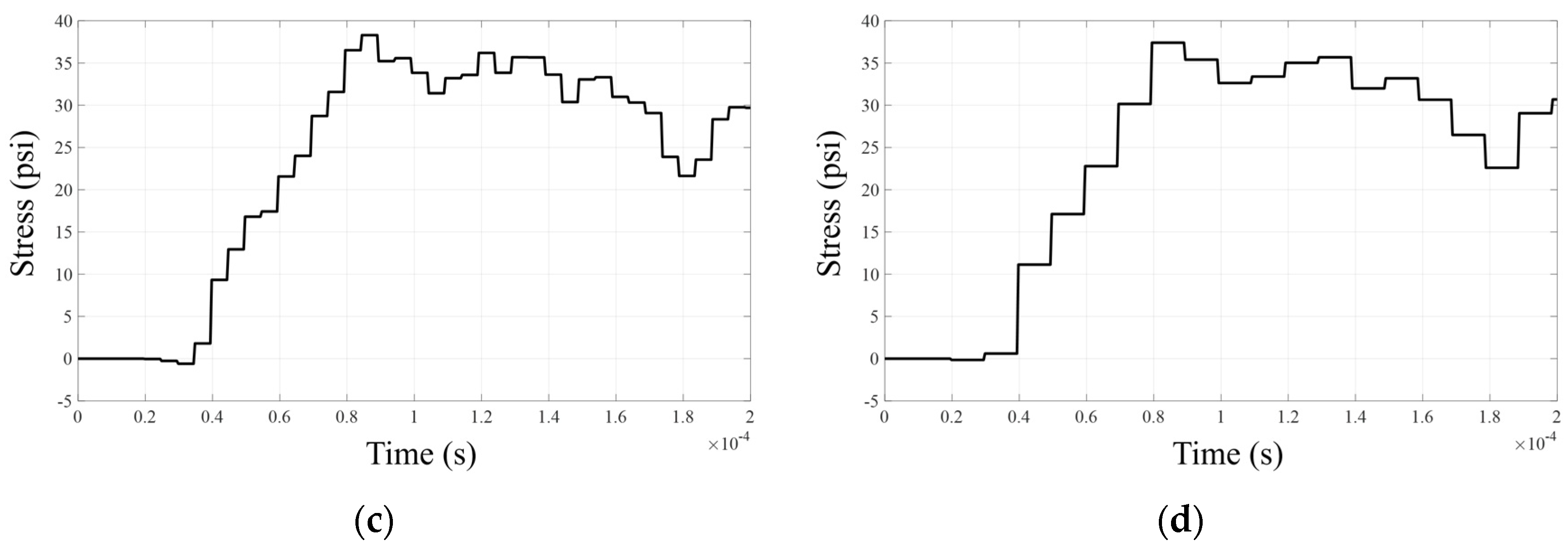
3.2. Analysis of the Accuracy Improvement with the Response Filtering Method
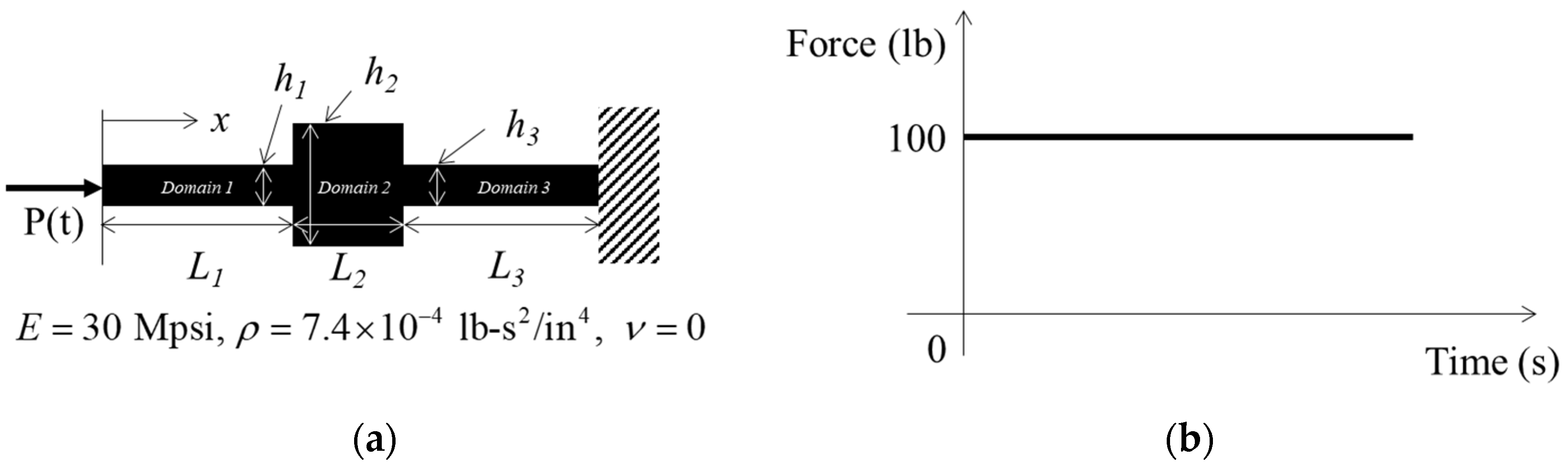
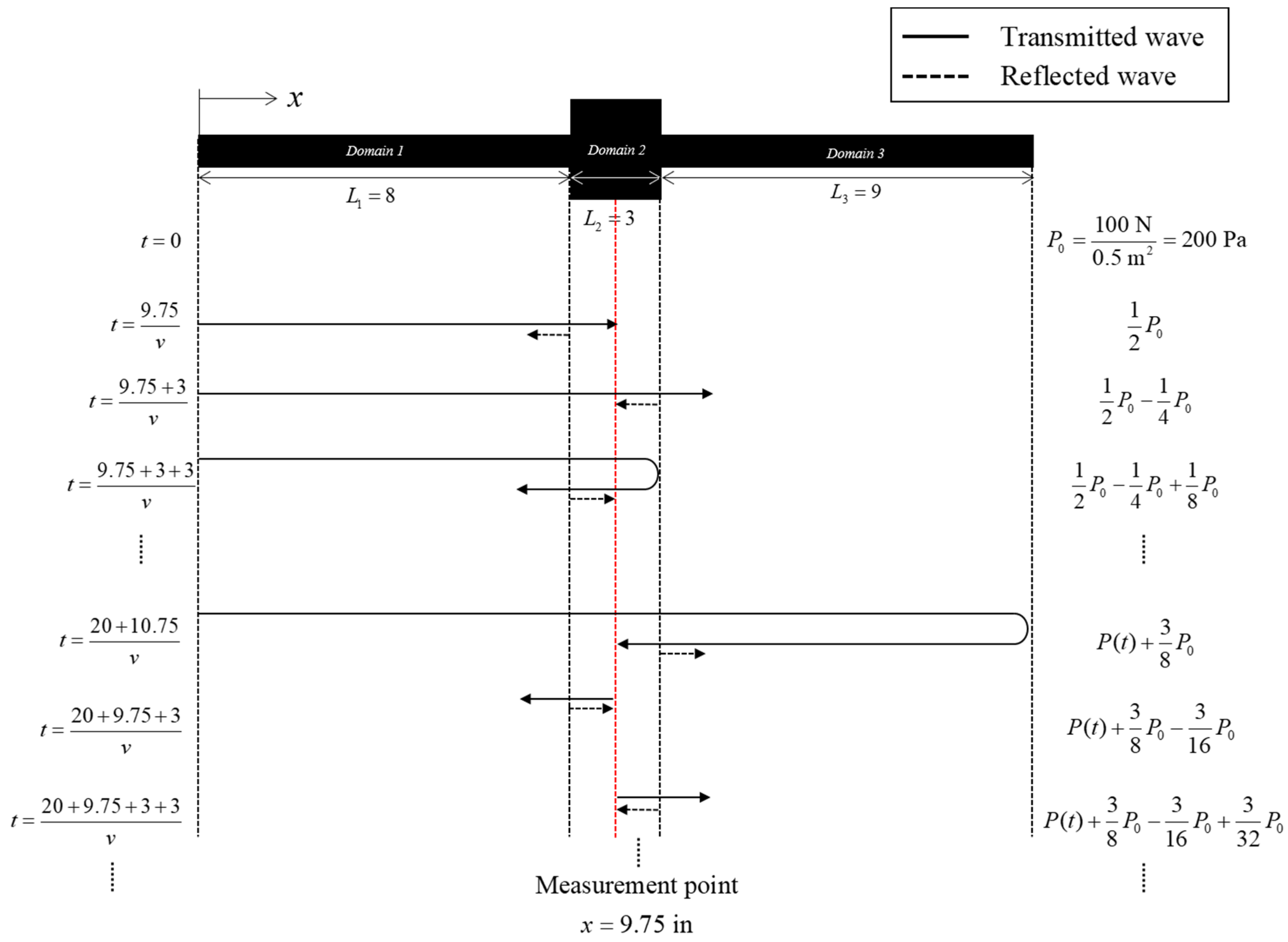
4. Numerical Examples
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kolsky, H. Stress waves in solids. J. Sound Vib. 1964, 1, 88–110. [Google Scholar] [CrossRef]
- Kang, W.J.; Huh, H. Crash Analysis of Auto-Body Structures Considering the Strain-Rate Hardening Effect; SAE International: Warrendale, PA, USA, 2000. [Google Scholar]
- Bathe, K.-J. Finite Element Procedures; Prentice Hall: Upper Saddle River, NJ, USA, 2006. [Google Scholar]
- Bathe, K.-J.; Noh, G. Insight into an implicit time integration scheme for structural dynamics. Comput. Struct. 2012, 98, 1–6. [Google Scholar] [CrossRef]
- Cook, R.D. Concepts and Applications of Finite Element Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Logan, D.L. A First Course in the Finite Element Method; Cengage Learning: Boston, MA, USA, 2011. [Google Scholar]
- Kolsky, H. Stress Waves in Solids; Courier Corporation: Chelmsford, MA, USA, 1963; Volume 1098. [Google Scholar]
- Givoli, D.; Harari, I. Special issue on new computational methods for wave propagation. Wave Motion 2004, 4, 279–280. [Google Scholar] [CrossRef]
- Cho, S.; Huh, H.; Park, K. A time-discontinuous implicit variational integrator for stress wave propagation analysis in solids. Comput. Methods Appl. Mech. Eng. 2011, 200, 649–664. [Google Scholar] [CrossRef]
- Chung, J.; Hulbert, G.M. A Time Integration Algorithm for Structural Dynamics With Improved Numerical Dissipation: The Generalized-α Method. J. Appl. Mech. 1993, 60, 371–375. [Google Scholar] [CrossRef]
- Reed, W.H.; Hill, T. Triangular Mesh Methods for the Neutron Transport Equation; Los Alamos Scientific Lab.: Los Alamos, NM, USA, 1973.
- Hughes, T.J.; Hulbert, G.M. Space-time finite element methods for elastodynamics: Formulations and error estimates. Comput. Methods Appl. Mech. Eng. 1988, 66, 339–363. [Google Scholar] [CrossRef]
- Hulbert, G.M.; Hughes, T.J. Space-time finite element methods for second-order hyperbolic equations. Comput. Methods Appl. Mech. Eng. 1990, 84, 327–348. [Google Scholar] [CrossRef]
- Arnold, D.N.; Brezzi, F.; Cockburn, B.; Marini, L.D. Unified analysis of discontinuous Galerkin methods for elliptic problems. Siam J. Numer. Anal. 2002, 39, 1749–1779. [Google Scholar] [CrossRef]
- Huang, H.; Costanzo, F. On the use of space–time finite elements in the solution of elasto-dynamic problems with strain discontinuities. Comput. Methods Appl. Mech. Eng. 2002, 191, 5315–5343. [Google Scholar] [CrossRef]
- Ham, S.; Bathe, K.-J. A finite element method enriched for wave propagation problems. Comput. Struct. 2012, 94, 1–12. [Google Scholar] [CrossRef]
- Noh, G.; Bathe, K.-J. An explicit time integration scheme for the analysis of wave propagations. Comput. Struct. 2013, 129, 178–193. [Google Scholar] [CrossRef]
- Mullen, R.; Belytschko, T. Dispersion analysis of finite element semidiscretizations of the two-dimensional wave equation. Int. J. Numer. Methods Eng. 1982, 18, 11–29. [Google Scholar] [CrossRef]
- Krenk, S. Dispersion-corrected explicit integration of the wave equation. Comput. Methods Appl. Mech. Eng. 2001, 191, 975–987. [Google Scholar] [CrossRef]
- Christon, M.A. The influence of the mass matrix on the dispersive nature of the semi-discrete, second-order wave equation. Comput. Methods Appl. Mech. Eng. 1999, 173, 147–166. [Google Scholar] [CrossRef]
- Idesman, A.; Schmidt, M.; Foley, J. Accurate finite element modeling of linear elastodynamics problems with the reduced dispersion error. Comput. Mech. 2011, 47, 555–572. [Google Scholar] [CrossRef]
- Guddati, M.N.; Yue, B. Modified integration rules for reducing dispersion error in finite element methods. Comput. Methods Appl. Mech. Eng. 2004, 193, 275–287. [Google Scholar] [CrossRef]
- Idesman, A.; Samajder, H.; Aulisa, E.; Seshaiyer, P. Benchmark problems for wave propagation in elastic materials. Comput. Mech. 2009, 43, 797–814. [Google Scholar] [CrossRef]
- Holmes, N.; Belytschko, T. Postprocessing of finite element transient response calculations by digital filters. Comput. Struct. 1976, 6, 211–216. [Google Scholar] [CrossRef]
- Pryor, R.W. Multiphysics Modeling Using COMSOL®: A First Principles Approach; Jones & Bartlett Publishers: Burlington, MA, USA, 2009. [Google Scholar]
- Stolarski, T.; Nakasone, Y.; Yoshimoto, S. Engineering Analysis with ANSYS Software; Butterworth-Heinemann: Oxford, UK, 2018. [Google Scholar]
- Davison, L. Fundamentals of Shock Wave Propagation in Solids; Springer Science & Business Media: Berlin, Germany, 2008. [Google Scholar]
| (a) | ||||||||
| Central-difference method | ||||||||
| Filtering ratio (%) | w/o RFM | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 |
| Error indicator | 1.8472 | 1.8283 | 1.7097 | 1.5967 | 1.3808 | 1.2124 | 1.2241 | 1.1895 |
| Number of over (under) shoots | 67 | 65 | 58 | 45 | 28 | 21 | 19 | 19 |
| Newmark’s method | ||||||||
| Filtering ratio (%) | w/o RFM | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 |
| Error indicator | 1.7223 | 1.7053 | 1.5941 | 1.4387 | 1.3123 | 1.1205 | 1.1937 | 1.1340 |
| Number of over (under) shoots | 65 | 65 | 65 | 49 | 27 | 20 | 20 | 19 |
| (b) | ||||||||
| Central-difference method | ||||||||
| Filtering ratio (%) | w/o RFM | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 |
| Error indicator | 1.7883 | 1.7539 | 1.6543 | 1.4968 | 1.3046 | 1.3640 | 1.2136 | 1.0409 |
| Number of over (under) shoots | 65 | 64 | 59 | 41 | 26 | 19 | 19 | 17 |
| Newmark’s method | ||||||||
| Filtering ratio (%) | w/o RFM | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 |
| Error indicator | 1.7876 | 1.7515 | 1.6510 | 1.4962 | 1.3064 | 1.3618 | 1.2165 | 1.0495 |
| Number of over (under) shoots | 65 | 64 | 59 | 41 | 26 | 19 | 19 | 17 |
| Central-difference method | ||||||||
| Filtering ratio (%) | w/o RFM | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 |
| Error indicator | 1.6710 | 1.6400 | 1.5039 | 1.3723 | 1.0918 | 1.1012 | 0.9666 | 0.9809 |
| Number of over (under) shoots | 73 | 73 | 73 | 47 | 19 | 15 | 23 | 23 |
| Newmark’s method | ||||||||
| Filtering ratio (%) | w/o RFM | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 |
| Error indicator | 1.6025 | 1.5811 | 1.4269 | 1.3339 | 1.1746 | 0.9752 | 0.9827 | 0.9688 |
| Number of over (under) shoots | 71 | 71 | 71 | 51 | 21 | 13 | 21 | 23 |
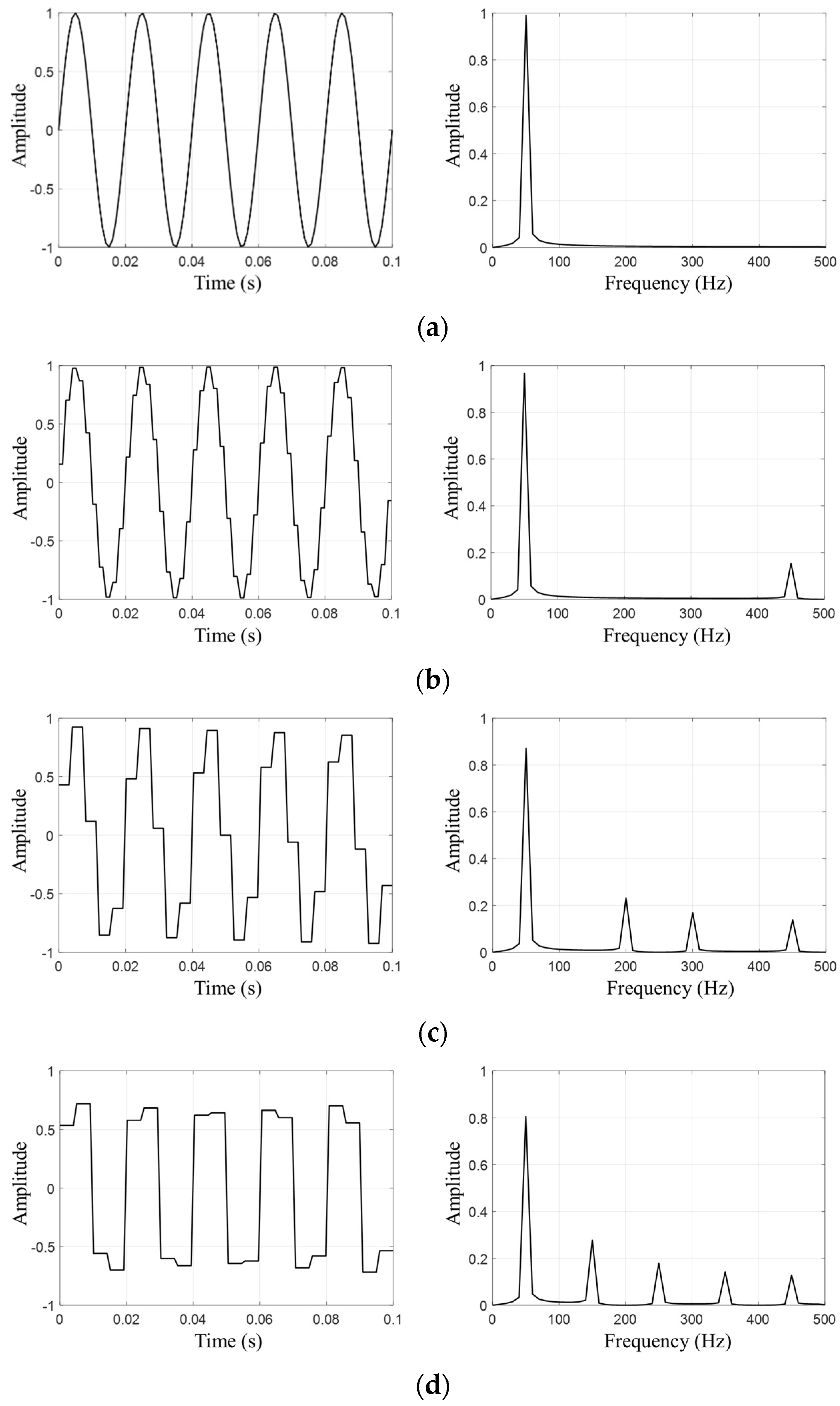
| 1 | 50 Hz |
| 2 | 50 Hz, 450 Hz |
| 4 | 50 Hz, 200 Hz, 300 Hz, 450 Hz |
| 5 | 50 Hz, 150 Hz, 250 Hz, 350 Hz, 450 Hz |
| Newmark’s Method | ||||||||
|---|---|---|---|---|---|---|---|---|
| Filtering ratio (%) | w/o RFM | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 |
| Error indicator | 2.5622 | 2.5463 | 2.4712 | 2.3883 | 2.3330 | 2.0453 | 2.0096 | 2.0617 |
| Number of over (under) shoots | 40 | 40 | 40 | 34 | 28 | 22 | 22 | 22 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koh, H.S.; Lee, J.W.; Kwon, K.; Yoon, G.H. Development of Post Processing for Wave Propagation Problem: Response Filtering Method. Appl. Sci. 2020, 10, 9032. https://doi.org/10.3390/app10249032
Koh HS, Lee JW, Kwon K, Yoon GH. Development of Post Processing for Wave Propagation Problem: Response Filtering Method. Applied Sciences. 2020; 10(24):9032. https://doi.org/10.3390/app10249032
Chicago/Turabian StyleKoh, Hyeong Seok, Jong Wook Lee, Kiwoon Kwon, and Gil Ho Yoon. 2020. "Development of Post Processing for Wave Propagation Problem: Response Filtering Method" Applied Sciences 10, no. 24: 9032. https://doi.org/10.3390/app10249032
APA StyleKoh, H. S., Lee, J. W., Kwon, K., & Yoon, G. H. (2020). Development of Post Processing for Wave Propagation Problem: Response Filtering Method. Applied Sciences, 10(24), 9032. https://doi.org/10.3390/app10249032






