Abstract
In this paper, the stability problem of a class of multi-agent tracking systems with quasi-cyclic switching topologies is investigated. The existing results of systems with switching topologies are usually achieved based on the assumption that the piecewise constant communication topologies are connected and the switchings are cyclic. The communication topologies are possible to be unconnected and it is difficult to guarantee the topologies switch circularly. The piecewise unconnected topology makes the interactive multi-agent tracking system to be an unstable subsystem over this time interval. In order to relax the assumption constraint, a quasi-cyclic method is proposed, which allows the topologies of multi-agent systems to switch in a less conservative way. Moreover, the stability of the tracking system with the existence of unstable subsystems is analyzed based on switched control theory. It is obtained that the convergence rate is affected by the maximum dwell time of unstable subsystems. Finally, a numerical example is provided to demonstrate the effectiveness of the theoretical results.
1. Introduction
Multi-agent systems (MASs), with entities possessing flexibility and autonomy, have been extensively studied to analyze and simulate complex systems in the past few years [1,2,3,4]. As an essential category of distributed artificial intelligence, MASs have been applied in the field of control engineering, such as the formation of spacecraft systems [5], robot systems [6,7], underwater vehicle systems [8], and unmanned aerial vehicles [9], etc. Tracking approaches for MASs have been widely used in areas of collaborative target tracking [10], convoy protection [11] and defensive navigation [12].
During the multi-agent tracking process, where some tracking agents aim to track the target agent, the communication topology between agents may change or even be unconnected due to obstacles, communication limitations and unknown disturbances. In terms of the case where the communication topology of the agents is connected, the whole interactive multi-agent tracking system is stable, while the unconnected topologies of the agents lead to the intermittent existence of unstable subsystems. In this paper, the division of the stable subsystem and the unstable subsystem results from the change of communication topology. Thus, it is not based on the system of the agent itself, but on the whole system between multiple agents. The time-varying topologies of the agents are generally described as switching topologies. The switching topology is an essential but challenging issue in MASs practical applications. The process of MASs switching topology is usually complicated because many kinds of scenarios must be considered when designing the switching rules [13,14,15,16].
Up to now, some researchers have focused on switching topologies of multi-agent systems, and numerous valuable research results were obtained with different models and control strategies [17,18,19,20,21,22,23]. To be more specific, consensus problems for networks of dynamic agents with switching topologies were addressed in [24,25,26,27]. Multi-agent systems with Lipschitz-type node dynamics was studied in [28], which obtained sufficient conditions for consensus tracking under weakly connected and switched topologies. The authors in [29] achieved exponential tracking of heterogeneous second-order time-varying nonlinear multi-agent systems under directed switching topology through constructing the topology-dependent Lyapunov function and designing appropriate time-varying regulation factors. In [30], a coordinated formation control task was accomplished with an iterative update algorithm based on the nearest neighbor relative distances under the condition that the topology has a spanning tree over iteration intervals with finite lengths. The core of the approaches in [31,32,33] was the achievements of the switching controllability in discrete-time multi-agent systems with time-delays on undirected networks. But, these results only considered multi-agent systems which switch among stable subsystems, in other words, the switching topologies were all-connected.
The complexity is significantly increased if there are unstable subsystems in multi-agent switching systems [34]. The work in [35] focused on a class of cyclic switched nonlinear systems, and achieved the finite-time stability by making the most of the trade-off among impulsive dynamics, initial conditions, and the dynamics of each mode. The authors in [36] discussed the case that switching subsystems were unstable, designed the dwell-time and proposed an event-triggered controller so as to achieve global stability. The multi-agent relay tracking problems with changing the number of agents, jumping of tracking errors, and communication time delays were solved in [37]. However, these studies were based on the premise that the sequence of topologies follows a strict cyclic period.
Based on the above discussions, this paper proposes a quasi-cyclic method that allows the topologies of multi-agent tracking systems with unstable subsystems to switch in a less conservative way. In comparison with the existing literature, the main contributions of the paper are mainly twofold. Firstly, the concept of quasi-cyclic switching signals (QCSS) is introduced to describe a more practical scenario, compared with the multi-agent systems with connected switching topologies [28,29,30,31,32,33] or strict cyclic switching topologies including unconnected cases [35,36,37]. Secondly, the stability of the multi-agent tracking system with both stable subsystems and unstable subsystems is guaranteed as well as the conservativeness of switched system conditions is reduced by finding a set of switching signals with admissible quasi-cyclic signals.
The remainder of the paper is organized as follows. Some preliminaries and the model formulation are presented in Section 2. The switched system with quasi-cyclic switching topologies (QCST) are introduced and the main theoretical results are established and proved in Section 3, followed by the simulation results with illustration of theoretical analysis in Section 4. Finally, the conclusions are drawn in Section 5.
2. Preliminaries and Problem Formulation
2.1. Notations
The following notations are used throughout the paper. Let be the set of nonnegative integers. represents Euclidean norm. refers to the set of all n-dimensional real column vectors. stands for a identity matrix. The Kronecker product is denoted by ⊗, and the operation ⊗ on matrix and matrix results in a block matrix . The floor and ceiling functions are defined as and respectively. refers to the time interval . and stands for the total time length of stable and unstable subsystems from initial time till the present time t, respectively. And the main parameters of the model in this paper are introduced in Table 1.

Table 1.
Nomenclature.
2.2. Graph Theory
In this work, we focus on the overall behavior of dynamic systems relying on interactive communication networks. Each agent can be treated as a node and the path of information interaction between agents can be treated as an edge. Then the whole multi-agent system network can be described by a graph with nodes and edges. There is a communication link between two tracking nodes , if node j is within the communication range of node i. A weighted graph containing N nodes is composed of a node set , an edge set and a weighted adjacency matrix , where i and j denote tracking agents. Nodes within the communication radius of node i are called neighbors of node i, which is denoted as . When node j is out of the communication range of node i (), the connection weight between the two tracking nodes is 0, which is denoted by , otherwise . In this work, we consider each node without self-loop i.e., . Let denote of connection weight between tracking agent i and the target agent, if the former can communicate with the latter, otherwise . Denote the Laplacian matrix of communication topology with target agent as , where
2.3. Problem Formulation
Consider a set of agents committing the task of tracking a target agent, the dynamics of the i-th tracking agent is described as follows:
where , is state vector of the i-th agent, and are dynamic matrices of the system, and is the control input of the i-th tracking agent.
The dynamics of the target agent is described by
where is the state vector of the target agent.
If for any initial condition, the tracking agents in the system presented by Equation (1) can accommodate themselves to the target agent’s state described by Equation (2) with the effect of designed controller such that
then it is said that the tracking agents successfully track the target agent.
In the practical tracking process, due to obstacles or the interference of external communication signals, the communication topology of multi-agent systems is likely to be different over different time intervals. If the topology is connected, the whole interactive tracking system is a stable subsystem over this corresponding time interval, otherwise, it is called unstable subsystems. Additionally, the stable subsystems and the unstable subsystems appear alternately, the switching law of which does not conform to the complete periodicity. Therefore, this paper proposes a quasi-cyclic method to solve this practical problem.
The switching signal is piecewise constant, where is the number of subsystems. is continuous from right everywhere and may be either autonomous or controlled in general. Generally, the more information we know about the switching signals, the more refined conclusions we could obtain.
In practice, switching topologies of the multi-agent tracking systems are usually not arbitrary due to some restrictions of physical entities, such as unknowable environmental impact, component failure and sensors. Therefore, in this section, we assume the switching signals satisfy the following assumption.
Assumption 1.
For a given set , is the length of the period of quasi-switching, and a mapping satisfy
Set . The switching law satisfies the following conditions, let .
- If , ;
- If , ;
- If , ;
- If , .
The switching signal that satisfies Assumption 1 is called quasi-cyclic switching signal. As shown in Table 2, belongs to a quasi-cyclic switching topology set of stable subsystems, belongs to a quasi-cyclic switching topology set of unstable subsystems. Let , be the length of the period of stable subsystems and unstable subsystems respectively, so that .

Table 2.
The schematic table for Assumption 1.
Figure 1 displays a possible case of Table 2, where the quasi-switching follows Assumption 1. As shown in Figure 1, the switching times are represented by , which consist of the switching not only among consecutive stable subsystems or consecutive unstable subsystems but also between stable and unstable subsystems. The time series is introduced to denote the switching times between stable and unstable subsystems. When , the systems are switched between stable and unstable systems.

Figure 1.
Illustration of quasi-cyclic switching times.
3. Controller Design and Stability Analysis
3.1. Controller Design
The distributed controller of i-th tracking agent is designed as
where are the control matrices. is the tracking error between the i-th tracking agent and the j-th tracking agent, is the tracking error between the i-th tracking agent and the target agent.
Define the collective tracking error . Then the error dynamics can be obtained through combining the tracking agent’s dynamics (1), the target agent’s dynamics (2), and the controller (4), which is designed with tracking errors based on distributed control protocol.
where , are the corresponding Laplacian matrices of dynamic graph at tracking time t related to switching signal . Denote , tracking error system (5) is reorganized as
Since , is related to control matrices , , and the Laplacian matrix of tracking topology with target agent , . Thus, according to the definition of successful tracking, the tracking problem can be elaborated as the stability of the above tracking error system.
Then the collective tracking error of the multi-agent system is obtained:
Let , where , such that [38]
where , is the set of a quasi-cyclic switching sets of stable subsystems and unstable subsystems respectively. and , are the eigenvalues of and respectively. and are related to the Laplacian matrix , and control matrix , .
Remark 1.
According to the Equations (4)–(8), the eigenvalue of the subsystem is related to the Laplacian matrices of topology among multiple agents. The positive and negative eigenvalues correspond to the unstable and stable subsystem respectively. Different from cyclic switching in [37], quasi-cyclic switching system does not follow a strict cycle, and could jump from any subsystem in stable quasi-cyclic period to the first subsystem in unstable quasi-cyclic period and vice versa.
3.2. Stability Analysis
Theorem 1.
Consider the multi-agent system (6), if there exist positive numbers , , and such that
where , . and refer to the maximum dwell time of unstable subsystems and the minimum dwell time of stable subsystems, respectively. Then if there exists , which satisfies
the tracking multi-agent system (6) with quasi-cyclic switching signals is exponentially stable, and the rate of stability equals Γ which is a positive number related to γ.
Proof.
Select the Lyapunov candidate for the tracking system (6) as
According to the collective tracking error of the multi-agent system (7), it has
Without loss of generality, suppose the subsystem is stable at the first time interval. Then, over the time interval , according to (8), it has
At time , the multi-agent tracking system switches from a stable subsystem to an unstable subsystem.
With iterations and derivations, at time , we have
where . From the condition in Theorem 1, it can be derived that
Substituting (18) into (17), we have
where , , , , . There must be a positive number satisfying , namely, so that
which implies the exponential stability of the tracking error (7). Therefore, with the proposed tracking strategy, the tracking error between each tracking agent and target agent is 0 when even if unstable subsystems exist. Thus, the proof is complete. □
4. A Numerical Example
In this section, a numerical example is provided to validate the effectiveness of the aforementioned theoretical results.
Consider a multi-agent system with one target agent followed by three tracking agents under the quasi-cyclic switched topologies, which is shown in Figure 2, where (, , ) and (, ).
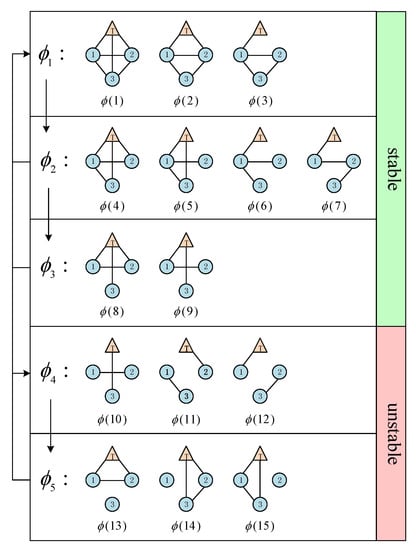
Figure 2.
An example of quasi-cyclic switching topologies.
According to the dynamic feedback linearization technology [39] that has adopted in distributed control of multi-agent systems with nonholonomic mobile robots [40,41], the dynamics of the system (1) can be linearized with the following matrices
The controller (4) of each tracking agent is designed with parameters
which have been verified that guarantee the stability of the system when the agents are topologically connected and meet the requirements of Theorem 1.
Consider a scenario where a team of three agents track a maneuvering target in a two-dimensional space. The initial position of the target agent is . The initial positions of the three tracking agents are , and .
Tracking trajectories of the agents are shown in Figure 3, from which we can see that successful tracking is eventually achieved.
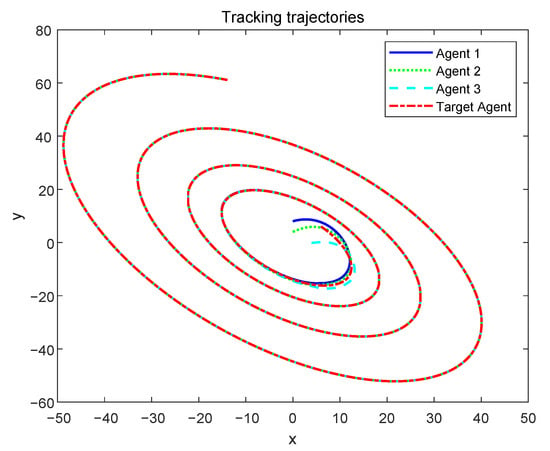
Figure 3.
Tracking trajectories of the system.
Errors of position between target agent and each tracking agent are plotted in Figure 4. The errors of tracking agents decreased to less than 0.01 within 5 s. Apparently every tracking agent successfully tracks the target agent under the quasi-cyclic topologies with the proposed tracking strategy (4).
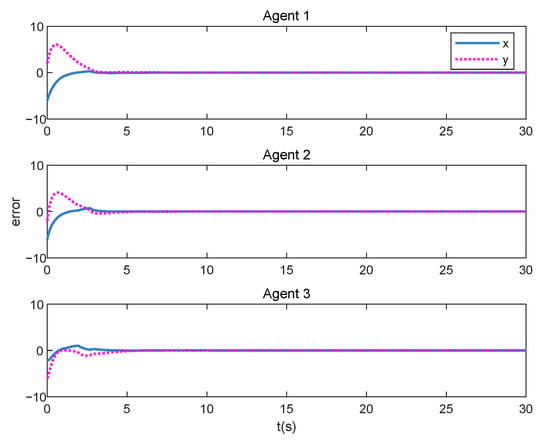
Figure 4.
Errors between target agent and each tracking agent.
The switching signal in the simulation is depicted in Figure 5. The switching sequence is: which can also be represented as It obviously conforms to the quasi-cyclic law compared to Figure 2.
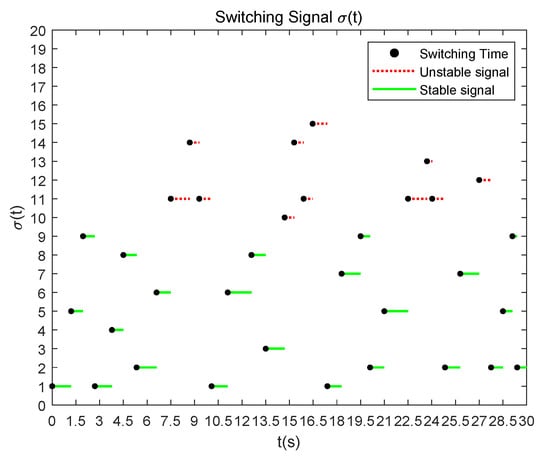
Figure 5.
Switching signal of the tracking process.
The topology of the multi-agent system switches 33 times during the tracking process. The profiles of the norm of tracking errors are plotted in Figure 6. It can be clearly seen that the tracking error eventually converges to zero even though it increases at some instants due to the occurrence of unstable subsystems. From the above results in Figure 3, Figure 4, Figure 5 and Figure 6, we can see that the states of tracking agents can track the target’s state successfully with the quasi-cyclic switched topologies.
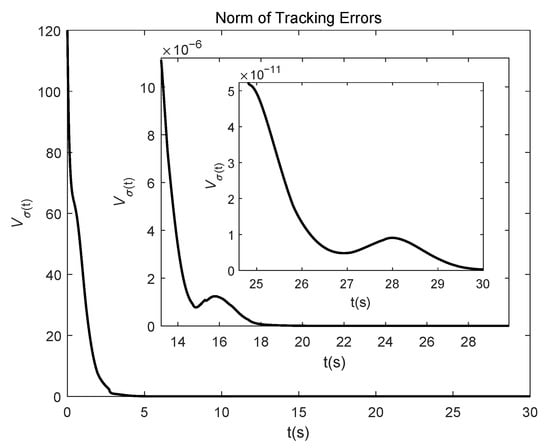
Figure 6.
Norm of tracking errors.
According to Equations (17)–(20), the value of is related to the convergence rate. It can be seen from the Equation (11) that the value of is also positively correlated with maximum dwell time of unstable subsystems. Thus, there exists a trade-off in between the convergence rate and the maximum dwell time of unstable subsystems. In this example, with the trade-off factor , we obtain , , , , , , , , , . , , then , which apparently satisfies the condition in Theorem 1. As analyzed, the stability of the multi-agent tracking systems with quasi-cyclic topologies is related to the ratio of the maximum dwell time of unstable subsystems and the minimum dwell time of stable subsystems, which effectively verifies the correctness of theoretical results.
5. Conclusions
In the paper, the switching problem of the multi-agent tracking systems with quasi-cyclic communication topologies is investigated. During this tracking process, several tracking agents have to cooperate and communicate with each other to track a maneuvering target. The communication links among the multiple agents may be interrupted due to the limitation of communication range or the appearance of obstacles, leading to unconnected communication topologies, which correspond to unstable subsystems. Existing results usually require the piecewise topologies to be connected or switch circularly. In order to relax the constraints, this paper proposes a quasi-cyclic method for MASs which contain a more practical switching rule with respect to a looser dwell time criterion. Moreover, it is proved that the tracking error converges exponentially in a less conservative way. Sufficient conditions that guarantee the stability of MASs with unstable subsystems are achieved. A numerical simulation is carried out to illustrate the validity of the theoretical results. It is concluded that the convergence rate and the maximum allowable dwell time of unstable subsystems are contradictory. Besides, the proposed method may be used not only in such scenarios as collaborative target tracking and convoy of vehicles, but also be promising in surveillance of a specific area and multi-robot coordination, in the case that the communication topologies of multiple agents are quasi-cyclic switched. However, there are still some challenging problems for MASs with switching topologies to be solved. In our future work, we will try to investigate a more widely applicable approach, considering the systems with nonlinear agents, and unknown time-varying communication delays.
Author Contributions
Conceptualization, D.F. and L.D.; methodology, D.F. and L.D.; software, D.F. and L.D.; validation, D.F.; formal analysis, H.S.; investigation, D.F.; resources, H.S.; data curation, D.F.; writing—original draft preparation, D.F.; writing—review and editing, L.D.; visualization, D.F.; supervision, H.S.; project administration, H.S.; funding acquisition, H.S. and L.D. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China under Grant 61903022, and funded by Beijing Advanced Innovation Center for Intelligent Robots and Systems under Grant 2019IRS11.
Conflicts of Interest
The authors declare no conflict of interest.The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| MASs | Multi-agent Systems |
| QCSS | Quasi-cyclic Switching Signals |
| QCST | Quasi-cyclic Switching Topologies |
References
- Nguyen, T.T.; Nguyen, N.D.; Nahavandi, S. Deep Reinforcement Learning for Multiagent Systems: A Review of Challenges, Solutions, and Applications. IEEE Trans. Cybern. 2020, 50, 3826–3839. [Google Scholar] [CrossRef] [PubMed]
- Dorri, A.; Kanhere, S.S.; Jurdak, R. Multi-Agent Systems: A Survey. IEEE Access 2018, 6, 28573–28593. [Google Scholar] [CrossRef]
- Kamdar, R.; Paliwal, P.; Kumar, Y. A State of Art Review on Various Aspects of Multi-Agent System. J. Circuits Syst. Comput. 2018, 27, 1830006. [Google Scholar] [CrossRef]
- Qin, J.; Ma, Q.; Yang, S.; Long, W. Recent Advances in Consensus of Multi-Agent Systems: A Brief Survey. IEEE Trans. Ind. Electron. 2017, 64, 4972–4983. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, J.; Zhang, D.; Shao, X. Fault-tolerant Adaptive Finite-time Attitude Synchronization and Tracking Control for Multi-spacecraft Formation. Aerosp. Sci. Technol. 2018, 73, 197–209. [Google Scholar] [CrossRef]
- Cardona, G.A.; Calderon, J.M. Robot Swarm Navigation and Victim Detection Using Rendezvous Consensus in Search and Rescue Operations. Appl. Sci. 2019, 9, 1702. [Google Scholar] [CrossRef]
- Kim, H.; Kim, D.; Kim, H.; Shin, J.U.; Myung, H. An Extended Any-angle Path Planning Algorithm for Maintaining Formation of Multi-agent Jellyfish Elimination Robot System. Int. J. Control Autom. Syst. 2016, 14, 598–607. [Google Scholar] [CrossRef]
- Kim, J. Cooperative Localization and Unknown Currents Estimation Using Multiple Autonomous Underwater Vehicles. IEEE Robot. Autom. Lett. 2020, 5, 2365–2371. [Google Scholar] [CrossRef]
- Pantelimon, G.; Tepe, K.; Carriveau, R.; Ahmed, S. Survey of Multi-agent Communication Strategies for Information Exchange and Mission Control of Drone Deployments. J. Intell. Robot. Syst. 2019, 95, 779–788. [Google Scholar] [CrossRef]
- Adamey, E.; Oguz, A.E.; Ozguner, U. Collaborative Multi-MSA Multi-Target Tracking and Surveillance: A Divide & Conquer Method Using Region Allocation Trees. J. Intell. Robot. Syst. 2017, 87, 471–485. [Google Scholar]
- Polyakov, I.; Shvets, E. Algorithm for Covert Convoy of a Moving Target Using a Group of Autonomous Robots. In Proceedings of the Tenth International Conference on Machine Vision (ICMV), Vienna, Austria, 13–15 November 2017; pp. 119–127. [Google Scholar]
- Hasan, Y.A.; Garg, A.; Sugaya, S.; Tapia, L. Defensive Escort Teams for Navigation in Crowds via Multi-Agent Deep Reinforcement Learning. IEEE Robot. Autom. Lett. 2020, 5, 5645–5652. [Google Scholar] [CrossRef]
- Cao, Y.; Yu, W.; Ren, W.; Chen, G. An Overview of Recent Progress in the Study of Distributed Multi-Agent Coordination. IEEE Trans. Ind. Inf. 2013, 9, 427–438. [Google Scholar] [CrossRef]
- Dong, X.; Yan, Z.; Zhang, R.; Zhong, Y. Time-varying Formation Tracking for Second-order Multi-agent Systems Subjected to Switching Topologies with Application to Quadrotor Formation Flying. IEEE Trans. Ind. Electron. 2017, 64, 5014–5024. [Google Scholar] [CrossRef]
- Wang, Y.; Long, C.; Wei, R.; Hou, Z.G.; Min, T. Seeking Consensus in Networks of Linear Agents: Communication Noises and Markovian Switching Topologies. IEEE Trans. Autom. Control 2015, 60, 1374–1379. [Google Scholar] [CrossRef]
- Chen, M.Z.Q.; Su, H. Multi-agent Containment Control with Input Saturation on Switching Topologies. IET Control Theory Appl. 2015, 9, 399–409. [Google Scholar]
- Mu, C.; Zhao, Q.; Sun, C. Optimal Model-Free Output Synchronization of Heterogeneous Multiagent Systems Under Switching Topologies. IEEE Trans. Ind. Electron. 2020, 67, 10951–10964. [Google Scholar] [CrossRef]
- Zhu, J.W.; Yang, Y.P.; Zhang, W.A.; Yu, L.; Wang, X. Cooperative Attack Tolerant Tracking Control for Multi-agent System with a Resilient Switching Scheme. Neurocomputing 2020, 409, 372–380. [Google Scholar] [CrossRef]
- Luo, Z.; Xiong, W.; He, W. Observer-based State Tracking for Discrete Linear Multi-agent Systems with Switching Topologies via Learning Control Strategies. IET Control Theory Appl. 2020, 14, 1639–1647. [Google Scholar] [CrossRef]
- Tanner, H.G.; Jadbabaie, A. Flocking in Fixed and Switching Networks. IEEE Trans. Autom. Control 2007, 52, 863–868. [Google Scholar] [CrossRef]
- Yu, D.; Chen, C.L.P. Automatic Leader–Follower Persistent Formation Generation with Minimum Agent-Movement in Various Switching Topologies. IEEE Trans. Cybern. 2020, 50, 1569–1581. [Google Scholar] [CrossRef]
- Xie, D.; Xu, S.; Chu, Y.; Zou, Y. Event-triggered Average Consensus for Multi-agent Systems with Nonlinear Dynamics and Switching topology. J. Frankl. Inst. 2014, 352, 1080–1098. [Google Scholar] [CrossRef]
- Wu, X.; Tang, Y.; Cao, J.; Zhang, W. Distributed Consensus of Stochastic Delayed Multi-agent Systems under Asynchronous Switching. IEEE Trans. Cybern. 2016, 46, 1817–1827. [Google Scholar] [CrossRef]
- Liu, K.; Ji, Z.; Xie, G.; Long, W. Consensus for Heterogeneous Multi-agent Systems under Fixed and Switching Topologies. J. Frankl. Inst. 2015, 352, 3670–3683. [Google Scholar] [CrossRef]
- Xi, J.; Fan, Z.; Hao, L.; Tang, Z. Guaranteed-cost Consensus for Multiagent Networks with Lipschitz Nonlinear Dynamics and Switching Topologies. Int. J. Robust Nonlinear Control 2018, 28, 2841–2852. [Google Scholar] [CrossRef]
- Hao, Z.; Yang, R.; Yan, H.; Yang, F. H∞ Consensus of Event-based Multi-agent Systems with Switching Topology. Inf. Sci. 2016, 370, 623–635. [Google Scholar]
- Meng, D.; Jia, Y.; Du, J. Robust Consensus Tracking Control for Multiagent Systems with Initial State Shifts, Disturbances, and Switching Topologies. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 809–824. [Google Scholar] [CrossRef]
- Wen, G.; Duan, Z.; Chen, G. Consensus Tracking of Multi-Agent Systems with Lipschitz-type Node Dynamics and Switching Topologies. IEEE Trans. Circuits Syst. I Regul. Pap. 2014, 61, 499–511. [Google Scholar] [CrossRef]
- Cai, Y.; Zhang, H.; Zhang, K.; Liang, Y. Distributed Leader-following Consensus of Heterogeneous Second-order Time-varying Nonlinear Multi-agent Systems under Directed Switching Topology. Neurocomputing 2019, 325, 31–47. [Google Scholar] [CrossRef]
- Meng, D.; Moore, K.L. Learning to Cooperate: Networks of Formation Agents with Switching Topologies. Automatica 2016, 64, 278–293. [Google Scholar] [CrossRef]
- Liu, B.; Su, H.; Li, R.; Sun, D.; Hu, W. Switching Controllability of Discrete-time Multi-agent Systems with Multiple Leaders and Time-delays. Appl. Math. Comput. 2014, 228, 571–588. [Google Scholar] [CrossRef]
- Han, F.; Gao, L.; Yang, H. Sampling Control on Collaborative Flocking Motion of Discrete-time System with Time-delays. Neurocomputing 2016, 216, 242–249. [Google Scholar]
- Yan, Y.; Huang, J. Cooperative Output Regulation of Discrete-time Linear Time-delay Multi-agent Systems under Switching Network. Neurocomputing 2017, 241, 108–114. [Google Scholar] [CrossRef]
- Dong, L.; Chai, S.; Zhang, B.; Nguang, S.K.; Savvaris, A. Stability of a Class of Multiagent Tracking Systems with Unstable Subsystems. IEEE Trans. Cybern. 2017, 47, 2193–2202. [Google Scholar] [CrossRef]
- Yang, H.; Jiang, B.; Zhao, J. On Finite-Time Stability of Cyclic Switched Nonlinear Systems. IEEE Trans. Autom. Control 2015, 60, 2201–2206. [Google Scholar] [CrossRef]
- Wu, Z.G.; Yong, X.; Lu, R.; Wu, Y.; Huang, T. Event-Triggered Control for Consensus of Multiagent Systems with Fixed/Switching Topologies. IEEE Trans. Syst. Man Cybern. Syst. 2018, 48, 1736–1746. [Google Scholar] [CrossRef]
- Dong, L. A Class of Cooperative Relay Analysis of Multi-agent Systems with Tracking Number Switching and Time Delays. ISA Trans. 2019, 90, 138–146. [Google Scholar] [CrossRef]
- Yu, Q.; Wu, B. Robust Stability Analysis of Uncertain Switched Linear Systems with Unstable Subsystems. Int. J. Syst. Sci. 2015, 46, 1278–1287. [Google Scholar] [CrossRef]
- Liu, T.; Jiang, Z.P. Distributed Formation Control of Nonholonomic Mobile Robots without Global Position Measurements. Automatica 2013, 49, 592–600. [Google Scholar] [CrossRef]
- Zhang, X.; Han, W.; Liu, X. Bipartite Tracking Consensus of Linear Multi-agent Systems with a Dynamic Leader under Signed Digraph. IET Control Theory Appl. 2020, 14, 2127–2133. [Google Scholar] [CrossRef]
- Zhang, J.; Lyu, M.; Shen, T.; Liu, L.; Bo, Y. Sliding Mode Control for a Class of Nonlinear Multi-agent System with Time Delay and Uncertainties. IEEE Trans. Ind. Electron. 2018, 65, 865–875. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).