1. Introduction
Recently, a large amount of literature on cooperative control of multi-agent systems (MAS) has emerged, which investigate this problem from different aspects, such as event-triggered and finite-time cooperative control [
1,
2]. Besides homogeneous MAS, research on heterogeneous MAS is also significant. As an effective method to realise cooperative control of heterogeneous MAS, for instance, a network of unmanned aerial vehicles (UAVs) with different dynamics, cooperative output regulation (COR) has attracted intensive research attention during the past decade [
3,
4,
5,
6], which was based on output regulation theory, where the influence of mismatched disturbance generated by an exosystem could be completely rejected via converting mismatched forms into matched forms [
7]. Specifically, H. Basu and S. Y. Yoon considered the condition that only partial information of an exosystem matrix was accessible to each agent, where a distinct estimator network was proposed to cooperatively estimate the value of the exosystem state [
8]. As some agents may destroy other healthy agents due to the influence of unexpected faults, security operation of heterogeneous MAS has attracted some researchers’ attention.
Existing security operation schemes of heterogeneous MAS are passive, where the fault tolerant COR is ensured by the designed passive fault tolerant controllers in each agent. In [
9], Deng et al. designed a distributed adaptive fault tolerant control law to attenuate partial loss of actuator effectiveness faults. Furthermore, they considered the condition that actuators suffered from both partial loss of effectiveness faults and stuck faults [
10,
11]. Besides designing passive fault tolerant control laws for each agent, detecting and removing faulty agents is the other effective method to ensure the security operation of MAS. Hence, some literature on FD schemes for MAS has emerged during the past decade. The basic idea is to design an additional FD algorithm for MAS, and run the FD and control algorithms simultaneously; the FD algorithm will locate and remove faulty agents in time, where the FD algorithm could be seen as a redundant algorithm to make the MAS operate well. In [
12], N. Meskin et al. proposed a centralised FD scheme for a group of unmanned vehicles, a bank of observers for FD were installed in one vehicle to monitor the remaining vehicles, where the observers needed to utilise all the nodes’ information. Furthermore, they considered the condition that agents suffered from external disturbances [
13]. In [
14], the authors proposed an FD scheme for linear MAS based on sliding mode fault estimators, where the design of fault estimators also utilised all the nodes’ input information. In summary, centralised FD schemes require one agent to have ability to obtain all the nodes’ information, which is contradicted with the distributed nature of MAS. Hence, researchers start considering distributed FD, where each agent just needs to have ability to obtain itself and its neighbours’ measurable information. I. Shames and K. H. Johansson et al. proposed a distributed FD scheme for a group of double integrators based on unknown input observer (UIO) [
15,
16], where the disturbance decoupling idea was widely utilised [
17,
18]. The basic idea was to adopt a distributed consensus law for each agent, and construct some FD observers for the MAS closed-loop system in one agent to judge whether a fault occurred in itself or its neighbours, then the utilisation or influence of agents’ control inputs for FD results was avoided. Furthermore, the authors proposed a distributed FD scheme for second-order MAS with uncertain communication topology, where the design process of some agent’s FD observers just utilised local topology information [
19]. As above framework possesses distributed characteristics, some researchers have extended above framework to MAS with different kinds of agent dynamics. Shi et al. designed robust FD observers for a group of discrete-time double integrators with both process and measurement noise [
20]. Jia and Wang proposed a distributed anti-disturbance FD scheme for disturbed second-order MAS, where the influence of exogenous disturbances for FD results was actively rejected [
21]. Besides MAS with double-integrator dynamics, Liu et al. considered linear MAS with Lipschitz nonlinearity [
22], and adopted a reduced-order observer design to lower the computational burden of each agent [
23].
To the best of the authors’ knowledge, there has been little published research on distributed FD schemes for heterogeneous MAS. M. R. Davoodi et al. designed a distributed FD scheme for heterogeneous MAS [
24], where the observer in one agent judged whether a fault occurred in itself and its neighbours or not. However, the above observer was not decoupled from control inputs, which meant that the FD results would be influenced by control inputs. In [
25], the authors considered a heterogeneous MAS with sensor faults, where fault estimators were designed in each agent to detect the fault. However, the considered agent dynamics did not contain exogenous disturbances, which were assumed to affect each agent and unknown for most agents in the MAS [
3,
4,
5,
6], and it seemed costly that all agents were equipped with fault estimators. Motivated by existing works mentioned above, we design a distributed FD scheme for disturbed MAS with heterogeneous dynamics based on UIO. As the exogenous disturbance is unknown for most agents of the MAS [
3,
4,
5,
6], above agents need to estimate the exogenous disturbance through cooperating with its neighbours, therefore, a bank of UIOs are designed according to the formed closed-loop system with the information of communication topology, which utilise exogenous disturbance estimate as feedback information, i.e., avoids utilising unknown exogenous disturbance. The contributions of this paper are listed as follows: First, a state-feedback-based distributed FD scheme for heterogeneous MAS is proposed in this paper, as well as an output-feedback-based distributed FD scheme. Second, unlike [
24], the FD results will not be influenced by agents’ control inputs, since FD observers are designed for closed-loop systems. Third, in comparison with [
25], the considered agent dynamics contain exogenous disturbances in this paper. FD observers could still be designed for those agents, which cannot obtain exogenous signal directly, and only partial agents need to be equipped with observers.
The rest of this paper is organised as follows:
Section 2 gives the preliminaries and problem formulation, where
Section 2.1 and
Section 2.2 introduce relevant knowledge of graph theory and UIO, and
Section 2.3 gives the problem formulation.
Section 3 gives results of this paper, state-feedback-based and output-feedback-based distributed FD schemes are proposed in
Section 3.1 and
Section 3.2.
Section 4 gives two simulation examples to verify that the proposed FD schemes are effective. Finally,
Section 5 gives conclusions and future directions.
Notation: Some standard notation will be adopted in this paper. and denote the set of complex numbers and n-dimensional Euclidean space, respectively. and I denote an identity matrix with dimension N and appropriate dimension, respectively. ⊗ denotes the Kronecker product. represents a column with only one nonzero entry ‘1’, which locates in the i-th row. represents the real part of , where . represents a block-diagonal matrix with matrices , . denotes the i-th eigenvalue of A. means that A is positive definite. ‘!’ denotes the factorial of a non-negative integer, and , where are non-negative integers, and . The superscript ‘T’ represents the transpose of a matrix.
2. Preliminaries and Problem Formulation
2.1. Graph Theory
A graph could represent communication links among one leader agent and several follower agents, where and represent the vertex and edge sets of , agent i could receive information from agent j if , where is also called the neighbour of . If means that , graph is called undirected. A path from to is a sequence of distinct nodes , where and . An induced subgraph is a graph such that , and indicates that . Subgraph with the vertex set represents the communication relationship among follower agents. The adjacency matrix associated with is defined as and if . What is more, define the in-degree of each agent as , and define the Laplacian matrix associated with as , where and .
For the convenience of analysis, denote as the Laplacian matrix associated with , and define and . Furthermore, define as the neighbour set of node in , and define , where is the cardinality of , and are sequence numbers of nodes in from small to large.
Lemma 1 ([
26])
. If the subgraph is undirected, and each follower agent has paths to the leader in the graph , is positive definite. 2.2. Unknown Input Observer
Consider the following system with unknown input:
where
is the state.
and
are the known and unknown inputs, and
W and
Y represent their input channels, respectively.
is the measurement output, and
H represents the measurement matrix.
In order to estimate the actual state of System (1), the following observer is designed.
where
and
are the estimated state and observer’s state, respectively. Parameter matrices of observer (2) need to be designed to make the state estimation error be not influenced by unknown input
w, where the design method is shown as follows:
then the state estimation error dynamics is shown as follows:
where
. If the designed
makes
G Hurwitz stable,
e will converge to zero asymptotically. Observer (2) is usually called unknown input observer (UIO). Lemma 2 gives the existence conditions of a UIO.
Lemma 2 ([
16])
. A UIO for System (1) exists if- (i)
rank() = rank(Y)
- (ii)
is of full column rank for , , i.e., is detectable.
Remark 1. The above two conditions guarantee existence of H and in (3), respectively, where makes G Hurwitz stable.
2.3. Problem Formulation
The considered heterogeneous MAS consists of the following
N agents:
where
,
,
,
and
are the state, tracking error, measurement output, control input and fault signal of the
i-th agent, respectively. Columns of
are linearly independent, and
are stabilisable and detectable.
is the reference input to be tracked or the disturbance to be rejected, which is assumed to be generated by the following exosystem:
In this paper, the leader labelled as 0 could represent the exosystem. System (5) could be seen as follower agents, where only some follower agents of the MAS could utilise v directly, i.e., the leader is their neighbour in the graph , and the remaining follower agents just have paths to the leader. The above two facts mean that the leader has paths to all follower agents in the graph .
System (5) also needs to satisfy the following assumptions.
Assumption 1. , .
Assumption 2. The following equationshave solution pairs , respectively. Remark 2.
According to Theorem 1.9 in [27], solution pairs are determined to exist if rank for any . In fact, is of full row rank for if System (5) are minimum phase systems, combined with Assumption 1, matrix Equation (6) will always have solutions if System (5) are minimum phase systems. Furthermore, the solution pair will be unique if .
Assumption 3. There exists only one faulty agent in each , .
For System (5), a state-feedback-based distributed control law is proposed in [
1].
where
is a dynamic compensator,
c is a positive scalar to design,
and
are parameter matrices to design. Let
be as follows:
and
are determined by matrix equations in Assumption 2. If
are Hurwitz stable,
, and the leader has paths to all follower agents, control law (7) will realise COR when there exists no faulty agent [
3], i.e., tracking errors
converge to zero asymptotically. However, the given exosystem under Assumption 1 just has an unforced purely oscillatory solution, which cannot include some kinds of solutions such as those of a damped differential system or the solution of a forced differential system or dynamic system, i.e., some kinds of practical signals cannot be generated by the given exosystem, where the application prospect is limited. This is due to the fact that the given exosystem needs to ensure that matrix Equation (6) has solutions, and the following Theorems 2 and 3 hold. Furthermore, COR will not realise if some agent suffers from fault signals. Hence, there exists a need to detect the faulty agent.
This paper aims at adopting a distributed control law for the MAS, and designing distributed observers in some agents to detect the possibly faulty agent. Running the observers and control law simultaneously, the observers could detect the faulty agent if there occurs a fault, and the distributed control law could also realise COR if no fault occurs. It is worth indicating that if the solution pair is not unique, we just need to select one of them to design the control law (7), and design FD observers (15) and (29), where the parameters of FD observers contain the selected solution pairs . What is more, the designed control law (7) with any chosen solution pair will realise consensus control when there exists no faulty agent, and existence of the designed FD observers will also hold under any chosen solution pair .
4. Simulation Example
In this section, we will provide an example to illustrate the effectiveness of the two proposed distributed FD schemes.
Consider the following agent dynamics in Reference [
31]:
where the parameters
are modelled as
,
,
and
, respectively.
Assume the communication graph
among all the follower agents and the exosystem can be described by
Figure 1, where node 0 represents the exosystem and the other nodes represent four follower agents, where agent 2 is assumed as faulty, it can be observed that only agent 3 can access the exosystem state
v,
v is generated by the exosystem
, where
Then, it can be verified that Assumptions 1–3 are satisfied,
are stabilisable,
are detectable, and four follower agents have paths to the leader in the graph
. What is more,
which satisfy Assumption 4. The solutions of (6) are given by
where
.
Choose the coupling gain coefficient c, parameter matrices of control laws as Theorems 2 and 3, which correspond to the state-feedback-based and output-feedback-based distributed FD schemes, respectively, as well as parameter matrices of the observers for FD.
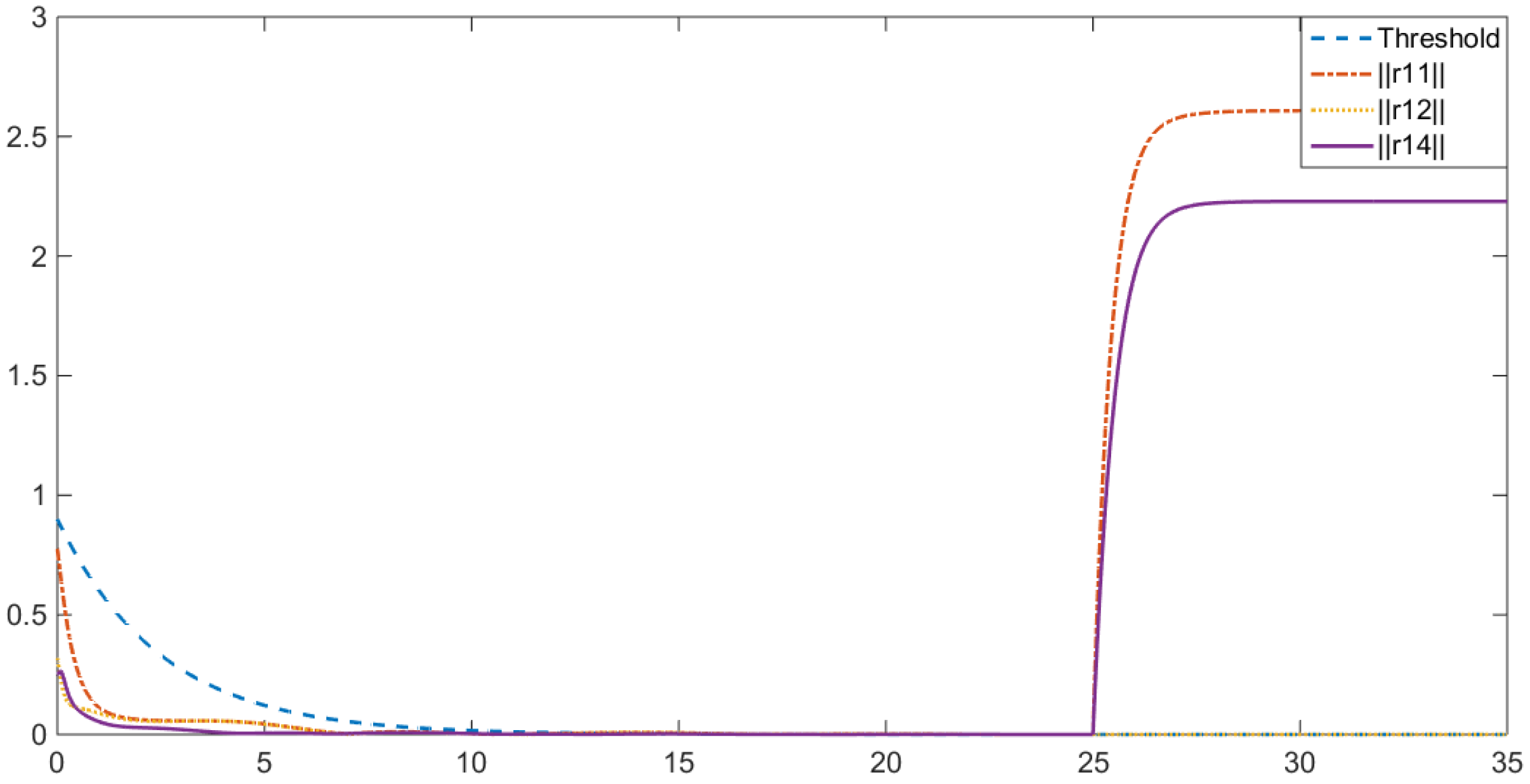
For the condition that state information is measurable, run control law (7) and observers (15) for FD.
The fault is assumed to be a constant and occur in the first element of
, i.e.,
, which occurs after 25 s. Residual generators
,
and
in agent 1 are shown as
Figure 2, which are represented by 2-norm type. According to Remark 8, we could choose a positive scalar
, which is larger than
,
and
, and
, which is larger than
,
and
, combined with
. Then, the isolation threshold could be set as
.
It is shown that above residuals converge to little enough values before the fault occurs, then and fluctuate when the fault occurs at the time of 25 s. However, does not fluctuate as and when the fault occurs, then according to Algorithm 1, the fault occurs in agent 2.
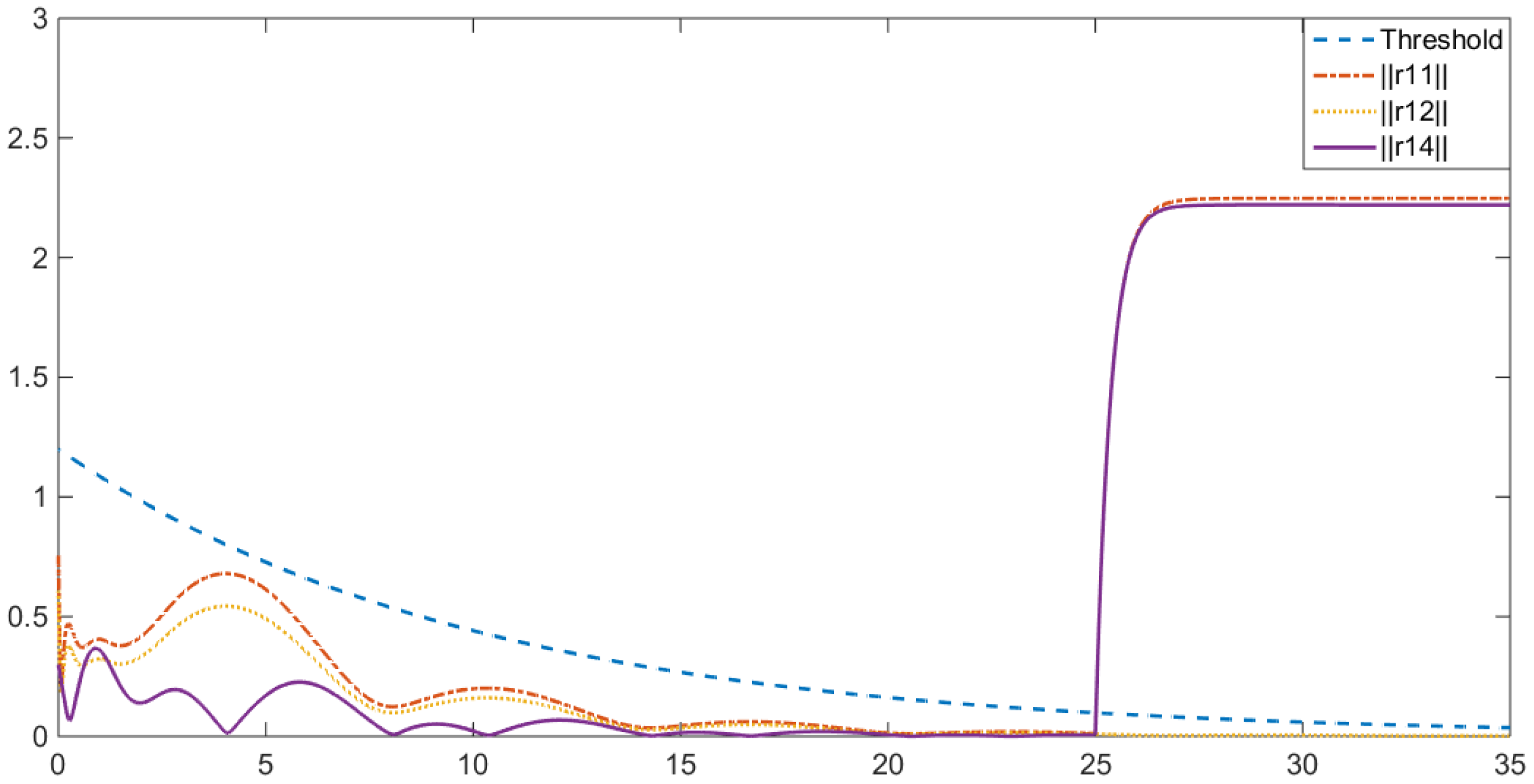
For the condition that state information is unmeasurable, run control law (21) and observers (29) for FD.
The fault signal is the same as the state feedback case, as well as the isolation threshold selection method. Simulation results of residual generators
,
and
in agent 1 are shown as
Figure 3, and still represented by 2-norm type. It is shown that
remains converging after the fault occurs, where
and
fluctuate; therefore, the fault occurs in agent 2.