Predicting and Modeling Wildfire Propagation Areas with BAT and Maximum-State PageRank
Abstract
Featured Application
Abstract
1. Introduction
2. Overview of Wildfire Propagation, Scale-Free Network, Barabási-Albert Model, and BAT
2.1. Wildfire Propagation
2.2. Scale-Free and Barabási-Albert Model
- STEP B1.
- Growth: Nodes are individually added into the network such that the network size, i.e., the number of nodes, increases over time.
- STEP B2.
- Preferential attachment: The probability of the newly added node being connected with an old node is dependent on the degree of the old node.
2.3. PageRank
- i1, i2, …, ini are nodes with links to node i
- damping factor d is a number between 0 and 1 and it accounts for the (1 − d) chance of jumping into an arbitrary node.
- Degout(j) is the out-degree number of a node, i.e., the number of links going from node j.
| Algorithm 1 PageRank Algorithm [53] |
| Input A scale-free network G(V, E) with node set V = {0, 1, …, (n − 1)} and link set E. Output Probability distribution, i.e., the PageRank value, PR(i) for all nodes i ∈ V. 1: Let time t = 0. Set the initial PR(i) as 1/n for node i and i = 0, 1, …, (n − 1). 2: Update PR(i) based on Equation (4) for all i ∈ V. 3: Redistribute PR(i) equally among the other nodes for all nodes i with Degout(i) = 0. 4: if there is no change in PR(i) for i = 0, 1, 2, …, (n − 1) then go to Stop. 5: else if let t = t + 1 return to line 2. |
2.4. BAT
| Algorithm 2 BAT Algorithm [46] |
| Input A binary-state network G(V, E) with two states, either 0 or 1, to each link and V = {0, 1, 2, …, n − 1} Output All possible non-duplicate link-based state vectors. 1: Let SUM = 0, vector index k = 1, and Y1 = Y be a zero vector with m coordinates which represented the states of the related links. 2: Let coordinate index i = m. 3: If Y(i) = 0, let Y(i) = 1, k = k + 1, Yk = Y, SUM = SUM + 1 then go to line 5. 4: Let Y(i) = 0. If i > 1, let i = i − 1 then go to line 3. 5: If SUM = m, halt, and Y1, Y2, …, Yk are all possible state vectors return line 2. |
3. Novel Dynamic BAT and States
3.1. States and Maximum-State
- the state of node i can be an empty node subset because it is possible that no area is affected by the wildfire in node i,
- these nodes in each state are subsets of V(i) because the neighbor areas can face a wildfire spread from node i.
3.2. State Labels
- the number of digits is equal to Deg(i) in the binary state label;
- the nodes in the states of i are arranged in the decreasing order of their node labels in V(i);
- the ith digit in the binary state label is equal to 0 or 1 if the ith node is included or excluded in the state, respectively.
3.3. State Vectors
3.4. State Pagerank, State Probability, and Maximum-State Pagerank
3.5. The New BAT
| Algorithm 3 New-BAT Algorithm. |
| InputG(V, E), V(i), Sk(i), and the node s where the wildfire is first identified, for all k = 0, 1, …, 2|Deg(i)| − 1 and i ∈ V. Output the probability Pr(s, Narea) that the wildfire spreads to at least Narea (≥1) areas (including the first area of wildfire identified). 1: Let i = s be the node that the wildfire was first found, l = 0, the current sum of probabilities that the wildfire are spread out to at least Narea areas R = 0, Tl = {i}, T−1 = ∅, the state label X(i) = 1. 2: If X(i) = 2|Deg(i)| − 1, i.e., node i reaches its the maximum-state then go to line 11. 3: Let X(i) = X(i) + 1 and T* = {j | j ∈ [V(i) − Tl]}. 4: If T* = ∅ then go to line 7. 5: Let Tl = Tl-1 ∪ T*, X(j) = 0 for all j ∈ T*, and Pl = P(l−1) × Pr(SX(i)(i)). 6: If |Sl| ≥ Nneighbor, let R = R + Pl then go to line 3. 7: Let new node i be the node right after the current node i in Tl then go to line 4. 8: If there is no such node in line 7 then go to line 3. 9: Let l = l − 1, i be the node right before the current node i in Tl, and go to line 2. If there is no such node i, halt, and Pr(s, Narea) = R is the final probability that the wildfire can be spread out at least Narea areas. |
3.6. Overall Procedure of the Proposed Method
| Algorithm 4 The overall procedure of we proposed methof. |
| Input The map including all areas we are interested in estimating the wildfire propagation Output The total probabilities of the wildfire propagation areas. 1: Build the network model for the area map by letting the city/down/important area to be node and links to connect these areas that are neighbor to each other. 2: Generate and normalize the adjacency matrix based on each column. 3: Calculate the PageRank values for each node based on the degree of nodes as shown in Equation (4). 4: Find out all node subsets of each node as discussed in Section 3.1. 5: Calculate the state PageRank values (including the maximum-state PageRank values) and state probabilities based on Section 3.4. 6: Use the maximum-state PageRank values to decide which areas need to protect in the beginning, middle, and final stages of the wildfire propagation. 7: Use the proposed the New BAT provided in Section 3.5 to calculate Pr(i, Narea) for all nodes i and Narea = 1, 2, …, |V|. |
4. Experimental Results
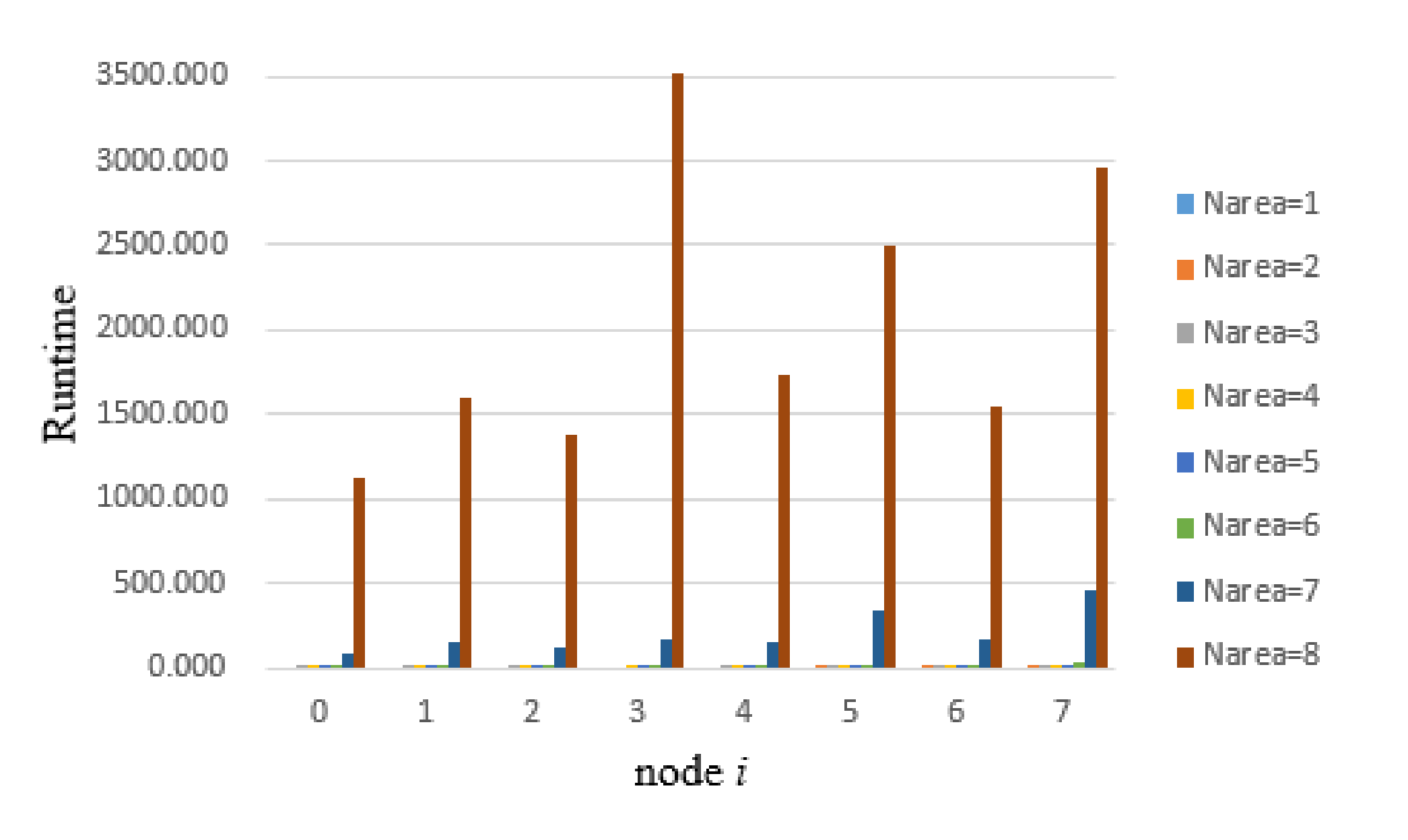
4.1. General Results
4.2. Pr(i, Narea) and Deg(i)
4.3. Pr(i, Narea) and the Maximum-State PageRank
4.4. Maximum-State PageRank
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wei, S.C.; Yeh, W.C. Resource allocation decision model for dependable and cost-effective grid applications based on Grid Bank. Future Gener. Comput. Syst. 2017, 77, 12–28. [Google Scholar] [CrossRef]
- Wang, M.; Yeh, W.C.; Chu, T.C.; Zhang, X.; Huang, C.L.; Yang, J. Solving Multi-Objective Fuzzy Optimization in Wireless Smart Sensor Networks under Uncertainty Using a Hybrid of IFR and SSO Algorithm. Energies 2018, 11, 2385. [Google Scholar] [CrossRef]
- Huang, C.L.; Huang, S.Y.; Yeh, W.C.; Wang, J. Fuzzy System and Time Window Applied to Traffic Service Network Problems under a Multi-Demand Random Network. Electronics 2019, 8, 539. [Google Scholar] [CrossRef]
- Wang, J.H.; Yeh, W.C.; Xiong, N.N.; Wang, J.; He, X.; Huang, C.L. Building an Improved Internet of Things Smart Sensor Network Based on a Three-Phase Methodology. IEEE Access 2019, 7, 141728–141737. [Google Scholar] [CrossRef]
- Yeh, W.C.; Lin, J.S. New Parallel Swarm Algorithm for Smart Sensor Systems Redundancy Allocation Problems in the Internet of Things. J. Supercomput. 2018, 74, 4358–4384. [Google Scholar] [CrossRef]
- Yeh, W.C. A squeezed artificial neural network for the symbolic network reliability functions of binary-state networks. IEEE Trans. Neural Netw. Learn. Syst. 2016, 28, 2822–2825. [Google Scholar] [CrossRef] [PubMed]
- Lai, C.M.; Yeh, W.C. Two-stage simplified swarm optimization for the redundancy allocation problem in a multi-state bridge system. Reliab. Eng. Syst. Saf. 2016, 156, 148–158. [Google Scholar] [CrossRef]
- Yeh, W.C. Solving cold-standby reliability redundancy allocation problems using a new swarm intelligence algorithm. Appl. Soft Comput. 2019, 83, 105582. [Google Scholar] [CrossRef]
- Zhu, W.; Yeh, W.C.; Cao, L.; Zhu, Z.; Chen, D.; Chen, J.; Li, A.; Lin, Y. Faster Evolutionary Convolutional Neural Networks Based on iSSO for Lesion Recognition in Medical Images. Basic Clin. Pharmacol. Toxicol. 2019, 124, 329. [Google Scholar]
- Yeh, W.C.; Zuo, M.J. A New Subtraction-based Algorithm for the d-MPs for all d Problem. IEEE Trans. Reliab. 2019, 68, 999–1008. [Google Scholar] [CrossRef]
- Hao, Z.; Yeh, W.C.; Hu, C.F. A Novel Multistate Minimal Cut Vectors Problem. IEEE Trans. Reliab. 2019, 68, 291–301. [Google Scholar] [CrossRef]
- Yeh, W.C.; Chu, T.C. A Novel Multi-Distribution Multi-State Flow Network and its Reliability Optimization Problem. Reliab. Eng. Syst. Saf. 2018, 176, 209–217. [Google Scholar] [CrossRef]
- Yeh, W.C. A Novel Boundary Swarm Optimization for Reliability Redundancy Allocation Problems. Reliab. Eng. Syst. Saf. 2018, 192, 106060. [Google Scholar] [CrossRef]
- Yeh, W.C. Fast algorithm for searching d-MPs for all possible d. IEEE Trans. Reliab. 2018, 67, 308–315. [Google Scholar] [CrossRef]
- Yeh, W.C. Methodology for the reliability evaluation of the novel learning-effect multi-state flow network. IISE Trans. 2017, 49, 1078–1085. [Google Scholar] [CrossRef]
- Yeh, W.C. A New Exact Solution Algorithm for a Novel Generalized Redundancy Allocation Problem. Inf. Sci. 2017, 408, 182–197. [Google Scholar] [CrossRef]
- Yeh, W.C. Evaluation of the One-to-all-target-subsets Reliability of a Novel Deterioration-Effect Acyclic Multi-state Information Network. Reliab. Eng. Syst. Saf. 2017, 166, 132–137. [Google Scholar] [CrossRef]
- Yeh, W.C. A Fast Algorithm for Quickest Path Reliability Evaluations in Multi-State Flow Networks. IEEE Trans. Reliab. 2015, 64, 1175–1184. [Google Scholar] [CrossRef]
- Yeh, W.C.; Bae, C.; Huang, C.L. A New Cut-based Algorithm for the Multi-state Flow Network Reliability Problem. Reliab. Eng. Syst. Saf. 2015, 136, 1–7. [Google Scholar] [CrossRef]
- Yeh, W.C. A Novel Node-based Sequential Implicit Enumeration Method for finding all d-MPs in a Multistate Flow Network. Inf. Sci. 2015, 297, 283–292. [Google Scholar] [CrossRef]
- Yeh, W.C. Orthogonal Simplified Swarm Optimization for the Series-Parallel Redundancy Allocation Problem with a Mix of Components. Knowl.-Based Syst. 2014, 64, 1–12. [Google Scholar] [CrossRef]
- Hao, Z.; Yeh, W.C.; Wang, J.; Wang, G.G.; Sun, B. A Quick Inclusion-Exclusion technique. Inf. Sci. 2019, 486, 20–30. [Google Scholar] [CrossRef]
- Yeh, W.C. An improved sum-of-disjoint-products technique for symbolic multi-state flow network reliability. IEEE Trans. Reliab. 2016, 64, 1185–1193. [Google Scholar] [CrossRef]
- Yeh, W.C. New method in searching for all minimal paths for the directed acyclic network reliability problem. IEEE Trans. Reliab. 2016, 65, 1263–1270. [Google Scholar] [CrossRef]
- Yeh, W.C. A simple heuristic algorithm for generating all minimal paths. IEEE Trans. Reliab. 2007, 56, 488–494. [Google Scholar] [CrossRef]
- Yeh, W.C. A simple universal generating function method to search for all minimal paths in networks. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 2009, 39, 1247–1254. [Google Scholar]
- Yeh, W.C. A Simple Algorithm to Search for All MCs in Networks. Eur. J. Oper. Res. 2006, 174, 1694–1705. [Google Scholar] [CrossRef]
- Firewise. Wildfire News and Notes. Wildland Fire Management Terminology; No. 1; Firewise: North Central Washington, DC, USA, 1998; Volume 12, p. 10. Available online: http://www.firewise.org/pubs/wnn/vol12/no1/pp-10.html (accessed on 1 November 2020).
- Khakzad, N. Modeling wildfire spread in wildland-industrial interfaces using dynamic Bayesian network. Reliab. Eng. Syst. Saf. 2019, 189, 165–176. [Google Scholar] [CrossRef]
- Fasullo, J.T.; Otto-Bliesner, B.L.; Stevenson, S. ENSO’s changing influence on temperature, precipitation, and wildfire in a warming climate. Geophys. Res. Lett. 2018. [Google Scholar] [CrossRef]
- Duane, A.; Aquilué, N.; Gil-Tena, A.; Brotons, L. Integrating fire spread patterns in fire modelling at landscape scale. Environ. Model. Softw. 2016, 86, 219–231. [Google Scholar] [CrossRef]
- Hajian, M.; Melachrinoudis, E.; Kubat, P. Modeling wildfire propagation with the stochastic shortest path: A fast simulation approach. Environ. Model. Softw. 2016, 82, 73–88. [Google Scholar] [CrossRef]
- Stepanov, A.; Smith, J.M. Modeling wildfire propagation with delaunay triangulation and shortest path algorithms. Eur. J. Oper. Res. 2012, 218, 775–788. [Google Scholar] [CrossRef]
- Demange, M.; Gabrel, V.; Haddad, M.A.; Murat, C. A robust p-Center problem under pressure to locate shelters in wildfire context. J. Comput. Optim. 2020, 8, 103–139. [Google Scholar] [CrossRef]
- Alexandre, M.E.; Cruz, M.G. Limitations on the accuracy of model predictions of wildland fire behavior: A state-of-the-knowledge overview. For. Chron. 2013, 89, 370–381. [Google Scholar]
- Byram, G.M. Forest fire: Control and use. In Combustion of Forest Fuels; Davis, K.P., Ed.; McGraw-Hill: New York, NY, USA, 1959; pp. 61–89. [Google Scholar]
- Cruz, M.G.; Alexander, M.E. Uncertainty associated with model predictions of surface and crown fire rates of spread. Environ. Model. Softw. 2013, 7, 16–28. [Google Scholar] [CrossRef]
- Doerr, S.H.; Santín, C. Global trends in wildfire and its impacts: Perceptions versus realities in a changing world. Philos. Trans. R. Soc. B Biol. Sci. 2016, 371. [Google Scholar] [CrossRef]
- Niu, Y.; Gao, Z.; Sun, H. An improved algorithm for solving all d-MPs in multi-state network. J. Syst. Sci. Syst. Eng. 2017, 26, 711–731. [Google Scholar] [CrossRef]
- Ramirez-Marquez, J.E. Assessment of the transition-rates importance of Markovian systems at steady state using the unscented transformation. Reliab. Eng. Syst. Saf. 2015, 142, 212–220. [Google Scholar]
- Boychuk, D.; Braun, W.J.; Kulperger, R.J.; Krougly, Z.L.; Stanford, D.A. A stochastic forest fire growth model. Environ. Ecol. Stat. 2019, 16, 133–151. [Google Scholar] [CrossRef]
- Clauset, A.; Shalizi, C.R.; Newman, M.E.J. Power-law distributions in empirical data. Siam Rev. 2009, 51, 661–703. [Google Scholar] [CrossRef]
- Onnela, J.P.; Saramäki, J.; Hyvönen, J.; Szabó, G.; Lazer, D.; Kaski, K.; Kertész, J.; Barabási, A.L. Structure and tie strengths in mobile communication networks. Proc. Natl. Acad. Sci. USA 2007, 104, 7332–7336. [Google Scholar] [CrossRef] [PubMed]
- Bomholdt, S.; Ebel, H. World Wide Web scaling exponent from Simon’s 1955 model. Phys. Rev. E 2001, 64, 035104. [Google Scholar] [CrossRef] [PubMed]
- Barabási, A.L.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar]
- Yeh, W.C. Novel binary-addition tree algorithm (BAT) for binary-state network reliability problem. arXiv 2020, arXiv:2004.08238. [Google Scholar]
- Yeh, W.C. A greedy branch-and-bound inclusion-exclusion algorithm for calculating the exact multi-state network reliability. IEEE Trans. Reliab. 2008, 57, 88–93. [Google Scholar]
- Yeh, W.C.; Lin, Y.C.; Chung, Y.Y. Performance analysis of cellular automata Monte Carlo Simulation for estimating network reliability. Expert Syst. Appl. 2010, 37, 3537–3544. [Google Scholar] [CrossRef]
- Yeh, W.C. An improved sum-of-disjoint-products technique for the symbolic network reliability analysis with known minimal paths. Reliab. Eng. Syst. Saf. 2007, 92, 260–268. [Google Scholar] [CrossRef]
- Levitin, G. The Universal Generating Function in Reliability Analysis and Optimization; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Yeh, W.C. A novel cut-based universal generating function method. IEEE Trans. Reliab. 2013, 62, 628–636. [Google Scholar] [CrossRef]
- Yeh, W.C. A simple universal generating function method for estimating the reliability of general multi-state node networks. Iie Trans. 2008, 41, 3–11. [Google Scholar] [CrossRef]
- Yeh, W.C.; El Khadiri, M. A new universal generating function method for solving the single (d, τ)-quick path problem in multistate flow networks. IEEE Trans. Syst. Man Cybern. 2012, 42, 1476–1484. [Google Scholar]
- Google Press Center: Fun Facts. Available online: https://pulseagency.com.au/wp-content/uploads/2018/06/funfacts.html (accessed on 15 July 2001).
- Facts about Google and Competition. Available online: https://blog.google/competition#facts (accessed on 4 November 2011).
- Viegas, D. Forest fire propagation. Philosophical transactions. Math. Phys. Eng. Sci. 1998, 356, 2907–2928. Available online: http://www.jstor.org/stable/55054 (accessed on 10 November 2020). [CrossRef]
- André, J.C.S.; Lopes, A.M.G.; Viegas, D.X. A broad synthesis of research on physical aspects of forest fires. In Cadernos Cientificos Sobre Incendios Florestais; Viegas, D.X., Ed.; Fluid Mechanics Group, Mechanical Engineering Department, Faculty of Science and Technology, University of Coimbra: Coimbra, Portugal, 1992; Volume 3, p. 148. [Google Scholar]
- Rothermel, R.C. Modelling fire behaviour. In Proceedings of the 1st International Conference on Forest Fire Research, Coimbra, Portugal, 19–22 November 1990. [Google Scholar]
- Tricaud, C.; Chen, Y.Q. Optimal Mobile Sensing and Actuation Policies in Cyber-Physical Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Nemhauser, G.L.; Wolsey, L.A. Integer and Combinatorial Optimization; Wiley-Interscience: New York, NY, USA, 1999. [Google Scholar]
- Yeh, W.C. A Novel Method for the Network Reliability in terms of Capacitated-Minimum-Paths without Knowing Minimum-Paths in Advance. J. Oper. Res. Soc. 2005, 56, 1235–1240. [Google Scholar] [CrossRef]






| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0.166667 | 0 | 0.2 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0.166667 | 0.166667 | 0.2 |
| 2 | 0 | 0 | 0 | 0 | 0 | 0.166667 | 0.166667 | 0 |
| 3 | 0 | 0 | 0 | 0 | 0 | 0.166667 | 0.166667 | 0.2 |
| 4 | 0 | 0 | 0 | 0 | 0 | 0.166667 | 0.166667 | 0.2 |
| 5 | 0.5 | 0.333333 | 0.5 | 0.333333 | 0.333333 | 0 | 0.166667 | 0 |
| 6 | 0 | 0.333333 | 0.5 | 0.333333 | 0.333333 | 0.166667 | 0 | 0.2 |
| 7 | 0.5 | 0.333333 | 0 | 0.333333 | 0.333333 | 0 | 0.166667 | 0 |
| Bi | Yi | i | Bi | Yi | |
|---|---|---|---|---|---|
| 1 | 00000 | (0, 0, 0, 0, 0) | 17 | 10000 | (1, 0, 0, 0, 0) |
| 2 | 00001 | (0, 0, 0, 0, 1) | 18 | 10001 | (1, 0, 0, 0, 1) |
| 3 | 00010 | (0, 0, 0, 1, 0) | 19 | 10010 | (1, 0, 0, 1, 0) |
| 4 | 00011 | (0, 0, 0, 1, 1) | 20 | 10011 | (1, 0, 0, 1, 1) |
| 5 | 00100 | (0, 0, 1, 0, 0) | 21 | 10100 | (1, 0, 1, 0, 0) |
| 6 | 00101 | (0, 0, 1, 0, 1) | 22 | 10101 | (1, 0, 1, 0, 1) |
| 7 | 00110 | (0, 0, 1, 1, 0) | 23 | 10110 | (1, 0, 1, 1, 0) |
| 8 | 00111 | (0, 0, 1, 1, 1) | 24 | 10111 | (1, 0, 1, 1, 1) |
| 9 | 01000 | (0, 1, 0, 0, 0) | 25 | 11000 | (1, 1, 0, 0, 0) |
| 10 | 01001 | (0, 1, 0, 0, 1) | 26 | 11001 | (1, 1, 0, 0, 1) |
| 11 | 01010 | (0, 1, 0, 1, 0) | 27 | 11010 | (1, 1, 0, 1, 0) |
| 12 | 01011 | (0, 1, 0, 1, 1) | 28 | 11011 | (1, 1, 0, 1, 1) |
| 13 | 01100 | (0, 1, 1, 0, 0) | 29 | 11100 | (1, 1, 1, 0, 0) |
| 14 | 01101 | (0, 1, 1, 0, 1) | 30 | 11101 | (1, 1, 1, 0, 1) |
| 15 | 01110 | (0, 1, 1, 1, 0) | 31 | 11110 | (1, 1, 1, 1, 0) |
| 16 | 01111 | (0, 1, 1, 1, 1) | 32 | 11111 | (1, 1, 1, 1, 1) |
| i | Deg(i) | V(i) | C(i) | PR(i) | PR(V(i)) | 1 - PR(V(i)) |
|---|---|---|---|---|---|---|
| 0 | 2 | {5, 7} | 4 | 0.074066 | 0.357809 | 0.642191 |
| 1 | 3 | {5, 6, 7} | 8 | 0.101160 | 0.549056 | 0.450944 |
| 2 | 2 | {6, 7} | 4 | 0.073398 | 0.357809 | 0.642191 |
| 3 | 3 | {5, 6, 7} | 8 | 0.101160 | 0.549056 | 0.450944 |
| 4 | 3 | {5, 6, 7} | 8 | 0.101160 | 0.549056 | 0.450944 |
| 5 | 6 | {0, 1, 2, 3, 4, 6} | 64 | 0.194502 | 0.642191 | 0.357809 |
| 6 | 6 | {1, 2, 3, 4, 5, 7} | 64 | 0.191247 | 0.734687 | 0.265313 |
| 7 | 5 | {0, 1, 3, 4, 6} | 32 | 0.163307 | 0.568793 | 0.431207 |
| State | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|---|---|---|
| Node | |||||||||
| 0 | ∅ | {5} | {7} | {5, 7} | |||||
| 1 | ∅ | {5} | {6} | {7} | {5, 6} | {5, 7} | {6, 7} | {5, 6, 7} | |
| 2 | ∅ | {5} | {6} | {6, 7} | |||||
| 3 | ∅ | {5} | {6} | {7} | {5, 6} | {5, 7} | {6, 7} | {5, 6, 7} | |
| 4 | ∅ | {5} | {6} | {7} | {5, 6} | {5, 7} | {6, 7} | {5, 6, 7} | |
| 5 | ∅ | {0} | {1} | {2} | {0, 1} | {0, 2} | {1, 2} | {0, 1, 2} | |
| 6 | ∅ | {1} | {2} | {3} | {1, 2} | {1, 3} | {2, 3} | {1, 2, 3} | |
| 7 | ∅ | {0} | {1} | {3} | {0, 1} | {0, 3} | {1, 3} | {0, 1, 3} | |
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| 0 | 0.0816538 | 0.194502 | 0.163308 | 0.357809 | ||||
| 1 | 0.0816538 | 0.194502 | 0.191247 | 0.385748 | 0.163308 | 0.357809 | 0.354554 | 0.549056 |
| 2 | 0.0956233 | 0.194502 | 0.191247 | 0.385748 | ||||
| 3 | 0.0816538 | 0.194502 | 0.191247 | 0.385748 | 0.163308 | 0.357809 | 0.354554 | 0.549056 |
| 4 | 0.0816538 | 0.194502 | 0.191247 | 0.385748 | 0.163308 | 0.357809 | 0.354554 | 0.549056 |
| 5 | 0.0366988 | 0.0740667 | 0.10116 | 0.175227 | 0.0733977 | 0.147464 | 0.174558 | 0.248624 |
| 6 | 0.0366988 | 0.10116 | 0.0733977 | 0.174558 | 0.10116 | 0.20232 | 0.174558 | 0.275718 |
| 7 | 0.0370333 | 0.0740667 | 0.10116 | 0.175227 | 0.10116 | 0.175227 | 0.20232 | 0.276387 |
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| 0 | 0.10241600 | 0.24395900 | 0.20483300 | 0.44879200 | ||||
| 1 | 0.03584640 | 0.08538720 | 0.08395830 | 0.16934600 | 0.07169290 | 0.15708000 | 0.15565100 | 0.24103800 |
| 2 | 0.11027700 | 0.22430800 | 0.22055400 | 0.44486200 | ||||
| 3 | 0.03584640 | 0.08538720 | 0.08395830 | 0.16934600 | 0.07169290 | 0.15708000 | 0.15565100 | 0.24103800 |
| 4 | 0.03584640 | 0.08538720 | 0.08395830 | 0.16934600 | 0.07169290 | 0.15708000 | 0.15565100 | 0.24103800 |
| 5 | 0.00178264 | 0.00359777 | 0.00491382 | 0.00851160 | 0.00356528 | 0.00716305 | 0.00847910 | 0.01207690 |
| 6 | 0.00155856 | 0.00429615 | 0.00311711 | 0.00741326 | 0.00429615 | 0.00859229 | 0.00741326 | 0.01170940 |
| 7 | 0.00405280 | 0.00810559 | 0.01107060 | 0.01917620 | 0.01107060 | 0.01917620 | 0.02214120 | 0.03024680 |
| l | i | V(i) | Label 1 | Label 2 | X(i) | T# | Tl = Tl−1∪S# | X | Probability * |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 3 | {7, 6, 5} | 1 | 001 | 1 | {5} | {3, 5} | (1/3) | p3,{5} |
| 1 | 5 | {6, 4, 3, 2, 1, 0} | 0 | 000000 | 0 | ∅ | {3, 5} | (1/3, 0/5) | p3,{5}p5,∅ |
| 2 | 5 | {6, 4, 3, 2, 1, 0} | 1 | 000001 | 1 | {5,7} | {3, 5, 0, 7} | (1/3, 1/5) | p3,{5}p5,{0} |
| 3 | 0 | {7, 5} | 0 | 00 | 0 | ∅ | {3, 5, 0, 7} | (1/3, 1/5, 0/0) | p3,{5}p5,{0}p0,∅ |
| 4 | 7 | {6, 4, 3, 2, 1, 0} | 0 | 000000 | 0 | ∅ | {3, 5, 0, 7} | (1/3, 1/5, 0/0, 0/7) | p3,{5}p5,{0}p0,{7}p7,∅ |
| 5 | 7 | {6, 4, 3, 2, 1, 0} | 1 | 000001 | 1 | ∅ | {3, 5, 0, 7} | (1/3, 1/5, 0/0, 1/7) | p3,{5}p5,{0}p0,{7}p7,{1} |
| i | Narea | Vector Number | Runtime | R1 = R0.85 | R2 = R0.15 | R1-R2 |
|---|---|---|---|---|---|---|
| 0 | 1 | 1 | 0.000 | 1.0000 | 1.0000 | 0.0000 |
| 2 | 5 | 0.000 | 0.8976 | 0.8919 | 0.0057 | |
| 3 | 191 | 0.003 | 0.8938 | 0.8864 | 0.0074 | |
| 4 | 1106 | 0.011 | 0.8895 | 0.8811 | 0.0084 | |
| 5 | 18036 | 0.377 | 0.8863 | 0.8776 | 0.0087 | |
| 6 | 356664 | 6.448 | 0.8776 | 0.8689 | 0.0087 | |
| 7 | 7510836 | 84.470 | 0.8283 | 0.8253 | 0.0031 | |
| 8 | 87742588 | 1131.378 | 0.5518 | 0.5654 | −0.0136 | |
| 1 | 1 | 1 | 0.000 | 1.0000 | 1.0000 | 0.0000 |
| 2 | 13 | 0.000 | 0.9642 | 0.9612 | 0.0030 | |
| 3 | 324 | 0.007 | 0.9620 | 0.9586 | 0.0034 | |
| 4 | 2607 | 0.022 | 0.9586 | 0.9547 | 0.0040 | |
| 5 | 36276 | 0.324 | 0.9524 | 0.9487 | 0.0038 | |
| 6 | 773828 | 6.779 | 0.9349 | 0.9325 | 0.0025 | |
| 7 | 13814130 | 152.826 | 0.8530 | 0.8617 | −0.0087 | |
| 8 | 122668428 | 1591.609 | 0.5144 | 0.5412 | −0.0268 | |
| 2 | 1 | 1 | 0.000 | 1.0000 | 1.0000 | 0.0000 |
| 2 | 5 | 0.000 | 0.8897 | 0.8904 | −0.0007 | |
| 3 | 255 | 0.016 | 0.8875 | 0.8872 | 0.0003 | |
| 4 | 1654 | 0.031 | 0.8840 | 0.8832 | 0.0008 | |
| 5 | 21394 | 0.527 | 0.8782 | 0.8776 | 0.0005 | |
| 6 | 415994 | 8.519 | 0.8647 | 0.8649 | −0.0003 | |
| 7 | 8604502 | 117.473 | 0.8158 | 0.8213 | −0.0055 | |
| 8 | 95178046 | 1374.070 | 0.5484 | 0.5675 | −0.0191 | |
| 3 | 1 | 1 | 0.000 | 1.0000 | 1.0000 | 0.0000 |
| 2 | 13 | 0.000 | 0.9642 | 0.9612 | 0.0030 | |
| 3 | 324 | 0.000 | 0.9620 | 0.9586 | 0.0034 | |
| 4 | 2607 | 0.031 | 0.9586 | 0.9547 | 0.0040 | |
| 5 | 36212 | 0.347 | 0.9524 | 0.9487 | 0.0038 | |
| 6 | 771940 | 7.105 | 0.9349 | 0.9325 | 0.0025 | |
| 7 | 13797962 | 167.760 | 0.8530 | 0.8617 | −0.0087 | |
| 8 | 122821892 | 3518.926 | 0.5144 | 0.5412 | −0.0268 | |
| 4 | 1 | 1 | 0.000 | 1.0000 | 1.0000 | 0.0000 |
| 2 | 13 | 0.000 | 0.9642 | 0.9612 | 0.0030 | |
| 3 | 324 | 0.004 | 0.9620 | 0.9586 | 0.0034 | |
| 4 | 2607 | 0.026 | 0.9586 | 0.9547 | 0.0040 | |
| 5 | 36180 | 0.346 | 0.9524 | 0.9487 | 0.0038 | |
| 6 | 771732 | 7.075 | 0.9349 | 0.9325 | 0.0025 | |
| 7 | 13791562 | 156.802 | 0.8530 | 0.8617 | −0.0087 | |
| 8 | 123244356 | 1742.573 | 0.5144 | 0.5412 | −0.0268 | |
| 5 | 1 | 1 | 0.000 | 1.0000 | 1.0000 | 0.0000 |
| 2 | 252 | 0.003 | 0.9949 | 0.9963 | −0.0014 | |
| 3 | 594 | 0.006 | 0.9865 | 0.9892 | −0.0027 | |
| 4 | 8664 | 0.075 | 0.9798 | 0.9834 | −0.0036 | |
| 5 | 119914 | 1.082 | 0.9696 | 0.9753 | −0.0057 | |
| 6 | 2050424 | 18.796 | 0.9426 | 0.9540 | −0.0113 | |
| 7 | 26321044 | 339.085 | 0.8306 | 0.8604 | −0.0298 | |
| 8 | 183961358 | 2505.281 | 0.4628 | 0.5074 | −0.0446 | |
| 6 | 1 | 1 | 0.000 | 1.0000 | 1.0000 | 0.0000 |
| 2 | 125 | 0.002 | 0.9984 | 0.9976 | 0.0008 | |
| 3 | 355 | 0.005 | 0.9956 | 0.9942 | 0.0014 | |
| 4 | 5216 | 0.077 | 0.9916 | 0.9904 | 0.0012 | |
| 5 | 70006 | 1.172 | 0.9815 | 0.9811 | 0.0004 | |
| 6 | 1153321 | 18.114 | 0.9573 | 0.9596 | −0.0023 | |
| 7 | 14700763 | 178.070 | 0.8552 | 0.8706 | −0.0154 | |
| 8 | 120803944 | 1547.187 | 0.4911 | 0.5204 | −0.0292 | |
| 7 | 1 | 1 | 0.000 | 1.0000 | 1.0000 | 0.0000 |
| 2 | 124 | 0.002 | 0.9900 | 0.9918 | −0.0018 | |
| 3 | 456 | 0.007 | 0.9787 | 0.9810 | −0.0022 | |
| 4 | 7998 | 0.160 | 0.9725 | 0.9753 | −0.0028 | |
| 5 | 130986 | 1.845 | 0.9650 | 0.9689 | −0.0039 | |
| 6 | 2571160 | 35.229 | 0.9452 | 0.9528 | −0.0077 | |
| 7 | 29212442 | 461.061 | 0.8386 | 0.8641 | −0.0255 | |
| 8 | 179307046 | 2957.642 | 0.4680 | 0.5105 | −0.0425 |
| Narea | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | PR | 1-PR | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| i | |||||||||||
| 0 | 1 | 7 | 7 | 7 | 7 | 7 | 7 | 1 | 8 | 1 | |
| 1 | 1 | 4 | 4 | 4 | 4 | 4 | 2 | 3 | 4 | 3 | |
| 2 | 1 | 8 | 8 | 8 | 8 | 8 | 8 | 2 | 7 | 1 | |
| 3 | 1 | 4 | 4 | 4 | 4 | 4 | 2 | 3 | 4 | 3 | |
| 4 | 1 | 4 | 4 | 4 | 4 | 4 | 2 | 3 | 4 | 3 | |
| 5 | 1 | 2 | 2 | 2 | 2 | 3 | 6 | 8 | 2 | 7 | |
| 6 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 6 | 1 | 8 | |
| 7 | 1 | 3 | 3 | 3 | 3 | 2 | 5 | 7 | 3 | 6 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yeh, W.-C.; Kuo, C.-C. Predicting and Modeling Wildfire Propagation Areas with BAT and Maximum-State PageRank. Appl. Sci. 2020, 10, 8349. https://doi.org/10.3390/app10238349
Yeh W-C, Kuo C-C. Predicting and Modeling Wildfire Propagation Areas with BAT and Maximum-State PageRank. Applied Sciences. 2020; 10(23):8349. https://doi.org/10.3390/app10238349
Chicago/Turabian StyleYeh, Wei-Chang, and Chia-Chen Kuo. 2020. "Predicting and Modeling Wildfire Propagation Areas with BAT and Maximum-State PageRank" Applied Sciences 10, no. 23: 8349. https://doi.org/10.3390/app10238349
APA StyleYeh, W.-C., & Kuo, C.-C. (2020). Predicting and Modeling Wildfire Propagation Areas with BAT and Maximum-State PageRank. Applied Sciences, 10(23), 8349. https://doi.org/10.3390/app10238349





