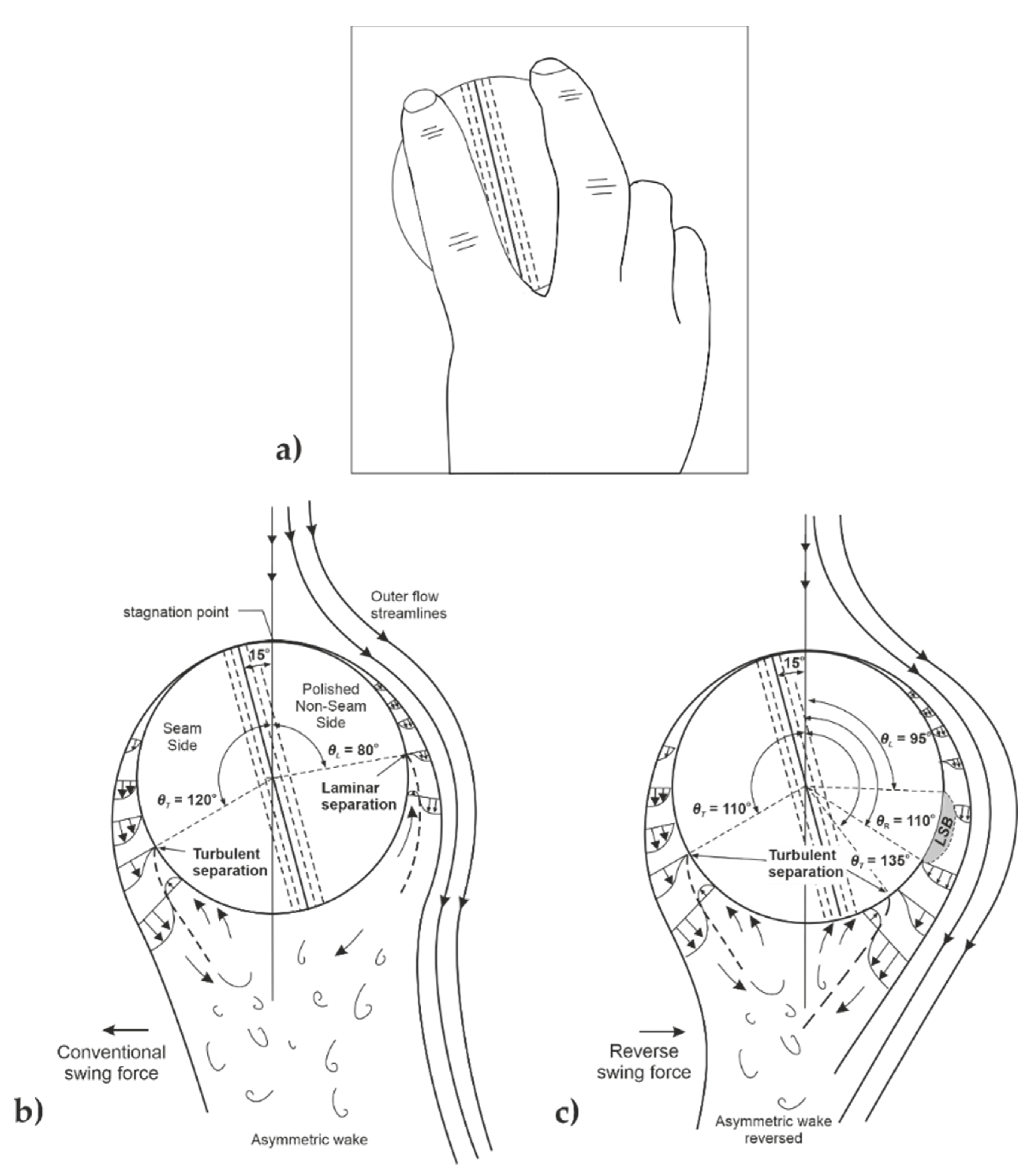
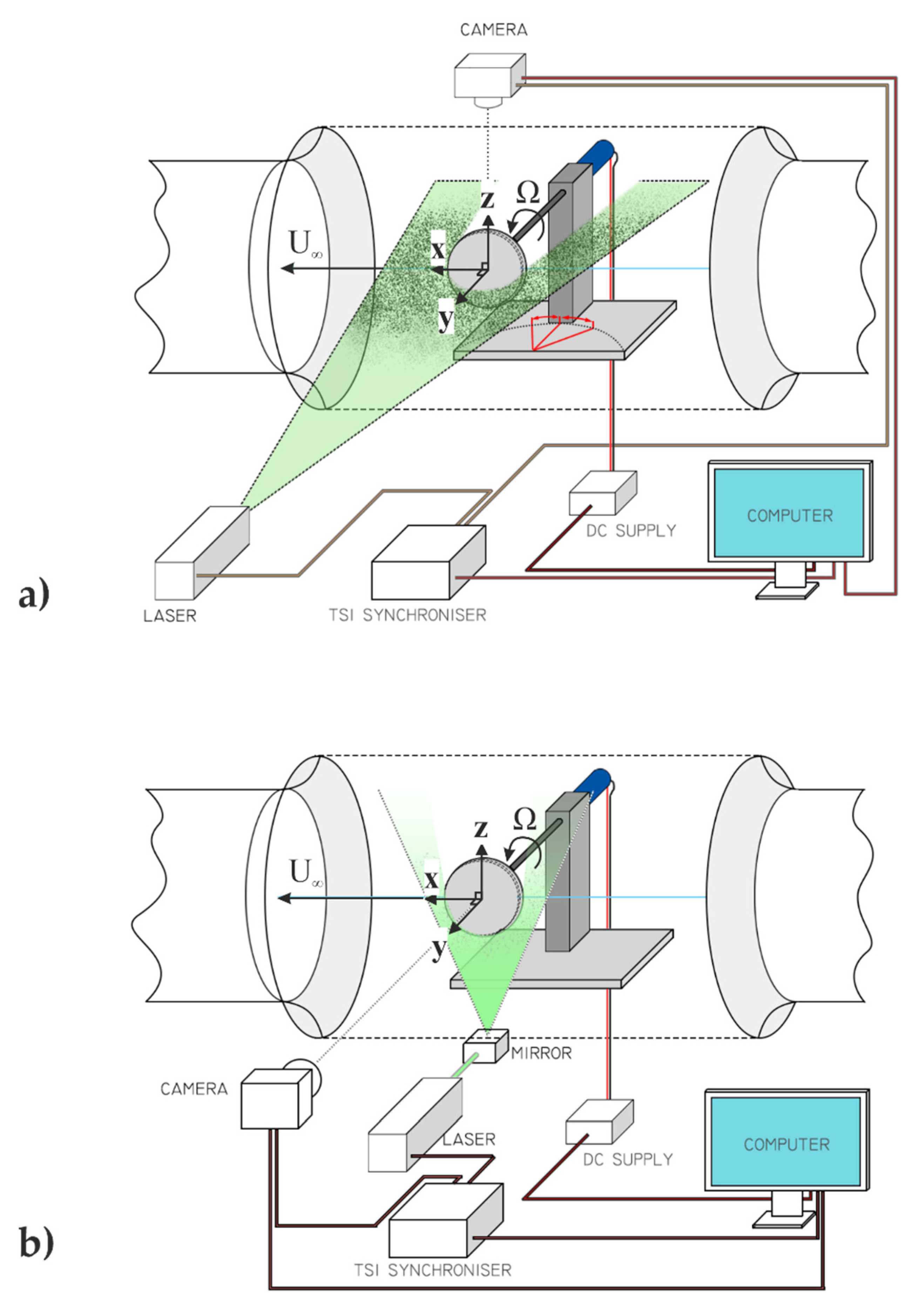
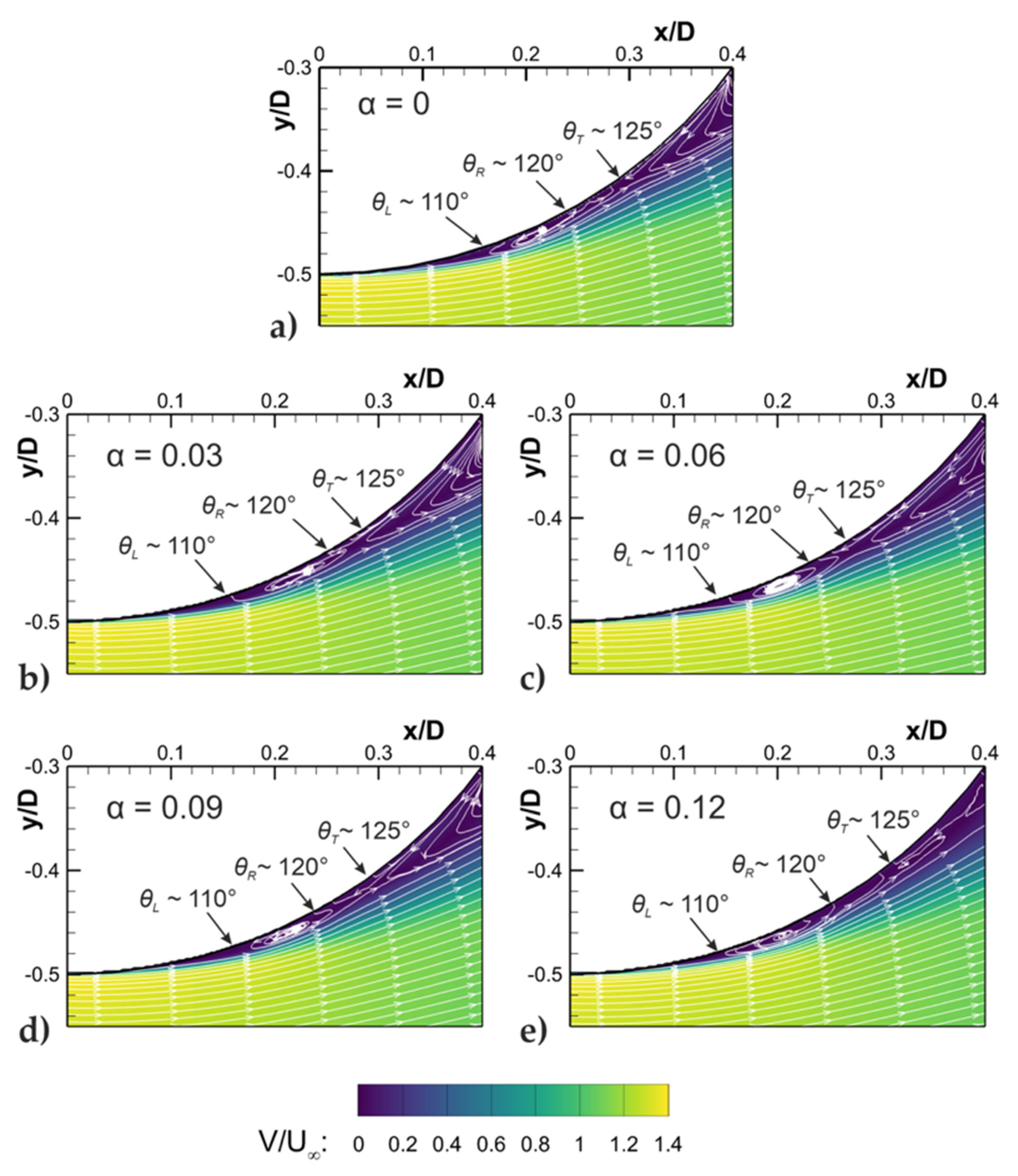
2.1. Flow Separation on Spheres and Cricket Balls
Achenbach published the results from a definitive set of experiments showing how the Reynolds number affects the location of boundary layer separation on hydraulically-smooth spheres [
6]. These locations were derived from skin-friction measurements; the results are presented in
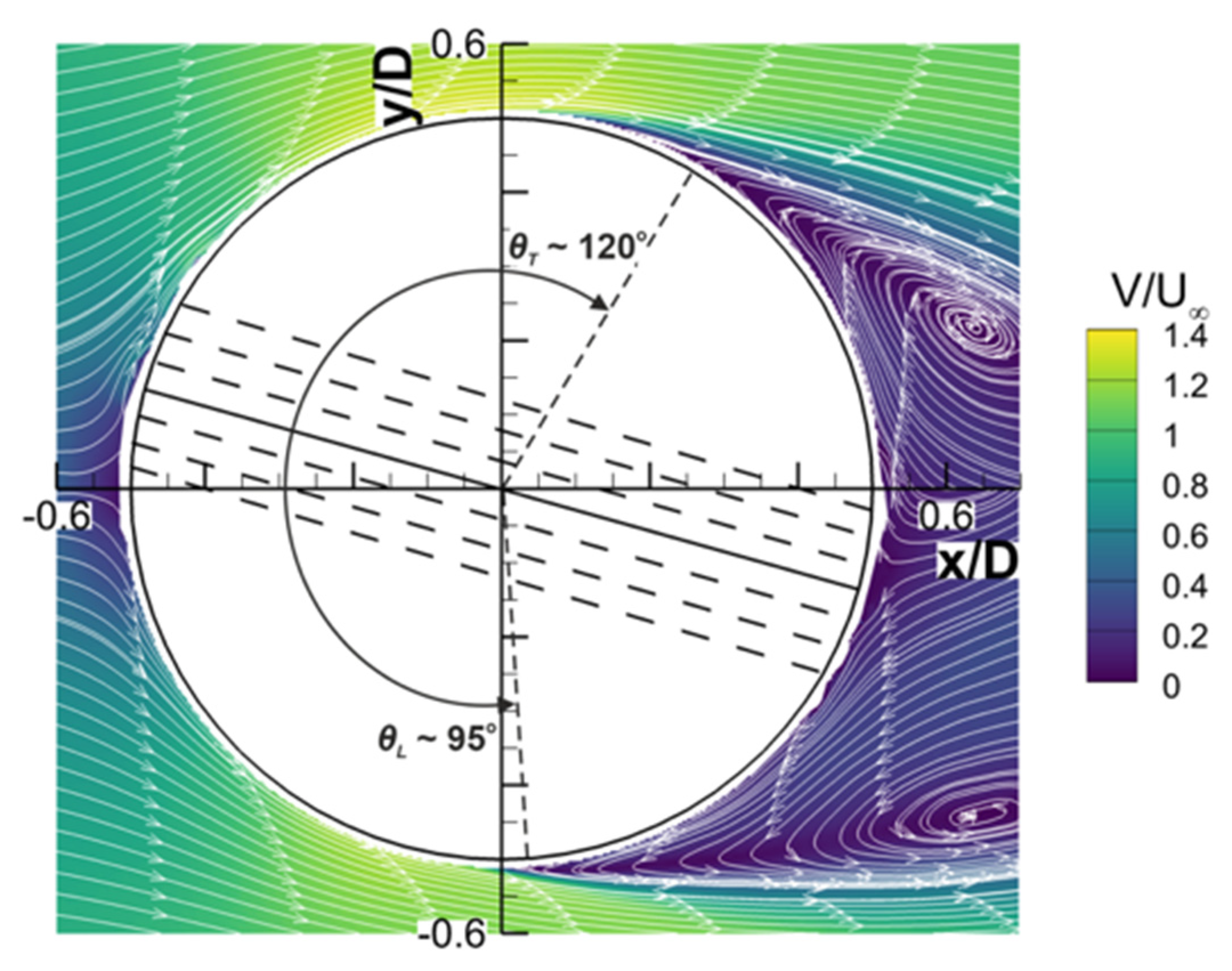
Figure 2, denoted by the open circles. Below a critical Reynolds number of Re = 2 × 10
5 (i.e., sub-critical flow), Achenbach showed that the boundary layer is laminar and the adverse pressure gradient on the sphere causes it to separate at around θ
L~80°. Within the critical flow regime (2 × 10
5 < Re < 4 × 10
5), the boundary layer transitions to turbulence and the separation angle is delayed to θ
T~120°. As the Reynolds number increases beyond critical flow to a supercritical flow regime, the point of boundary layer separation gradually retreats upstream. It was later shown by Taneda, using oil flow visualization on a smooth sphere, that the increase in separation angle at the critical Reynolds number is associated with an LSB—see inset in
Figure 2 [
7]. An LSB forms as the laminar boundary layer separates from the sphere (θ
L) before transitioning to turbulence and reattaching downstream (θ
R); the turbulent boundary layer separates yet further downstream (θ
T). Taneda measured 92° < θ
L < 110°, 107° < θ
R < 127°, and 123° < θ
T < 147° (depending on Re). Importantly, θ
T is larger in the presence of an LSB during the critical flow regime, than in the absence of the LSB during the supercritical flow regime.
Achenbach later investigated the effect of surface roughness on the separation angles of spheres [
8]. He found that the value of Re in the critical regime reduces with increasing roughness, as the roughness destabilizes the boundary layer and causes it to transition to turbulence earlier. The size of the critical region also increases, described by the range of Re across which the flow regime changes. These results are also shown in
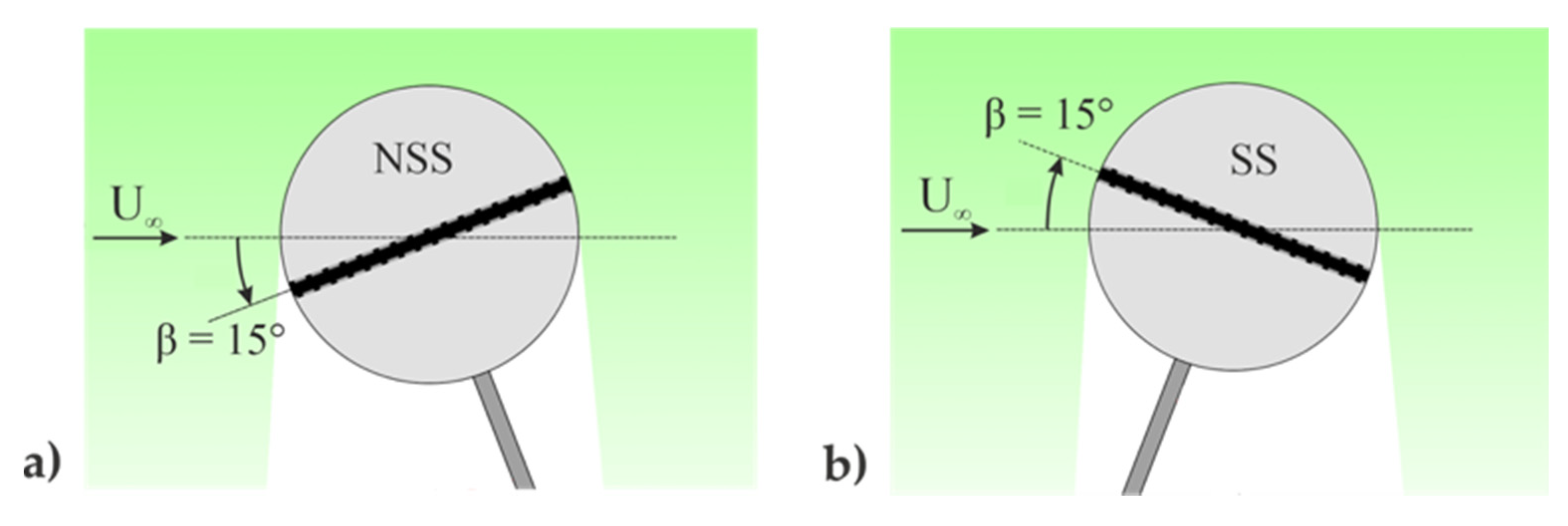
Figure 2 by the open triangle and square symbols. In the scenario of a cricket ball with an angled seam, the two hemispheres will feature a different roughness, the separation angles will be different, and a lateral aerodynamic force will be caused by the asymmetric distribution of pressure.
Figure 2 demonstrates this asymmetry for CS and RS in the context of a cricket match. Consider a swing bowler delivering a new ball at 90 mph (Re~2 × 10
5). The relative size of the primary seam (hence primary, dominating roughness) on the SS is approximately equivalent to
k/d = 1250 × 10
−5 (denoted by the squares). For the sake of demonstration, it is assumed that the surface of the NSS for a new ball is hydraulically-smooth. At these conditions, θ
L = 82° on the NSS (in the sub-critical regime) and θ
T = 100° on the SS (in the super-critical regime), resulting in CS. As the ball ages during the course of play, the NSS roughens slightly to
k/d = 250 × 10
−5 (despite careful polishing of the ball by the fielding side). Assuming the bowler delivers the ball at the same speed (and therefore, same Re), now θ
T = 120° on the NSS (in the critical regime) and θ
T = 100° on the SS (in the super-critical regime), resulting in RS. The red region demonstrates where the separation angle on the NSS is less than the SS, corresponding to CS, and the solid blue region corresponds to RS for an aged ball. At larger Re, the hatched blue region corresponds to RS for a new ball.
Achenbach’s results show that RS for a new cricket ball would occur if it were bowled at an impossible speed of >75 m/s (Re > 3 × 10
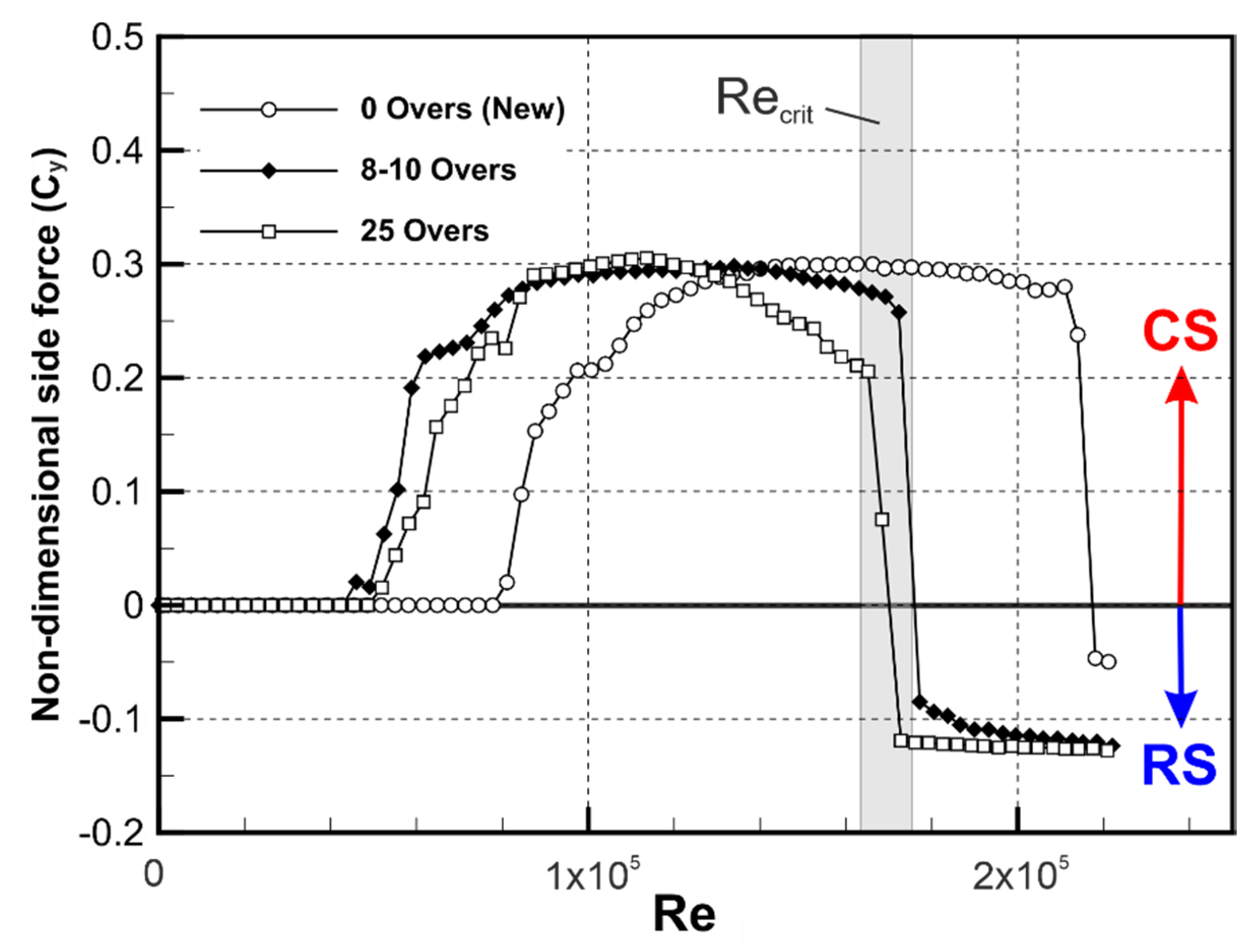
5); here the surface on the NSS is assumed to be hydraulically-smooth and the ball to be a perfect sphere. In practice, cricket balls are imperfect spheres with manufacturing irregularities and an inherent surface roughness, which are exacerbated as the ball ages and wears. Direct side force measurements on new and aged stationary Dukes cricket balls in a wind tunnel by Scobie et al. [
4] are presented in
Figure 3 as a function of Re. Note that Scobie et al. [
4,
5] investigated an extensive series of balls aged under first-class match conditions and provided by professional cricketers. For the results presented in
Figure 3, the seam angle was set at
= 15°. The critical Re reduces as the ball ages, due to the increasing surface roughness. Interestingly, it shows that RS on a new Dukes ball can be achieved if bowled at 100 mph (Re~2.2 × 10
5), suggesting that the surface roughness of a new ball is in the range 0 <
k/
d < 250 × 10
−5. Scobie et al. [
5] collected side force measurements on a double-sized scaled model (of the same dimensions and surface roughness as that used in this study) and showed that this 3D printed double-sized model had a similar aerodynamic behavior to a real Dukes ball that is approximately 25 overs old. The critical region (1.65 × 10
5 < Re < 1.75 × 10
5) is marked in
Figure 3. The non-dimensional side force coefficients for CS (C
Z~0.3) are comparable with the results of other studies on stationary balls [
9,
10]. Note that the magnitude of C
Z for RS is less than that for CS either side of the critical Re (Re
crit). Sustained swing over the full trajectory of flight is further complicated by aerodynamic drag, which will continually decrease Re; the net lateral movement will be reduced if the ball experiences a combination of both CS and RS. Swing can be elusive and the appropriate conditions for its manifestation, even with experience, may be elusive.
In practice, the bowler will impart a small backspin on the ball. Bentley et al. [
11] found that the optimum spin rate to achieve maximum swing is around 10 rev/s. However, it has been shown that a high backspin can reduce the lateral force [
12]. It is argued that the rotation exaggerates the surface roughness and any other protrusions or irregularities, including the quarter seams and logo embossments, disrupting the boundary layer. This rotation effect has been put forth as a skeptical argument against the existence of an LSB on the NSS of a rotating cricket ball in the context of a match [
13].
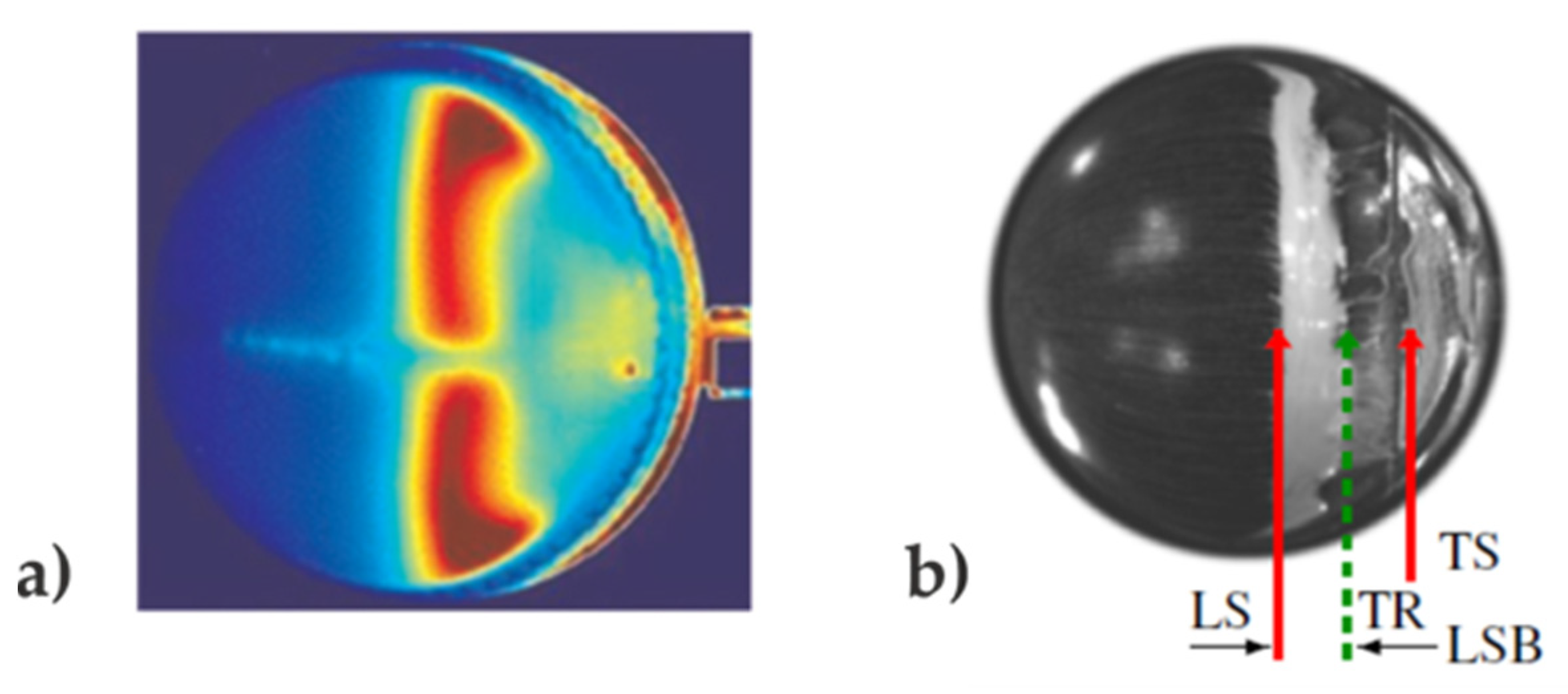
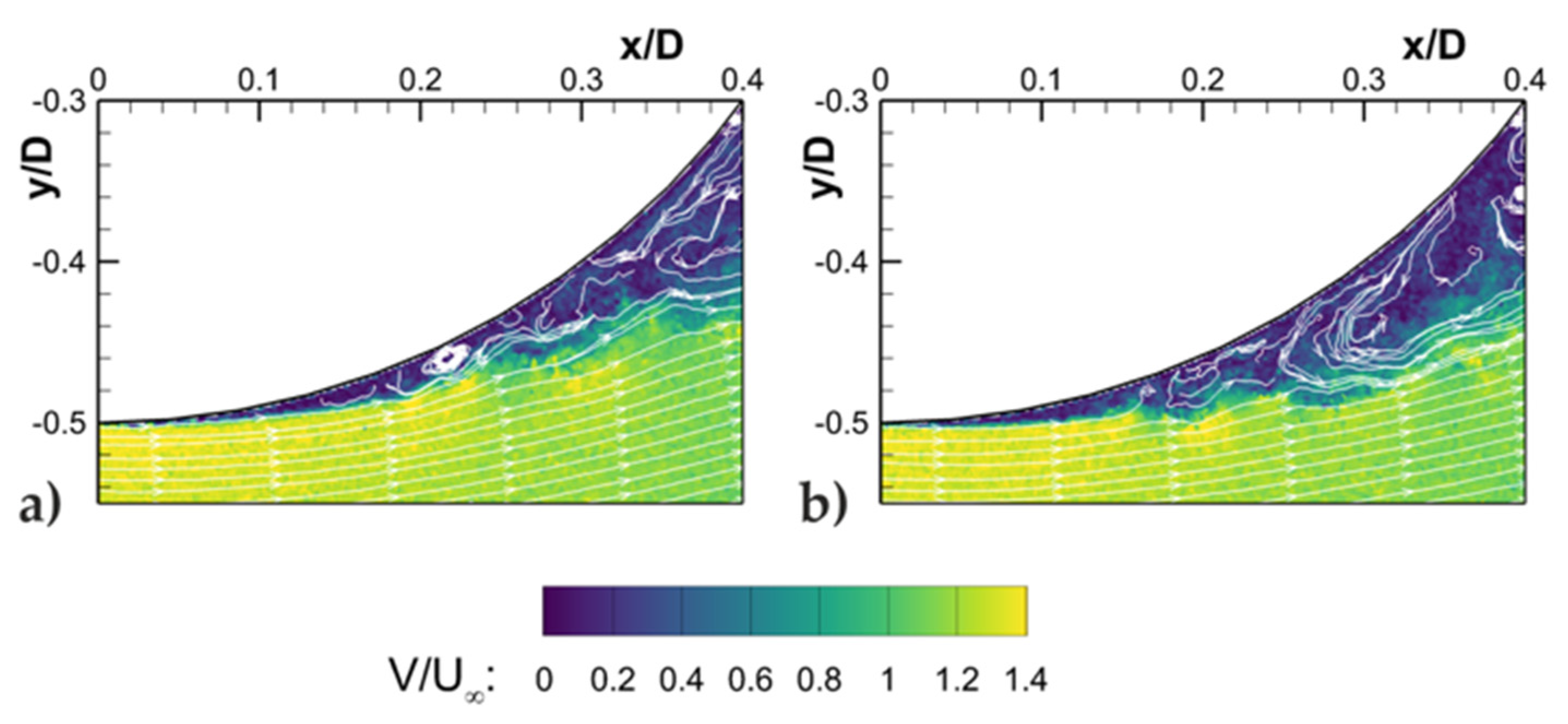
The presence of the LSB on a non-rotating cricket ball was first demonstrated by Scobie et al. [
5] and later validated by Deshpande et al. [
14]. Scobie et al. demonstrated this phenomenon using heated flow visualization and pressure measurements on both a double-scaled ball and on actual cricket balls aged under first-class match conditions. Deshpande et al. modelled a cricket ball as a sphere with a trip to act as the seam, showing the formation of the LSB using oil flow visualization experiments in a wind tunnel. Images from the above papers are shown in
Figure 4. Deshpande et al. also showed that an LSB forms over the SS at low Re during the CS regime. Earlier experiments by Deshpande et al. [
15] demonstrated the instability and intermittency of an LSB over a smooth sphere, by means of unsteady force and pressure measurements. They found that the critical flow regime can be further categorized into three sub-regimes based on the nature of the LSB.
The method of PIV has not been used to identify the LSB on a cricket ball (rotating or non-rotating), but it has been used to show the boundary layer separation angles on a stationary sphere with a trip at the sub-critical and critical flow regimes, demonstrating CS and RS [
10]. The image resolution of their system was too low to be able to resolve an LSB. This paper aims to show that an LSB is present on a cricket ball subject to backspin.
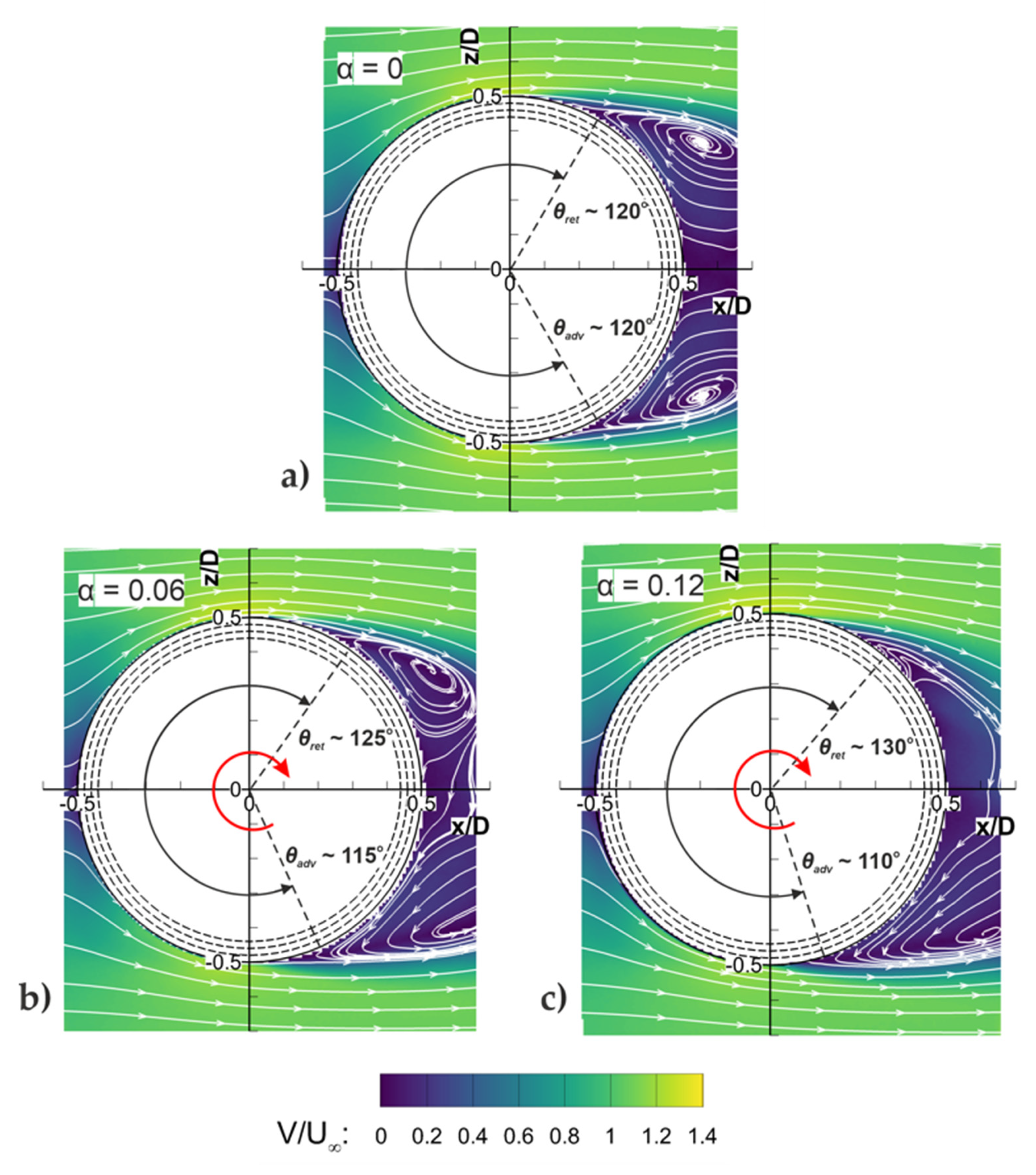
2.2. Magnus Effect
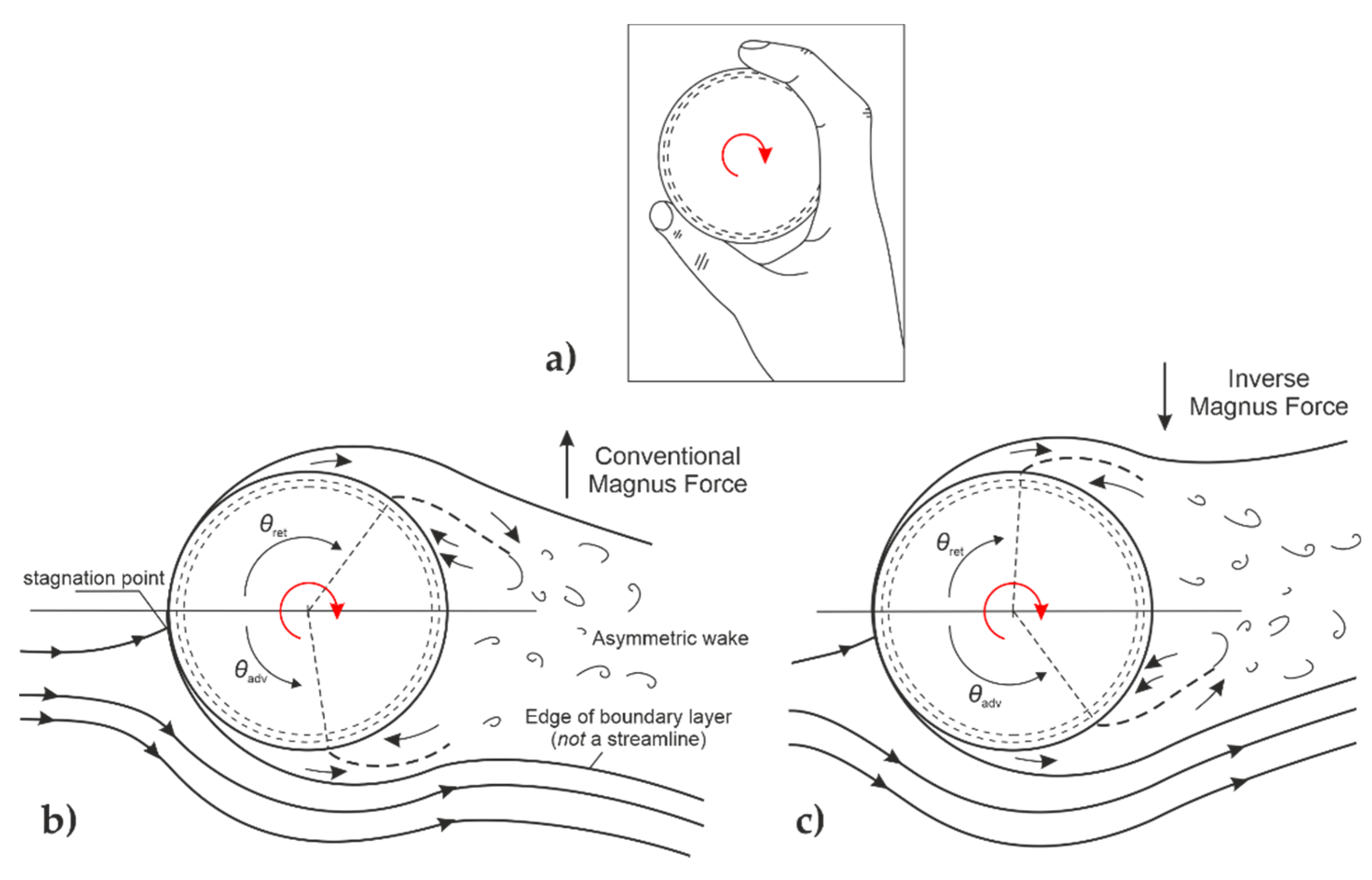
Video analysis reveals that swing bowlers apply a typical backspin of around 10 rev/s when they release the ball. In addition to stabilizing the seam, the rotation of the ball induces a Magnus force in the vertical axis (orthogonal to the direction of any swing). This deviation from the main trajectory influences the location of where the ball pitches and is also important to spin bowling. The bowler’s hand position to apply backspin is illustrated in
Figure 5a. The Magnus force is governed by Re and the spin ratio,
α (see nomenclature), which describes the ratio of the tangential velocity on the surface of a rotating body to the velocity of the freestream. A typical swing bowler, operating at 40 m/s (~90 mph) with a backspin of 10 rev/s, will therefore create a spin ratio of α~0.06.
Mehta [
13] has demonstrated the Magnus effect on a cricket ball in a water channel using dye flow visualization. Sayers and Lelimo [
9] collected lift force measurements on a cricket ball rotating about its axis (i.e.,
= 0°) up to spin ratios of
α = 0.3, showing that the lift coefficient can reach C
L = 0.3.
For a rotating sphere in the conventional Magnus regime (
Figure 5b), the upper (retreating) side of the ball provides extra momentum to the boundary layer, and so separation is delayed. In addition, if Re is in the super-critical or trans-critical flow regime, the increased relative speed between the surface and the freestream will cause earlier boundary layer separation on the lower (advancing) side. For θ
ret > θ
adv, the Magnus force provides lift, and this is classified as conventional Magnus. The boundary layers can be laminar or turbulent, as long as they are operating in the same flow regime.
It has been theorized that if bowlers impart a large enough backspin on the ball, then the Magnus effect is inversed and the pressure asymmetry and wake switch direction, as illustrated in
Figure 5c. (Mittal has speculated in sports journalist articles that this is exploited in a singular fashion, such that the ball pitches further from the batsman than expected.) This inversion effect has been demonstrated computationally and experimentally on smooth rotating spheres [
16,
17,
18] and dimpled golf balls [
19]. It is often explained by an effective Re on the advancing and retreating sides based on the velocity difference, which is the combination of Re and
α. Sakib and Smith [
19] identified that the inverse Magnus effect on a golf ball only occurs when Re is close to the critical regime. For a dimpled golf ball, which has a roughness that is comparable to the seam of a cricket ball, they found that a sufficient backspin causes the effective Re on the retreating side to reduce to the sub-critical regime, where laminar separation occurs. At this point θ
ret < θ
adv and an inverse Magnus force is generated. It is expected that a similar behavior would occur for a cricket ball, under appropriate conditions.