Techno-Economic Analysis of a Heat Pump Cycle Including a Three-Media Refrigerant/Phase Change Material/Water Heat Exchanger in the Hot Superheated Section for Efficient Domestic Hot Water Generation
Abstract
1. Introduction
- the possibility to pre-heat the process water with the HP’s condenser during energy efficient DHW generation (compared with operating mode (c) in Section 2.1 and Appendix A);
- the limitations in the storage capacity of the RPW-HEX and the DHW storage devices;
- the heat losses to the surrounding of the RPW-HEX and the decentralized DHW storage devices;
- the solar radiation, ventilation rates and many other constraints of the building;
- the control strategy.
2. Case Studies and Operation Modes of the System
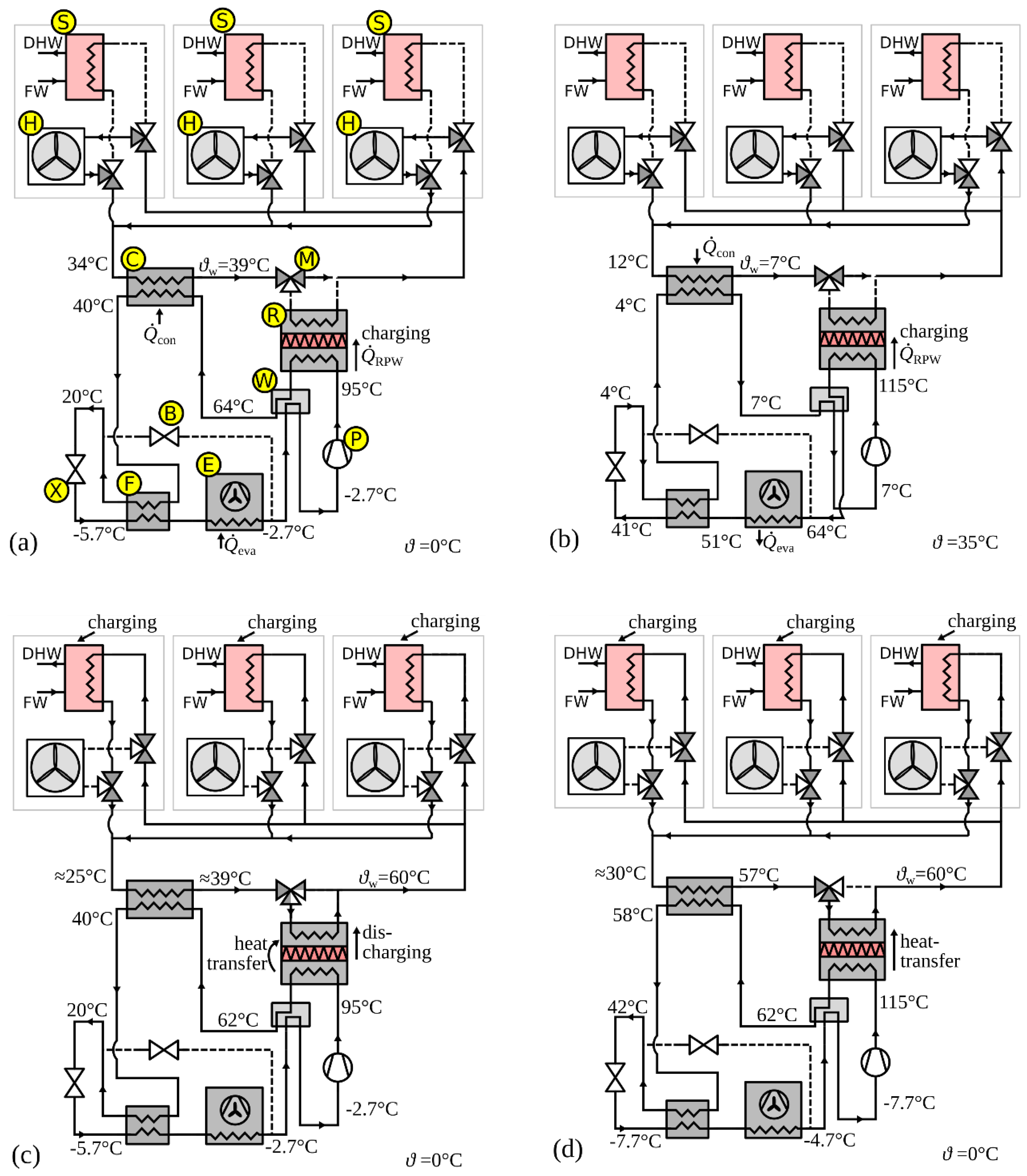
2.1. Operation Modes of the HP with Integrated RPW-HEX
- (a)
- heating operation and charging the RPW-HEX (0 < SoC↑ ≤ 1)
- (b)
- cooling operation and charging the RPW-HEX (0 < SoC↑ ≤ 1)
- (c)
- energy efficient DHW generation by discharging the RPW-HEX and pre-heating via the condenser (0 ≤ SoC↓ ≤ 1)
- (d)
- conventional (inefficient) direct DHW generation (SoC = 0)
- (e)
- heating operation when the RPW-HEX is fully charged (SoC = 1)
- (f)
- cooling operation when the RPW-HEX is fully charged (SoC = 1)
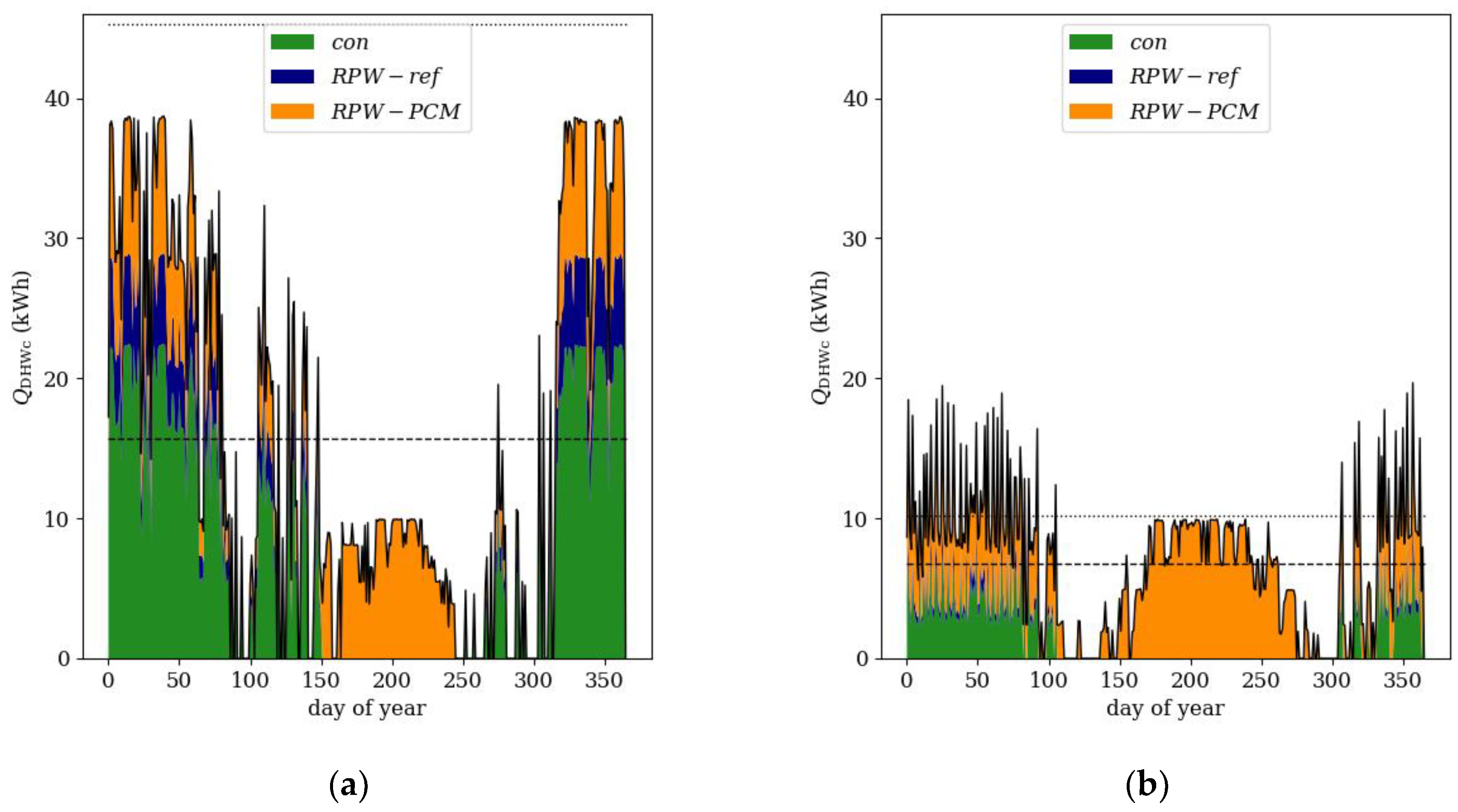
2.2. Control Strategy
2.3. Case Studies
- Case #1: A passive house located in Helsinki with a “low-temperature heating” distribution system and a PCM with a phase transition at 64 °C
- Case #2: A low energy building located in Strasbourg with an “intermediate-temperature heating” distribution system and a PCM with a phase transition at 64 °C
- Case #3: A refurbished building located in Athens with an “intermediate-temperature heating” system and a PCM with a phase transition at 64 °C
- The ground floor of the standard apartment is a square with 75 m2 and the room height is 3 m.
- Two outer walls are considered which are oriented to the south and the west. The U-values for the walls are 0.09, 0.11, and 3 Wm−2 K−1 for the buildings located in Helsinki, Strasbourg, and Athens, respectively
- The wall (south and west) to window ratio is 20% and the U-values for the windows are 0.75, 0.9, and 5 Wm−2 K−1 for the buildings located in Helsinki, Strasbourg, and Athens, respectively.
- If cooling is needed, the windows are shaded with a solar radiation transmittance of 15%.
- The ventilation rate is 0.8 m3m−2h−1
- The air heat recovery efficiency is 75% for the passive house located in Helsinki
- The heat gains from lights and equipment are 5 Wm−2
- The DHW consumption of each full-scale apartment was 5.845 kWh, which is comparable to a medium water consumption as defined in [18].
- The apartments were scaled to multiples of 1/4 of the full-scale. The DHW storage devices were considered in full-scale for each apartment.
- Fresh water for the decentralized DHW storage devices is provided at 12 °C.
3. Methodology
3.1. Simulation Models
3.2. Annual Energy Efficiency Calculations
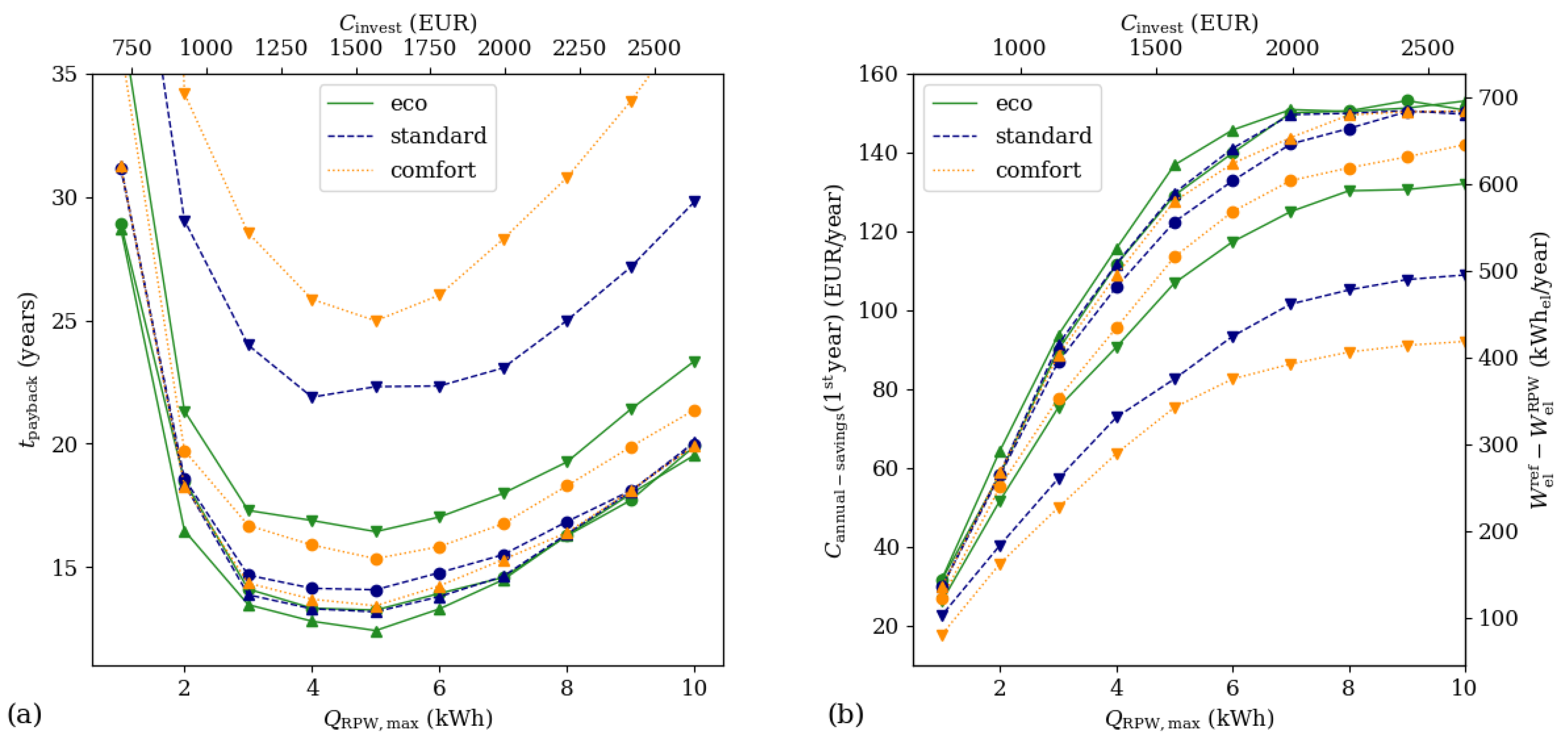
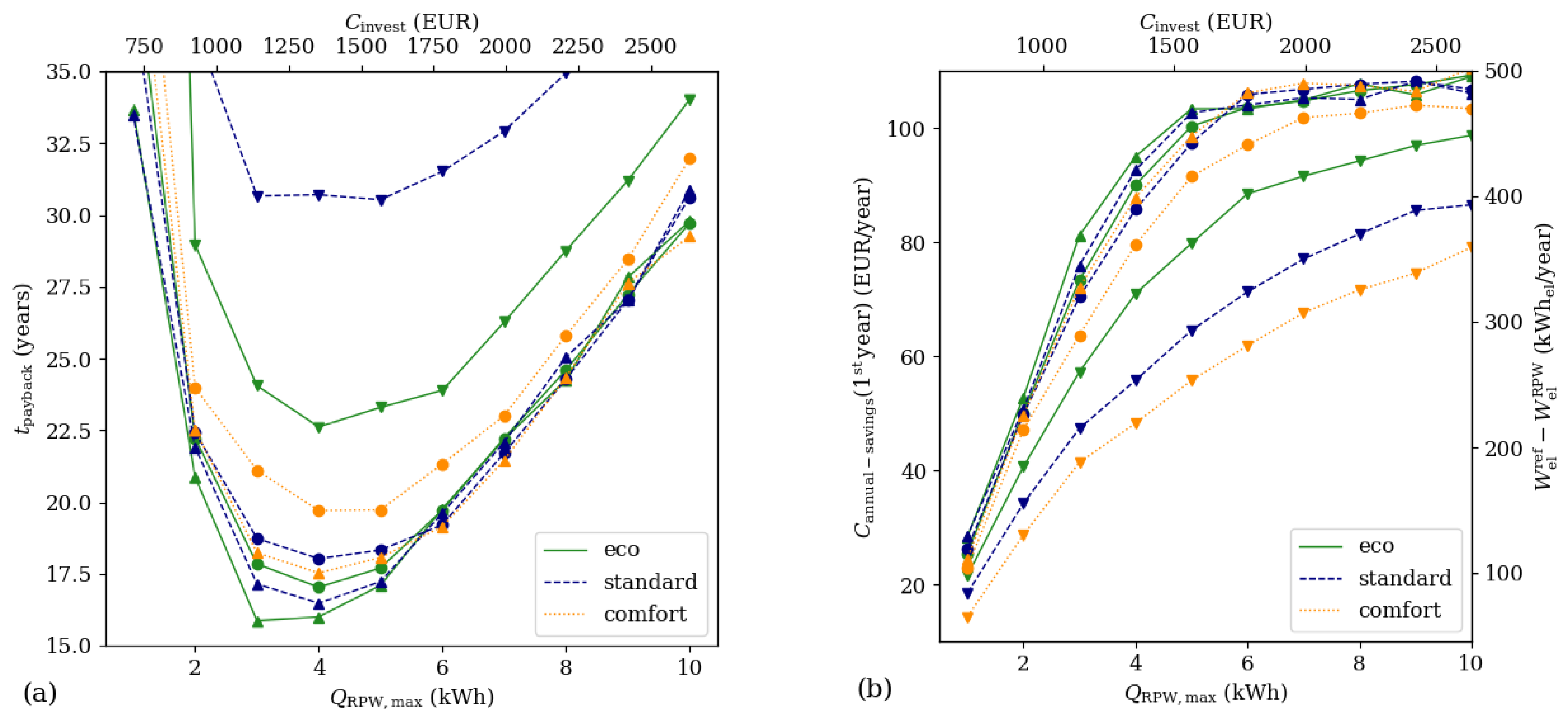
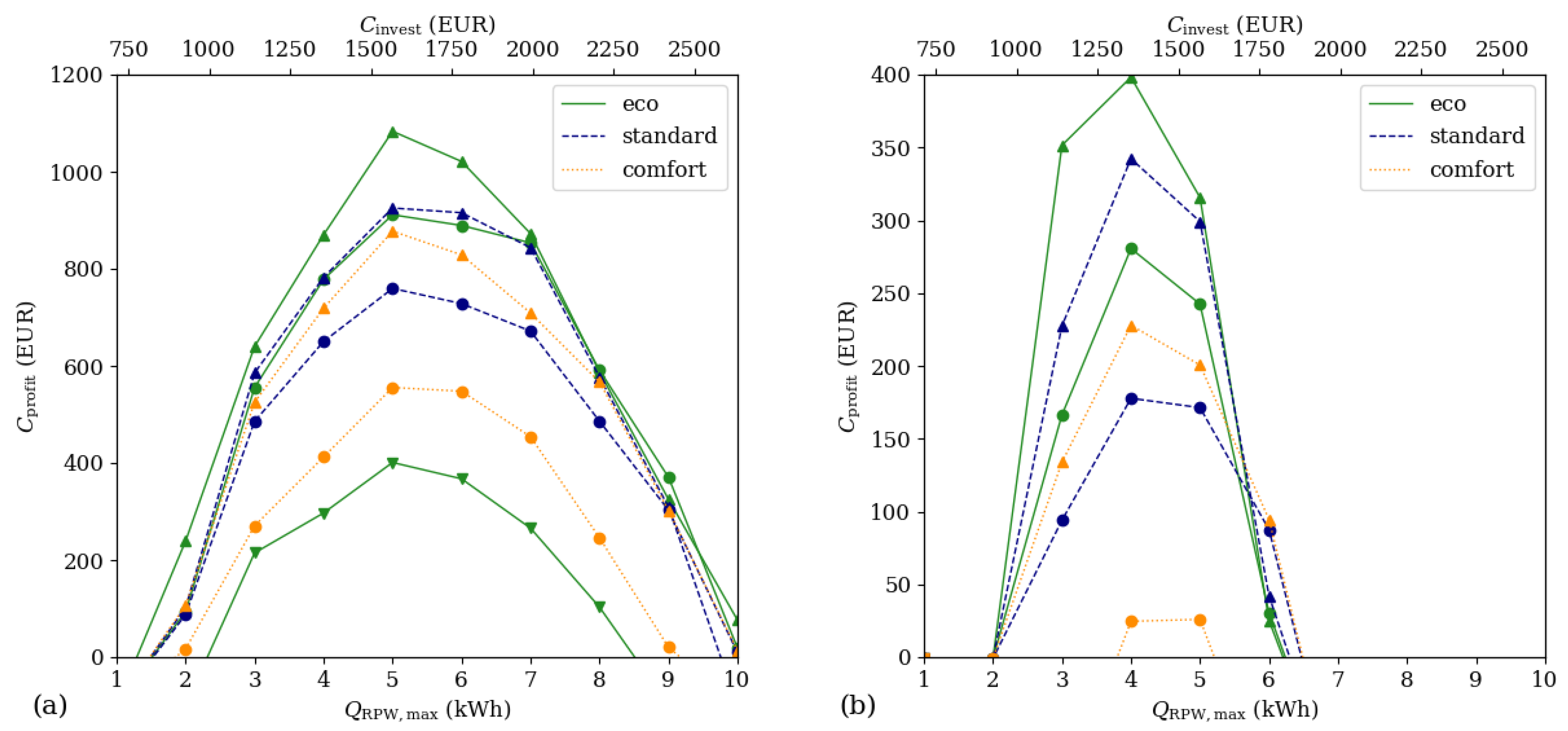
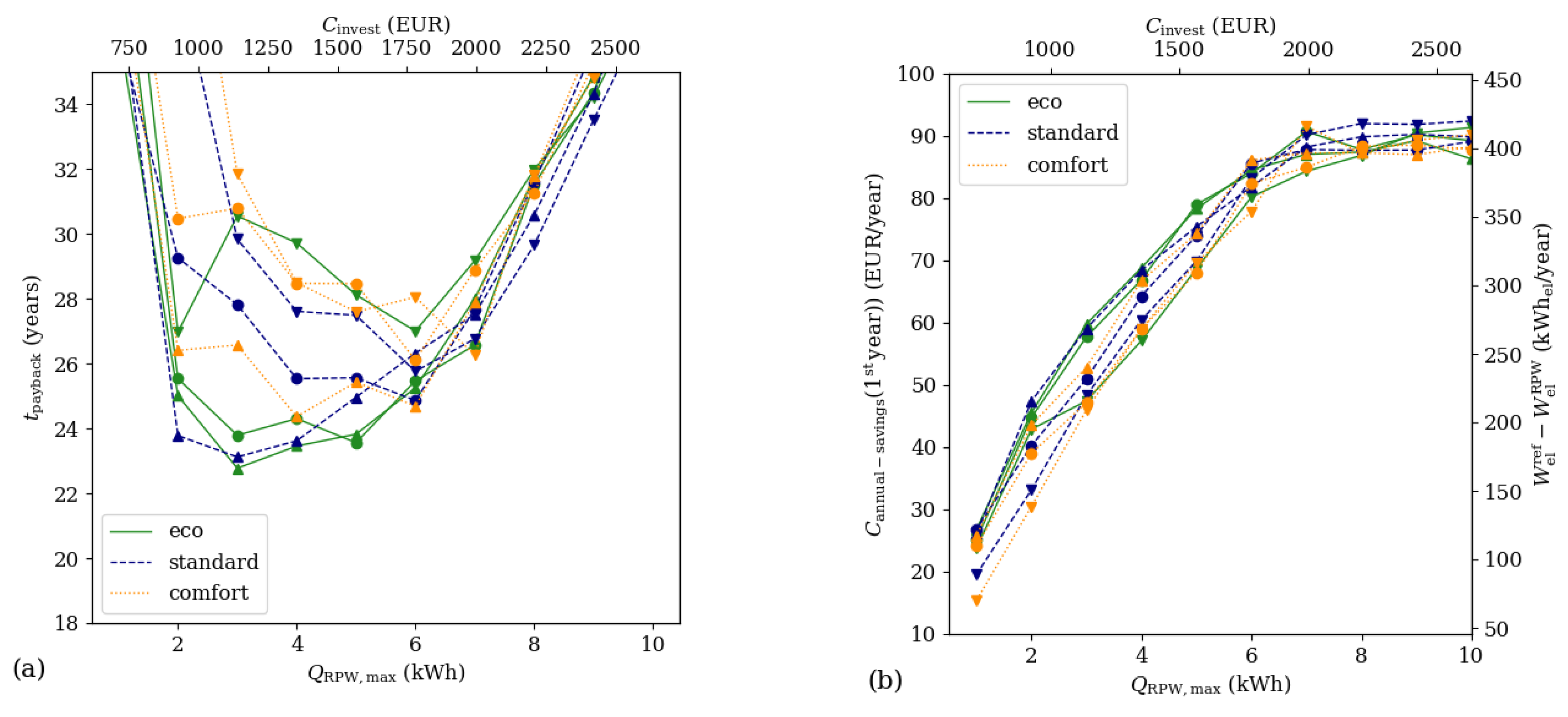
3.3. Parameter Variations
- eco-mode: charging starts if hot water (in a perfect thermocline) is below 40 L and stops at 90 L
- standard-mode: DHW generation is initiated if hot water is below 55 L and stops at 105 L
- comfort-mode: charging starts if hot water is below 70 L and stops at 120 L
3.4. Economic Performance Indicators
4. Results and Discussion
5. Conclusions and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbols | |
| a,b,d,k1 | Constants of the moving boundary model for the DHW storage (W, -, J−1, J) |
| ADHW | Ground area of the DHW storage (m2) |
| Specific costs (EUR/kWhel) | |
| cp,w | Specific heat capacity of water (Jkg−1K−1) |
| C | Costs (EUR) |
| COP | Coefficient of Performance |
| L | Height of the DHW storage (in the moving boundary model) (m) |
| Mass flow rate (kg s−1) | |
| Q | Thermal energy (J or kWh) |
| Heat flow rate (W) | |
| t | Time (years) |
| w | Width of the heat transfer cross-section of the DHW storage |
| Wel | Electric energy (kWh) |
| εRPW | Ratio of thermal energy that can be transferred to the RPW-HEX |
| ℓ | Length of the cold section in the moving boundary model of the DHW storage (m) |
| ϑ | Temperature (°C) |
| τ | Time span of the DHW charging process(s) |
| Abbreviations | |
| c | Cold |
| con | Condenser |
| DHW | Domestic Hot Water |
| HP | Heat Pump |
| msc | Minimum speed of compressor |
| PCM | Phase Change Material |
| RPW-HEX | Refrigerant-PCM-water heat exchanger |
| RPW,P | Contribution of PCM in RPW-HEX |
| RPW,R | Contribution of refrigerant in PCM |
| REF | Reference system without RPW-HEX |
| SoC | State of Charge |
| sp | Set-point |
| w | Water |
Appendix A
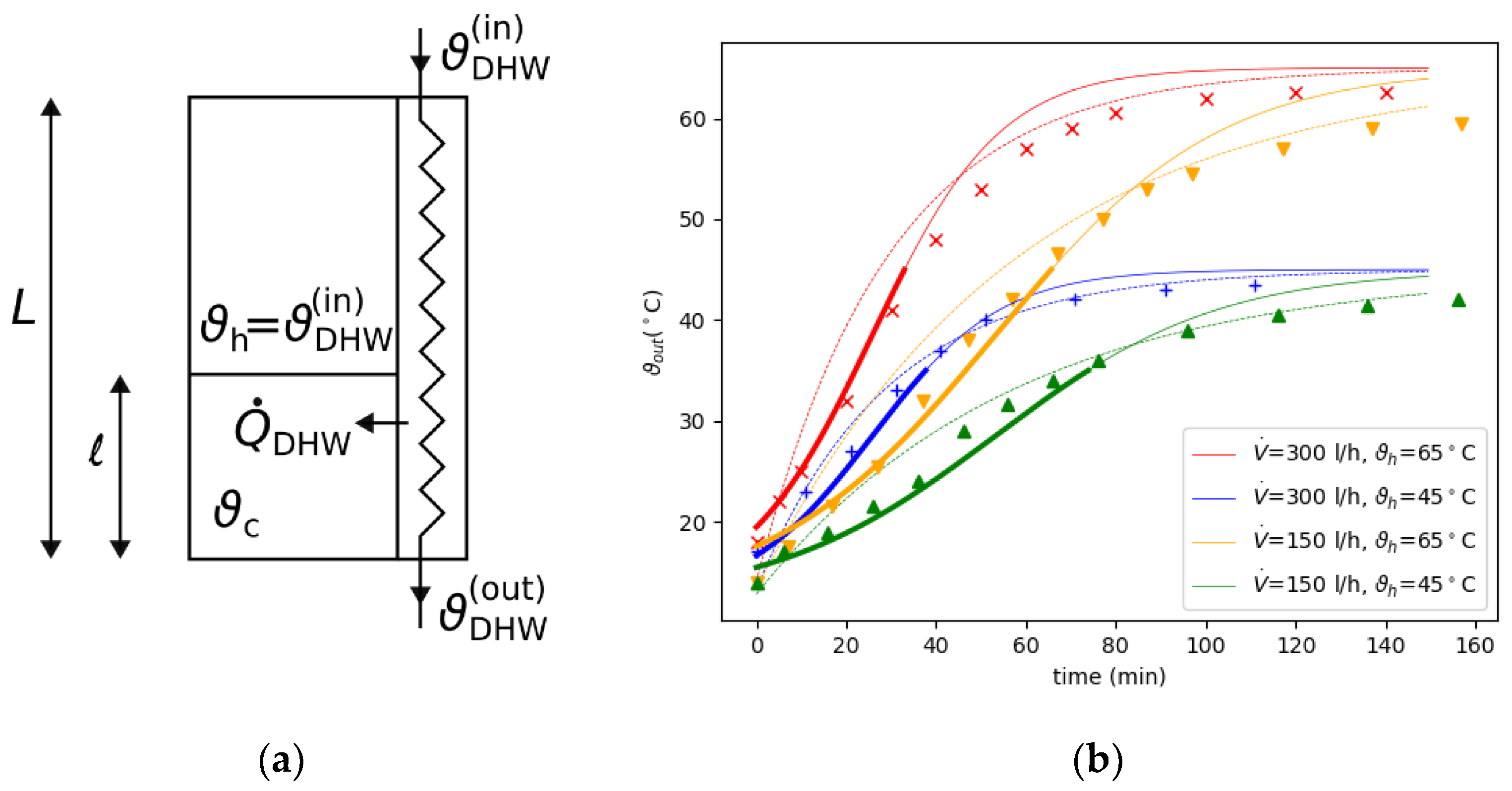
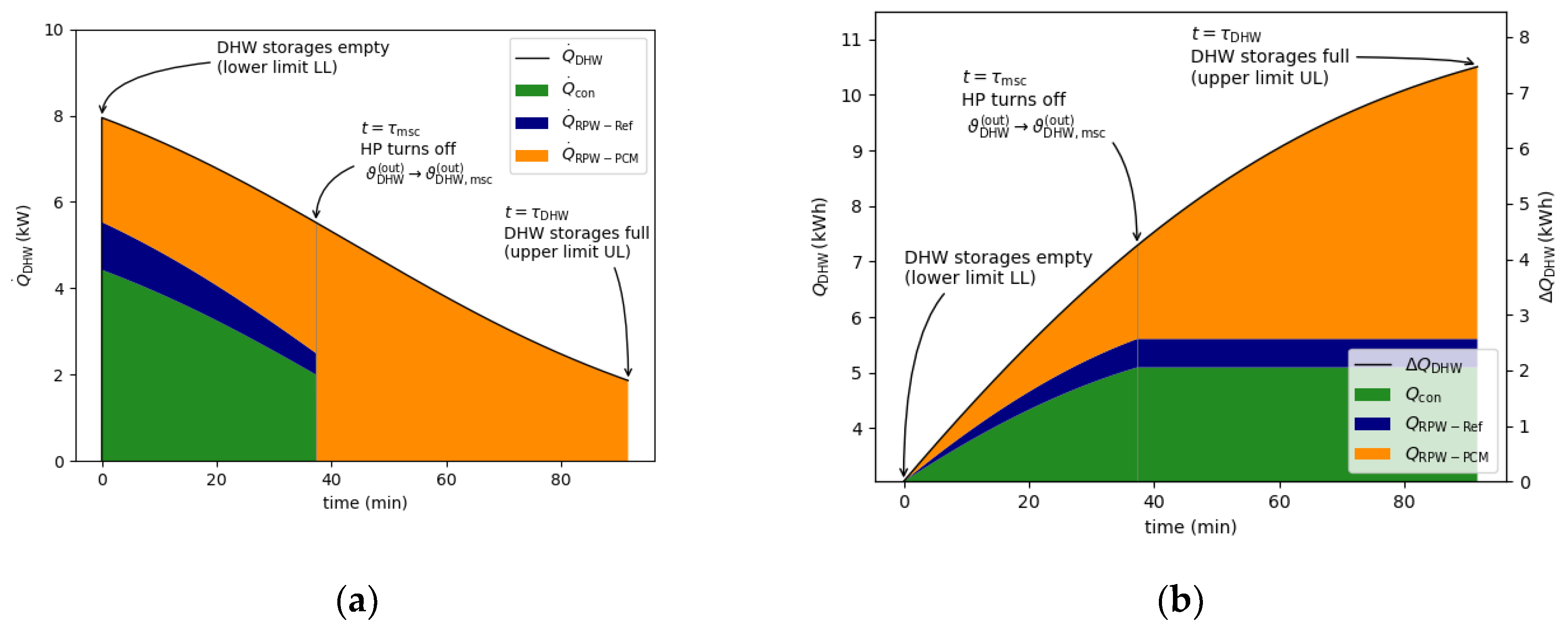
References
- IEA. Heat Pumps, IEA, Paris. 2020. Available online: https://www.iea.org/reports/heat-pumps (accessed on 8 September 2020).
- Pardiñas, A.A.; Alonso, M.J.; Diz, R.; Kvalsvik, K.H.; Fernández-Seara, J. State-of-the-art for the use of phase-change materials in tanks coupled with heat pumps. Energy Build. 2017, 140, 28–41. [Google Scholar] [CrossRef]
- Li, Y.; Nord, N.; Xiao, Q.; Tereshchenko, T. Building heating applications with phase change material: A comprehensive review. J. Energy Storage 2020, 31, 101634. [Google Scholar] [CrossRef]
- Kapsalis, V.; Karamanis, D. Solar thermal energy storage and heat pumps with phase change materials. Appl. Therm. Eng. 2016, 99, 1212–1224. [Google Scholar] [CrossRef]
- Zou, D.; Ma, X.; Liu, X.; Zheng, P.; Cai, B.; Huang, J.; Guo, J.; Liu, M. Experimental research of an air-source heat pump water heater using water-PCM for heat storage. Appl. Energy 2017, 206, 784–792. [Google Scholar] [CrossRef]
- Song, M.; Deng, S.; Dang, C.; Mao, N.; Wang, Z. Review on improvement for air source heat pump units during frosting and defrosting. Appl. Energy 2018, 211, 1150–1170. [Google Scholar] [CrossRef]
- Spitler, J.; Bernier, M. Ground-source heat pump systems: The first century and beyond. HVAC R Res. 2011, 17, 891–894. [Google Scholar]
- Cabeza, L.F.; Castell, A.; Barreneche, C.; de Gracia, A.; Fernández, A.I. Materials used as PCM in thermal energy storage in buildings: A review. Renew. Sustain. Energy Rev. 2011, 15, 1675–1695. [Google Scholar] [CrossRef]
- Ravotti, R.; Fellmann, O.; Lardon, N.; Fischer, L.J.; Stamatiou, A.; Worlitschek, J. Synthesis and Investigation of Thermal Properties of Highly Pure Carboxylic Fatty Esters to Be Used as PCM. Appl. Sci. 2018, 8, 1069. [Google Scholar] [CrossRef]
- Du, K.; Calautit, J.; Wang, Z.; Wu, Y.; Liu, H. A review of the applications of phase change materials in cooling, heating and power generation in different temperature ranges. Appl. Energy 2018, 220, 242–273. [Google Scholar] [CrossRef]
- Baxter, V.D. Comparison of Field Performance of a High-Efficiency Heat Pump with and without a Desuperheater Water Heater. ASHRAE Trans. 1984, 90, 180. [Google Scholar]
- Lee, A.H.W.; Jones, J.W. Thermal performance of a residential desuperheater/water heater system. Energy Convers. Manag. 1996, 37, 389–397. [Google Scholar] [CrossRef]
- Heinz, A.; Lerch, W.; Heimrath, R. Heat pump condenser and desuperheater integrated into a storage tank: Model development and comparison with measurements. Appl. Therm. Eng. 2016, 102, 465–475. [Google Scholar] [CrossRef]
- Shao, S.; Shi, W.; Li, X.; Ma, J. A new inverter heat pump operated all year round with domestic hot water. Energy Convers. Manag. 2004, 45, 2255–2268. [Google Scholar] [CrossRef]
- Emhofer, J.; Barz, T.; Marx, K.; Hochwallner, F.; Cabeza, L.F.; Zsembinszki, G.; Strehlow, A.; Nitsch, B.; Weiss, M. Integration of a compact two fluid PCM heat exchanger into the hot superheated section of an air source heat pump cycle for optimized DHW generation. In Proceedings of the 25th IIR International Congress of Refrigeration, Montreal, Canada, 24−30 August 2019. [Google Scholar]
- EN 14825:2018. Air Conditioners, Liquid Chilling Packages and Heat Pumps, with Electrically Driven Compressors, for Space Heating and Cooling—Testing and Rating at Part Load Conditions and Calculation of Seasonal Performance; British Standards Institution: London, UK, 2018. [Google Scholar]
- Barz, T.; Seliger, D.; Marx, K.; Sommer, A.; Walter, S.F.; Bock, H.G.; Körkel, S. State and state of charge estimation for a latent heat storage. Control Eng. Pract. 2018, 72, 151–166. [Google Scholar] [CrossRef]
- EN 16147:2017. Heat Pumps with Electrically Driven Compressors–Testing, Performance Rating and Requirements for Marking of Domestic Hot Water Units; British Standards Institution: London, UK, 2017. [Google Scholar]
- Hauer, S.; Judex, F.; Bres, A. BMG- Building Model Generator: Reducing the effort for thermal building simulation by automation. In Proceedings of the e-nova International Congress 2016, Pinkafeld, Austria, 24–25 November 2016; pp. 229–236. [Google Scholar]
- Bres, A.; Eder, K.; Hauer, S.; Judex, F. Case study of energy performance analyses on different scales. Energy Procedia 2015, 78, 1847–1852. [Google Scholar] [CrossRef]
- Quoilin, S.; Desideri, A.; Wronski, J.; Bell, I.; Lemort, V. ThermoCycle: A Modelica library for the simulation of thermodynamic systems. In Proceedings of the 10th International Modelica Conference 2014, Lund, Sweden, 10–12 March 2014. [Google Scholar]
- Emhofer, J.; Barz, T.; Palomba, V.; Frazzica, A.; Sergi, F.; Varvagiannis, S.; Karellas, S.; Oró, E.; Zsembinszki, G.; Cabeza, L.F. Deliverable D3.1 of the HYBUILD-Project: Modular Flow Sheet Simulation of the Hybrid (sub-)System. Available online: http://www.hybuild.eu/publications/deliverables/ (accessed on 8 September 2020).
- Frazzica, A.; Palomba, V.; Sergi, F.; Ferraro, M.; Cabeza, L.F.; Zsembinszki, G.; Oró, E.; Karellas, S.; Varvagiannis, S.; Emhofer, J.; et al. Dynamic Modelling of a Hybrid Solar Thermal/electric Energy Storage System for Application in Residential Buildings. In Proceedings of the 12th International Conference on Solar Energy for Buildings and Industry, Raperswil, Switzerland, 10–13 September 2018. [Google Scholar]
- Bell, I.H.; Wronski, J.; Quoilin, S.; Lemort, V. Pure and Pseudo-pure Fluid Thermophysical Property Evaluation and the Open-Source Thermophysical Property Library CoolProp. Ind. Eng. Chem. 2014, 53, 2498–2508. [Google Scholar] [CrossRef] [PubMed]
- Marx, K.; Emhofer, J.; Barz, T.; Krämer, J.; Cabeza, L.F.; Zsembinszki, G.; Strehlow, A.; Nitsch, B.; Wiesflecker, M.; Zitzenbacher, R.; et al. Dynamic Performance Tests of a Heat Pump Cycle Integrated Latent Heat Thermal Energy Storage for Optimized DHW Generation. Unpublished work. 2020. [Google Scholar]
- EUROSTAT, Electricity Price Statistics–Statistics Explained. Available online: https://ec.europa.eu/eurostat/statistics-explained/index.php/Electricity_price_statistics#Electricity_prices_for_household_consumers (accessed on 8 September 2020).
- Zsembinszki, G.; Fernández, A.G.; Cabeza, L.F. Selection of the Appropriate Phase Change Material for Two Innovative Compact Energy Storage Systems in Residential Buildings. Appl. Sci. 2020, 10, 2116. [Google Scholar] [CrossRef]
- HYBUILD Project, Innovative Compact Hybrid Storage Systems for Low Energy Buildings. Available online: http://www.hybuild.eu/ (accessed on 8 September 2020).
| Constraint | Case #1 Passive House in Helsinki | Case #2 Low Energy Building in Strasbourg | Case #3 Refurbished Building in Athens |
|---|---|---|---|
| Apartments and total floor area per building | 7.75, 581 m2 | 5.25, 394 m2 | 1.75, 131 m2 |
| Heating demand per year and m2 (kWh year−1 m−2) | 14.8 | 31.5 | 61.7 |
| Maximum heating demand (kW) | 6.97 | 9.89 | 7.15 |
| Maximum cooling demand (kW) | 10.8 | 9.68 | 10.67 |
| Daily DHW demand without losses (kWh) | 45.3 | 30.7 | 10.2 |
| Annual heating demand (kWh) | 8598 | 12,413 | 8096 |
| Annual cooling demand (kWh) | 6903 | 5360 | 9401 |
| Annual DHW demand without losses (kWh) | 16,534 | 11,200 | 3733 |
| HP design load heating Pdesign,heating (kW) | 7.22 (at −22 °C) | 9.66 (at −10 °C) | 13.0 (at 2 °C) |
| HP design load cooling Pdesign,cooling (kW) | 10.843 (at 35 °C) | 10.843 (at 35 °C) | 10.843 (at 35 °C) |
| ϑwater,heating,distribution,in (°C) | 22–35 | 24–45 | 24–45 |
| ϑwater,cooling,distribution,in (°C) | 7–11.5 | 7–11.5 | 7–11.5 |
| Main purpose | mostly heating | heating | mostly cooling |
| Manufacturing costs RPW-HEX | 500 | Aluminum | 137.0 |
| Three-way valve and additional piping | 20 | PCM | 61.7 |
| Insulation (mineral wool) | 2.6 | ||
| Total | 520 | 201.3 |
| Case #1 | Case #2 | Case #3 | |
|---|---|---|---|
| Energy demand for heat-ing per year (RPW/REF) | 2990 kWhel/ | 3972 kWhel/ | 2231 kWhel/ |
| 2939 kWhel | 3918 kWhel | 2180 kWhel | |
| Energy demand for cool-ing per year (RPW/REF) | 2000 kWhel/ | 1692 kWhel/ | 3520 kWhel/ |
| 2059 kWhel | 1753 kWhel | 3616 kWhel | |
| Energy demand for DHW per year (RPW/REF) | 6086 kWhel/ | 3713 kWhel/ | 900 kWhel/ |
| 6634 kWhel | 4150 kWhel | 1191 kWhel | |
| Energy savings for heating per year | −51.2 kWhel (−1.74%) | −55.5 kWhel (−1.42%) | −50.5 kWhel (−2.32%) |
| Energy savings for cooling per year | 59.0 kWhel (2.86%) | 61.6 kWhel (3.51%) | 95.8 kWhel (2.65%) |
| Energy savings for DHW per year | 549 kWhel (8.27%) | 436 kWhel (10.5%) | 291 kWhel (24.4%) |
| Total energy savings per year | 557 kWhel (4.78%) | 442 kWhel (4.50%) | 336 kWhel (4.81%) |
| Investment costs | 1526 EUR | 1526 EUR | 1526 EUR |
| Payback time | 14.1 years | 18.3 years | 25.6 years |
| Minimum cost savings per year (based on first year) | 122 EUR | 97.3 EUR | 74.0 EUR |
| Profit after 20 years | 760 EUR | 171 EUR | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Emhofer, J.; Marx, K.; Barz, T.; Hochwallner, F.; Cabeza, L.F.; Zsembinszki, G.; Strehlow, A.; Nitsch, B.; Wiesflecker, M.; Pink, W. Techno-Economic Analysis of a Heat Pump Cycle Including a Three-Media Refrigerant/Phase Change Material/Water Heat Exchanger in the Hot Superheated Section for Efficient Domestic Hot Water Generation. Appl. Sci. 2020, 10, 7873. https://doi.org/10.3390/app10217873
Emhofer J, Marx K, Barz T, Hochwallner F, Cabeza LF, Zsembinszki G, Strehlow A, Nitsch B, Wiesflecker M, Pink W. Techno-Economic Analysis of a Heat Pump Cycle Including a Three-Media Refrigerant/Phase Change Material/Water Heat Exchanger in the Hot Superheated Section for Efficient Domestic Hot Water Generation. Applied Sciences. 2020; 10(21):7873. https://doi.org/10.3390/app10217873
Chicago/Turabian StyleEmhofer, Johann, Klemens Marx, Tilman Barz, Felix Hochwallner, Luisa F. Cabeza, Gabriel Zsembinszki, Andreas Strehlow, Birgo Nitsch, Michael Wiesflecker, and Werner Pink. 2020. "Techno-Economic Analysis of a Heat Pump Cycle Including a Three-Media Refrigerant/Phase Change Material/Water Heat Exchanger in the Hot Superheated Section for Efficient Domestic Hot Water Generation" Applied Sciences 10, no. 21: 7873. https://doi.org/10.3390/app10217873
APA StyleEmhofer, J., Marx, K., Barz, T., Hochwallner, F., Cabeza, L. F., Zsembinszki, G., Strehlow, A., Nitsch, B., Wiesflecker, M., & Pink, W. (2020). Techno-Economic Analysis of a Heat Pump Cycle Including a Three-Media Refrigerant/Phase Change Material/Water Heat Exchanger in the Hot Superheated Section for Efficient Domestic Hot Water Generation. Applied Sciences, 10(21), 7873. https://doi.org/10.3390/app10217873








