The new rating model aims to estimate offensive and defensive ratings for each player. These ratings are entirely data driven, and are defined so that the sum of the offensive ratings of the home team minus the sum of the defensive ratings of the away team should approximately equal the number of goals scored by the home team. Similarly, the number of goals scored by the away team should be approximately equal to the sum of the offensive ratings of the away team minus the sum of the defensive ratings of the home team. However, the goals scored and conceded by the home team are also expected to vary depending on the home field advantage and the number of player dismissals. The ratings of players are not assumed to be constant over time, but rather to be a function of the player’s age: young players tend to be improving over time, while the playing strength of older players tend to decline.
Considering a part of a match where the players are fixed, ratings are determined by minimizing the squared difference between the actual number of goals scored and the number of goals expected based on the players’ ratings, other effects such as the home field advantage, and the duration of a segment. Hence, the numerical values of the ratings obtained are interpreted as the contribution of a player towards goals scored per 90 min. To calculate ratings, data must be available regarding the starting line-ups of both teams, the time of goals, red cards, and substitutions, as well as the players involved in red cards and substitutions. Furthermore, the new ratings require knowledge about the birth date of players and their playing position.
3.1. Rating Model
Following Pantuso and Hvattum [
16], the new offensive–defensive plus–minus ratings for soccer are calculated by solving an unconstrained quadratic program. Let
M be a set of matches, with each match
divided into segments
, defined as a maximal period of time without changes to the players appearing on the pitch. The duration of segment
s is
minutes.
Let and be the two teams involved in match m, where h is the home team. In the case that the match is played on neutral ground, one of the two teams is arbitrarily assigned as h and the other as a. Let be the number of goals scored by team h in segment s of match m, whereas the number of goals scored by a is . Past plus–minus rating models have used as the dependent variable of the observation associated to the segment. Here, to facilitate both offensive and defensive ratings, each segment corresponds to two observations. One observation is from the perspective of team h, and has as the dependent variable, whereas the other is from the perspective of a, with as the dependent variable.
In addition, define
as the goal difference in favour of
h at the beginning of the segment, and
as the goal difference at the end of the segment. The change of the goal difference in favour of
h in segment
s of match
m then becomes
. Let
denote the time that match
m is played, and let
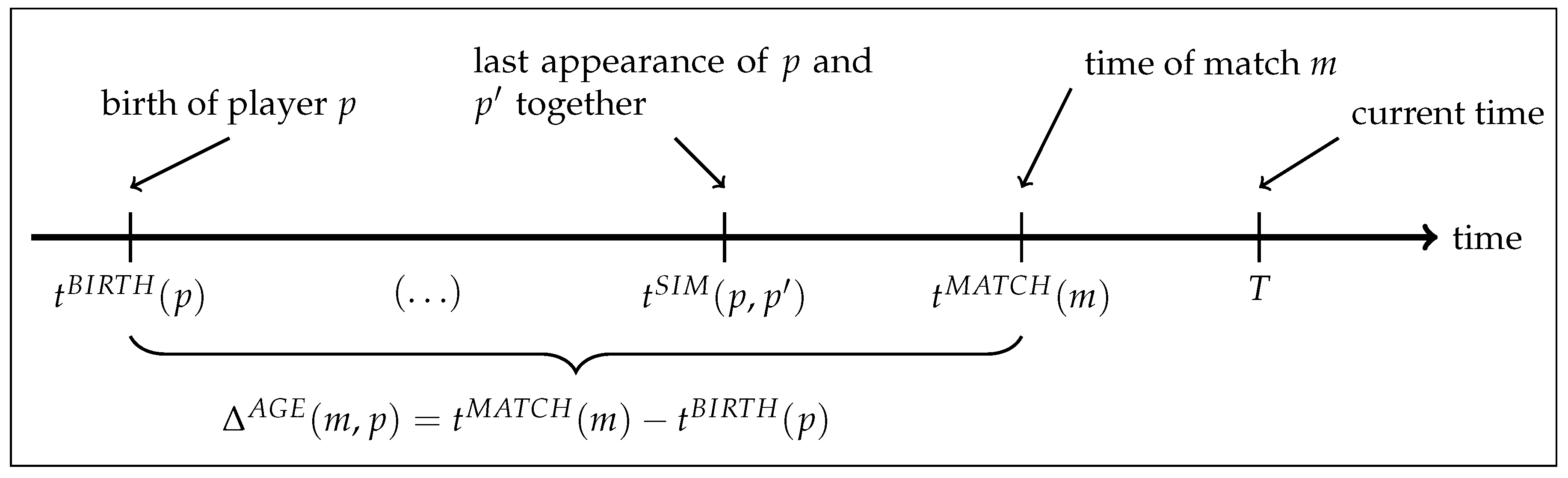
T be the time at which ratings are calculated, as illustrated in
Figure 1.
Let P be the set of all players. The set of players for team t that appears on the pitch for a given segment s are denoted by . The set of players that are involved in offensive contributions is denoted by , and the set of players involved in defensive contributions is denoted by . For , define if team h has received n or more red cards before the beginning of segment s and team a has not, if team a has received n or more red cards and team h has not, and otherwise. If a team has made all its available substitutions and a player on the team becomes injured and must leave the pitch, the situation is modelled in the same way as a red card.
Each match m belongs to a competition organized by an association. Let be the association organizing the match. This could be a national organization, a continental federation such as UEFA, or FIFA. The model allows the home field advantage of match m to depend on . Furthermore, a set of domestic league competitions C is considered, with being the subset of such competitions in which player p has participated. For example, a given player could have appeared in the French Ligue 2, the English Championship, and the English Premier League, resulting in these three leagues being members of .
Each player
p is associated to a set
of players that are considered to be similar. This set is based on which players have appeared together on the same team for the most minutes of playing time. The time of the last match where players
p and
appeared together is denoted by
(see
Figure 1).
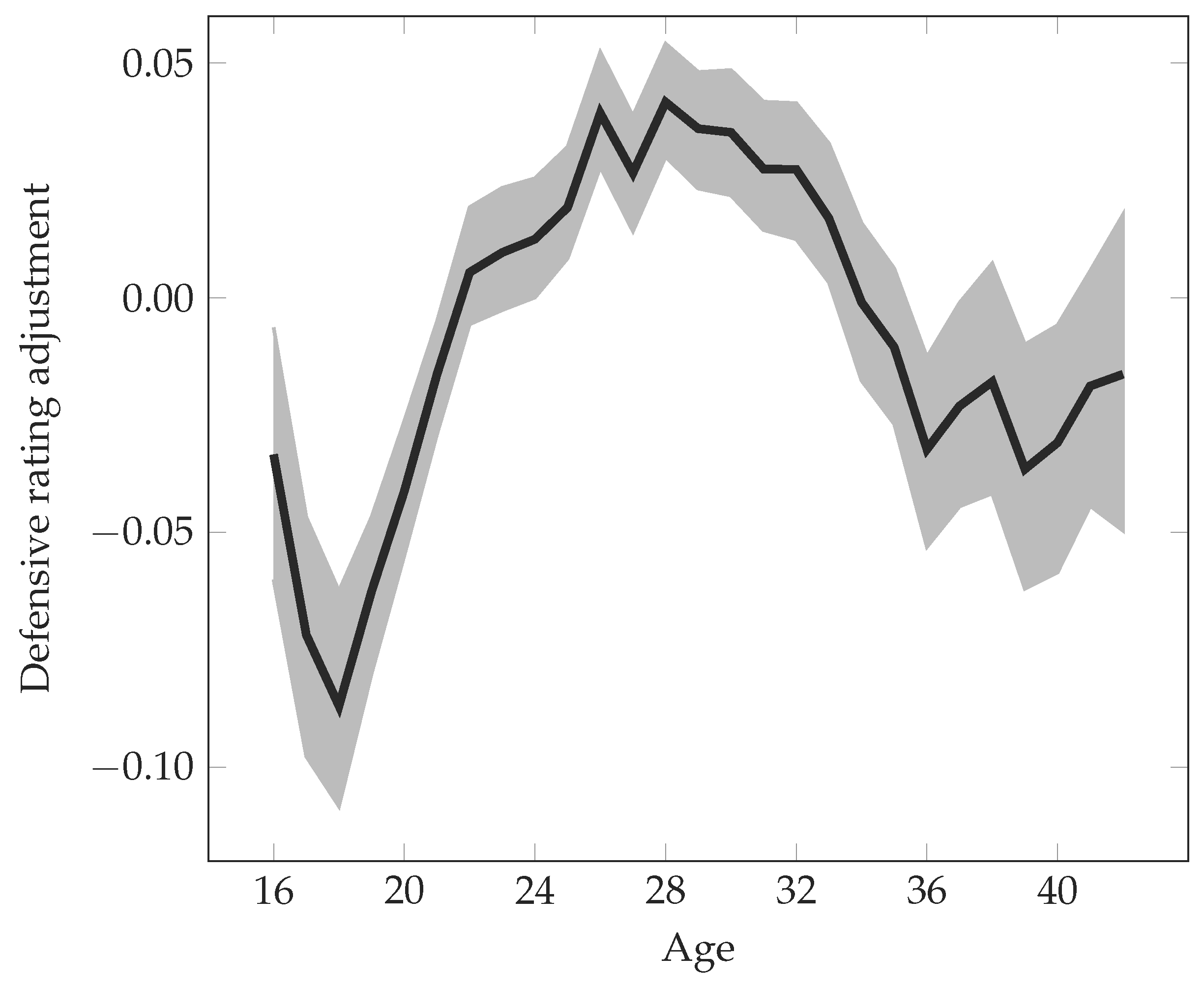
The quality of players is assumed to depend on their age, allowing the model to capture their typical improvement in early years as well as their decline when getting older. Let
be the time of birth for player
p. The age of player
p at the time of match
m is then
, as illustrated in
Figure 1. The average effect of age on the ratings of players is modelled as a piecewise linear function. To this end, an ordered set of
k age values
is defined. For a given match and player, the exact age of the player is expressed as a convex combination of the nearest two ages in
Y. Thus, weights
,
, are defined as
Thus, after censoring so that it lies within , it holds that . In addition, at most two of the values are non-zero, and any two non-zero values are for consecutive values of i. As a concrete example, assuming that , , and , then and uniquely identifies the age of player p at the time of match m.
To improve the calculations of offensive and defensive ratings, a set of positional roles is considered: , where the elements refer to goalkeeper, defender, midfielder, and forward, respectively. Let be the subset of positions covered by player p. This notation is used to improve the distribution of a player’s overall rating into offensive and defensive components, in particular for players with few minutes played.
The following parameters are defined to control the behavior of the model: , , and are regularization factors, with being the main regularization factor, and the others being adjustments made for specific regularization terms. The parameter is a discount factor for older observations, and are parameters regarding the importance of the duration of a segment, while is a parameter for the importance of a segment based on the goal difference at the start and end of the segment. To balance the importance of the age factors when considering similarity of players, the weight is introduced. Finally, is a weight that controls the extent to which overall ratings of players with few minutes played are shrunk towards zero or towards the overall ratings of similar players.
The variables used in the quadratic program can be stated as follows: the offensive base rating of player p is denoted by , and the defensive base rating is ; the value of the home advantage in competitions organized by is represented by and —the former measures the home field advantage in terms of goals scored, and the latter in terms of goals conceded for the home team; for a given age , the age effect is denoted by and for, respectively, the offensive and defensive contribution of a player.
The influence of red cards is also split into an offensive and a defensive contribution, as captured by the variables and for missing players of the home team, and and for missing players of the away team. These variables are defined for . A potential adjustment for player ratings based on the participation in a domestic league competition is given by the variables and . Moreover, is introduced to indicate the average difference between offensive and defensive ratings for players in position .
The model to calculate offensive and defensive plus–minus ratings can now be stated as
The complete model (1)–(8) consists of two main parts: expressions that link the observed number of goals scored and conceded in each segment of each match with the player ratings to be estimated, and regularization terms that are used to guide the estimation of player ratings, in particular for players that are involved in few observations or whose appearances are highly correlated with appearances of other players.
The observations are based on segments that are weighted using
. The weights depend on the time since the segment was played, the duration of the segment, and on the goal difference at the start and the end of the segment:
The two observations based on each segment can now be specified in more detail. The quadratic terms in (1) and (2) arise in an attempt to minimize the squared error between a right-hand side consisting of the observed number of goals scored or conceded, and a left-hand side comprising explanatory terms corresponding to players involved in the segment, to attributes of the particular segment, and to attributes of the match to which the segment is associated. The factor
is used to scale the explanatory terms so that they can be interpreted as contributions per 90 min of play:
Attributes specific to a segment involve compensating for missing players following red cards and injured platers who are not replaced. For segments of matches where there is a home field advantage present, this is expressed as follows:
However, for matches played on neutral ground, the effect of missing players is modelled as:
Regarding a specific match, the relevant contribution to explain the observed number of goals comes from the home field advantage, which is modelled as being specific to a given association organizing the match:
The remaining terms to explain the observed goals represent the ratings of players at the time of the match. These ratings consist of a base rating plus adjustments based on the age of the player and based on the domestic league competitions where the player has appeared:
The model then includes a set of quadratic terms (3)–(8) known as regularization terms. The purpose of these is to dampen the ratings and other estimated effects, so that very high or very low ratings are avoided for players with few observations in the data set. First, a regularization term ensures that the overall rating of a player is not too different from the overall ratings of similar players:
Second, the following ensures that the difference between the offensive and the defensive rating of a player is not too different from the typical difference for players in similar positions:
The two types of regularization applied above aim to control the player ratings directly. Regularization is not applied to all the other estimates made by the model, such as the home field advantages and the effects of red cards. However, the age effects are subject to regularization, partly to ensure model identifiability, and partly to make sure the age effects are smoothed out when applied to smaller data sets:
The model (1)–(8) constitutes an unconstrained quadratic program. Due to the large dimensions of the problem, a gradient descent search is used to determine its solution. This is coded in C++, and several calculations, such as finding the gradient at a given step, are parallelized over several threads. Once the model has been estimated, the offensive rating of player p at time T corresponds to , while the defensive rating is . The overall rating for player p becomes .
3.2. Example Segment
To illustrate the model, a segment is selected from a match played between Barcelona and Athletic Bilbao in the Spanish Primera División on 17 January 2016. The selected segment of the match started after a substitution in minute 6 and ended with a new substitution in minute 46. Before this, the goalkeeper of the away team had been shown a red card, and the home team had been awarded a penalty shot, which would be taken by Lionel Messi in minute 7. The match was tied when the segment started. The following assumes that the ratings are being estimated on 21 June 2017, and the notation is simplified by dropping references to the match m and the segment s.
The duration of the selected segment is min, and the home team scored twice and the away team zero times during these minutes. The rating model contains two quadratic terms tied directly to this segment, having, respectively, and as the constant terms, representing the goals scored by each team. The weights of the segment become , , and , resulting in .
The number of non-zero linear terms of and , as appearing in the objective function terms (1) and (2), is 44 and 45, respectively. As there is one player sent off for the away team, the segment specific terms are and . The match specific terms represent the home field advantage, with and , with the Spanish league represented by .
As goalkeepers do not have offensive ratings, and since the away team has one player missing, the number of players contributing offensively is and for the two teams, while the number of players contributing defensively is and . These numbers are used to normalize the sum of contributions from player ratings, and , to and .
Table 1 shows the coefficients for the age variables in the selected segment, before scaling by
and multiplying by the segment weight
w. These coefficients arise from summing over the players appearing in the segment. Based on the coefficients, one can see that the home team has one player aged between 23 and 24, and two players aged between 31 and 32, excluding the goalkeeper: the sum of coefficients for offensive contributions related to age sum up to 1.1 for ages 23 and 24 and to 2.2 for ages 31 and 32, corresponding to the fact that these coefficients have been scaled by 11 and divided by the number of offensive players.
The coefficients of the league components,
and
are given in
Table 2. The players involved in the match had previously appeared in five different league competitions, most commonly being the Spanish Primera División. The away team had six players previously appearing in the Spanish Segunda División, each contributing with
and
to the given coefficients, with
, as these players only appeared in two different league competitions.
Finally, both
and
have, in total, twenty occurrences of
and
, representing the main player rating components. With the proposed model, each match is, on average, divided into around 6.3 segments, each of which provides two squared expressions for the objective function. Less than half of the terms in these expression relate directly to player ratings, whereas the rest are used to estimate home field advantages, age effects, and league effects. Taking again the example segment, and focusing on the observation of goals scored by the home team, after factoring in all the weights, the corresponding objective function expression can be stated as