Featured Application
The paper presents a method for the classification of sports disciplines from images using fine-tuning of transfer learning for training a convolutional neural network with hyper-parameter optimization based on differential evolution.
Abstract
With the exponential growth of the presence of sport in the media, the need for effective classification of sports images has become crucial. The traditional approaches require carefully hand-crafted features, which make them impractical for massive-scale data and less accurate in distinguishing images that are very similar in appearance. As the deep learning methods can automatically extract deep representation of training data and have achieved impressive performance in image classification, our goal was to apply them to automatic classification of very similar sports disciplines. For this purpose, we developed a CNN-TL-DE method for image classification using the fine-tuning of transfer learning for training a convolutional neural network model with the use of hyper-parameter optimization based on differential evolution. Through the automatic optimization of neural network topology and essential training parameters, we significantly improved the classification performance evaluated on a dataset composed from images of four similar sports—American football, rugby, soccer, and field hockey. The analysis of interpretable representation of the trained model additionally revealed interesting insights into how our model perceives images which contributed to a greater confidence in the model prediction. The performed experiments showed our proposed method to be a very competitive image classification method for distinguishing very similar sports and sport situations.
1. Introduction
A huge increase of the amount of non-textual information available in electronic form in mass media requires dealing with it as a major source of content [1]. Digital archiving and multimedia analysis are needed to improve the processing efficiency of this material. Specifically, multimedia intelligent systems count on effective classification and indexing of multimedia (e.g., images and videos) in various domains, including sports. The presence of sports in the media has grown exponentially over the last few decades [2], as the broadcasters produce enormous numbers of sports content in cyberspace due to massive viewership and commercial benefits [3]. To deal with such an amount of information, computational intelligence methods are increasingly used in sports [4].
Image classification, as one of the enabling techniques for effective manipulation over large-scale images and videos, is challenging [5]. The intent of the classification process is to decide whether an image belongs to a certain category. Traditional algorithms for sports image classification require carefully hand-crafted features, such as color, texture, object shape, and contour [6]. Notwithstanding the fact that this kind of use is very impractical due to the emergence of massive-scale data, such algorithms have the most difficulty in distinguishing sports disciplines that are very similar in appearance.
In recent years, we have witnessed an enormous advancement of deep learning (DL) methods and techniques utilizing convolutional neural networks (CNNs). CNN-based algorithms, which can automatically extract deep representation of training data, have achieved impressive performance in image classification [6], providing results that achieved near-human performance or have even outperformed humans [7]. Various research works have proved that the application of such methods is very encouraging also for sports images classification [8,9].
However, in order for CNNs to be able to train a good predictive model with high predictive performance, a large enough dataset with reliable ground truth is needed. While the human annotation is impossible for large image datasets, for smaller datasets the manual process also may not be accurate due to human mistakes and perception subjectivity [1]. In the last years, the lack of adequate datasets is most commonly addressed with the utilization of transfer learning approaches [10]. Transfer learning enables one to transfer the weights of a CNN model, previously trained for a specific task, to a new model solving different, but related tasks. With the use of transfer learning, CNN-based classification models of high predictive performance can be produced, even when a large annotated dataset is not available. Furthermore, the training of such models generally requires less time, since the models are already somewhat pre-trained.
To fit a CNN model into different problems, its hyper-parameters must be properly tuned [11]. One of the major issues of using CNN for image classification is thus finding the right learning parameters and network topology to achieve the best performance [12]. Namely, there is no general rule to follow which would guarantee a good outcome, so it commonly depends on previous experience and trying out different parameter settings. Selecting the best hyper-parameter configuration often requires deep knowledge of machine learning (ML) algorithms and a lot of burdensome work. To automatize this process, hyper-parameter optimization (HPO) techniques may be the right approach [11].
Based on our previous experience with image classification using CNNs with HPO [13,14], we set our goals to develop an advanced CNN based image classification method tailored to the task of identifying a sports discipline from a small image dataset of very similar sports, namely American football, rugby, soccer, and field hockey. For this purpose, we adopted a pre-trained CNN architecture, utilized a transfer learning approach to fine-tune the pre-trained CNN model to the task of sports images classification, and optimized the training of hyper-parameters with the use of differential evolution (DE).
In addition to pure quantitative evaluation of our proposed classification model, we also generated various interpretive representations of the trained classification model in order to analyze how it perceives the images of various sports disciplines and also to evaluate the model’s decisions from a qualitative perspective.
The main contributions of this paper are as follows:
- We prepared a new image dataset of four similar sports—American football, rugby, soccer, and field hockey.
- We developed a method for the classification of sports disciplines from images using the transfer learning of CNN with HPO.
- We compared our proposed method with a conventional CNN as well as with the CNN using the transfer learning methodology with handpicked hyper-parameters for fine tuning.
- We provide detailed results of the performed experiments alongside with the statistical analysis and the analysis of interpretable representations of the trained image classification models.
The remaining of the paper is structured as follows. In Section 2, the related work of classifying sports images is presented briefly. The background and utilized methods are presented in Section 3. Section 4 explains our proposed image classification method. Section 5 describes the conducted experiments and experimental settings. Section 6 presents the obtained results in detail. Section 7 concludes our work with some final thoughts and possible future work.
2. Related Work
The use of image classification methods and techniques in sports is not new. Previous works on image and video classification for sports related content can be generally divided into traditional ML algorithms and the more recently developed DL techniques [9]. While in the traditional ML approaches one of the major challenges is to define and extract the appropriate features from images, in the case of DL approaches, both the features and the classifier are automatically compiled in the learning process.
In [15], the authors proposed a method for classifying sports images, which is based on the Bayesian framework and employs four important color features to exploit the properties of sports images. For this purpose, color histogram, color coherence vector, edge direction histogram, and edge direction coherence vector are extracted from images, on which a Bayesian classifier is trained to automatically assign a class to a sports image.
Another well known traditional classification method was used by Capodiferro et al. [16], who proposed a classification method based on the Support Vector Machine (SVM) and key frames features extraction to classify sport video contents from the 1960 Olympic games. For the extracted key frame images, feature vectors were computed in the Laguerre–Gauss transformed domain, which represented the input of the SVM classifier. The SVM was also used for the classification of sports images by Hatem et al. [17], who compared it with another traditional classification technique, decision trees, showing the advantage of SVM.
To achieve better performance, in general, many low-level features are extracted from images to discriminate different types of images. Beside requiring additional effort and posing a computational overhead, the classification model may also tend to overfit, resulting in poor performance. To avoid such problems in the domain of sports images, in [1], the authors proposed feature dimensionality reduction techniques for the annotation of image datasets. They investigated different techniques, such as Chi-square, information gain, gain ratio, and Latent Semantic Analysis (LSA), and applied them for sports images classification using a SVM classifier. A comparison between the performances of applying SVM alone and when incorporating the different reduction methods showed a raise in the accuracy.
An early attempt to move from traditional ML approaches to neural networks was made by Breen et al. [18], who trained a shallow neural network following a domain-dependent ontology to perform classification, resulting in a scalable system capable of examining images and classifying them based on their visual content. After classifying the objects within an image into predefined classes, the ontology is traversed in order to find a possible semantic relationship among those objects.
An extensive evaluation of CNNs on video classification is presented in [8], where the authors used a dataset of one million YouTube sports videos to train a CNN. Their best produced spatiotemporal networks display significant performance improvements compared to strong feature-based baselines. The research included a transfer learning approach, where the authors studied the generalization performance of their best model by retraining the top layers on the UCF-101 Action Recognition dataset and observed significant performance improvements compared to the UCF-101 baseline model.
A recent interesting approach to shot classification of field sports videos is presented in [3], where the authors proposed an effective shot classification method based on AlexNet CNN. The method proposes a neural network consisting of five convolutional and three fully connected layers to classify the shots into long, medium, close-up, and out-of-the-field shots. Through the response normalization and the dropout layers on the feature maps, the overall training and validation performance evaluated over a diverse dataset of cricket and soccer videos was boosted. A comparison with SVM, Extreme Learning Machine, K-Nearest Neighbors, and standard CNN showed the method’s classification improvement.
3. Background and Methods
Neural networks have been used for many years as a very effective and successful method for image classification and recognition [19]. As image classification from the ML algorithms point of view is a demanding and complex task, researchers tried to improve the performance of traditional neural networks by introducing more hidden levels with multi layer perceptrons [20] or creating ensembles of neural networks [21]. Significant progress in this area has been achieved by the introduction of CNNs [22], which have become the de facto standard for classifying images with the improvement of computing power and the proliferation of large amounts of image data on which the advanced CNN architectures can be trained. CNNs achieved excellent results in a wide variety of domains [23]: medicine [14,24,25], biology [26], information security [27], agriculture [28], etc.
Compared to traditional neural networks, CNNs have sparse interactions between the input and output units, which are achieved by using kernels smaller than the input. Such kernels allow us to recognize small, semantically expressive features, occupying a small number of pixels. Together with the parameter sharing mechanism, the use of such kernels achieves greater training efficiency of the neural network, which results in better predictive performance, consumes less time, and requires lower memory consumption. The equivariance of convolutional layers enables memorizing the position of a certain feature in the input images, which can be easily recognized even when their position change.
To make the best use of the mentioned advantages of CNNs, we need a sufficiently large dataset of tagged images from the selected specific area to train CNNs. As a suitable image collection of this kind for a selected specific task is often not available, but huge amounts of tagged images from many general areas are available, transfer learning methods with fine-tuning have been developed. They allow us to build a pre-trained model over the multitude of tagged images that are available, and then adapt and retrain the pre-trained model to the selected specific case. Namely, the pre-trained model can be successfully trained over a significantly smaller set of annotated specific images when utilizing the transfer learning approach.
3.1. Transfer Learning
Transfer learning can be defined as a technique that enables the improvement of learning a specific task by applying pre-learned knowledge from a similar other task. When using neural networks, training usually begins on a neural network model in which weights are randomly initialized. In the learning phase, we want to adjust the weights in the model so that the model will map the given input data to the known outputs as accurate as possible. Because the initial, randomly initialized weight values are generally far from optimal, we need a lot of time and a large number of training instances to successfully train the model. Using transfer learning, training of the selected specific task starts on a pre-trained model, where the weight values are not random, but are already adapted to the previous learning situation. Therefore, if we use an appropriate pre-learned model, we can generally consume much less time to adapt such a model to the selected specific task and often achieve even better predictive performance even on a smaller training set.
The idea of transferring the learned knowledge is not new [29] and appears in the literature under various names—as inductive transfer [30], incremental or cumulative learning [31], and multitask learning [32], which is the most closely related to modern transfer learning techniques. One of the most common ways to use transfer learning when training CNNs is fine-tuning. In fine-tuning, we transfer weight values from the convolutional base of the pre-trained CNN model, since the bottom convolutional layers of the neural network are intended for the extraction of general, more abstract features. In classifying images and recognizing objects on them, these general features are usually quite similar regardless of the domain from which the images come. Specific domain features, on the other hand, are extracted mainly in the top layers of the CNN. By utilizing fine-tuning, we primarily want to adjust these specific top layers of the neural network, while leaving the rest more or less unchanged.
The success of implementing the transfer learning with fine-tuning depends largely on the appropriate setting of training parameters. The use of an approach that ensures the appropriate setting of hyper-parameters is thus crucial to achieve a high learning ability of the CNN model.
3.2. Hyper-Parameter Optimization in Machine Learning
HPO is the process of finding optimal values of hyper-parameters. It is used for various purposes, where optimal values of parameters are not known in advance or they cannot be simply determined analytically. In ML, we want to use HPO to determine the values of hyper-parameters, which significantly contribute to improving the efficiency of the learning process, and especially to the predictive performance of the trained predictive model. Thus, the set of possible values of hyper-parameters represents the search space, within which, using the search algorithm or optimization method, we are looking for such a combination of value settings (hyper-parameter configuration), which will enable the selected ML algorithm to build the best possible prediction model according to the given evaluation function [11]. The search for optimal values is usually iterative, where the setting of hyper-parameter values is being constantly improved throughout iterations. The values can be continuous, discrete, binary, or categorical and have different constraints, so their optimization is often a complex constrained optimization problem [33].
In supervised ML, such as classification, the goal is to build an optimal predictive model that minimizes the difference between actual ground-truth and predicted values [11]. If the mapping between input values and outputs in the predictive model is denoted as a model function f from a set of possible models F, the optimal predictive model can be obtained by [34]:
where n is the number of training instances, is the feature vector of the ith instance, is the corresponding actual output, and is the cost function value of each sample.
In DL, there are two main types of hyper-parameters that could be optimized. While the model design hyper-parameters are used to improve the resulting NN architecture, the optimizer hyper-parameters are mainly used to fine-tune the learning process on the selected NN architecture. To achieve the best possible result, hyper-parameters from both two sets can be used simultaneously.
3.3. Differential Evolution
Differential Evolution (DE) is one of the most popular population-based meta-heuristic algorithms, introduced by Storn and Price in 1997 [39], and is considered as one of the most appropriate algorithms for continuous optimization. Besides the general popularity of DE algorithm for solving optimization tasks, it was also successfully applied to various ML problems such as HPO problem [40], problem of designing neural network architecture [41] or feature selection problem [42].
The DE algorithm is composed of real-coded vectors and three operators: mutation, crossover, and selection. The real-coded vectors are representing the candidate solutions (individuals) which can be formally defined as presented in Equation (2), where each element of the solution is in the interval , while and denote the lower and upper bounds of the ith variable, respectively.
DE’s basic strategy consists of mutation, crossover, and selection operations. The mutation operation can be formally expressed as follows:
where F represents the scaling factor as a positive real number that scales the rate of modification while , , and are randomly selected values in the interval .
To increase the diversity of the parameter vectors, the crossover operator is introduced as presented in Equation (4), where controls the fraction of parameters that are copied to the trial solution.
Finally, the selection operator is utilized to decide whether or not the produced vector should become a member of generation utilizing the greedy criterion. The selection could be formally expressed as follows:
where denotes the fitness function defined for solving specific optimization problem. The DE algorithm works in an iterative manner, where each produced solution is evaluated using the given fitness function. Based on the selection operator, presented in Equation (5), the DE algorithm’s search mechanism seeks for solutions of ever better fitness scores. Naturally, the DE algorithm is optimized for solving the minimization optimization problems and therefore the fitness function should be tailored to give the lower score to the preferred solutions.
In order for a DE algorithm to yield good performance, the DE parameters, namely , F, and , need to be set appropriately. The parameter, as presented, denotes the population size of real-coded vectors (individuals) on top of which the mutation, crossover, and selection operators are applied. If the population size is too small, it may lead to premature convergence and stagnation, while a too big population slows down the search by wasting time on too many unpromising moves [43]. The F parameter denotes the differential weight that determines how far from point the offspring should be generated [44]. The parameter is called crossover probability and controls how many parameters in expectation are changed in a population member [45].
3.4. Interpretable Representation
When using a classification in a specific domain, it is often not enough to obtain only the information in which final class instances belong (e.g., just to find out which sport is shown in the picture), but also to find out why a specific instance was classified in this class (e.g., which are the indicators that strongly indicate a specific sport). Understanding the built model also contributes to greater confidence in the model prediction. To detect possible errors, observe model behavior, and identify what significantly influenced the decision, various interpretive methods have been developed [46]. In our research, we used two of the most widely used interpretation methods, which allow the interpretation of models built above images: the Local Interpretable Model-Agnostic Explanations (LIME) and the SHapley Additive exPlanations (SHAP).
In its interpretation, LIME focuses on each instance separately (this is also called a local explanation). The results of the interpretation for the individual instance are obtained by sampling its neighboring inputs and building a sparse linear model based on the predictions of these inputs. The features, included in this model, for which a high value of the coefficients was calculated are in this case considered more important for decision making [47]. The main goal of the LIME method is to provide interpretive representations for black-box classifiers. When classifying images, the LIME provides one or more pixel regions, indicating parts of an image that contain features, because of which the image can be classified to one of the possible classes. For its operation, LIME needs an implemented classifier function that returns classification probabilities for a list of possible classes.
When we describe the above-mentioned process of generating an interpretation with Equation (6), x represents an individual instance for which we obtain interpretation, while g is a model from a set of potential interpretative models G:
The model to be explained is denoted with f while represents the probability distribution around x. denotes how complex it is to interpret the model g, which we want to minimize in order for an interpretive model to be as comprehensible as possible. denotes how similar the values of a linear model g are to the values of the built model f at the location defined by . For good interpretation of a classifier, we want to keep this value to a minimum [46].
The segmentation of an individual image with LIME is automated and is performed by combining similar neighboring pixels into so-called super-pixels. One super-pixel illustrates one area that represents an individual interpretive feature. Into how many of these areas the image will be divided is determined using an image segmentation algorithm such as Quick-Shift algorithm [48].
SHAP represents a game theory-based approach designed to explain the output of any machine learning model. Lundberg and Lee defined it as an optimal evaluation of the influence of individual features in association with local explanations using classical Shapley values from game theory and related extensions [49]. It implements six classes: TreeExplainer, GradientExplainer, DeepExplainer, KernelExplainer, SamplingExplainer, and PartitionExplainer. Each class is adapted to operate on a specific type of built model. TreeExplainer is intended to explain the outputs of a simple tree and tree-ensemble models, GradientExplainer explains a model using expected gradients, DeepExplainer is used to compute SHAP values in DL models, SamplingExplainer computes SHAP values under the assumption of feature independence, and PartitionExplainer allows creating common dependent variables that are available for reuse. It allows the interpretation of each instance of any classifier, as well as the interpretation of the learned model in a comprehensive form [50].
If we focus in more detail on the operation of the SAHP method, we can say that it explains the prediction of a specific instance by computing the contribution of each feature to the prediction. Features’ values can be thought of as parts of a whole. This part can be an individual feature value or a group of feature values. Calculated Shapley values tell us how to fairly distribute the prediction among the features. When interpreting image classification, pixels can be grouped into super-pixels and then the prediction distributed among them. SHAP explanation is obtained by the formula
where g presents the model we want to explain, is a simplified feature or group of features (coalition), M is the maximum coalition size, and is the Shapley value feature attribution for a feature n [51].
4. Image Classification with CNN Using Optimized Transfer Learning
To solve the problem of classifying similar sports images into proper disciplines, we developed the adaptive CNN training method, which is based on an adopted CNN architecture, trained using the transfer learning approach where the hyper-parameters for fine tuning are optimized with the use of DE—we named the method CNN-TL-DE. The pseudo-code of the whole method is presented in Algorithm 1. The method accepts as input a training dataset, a pre-trained CNN model, and the number of hyper-parameters to be optimized. The control parameters for both the DE (Np, CR, F, and number of model evaluations) and CNN training (number of epochs for each individual within the DE, number of epochs for the final model, early stopping criteria, and batch size) also need to be defined. The output of the method is the trained CNN model for the classification of sports images.
| Algorithm 1 CNN-TL-DE algorithm. |
| Input: training dataset D, pre-trained CNN model, number of hyper-parameters to be optimized n |
| Output: trained CNN model |
|
The architecture of our CNN model is presented in Figure 1 and is based on a well known and often used CNN model VGG19 by Simonyan et. al. [52]. While we kept the convolutional layers, represented by the blocks from Block1 to Block5, as defined in VGG19, the classification part of the adopted VGG19 model, consisting of six layers, was tailored to our specific task of identifying sports disciplines from image. On top of Block5, we appended the spatial two-dimensional dropout layer denoted in the figure as , two-dimensional global average pooling layer denoted as , batch normalization layer denoted as , fully-connected layer denoted as , dropout layer, and finally fully-connected output layer with a sigmoid activation function denoted as . The introduction of two dropout layers was needed to reduce the over-fitting problem, which commonly occurs when fine-tuning a large CNN architecture such as VGG19 against rather small dataset as in our case.
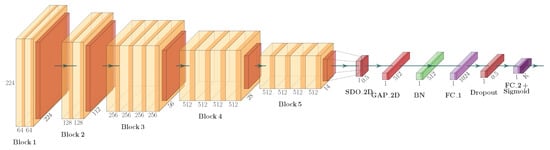
Figure 1.
The architecture of the adapted VGG19 convolutional neural network model.
For training our adapted VGG19 CNN model, we applied the transfer learning approach with fine-tuning. In this manner, all the convolutional layers were first pre-trained on the ImageNet dataset [53]. Then, the model was fine-tuned on our sports images dataset. During fine-tuning, the convolutional blocks from Block1 to Block4 remained disabled (their weights remained unchanged), while the convolutional Block5 and all the classification layers were fully trained.
The five hyper-parameters optimized with the use of the DE are:
- the dropout probability value of the spatial two-dimensional dropout layer ;
- the number of neurons in the last fully connected dense layer ;
- the dropout probability value of the second dropout layer;
- the optimizer type; and
- the learning rate.
Hyper-Parameter Optimization of Transfer Learning with Differential Evolution
Formally, the individuals of CNN-TL-DE produced solutions can be presented as vectors:
where each element of the solution is a real value in the interval . In order for these vectors to represent possible solutions (hyper-parameter configurations), they need to be mapped to proper hyper-parameter values in accordance with Equations (9)–(13), where denotes dropout probability of a spatial two-dimensional dropout layer, denotes the number of neurons in last fully connected layer, denotes the dropout probability of a dropout layer, denotes optimizer function, and denotes the learning rate value. Each and value is mapped to the particular member of the population according to the members position in the population, which in the case of represents a group of available dropout probability values for spatial two-dimensional dropout layer and in the case of represents a group of available dropout values for regular dropout layer. Similarly, is used to define the number of neurons in the last fully connected layer from the population , defines the optimizer type from , while defines the learning rate from a set of possible values .
For calculating the appropriateness of a single solution (hyper-parameter configuration), the fitness value is calculated as:
where represents a hyper-parameter configuration with which the model has been trained and represents the accuracy of the trained model on the validation part of the training set. The calculated fitness value for each individual is used by the DE to produce new solutions in an iterative manner.
5. Experiments
For the purpose of objectively evaluating the proposed method’s predictive performance, we conducted three experiments using the 10-fold cross-validation methodology:
- CNN, where the conventional approach for training the adapted VGG19 CNN model was used;
- CNN-TL, where the transfer learning methodology was used with handpicked hyper-parameters for fine tuning; and
- CNN-TL-DE, where our proposed method which utilizes the DE for the optimization of hyper-parameters for fine tuning of the transfer learning was exploited.
5.1. Dataset
We evaluated the proposed CNN-TL-DE method on the problem of classifying images to one of four sports—American football, rugby, soccer, and field hockey. For this purpose, we composed a new image dataset, containing different images representing one of the four sports disciplines. The images were first automatically collected from various web repositories, and then manually checked and annotated. By manually double-checking all the images, we confirmed that they were correctly distributed into four classes. The images were not manipulated in any way, but the images containing only logos, drawings, or similar, which did not correspond to real world pictures, were removed. In this manner, a collection of 1359 images was compiled. The distribution of images into four classes is presented in Table 1.

Table 1.
The basic information about sports image dataset.
In the data pre-processing phase, we scaled down images to 224 × 224 px, which is the input size of the utilized VGG19 CNN model. Various studies have shown [13,54] that such scaling when utilizing VGG19 architectures results in great classification performance. Figure 2 presents samples of individual target classes, where we can see how the four sports disciplines are very similar in appearance and therefore difficult for an automatic classifier.

Figure 2.
Sample images from the dataset. We can see that the four sports disciplines are indeed very similar in appearance.
5.2. CNN-TL-DE Settings
To objectively compare the methods, we adopted the 10-fold cross-validation methodology. The CNN-TL-DE is an iterative method, which produces new solutions (within the DE loop) based on the evaluation of the previous ones. In this manner, a proper evaluation function that calculates the fitness of each solution is of great importance. However, in ML, the evaluation should not be based solely on training results in order to avoid overfitting. For this purpose, in contrast to the CNN and CNN-TL methods, which use the whole training set for training the CNN model, for the CNN-TL-DE method, the training set was additionally divided into the 80:20 ratio, where the larger subset (true training set) was used for training the solutions, while the smaller subset (validation set) was used for evaluating the solutions produced with the use of DE. In this manner, the whole HPO process was performed properly on the training dataset alone without any data leakage from the test set.
For each fold, the CNN-TL-DE produced and evaluated 50 solutions—hyper-parameter configurations—by first training the adapted VGG19 model using their values and then testing it against the validation subset of the initial training set. The best performing solution (having the best fitness) was then finally evaluated on the test set. The iterative nature of the CNN-TL-DE method is computationally demanding, therefore we applied the early stopping criteria, where the training of the models without improvement in five consecutive epochs was interrupted.
5.3. Experimental Settings
Table 2 presents the used parameter settings for the conducted experiments. The values of all the parameters were picked based on previous experience utilizing CNNs for various image recognition tasks [13,14,24,25], which showed very good classification performances. Every method was provided with 100 epochs, except the CNN-TL-DE method which could use up to a total of 5100 epochs in the worst case (100 epochs for each of the 50 model evaluations within the DE plus 100 epochs for training the final CNN model). The batch size was set equally to 32 for all compared methods. The CNN and CNN-TL experiments were trained using RMSprop optimizer with learning rate set to , while the learning rate and the optimizer type for the CNN-TL-DE method were set (optimized) by the method itself using DE. The dropout probability for spatial two-dimensional dropout layer, the number of neurons in last fully-connected layer, and dropout probability for regular dropout layer were set to , 1024, and , respectively, for both CNN and CNN-TL experiments. For the CNN-TL-DE, the method configured those parameters automatically.

Table 2.
Parameter settings for the performed experiments.
For the DE, the parameters values were set as presented in Table 3. The parameters were set based on our previous experience with DE and general recommendations [55]. Our main goal when setting the DE parameters was to find a reasonable solution in the shortest time. Thus, we chose the recommended minimum population size as two times the dimensionality of the problem, high for speedier (but risky) convergence, the lowest number of function evaluations as times five (the minimum number of epochs for early stopping criteria), and the recommended default value of scale factor F.

Table 3.
Used parameter values for the DE optimization method.
6. Results
6.1. Classification Performance
To evaluate sports images classification results objectively, we compared the proposed CNN-TL-DE method with the CNN method for training the CNN model in an conventional manner and CNN-TL method that performs transfer learning upon the same CNN architecture. For the conventional CNN method, we used the VGG19 [52] CNN architecture and trained the models from scratch. For both the CNN-TL and CNN-TL-DE methods, we applied the transfer learning approach on the same VGG19 CNN architecture, but pre-trained on the ImageNet dataset [53]; however, in the CNN-TL-DE method, the hyper-parameters were automatically optimized using the described DE approach. In this way, the classification performance results depend only on different training methods used. The results were obtained through the conducted experiments on the sports images dataset using the 10-fold cross-validation.
The obtained classification performance results are summarized in Table 4. Our proposed CNN-TL-DE method achieved the best scores by a significant margin in six performance metrics (accuracy, AUNP, precision, recall, F-1 score, and Cohen’s kappa), while lagging behind in terms of consumed time and number of epochs. From the compared two methods, the CNN-TL method performed much better than the conventional CNN in all aspects but the number of consumed epochs, where the difference was not very dramatic.

Table 4.
Comparison of average accuracy, AUNP, precision, recall, F-1 score, kappa coefficient, consumed training time (in seconds), and consumed epochs over 10-folds on test data.
Figure 3a presents test accuracy results obtained by the three compared methods for all 10 folds on the sports images dataset. From 10 folds, the CNN-TL-DE method was the most accurate in eight cases and the CNN-TL in three cases (there was one tied win between CNN-TL and CNN-TL-DE), while the CNN method lag quite distinctively behind. The great advantage of the CNN-TL-DE method with regard to accuracy can be well seen on a violin plot of the comparison of the three methods (Figure 3b). As the standard deviation of the CNN-TL-DE method is also the lowest, we can conclude that it is a very accurate and robust method when compared to the other two methods.
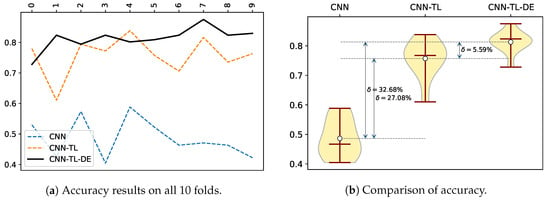
Figure 3.
Comparison of accuracy results for the compared methods over 10 folds.
Similarly, Figure 4a shows a comparison of test AUC (Area under the ROC Curve) results. As we are dealing with multi-class classification problem, we utilized the AUC metric for multi-classification problems, namely AUNP. The AUNP metric is calculated as AUC of each class against the rest, using the a priori class distribution. It was introduced in 2001 by Fawcett [56] and computes the AUC treating a c-dimensional classifier as c two-dimensional classifiers, taking into account the prior probability of each class (). Formally, the AUNP can be expressed as follows:
where represents all classes different from class j.
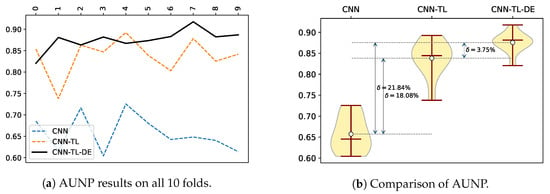
Figure 4.
Comparison of AUNP results for the compared methods over 10 folds.
The AUNP results were very similar to accuracy, with the CNN-TL-DE method dominating in eight out of 10 folds, while in the remaining two folds it was not far behind the CNN-TL method. The violin plot of the AUNP results is presented on Figure 4b.
Figure 5 shows a comparison of Cohen’s Kappa coefficient values for all of the compared methods. Essentially the Cohen’s Kappa metric compares an observed accuracy with an expected accuracy (random chance), which is generally less misleading than the accuracy metric itself, due to the Cohen’s Kappa taking into the account the random chance. By the Fleiss’s characterization [57], the Kappa coefficient values are translated into poor agreement when the value is <0.40, fair to good agreement when the the value is 0.40–0.75, and excellent agreement when the value is >0.75. Following the mentioned characterization of Cohen’s Kappa coefficient values, our proposed CNN-TL-DE method achieves excellent agreement in seven out of 10 folds, which results in an excellent agreement with an average of 0.7508. The CNN-TL method achieves on average fair to good agreement, while the CNN method achieves on average a poor agreement (see Table 4).
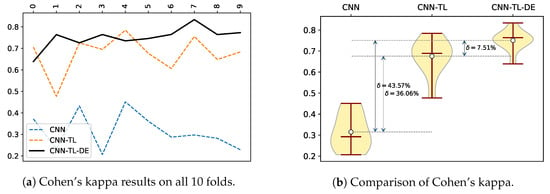
Figure 5.
Comparison of Cohen’s kappa results for the compared methods over 10 folds.
6.1.1. Statistical Comparison
To evaluate the statistical significance of the obtained results, we first applied the Friedman test as proposed by Demšar [58] by calculating the Friedman asymptotic significance and p-values for eight measures (Table 5). The results show statistically significant differences between the methods for all eight metrics. To statistically compare the CNN-TL-DE method with the two baseline methods CNN and CNN-TL, the Wilcoxon signed-rank test was applied. If the Wilcoxon test resulted in statistically significant difference between the two methods, the method with the better average rank can be regarded as the better method. Our proposed CNN-TL-DE method significantly outperforms the other two methods in all six classification performance metrics (acc, AUNP, precision, recall, F-1 score, and Cohen’s kappa). On the other hand, the CNN-TL-DE method lags significantly behind with regard to computational complexity (consumed training time and number of epochs).

Table 5.
Statistical comparison of the three compared methods (all results are statistically significant).
6.1.2. Using Alternative Optimization Techniques
Beside DE, there are other optimization techniques that are commonly used for HPO tasks, with Genetic Algorithms (GA) and Particle Swarm Optimization (PSO) being two of the most known ones. To compare the results of our proposed CNN-TL-DE method, we performed two additional experiments:
- CNN-TL-GA, where GA was used instead of DE for the optimization of hyper-parameters for fine tuning of the transfer learning; and
- CNN-TL-PSO, where PSO was used instead of DE for the same purpose.
In the two cases of using GA and PSO for performing HPO, the whole training process was completely the same as explained in the case of using DE, only the optimization technique was different. The parameters were set in the same manner as for the DE. For GA, the dimension of the problem D = 5, population size = 10, mutation rate = 0.25, and crossover rate = 0.25. For PSO, the dimension of the problem D = 5, population size = 10, cognitive component = 2.0, social component = 2.0, inertial weight w = 0.7, minimal velocity = −1.5, and maximal velocity = 1.5. For all optimization techniques, the number of function evaluations was limited to 50.
The obtained classification performance results are summarized in Table 6. The CNN-TL-GA and CNN-TL-PSO performed very similarly in all the presented metrics, and generally not as good as the CNN-TL-DE. The only two exceptions are a bit shorter training time and slightly lower number of consumed epochs in the case of CNN-TL-GA. On the other hand, both alternative optimization techniques performed better than the two baseline methods CNN and CNN-TL, which speaks in favor of using a proper HPO method in general.

Table 6.
Comparison of classification performance results with alternative optimization techniques.
6.1.3. Using Different CNN Architectures
To even more exhaustively evaluate the performance of CNN-TL-DE algorithm, we evaluated the performance against two additional commonly used CNN architectures: Inception-V3 [59] and DenseNet-121 [60].
The Inception-V3 CNN architecture was first introduced by Szegedy et al. in 2015 [61], where the authors presented GoogleNet architecture, which would serve as an alternative to VGGNet with the ability to perform well under strict constraints on memory and computational budget [59]. The Inception-V3 architecture presented in [59] is an upgrade to the original one, where the authors introduced some general principles and optimization ideas such as factorizing convolutions with large filter sizes and utilization of auxiliary classifiers that proved to be useful for scaling up convolution networks in efficient ways. For the purpose of evaluation of our CNN-TL-DE algorithm, we adapted the Inception-V3 architecture in a manner where all but the last inception module layers are frozen, while the inception module layers are enabled for fine-tuning.
The DenseNet-121 architecture was presented in 2017 by Huang et al. [60]. The architecture features a simple connectivity pattern which enables the maximum information flow between the layers. To achieve this, the authors connected all layers with matching feature-map sizes directly with each other. In addition, each layer also obtains inputs from all preceding layers and passes on its own feature-maps to all subsequent layers, which enables to preserve the feed-forward nature [60]. We adapted the DenseNet-121 architecture in a way that the layers constructing a fourth (last) dense block are enabled for fine-tuning, while other layers are frozen.
The obtained classification performance results on three different CNN architectures are summarized in Table 7. The results obtained on Inception-V3 lag somewhat behind, while the results on the other two are very similar, within the range of 1%, with the exception of consumed training time. While the predictive performance results on DenseNet-121 are a bit higher, they exhibit much higher variance. On the other hand, both Inception-V3 and especially DenseNet-121 consumed much more time for training than the VGG19 architecture.

Table 7.
Comparison of classification performance of CNN-TL-DE on different CNN architectures.
6.2. The Analysis of Confusion Matrices
Besides comparing the general classification performance, we wanted to see how the methods classify images of specific sports and what are the most common misclassifications of one sport for another. For this purpose, we prepared a confusion matrix of test data classification from all ten folds for each of the methods (Figure 6).
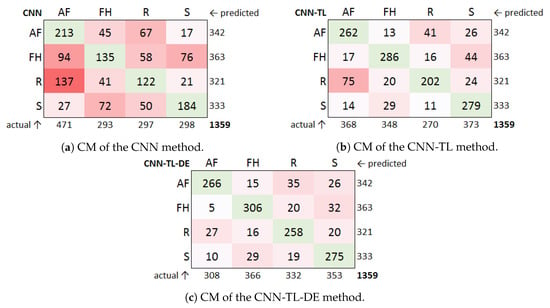
Figure 6.
Comparison of confusion matrices of the three methods on test data (AF, American football; FH, field hockey; R, rugby; S, soccer).
The proposed CNN-TL-DE method achieved the best results in the vast majority of situations. When compared to the CNN method, there is only one situation (out of 16 possible) where it lags slightly behind—namely, it misclassified a few more American football images as soccer (26 vs. 17 mistakes). In all other situations the CNN-TL-DE performed much better. When compared to CNN-TL, there are four situations (out of 16) where CNN-TL-DE performed slightly worse—when misclassifying American football images as field hockey (15 vs. 13 mistakes), field hockey images as rugby (20 vs. 16 mistakes), and soccer images as rugby (19 vs. 11 mistakes), and also when classifying soccer images correctly (275 vs. 279 cases).
It is interesting to see that all three methods made the most mistakes when misclassifying American football as rugby or vice versa. Mistakenly identifying one instead of the other is quite natural because of their similar game concepts, formations and postures of athletes, shape of the ball, etc. On the other hand, field hockey can be considered as the most different of the four sports, with hockey sticks, smaller ball, etc. While this proved to be the case with the CNN-TL-DE method, the other two methods (especially the CNN) made more misclassifications of field hockey images—the CNN-TL primarily confused them with soccer, and the CNN confused them with soccer and American football (see Figure 6).
Overall, the CNN-TL-DE method turned out to be the most balanced, with very similar results on all four sports and all possible misclassifications. The CNN-TL classified rugby noticeably worse than other sports, while the CNN over-predicted American football and performed much worse on the other three sports. Thus, the CNN-TL-DE performed the most up to one’s expectations.
6.3. The Analysis of the Obtained Hyper-Parameters
As the key aspect of the proposed method is to find the optimal values of hyper-parameters using the DE approach, we wanted to see what were the actual final values as obtained by the CNN-TL-DE method. All the obtained values for all ten folds are presented in Table 8. The optimal values differ from one fold to another. Unfortunately, this does not allow one to find and fix one general set of optimal hyper-parameters and then just use them for training. From the results, we can see that the most often used optimizer type is adam and the most optimal learning rate is between 0.00005 and 0.0001. The dropout probability of the spatial two-dimensional dropout layer should be lower (0.1–0.4) than that of the regular dropout layer (typically 0.4–0.7, but with higher variance). Finally, the number of neurons in last fully-connected layer was set quite diverse, from the lowest 64 neurons to the highest 2048, with the later being the most frequent choice.

Table 8.
Obtained hyper-parameters per fold using the CNN-TL-DE method.
When compared to manually set parameters (see Table 2), we can see that the learning rates and the probabilities of the regular dropout layer are quite similar. Although being pretty much the same on average (1241 neurons), the optimal number of neurons turned out to be very diverse, as opposed to manually fixed value of 1024. The most different, however, are the optimizer types (adam as opposed to fixed RMSprop) and the dropout probabilities of the spatial two-dimensional dropout layer, which were manually fixed to the same value as the regular dropout layer (0.5), but it turned out that the optimal value should be lower (0.1–0.4).
6.4. Explaining the Classification Model
Finally, we inspected how the classification model produced by the proposed CNN-TL-DE method performs classification on specific images from the interpretability point of view. For this purpose, we used two surrogate models techniques, LIME and SHAP, to explain the deep neural network model and to gain useful insights on how the model perceives individual images and their various features. Using interpretive representations of a trained model also increases the trust in the predictive model.
Figure 7, Figure 8, Figure 9 and Figure 10 present some images with their corresponding interpretable representations generated with the LIME technique. Green colored pixel groups (super-pixels) indicate identified regions with a positive impact towards a particular sports discipline, while the red pixel groups indicate the regions with a negative impact towards this same discipline. In other words, the green regions represent the decisive features, because of which an image has been classified to a specific sport.

Figure 7.
Examples of how LIME explained classifying images as American football. We can see that the equipment, such as helmets, visors, and shoulder pads, of athletes is decisive for classification.

Figure 8.
Examples of how LIME explained classifying images as field hockey. The hockey sticks are decisive for classification, while general features, such as faces and hair, do not contribute.

Figure 9.
Examples of how LIME explained classifying images as rugby. Here, the packed formation of athletes and the rugby ball are decisive for classification; again, general features of athletes do not contribute to classification.

Figure 10.
Examples of how LIME explained classifying images as soccer. Here, the shape of the soccer ball or specialties of the soccer shoes are decisive for classification.
Similarly, Figure 11 shows some images with their interpretable representations generated with the SHAP method. SHAP provides a separate interpretation for each class, where red pixels indicate parts of image with a positive impact towards specific class, while blue pixels indicate parts with a negative impact. It can be easily seen how the hockey stick, for example, is decisive for classifying an image as field hockey, or the soccer ball for soccer.
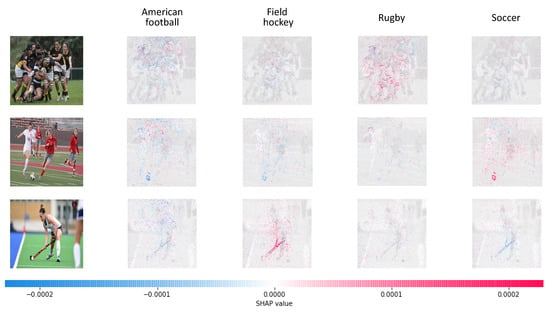
Figure 11.
Examples of SHAP explanations: red pixels indicate parts of image with a positive impact towards specific sport, while blue pixels indicate parts with a negative impact. In the top row, we can see how the packed formation of athletes contributed towards recognizing rugby. In the middle row, the soccer ball was decisive. In the bottom row, the hockey stick was the most informative feature for identifying field hockey.
7. Conclusions
In this paper, we present a CNN-TL-DE method for image classification using the fine-tuning of transfer learning for training an adapted VGG19 CNN model with the use of HPO based on DE. The method addresses the problem of automatic classification of images of very similar sports disciplines. In order for the method to be able to train an accurate classification model efficiently on a rather small image dataset, the essential hyper-parameters, which influence the training process and the resulting model, were optimized with the utilization of DE.
The presented method was evaluated against two other methods, one where the model is trained in a conventional way (from scratch), and the other where the model is trained using the transfer learning approach with convolutional layers of the neural network pre-trained on ImageNet dataset. All the hyper-parameters in this case were handpicked based on general recommendations and our previous experiences. As the target, we selected the task of classifying images, representing four similar sports, into their respective disciplines. The results obtained from the conducted experiments show that our proposed CNN-TL-DE method outperformed the compared methods in all predictive performance metrics by quite a margin. On the other hand, the proposed method is significantly more time-consuming.
In conclusion, the main contribution and purpose of the proposed method is to provide a robust and automatic approach to HPO, which then significantly improves the classification performance. With the use of DE for performing HPO, the accuracy results on unseen images improved by 32.68% with regard to baseline CNN without HPO and by 5.59% with regard to manually optimized hyper-parameters, which requires a deep understanding of CNNs; similar improvements were shown for all other classification performance metrics. The proposed method, thus, allows one to achieve very good classification results in a quite automatic manner—at the expense of training time.
In the future, we would like to research on how to improve the time-complexity of the proposed method without compromising its predictive performance. For this purpose, we are currently investigating the utilization of some other promising optimization algorithms, such as Grey Wolf Optimizer, to see whether they could bring any improvement. Additionally, we would like to evaluate the proposed method on other image datasets.
Author Contributions
Conceptualization, V.P. and G.V.; methodology, V.P.; validation, V.P., Š.P., and G.V.; software and programming, G.V. and Š.P.; results analysis, V.P.; writing—original draft, V.P.; writing—review and editing, V.P., Š.P., and G.V.; visualization, V.P., Š.P., and G.V.; and funding acquisition, V.P. All authors have read and agreed to the published version of the manuscript.
Funding
The authors acknowledge the financial support from the Slovenian Research Agency (Research Core Funding No. P2-0057).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hatem, Y.; Rady, S. Exploring feature dimensionality reduction methods for enhancing automatic sport image annotation. Multimed. Tools Appl. 2018, 77, 9171–9188. [Google Scholar] [CrossRef]
- Pilar, P.M.; Rafael, M.C.; Félix, Z.O.; Gabriel, G.V. Impact of sports mass media on the behavior and health of society. A systematic review. Int. J. Environ. Res. Public Health 2019, 16, 486. [Google Scholar] [CrossRef] [PubMed]
- Minhas, R.A.; Javed, A.; Irtaza, A.; Mahmood, M.T.; Joo, Y.B. Shot classification of field sports videos using AlexNet Convolutional Neural Network. Appl. Sci. 2019, 9, 483. [Google Scholar] [CrossRef]
- Fister, I.; Fister, I., Jr.; Fister, D. Computational Intelligence in Sports; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Wang, S.Y.; Liao, W.S.; Hsieh, L.C.; Chen, Y.Y.; Hsu, W.H. Learning by expansion: Exploiting social media for image classification with few training examples. Neurocomputing 2012, 95, 117–125. [Google Scholar] [CrossRef]
- Lu, C.; Zhai, F. Weakly-supervised large-scale image modeling for sport scenes and its applications. J. Vis. Commun. Image Represent. 2020, 71, 102718. [Google Scholar] [CrossRef]
- Ciregan, D.; Meier, U.; Schmidhuber, J. Multi-column deep neural networks for image classification. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 3642–3649. [Google Scholar]
- Karpathy, A.; Toderici, G.; Shetty, S.; Leung, T.; Sukthankar, R.; Fei-Fei, L. Large-scale video classification with convolutional neural networks. In Proceedings of the IEEE conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 24–27 June 2014; pp. 1725–1732. [Google Scholar]
- Moreira, D.; Vasconcelos, C.; Paes, A.; Velho, L. Deep Image Classification of a Wild Data Set for Olympic Sports. 2016. Available online: https://www.visgraf.impa.br/Data/RefBib/PS_PDF/workpedia2016/Workpedia_2016_paper_18.pdf (accessed on 20 August 2020).
- Hussain, M.; Bird, J.J.; Faria, D.R. A study on cnn transfer learning for image classification. In UK Workshop on Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2018; pp. 191–202. [Google Scholar]
- Yang, L.; Shami, A. On hyperparameter optimization of machine learning algorithms: Theory and practice. Neurocomputing 2020, 415, 295–316. [Google Scholar] [CrossRef]
- Vrbančič, G.; Fister, I.J.; Podgorelec, V. Parameter Setting for Deep Neural Networks Using Swarm Intelligence on Phishing Websites Classification. Int. J. Artif. Intell. Tools 2019, 28, 1960008. [Google Scholar] [CrossRef]
- Vrbančič, G.; Zorman, M.; Podgorelec, V. Transfer Learning Tuning Utilizing Grey Wolf Optimizer for Identification of Brain Hemorrhage from Head CT Images. In Proceedings of the 2019 6th Student Computer Science Research Conference, Koper, Slovenia, 10 October 2019; pp. 61–66. [Google Scholar]
- Vrbančič, G.; Pečnik, Š.; Podgorelec, V. Identification of COVID-19 X-ray Images using CNN with Optimized Tuning of Transfer Learning. In Proceedings of the 2020 International Conference on INnovations in Intelligent SysTems and Applications (INISTA), Novi Sad, Serbia, 24–26 August 2020; pp. 1–8. [Google Scholar]
- Jung, Y.; Hwang, E.; Kim, W. Sports image classification through Bayesian classifier. In Lecture Notes in Computer Science, Proceedings of the Conference on Technology Transfer, San Sebastian, Spain, 12–14 November 2003; Springer: Berlin/Heidelberg, Germany, 2003; pp. 546–555. [Google Scholar]
- Capodiferro, L.; Costantini, L.; Mangiatordi, F.; Pallotti, E. SVM for historical sport video classification. In Proceedings of the 2012 5th International Symposium on Communications, Control and Signal Processing, Rome, Italy, 2–4 May 2012; pp. 1–4. [Google Scholar]
- Hatem, Y.; Rady, S.; Ismail, R.; Bahnasy, K. Automatic content description and annotation of sport images using classification techniques. In Proceedings of the 10th International Conference on Informatics and Systems, Cairo, Egypt, 9–11 May 2016; pp. 88–94. [Google Scholar]
- Breen, C.; Khan, L.; Ponnusamy, A. Image classification using neural networks and ontologies. In Proceedings of the 13th International Workshop on Database and Expert Systems Applications, Aix-en-Provence, France, 6 September 2002; pp. 98–102. [Google Scholar]
- Kanellopoulos, I.; Wilkinson, G.G. Strategies and best practice for neural network image classification. Int. J. Remote Sens. 1997, 18, 711–725. [Google Scholar] [CrossRef]
- Foody, G. Supervised image classification by MLP and RBF neural networks with and without an exhaustively defined set of classes. Int. J. Remote Sens. 2004, 25, 3091–3104. [Google Scholar] [CrossRef]
- Giacinto, G.; Roli, F. Design of effective neural network ensembles for image classification purposes. Image Vis. Comput. 2001, 19, 699–707. [Google Scholar] [CrossRef]
- Fukushima, K.; Miyake, S. Neocognitron: A self-organizing neural network model for a mechanism of visual pattern recognition. In Competition and Cooperation in nEural Nets; Amari, S., Arbib, M.A., Eds.; Springer: Berlin/Heidelberg, Germany, 1982; pp. 267–285. [Google Scholar]
- Rawat, W.; Wang, Z. Deep convolutional neural networks for image classification: A comprehensive review. Neural Comput. 2017, 29, 2352–2449. [Google Scholar] [CrossRef] [PubMed]
- Vrbančič, G.; Podgorelec, V. Automatic Classification of Motor Impairment Neural Disorders from EEG Signals Using Deep Convolutional Neural Networks. Elektron. Elektrotech. 2018, 24, 3–7. [Google Scholar] [CrossRef]
- Vrbančič, G.; Fister, I.J.; Podgorelec, V. Automatic Detection of Heartbeats in Heart Sound Signals Using Deep Convolutional Neural Networks. Elektron. Elektrotech. 2019, 25, 71–76. [Google Scholar] [CrossRef]
- McQuin, C.; Goodman, A.; Chernyshev, V.; Kamentsky, L.; Cimini, B.A.; Karhohs, K.W.; Doan, M.; Ding, L.; Rafelski, S.M.; Thirstrup, D.; et al. CellProfiler 3.0: Next-generation image processing for biology. PLoS Biol. 2018, 16, e2005970. [Google Scholar] [CrossRef] [PubMed]
- Javaid, A.; Niyaz, Q.; Sun, W.; Alam, M. A deep learning approach for network intrusion detection system. In Proceedings of the 9th EAI International Conference on Bio-Inspired Information and Communications Technologies (Formerly BIONETICS), New York, NY, USA, 3–5 December 2015; pp. 21–26. [Google Scholar]
- Kamilaris, A.; Prenafeta-Boldú, F.X. Deep learning in agriculture: A survey. Comput. Electron. Agric. 2018, 147, 70–90. [Google Scholar] [CrossRef]
- Ching, J.Y.; Wong, A.K.C.; Chan, K.C.C. Class-dependent discretization for inductive learning from continuous and mixed-mode data. IEEE Trans. Pattern Anal. Mach. Intell. 1995, 17, 641–651. [Google Scholar] [CrossRef]
- Dumais, S.; Platt, J.; Heckerman, D.; Sahami, M. Inductive Learning Algorithms and Representations for Text Categorization. In Proceedings of the 7th International Conference on Information and Knowledge Management, Bethesda, MD, USA, 3–7 November 1998; pp. 148–152. [Google Scholar]
- Zhu, X.; Wu, X. Class noise handling for effective cost-sensitive learning by cost-guided iterative classification filtering. IEEE Trans. Knowl. Data Eng. 2006, 18, 1435–1440. [Google Scholar]
- Yang, Q.; Ling, C.; Chai, X.; Pan, R. Test-cost sensitive classification on data with missing values. IEEE Trans. Knowl. Data Eng. 2006, 18, 626–638. [Google Scholar] [CrossRef]
- Diaz, G.I.; Fokoue-Nkoutche, A.; Nannicini, G.; Samulowitz, H. An effective algorithm for hyperparameter optimization of neural networks. IBM J. Res. Dev. 2017, 61, 9:1–9:11. [Google Scholar] [CrossRef]
- Gambella, C.; Ghaddar, B.; Naoum-Sawaya, J. Optimization models for machine learning: A survey. arXiv 2019, arXiv:1901.05331. [Google Scholar]
- Bergstra, J.S.; Bardenet, R.; Bengio, Y.; Kégl, B. Algorithms for hyper-parameter optimization. In Proceedings of the Advances in Neural Information Processing Systems, Granada, Spain, 12–17 December 2011; pp. 2546–2554. [Google Scholar]
- Bergstra, J.; Bengio, Y. Random search for hyper-parameter optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Bacanin, N.; Bezdan, T.; Tuba, E.; Strumberger, I.; Tuba, M. Optimizing Convolutional Neural Network Hyperparameters by Enhanced Swarm Intelligence Metaheuristics. Algorithms 2020, 13, 67. [Google Scholar] [CrossRef]
- Bibaeva, V. Using metaheuristics for hyper-parameter optimization of convolutional neural networks. In Proceedings of the 2018 IEEE 28th International Workshop on Machine Learning for Signal Processing (MLSP), Aalborg, Denmark, 17–20 September 2018; pp. 1–6. [Google Scholar]
- Storn, R.; Price, K. Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Nakisa, B.; Rastgoo, M.N.; Rakotonirainy, A.; Maire, F.; Chandran, V. Long short term memory hyperparameter optimization for a neural network based emotion recognition framework. IEEE Access 2018, 6, 49325–49338. [Google Scholar] [CrossRef]
- Xue, N.; Triguero, I.; Figueredo, G.P.; Landa-Silva, D. Evolving Deep CNN-LSTMs for Inventory Time Series Prediction. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation (CEC), Wellington, New Zealand, 10–13 June 2019; pp. 1517–1524. [Google Scholar]
- Brezočnik, L.; Fister, I.; Vrbančič, G. Applying Differential Evolution with Threshold Mechanism for Feature Selection on a Phishing Websites Classification. In New Trends in Databases and Information Systems; Welzer, T., Eder, J., Podgorelec, V., Wrembel, R., Ivanović, M., Gamper, J., Morzy, M., Tzouramanis, T., Darmont, J., Kamišalić Latifić, A., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 11–18. [Google Scholar]
- Piotrowski, A.P. Review of differential evolution population size. Swarm Evol. Comput. 2017, 32, 1–24. [Google Scholar] [CrossRef]
- Mininno, E.; Neri, F. A memetic differential evolution approach in noisy optimization. Memetic Comput. 2010, 2, 111–135. [Google Scholar] [CrossRef]
- Das, S.; Suganthan, P.N. Differential Evolution: A Survey of the State-of-the-Art. IEEE Trans. Evol. Comput. 2011, 15, 4–31. [Google Scholar] [CrossRef]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. “Why should i trust you?” Explaining the predictions of any classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 1135–1144. [Google Scholar]
- Zhang, Y.; Song, K.; Sun, Y.; Tan, S.; Udell, M. “Why Should You Trust My Explanation?” Understanding Uncertainty in LIME Explanations. arXiv 2014, arXiv:1904.12991. [Google Scholar]
- Schallner, L.; Rabold, J.; Scholz, O.; Schmid, U. Effect of Superpixel Aggregation on Explanations in LIME–A Case Study with Biological Data. In Communications in Computer and Information Science, Proceedings of the Joint European Conference on Machine Learning and Knowledge Discovery in Databases, Würzburg, Germany, 16–20 September 2019; Springer: Cham, Switzerland, 2019; pp. 147–158. [Google Scholar]
- Lundberg, S.M.; Lee, S.I. A Unified Approach to Interpreting Model Predictions. In Advances in Neural Information Processing Systems 30; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2017; pp. 4765–4774. [Google Scholar]
- Lundberg, S. SHAP Documentation. 2018. Available online: https://shap.readthedocs.io/en/latest/index.html (accessed on 28 September 2020).
- Molnar, C. Interpretable Machine Learning: A Guide for Making Black Box Models Explainable, 1st ed.; Lulu: Morrisville, NC, USA, 2019. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. Imagenet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Gómez-Valverde, J.J.; Antón, A.; Fatti, G.; Liefers, B.; Herranz, A.; Santos, A.; Sánchez, C.I.; Ledesma-Carbayo, M.J. Automatic glaucoma classification using color fundus images based on convolutional neural networks and transfer learning. Biomed. Opt. Express 2019, 10, 892–913. [Google Scholar] [CrossRef]
- Mayer, D.G.; Kinghorn, B.; Archer, A.A. Differential evolution–an easy and efficient evolutionary algorithm for model optimisation. Agric. Syst. 2005, 83, 315–328. [Google Scholar] [CrossRef]
- Fawcett, T. Using rule sets to maximize ROC performance. In Proceedings of the 2001 IEEE International Conference on Data Mining, San Jose, CA, USA, 29 November–2 December 2001; pp. 131–138. [Google Scholar]
- Fleiss, J.L.; Levin, B.; Paik, M.C. Statistical Methods for Rates and Proportions, 3rd ed.; Wiley-Interscience: Hoboken, NJ, USA, 2003. [Google Scholar]
- Demsar, J. Statistical Comparisons of Classifiers over Multiple Data Sets. J. Mach. Learn. Res. 2006, 1–30. [Google Scholar] [CrossRef]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the inception architecture for computer vision. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2017; pp. 2818–2826. [Google Scholar]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Hoholulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).