1. Introduction
In recent years, with continuous attention focused on energy issues, the traditional power grid is facing a major challenge of renewable energy generation. In Korea, with the promulgation of the “2030 renewable energy” plan, the power generation of renewable sources will reach 20% of the total power generation in 2030, as proposed in the plan. The penetration level of renewable energy sources will increase to a large extent in the next 10 years, that is, it will penetrate the traditional power grid. In particular, maintaining the stability of the power system despite increase in the penetration level of offshore wind turbines is a significant challenge.
Type 4 (full-scale converter wind turbines, or FSC-WTs) is a variable-speed wind turbine that is widely used for offshore wind-power generation. However, extensive type-4 penetration into the power system causes the onshore-power-grid inertia to decrease, debilitating the onshore AC power grid and making it difficult to maintain its frequency stability. As the type-4 wind turbine has a series connected to a back-to-back converter, in severe cases, it may cause power outages [
1]. In a previous study [
2], it was proposed that the type-4 wind turbine be integrated with a weaker grid because the phase-locked-loop parameters may cause low-frequency and synchronous-oscillation problems, as proven via dynamic modeling and eigenvalue analysis. In [
3], it was recommended that the system inertia be controlled by measuring the DC voltage of the converter instead of using the conventional method of measuring the system frequency. This method was verified using the hardware-in-loop method. The authors in [
4] suggested that the inertial response constant of a single wind turbine was not the inertial response constant of the wind power system; this was verified using field measurements and simulations. In [
5], the author explained in detail the calculation method of the inertia constant of the wind turbine with a formula.
The authors in [
6,
7,
8,
9] presented several different frequency control strategies for the entire power grid, which consisted of offshore wind power plants and line-commutated converter high-voltage direct-current transmission systems (LCC–HVDC). A control strategy that controls the grid frequency instead of reactive power control is used to control the firing angle of the HVDC rectifier or the DC-link current in [
6] because of the reactive power controlled by the rotor-side converter and rectifier converter. A coordinated control strategy provides primary frequency control for the grid, which consists of the LCC-HVDC and offshore wind turbines [
7].
The authors in [
8] state that the modeling of the weak grid is highly sensitive to the effective DC inertia constant and effective short circuit ratio, which connect to the LCC-HVDC. The authors in [
9] presented a full-order and four-state model to verify the frequency droop control strategy proposed in this paper, which can improve the frequency response speed of the weak grid. The voltage-source converter HVDC (VSC-HVDC) has more advantages than the traditional HVDC system. As is well-known, the LCC-HVDC is required to consider commutation failure, especially in the case of weak AC grids, and this may be more likely to cause grid failures. The short board of LCC-HVDC is mentioned in [
10]. Compared with VSC-HVDC, LCC-HVDC has a high risk of the stability.
The VSC-HVDC is not required to consider commutation failure and can compensate for a weak AC grid owing to its good active-power and reactive-power regulation ability. In [
11], a virtual impedance control strategy is proposed to improve the dynamic adjustment ability. Furthermore, the VSC–HVDC can also transmit energy to the system via the passive power grid, especially when the wind turbine is subject to external interference. In a previous study [
12], the stability of the power system was verified by the root-locus method. The system consists of hybrid offshore wind power plants and VSC-HVDC. The authors in [
13] proposed a method for maintaining the system frequency through coordinated control of the DC voltage. A similar power synchronization control is adopted to regulate the fault ride-through capability into a combined power grid of offshore wind power plants and VSC-HVDC [
14,
15,
16]. But the proposed method increases the communication risk at both converter sides, which makes the control method more complicated.
As mentioned in [
17,
18], a new method called inertia emulation control is used to help the VSC-HVDC evaluate the inertia of the synchronous generator (SG) when faults occur and the load is changed. This method mainly uses DC link capacitors. Because of capacity limitations, compensation capabilities are limited. The authors in [
19] proposed inertial and primary frequency support to control the frequency of the VSC-HVDC and wind turbines. The majority of modern modular multilevel converter high-voltage direct-current systems (MMC-HVDC) use half-bridge modeling with a DC breaker. The detailed MMC-HVDC model in [
20,
21] uses average-value models, which can simplify the calculation. In [
4], a high-level capacity of a type-4 wind turbine farm replaces the traditional SG and penetrates the system, resulting in a reduction in the available inertia of the system and oscillation of the system frequency stability.
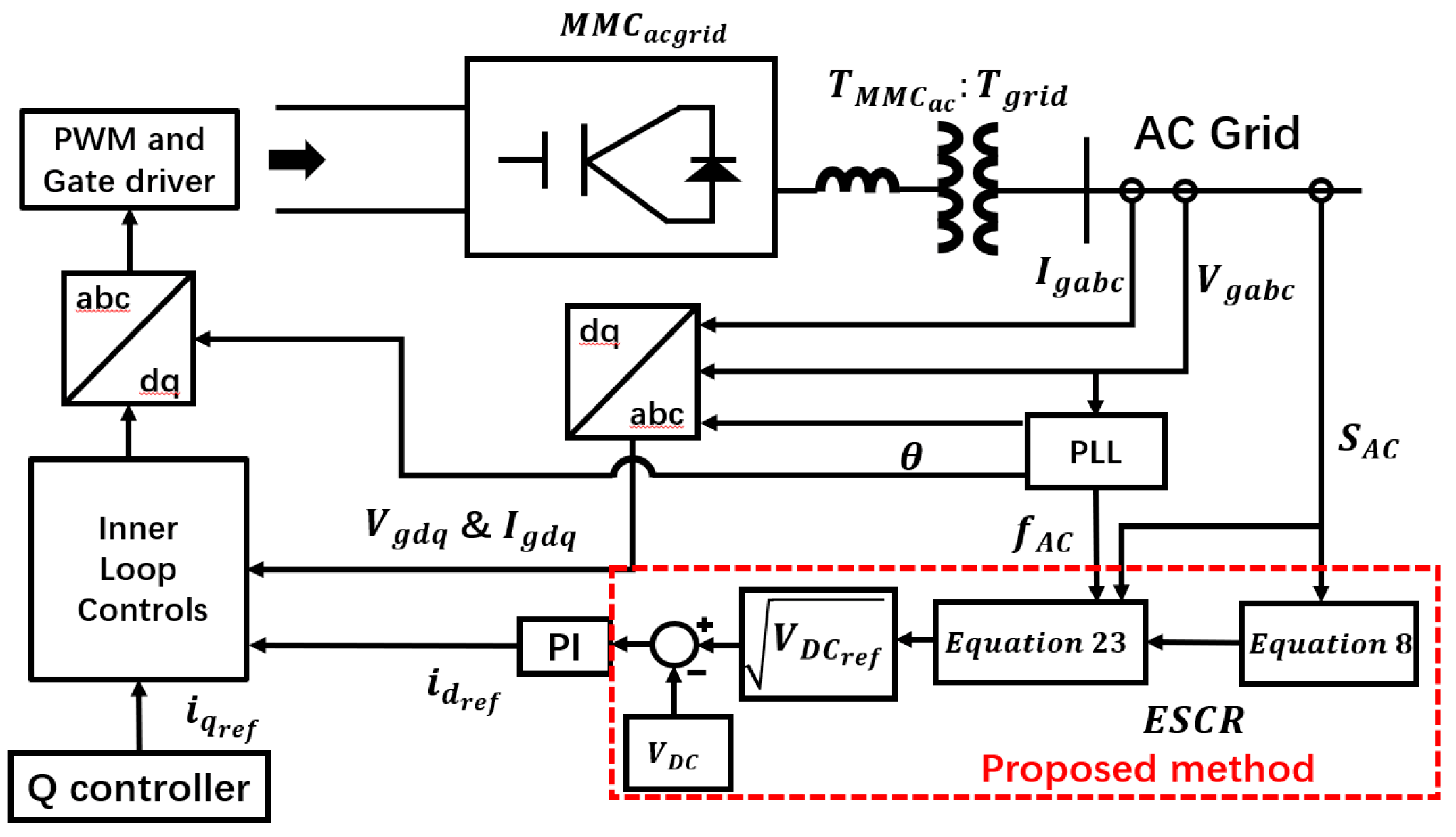
In this paper, an improved inertia control method is presented to evaluate the frequency stability of a hybrid system consisting of a full-scale-converter-wind-turbine (FSCWT) farm connected to an onshore AC system via an MMC-HVDC. The derivation of the improved control method is based on a synchronous-generator inertial mathematical model and hybrid AC/DC mathematical model. The inertia index is based on the inertia emulation control presented in [
16,
17]. First, it uses the capacitor of the MMC-HVDC sub-modulation instead of the DC link capacitor to provide the virtual inertia constant without capacity limitation. The index is also calculated based on the effective short circuit ratio (ESCR) of the AC system. An improved method can aid the AC system in maintaining its frequency stability. The index is intended to provide a simpler and faster calculation method for the system inertia constant. As the strength of the onshore AC system is different, this index will provide the minimum inertia constant required for system frequency stability. This function eliminates the inconvenience caused by other auxiliary measurement methods.
The rest of this paper is organized as follows.
Section 2 presents the inertia of the power system.
Section 3 describes the mathematical model of the MMC-HVDC, and the new index is calculated to evaluate the stability of the hybrid AC/DC system according to the ESCR of the AC system. Furthermore, in this section, the advantages of the proposed method are considered. The obtained results represent the stability of the entire system under AC faults or a small disturbance, and the verification of the correctness of the method is presented in
Section 4. The conclusions of this study are presented in
Section 5.
2. Inertia of Power System
In recent years, power electronics has significantly improved. Many types of power equipment are no longer directly connected to the power grid. However, they are connected to the power grid through various types of converters. This can greatly improve the power quality of the entire grid, but it also poses a great challenge in maintaining the stability of the power system. This article presents an investigation of the challenge of maintaining frequency stability caused by the popularity of converter technology. In this study, the offshore wind turbines considered were FSCWTs.
The generator directly connects to the back-to-back converter in series. As its output power is regulated by the converter, it loses the inertial constant. The penetration capacity of the renewable source is significantly high. The grid can be operated in a low-inertia state. Therefore, the power system cannot maintain its frequency stability under normal conditions [
4,
5]. To consider the transmission distance and system stability adjustment of offshore wind power, it is considered that the MMC-HVDC is used to connect the offshore wind power and onshore AC system, and the active power and reactive power control of MMC-HVDC can provide system stability control for AC systems.
The virtual inertia control proposed in this article will accurately and quickly provide the required minimum inertia constant based on the strength of the AC system without the root locus analysis method or eigenvalue analysis method [
12]. The detailed results are discussed in
Section 5. In addition, this consideration combines the above advantages with those of the onshore AC system to provide a more suitable inertial control for the system. This also means that we are still able to clearly determine whether the system is in a stable state without confirming the eigenvalue.
3. Control Method of MMC-HVDC System
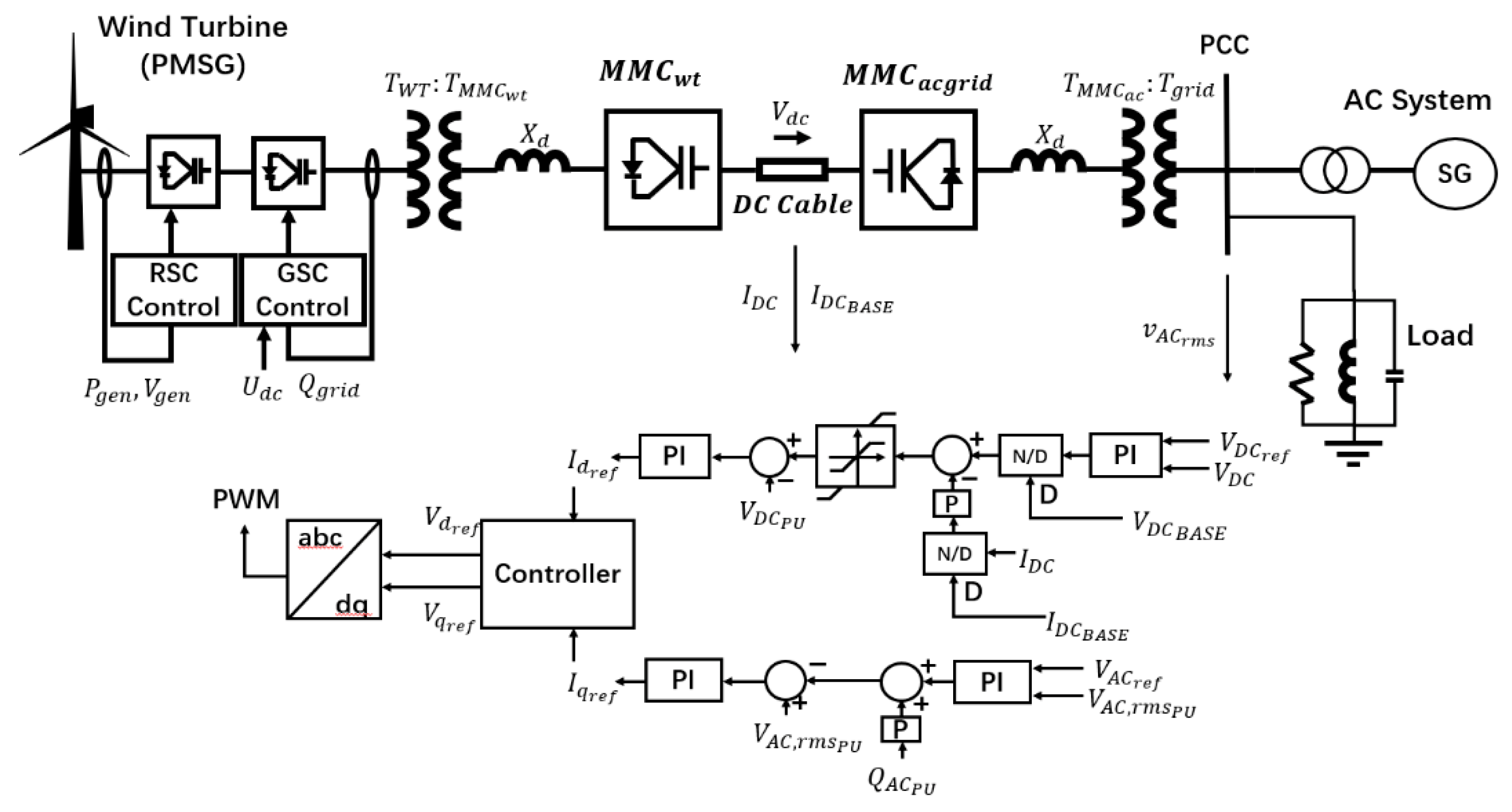
As shown in
Figure 1, the entire system consists of three parts: offshore wind power farm, onshore AC system, and MMC-HVDC system. In addition, the system has an HVDC cable and an AC cable in the modeling. In the MMC converter on the side of the offshore wind power farm, the P-Q control strategy is adopted, and on the side of the MMC converter connected to the onshore AC system, the Vdc-Q control strategy is adopted. The Vdc control strategy is used to quickly adjust the output active power from the MMC converter side. The reactive power control strategy aids the AC system in quickly adjusting the voltage level by using a set-point value. First, the detailed modeling of the controller of the MMC-HVDC is described in this section.
The MMC-HVDC model contains three-phase legs, and each phase contains an upper and lower arm. Each item’s upper and lower arms have an equal number of submodules in series. There is a capacitor inside each submodule for storing energy. Therefore, a DC-link capacitor is not required for MMC-HVDC [
20,
22]. For detailed information on MMC-HVDC modeling, please refer to [
20,
22].
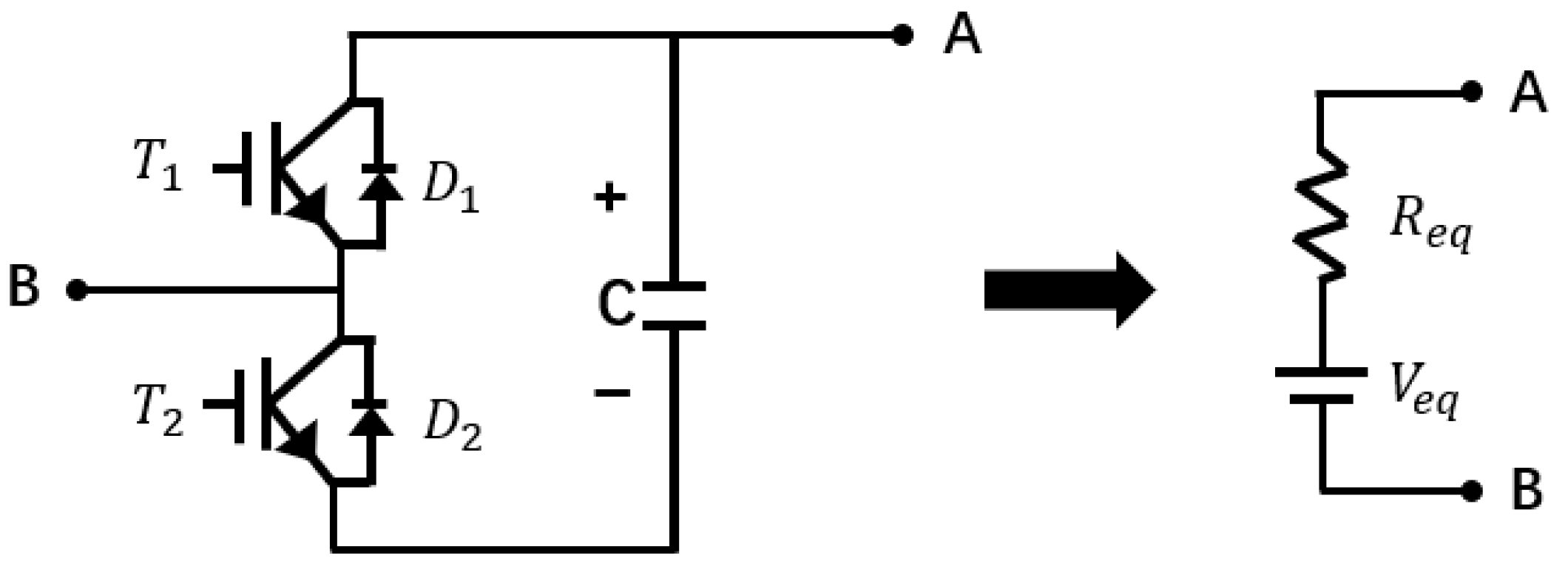
Figure 2 shows a detailed model of the half-bridge submodule, which contains two insulated-gate bipolar transistor (IGBT) switches and a capacitor for energy storage.
Figure 2 presents the equivalent circuit of the submodule, which simplifies the mathematical formula.
and
are the corresponding resistances of the IGBT switches,
is the voltage of the capacitors, and
is the resistance of the capacitor. The changes in these values depend on changes in the time and state of the IGBT switch. Therefore, the time-varying formula can be expressed as follows:
where
is the time-varying voltage value of the upper/lower arm of the MMC-HVDC.
Figure 1 shows the basic control strategy logic for the MMC-HVDC control.
Figure 1 presents a d-axis control strategy that provides two control strategies—active power control and DC voltage control—for calculating the d-axis current reference.
Figure 1 also presents a q-axis control strategy that provides two control strategies—reactive power control and AC voltage control—for calculating the q-axis current reference. The proportional-integral (PI) controller is used primarily in the control strategy loop of this study.
To ensure that the voltage components of the HVDC and the point of common coupling (PCC) are the same, we use a phase-locked loop (PLL) to realize control. When the voltage of the PCC is maintained at a constant value and balanced (
), the MMC dynamic formula is as follows:
where
is the d-component voltage of the DC side,
is the d-component voltage of the AC side, and R, L, and X are the equivalent resistance, inductance, and impedance of the three-phase reactor and transformer, respectively. The current component required for control by the proportional-integral (PI) controller is calculated, and the MMC voltage reference component is then calculated. Using these calculated values, the active power and reactive power output of the MMC-HVDC injected into the AC system through the dq-to-abc transformer is then calculated. This formula is as follows:
where
is the active power injected into the AC system for calculating the d-component reference current, and
is the reactive power injected into the AC system for calculating the q-component reference current.
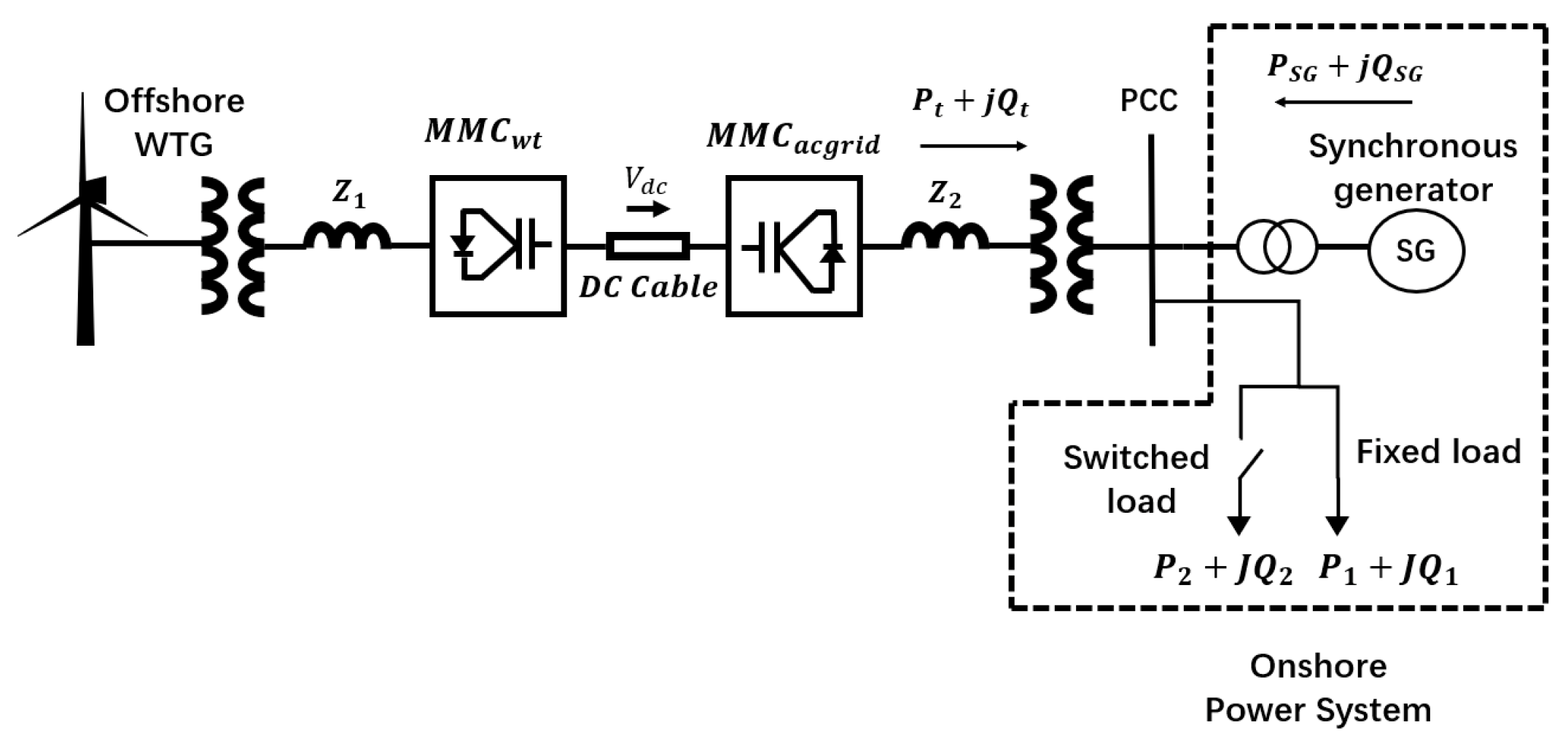
5. Case Study
The simulation system diagram is shown in
Figure 4. The ends of the MMC-HVDC are connected to the offshore wind turbine and onshore AC system. The offshore system is wind turbine generators. They transmit constant power energy to the onshore load system by using MMC-HVDC. The rated capacity of the type-4 offshore wind turbine is 5 MW. The onshore power system includes a synchronous generator and load system. There are two passive load connections on the onshore-AC-system side:
is the fixed passive load, and
is the other passive load caused by switching in or out. As the simulation is performed at different strengths of the AC system, the capacity of the passive load and parameters are detailed in a subsequent subsection. The inertia constant is calculated under the worst case of the allowable range. The 16 s before the simulation in this article is the initialization time of the system, which means that the system is not stable before 16 s. Therefore, the simulations in this article are all carried out after the 16 s. At 17 s, the switched load was disconnected from the system because of the opening of the switch.
For example, when the system is subjected to an external disturbance, the frequency fluctuation of the system is controlled within 49.2 Hz. Therefore, the calculated system frequency variation is 0.8 Hz. In addition, as the system does not consider the third resonance, the maximum range of the allowable voltage variation is 0.1 p.u. From the above data, the minimum inertia constant required for the MMC-HVDC inertia control is calculated. In this section, the improved inertia control and commonly used control are compared based on the simulation results. In addition, the simulation also takes into consideration the relationship between the inertia constant and the onshore-AC-system strength.
In
Table 1, for detailed parameters refer to [
26,
27]. Through [
26], we can know that the detailed parameters reference comes from the design of an MMC-HVDC system, which interconnected the 400-kV systems of France and Spain by 2013. This system has been put into use in practical applications, so the data of this system is reliable. In addition, the [
26,
27] have further proved the reliability of the parameters through simulation.
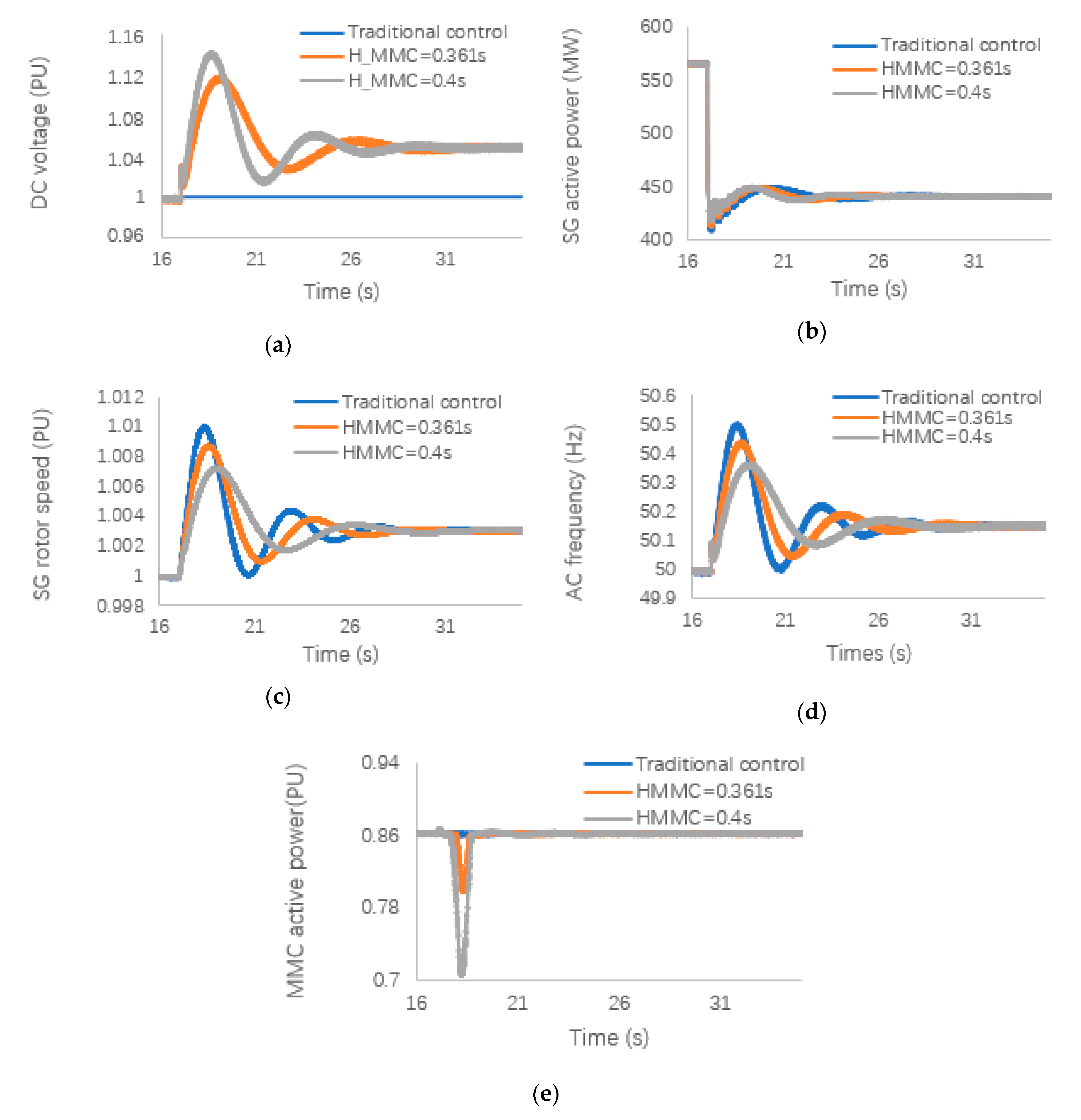
5.1. ESCR Is Low and 10% Changes in Load (ESCR = 1.7)
Case 1 was simulated when the onshore AC system was relatively weak. Thus, when the ESCR of the AC system is 1.7, the variable load
is disconnected from the system when the system is under the stability condition.
Figure 5 shows the changes in the AC-side MMC converter and onshore AC system when the system loses 10% of the load.
Figure 5a shows the curve of the DC voltage of the AC-side MMC converter. From the figure, we observe that when the ESCR is 1.7, the corresponding
value is 0.361 s.
When we increase
to 0.4 s, we find that the curve amplitude increases, which indicates improved support of the inertia control for realizing system stability. It can also be observed that the output increases as
increases, and the effective support of the inertia control for the system frequency regulation also increases.
Figure 5b,c presents the active power and rotor speed of the SG in the AC system, respectively. It is clearly observed that when the system load is reduced, the SG’s rotor-speed change and active-power change are effectively obtained.
Figure 5d shows the frequency variation curve of the onshore AC system.
Figure 5e shows the changes of MMC active power when the system is weak. As the load decreases, the active power is affected to a certain extent, but the normal operation of the system can still be guaranteed. As the system inertia constant increases, the system frequency stability is also greatly enhanced. The increase of the inertia constant can further reduce the oscillation of the system frequency. This once again verifies that the improved inertia control effectively supports the frequency stability of the system.
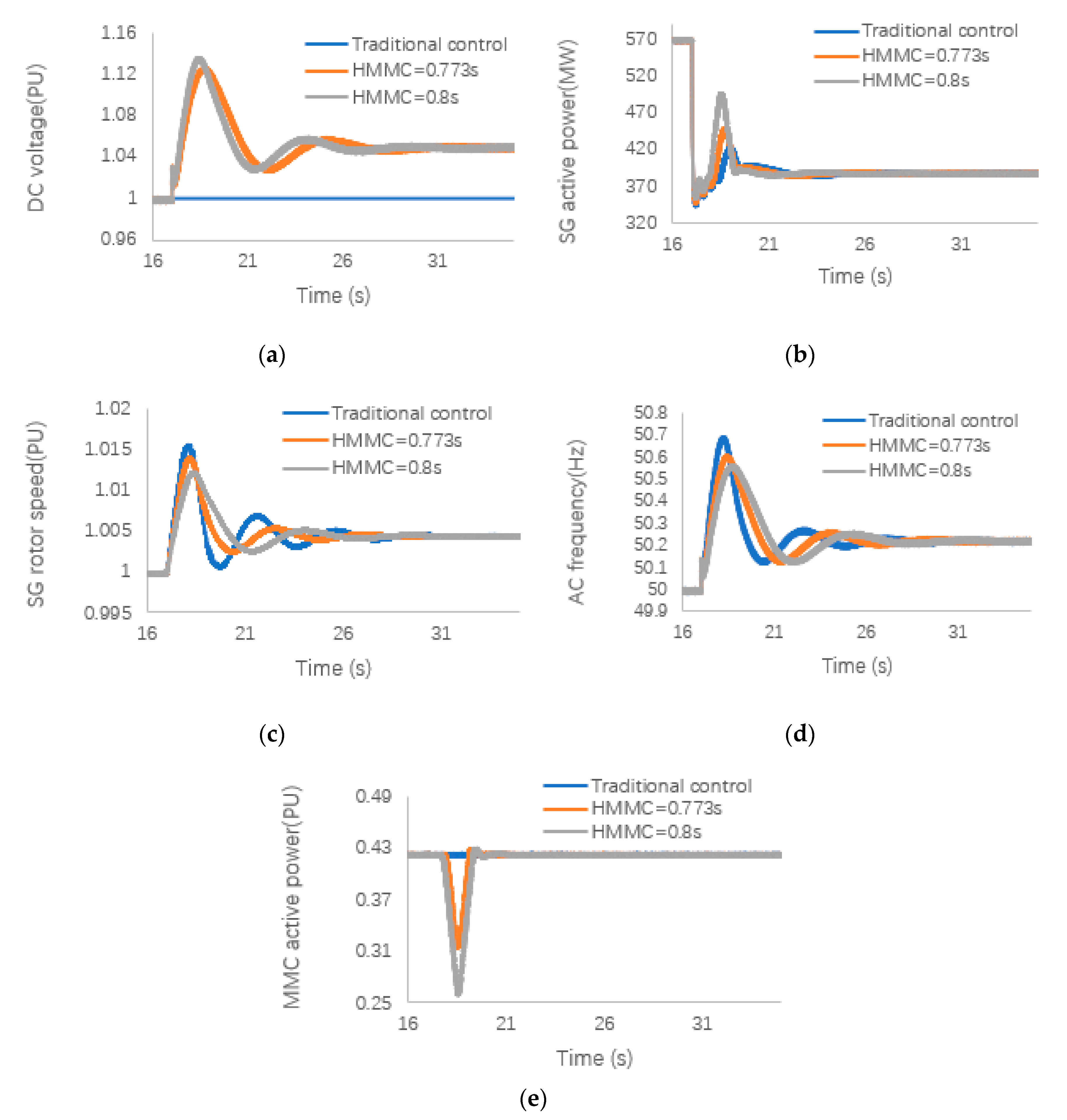
5.2. ESCR Is High and 10% Changes in Load (ESCR = 2.5)
In Case 2, the load decreased in the system when the strength of the AC system increased to 2.5. When the AC system became stronger, its frequency stability was enhanced compared to that in Case 1. As the strength of the AC system increased to 2.5, the corresponding
also increased to 0.773 s.
Figure 6a shows that the DC voltage can be effectively supported as
increases. Both the MMC converter and the improved inertia control can be observed in
Figure 6d,c, which further demonstrates that the improved control method is effective for maintaining the system stability,
Figure 6e. When the system becomes a stronger system, it can be found that while its own stability has been improved, the impact on it is also reduced.
As the system becomes stronger, the required inertia constant also increases. With the enhancement of the AC system’s stability, the system’s inertia constant also increases, which implies that the MMC controller can provide a lower inertia constant to maintain the frequency stability of the system. The AC system variation in
Figure 6d demonstrates that an improved inertia control can effectively control the system frequency stability.
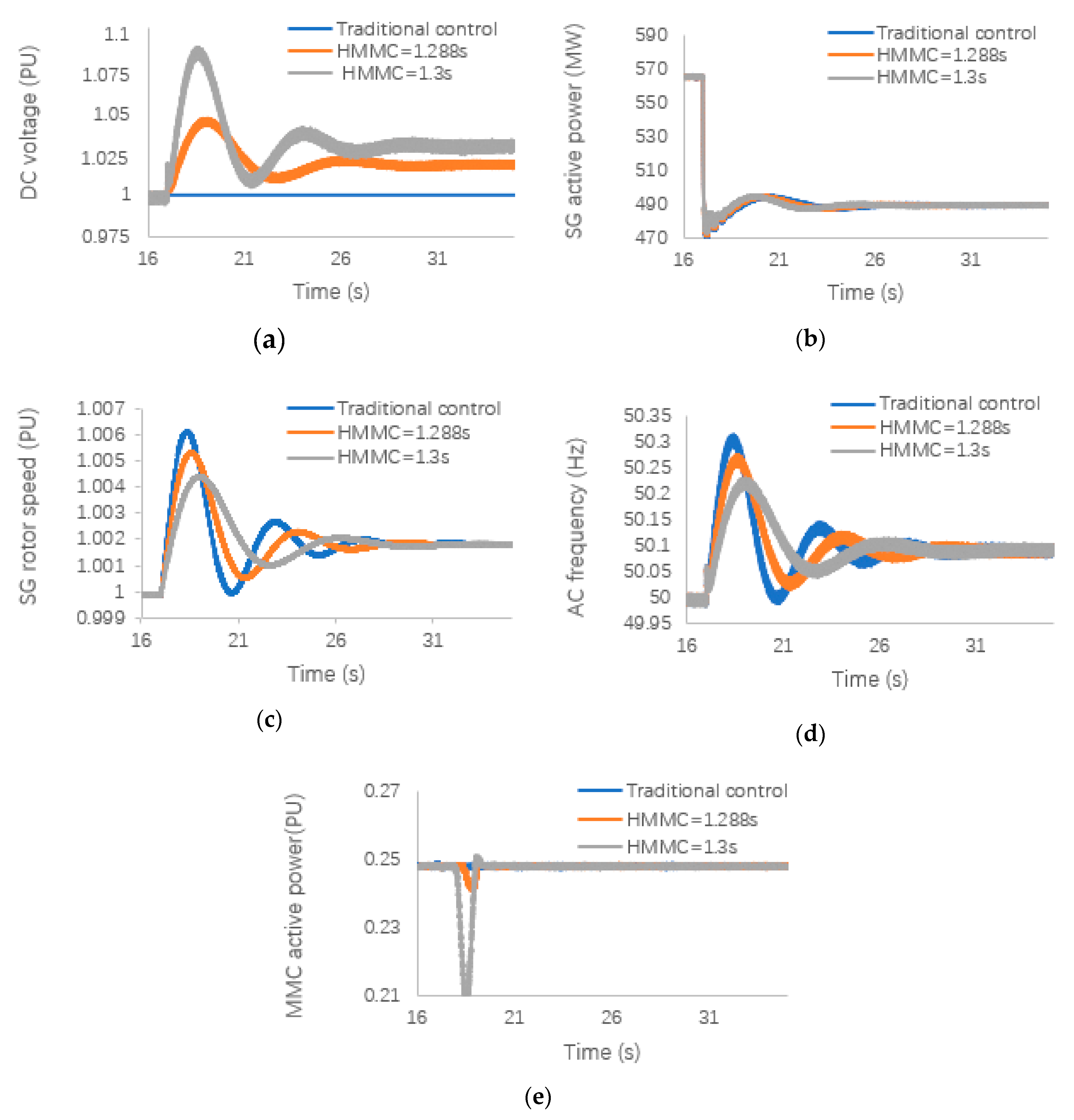
5.3. ESCR Is Higher and 10% Changes in Load (ESCR = 3.5)
According to international standards, when the ESCR value of the AC system exceeds 3, the system can be defined as a strong system. The AC system used in Case 3 had an ESCR of 3.5. The system was truly powerful. As the ESCR of the AC system increased to 3.5,
correspondingly increased to 1.288 s.
Figure 7a shows that although the system itself is strong, the improved inertia control can still effectively support the stability of the DC voltage. This also influences the active power and rotor speed of the SG in the AC system.
The results presented in
Figure 7b,c show that when
is increased by 1.3 s, the change in inertia constant can still be effectively suppressed. As the AC system becomes stronger, the system inertia constant increases. Regardless of how high a system inertia constant is provided by the MMC virtual inertia control, it will not have a significant impact on the system frequency stability. Finally, in
Figure 7d, it can be observed that the improved inertia constant provides effective support for the system frequency stability. When the MMC provides a minimum
that is higher than the system requirement, further system changes are contained.
Figure 7e also progresses to verify that when the system becomes stronger, its own anti-interference ability is stronger and can cope with more complex changes.
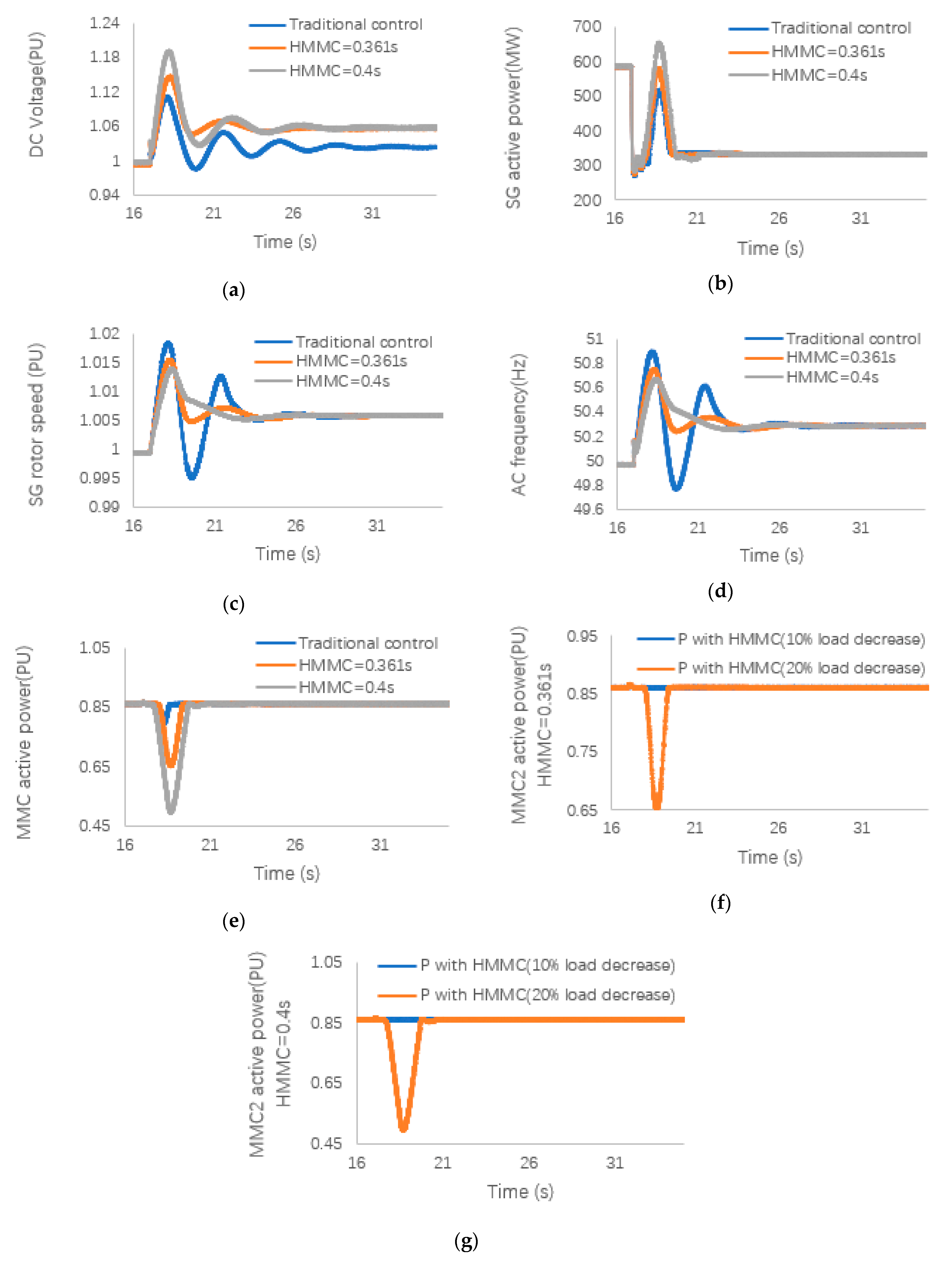
5.4. ESCR Is Low and 20% Changes in Load (ESCR = 1.7)
Case 4 simulates the situation where 20% of load decrease with the weak onshore AC system.
Figure 8 shows the response of the system after the load decreases when the onshore power system is weak.
Figure 8a shows the changes of DC voltage during the 20% load decreases. The value of HMMC directly affects the variation of DC voltage. With the increase of
, the variation of DC voltage also increases.
Figure 8b can clearly find that onshore SG has temporarily increased the power output during the load decreases. At the same time, the onshore MMC temporarily reduces the active power output to deal with the power mismatch of the onshore system in
Figure 8e. Improved inertia control still helps the system’s active power return to normal levels through its own rapid adjustment capabilities. It means that improved inertia control can also support the main frequency stability of the system under more complicated conditions.
Figure 8c shows that as the
value increases, the rotor speed of the SG is effectively damped. It means that the inertia constant provided by the improved inertia control effectively improves the stability of the system frequency. By observing
Figure 8d, the improved inertia control strategy effectively gives the system frequency support. When
, the system device response is greatly improved than before, and it is better than the system under the traditional control strategy.
In addition, by observing
Figure 8f,g, the two figures show the changes of offshore side MMC active power when the load is reduced by 10% and 20% under weak onshore AC system conditions. When the load is decreased by 10%, it affects the system which is close to the onshore side, but it does not affect the offshore side under the control of the improved inertia control strategy. When the load is decreased by 20%, the system is more affected, which also causes the active power on the offshore side to be affected, but it is still restored to a normal level under the control of improved inertia control. Although it has been more affected than the previous loading conditions, the improved inertia control strategy still effectively supports the system with a good blocking capability. When the onshore system is weak, it still has an impact on the offshore side MMC converter. But this impact is quickly corrected, then the normal operation of the system is guaranteed. Case 5 and case 6 systems have become stronger. Under the control of improved inertia control, neither a 10% load reduction nor a 20% load reduction can affect the offshore side. Therefore, case 5 and case 6 will no longer represent the active power graphics on the offshore side.
5.5. ESCR Is High and 20% Changes in Load (ESCR = 2.5)
In case 5, the 20% load decreased in the system when the strength of the AC system increased to 2.5.
Figure 9 shows the result of system response to load decrease when the onshore system becomes stronger. In
Figure 9, the results show that the onshore power system becomes stronger, the system’s own frequency stability enhanced, and it can cope with more complex changing conditions. In
Figure 9a, with the enhancement of the onshore system, the inertia constant provided by the improved inertia control still makes the DC variation. In addition, as the ESCR value of the onshore system increases, it can be found through the proposed method that the minimum inertia constant required by the system also increases. The active power of the SG changed under the stronger onshore system in
Figure 9b. In
Figure 9c, with the enhancement of the onshore system, the improved inertia control is still effective to damp the rotor speed of the SG. With the effective support of improved inertia control, the system frequency variation decreases in
Figure 9d. It also has a good control effect for MMC output active power as shown in
Figure 9e. Similarly, when
is increased to 0.8, the response result of the system is better than before.
5.6. ESCR Is Higher and 20% Load Changes (ESCR = 3.5)
The results in
Figure 10 show that when the system becomes a strong system, its own stability will be greatly improved, and the minimum inertia constant required by the system will also increase.
Figure 10a shows that the inertia constant provided by improved inertia control still causes changes in the DC voltage. The response of the active power is shown in
Figure 10b. The results in
Figure 10c show that the rotor speed of SG can be well controlled under the condition of strong onshore AC system. Improved inertia control still effectively controls the frequency of the AC system. From
Figure 10d, improved inertia control still effectively controls the frequency of the AC system. When the
is further increased to 1.3 s, the response result of the system is also satisfactory. It has a superior control effect for MMC active power in
Figure 10e.
5.7. Relationship between Inertia Constant and ESCR
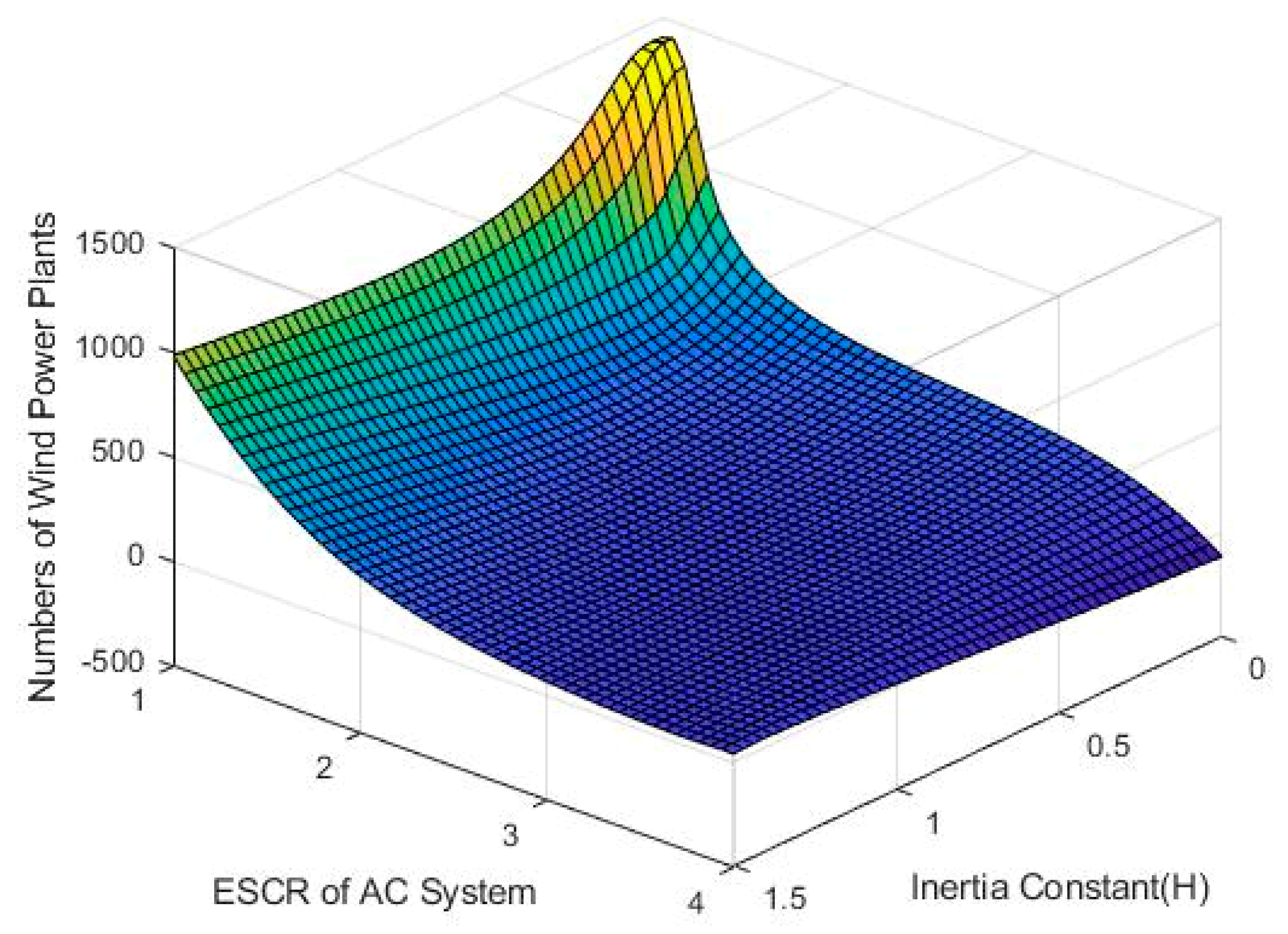
In this subsection, we discuss the relationship between the inertia constant and AC system robustness based on (22). Additionally, the ESCR is affected by the AC-rated capacity and DC-rated active power. In other words, the total capacity of offshore wind turbines directly affects the rated active power of the MMC-HVDC. As the capacity of each type-4 wind turbine is fixed, the number of generators that penetrate the system determines the transmission power. As shown in
Figure 8, we provided an ESCR ranging from weak to strong (e.g., ESCR of 1 to 4), an inertia constant, and the number of wind turbines infiltrating the system.
In
Figure 11, it can be observed from the results that the value of the inertia constant depends to a certain extent on the value of the ESCR, which maintains the same DC voltage level. If the number of wind turbines infiltrating the grid is reduced, then the inertia of the system increases. Therefore, as the capacity of a single motor is fixed, the penetration level of the wind turbine will also present great challenges to the stability of the grid.
6. Conclusions
In this paper, an improved inertia constant control that uses the ESCR value of the AC system is presented. This method aids the system in maintaining its frequency stability by using the energy stored in the capacitor of the MMC submodules and via effective damping of the frequency oscillations owing to load loss. The simulation results show that improved inertia control can better support the frequency stability of the AC system under various conditions. Whether it is under 10% load reduction or 20% load reduction, the improved inertia control strategy provides good support for system stability. In addition, the control accuracy of this method is higher even if the system is in a relatively weaker state (and even in the case of a system with an extremely low inertia constant). The improved inertia control can also help the generators connected to it, which can effectively contain the fault effect and provide better stability support and primary frequency control for the system.
As the type-4 wind-turbine penetration level decreases, the inertia constant of the MMC-HVDC improves significantly. The stability of the system itself was strengthened to ensure the stability of the system frequency when the regenerative-energy penetration level increases in the future, and a fault crossing capability was realized.