Cavitating Jet: A Review
Abstract
Featured Application
Abstract
1. Introduction
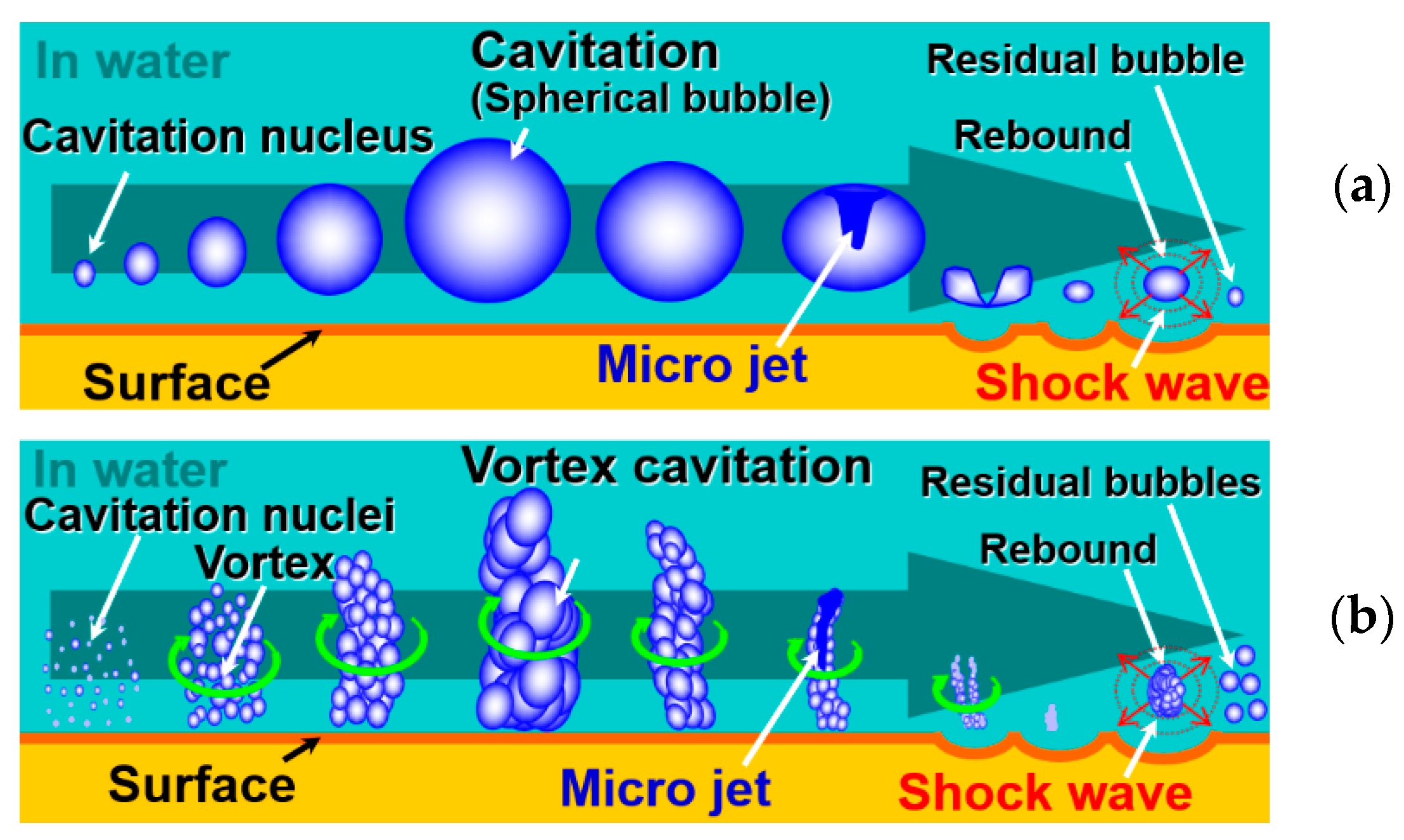
2. Cavitation
3. Cavitating Jet
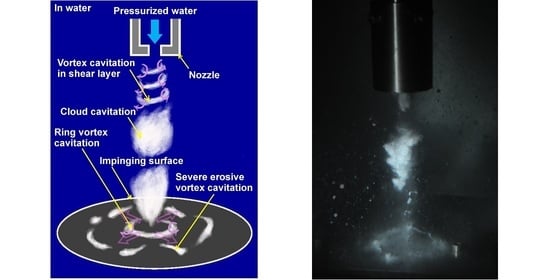
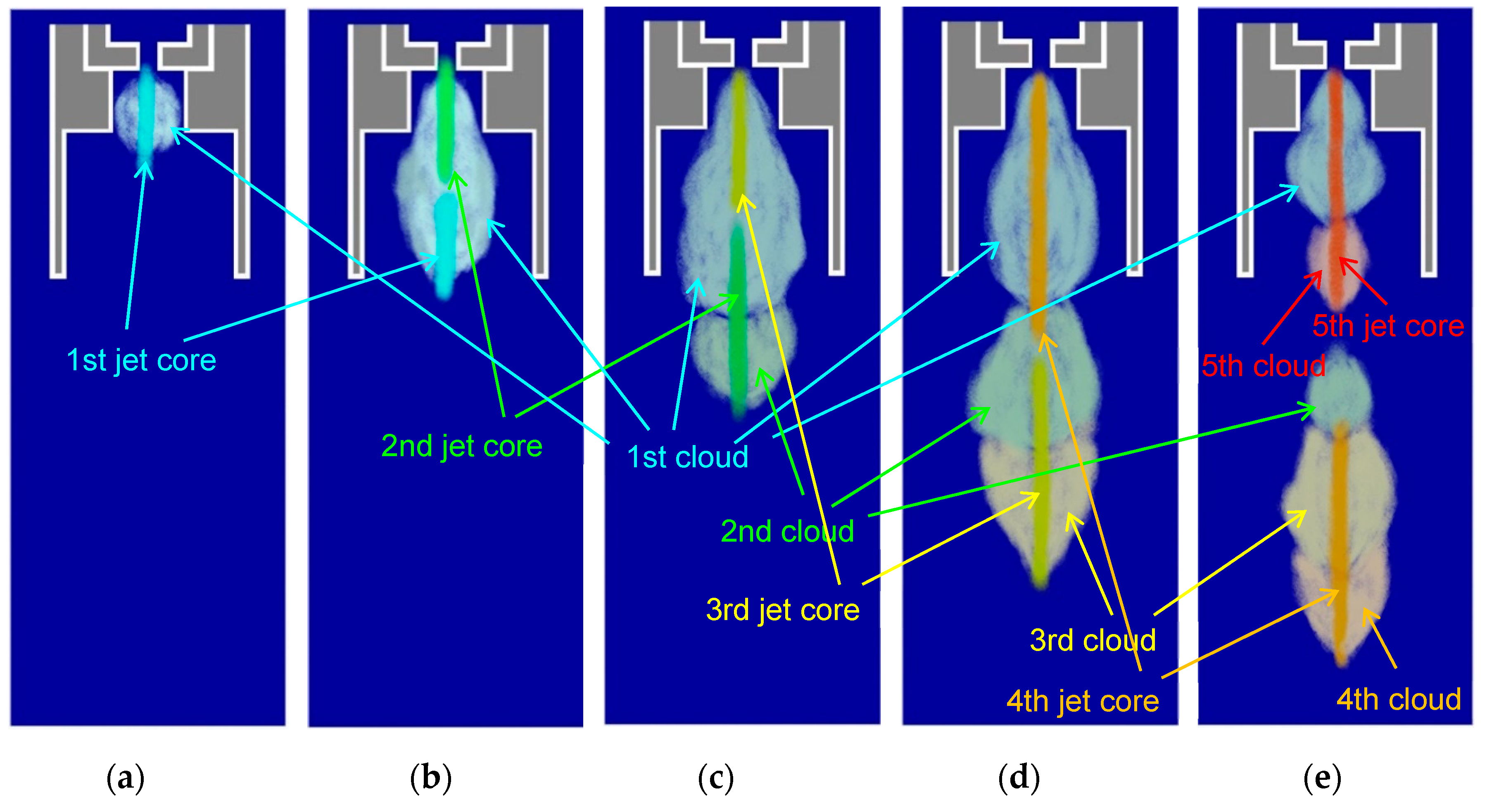
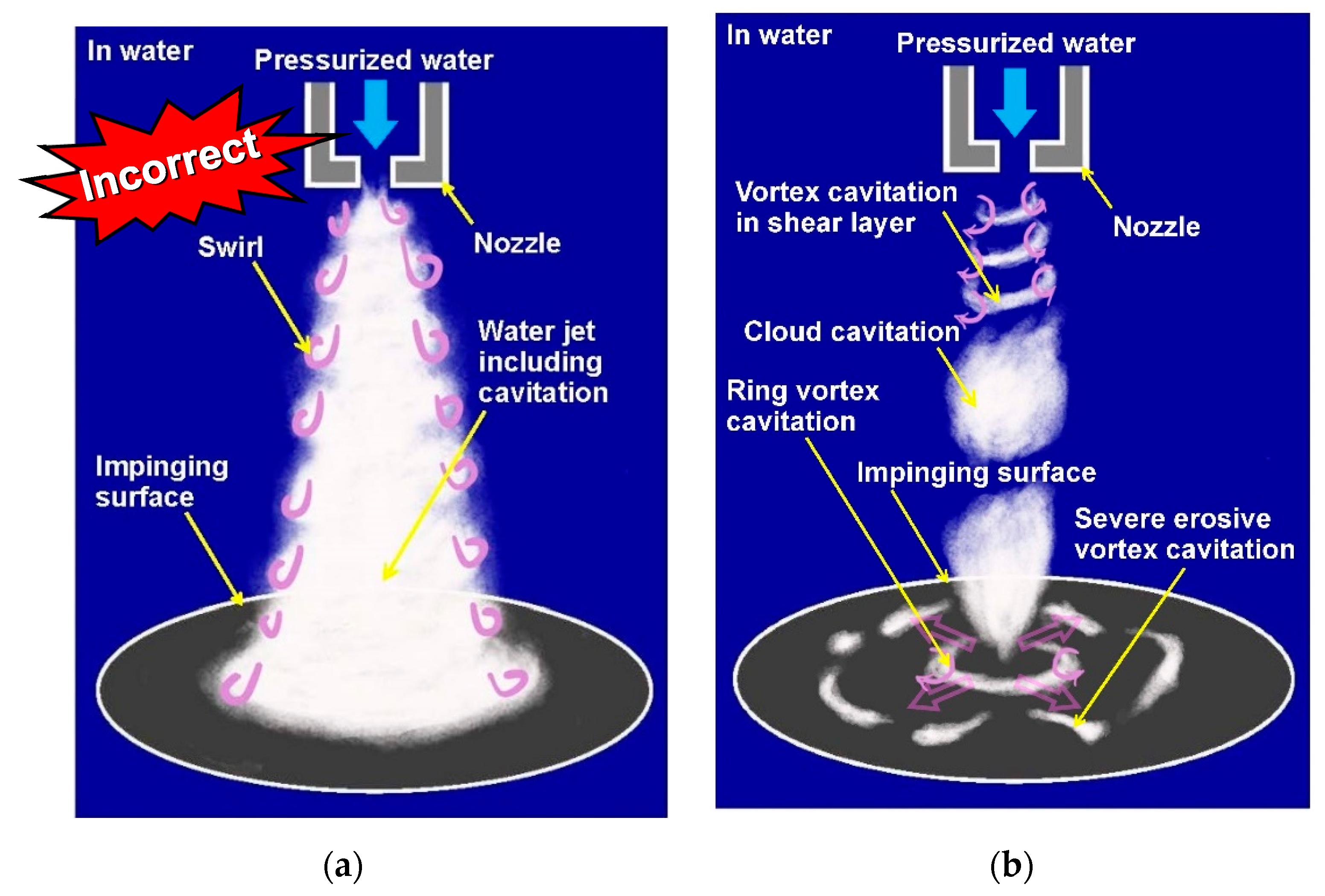
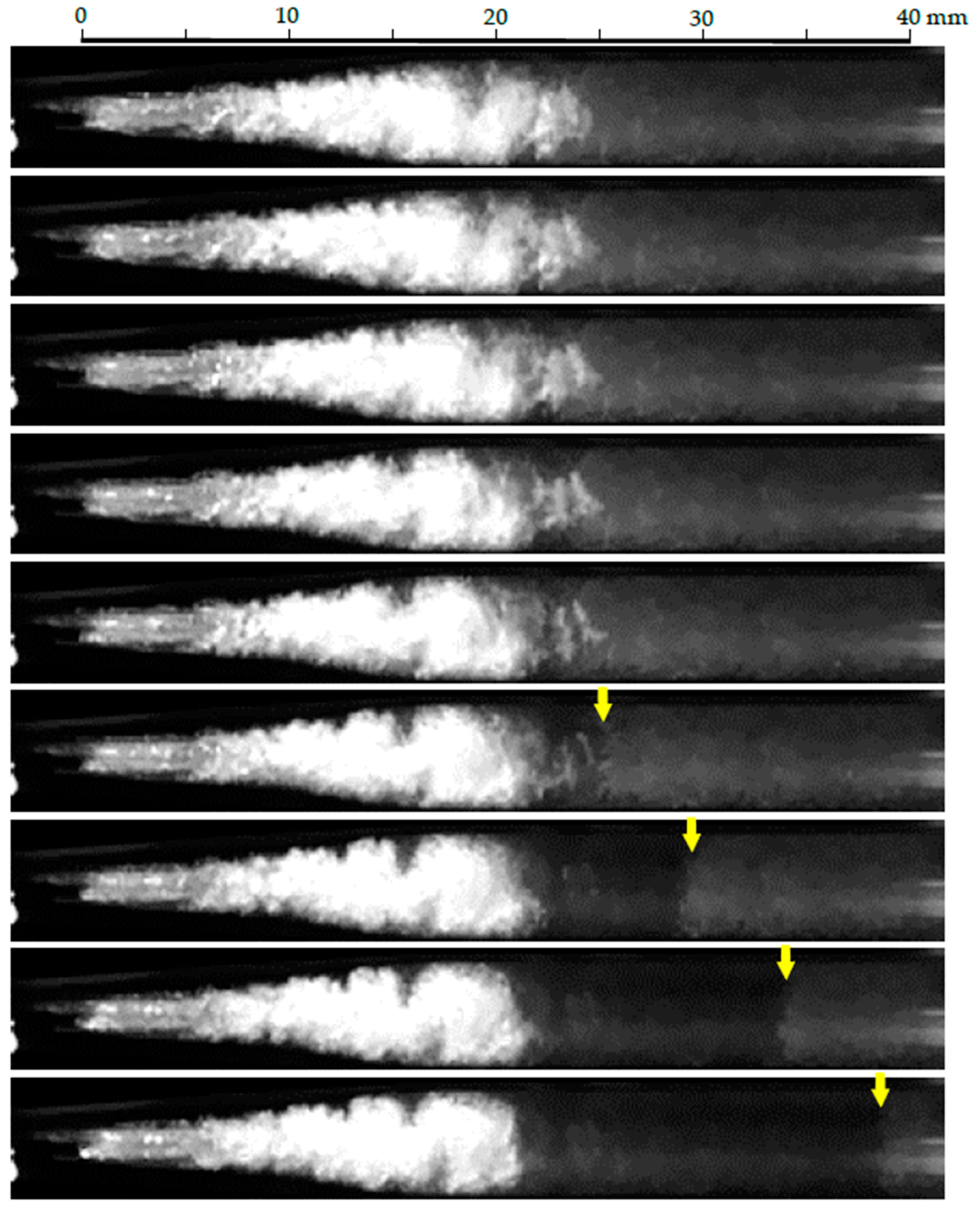
3.1. Structure of Cavitating Jet
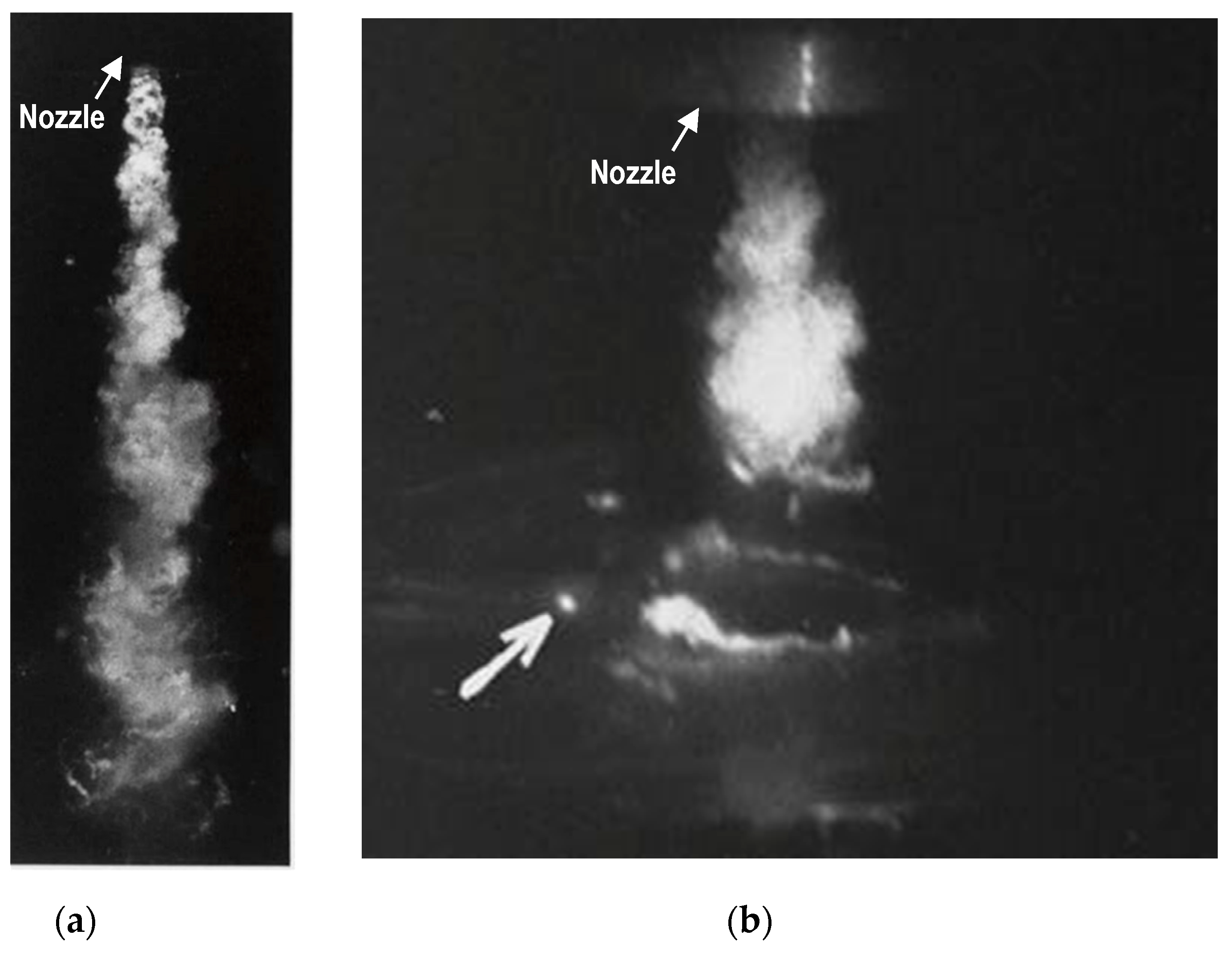
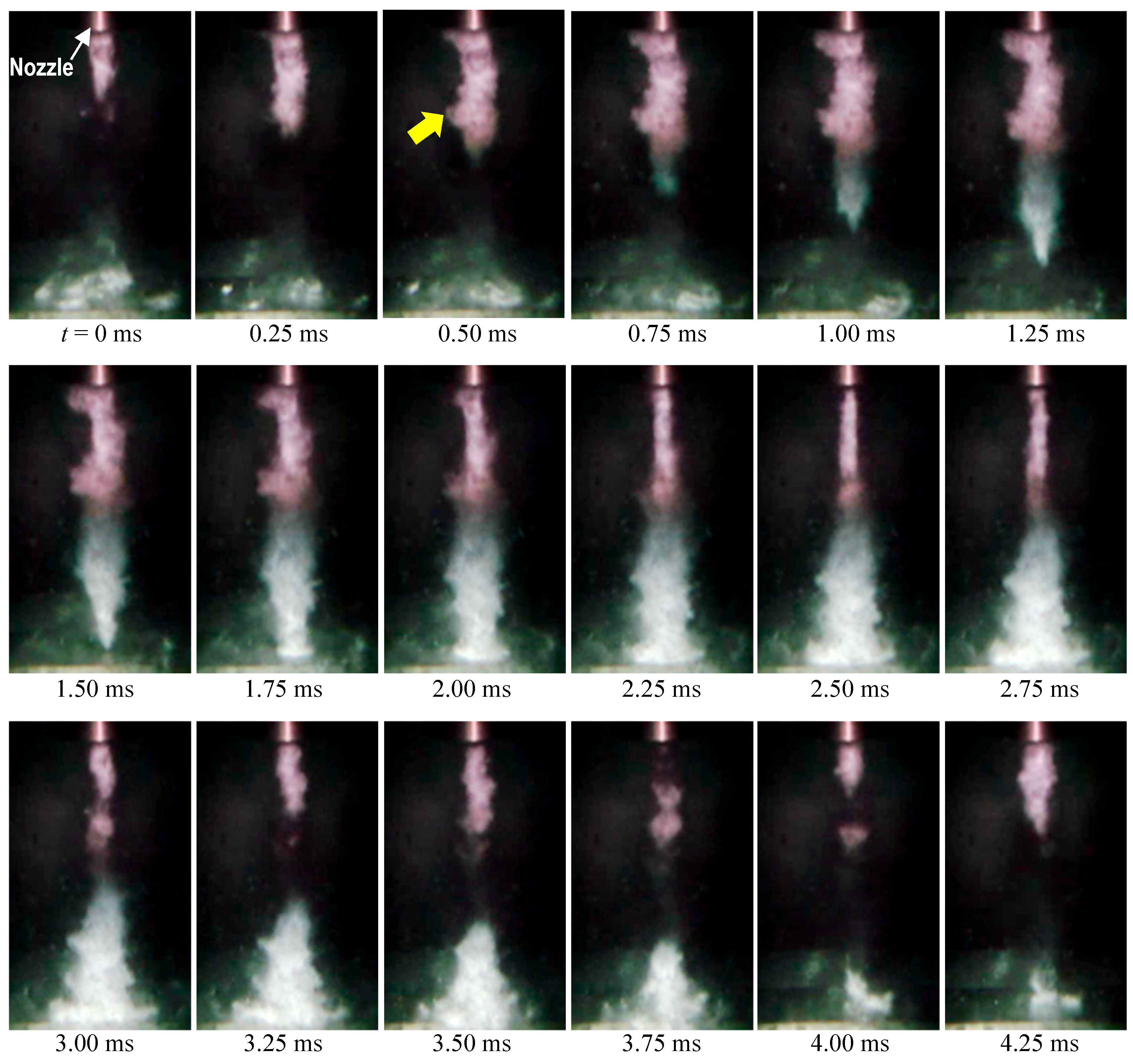
3.2. Periodical Shedding of Cavitation Cloud
4. Key Parameters of Cavitating Jet
4.1. Type of Cavitating Jet
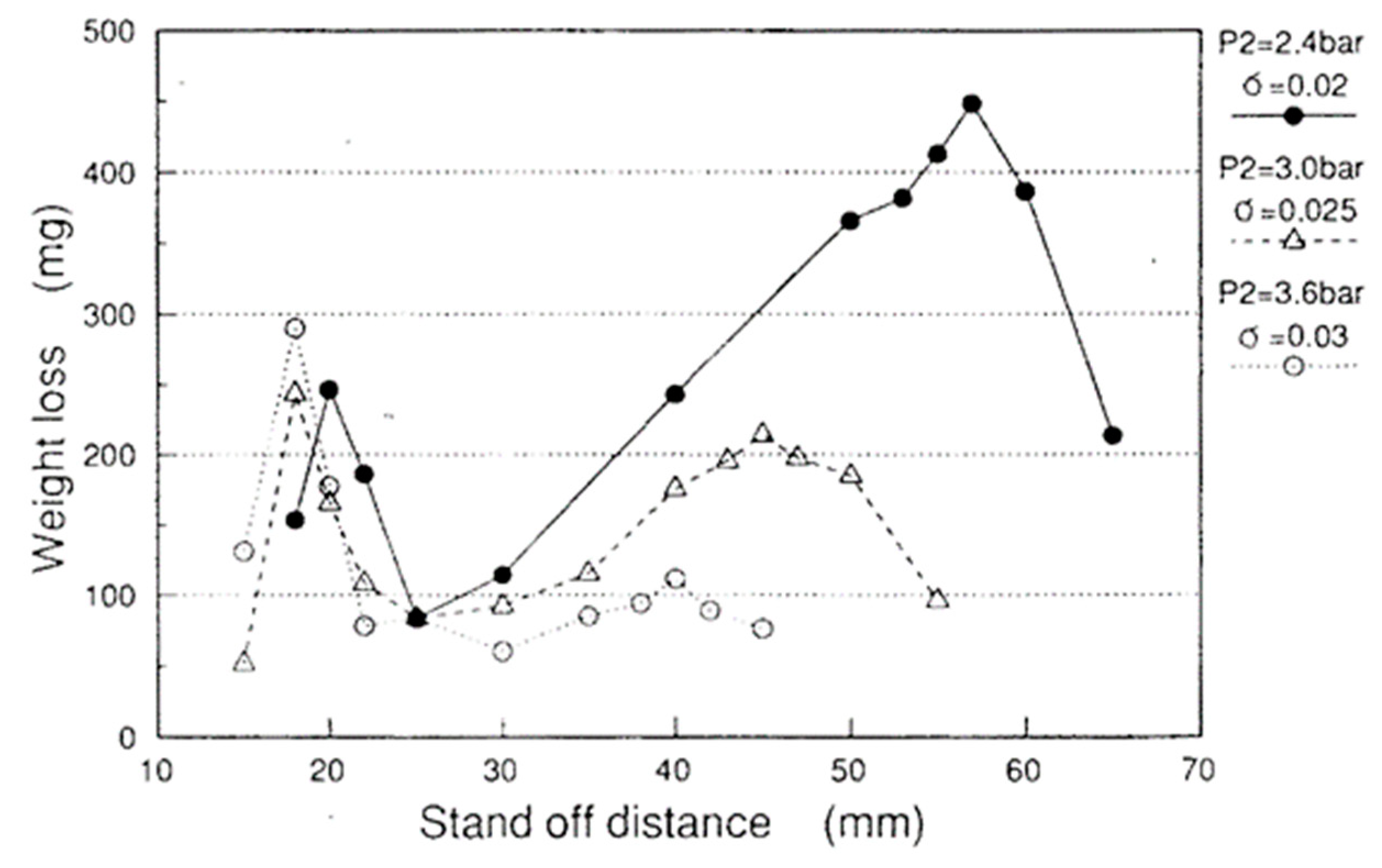
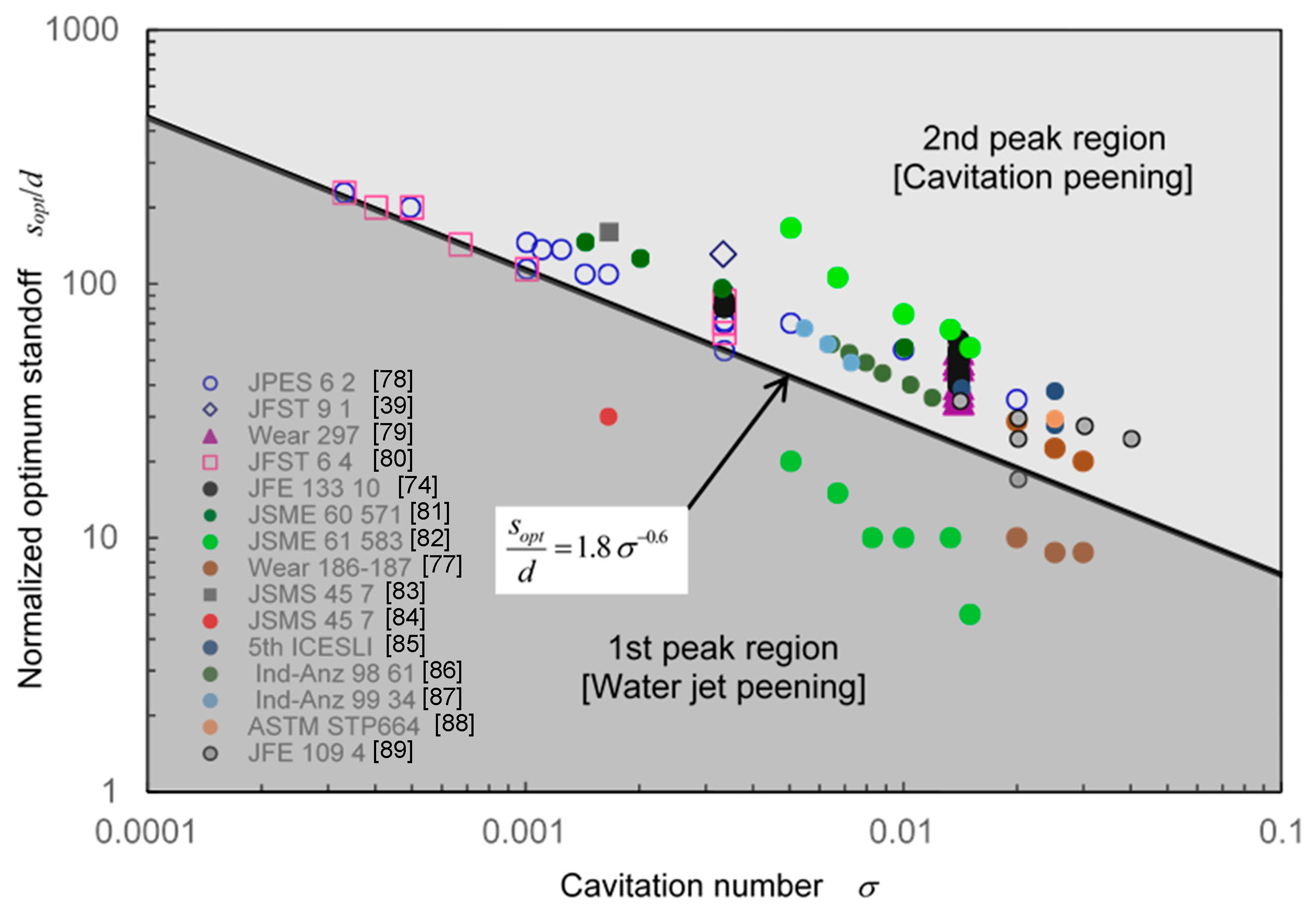
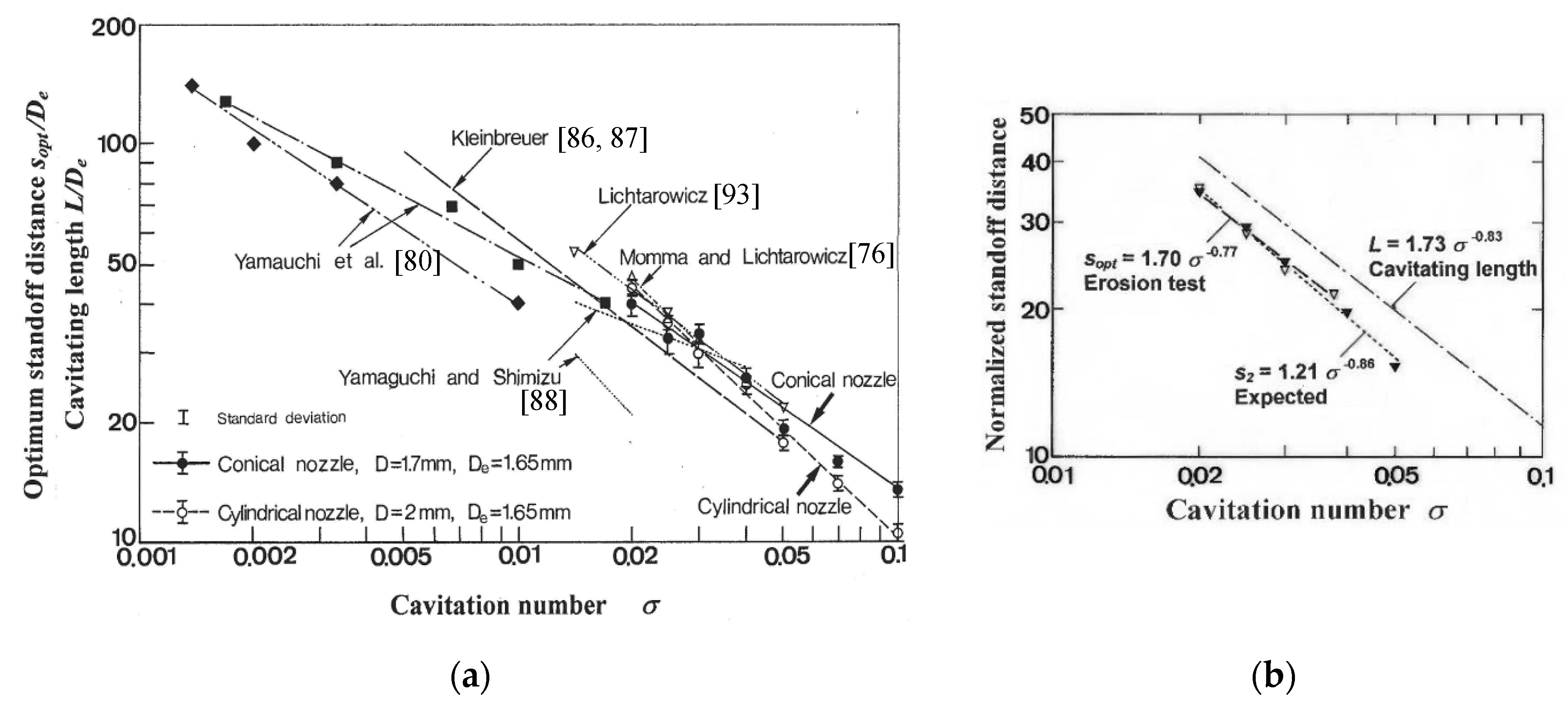
4.2. Standoff Distance
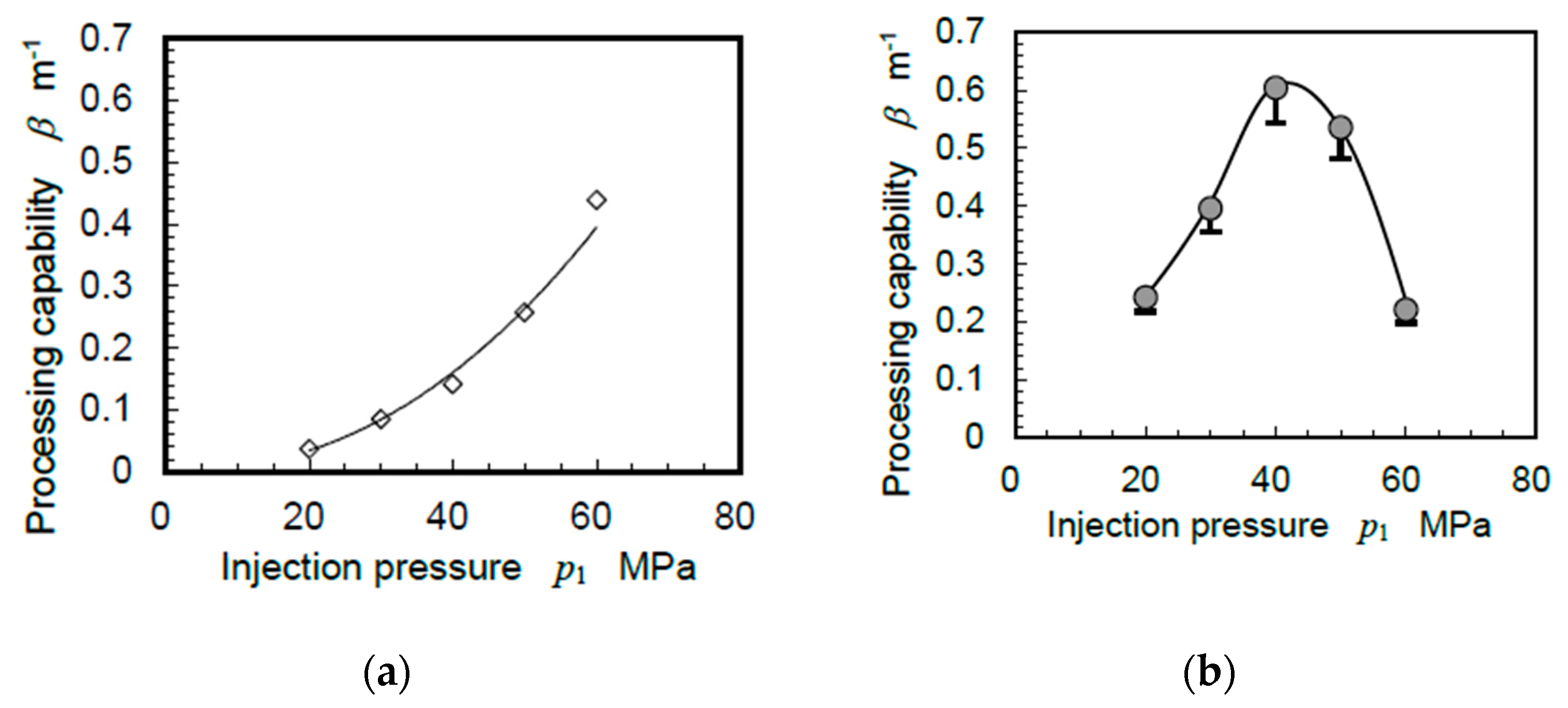
4.3. Injection Pressure
4.4. Cavitation Number
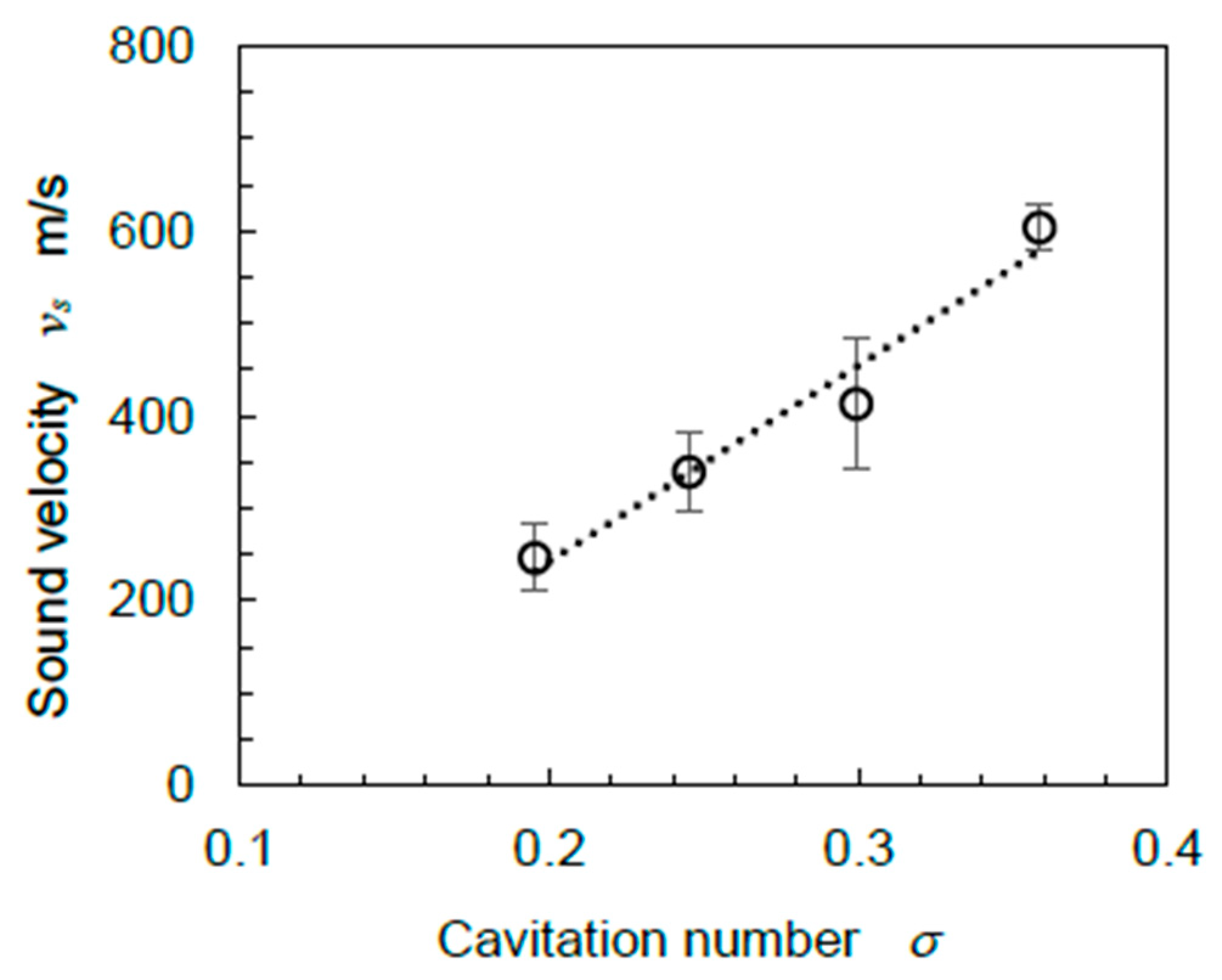
4.5. Sound Velocity in Cavitating Flow Field
4.6. Nozzle Geometry and Diameter
4.7. Water Qualities
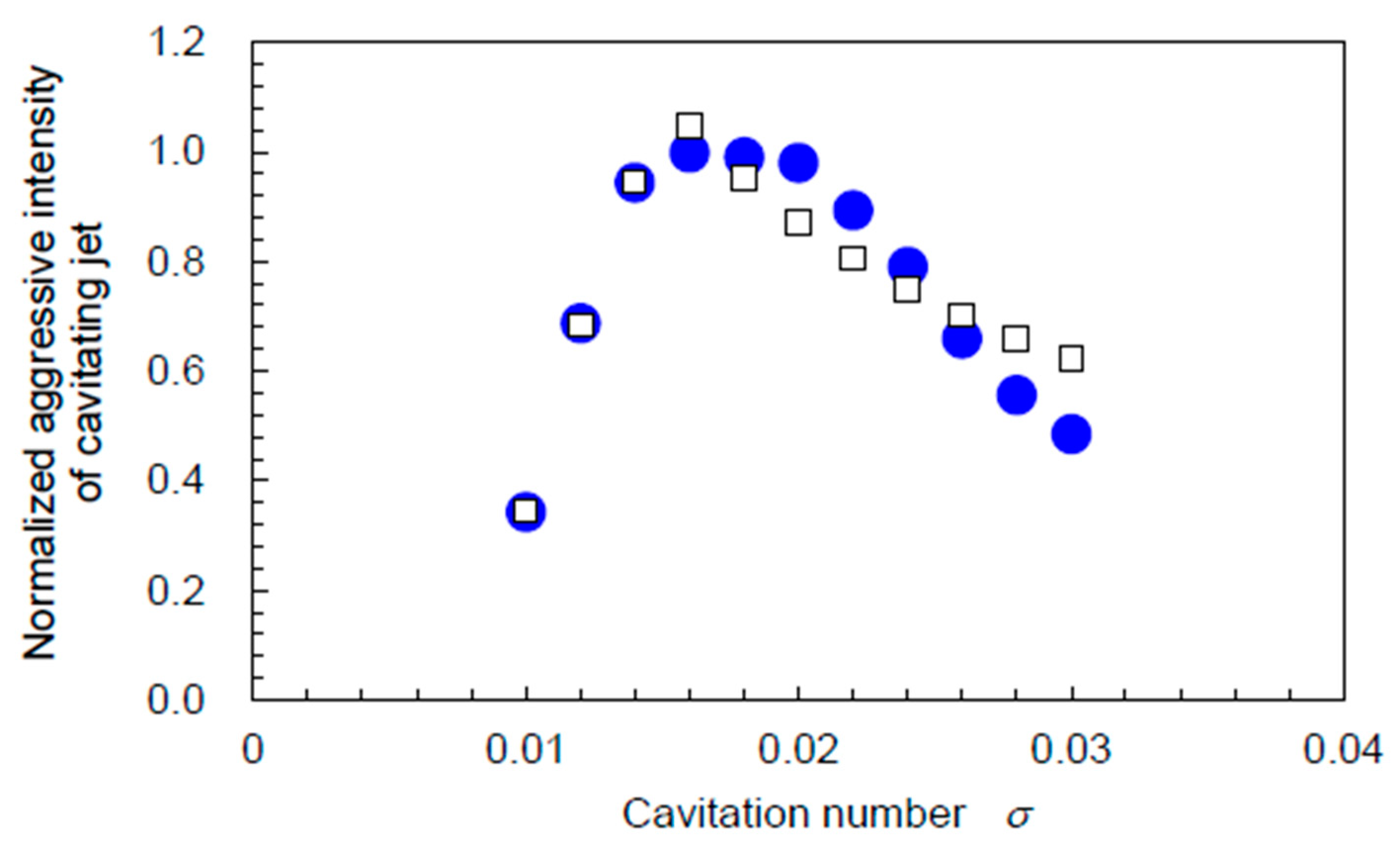
5. Estimation of Aggressive Intensity of Cavitating Jet
6. Applications of Cavitating Jet
7. Conclusions
- (1)
- The cavitation is initiated inside and/or outside of the nozzle as a ring or helical vortex cavitation. These vortex cavitations become cloud cavitations combining with each other, and the cloud cavitation sheds periodically;
- (2)
- Cloud shedding is a phenomenon governed by a constant Strouhal number, which is defined by the shedding frequency, the flow velocity and the width of the cavitating region;
- (3)
- The cloud cavitation forms a ring vortex cavitation on the impinging surface and then collapses producing impacts;
- (4)
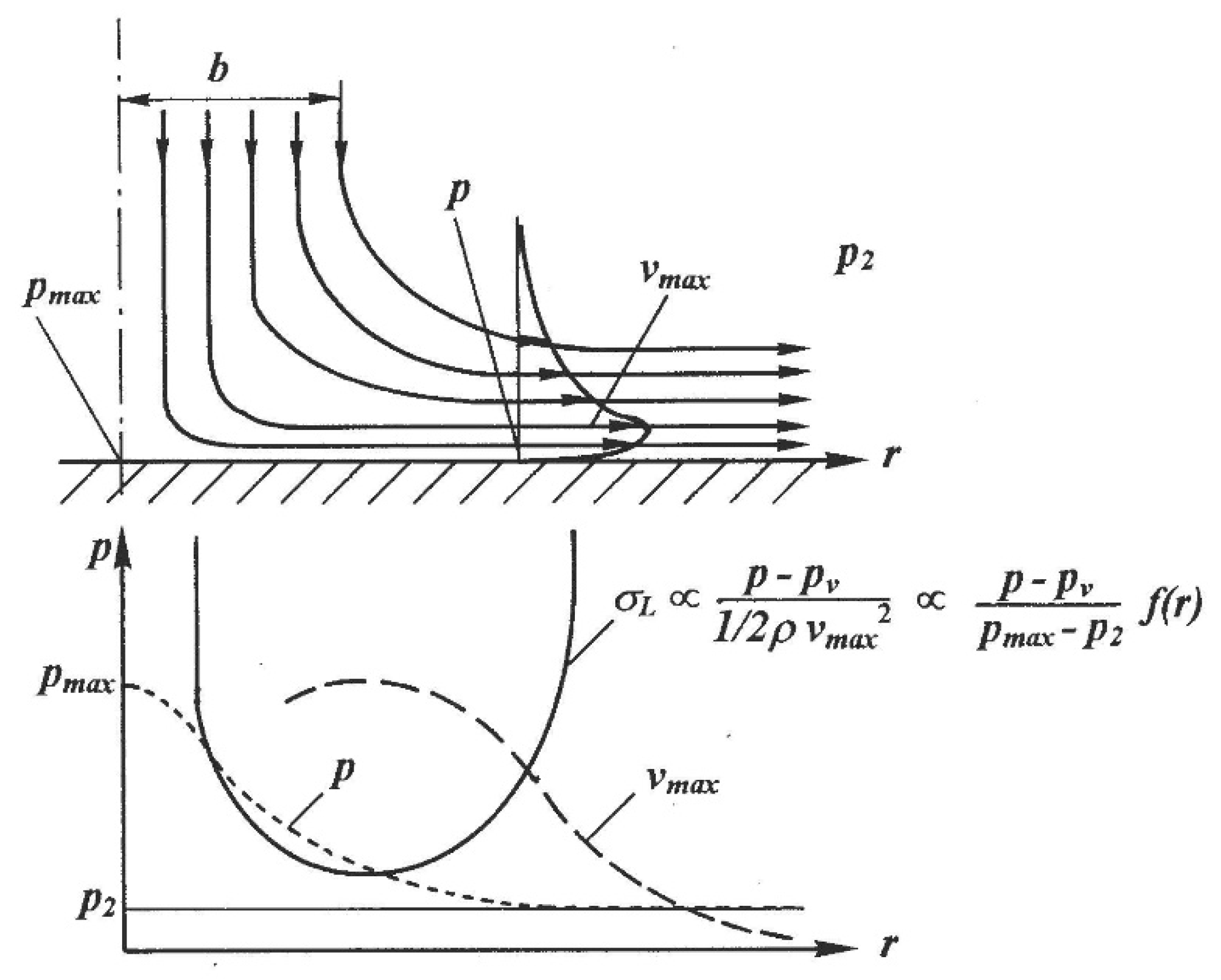
- At optimum conditions, the affected area on the flat target by the impinging cavitating jet is a ring. The mechanism of the ring region can be explained by considering the local cavitation number on the surface. Note that the ring does not directly result from the swirl around the cavitating jet;
- (5)
- At constant downstream pressure conditions, the aggressive intensity of the cavitating jet increases with the injection pressure, and it saturates at a certain pressure and then decreases. At too high an injection pressure, the aggressive intensity decreases.;
- (6)
- At constant injection pressure conditions, the aggressive intensity of the cavitating jet increases with a decrease in cavitation number σ, and it saturates at σ = 0.01 − 0.02 and then decreases at too low σ;
- (7)
- One reason why the aggressive intensity of the cavitating jet decreases at too high an injection pressure, i.e., too low a cavitation number, is the decrease in sound velocity in the cavitating flow field.
Funding
Conflicts of Interest
References
- Soyama, H.; Oba, R.; Kato, H. Cavitation Observations of Severely Erosive Vortex Cavitation Arising in a Centrifugal Pump. In Proceedings of the Institution of Mechanical Engineers, 3rd International Conference on Cavitation, Cambrige, UK, 9–11 December 1992; pp. 103–110. [Google Scholar]
- Brennen, C.E. Cavitation and Bubble Dynamics; Oxford University Press: New York, NY, USA, 1995. [Google Scholar]
- Soyama, H. Cavitation peening: A review. Metals 2020, 10, 270. [Google Scholar] [CrossRef]
- Soyama, H. Key factors and applications of cavitation peening. Inter. J. Peen. Sci. Technol. 2017, 1, 3–60. [Google Scholar]
- Soyama, H.; Saito, K.; Saka, M. Improvement of fatigue strength of aluminum alloy by cavitation shotless peening. J. Eng. Mater. Technol. 2002, 124, 135–139. [Google Scholar] [CrossRef]
- Soyama, H.; Chighizola, C.R.; Hill, M.R. Effect of compressive residual stress introduced by cavitation peening and shot peening on the improvement of fatigue strength of stainless steel. J. Mater. Process. Technol. 2021, 288, 1168771–11687710, paper No. 116877. [Google Scholar] [CrossRef]
- Mankbadi, R.R. Dynamics and control of coherent structure in turbulent jets. Appl. Mech. Rev. 1992, 45, 219–248. [Google Scholar] [CrossRef]
- Taghavi, R. Cavitation Inception in Axisymmertric Jets. Ph.D. Thesis, University of Minnesota, Minneapolis, MN, USA, 1985. [Google Scholar]
- Soyama, H.; Lichtarowicz, A.; Momma, T. Vortex Cavitation in a Submerged Jet. In Proceedings of the 1996 ASME Fluids Engineering Division Summer Meeting, San Diego, CA, USA, 7–11 July 1996; pp. 415–422, FED-236. [Google Scholar]
- Arndt, R.E.A. Cavitation in vortical flows. Annu. Rev. Fluid Mech. 2002, 34, 143–175. [Google Scholar] [CrossRef]
- Lichtarowicz, A. Use of a simple cavitating nozzle for cavitation erosion testing and cutting. Nat. Phys. Sci. 1972, 239, 63–64. [Google Scholar] [CrossRef]
- Yamauchi, Y.; Soyama, H.; Adachi, Y.; Sato, K.; Shindo, T.; Oba, R.; Oshima, R.; Yamabe, M. Suitable region of high-speed submerged water jets for cutting and peening. JSME Int. J. 1995, 38B, 31–38. [Google Scholar] [CrossRef]
- Soyama, H.; Yamauchi, Y.; Ikohagi, T.; Oba, R.; Sato, K.; Shindo, T.; Oshima, R. Marked peening effects by highspeed submerged-water-jets—Residual stress change on SUS304. Jet Flow Eng. 1996, 13, 25–32. [Google Scholar]
- Hutli, E.; Nedeljkovic, M.S.; Bonyar, A.; Legrady, D. Experimental study on the influence of geometrical parameters on the cavitation erosion characteristics of high speed submerged jets. Exp. Fluid Sci. 2017, 80, 281–292. [Google Scholar] [CrossRef]
- G134-17 Standard test method for erosion of solid materials by a cavitating liquid jet. ASTM Stand. 2017, 03.02, 1–17.
- Peng, C.; Tian, S.C.; Li, G.S. Joint experiments of cavitation jet: High-speed visualization and erosion test. Ocean Eng. 2018, 149, 1–13. [Google Scholar] [CrossRef]
- Soyama, H. Comparison between the improvements made to the fatigue strength of stainless steel by cavitation peening, water jet peening, shot peening and laser peening. J. Mater. Process. Technol. 2019, 269, 65–78. [Google Scholar] [CrossRef]
- Soyama, H.; Yamauchi, Y.; Adachi, Y.; Sato, K.; Shindo, T.; Oba, R. High-speed observations of the cavitation cloud around a high-speed submerged water-jet. JSME Int. J. 1995, 38B, 245–251. [Google Scholar] [CrossRef]
- Hutli, E.A.F.; Nedeljkovic, M.S. Frequency in shedding/discharging cavitation clouds determined by visualization of a submerged cavitating jet. J. Fluids Eng. 2008, 130, 1–8, paper No. 021304. [Google Scholar] [CrossRef]
- Sato, K.; Sugimoto, Y.; Ohjimi, S. Structure of periodic cavitation clouds in submerged impinging water-jet issued from horn-type nozzle. In Proceedings of the 9th Pacific Rim International Conference on Water Jetting Technology, Koriyama, Japan, 20–23 November 2009. [Google Scholar]
- Nishimura, S.; Takakuwa, O.; Soyama, H. Similarity law on shedding frequency of cavitation cloud induced by a cavitating jet. J. Fluid Sci. Technol. 2012, 7, 405–420. [Google Scholar] [CrossRef][Green Version]
- Wright, M.M.; Epps, B.; Dropkin, A.; Truscott, T.T. Cavitation of a submerged jet. Exp. Fluids 2013, 54, 21. [Google Scholar] [CrossRef]
- Sato, K.; Taguchi, Y.; Hayashi, S. High speed observation of periodic cavity behavior in a convergent-divergent nozzle for cavitating water jet. J. Flow Control Meas. Vis. 2013, 1, 102–107. [Google Scholar] [CrossRef]
- Liu, H.X.; Kang, C.; Zhang, W.; Zhang, T. Flow structures and cavitation in submerged waterjet at high jet pressure. Exp. Fluid Sci. 2017, 88, 504–512. [Google Scholar] [CrossRef]
- Hutli, E.; Nedeljkovic, M.; Bonyar, A. Dynamic behaviour of cavitation clouds: Visualization and statistical analysis. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 15. [Google Scholar] [CrossRef]
- Wu, Q.; Wei, W.; Deng, B.; Jiang, P.; Li, D.; Zhang, M.D.; Fang, Z.L. Dynamic characteristics of the cavitation clouds of submerged helmholtz self-sustained oscillation jets from high-speed photography. J. Mech. Sci. Technol. 2019, 33, 621–630. [Google Scholar] [CrossRef]
- Liu, B.; Pan, Y.; Ma, F. Pulse pressure loading and erosion pattern of cavitating jet. Eng. Appl. Comp. Fluid Mech. 2020, 14, 136–150. [Google Scholar] [CrossRef]
- Kamisaka, H.; Soyama, H. Enhancing the aggressive intensity of a cavitating jet by introducing water flow holes and a long guide pipe. J. Fluids Eng.Trans. ASME 2020, in press. [Google Scholar] [CrossRef]
- Gopalan, S.; Katz, J.; Knio, O. The flow structure in the near field of jets and its effect on cavitation inception. J. Fluid Mech. 1999, 398, 1–43. [Google Scholar] [CrossRef]
- Arndt, R.E.A.; Amromin, E.L.; Hambleton, W. Cavitation inception in the wake of a jet-driven body. J. Fluids Eng.Trans. ASME 2009, 131, 8. [Google Scholar] [CrossRef]
- Brandner, P.A.; Pearce, B.W.; de Graaf, K.L. Cavitation about a jet in crossflow. J. Fluid Mech. 2015, 768, 34. [Google Scholar] [CrossRef]
- Yuan, C.; Song, J.C.; Liu, M.H. Comparison of compressible and incompressible numerical methods in simulation of a cavitating jet through a poppet valve. Eng. Appl. Comp. Fluid Mech. 2019, 13, 67–90. [Google Scholar] [CrossRef]
- Soyama, H. Introduction of compressive residual stress using a cavitating jet in air. J. Eng. Mater. Technol. 2004, 126, 123–128. [Google Scholar] [CrossRef]
- Soyama, H.; Kikuchi, T.; Nishikawa, M.; Takakuwa, O. Introduction of compressive residual stress into stainless steel by employing a cavitating jet in air. Surf. Coat. Technol. 2011, 205, 3167–3174. [Google Scholar] [CrossRef]
- Soyama, H. High-speed observation of a cavitating jet in air. J. Fluids Eng. 2005, 127, 1095–1108. [Google Scholar] [CrossRef]
- Soyama, H. Improvement of fatigue strength by using cavitating jets in air and water. J. Mater. Sci. 2007, 42, 6638–6641. [Google Scholar] [CrossRef]
- Marcon, A.; Melkote, S.N.; Yoda, M. Effect of nozzle size scaling in co-flow water cavitation jet peening. J. Manuf. Process. 2018, 31, 372–381. [Google Scholar] [CrossRef]
- Marcon, A.; Melkote, S.N.; Yoda, M.; Sanders, D. Analysis of co-flow water cavitation peening of Al7075-T651 alloy using high-speed imaging and surface pitting tests. Mater. Perform. Charact. 2018, 7, 1018–1040. [Google Scholar] [CrossRef]
- Soyama, H. Enhancing the aggressive intensity of a cavitating jet by introducing a cavitator and a guide pipe. J. Fluid Sci. Technol. 2014, 9, 1–12, paper No. 13-00238. [Google Scholar] [CrossRef]
- Kamisaka, H.; Soyama, H. Periodical shedding of cavitation cloud induced by a cavitating jet. In Proceedings of the 24th International Conference on Water Jetting, Manchester, UK, 5–6 September 2018; 2018; pp. 111–123. [Google Scholar]
- Soyama, H.; Lichtarowicz, A.; Momma, T.; Williams, E.J. A new calibration method for dynamically loaded transducers and its application to cavitation impact measurement. J. Fluids Eng. 1998, 120, 712–718. [Google Scholar] [CrossRef]
- Soyama, H.; Sekine, Y.; Saito, K. Evaluation of the enhanced cavitation impact energy using a PVDF transducer with an acrylic resin backing. Measurement 2011, 44, 1279–1283. [Google Scholar] [CrossRef]
- Soyama, H.; Kumano, H. The fundamental threshold level—A new parameter for predicting cavitation erosion resistance. J. Test. Eval. 2002, 30, 421–431. [Google Scholar]
- Schnerr, G.H.; Sezal, I.H.; Schmidt, S.J. Numerical investigation of three-dimensional cloud cavitation with special emphasis on collapse induced shock dynamics. Phys. Fluids 2008, 20, 9. [Google Scholar] [CrossRef]
- Bensow, R.E.; Bark, G. Implicit les predictions of the cavitating flow on a propeller. J. Fluids Eng.Trans. ASME 2010, 132, 10. [Google Scholar] [CrossRef]
- Ji, B.; Luo, X.W.; Wu, Y.L.; Peng, X.X.; Duan, Y.L. Numerical analysis of unsteady cavitating turbulent flow and shedding horse-shoe vortex structure around a twisted hydrofoil. Int. J. Multiph. Flow 2013, 51, 33–43. [Google Scholar] [CrossRef]
- Xing, T.; Li, Z.Y.; Frankel, S.H. Numerical simulation of vortex cavitation in a three-dimensional submerged transitional jet. J. Fluids Eng.Trans. ASME 2005, 127, 714–725. [Google Scholar] [CrossRef]
- Alehossein, H.; Qin, Z. Numerical analysis of rayleigh-plesset equation for cavitating water jets. Int. J. Numer. Methods Eng. 2007, 72, 780–807. [Google Scholar] [CrossRef]
- Sonde, E.; Chaise, T.; Boisson, N.; Nelias, D. Modeling of cavitation peening: Jet, bubble growth and collapse, micro-jet and residual stresses. J. Mater. Process. Technol. 2018, 262, 479–491. [Google Scholar] [CrossRef]
- Dittakavi, N.; Chunekar, A.; Frankel, S. Large eddy simulation of turbulent-cavitation interactions in a venturi nozzle. J. Fluids Eng.Trans. ASME 2010, 132, 11. [Google Scholar] [CrossRef]
- Peng, G.Y.; Shimizu, S. Progress in numerical simulation of cavitating water jets. J. Hydrodyn. 2013, 25, 502–509. [Google Scholar] [CrossRef]
- Peng, G.Y.; Yang, C.X.; Oguma, Y.; Shimizui, S. Numerical analysis of cavitation cloud shedding in a submerged water jet. J. Hydrodyn. 2016, 28, 986–993. [Google Scholar] [CrossRef]
- Hsiao, C.T.; Jayaprakash, A.; Kapahi, A.; Choi, J.K.; Chahine, G.L. Modelling of material pitting from cavitation bubble collapse. J. Fluid Mech. 2014, 755, 142–175. [Google Scholar] [CrossRef]
- Choi, J.K.; Chahine, G.L. Relationship between material pitting and cavitation field impulsive pressures. Wear 2016, 352–353, 42–53. [Google Scholar] [CrossRef]
- Ma, J.S.; Hsiao, C.T.; Chahine, G.L. Numerical study of acoustically driven bubble cloud dynamics near a rigid wall. Ultrason. Sonochem. 2018, 40, 944–954. [Google Scholar] [CrossRef]
- Sasaki, H.; Iga, Y.; Soyama, H. Effect of Bubble Radius on Ability of Submerged Laser Peening. In Advanced Surface Enhancement, INCASE 2019, Lecture Notes in Mechanical Engineering; Springer Nature Singapore Pte Ltd.: Singapore, 2020; pp. 283–291. [Google Scholar]
- Lauterborn, W.; Bolle, H. Experimental investigations of cavitation-bubble collapse in neighborhood of a solid boundary. J. Fluid Mech. 1975, 72, 391–399. [Google Scholar] [CrossRef]
- Soyama, H. Corrosion behavior of pressure vessel steel exposed to residual bubbles after cavitation bubble collapse. Corrosion 2011, 67, 1–8, paper No. 025001. [Google Scholar] [CrossRef]
- Plesset, M.S.; Chapman, R.B. Collapse of an initially spherical vapour cavity in neighbourhood of a solid boundary. J. Fluid Mech. 1971, 47, 283–290. [Google Scholar] [CrossRef]
- Crum, L.A. Surface oscillations and jet development in pulsating bubbles. J. Phys. Colloq. 1979, 40, 285–288. [Google Scholar] [CrossRef]
- Lauterborn, W.; Ohl, C.D. Cavitation bubble dynamics. Ultrason. Sonochem. 1997, 4, 65–75. [Google Scholar] [CrossRef]
- Lauterborn, W.; Kurz, T. Physics of bubble oscillations. Rep. Prog. Phys. 2010, 73, 88. [Google Scholar] [CrossRef]
- Soyama, H.; Ohba, K.; Takeda, S.; Oba, R. High-speed observations of highly erosive vortex cavitation around butterfly valve. Trans. JSME 1994, 60B, 1133–1138. [Google Scholar] [CrossRef]
- Ohba, K.; Soyama, H.; Takeda, S.; Inooka, H.; Oba, R. High-speed observations of highly erosive vortex cavitation using image processing. J. Flow Vis. Image Process. 1995, 2, 161–172. [Google Scholar] [CrossRef]
- Soyama, H.; Li, S.R.; Tonosaki, M.; Uranishi, K.; Kato, H.; Oba, R. High-speed observations of severe cavitation erosion in a high-specific-speed centrifugal pump. Trans. JSME 1995, 61B, 3945–3951. [Google Scholar] [CrossRef]
- Dominguez Cortazar, M.A.; Franc, J.P.; Michel, J.M. The erosive axial collapse of a cavitating vortex: An experimental study. J. Fluids Eng. 1997, 119, 686–691. [Google Scholar] [CrossRef]
- Takakuwa, O.; Soyama, H. The effect of scanning pitch of nozzle for a cavitating jet during overlapping peening treatment. Surf. Coat. Technol. 2012, 206, 4756–4762. [Google Scholar] [CrossRef]
- Ohya, T.; Okimura, K.; Ohta, T.; Ichioka, T. Residual Stress Improved by Water Jet Peening for Small-Diameter Pipe Inner Surfaces. In Mitsubishi Heavy Industries, Ltd. Technical Review; Mitsubishi: Tokyo, Japan, 2000; Volume 37, pp. 52–55. [Google Scholar]
- Demma, A.; Frederick, G. Program on Technology Innovation: An Evaluation of Surface Stress Improvement Technologies for Pwscc Mitigation of Alloy 600 Nuclear Components. In Materials Reliability Program (MRP-162); Electric Power Research Institute: Palo Alto, CA, USA, 2006; pp. 1–104. [Google Scholar]
- Crooker, P.; Lian, T. Materials Reliability Program: Technical Basis for Primary Water Stress Corrosion Cracking Mitigation by Surface Stress Improvement (MRP-267, Revision 1); Electric Research Power Institute: Palo Alto, CA, USA, 2012; pp. 1–330. [Google Scholar]
- Hutli, E.; Nedeljkovic, M.S.; Radovic, N.A.; Bonyar, A. The relation between the high speed submerged cavitating jet behaviour and the cavitation erosion process. Int. J. Multiph. Flow 2016, 83, 27–38. [Google Scholar] [CrossRef]
- Soyama, H.; Lichtarowicz, A. Cavitating jets—Similarity correlations. J. Jet Flow Eng. 1996, 13, 9–19. [Google Scholar]
- Nobel, A.J.; Talmon, A.M. Measurements of the stagnation pressure in the center of a cavitating jet. Exp. Fluids 2012, 52, 403–415. [Google Scholar] [CrossRef][Green Version]
- Soyama, H. Enhancing the aggressive intensity of a cavitating jet by means of the nozzle outlet geometry. J. Fluids Eng. 2011, 133, 1–11, paper No. 101301. [Google Scholar] [CrossRef]
- Kamisaka, H.; Soyama, H. Enhancement of an aggressive intensity of a cavitating jet by water flow holes near nozzle outlet. Trans. JSME 2019, 85. paper No. 19-00280. [Google Scholar] [CrossRef]
- Soyama, H. Fundamentals and Applications of Cavitation Peening Comparing with Shot Peening and Laser Peening. In Advanced Surface Enhancement, INCASE 2019, Lecture Notes in Mechanical Engineering; Springer Nature Singapore Pte Ltd.: Singapore, 2020; pp. 76–87. [Google Scholar]
- Momma, T.; Lichtarowicz, A. A study of pressure and erosion produced by collapsing cavitation. Wear 1995, 186, 425–436. [Google Scholar] [CrossRef]
- Soyama, H.; Nagasaka, K.; Takakuwa, O.; Naito, A. Optimum injection pressure of a cavitating jet for introducing compressive residual stress into stainless steel. J. Power Energy Syst. 2012, 6, 63–75. [Google Scholar] [CrossRef]
- Soyama, H. Effect of nozzle geometry on a standard cavitation erosion test using a cavitating jet. Wear 2013, 297, 895–902. [Google Scholar] [CrossRef]
- Soyama, H.; Takakuwa, O. Enhancing the aggressive strength of a cavitating jet and its practical application. J. Fluid Sci. Technol. 2011, 6, 510–521. [Google Scholar] [CrossRef]
- Yamauchi, Y.; Soyama, H.; Sato, K.; Ikohagi, T.; Oba, R. Development of erosion in high-speed submerged water jets. Trans. JSME 1994, 60B, 736–743. [Google Scholar] [CrossRef][Green Version]
- Yamauchi, Y.; Asami, K.; Soyama, H.; Sato, K.; Ikohagi, T.; Oba, R. Marked effects of ambient pressure on impinging erosion induced by high-speed submerged water jets. Trans. JSME 1995, 61B, 785–792. [Google Scholar] [CrossRef][Green Version]
- Hirano, K.; Enomoto, K.; Hayashi, E.; Kurosawa, K. Effect of water jet peening on corrosion resistance and fatigue strength of type 304 stainless steel. J. Soc. Mater. Soc. Jpn. 1996, 45, 740–745. [Google Scholar] [CrossRef]
- Enomoto, K.; Hirano, K.; Mochizuki, M.; Kurosawa, K.; Saito, H.; Hayashi, E. Improvement of residual stress on material surface by water jet peening. J. Soc. Mater. Soc. Jpn. 1996, 45, 734–739. [Google Scholar] [CrossRef]
- Lichtarowicz, A.; Scott, P.J. Erosion Testing with Cavitating Jet. In Proceedings of 5th International Conference on Erosion by Liquid and Solid Impact; Office of Naval Research London: London, UK, 1979; paper No. 69. [Google Scholar]
- Kleinbreuer, W. Werkstoffzerstorung durch kavitation in olhydralishen systemen. Ind. Anz. 1976, 98, 1096–1100. [Google Scholar]
- Kleinbreuer, W. Kavitationserosion in hydraulischen systemen. Ind. Anz. 1977, 99, 609–613. [Google Scholar]
- Lichtarowicz, A. Cavitating jet apparatus for cavitation erosion testing, erosion: Prevention and useful applications. ASTM STP 1979, 669, 530–549. [Google Scholar]
- Yamaguchi, A.; Shimizu, S. Erosion due to impingement of cavitating jet. J. Fluids Eng.Trans. ASME 1987, 109, 442–447. [Google Scholar] [CrossRef]
- Soyama, H. Surface mechanics design of metallic materials on mechanical surface treatments. Mech. Eng. Rev. 2015, 2, 1–20, paper No. 14-00192. [Google Scholar] [CrossRef]
- Soyama, H.; Sanders, D. Use of an abrasive water cavitating jet and peening process to improve the fatigue strength of titanium alloy 6Al-4V manufactured by the electron beam powder bed melting (EBPB) additive manufacturing method. JOM 2019, 71, 4311–4318. [Google Scholar] [CrossRef]
- Kamisaka, H.; Soyama, H. Effect of injection pressure on mechanical surface treatment using a submerged water jet. J. Jet Flow Eng. 2018, 33, 4–10. [Google Scholar]
- J443 Procedures for Using Standard Shot Peening Almen Strip. In SAE International Standards; SAE International: Warrendale, PA, USA, 2010; pp. 1–6.
- Lichtarowicz, A. Erosion testing with cavitating jet. In Proceedings of the Cavitation Erosion in Fluid Systems, ASME Fluids Engineering Conference, Boulder, CO, USA, 22–24 June 1981; pp. 153–161. [Google Scholar]
- Soyama, H. Estimation of luminescence intensity of hydrodynamic cavitation considering sound velocity in the cavitating flow field. In Proceedings of the 11th International Symposium on Cavitation, Daejeon, Korea, 9–13 May 2021. [Google Scholar]
- Wilson, R.W.; Graham, R. Cavitation of metal surfaces in contact with lubricants. Conf. Lubr. Wear IME 1957, 707–712. [Google Scholar]
- Hattori, S.; Motoi, Y.; Kikuta, K.; Tomaru, H. Cavitation Erosion Of Silver Plated Coating at Different Temperatures and Pressures. In 8th International Symposium on Measurement Techniques for Multiphase Flows; Li, Y., Zheng, Y., Eds.; American Institute of Physics: Melville, NY, USA, 2014; pp. 358–365. [Google Scholar]
- Bass, A.; Ruuth, S.J.; Camara, C.; Merriman, B.; Putterman, S. Molecular dynamics of extreme mass segregation in a rapidly collapsing bubble. Phys. Rev. Lett. 2008, 101, 4. [Google Scholar] [CrossRef] [PubMed]
- Soyama, H.; Hoshino, J. Enhancing the aggressive intensity of hydrodynamic cavitation through a venturi tube by increasing the pressure in the region where the bubbles collapse. AIP Adv. 2016, 6, 1–13, paper No. 045113. [Google Scholar] [CrossRef]
- Gielen, B.; Marchal, S.; Jordens, J.; Thomassen, L.C.J.; Braeken, L.; Van Gerven, T. Influence of dissolved gases on sonochemistry and sonoluminescence in a flow reactor. Ultrason. Sonochem. 2016, 31, 463–472. [Google Scholar] [CrossRef]
- Kang, B.K.; Kim, M.S.; Park, J.G. Effect of dissolved gases in water on acoustic cavitation and bubble growth rate in 0.83 MHz megasonic of interest to wafer cleaning. Ultrason. Sonochem. 2014, 21, 1496–1503. [Google Scholar] [CrossRef]
- Kieffer, S.W. Sound speed in liquid-gas mixtures—Water-air and water-steam. J. Geophys. Res. 1977, 82, 2895–2904. [Google Scholar] [CrossRef]
- Shimizu, S.; Tanioka, K.; Ikegami, N. Erosion due to ultra-high-speed cavitating jet. J. Jpn. Hydraul. Pneum. Soc. 1997, 28, 778–784. [Google Scholar]
- Soyama, H. Material testing and surface modification by using cavitating jet. J. Soc. Mater. Sci. Jpn. 1998, 47, 381–387. [Google Scholar] [CrossRef]
- Johnson, V.E.; Chahine, G.L.; Lindenmuth, W.T.; Conn, A.F.; Frederick, G.S.; Giacchino, G.J. Cavitating and structured jets for mechanical bits to increase drilling rate, 1. Tehory and concepts. J. Energy Resour. Technol. 1984, 106, 282–288. [Google Scholar] [CrossRef]
- Chahine, G.L.; Johnson, V.E., Jr.; Kalumuck, K.M.; Perdue, T.O.; Waxman, D.N.; Frederick, G.S.; Watson, R.E. Internal and external acoustics and large structure dynamics of cavitating self-resonating water jets. In Sandia National Laboratories, Contractor Report; OSTI.gov: Livermore, CA, USA, 1987; pp. 1–202. SAND86-7176. [Google Scholar]
- Soyama, H. Power law of injection pressure and nozzle diameter on aggressive intensity of a cavitating jet. In Proceedings of the 21st International Conference on Water Jetting, Ottawa, ON, Canada, 19–22 September 2012; pp. 343–354. [Google Scholar]
- Hattori, S.; Goto, Y.; Fukuyama, T. Influence of temperature on erosion by a cavitating liquid jet. Wear 2006, 260, 1217–1223. [Google Scholar] [CrossRef]
- Hutli, E.A.F.; Nedeljkovic, M.S.; Radovic, N.A. Mechanics of submerged jet cavitating action: Material properties, exposure time and temperature effects on erosion. Arch. Appl. Mech. 2008, 78, 329–341. [Google Scholar] [CrossRef]
- Dular, M. Hydrodynamic cavitation damage in water at elevated temperatures. Wear 2016, 346, 78–86. [Google Scholar] [CrossRef]
- Kamisaka, H.; Soyama, H. Effect of water depth on aggressive intensity of a cavitating jet. J. Jet Flow Eng. 2020, 35, 4–11. [Google Scholar]
- Soyama, H.; Takakuwa, O.; Naito, A. Effect of nozzle shape for high injection pressure on aggressivity of cavitating jet. In Proceedings of the 21st International Conference on Water Jetting, Ottawa, ON, Canada, 19–22 September 2012; pp. 367–378. [Google Scholar]
- Johnson, V.E.; Lindenmuth, W.T.; Conn, A.F.; Frederick, G.S. Feasibility study of tuned-resonator, pulsating cavitating water jet for deep-hole drilling. In Sandia National Laboratories, Contractor Report SAND81-7126; OSTI.gov: Livermore, CA, USA, 1981; pp. 1–131. [Google Scholar]
- Soyama, H.; Matsuda, K.; Mikami, M. Digging of concrete by a cavitating jet in air comparing with a conventional water jet. In Proceedings of the 23rd International Conference on Water Jetting, Seattle, WA, USA, 16–18 November 2016; pp. 209–214. [Google Scholar]
- Saitou, N.; Enomoto, K.; Kurosawa, K.; Morinaka, R.; Hayashi, E.; Ishikwa, T.; Yoshimura, T. Development of water jet peening technique for reactor internal components of nuclear power plant. J. Jet Flow Eng. 2003, 20, 4–12. [Google Scholar]
- Soyama, H. Improvement in fatigue strength of silicon manganese steel SUP7 by using a cavitating jet. JSME Int. J. 2000, 43A, 173–178. [Google Scholar] [CrossRef]
- Soyama, H.; Sasaki, K.; Odhiambo, D.; Saka, M. Cavitation shotless peening for surface modification of alloy tool steel. JSME Int. J. 2003, 46A, 398–402. [Google Scholar] [CrossRef]
- Odhiambo, D.; Soyama, H. Cavitation shotless peening for improvement of fatigue strength of carbonized steel. Int. J. Fatigue 2003, 25, 1217–1222. [Google Scholar] [CrossRef]
- Soyama, H.; Takano, Y.; Ishimoto, M. Peening of forging die by cavitation. In Technical Review of Forging Technology Institute of Japan; Forging Technology Insitute of Japan: Tokyo, Japan, 2000; Volume 25, pp. 53–57. [Google Scholar]
- Soyama, H.; Macodiyo, D.O. Fatigue strength improvement of gears using cavitation shotless peening. Tribol. Lett. 2005, 18, 181–184. [Google Scholar] [CrossRef]
- Soyama, H.; Sekine, Y. Sustainable surface modification using cavitation impact for enhancing fatigue strength demonstrated by a power circulating-type gear tester. Int. J. Sustain. Eng. 2010, 3, 25–32. [Google Scholar] [CrossRef]
- Soyama, H.; Shimizu, M.; Hattori, Y.; Nagasawa, Y. Improving the fatigue strength of the elements of a steel belt for CVT by cavitation shotless peening. J. Mater. Sci. 2008, 43, 5028–5030. [Google Scholar] [CrossRef]
- Seki, M.; Soyama, H.; Kobayashi, Y.; Gowa, D.; Fujii, M. Rolling contact fatigue life of steel rollers treated by cavitation peening and shot peening. J. Solid Mech. Mater. Eng. 2012, 6, 478–486. [Google Scholar] [CrossRef]
- Soyama, H. Improvement of fatigue strength of duralumin plate with a hole by a cavitating jet. In Proceedings of the 22nd International Conference on Water Jetting, Haarlem, The Netherlands, 3–5 September 2014; pp. 57–65. [Google Scholar]
- Soyama, H.; Takeo, F. Comparison between cavitation peening and shot peening for extending the fatigue life of a duralumin plate with a hole. J. Mater. Process. Technol. 2016, 227, 80–87. [Google Scholar] [CrossRef]
- Soyama, H.; Takeo, F. Effect of various peening methods on the fatigue properties of titanium alloy Ti6Al4V manufactured by direct metal laser sintering and electron beam melting. Materials 2020, 13. paper No. 13-02216. [Google Scholar] [CrossRef] [PubMed]
- Soyama, H. Comparison between shot peening, cavitation peening and laser peening by observation of crack initiation and crack growth in stainless steel. Metals 2020, 10, 63. [Google Scholar] [CrossRef]
- Grinspan, A.S.; Gnanamoorthy, R. Effect of nozzle-traveling velocity on oil cavitation jet peening of aluminum alloy, AA6063-T6. J. Eng. Mater. Technol.Trans. ASME 2007, 129, 609–613. [Google Scholar] [CrossRef]
- Lee, H.; Mall, S.; Soyama, H. Fretting fatigue behavior of cavitation shotless peened Ti-6Al-4V. Tribol. Lett. 2009, 36, 89–94. [Google Scholar] [CrossRef]
- Lee, H.; Mall, S. Analysis of fretting fatigue of cavitation shotless peened Ti-6Al-4V. Tribol. Lett. 2010, 38, 125–133. [Google Scholar] [CrossRef]
- Fukuda, S.; Matsui, K.; Ishigami, H.; Ando, K. Cavitation peening to improve the fatigue strength of nitrocarburized steel. Fatigue Fract. Eng. Mater. Struct. 2008, 31, 857–862. [Google Scholar] [CrossRef]
- Takahashi, K.; Osedo, H.; Suzuki, T.; Fukuda, S. Fatigue strength improvement of an aluminum alloy with a crack-like surface defect using shot peening and cavitation peening. Eng. Fract. Mech. 2018, 193, 151–161. [Google Scholar] [CrossRef]
- Takakuwa, O.; Soyama, H. Suppression of hydrogen-assisted fatigue crack growth in austenitic stainless steel by cavitation peening. Int. J. Hydrog. Energy 2012, 37, 5268–5276. [Google Scholar] [CrossRef]
- Kumagai, N.; Takakuwa, O.; Soyama, H. Improvement of delayed fracture resistance on chrome molybdenum steel bolt by cavitation peening. Trans. JSME 2016, 82, 1–13, paper No. 16-00111. [Google Scholar]
- Tsujimura, M.; Shirakashi, K.; Hamada, S.; Hiyama, H.; Tomita, H.; Nadahara, S.; Ota, M. Development of semi-conductor device cleaning by cavitation jet. Trans. JSME 2001, 67B, 88–94. [Google Scholar] [CrossRef][Green Version]
- Kumano, H.; Sasaki, T.; Soyama, H. Evaluation of the effectiveness of back-side damage gettering in silicon introduced by a cavitating jet. Appl. Phys. Lett. 2004, 85, 3935–3937. [Google Scholar] [CrossRef]
- G32-16 Standard test method for cavitation erosion using vibratory apparatus1. ASTM Stand. 2016, 3, 1–20.
- Goetzberger, A.; Shockley, W. Metal precipitates in silicon P-N junctions. J. Appl. Phys. 1960, 31, 1821–1824. [Google Scholar] [CrossRef]
- Tice, W.K.; Tan, T.Y. Nucleation of cusi precipitate colonies in oxygen-rich silicon. Appl. Phys. Lett. 1976, 28, 564–565. [Google Scholar] [CrossRef]
- Kang, J.S.; Schroder, D.K. Gettering in silicon. J. Appl. Phys. 1989, 65, 2974–2985. [Google Scholar] [CrossRef]
- Istratov, A.A.; Hieslmair, H.; Weber, E.R. Iron contamination in silicon technology. Appl. Phys. A Mater. Sci. Process. 2000, 70, 489–534. [Google Scholar] [CrossRef]
- Battaglia, C.; Cuevas, A.; De Wolf, S. High-efficiency crystalline silicon solar cells: Status and perspectives. Energy Environ. Sci. 2016, 9, 1552–1576. [Google Scholar] [CrossRef]
- Mikkelsen, J.C. Gettering of oxygen in Si wafers damaged by ion-implantation and mechanical abrasion. Appl. Phys. Lett. 1983, 42, 695–697. [Google Scholar] [CrossRef]
- Sawada, R. Durability of mechanical damage gettering effect in si wafers. Jpn. J. Appl. Phys. Part 1 Regul. Pap. Short Notes Rev. Pap. 1984, 23, 959–964. [Google Scholar] [CrossRef]
- Soyama, H.; Kumano, H. Oxidation-induced stacking faults introduced by using a cavitating jet for gettering in silicon. Electrochem. Solid State Lett. 2000, 3, 93–94. [Google Scholar] [CrossRef]
- Kumano, H.; Soyama, H. Back side damage gettering of cu using a cavitating jet. Electrochem. Solid State Lett. 2004, 7, G51–G52. [Google Scholar] [CrossRef]
- Kikuchi, M.; Takiguchi, T.; Yamada, J.; Yamamoto, M.; Soyama, H. Evaluation of the efficiency of cleaning dental plaque on titanium using a cavitating jet. J. Biomech. Sci. Eng. 2014, 9. paper No.14-00297. [Google Scholar] [CrossRef]
- Yamada, J.; Takiguchi, T.; Saito, A.; Odanaka, H.; Soyama, H.; Yamamoto, M. Removal of oral biofilm on an implant fixture by a cavitating jet. Implant Dent. 2017, 26, 904–910. [Google Scholar] [CrossRef]
- Yamada, J.; Peng, K.; Kokubun, T.; Takiguchi, T.; Li, G.; Yamamoto, M.; Soyama, H. Optimization of a cavitating jet for removing dental plaque from the surface of the screw of an implant and its practical application. J. Biomech. Sci. Eng. 2018, 13. paper No.17-00102. [Google Scholar] [CrossRef][Green Version]
- Lindhe, J.; Meyle, J.; European Workshop, P. Peri-implant diseases: Consensus report of the sixth european workshop on periodontology. J. Clin. Periodontol. 2008, 35, 282–285. [Google Scholar] [CrossRef]
- Heitz-Mayfield, L.J.A. Peri-implant diseases: Diagnosis and risk indicators. J. Clin. Periodontol. 2008, 35, 292–304. [Google Scholar] [CrossRef] [PubMed]
- Renvert, S.; Roos-Jansaker, A.M.; Claffey, N. Non-surgical treatment of peri-implant mucositis and peri-implantitis: A literature review. J. Clin. Periodontol. 2008, 35, 305–315. [Google Scholar] [CrossRef]
- Teughels, W.; Van Assche, N.; Sliepen, I.; Quirynen, M. Effect of material characteristics and/or surface topography on biofilm development. Clin. Oral Implant. Res. 2006, 17, 68–81. [Google Scholar] [CrossRef] [PubMed]
- Ley, S.V.; Low, C.M.R. Ultrasound in Synthesis; Springer-Verlag: Berlin, Germany, 1980. [Google Scholar]
- Sivakumar, M.; Pandit, A.B. Wastewater treatment: A novel energy efficient hydrodynamic cavitational technique. Ultrason. Sonochem. 2002, 9, 123–131. [Google Scholar] [CrossRef]
- Patil, P.N.; Bote, S.D.; Gogate, P.R. Degradation of imidacloprid using combined advanced oxidation processes based on hydrodynamic cavitation. Ultrason. Sonochem. 2014, 21, 1770–1777. [Google Scholar] [CrossRef] [PubMed]
- Bagal, M.V.; Gogate, P.R. Wastewater treatment using hybrid treatment schemes based on cavitation and fenton chemistry: A review. Ultrason. Sonochem. 2014, 21, 1–14. [Google Scholar] [CrossRef]
- Dular, M.; Griessler-Bulc, T.; Gutierrez-Aguirre, I.; Heath, E.; Kosjek, T.; Klemencic, A.K.; Oder, M.; Petkovsek, M.; Racki, N.; Ravnikar, M.; et al. Use of hydrodynamic cavitation in (waste)water treatment. Ultrason. Sonochem. 2016, 29, 577–588. [Google Scholar] [CrossRef]
- Thanekar, P.; Gogate, P. Application of hydrodynamic cavitation reactors for treatment of wastewater containing organic pollutants: Intensification using hybrid approaches. Fluids 2018, 3, 98. [Google Scholar] [CrossRef]
- Gagol, M.; Przyjazny, A.; Boczkaj, G. Wastewater treatment by means of advanced oxidation processes based on cavitation—A review. Chem. Eng. J. 2018, 338, 599–627. [Google Scholar] [CrossRef]
- Bandala, E.R.; Rodriguez-Narvaez, O.M. On the nature of hydrodynamic cavitation process and its application for the removal of water pollutants. Air Soil Water Res. 2019, 12, 6. [Google Scholar] [CrossRef]
- Burzio, E.; Bersani, F.; Caridi, G.C.A.; Vesipa, R.; Ridolfi, L.; Manes, C. Water disinfection by orifice-induced hydrodynamic cavitation. Ultrason. Sonochem. 2020, 60, 13. [Google Scholar] [CrossRef]
- Kalumuck, K.M.; Chahine, G.L. The use of cavitating jets to oxidize organic compounds in water. J. Fluids Eng.-Trans. Asme 2000, 122, 465–470. [Google Scholar] [CrossRef]
- Kato, H.; Oe, Y.; Honoki, M.; Mochiki, T.; Fukazawa, T. Dispersion of spilled oil by a cavitating jet at sea. J. Mar. Sci. Technol. 2006, 11, 131–138. [Google Scholar] [CrossRef]
- Nakashima, K.; Ebi, Y.; Shibasaki-Kitakawa, N.; Soyama, H.; Yonemoto, T. Hydrodynamic cavitation reactor for efficient pretreatment of lignocellulosic biomass. Ind. Eng. Chem. Res. 2016, 55, 1866–1871. [Google Scholar] [CrossRef]








Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soyama, H. Cavitating Jet: A Review. Appl. Sci. 2020, 10, 7280. https://doi.org/10.3390/app10207280
Soyama H. Cavitating Jet: A Review. Applied Sciences. 2020; 10(20):7280. https://doi.org/10.3390/app10207280
Chicago/Turabian StyleSoyama, Hitoshi. 2020. "Cavitating Jet: A Review" Applied Sciences 10, no. 20: 7280. https://doi.org/10.3390/app10207280
APA StyleSoyama, H. (2020). Cavitating Jet: A Review. Applied Sciences, 10(20), 7280. https://doi.org/10.3390/app10207280