Quantum Eigenstates of Curved and Varying Cross-Sectional Waveguides
Abstract
1. Introduction
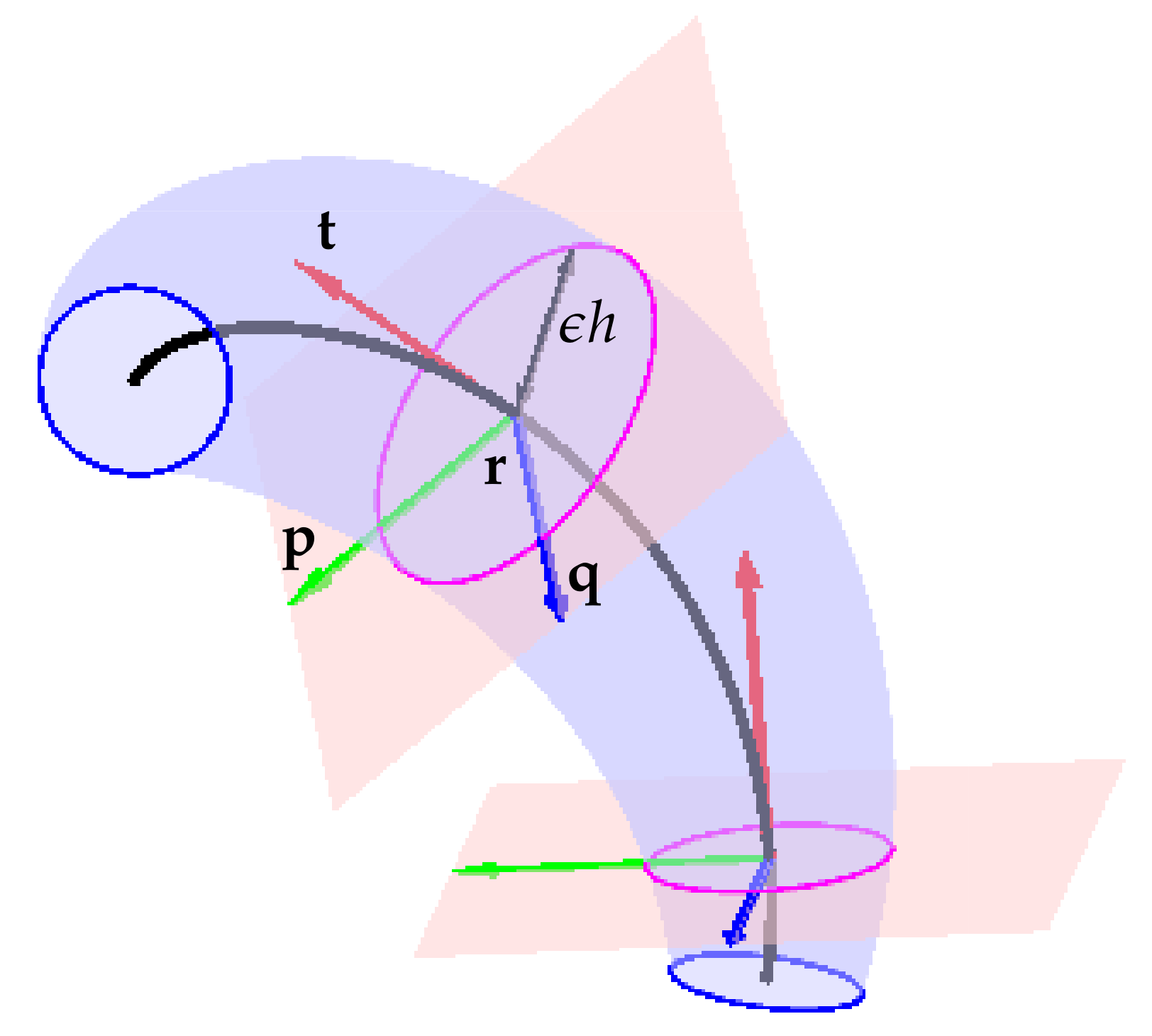
2. The General Equations
2.1. Constant Orientation
2.2. Variable Orientation
2.3. Non Arc Length Parametrisation
2.4. 2D Problems
2.5. Schrödinger Equation
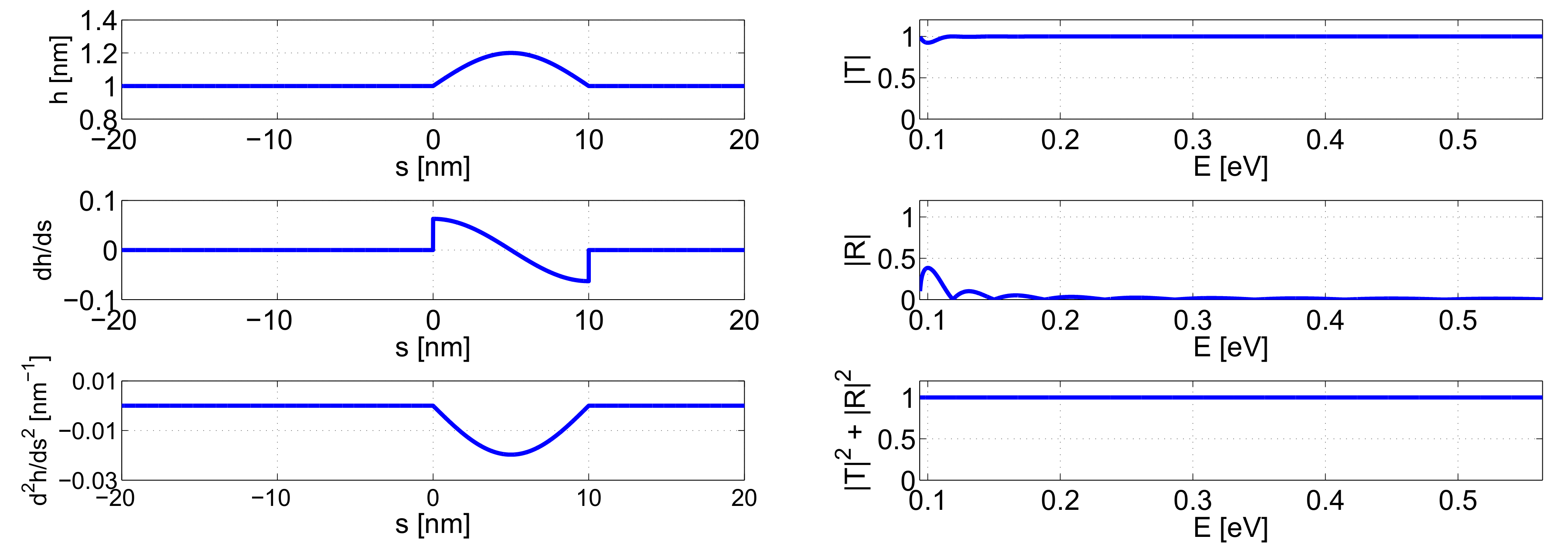
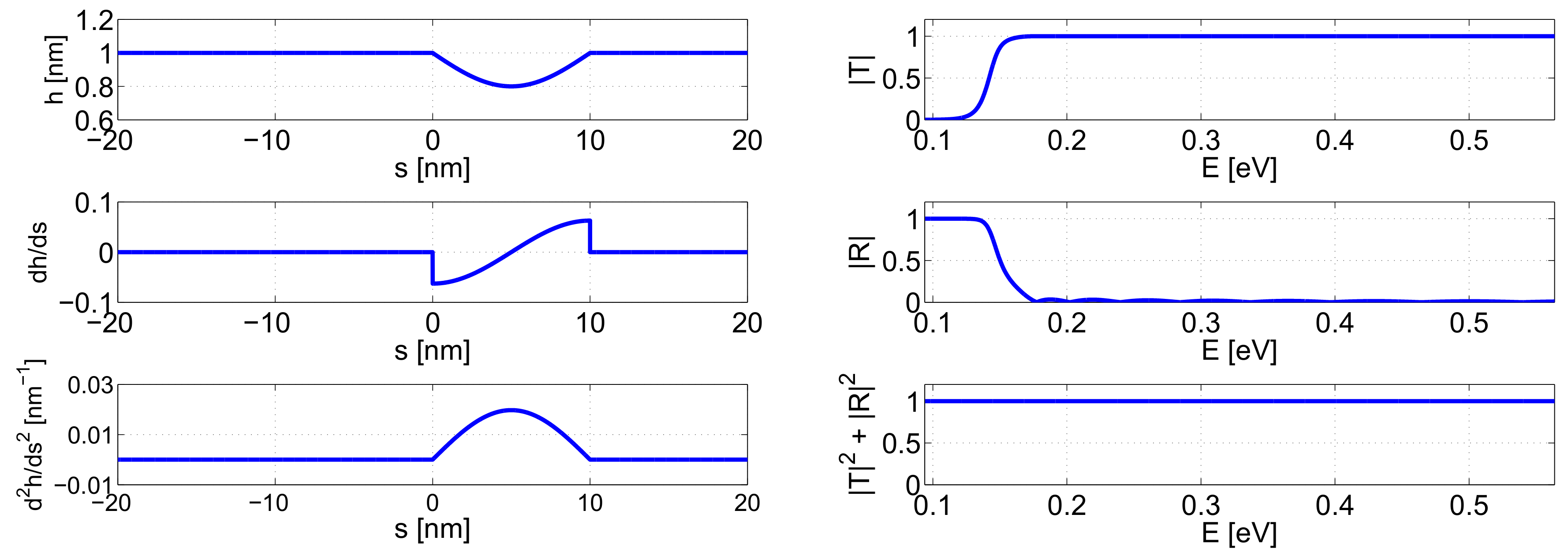
3. Transmission Studies through a Straight Waveguide with a Varying Thickness
4. 3D Eigenstate Problems
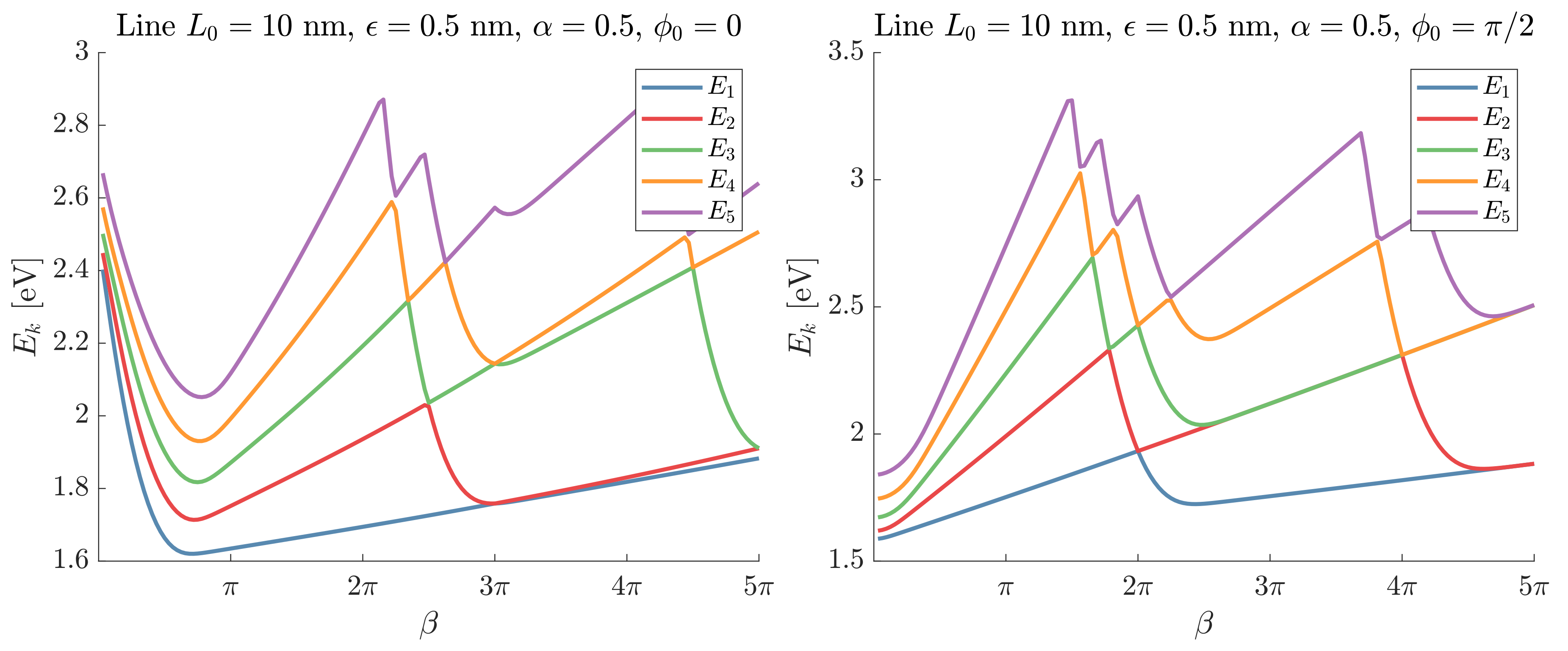
4.1. Line with Circular Cross Section
4.2. Elliptic Helix with Circular Cross Section
4.3. Closed Ellipse with Circular Cross Section
4.4. Tennis Ball Curve with a Square Cross Section
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Validation
Appendix A.1. Logarithmic Spiral

| 0.0 | 1D | 996.71 | 1026.32 | 1075.66 | 1144.75 | 1233.58 |
| 2D | 996.72 | 1026.34 | 1075.71 | 1144.82 | 1233.69 | |
| 0.2 | 1D | 925.10 | 1015.99 | 1094.11 | 1169.73 | 1255.79 |
| 2D | 925.12 | 1016.02 | 1094.15 | 1169.78 | 1255.88 | |
| 0.4 | 1D | 834.43 | 969.69 | 1088.59 | 1199.90 | 1307.49 |
| 2D | 834.45 | 969.72 | 1088.64 | 1199.95 | 1307.56 | |
| 0.6 | 1D | 752.84 | 918.86 | 1068.12 | 1210.19 | 1348.52 |
| 2D | 752.86 | 918.89 | 1068.16 | 1210.24 | 1348.57 | |
| 0.8 | 1D | 682.39 | 871.21 | 1044.48 | 1211.89 | 1376.83 |
| 2D | 682.39 | 871.22 | 1044.49 | 1211.89 | 1376.82 | |
| 1.0 | 1D | 622.31 | 828.74 | 1021.79 | 1210.85 | 1399.10 |
| 2D | 622.31 | 828.72 | 1021.74 | 1210.77 | 1398.99 |
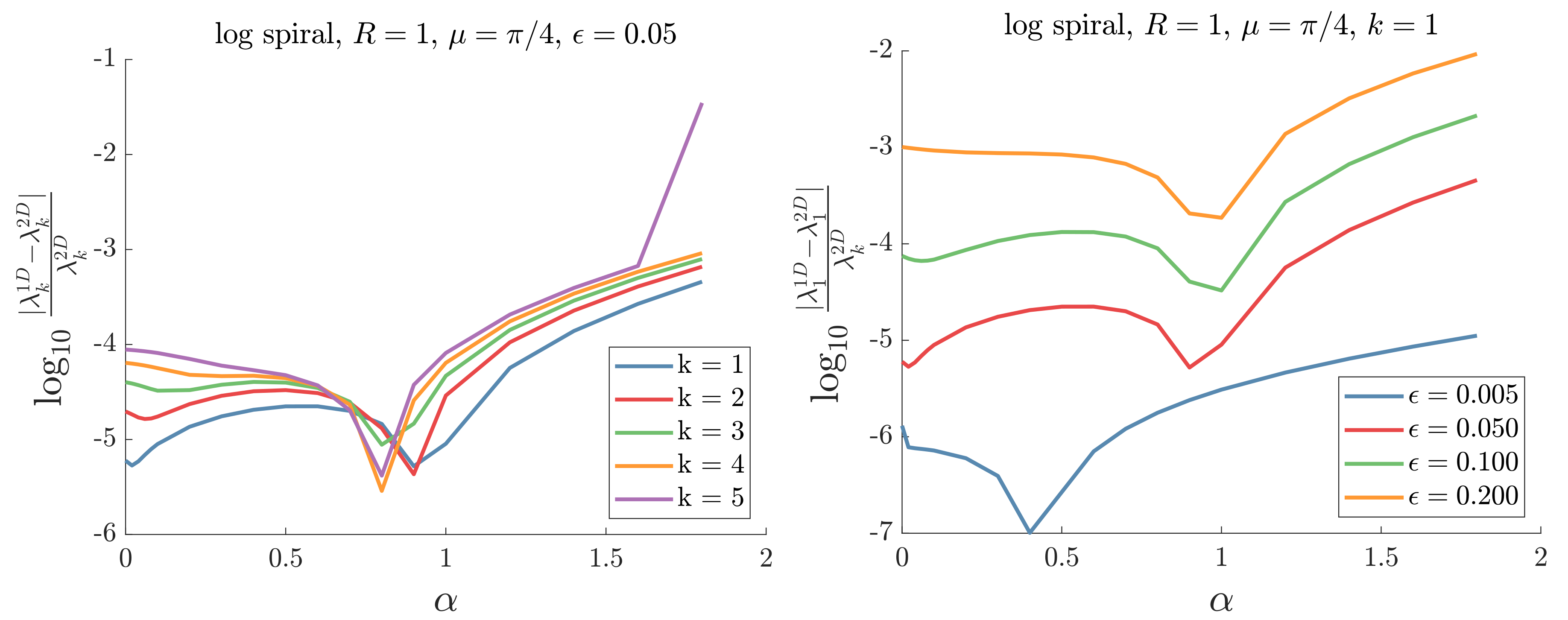
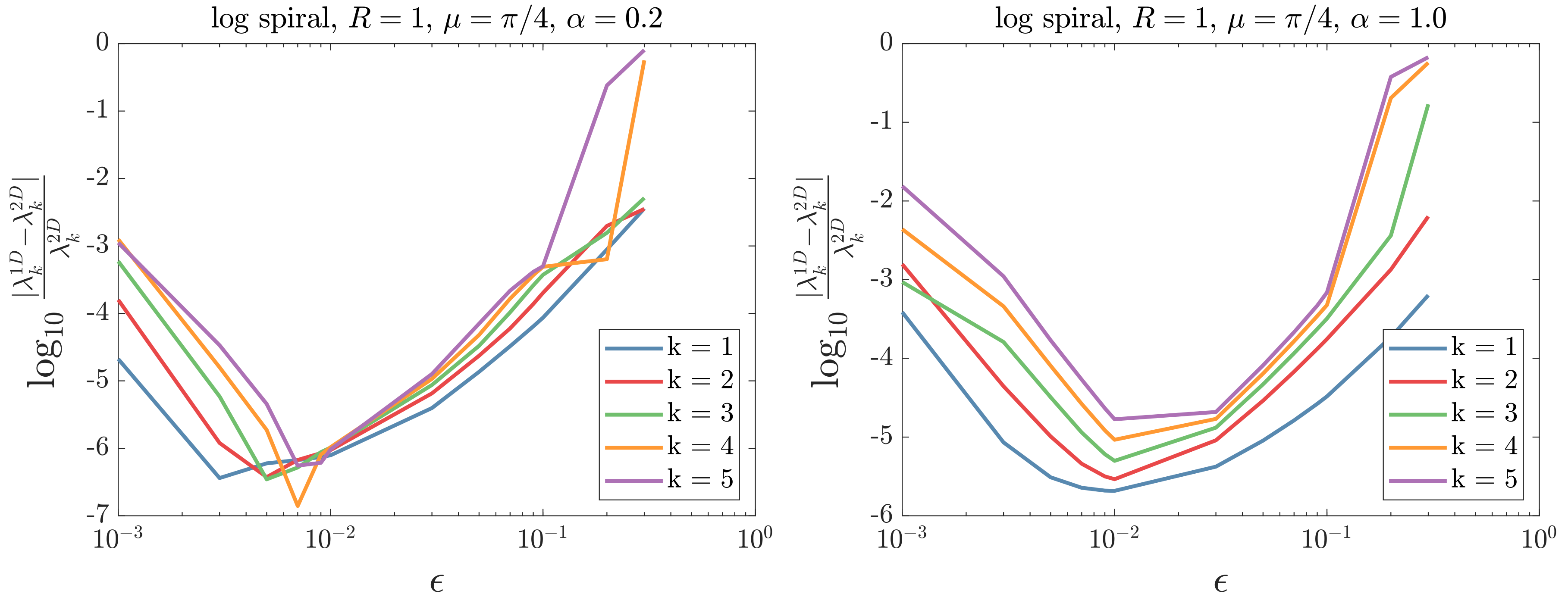

| −0.8 | 1D | 15.99 | 17.64 | 19.09 | 20.44 | 21.75 |
| 2D | 15.88 | 17.58 | 19.06 | 20.43 | 21.75 | |
| 0.8 | 1D | 16.00 | 17.65 | 19.09 | 20.45 | 21.75 |
| 2D | 15.99 | 17.64 | 19.08 | 20.44 | 21.75 |
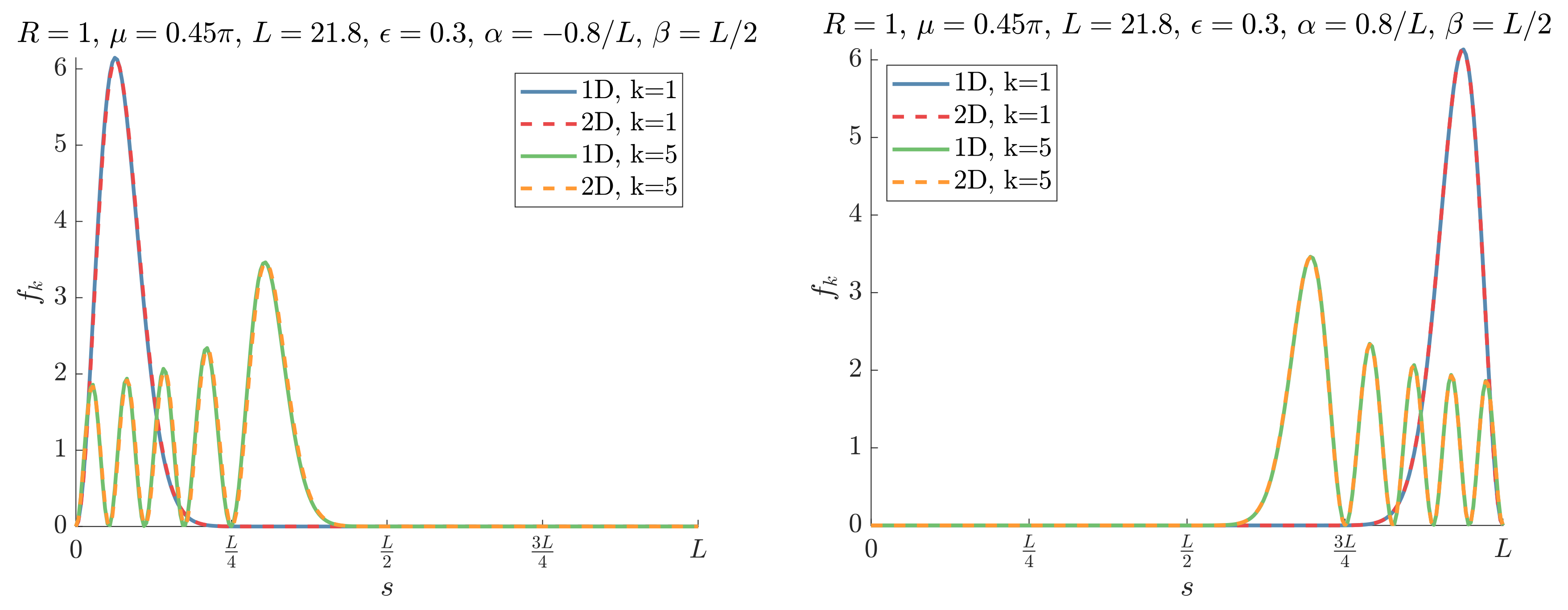
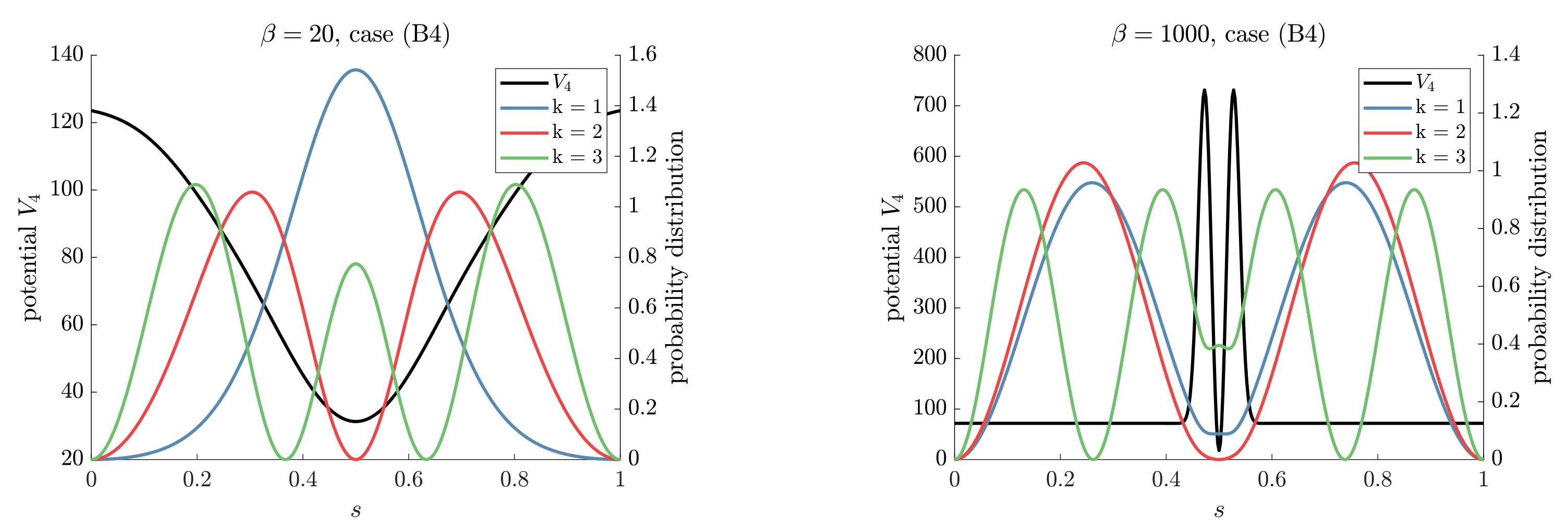
Appendix B. Significance of the Different Terms
| Case | |||||
|---|---|---|---|---|---|
| (A1) | 74.13 | 103.74 | 153.08 | 222.17 | 311.00 |
| (A2) | 81.25 | 112.16 | 157.22 | 228.03 | 316.90 |
| (A3) | 57.48 | 110.62 | 167.66 | 236.54 | 324.39 |
| (A4) | 63.80 | 120.12 | 173.19 | 241.69 | 330.02 |
| Case | |||||
| (A1) | 74.13 | 103.74 | 153.08 | 222.17 | 311.00 |
| (A2) | 101.52 | 105.88 | 210.91 | 230.51 | 385.76 |
| (A3) | 72.45 | 110.92 | 153.34 | 228.77 | 311.94 |
| (A4) | 108.18 | 113.17 | 215.24 | 237.46 | 386.54 |
References
- Varnava, C. Nanowire networks crack on. Varnava. Nat. Electron. 2018, 1, 326. [Google Scholar] [CrossRef]
- Chan, C.K.; Peng, H.; Liu, G.; Mcllwrath, K.; Zhang, X.F.; Huggins, R.A.; Cui, Y. High-performance lithium battery anodes using silicon nanowires. Nat. Nanotechnol. 2018, 3, 31–35. [Google Scholar] [CrossRef] [PubMed]
- Patolsky, F.; Zheng, G.; Lieber, C.M. Fabrication of silicon nanowire devices for ultrasensitive, label-free, real-time detection of biological and chemical species. Nat. Protoc. 2006, 1, 1711–1724. [Google Scholar] [CrossRef]
- Takei, K.; Takahashi, T.; Ho, J.C.; Ko, H.; Gillies, A.G.; Leu, P.W.; Fearing, R.S.; Javey, A. Nanowire active-matrix circuitry for low-voltage macroscale artificial skin. Nat. Mater. 2010, 9, 821–826. [Google Scholar] [CrossRef] [PubMed]
- Ramezany, A.; Mahdavi, M.; Pourkamali, S. Nanoelectromechanical resonant narrow-band amplifiers. Microsyst. Nanoeng. 2016, 2, 16004. [Google Scholar] [CrossRef] [PubMed]
- Feng, X.L.; He, R.; Yang, P.; Roukes, M.L. Very high frequency silicon nanowire electromechanical resonators. Nano Lett. 2007, 7, 1953–1959. [Google Scholar] [CrossRef]
- Liu, X.; Zhou, H.; Zhang, G.; Zhang, Y.-W. The effects of curvature on the thermal conduction of bent silicon nanowire. J. Appl. Phys. 2019, 125, 082505. [Google Scholar] [CrossRef]
- Fomin, V.M. Topology and geometry controlled properties of nanoarchitectures. Phys. Status Solidi RRL 2019, 13, 1800595. [Google Scholar] [CrossRef]
- Bocharov, D.; Piskunov, S.; Zhukovskii, Y.F.; Evarestov, R.A. Ab initio calculations on the electronic structure and photocatalytic properties of two-dimensional WS2 (0001) nanolayers of varying thickness. Phys. Status Solidi RRL 2018, 13, 1800253. [Google Scholar] [CrossRef]
- Dolgirev, P.E.; Kalenkov, M.S.; Zaikin, A.D. Topology-controlled thermopower oscillations in multiterminal Andreev interferometers. Phys. Status Solidi RRL 2019, 13, 1800252. [Google Scholar] [CrossRef]
- Rezaev, R.; Posenitskiy, E.; Smirnova, E.; Levchenko, E.; Schmidt, O.G.; Fomin, V.M. Voltage induced by superconducting vortices in open nanostructured microtubes. Phys. Status Solidi RRL 2019, 13, 1800251. [Google Scholar] [CrossRef]
- Córdoba, R.; Mailly, D.; Rezaev, R.O.; Smirnova, E.I.; Schmidt, O.G.; Fomin, V.M.; Zeitler, U.; Guillamón, I.; Suderow, H.; de Teresa, J.M. Three-Dimensional Superconducting Nanohelices Grown by He+-Focused-Ion-Beam Direct Writing. Nano Lett. 2019, 19, 8597–8604. [Google Scholar] [CrossRef] [PubMed]
- Rezaev, R.O.; Smirnova, E.I.; Schmidt, O.G.; Fomin, V.M. Topological transitions in superconductor nanomembranes under a strong transport current. Commun. Phys. 2020, 3, 144. [Google Scholar] [CrossRef]
- Gravesen, J.; Willatzen, M. The four-band spin-less Kane model in curvilinear coordinates. Phys. Status Solidi RRL 2019, 13, 1800305. [Google Scholar] [CrossRef]
- Gravesen, J.; Willatzen, M. On the geometry of nanowires and the role of torsion. Phys. Status Solidi RRL 2019, 13, 1800357. [Google Scholar] [CrossRef]
- Jensen, H.; Koppe, H. Quantum mechanics with constraints. Ann. Phys. 1971, 63, 586–591. [Google Scholar] [CrossRef]
- Da Costa, R.C.T. Quantum mechanics of a constrained particle. Phys. Rev. A 1981, 23, 1982. [Google Scholar] [CrossRef]
- Da Costa, R.C.T. Constraints in quantum mechanics. Phys. Rev. A 1982, 25, 2893. [Google Scholar] [CrossRef]
- Takagi, S.; Tanzawa, T. Quantum mechanics of a particle confined to a twisted ring. Prog. Theor. Phys. 1992, 87, 561–568. [Google Scholar] [CrossRef]
- Goldstone, J.; Jaffe, R.L. Bound states in twisting tubes. Phys. Rev. B 1992, 45, 14100. [Google Scholar] [CrossRef]
- Exner, P.; Seba, P. Bound states in curved quantum waveguides. J. Math. Phys. 1989, 30, 2574. [Google Scholar] [CrossRef]
- Gravesen, J.; Willatzen, M. Eigenstates of Möbius nanostructures including curvature effects. Phys. Rev. A 2005, 72, 32108. [Google Scholar] [CrossRef]
- Starostin, E.L.; van der Heijden, G.H.M. Tension-induced multistability in inextensible helical ribbons. Phys. Rev. Lett. 2008, 101, 84301. [Google Scholar] [CrossRef]
- Encinosa, M.; Eternadi, B. Energy shifts resulting from surface curvature of quantum nanostructures. Phys. Rev. A 1998, 58, 77. [Google Scholar] [CrossRef]
- Webster, A.G. Acoustical impedance and the theory of horns and of the phonograph. Proc. Natl. Acad. Sci. USA 1919, 5, 275. [Google Scholar] [CrossRef] [PubMed]
- Pierce, A.D. Acoustics—An Introduction to Its Physical Principles and Applications; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Stevenson, A.F. General theory of electromagnetic horns. J. Appl. Phys. 1951, 22, 1447. [Google Scholar] [CrossRef]
- Stevenson, A.F. Exact and approximate equations for wave propagation in acoustic horns. J. Appl. Phys. 1951, 22, 1461. [Google Scholar] [CrossRef]

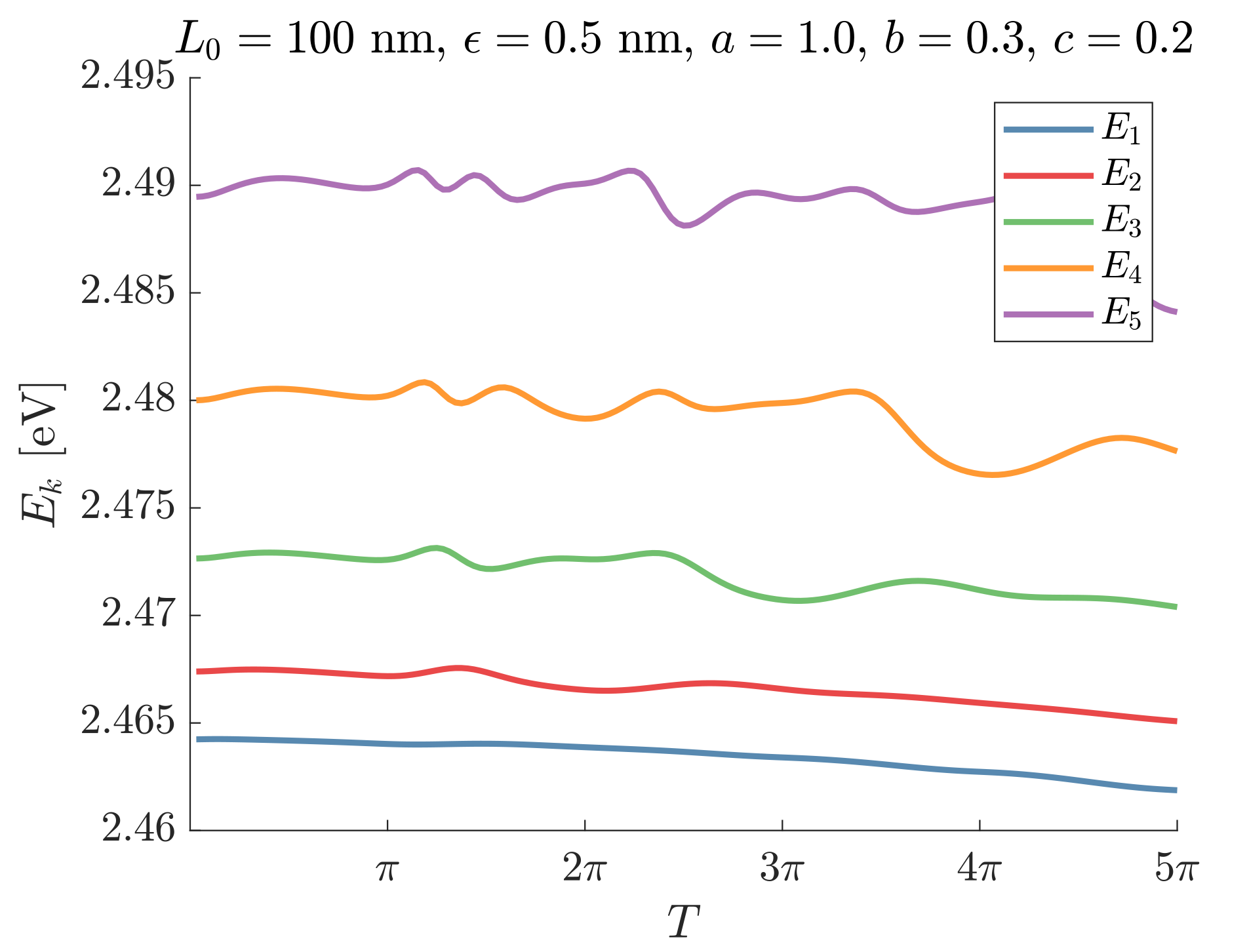
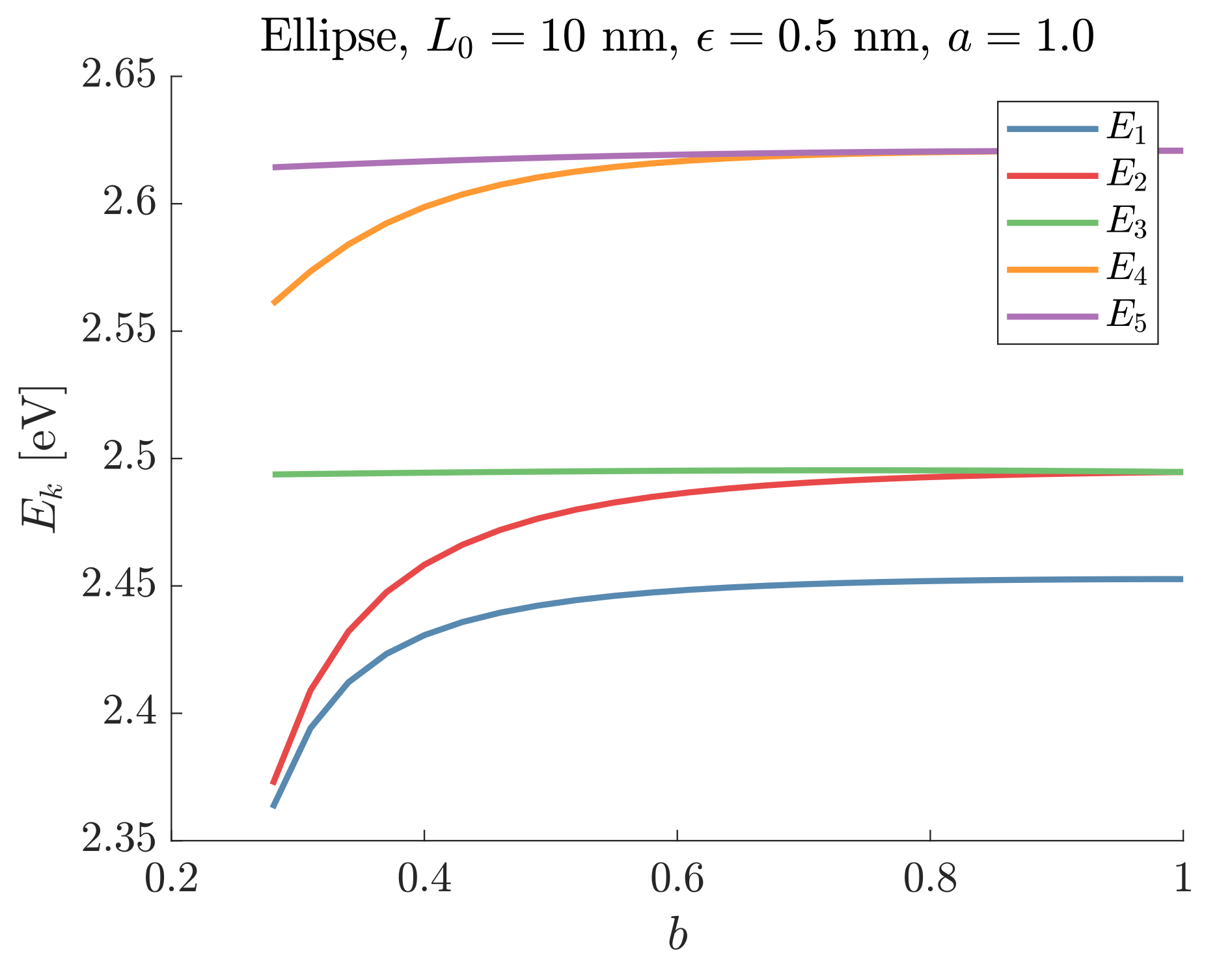

| [eV] | [eV] | [eV] | [eV] | [eV] | |
|---|---|---|---|---|---|
| 0 | 2.10 | 2.21 | 2.21 | 2.52 | 2.53 |
| 1.54 | 1.90 | 2.27 | 2.64 | 3.00 | |
| 1.80 | 1.80 | 2.54 | 2.56 | 3.17 | |
| 2.10 | 2.11 | 2.12 | 3.13 | 3.13 | |
| 2.41 | 2.46 | 2.46 | 2.53 | 3.48 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gravesen, J.; Willatzen, M. Quantum Eigenstates of Curved and Varying Cross-Sectional Waveguides. Appl. Sci. 2020, 10, 7240. https://doi.org/10.3390/app10207240
Gravesen J, Willatzen M. Quantum Eigenstates of Curved and Varying Cross-Sectional Waveguides. Applied Sciences. 2020; 10(20):7240. https://doi.org/10.3390/app10207240
Chicago/Turabian StyleGravesen, Jens, and Morten Willatzen. 2020. "Quantum Eigenstates of Curved and Varying Cross-Sectional Waveguides" Applied Sciences 10, no. 20: 7240. https://doi.org/10.3390/app10207240
APA StyleGravesen, J., & Willatzen, M. (2020). Quantum Eigenstates of Curved and Varying Cross-Sectional Waveguides. Applied Sciences, 10(20), 7240. https://doi.org/10.3390/app10207240





