High-Speed Time-Resolved Tomographic Particle Shadow Velocimetry Using Smartphones
Abstract
1. Introduction
2. Materials and Methods
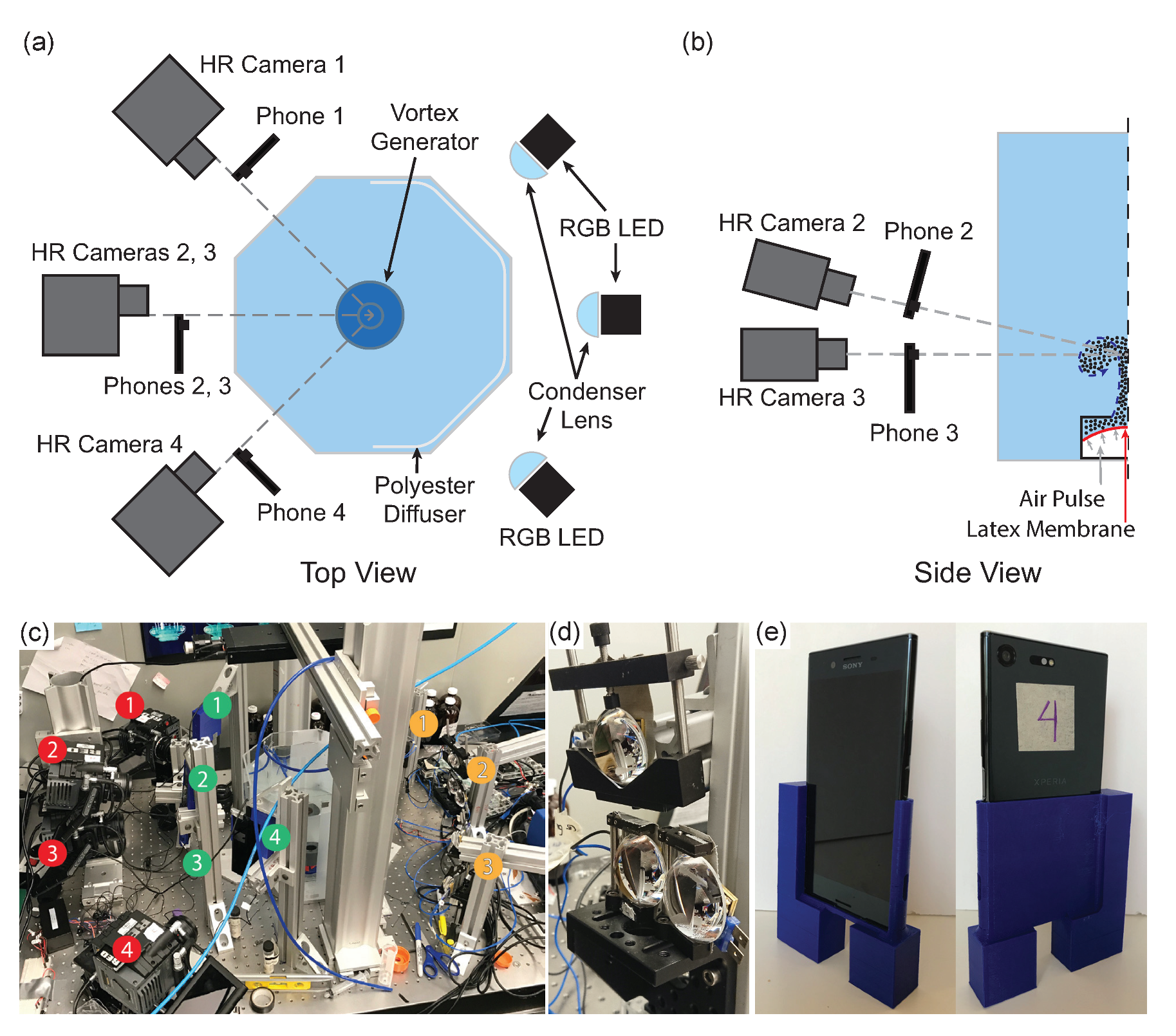
2.1. Overall Tomographic PIV Setup
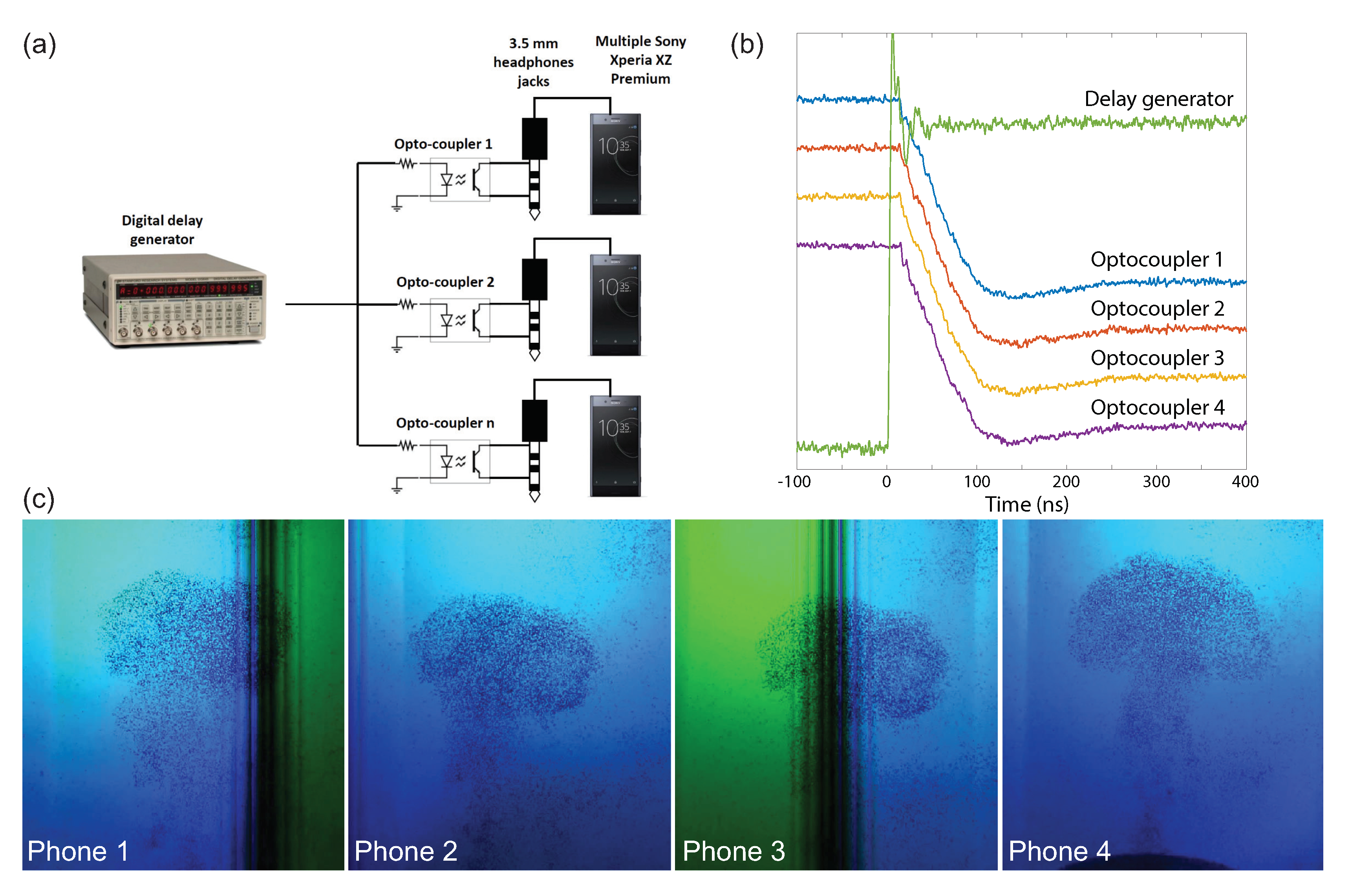
2.2. Smartphone Camera Triggering and Synchronization
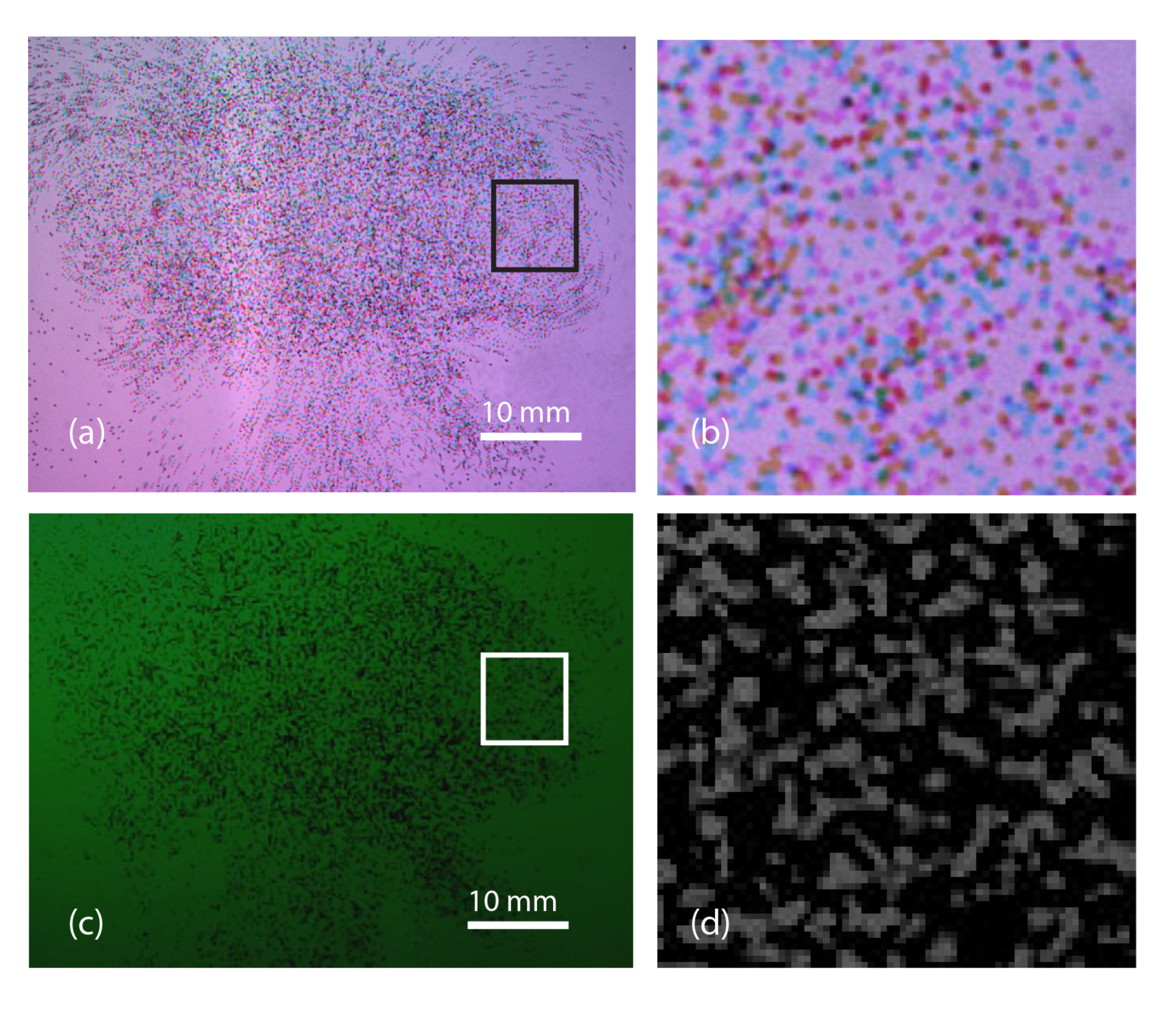
2.3. Image Pre-Processing
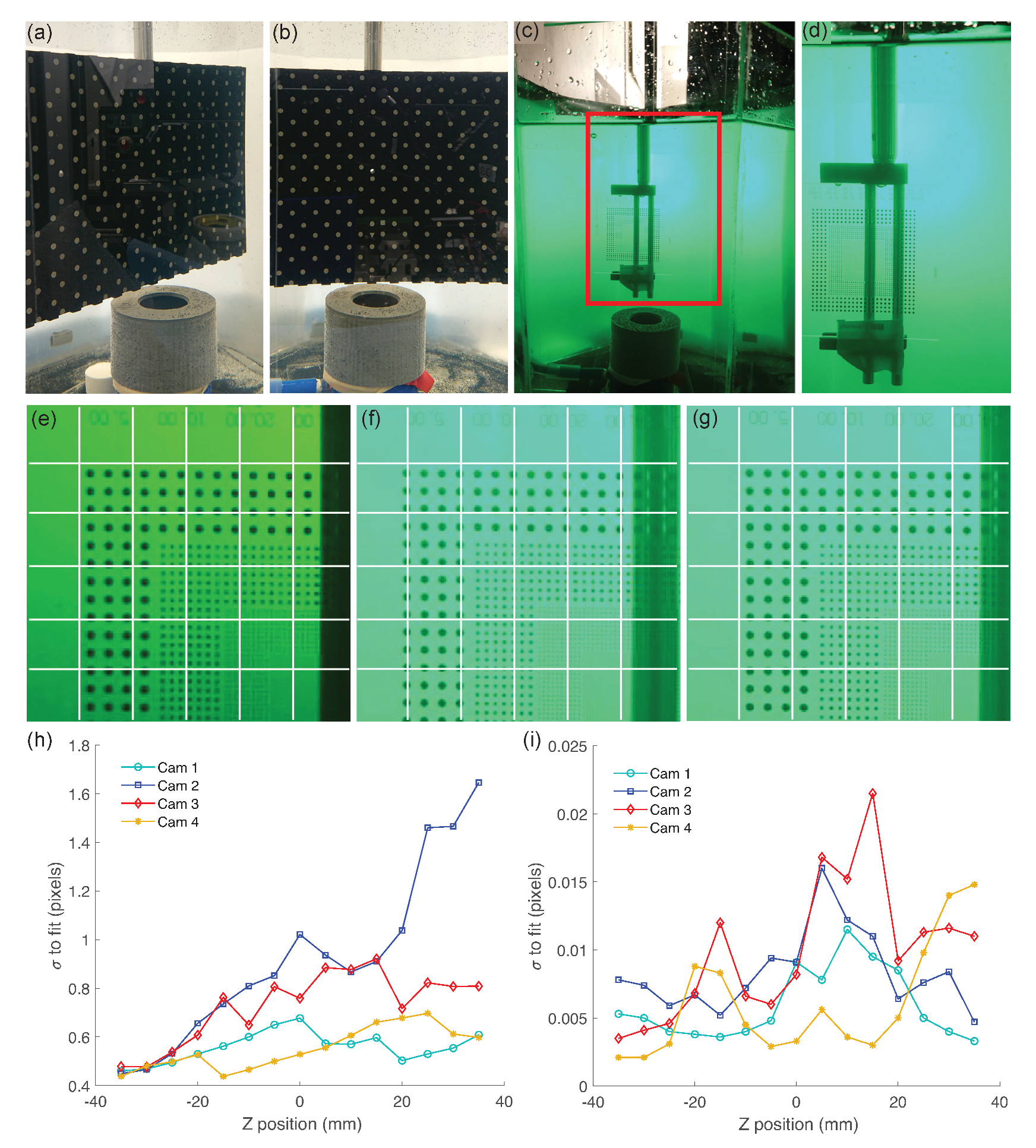
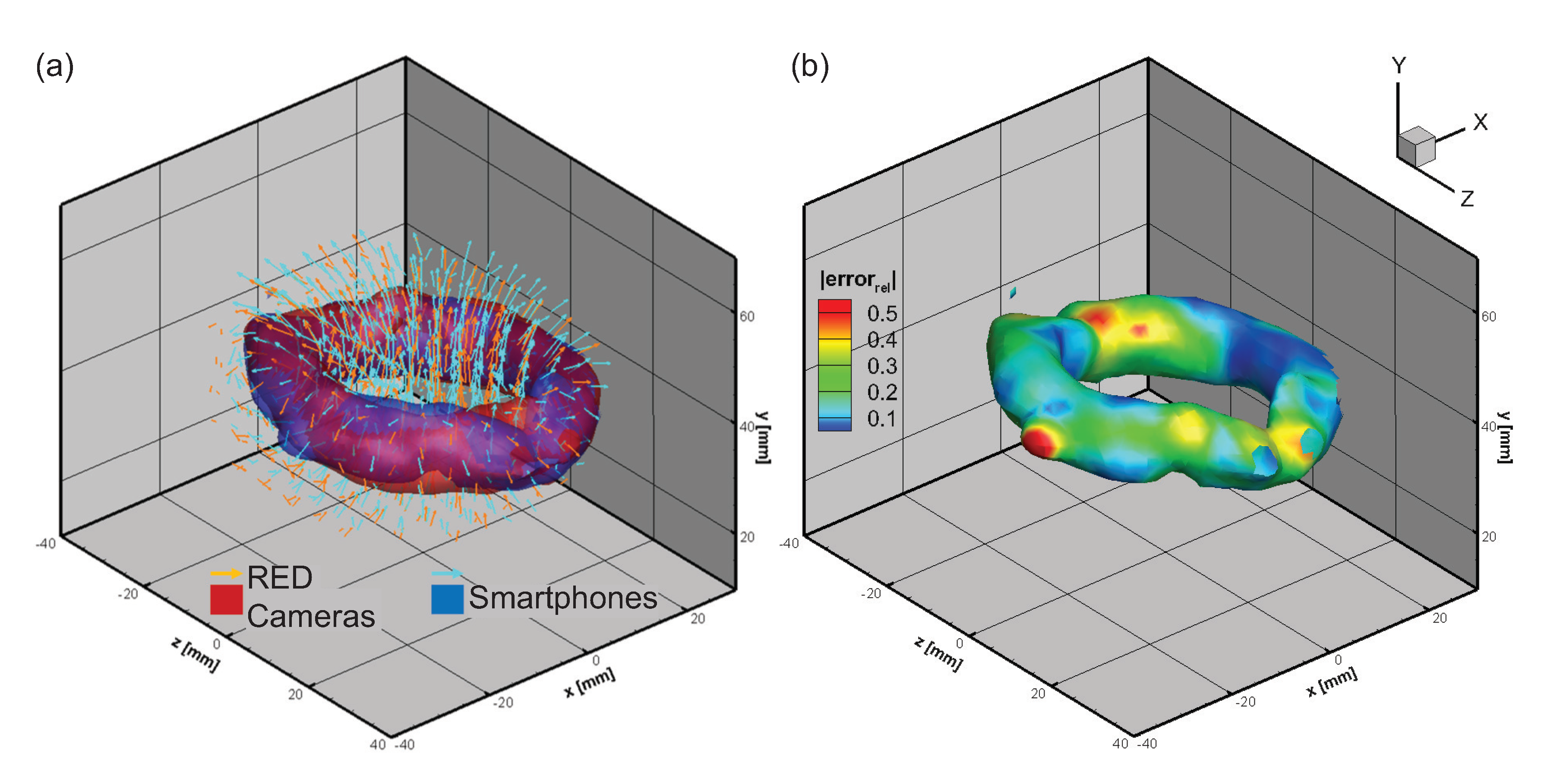
2.4. Tomographic PIV Calibration
2.5. Tomographic PIV Reconstruction and Correlation Procedures
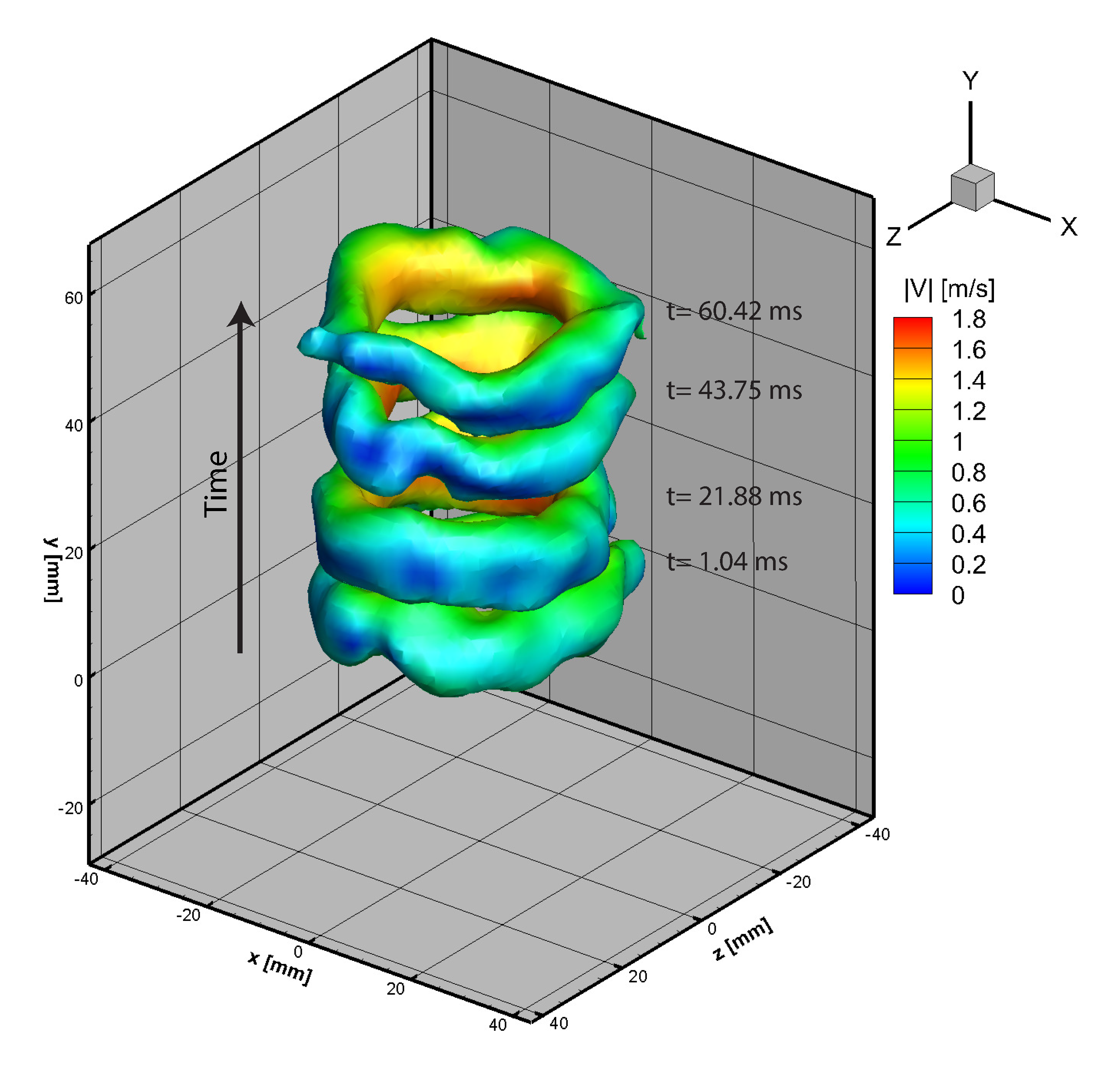
3. Results
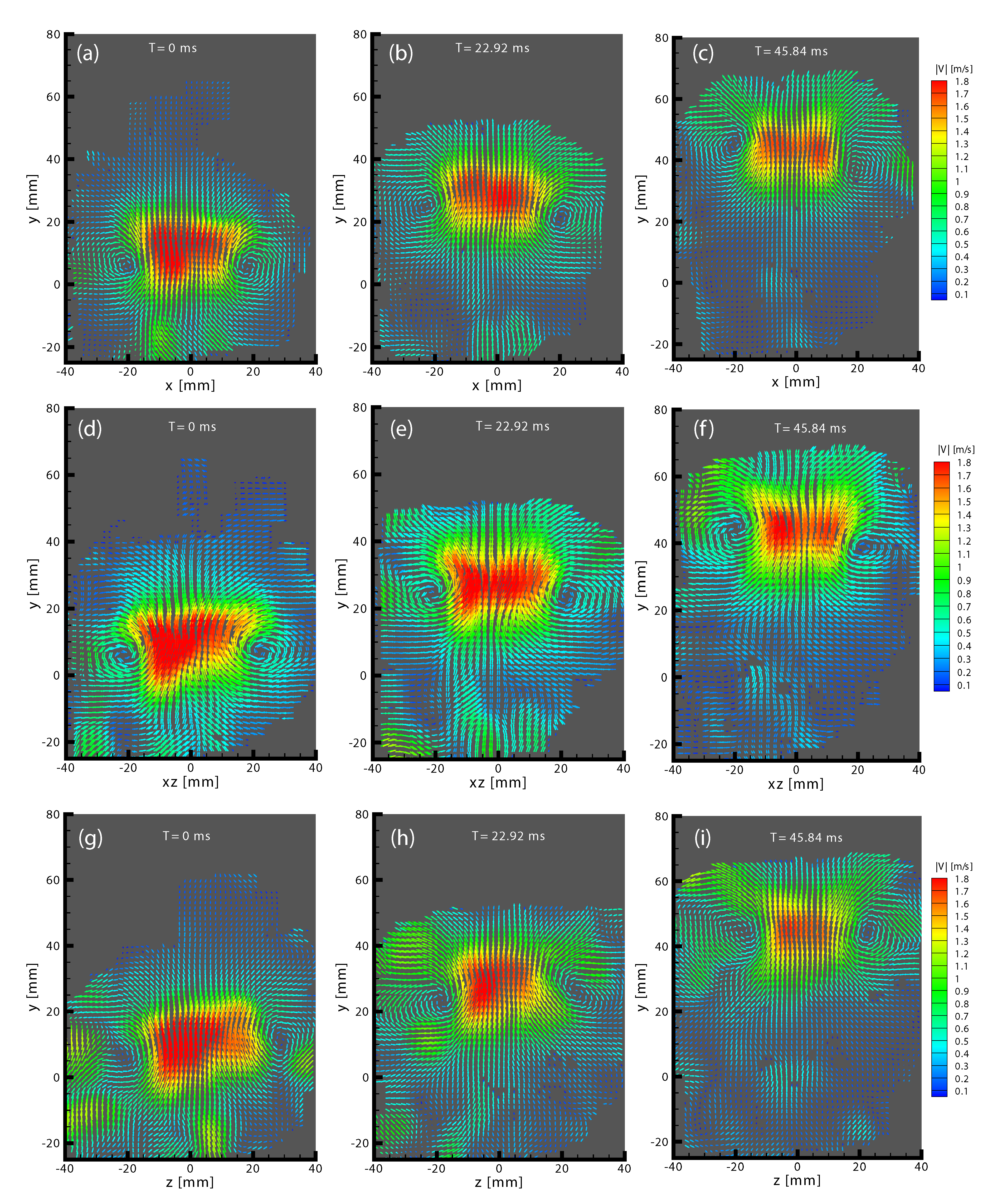
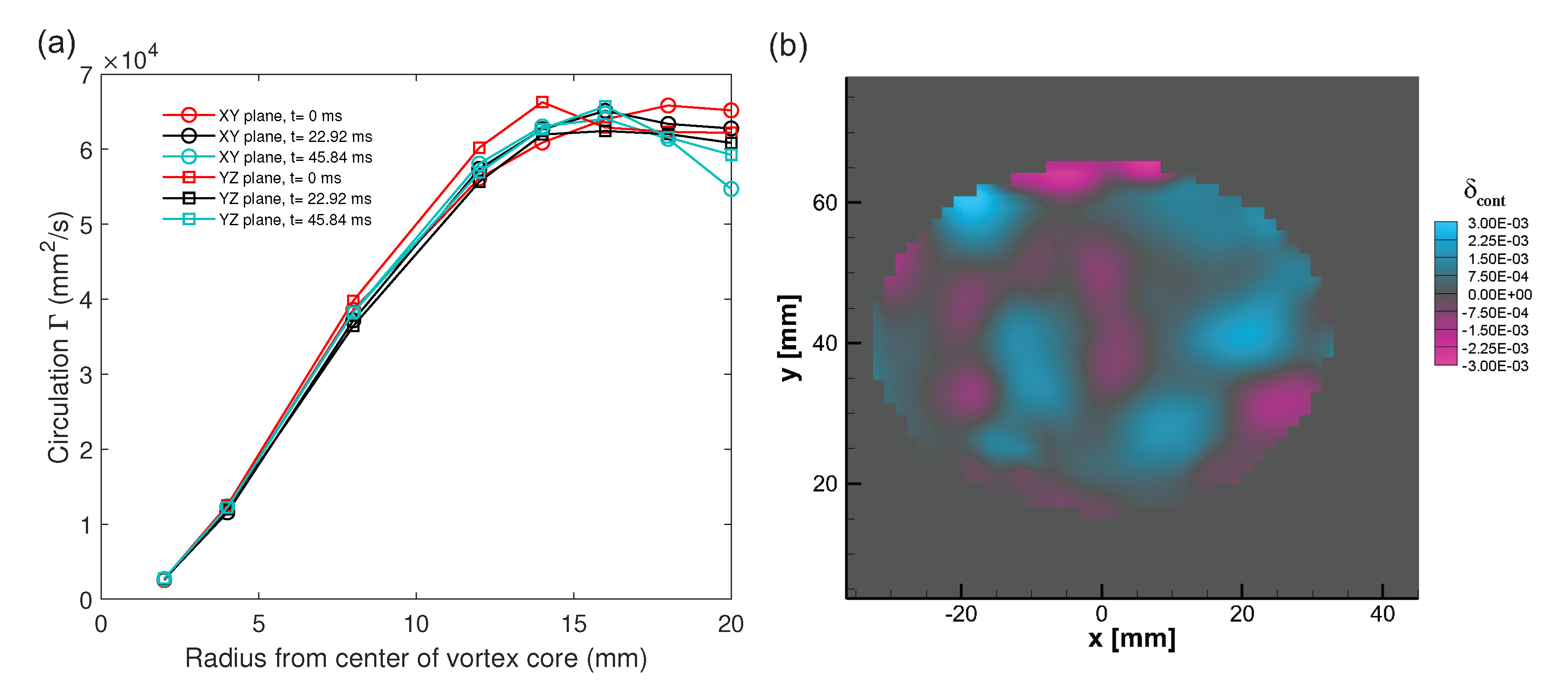
3.1. Circulation and Continuity Verification
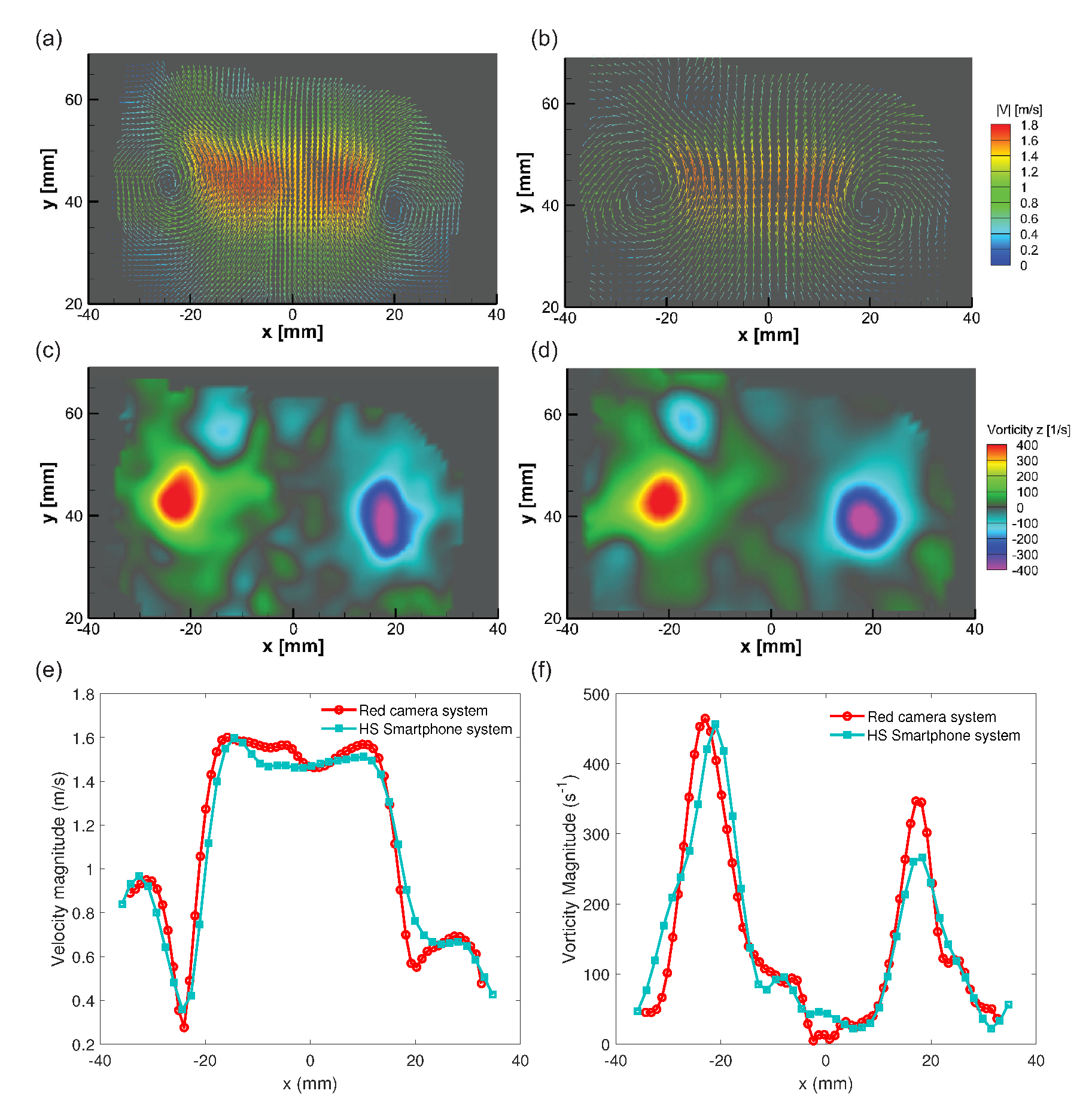
3.2. Comparison with High Resolution Tomographic PIV System
4. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Adrian, R.J. Particle-imaging techniques for experimental fluid mechanics. Ann. Rev. Fluid Mech. 1991, 23, 261–304. [Google Scholar] [CrossRef]
- Westerweel, J.; Elsinga, G.E.; Adrian, R.J. Particle image velocimetry for complex and turbulent flows. Ann. Rev. Fluid Mech. 2013, 45, 409–436. [Google Scholar] [CrossRef]
- Willert, C.E.; Gharib, M. Digital particle image velocimetry. Exp. Fluids 1991, 10, 181–193. [Google Scholar] [CrossRef]
- Hori, T.; Sakakibara, J. High-speed scanning stereoscopic PIV for 3D vorticity measurement in liquids. Meas. Sci. Technol. 2004, 15, 1067. [Google Scholar] [CrossRef]
- Elsinga, G.E.; Scarano, F.; Wieneke, B.; van Oudheusden, B.W. Tomographic particle image velocimetry. Exp. Fluids 2006, 41, 933–947. [Google Scholar] [CrossRef]
- Scarano, F. Tomographic PIV: Principles and practices. Meas. Sci. Technol. 2012, 24, 012001. [Google Scholar] [CrossRef]
- Belden, J.; Truscott, T.T.; Axiak, M.C.; Techet, A.H. Three-dimensional synthetic aperture particle image velocimetry. Meas. Sci. Technol. 2010, 21, 125403. [Google Scholar] [CrossRef]
- Bomphrey, R.J.; Henningsson, P.; Michaelis, D.; Hollis, D. Tomographic particle image velocimetry of desert locust wakes: Instantaneous volumes combine to reveal hidden vortex elements and rapid wake deformation. J. R. Soc. Interface 2012, 9, 3378–3386. [Google Scholar] [CrossRef]
- Langley, K.R.; Hardester, E.; Thomson, S.L.; Truscott, T.T. Three-dimensional flow measurements on flapping wings using synthetic aperture PIV. Exp. Fluids 2014, 55, 1831. [Google Scholar] [CrossRef]
- Casey, T.A.; Sakakibara, J.; Thoroddsen, S.T. Scanning tomographic particle image velocimetry applied to a turbulent jet. Phys. Fluids 2013, 25, 025102. [Google Scholar] [CrossRef]
- Ianiro, A.; Lynch, K.P.; Violato, D.; Cardone, G.; Scarano, F. Three-dimensional organization and dynamics of vortices in multichannel swirling jets. J. Fluid Mech. 2018, 843, 180. [Google Scholar] [CrossRef]
- Mugundhan, V.; Pugazenthi, R.; Speirs, N.B.; Samtaney, R.; Thoroddsen, S.T. The alignment of vortical structures in turbulent flow through a contraction. J. Fluid Mech. 2020, 884, A5. [Google Scholar] [CrossRef]
- Saaid, H.; Voorneveld, J.; Schinkel, C.; Westenberg, J.; Gijsen, F.; Segers, P.; Verdonck, P.; de Jong, N.; Bosch, J.G.; Kenjeres, S.; et al. Tomographic PIV in a model of the left ventricle: 3D flow past biological and mechanical heart valves. J. Biomech. 2019, 90, 40–49. [Google Scholar] [CrossRef] [PubMed]
- Willert, C.; Gharib, M. Three-dimensional particle imaging with a single camera. Exp. Fluids 1992, 12, 353–358. [Google Scholar] [CrossRef]
- Tien, W.H.; Dabiri, D.; Hove, J.R. Color-coded three-dimensional micro particle tracking velocimetry and application to micro backward-facing step flows. Exp. Fluids 2014, 55, 1684. [Google Scholar] [CrossRef]
- Kreizer, M.; Liberzon, A. Three-dimensional particle tracking method using FPGA-based real-time image processing and four-view image splitter. Exp. Fluids 2011, 50, 613–620. [Google Scholar] [CrossRef]
- Gao, Q.; Wang, H.P.; Wang, J.J. A single camera volumetric particle image velocimetry and its application. Sci. China Technol. Sci. 2012, 55, 2501–2510. [Google Scholar] [CrossRef]
- Cenedese, A.; Cenedese, C.; Furia, F.; Marchetti, M.; Moroni, M.; Shindler, L. 3D particle reconstruction using light field imaging. In Proceedings of the International Symposium on Applications of Laser Techniques to Fluid Mechanics, Lisbon, Portugal, 9–12 July 2012. [Google Scholar]
- Skupsch, C.; Brücker, C. Multiple-plane particle image velocimetry using a light-field camera. Opt. Express 2013, 21, 1726–1740. [Google Scholar] [CrossRef]
- Shi, S.; Ding, J.; Atkinson, C.; Soria, J.; New, T.H. A detailed comparison of single-camera light-field PIV and tomographic PIV. Exp. Fluids 2018, 59, 46. [Google Scholar] [CrossRef]
- Rice, B.E.; McKenzie, J.A.; Peltier, S.J.; Combs, C.S.; Thurow, B.S.; Clifford, C.J.; Johnson, K. Comparison of 4-camera Tomographic PIV and Single-camera Plenoptic PIV. In Proceedings of the 2018 AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8–12 January 2018; p. 2036. [Google Scholar]
- Ido, T.; Shimizu, H.; Nakajima, Y.; Ishikawa, M.; Murai, Y.; Yamamoto, F. Single-camera 3-D particle tracking velocimetry using liquid crystal image projector. In Proceedings of the ASME/JSME 2003 4th Joint Fluids Summer Engineering Conference, Honolulu, HI, USA, 6–10 July 2003; pp. 2257–2263. [Google Scholar]
- Zibret, D.; Bailly, Y.; Prenel, J.P.; Malfara, R.; Cudel, C. 3D flow investigations by rainbow volumic velocimetry (RVV): Recent progress. J. Flow Vis. Image Process. 2004, 11. [Google Scholar] [CrossRef]
- McGregor, T.J.; Spence, D.J.; Coutts, D.W. Laser-based volumetric colour-coded three-dimensional particle velocimetry. Opt. Lasers Eng. 2007, 45, 882–889. [Google Scholar] [CrossRef]
- Ruck, B. Colour-coded tomography in fluid mechanics. Opt. Laser Technol. 2011, 43, 375–380. [Google Scholar] [CrossRef]
- Xiong, J.; Idoughi, R.; Aguirre-Pablo, A.A.; Aljedaani, A.B.; Dun, X.; Fu, Q.; Thoroddsen, S.T.; Heidrich, W. Rainbow particle imaging velocimetry for dense 3D fluid velocity imaging. ACM Trans. Graphics (TOG) 2017, 36, 36. [Google Scholar] [CrossRef]
- Xiong, J.; Aguirre-Pablo, A.A.; Idoughi, R.; Thoroddsen, S.T.; Heidrich, W. Rainbow PIV with improved depth resolution—Design and comparative study with TomoPIV. Meas. Sci. Technol. 2020. [Google Scholar] [CrossRef]
- Aguirre-Pablo, A.; Aljedaani, A.B.; Xiong, J.; Idoughi, R.; Heidrich, W.; Thoroddsen, S.T. Single-camera 3D PTV using particle intensities and structured light. Exp. Fluids 2019, 60, 25. [Google Scholar] [CrossRef]
- Willert, C.; Stasicki, B.; Klinner, J.; Moessner, S. Pulsed operation of high-power light emitting diodes for imaging flow velocimetry. Meas. Sci. Technol. 2010, 21, 075402. [Google Scholar] [CrossRef]
- Buchmann, N.A.; Willert, C.E.; Soria, J. Pulsed, high-power LED illumination for tomographic particle image velocimetry. Exp. Fluids 2012, 53, 1545–1560. [Google Scholar] [CrossRef]
- Estevadeordal, J.; Goss, L. PIV with LED: Particle shadow velocimetry (PSV) technique. In Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 2005; p. 37. [Google Scholar]
- Cierpka, C.; Hain, R.; Buchmann, N.A. Flow visualization by mobile phone cameras. Exp. Fluids 2016, 57, 108. [Google Scholar] [CrossRef]
- Aguirre-Pablo, A.A.; Alarfaj, M.K.; Li, E.Q.; Hernández-Sánchez, J.F.; Thoroddsen, S.T. Tomographic Particle Image Velocimetry using Smartphones and Colored Shadows. Sci. Rep. 2017, 7, 3714. [Google Scholar] [CrossRef]
- Sonymobile. Sony Xperia XZ Premium. 2017. Available online: https://www.sonymobile.com/global-en/products/phones/xperia-xz-premium/ (accessed on 1 May 2017).
- Android Debug Bridge (adb): Android Developers. Available online: https://developer.android.com/studio/command-line/adb (accessed on 20 March 2020).
- Ansari, S.; Wadhwa, N.; Garg, R.; Chen, J. Wireless software synchronization of multiple distributed cameras. In Proceedings of the 2019 IEEE International Conference on Computational Photography (ICCP), Tokyo, Japan, 15–17 May 2019; pp. 1–9. [Google Scholar]
- Sternberg, S.R. Biomedical image processing. Computer 1983, 16, 22–34. [Google Scholar] [CrossRef]
- Wieneke, B. Volume self-calibration for 3D particle image velocimetry. Exp. Fluids 2008, 45, 549–556. [Google Scholar] [CrossRef]
- Atkinson, C.; Soria, J. An efficient simultaneous reconstruction technique for tomographic particle image velocimetry. Exp. Fluids 2009, 47, 553. [Google Scholar] [CrossRef]
- Gan, L.; Cardesa-Duenas, J.I.; Michaelis, D.; Dawson, J. Comparison of tomographic PIV algorithms on resolving coherent structures in locally isotropic turbulence. In Proceedings of the 16th International Symposium on Applications of Laser Techniques to Fluid Mechanics, Lisbon, Portugal, 9–12 July 2012. [Google Scholar]
- Malvar, H.S.; He, L.-W.; Cutler, R. High-quality linear interpolation for demosaicing of Bayer-patterned color images. In Proceedings of the 2004 IEEE International Conference on Acoustics, Speech, and Signal Processing, Montreal, QC, Canada, 17–21 May 2004; Volume 3, pp. iii-485–iii-488. [Google Scholar]
- McPhail, M.J.; Fontaine, A.A.; Krane, M.H.; Goss, L.; Crafton, J. Correcting for color crosstalk and chromatic aberration in multicolor particle shadow velocimetry. Meas. Sci. Technol. 2015, 26, 025302. [Google Scholar] [CrossRef] [PubMed]

| Platform | OS | Android 7.1 (Nougat) |
|---|---|---|
| Chipset | Qualcomm MSM8998 Snapdragon 835 | |
| CPU | Octa-core (4 × 2.45 GHz Kryo and 4 × 1.9 GHz Kryo) | |
| GPU | Adreno 540 | |
| Memory | Card Slot | microSD, up to 256 GB |
| Internal | 64 GB, 4 GB RAM | |
| Cameras | Primary | 19 Mpx, f/2.0, 25 mm, EIS (gyro), predictive phase detection and laser autofocus, LED flash |
| Features | 1/2.3-inch sensor size, 1.22 μm pixel size, geo-tagging, touch focus, face detection, HDR, panorama | |
| Video | 2160p@30 fps, 720p@960 fps, HDR | |
| Secondary | 13 Mpx, f/2.0, 22 mm, 1/3-inch sensor size, 1.12 μm pixel size, 1080 p |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aguirre-Pablo, A.A.; Langley, K.R.; Thoroddsen, S.T. High-Speed Time-Resolved Tomographic Particle Shadow Velocimetry Using Smartphones. Appl. Sci. 2020, 10, 7094. https://doi.org/10.3390/app10207094
Aguirre-Pablo AA, Langley KR, Thoroddsen ST. High-Speed Time-Resolved Tomographic Particle Shadow Velocimetry Using Smartphones. Applied Sciences. 2020; 10(20):7094. https://doi.org/10.3390/app10207094
Chicago/Turabian StyleAguirre-Pablo, Andres A., Kenneth R. Langley, and Sigurdur T. Thoroddsen. 2020. "High-Speed Time-Resolved Tomographic Particle Shadow Velocimetry Using Smartphones" Applied Sciences 10, no. 20: 7094. https://doi.org/10.3390/app10207094
APA StyleAguirre-Pablo, A. A., Langley, K. R., & Thoroddsen, S. T. (2020). High-Speed Time-Resolved Tomographic Particle Shadow Velocimetry Using Smartphones. Applied Sciences, 10(20), 7094. https://doi.org/10.3390/app10207094






