Abstract
A simplified numerical model is introduced to predict ice impact force acting on the ship hull in level ice condition. The model is based on ice-hull collision mechanisms and the essential ice breaking characteristics. The two critical ice failure modes, localized crushing and bending breaking, are addressed. An energy method is used to estimate the crushing force and the indentation displacement for different geometry schemes of ice-ship interaction. Ice bending breaking scenario is taken as a semi-infinite plate under a distributed load resting on an elastic foundation. An integrated complete ice-hull impact event is introduced with ice failure modes and breaking patterns. Impact location randomness and number of broken ice wedges are considered in order to establish a stochastic model. The analysis is validated by comparison with the model ice test of a shuttle passenger ferry performed in May 2017 for SSPA Sweden AB at Aker Arctic Technology Inc. Good agreement is achieved with appropriate parameter selection assumed from the model test and when ice bending failure is dominant. This model can be used to predict the ice impact load and create a bridge between design parameters (ice properties and ship geometry) and structure loads.
1. Introduction
According to the European Commission, inland waterway transportation (IWT) is classified as one of the five transport modes. It can release traffic congestion and reduce greenhouse gas emissions. For countries with strong winters, the development of IWT must take into account the impact of ice problems on ice-going ships. The most common problems are the ship resistance in icy waters and impact ice loading on the hull. There are many available empirical methods [1,2,3] for ice-induced resistance calculation. Hence the problem could as an initial step be solved by increasing the propulsion power. For ice impact load, several methods can be used. In principle, ice-hull collision occurs in the bow area. Therefore, it is critical to put focus on the bow structure in the design process and to study the hull design parameters and their influences on the ice impact load.
One way is to utilize the probabilistic method which simplifies the ice pressure in relation to the contact area,
where and are constants for a given ice condition, is pressure on structure in [MPa] and is contact area between ice floe and ship structure in [m2]. The probabilistic method aims to estimate extreme ice load and is easy to apply compared to other methods. However, this method is proposed for sea-ice going ships with severe ice conditions and the existing values of the two constants come from sea trial tests [4,5]. The inland waterway (IWW) ice condition is however drastically different compared to the sea ice condition and the discrepancies in ice properties are significant, resulting in a different scale of ice loading. It can result in extreme high pressure for light ice condition. The ship design with regards to the corresponding ice prediction is too conservative and not efficient. Moreover, concerning IWW ice conditions, there are uncertainties due to the lack of research and test data and that make it difficult to estimate the ice properties and ice loads accurately [6]. Nevertheless, it is still a good approach to estimate an extreme load even when several design parameters are unknown. Practically, when it comes to the ship design, more parameters and their effects on ice load are usually required. However, the direct ice load prediction needs more refined models as there are lots of influencing parameters both from hull geometry and ice properties.
Another approach is to consider the physical phenomena and reduce the complex scenario to single events by studying the ice-hull interaction mechanism and ice failure modes (e.g., crushing, bending, splitting, sliding). The studies based on ice-hull interaction process are more reliable and efficient for practical ice collision scenarios and ship design aspects. Studies, presented in the literature available either study ice crushing or ice bending, but the combination of the two failure modes are limited. Investigating the two modes together has a significant meaning. By considering the two failure modes simultaneously, a more reliable ice load prediction model should be obtained.
In this work, ice-hull impact is studied, and the focus is on both of the ice crushing and ice bending case, with the contact area connecting the two modes. Normally, ice bending failure is widely accepted as the dominant ice breaking pattern with the largest force. The same assumption is applied to the current model to ensure the accuracy of the model.
The purpose of the paper is to propose a feasible and reliable model for ice load prediction, especially the ice impact force, on ship hull. The energy method [7] is chosen as to calculate the crushing force and the contact area. The stem collision and the shoulder collision are evaluated with two different contact area cases respectively. The bending scenario is equivalent to a wedge-shaped beam failure model and is represented by a semi-plate resting on a Winkler foundation with the ice flexural strength, as the failure criterion. There are also other empirical equations widely used for predicting the ice bending breaking force, for example, in which is the ice thickness and is a constant based on previous research [8]. However, only ice flexural strength and ice thickness are taken into consideration. The bending scenario used in this paper is more suitable since many design parameters are considered. A parametric study is performed with the aim to reveal influences from the design parameters. The numerical model is constituted by repetition of a complete collision event with a set of ice failures happening in sequence.
2. Ice Load Prediction Model
The ship-ice interaction process is known as a complex phenomenon which highly depends on ice properties, hull geometry and relative speed [9]. Valanto [10] divided this interaction process into ice breaking, ice rotation, ice sliding, and ice clearing based on the main phenomena in breaking the level ice [11]. This break-displace process and ice forces are idealized in Figure 1.
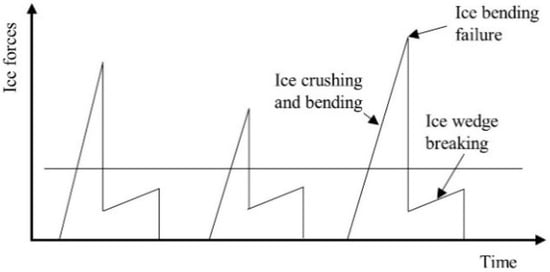
Figure 1.
Idealized time histories of ice forces.
The ship-ice interaction begins with a localized crushing of a free ice edge at the contact zone. When the ship keeps moving forward, both the contact area and the crushing force increase. The ship advance motion causes the ice sheet to deflect down along the hull surface, thus bending stresses are build up in ice sheet until it breaks off into small pieces, as shown in Figure 2. The ice flexural failure occurs at a distance, expressed as the ice breaking length, from the crushing region. It is mainly determined by the ice thickness and the ship speed among all other parameters. The final force to break the ice sheet is denoted as the ice breaking force .
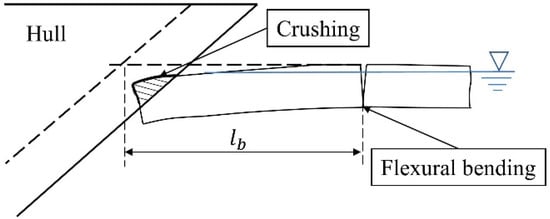
Figure 2.
Illustration of the ice breaking model between a ship bow and level ice.
The numerical model developed in this paper aims to provide an efficient way to compute ice-hull impact force with two primarily ice failure features. Ice is regarded as an isotropic material with flexural strength, which is used as the failure criterion. The process is assumed to be a repetition of the following steps: (1) initial contact and crushing, (2) cracking due to ice bending, (3) more cracks are triggered and both radial and circumferential cracks are generated. A detailed process of the periodic ice impact load prediction model and calculation procedure are well described herein.
2.1. Ice-Hull Contact Mechanism and Determination of Impact Load
Four ice failure occurrences are assumed to happen during one complete impact event. The forces for each occurrence can be computed. The time history ice force is thus a periodic function of every impact event.
2.1.1. Ice Crushing
Ice crushing is regarded to occur at the first stage during one impact event. Ship penetrates ice sheets with a constant speed. An ice sheet is unbreakable but localized fracture takes place with ice spalling and extruding. The crushing force, , indentation displacement, , and contact area, , are therefore determined by the energy method.
2.1.2. Initial Crack Propagation
The initial ice sheet defect due to bending failure usually happens along the free edge of ice sheet and the radial fracture is roughly perpendicular to the free boundary. A similar phenomenon is considered by Lu et al. [12] and is denoted as ice splitting failure. This occurs if ice floes are present with finite mass. The current case is applicable for infinite ice sheet. Shear force is not considered in ice bending as it is proven trivial. Thus, ice breaks when on the ice sheet free edge. An assumption is made that initial crack happens before the maximum stress is build up and corresponding force is not considered in the model.
2.1.3. Circumferential Ice Breaking
Circumferential cracks are assumed to form after any initial defect is created. The ice sheet starts to break up due to bending failure occurring at the maximum stress, . In the ice bending breaking model, with the failure criterion, , the position of the maximum stress can be located and the maximum ice sheet breaking force, , can be found. The ice breaking length, , as shown in Figure 2, occurs at a point where the maximum stress just exceeds the ice flexural strength. Here the computed value of ice breaking length from ice bending breaking model is denoted as ,
There are other empirical ways to calculate the ice breaking length. Usually it is proportional to the ice characteristic length, . Zhang et al. [6] assumed that the breaking length is one-third of . This assumption originates from the ice resistance prediction method proposed by Lindqvist [1]. The empirical ice breaking length value is denoted as .
where is the water density, is the ice Young’s modulus, is ice thickness and is the ice Poisson’s ratio.
2.1.4. Wedge Shaped Ice Floe with Radial Cracks
Eventually more radial cracks are produced as the floating ice wedges are broken off from the ice sheet. As introduced by Kerr [13], the failure load for a wedged ice with an opening angle θ can be calculated according to:
where is an empirical parameter and donates the magnitude of ice breaking force.
Kerr [13] related the ice failure load to the maximum ice force by multiplying a square of the ratio of opening angle to . Here the same analogy is applied. An expression is introduced to correlate the failure load of a wedged ice floe with a maximum ice breaking force, which is written as:
2.2. Stochasticity and Discretization in the Present Model
Ice-hull impact is a highly stochastic process. Normally, ice collision happens along the ship waterline plane randomly. Still, most impacts occur at the ship bow part which means that the stem and shoulder are more effective in terms of ice breaking. To estimate the ice breaking force, the periphery of waterline plane is discretized into small elements and the ice breaking force is computed in the time domain. In order to simplify the ice-hull interaction model and keep the dynamic feature, the ship stem and bow parts are highlighted in the model and discretized with infinite number of elements (points). Thus, several contact locations within the target area are evaluated in the model, as shown in Figure 3. In this paper, only five points are selected to demonstrate the concept. More points (elements) can be introduced to increase the model accuracy. In the model, the number of collisions is also randomized from one location to four locations for shoulder collision event.
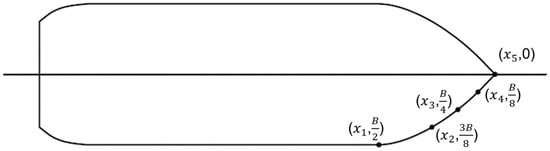
Figure 3.
Bow discretization and locations considered in the paper.
When ice sheet breaks, it may break into different number of pieces. In this paper, the ice sheet is assumed to break into small ice floes with the same angle and size. Here the number of ice floes evaluated are 1, 2, 3 and they correspond to wedge angle of 180°, 90°, 60°. Those parameters are randomly selected in the simulation. A random wedge angle, e.g., 35°, can be explored in further study. All the scenarios mentioned above are considered to happen randomly in the model.
2.3. Model Implementation
The model presented is this paper consists of ice crushing force and bending force at different scenarios. Extra attention is paid to when the maximum ice sheet breaking force is computed. The process is illustrated in Figure 4. The whole computation is realized by programming in Matlab.
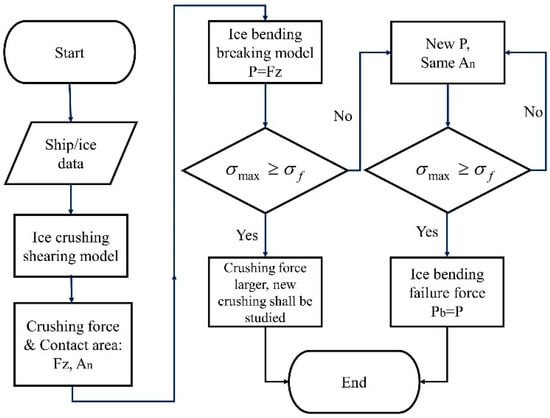
Figure 4.
Description of how to obtain ice breaking force in the current model.
Traditional numerical methods require computation at each time step. Consequently, the simulation usually takes substantial computation resource and time. Instead of running heavy computation, the impact forces are here evaluated at different locations and scenarios, after that the force history can be generated by introducing the randomness and following the collision mechanism. Computation steps are used rather than the real event time since the final force is not a function of time. Although it is possible to refine the model using the real time, the computation becomes more tedious.
3. Ice Load Prediction Sub Models
The fundamentals of the paper are based on the understanding and features of the ice-hull interaction described above. Currently, models evolved on such interaction are widely used in predicting the ice resistance, Lindqvist [1], Keinonen et al. [2], Riska et al. [3], and Su et al. [14]. In addition, this interaction decomposition offers a useful tool to predict the structural loads as well. Therefore, the model in this paper explores the potential to determine the structure load. This method would assist engineers to predict the ice load in an easy way and facilitate the hull structure design in accordance with ice loads and design parameters.
3.1. Ice Crushing-Shearing Model
The energy method proposed by Daley [7] and Propov et al. [15] provides an effective way to calculate the crushing force and indentation displacement for any ice-hull contact. The initial impact collision is triggered by a ship with kinetic energy and a stationary ice sheet with bulky mass. The inputs for calculation are the ice properties, e.g., ice thickness, ice crushing strength, and the hull geometry. Moreover, the method includes analytical formulas for the different geometric contact cases.
The hull geometry parameters are described and presented in Table 1 and Figure 5. The definitions of the hull angles from literature and Finnish-Swedish Ice Class Rules (FSICR) [16] are summarized and illustrated in Figure 6. The coordinate system is set with the origin at the mass center of a ship. The x-axis is along the longitudinal direction of the hull and positive forward. The y-axis is normal to the x-axis and is positive towards starboard. The z-axis is perpendicular to the xy-plane and positive downward [17].

Table 1.
Ship parameters.
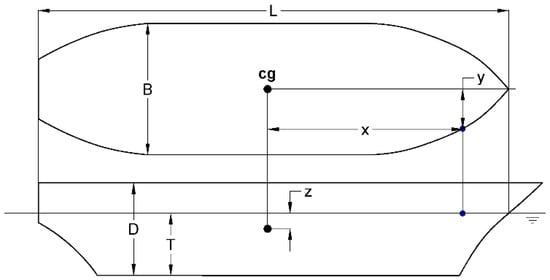
Figure 5.
Definitions of geometric parameters at a ship-ice collision point.
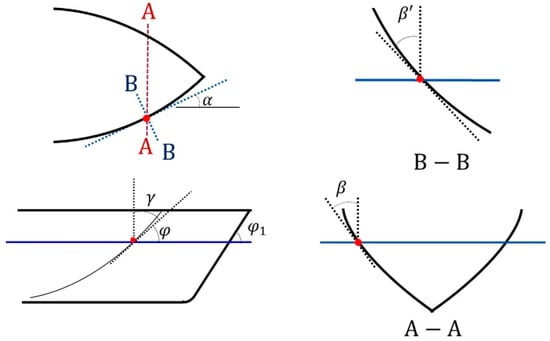
Figure 6.
Definitions of hull angles at a collision point.
The relationships between ship angles are given as below:
The energy method is applicable for an impact between two objects. It is assumed that one object is moving while another is still. During the process, the effective kinetic energy from the moving object is equivalent to the energy expanded to the another as crushing, or indentation, energy. The collided object is assumed to have infinite large mass, thus the effective kinetic energy is regarded the same as the total kinetic energy. This approach is used to determine the maximum force when all motions are ceased.
According to such assumption and based on Daley [7], the effective kinetic energy, , and the crushing energy, , are equal:
The indentation energy can be represented by the indentation force, , and the crushing indentation displacement, ; the kinetic energy is expressed by the ship effective mass and velocity:
where is the effective mass at the impact point; stands for the effective mass of the ship at the contact point; presents the mass reduction factor in six degrees of freedom; is the normal velocity at the impact point; is the ship velocity; is the x-direction cosine. They are defined based on Popov [15]:
For a symmetrical collision on the stem, the relationships become:
The roll, pitch, and yaw lever arm can be calculated, respectively:
The added mass terms in surge, sway, heave, roll, pitch, and yaw can be obtained from [15]:
The squared mass radii of gyration in roll, pitch and yaw can be expressed as:
The mass reduction coefficient thus can be obtained [15]:
The normal impact force and the energy can be calculated as:
where is the pressure on , and equivalent to the ice crushing strength, , it equals to is the ice indentation from the initial contact point along the normal direction of contact area and is a function of , where is constant. is a function of the geometric parameter.
Based on Equations (9) and (21), the kinetic energy can be expressed as:
with the normal indentation displacement as:
Substitute Equation (23) into Equation (20), the normal force can be calculated:
It can be observed that the indentation displacement plays an important role. It is affected by the impact geometry configuration. Two indentation geometry scenarios are introduced. They refer to the bow stem (or head on) collision and the bow shoulder collision respectively, as seen in Figure 7 and Figure 8. The two collision scenes are illustrated as a symmetrical- and an unsymmetrical-contact, as shown in Figure 7 and Figure 8. The indentation functions, and are defined in Daley et al. [15]. The ice sheet dimension and bow geometry at the collision area shown in Figure 9, and the indentation areas for the two collisions and two contact area cases can be derived based on the indentation functions [15].
Figure 7.
Case I-bow front collision: symmetric V wedge indentation. (a) Indentation does not go through the ice thickness; (b) Indentation penetrates through the ice thickness.
Figure 8.
Case II-shoulder collision: wedge-shaped edge indentation. (a) Indentation does not go through the ice thickness; (b) Indentation penetrates through the ice thickness.
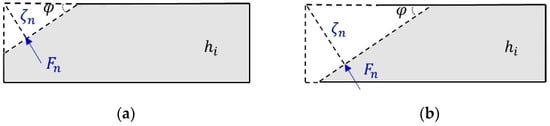
Figure 9.
Side view of the two contact areas: (a) Case I with an indentation that does not go through the ice thickness hi; (b) Case II with an indentation penetrating through the ice thickness hi.
Collision I: bow front collision,
Collision II: shoulder collision,
The normal contact force can be divided into two components, the vertical component, , and the horizontal component, [18]. In the presented model, these force components are related to the failure criterion of the ice floe and the ice resistance, respectively. The vertical component, , could cause bending failure of the ice floe. can be calculated according to the relationship in Figure 10, and based on the geometric relationships, the resistance component and bending force can be calculated and transformed.
where is the horizontal force, is the average dynamic coefficient of friction between the ice and the hull.
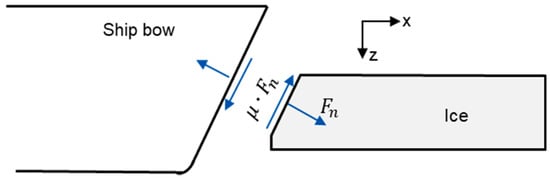
Figure 10.
The force components at contact area.
3.2. Ice Bending-Breaking Model
The problem of computing the stresses in a breakable ice floe caused by ice-hull impacts can be solved by reforming it into an infinite plate subjected to a uniform and distributed force on a Winkler (elastic) foundation, as shown in Figure 11. The stress in the ice wedges can be calculated using method described in the literature [19,20,21,22].
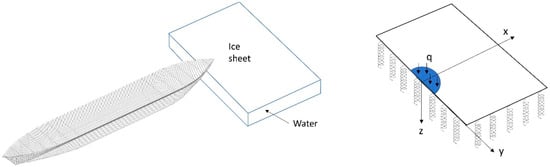
Figure 11.
The ice bending model illustration: a semi-infinite plate resting on an elastic foundation and subjected to a uniform distributed load.
The analysis is based on the differential equation:
where is the bending stiffness of the ice, is the vertical deflection, is the specific weight of water (is the foundation modulus for a pavement or the specific weight of the liquid base), and is the distributed load, with
where is Young’s modulus in [Pa], is Poison’s ratio, is water density in , gravitational constant in [].
It can be seen from Figure 11 that the applied force is uniformly distributed over a half circular area with a radius . As it is assumed that the contact area remains the same after ice crushing, the loading radius and distributed load can be computed as:
where is the horizonal area in the crushing zone. When the crushing force is not sufficient to break the ice sheet, a new variable is introduced to find the ice bending breaking force. The final breaking force can be found by iteration and is represented as .
To solve the special case in Equation (29), the problem can be further reformulated from a uniform distributed load to a concentrated load acting close to the ice edge. Based on the work by Lubbad and Løset [9], the point load location can be marked as , where
The general solution of the differential equation is as follows;
where
The bending moments and stresses in the x- and y-direction are calculated from the curvature of the deformed ice sheet along x-axis at y = 0.
Moreover, the stress at the breaking point along the ice sheet free edge can be obtained by Lubbad and Løset [9] as
By solving the equations, the stresses in the ice sheet can be calculated. Taking the yield stress as the criterion, the ice sheet bending capacity can be computed and it can be determined if the impact force can result in ice breaking by bending failure.
4. Model Validation
The model is validated by comparing the results from a model test performed at Aker Arctic. The details of the ferry model and the ice test conditions are described below as well as a summary and discussion of the results in comparison with the computed results from the current study.
4.1. Ice Model Test
The ice model tests for a shuttle passenger ferry were conducted in May 2017 for SSPA Sweden AB at Aker Arctic Technology Inc. [23]. The ferry model is shown in Figure 12. The vessel is designed to operate in the Stockholm archipelago and the main particulars are presented in Table 2. The model was built in scale 1:8.333 and its dimensions and the ice properties can be seen in Table 2. The level ice tests were performed at three speeds according to the specifications given in Table 3, where is ice breaking component and is ice resistance. The total resistance is calculated by dividing the resistance into breaking and submersion components. However, the breaking component in the test is independent of the ship velocity and is defined by the ITTC guidelines [24]. The breaking resistance is the total resistance in level ice minus the resistance in the pre-sawn ice which is assumed to represent the resistance without the breaking component.

Figure 12.
Side view and bottom view of the ferry model NB550 (In Appendix C of AARC Report A-555): (a) Side view; (b) Bottom view [23]. “Reproduced with permission from [Aker Arctic Technology Inc, SSPA Sweden AB and SLL], published by [Aker Arctic Technology Inc.], 2017”.

Table 2.
Principal particulars of the ferry NB550 and model ship.

Table 3.
Model test conditions.
Photos of the ice breaking patterns are taken during the model tests and are shown in Figure 13. Each color strap on the ruler is 10 cm, which indicates that the broken ice floe field (less than 1 m) is created by the stem and shoulder of the ship model. In Figure 13a, the broken ice floe can be observed and their boundaries can be depicted. It is be assumed that the out layer ice floe fail only once. The stem and shoulder collision can be roughly indicated by the black dot in Figure 13. Figure 13b shows small ice pieces and they may fail more than once. After they first break off due to ice bending failure, they break into more pieces when sliding along the ship hull. The ice breaking length is around 10–30 cm. Multi-contact seems to be happening around the shoulder area. By considering the ship symmetry, the ship geometry, and ice breaking pattern, it is assumed that the stem contact is a single event while the shoulder impact has multiple collision locations ranging from one to four on each side. The simulation is conducted according to such assumption.

Figure 13.
Two examples of Ice breaking pattern captured from ice model test (In Appendix B of AARC Report A-555): (a) an estimation of the breaking points indicated by back dots and ice floes marked with numbering for an average ice thickness of 26 mm, (b) ice breaking pattern with an average ice thickness of 31mm [23]. “Reproduced with permission from [Aker Arctic Technology Inc, SSPA Sweden AB and SLL], published by [Aker Arctic Technology Inc], 2017”.
4.2. Simulation Results
The computation of the impact force on the shuttle ferry is performed by using the ship model data at different speeds. The results are plotted in Figure 14, Figure 15 and Figure 16 and also given in Table 4. In Figure 14, Figure 15 and Figure 16, the blue vertical lines indicate the ice force at each time step. The red horizontal lines are the model test data while the black dashed lines are the mean values and the green lines indicate the standard deviation of computed results. It can be seen that the predicted ice force converges to the model test data with the increasing speed. However, the discrepancy is large at the lowest speed, case 1. For the two cases, Cases 2 and 3, a good agreement is observed with an error less than 10%.
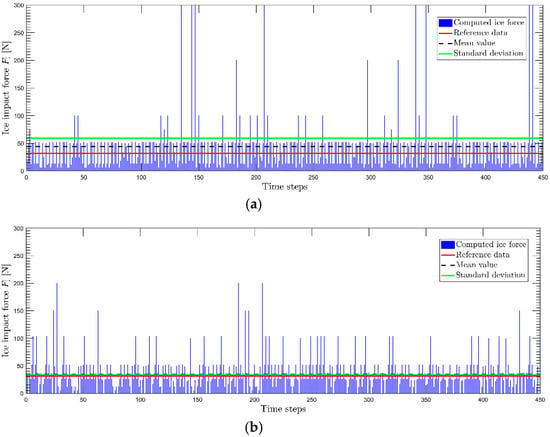
Figure 14.
Result comparison for V = 0.41 m/s: (a) Case 1: Initial setup; (b) Case 1.1: Modified setup.
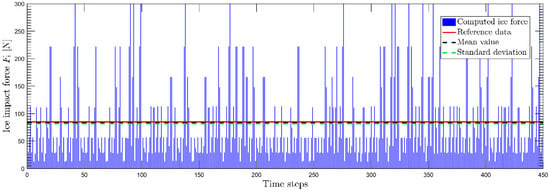
Figure 15.
Case 2: Result comparison for speed V = 0.92 m/s.
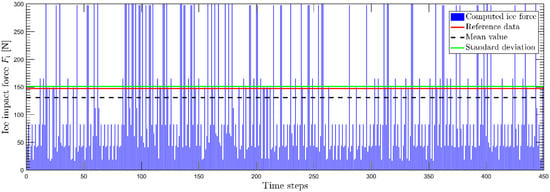
Figure 16.
Case 3: Result comparison for speed V = 1.38 m/s.

Table 4.
Ice force result summary and comparison.
For Case 1, the simulation result does not fit to the test data. A further study is conducted. It is assumed that crushing failure is dominant especially during shoulder collision. It turns out the new simulation, Case 1.1, matches the ice model test data with 8% discrepancy. The modified case demonstrates that the contact scenario, or breaking pattern, affect the outcome considerably. As the breaking pattern and speed relationship is not given in Figure 13, the original assumption may not be applicable for the low speed case. A fraction of the ice impact load history is extracted from Figure 14, as shown in Figure 17. The force pattern matches with Figure 1.
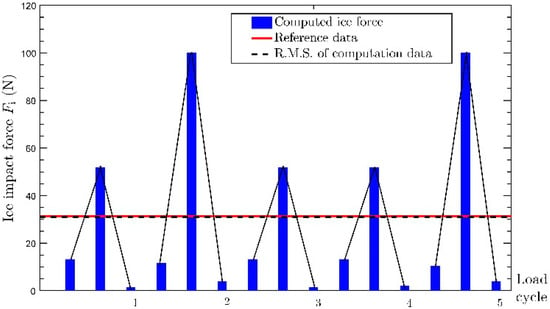
Figure 17.
A fraction of ice impact load extracted from Case 1.1.
The ice breaking lengths are calculated and compared with the reference one from empirical Equations (2) and (3), as shown in Table 5. The computed breaking length is larger than the , and both increase with increasing ship speed. Compared to the ice breaking patterns in Figure 13, the computed values of seem reasonable when studying the size of ice pieces in the outside layers from Figure 13. The small ice pieces in the middle are created by the ship body movement when the ice floes slide down along the hull surface, those ice floes deform several times thus cannot represent the ice breaking length.

Table 5.
Ice breaking length result summary and comparison (unit: m).
As the different collision locations are evaluated along the ship shoulder, it is interesting to investigate its influence on the discrepancy of the ice forces. Crushing forces in relation to collision locations at different speeds are presented in Figure 18. It clearly seen that the higher speed triggers higher contact forces and the closer to the ship stem, the bigger the force is. Usually, a shoulder collision is only evaluated at location (), but Figure 18 can be a good example to illustrate the effect of location on the deciding ice-shoulder impact force.
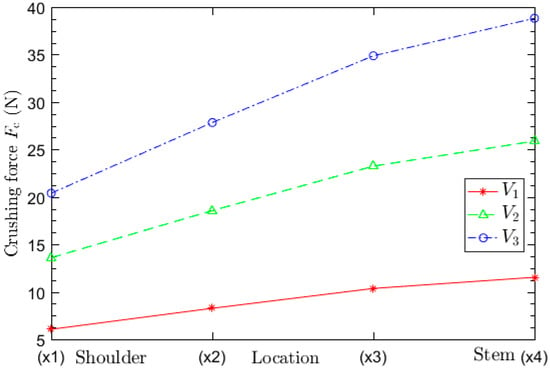
Figure 18.
Crushing force in relation to collision location at different speeds.
In order to understand the discrepancy in the predicted force and the model test results at the lower speeds, computed crushing and bending forces are plotted together with measured model test data in Figure 19. The maximum ice bending force and crushing force at () for both the stem and shoulder are selected to make a comparison. The red triangle represents the ice breaking force for the model test data. It can be seen from Figure 19, that the model test data, at the lowest speed, is approximately equivalent to the crushing force, while the second one is in between of crushing and bending force, while the third one, at the highest speed, matches the ice bending force. It can be observed that for low speeds, the ship model test data only indicates crushing not bending. The ice breaking force should be larger with a combination of two components from a statistical point of view. Ship speed also plays an important role in deciding the main failure mode. It can be concluded that the prediction model may be accurate when both crushing and bending occurs and the ice bending force is assumed to be the dominant component in the ice breaking modes.
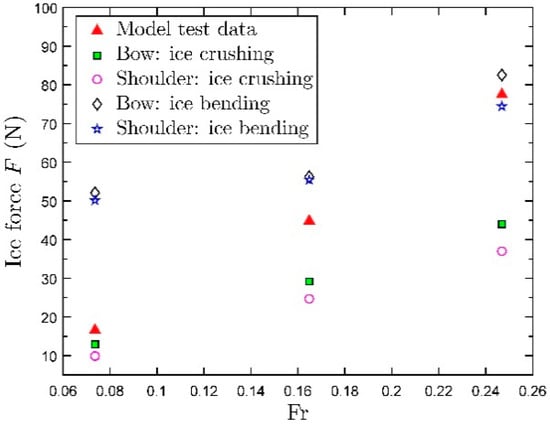
Figure 19.
Comparison among model test data and ice failure force components.
In the model test the ice breaking component is calculated in an indirect way using the ITTC guidelines. Considering the result discrepancy, the empirical method should only be used conditionally to compute ice impact force. It is recommended to compared results by ITTC guidelines and simulation, they together can give a good explanation.
5. Case Study
When designing a new ship that is supposed to operate in ice-covered waters it is important to identify the design ice force to assure structural performance. However, it is also crucial to identify the critical ice force as the ship structure needs to survive against extreme loading condition. It can clearly be seen that the critical force is the maximum ice bending breaking force and is significantly larger than the ice impact force. Only the ice critical force, , is considered in this Chapter. The simulation results show that ice bending breaking force is larger than ice crushing force, as seen in Figure 19. Thus, when calculating the ice critical force, the procedure for calculating maximum ice breaking force is used, as shown in Figure 4. A case study is conducted with a full-scale ship to investigate the influence from different design parameters. An IWW barge is chosen as the extreme ice pressure with regards to the ship that was previously evaluated by Zhang et al. [6] using the probabilistic method.
5.1. Barge Information
An IWW barge operating in Lake Mälaren is studied and the ship main particulars are seen in Table 6. The ice properties, e.g., crushing strength and flexural strength, of level ice used in the simulation are given in Table 7.

Table 6.
Main particulars of the barge.

Table 7.
Ice Properties.
5.2. Parameteric Study
Both the ship design parameters and the ice properties are assumed to have significant effect on the impact load. Therefore a parametric study is performed investigating the effect of variations of the rake angle, ship speed, and the ice thickness, see Table 8.

Table 8.
Parameters investigated in parametric studies.
The critical ice force with respect to ship speed and ice thickness are plotted in Figure 20 for both ship head-on and shoulder collision. It can be seen that the critical force varies with ship speed and ice thickness and the influence is significant. For example, for thinner ice thickness, the ice critical force hardly change with speed. The influence from the speed for thin ice, , can almost be neglected. When the ice thickness increases, the force increase becomes more and more significant. The figure can be used for guidance in ship operation. For example, assume the structure load capacity is , the ship speed can be when ice thickness is or be approximately when ice thickness is .
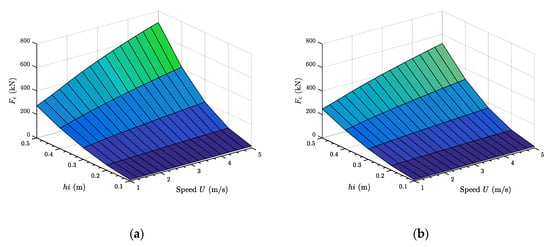
Figure 20.
Ice critical force ( ) in terms of ship speed and ice thickness for stem angle 25°. (a) Ship stem collision; (b) Ship shoulder collision.
The parametric study also investigates the influence of the ship stem angle, and the results are plotted in Figure 21. Usually, the stem angle for an ice-going ship is around . The figure shows that when the ice critical force takes the lowest value at 1 m/s. However, the critical force increases with ship speed. For a stem angle the ice critical force along the whole speed range is low. One explanation can be that the projection to the xy-plane of the contact area and vertical force becomes small based on the ice crushing model. This results in a small ice bending force. The suitable range of the stem angle should be smaller than , for instance, , which causes a larger force to bend the ice sheet. It is suggested that further studies may be conducted as to verify this hypothesis.
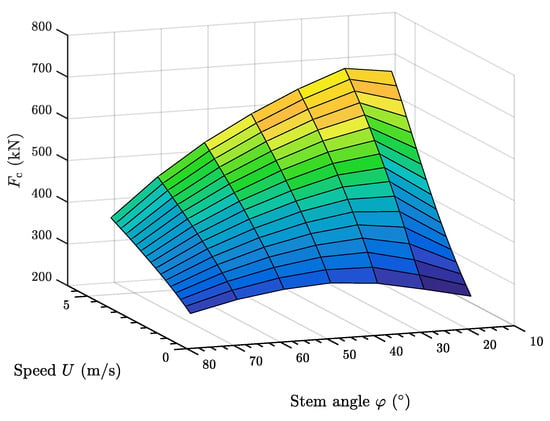
Figure 21.
Ship stem collision: ice bending failure force in terms of ship speed and stem angle with ice thickness of .
Ice breaking lengths in relation to ice thickness and ship speed are plotted in Figure 22. It can be clearly seen that the reference breaking length is smaller than the computed one, . However, the difference is decreasing with increasing ice thickness. It can also be deduced that the empirical value is very close to the computed one when ice thickness is approaching 0.5 m and it () exceed at lower speed. Figure 22 indicates that the Lindqvist [1] method has a limited validity range around ice thickness of half meter.
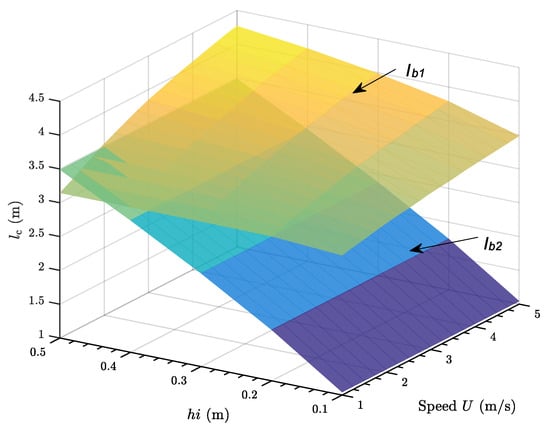
Figure 22.
Computed breaking length and reference breaking length for for bow collision scenario.
6. Discussion and Conclusions
A numerical model for predicting the ice impact force according to ice-hull collision mechanism is developed. The theoretical foundations of the model are explained in detail in this paper. For the realization of such complex ship-ice interaction model several assumptions and simplifications are made. Two ice failure modes, crushing and bending, are thoroughly evaluated. In addition, several different points of collision, i.e., ice ship impact, are considered. The proposed model is simpler than the traditional numerical simulations but still focuses on the essential phenomena and forces, thus, a computationally cost-effective and efficient prediction method is proposed.
6.1. Ice Crushing and Ice Bending
In this work, ice bending is assumed to be dominant over ice crushing. Nevertheless, the assumption does not work every time. Su and Riska [14] found irregularities in resistance values due to changes in the nature of icebreaking pattern: sometimes crushing dominates and sometimes bending. Some parts of the ice sheet are continuously crushed by the vertical parts of the ship hull, e.g., shoulder crushing, without bending failure, then the crushing forces becomes more severe. Croasdale et al. [25] presented a model to calculate the level ice action on wide conical structures. This model is adopted by the ISO Code, ISO/CD19906 [26]. Croasdale’s model shows that the contribution of the breaking load component accounts for 20%–30% of the total ice force. Devinder [27] found that ice crushing only occurred at 1% of the time during the observation of Molikpaq ship trial. Still, it caused some of the highest forces. Continuous brittle crushing takes place when an ice sheet moves against a structure at high speed. However, such crushing is mainly happening for relative thin ice. When ice sheet thickness increases, ice bending becomes dominant again. Devinder also found that for low indentation speed and low loading rate, a smooth variation in ice forces based on ice elastic and creep behavior results in ductile deformation [28]. The ejection phase or extrusion (ice sheet drifts away) gives rise to brittle ice failure and the ice force endures an abrupt decrease. Yet, the transition has not been clearly defined as it is ice and scale parameter depended. The energy force used in this model only considers brittle crushing which can cause result discrepancy at low speed. As a rule of thumb, the interaction can be assumed to be bending failure dominant. Another aspect can be the negligence of the different energy components and distributions during the interaction process [29], for instance friction energy.
To identify whether ice crushing or ice bending is dominant, ice crushing force can be plotted through together with the bending force. If crushing force is larger at a certain indentation displacement, then bending will not occur.
In numerical simulation, ice is usually regarded as an isotropic material. Still, ice is a non-isotropic, non-homogeneous and orthotropic material. The reasons behind irregularity and discrepancy between model test and simulation should always be kept in mind.
6.2. Ice Impact Load Prediction Model
The ice impact loads for the barge in the present case study was previously studied with the probabilistic method [6], with the predicted design loads or for ice thickness of depending on different reference dataset. From Figure 20, it can be seen that ice critical force varies from at same ice thickness. The model in this paper indicates that the predicted impact load of with a contact area of from empirical methods can be the more valid one. Nevertheless, the ice breaking force of stem collision is higher compared to the shoulder collision, while the contact area of stem collision is lower. This contradicts the conclusion that a smaller contact area results in a higher force according to the probabilistic method. It would be valuable to conduct further investigates on this. The ice breaking force predicted from the numerical model in this paper shows the same magnitude as in other studies, e.g., [12,30].
For the ice model test, ITTC guidelines are used to calculate the ice breaking force. Ice resistance is simplified as a composition of ship resistance in pre-sawn ice and ice-breaking resistance. Pre-sawn ice is level ice in which the approximate breaking pattern is cut prior to the model test. Thus, ice force from model test does not contain the ice breaking component. The guidance has barrier during application.
In the present study, several parameters are studied for ice bending failure. The ship speed and the ice thickness have a positive correlation. The ship speed is shown to have a great impact on the ice breaking in comparison to the other parameters considered. It is also worth mentioning that this parameter is sometimes ignored in empirical equations. The proposed model could assist in quantifying possible differences and improve those equations. For a certain stem angle, the ice loads increase with increasing ship speed. However, the influence from variations in stem angle is not perfectly clear.
The numerical model is sensitive to parameters such as number of wedges, number of collision event. As speed affects ice breaking length, contact case may change. Moreover, when a ship runs slowly, other ice forces, such as sliding or splitting, may become significant. Those possibilities can violate the assumption that bending is dominant and cause discrepancy. Moreover, it is also possible that continuous brittle crushing is happening at such speed. In general, the method works well once suitable parameters are selected. Thus, it facilitates the computation of ice forces for ship design purpose.
The current model indicates that the Lindqvist [1] method is limited regarding the prediction of the ice breaking length. Lindqvist does not work very well for ice thickness below 0.5 m. For IWW light ice conditions, it could be better to find another method.
6.3. Summary
The numerical model introduced herein can be applied in many scenarios. In this paper, the focus is to compute ice impact load based on ice crushing and bending failures. As ice breaking usually occurs at ship bow area, it is taken into consideration by selecting several discretized representative points along the hull. The numerical simulation results are comparable to the model test data, which demonstrates that the present mathematical model is rational. The ice impact force calculated with this method can be used to analyze ship structural response, especially in the bow area. The critical force is needed when accessing ship performance under extreme condition. Both global force and local force are calculated from this method. The numerical model can also be adopted to a more global application. More elements can be added to in order to describe the whole waterplane. More geometry contact cases can be analyzed as well for other ice-ship collision circumstances.
A parameter sensitivity analysis of this numerical model is valuable and worth considering in the future work. Moreover, the current model uses computation steps rather than real time steps. Further work can be done to update the time step and generate real time history ice force. Such work would be valuable to study the dynamic structural behaviors. In addition, the proposed model framework can be further developed by including additional ship and ice parameters.
Author Contributions
Conceptualization, M.Z., K.G., and M.B.; methodology, M.Z.; validation, M.Z. and L.Z.; formal analysis, M.Z.; writing—original draft preparation, M.Z.; writing—review and editing, K.G., M.B., and L.Z.; supervision, K.G. and L.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Sjöfartsverket (Swedish Transport Administration): Dnr 16-00778 and Trafikverket (Swedish Transport Administration): TRV 2017/64978. The work is also supported under Joint China-Sweden Mobility Project financed by Swedish Foundation for International Cooperation in Research and Higher Education with grant number Dnr: CH2018-7827 and National Natural Science Foundation of China with grant number 51911530156.
Acknowledgments
We thank SLL, Aker Arctic and SALTECH Consultants AB for their help.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lindqvist, G. A straightforward method for calculation of ice resistance of ships. In Proceedings of the 10th Int Port and Ocean Engineering under Arctic Conditions Conference, Luleå, Sweden, 12–16 June 1989. [Google Scholar]
- Keinonen, A.J.; Browne, R.P.R.; Reynolds, A. Ice breaker Characteristics Synthesis; TP 12812 E; Transportation Development Centre: Calgary, AL, Canada, 1996. [Google Scholar]
- Riska, K.; Patey, M.; Kishi, S.; Kamesaki, K. Influence of ice conditions on ship transit times in ice. In Proceedings of the Int Port and Ocean Engineering under Arctic Conditions Conf, Ottawa, ON, Canada, 12–17 August 2001; Volume 2, pp. 729–745. [Google Scholar]
- Rahman, M.S.; Taylor, R.S.; Kennedy, A.; Ré, A.S.; Veitch, B. Probabilistic Analysis of Local Ice Loads on a Lifeboat Measured in Full-Scale Field Trials. J. Offshore Mech. Arct. 2015, 137, 041501. [Google Scholar] [CrossRef]
- Taylor, R.S.; Jordaan, I.J.; Li, C.; Sudom, D. Local Design Pressures for Structures in Ice: Analysis of Full-Scale Data. J. Offshore Mech. Arct. 2010, 132, 031502. [Google Scholar] [CrossRef]
- Zhang, M.; Cheemakurthy, H.; Ehlers, S.; von Bock und Polach, F.; Garme, K.; Burman, M. Ice Pressure Prediction Based on the Probabilistic Method for Ice-Going Vessels in Inland Waterways. J. Offshore Mech. Arct. 2019, 41, 021501. [Google Scholar] [CrossRef]
- Daley, C. Energy based ice collision forces. In Proceedings of the 15th International Conference on Port and Ocean Engineering under Arctic Conditions, Helsinki, Finland, 24–29 May 1999. [Google Scholar]
- Kerr, A. The Bearing Capacity of Floating Ice Plates Subjected to Static or Quasi-Static Loads. J. Glaciol. 1976, 17, 76. [Google Scholar]
- Lubbad, R.; Løset, S. A numerical model for real-time simulation of ship–ice interaction. Cold Reg. Sci. Technol. 2011, 65, 111–127. [Google Scholar] [CrossRef]
- Valanto, P. The resistance of ships in level ice. SNAME Trans. 2001, 109, 53–83. [Google Scholar]
- Enkvist, E.; Varsta, P.; Riska, K. The Ship-Ice Interaction. In Proceedings of the International Conference on Port and Ocean Engineering under Arctic Conditions, Trondheim, Norway, 13–18 August 1979. [Google Scholar]
- Lu, W.; Lubbad, R.; Løset, S. In-plane fracture of an ice floe: A theoretical study on the splitting failure mode. Cold Reg. Sci. Technol. 2015, 110, 77–101. [Google Scholar] [CrossRef]
- Kerr, A.D. The Bearing Capacity of Floating Ice Plates Subjected to Static or Quasistatic Loads, a Critical Survey; Research Report; Cold Regions Research and Engineering Laboratory: Hanover, NH, USA, 1975; Volume 333. [Google Scholar]
- Su, B.; Riska, K.; Moan, T. A numerical method for the prediction of ship performance in level ice. Cold Reg. Sci. Technol. 2010, 60, 177–188. [Google Scholar] [CrossRef]
- Popov, Y.; Faddeyev, O.; Kheisin, D.; Yalovlev, A. Strength of Ships Sailing in Ice; Sudostroenie Publishing House: Leningrad, The Netherlands, 1967. [Google Scholar]
- Trafi. Finnish-Swedish Ice Class Rules 2010. In Ice Class Regulations 2010; Report No. TRAFI 31298; Finnish Transport Safety Agency: Espoo, Finland, 2010. [Google Scholar]
- Daley, C.; Liu, J. Assessment of Ship Ice Loads in Pack Ice; ICETECH: Anchorage, AK, USA, 2010. [Google Scholar]
- Croasdale, K.R. Ice Forces on fixed, rigid structures. In CRREL Special Report 80–26, Working Group on Ice Forces on Structures. A State-of-the-art Report; U.S. Army: Hanover, Germany, 1980. [Google Scholar]
- Kerr, A.D.; Palmer, W.T. The Deformations and Stresses in Floating Ice Plates. Acta Mech. 1972, 15, 57–72. [Google Scholar] [CrossRef]
- Kerr, A.D.; Kwak, S.S. The semi-infinite plate on a Winkler base, free along the edge, and subjected to a vertical force. Arch. Appl. Mech. 1993, 63, 210–218. [Google Scholar]
- Nevel, D.E. The Theory of a Narrow Infinite Wedge on an Elastic Foundation. Trans. Eng. Inst. Can. 1958, 2, 132–140. [Google Scholar]
- Nevel, D.E. The narrow free infinite wedge on elastic foundation. CRREL Res. Rep. 1961, 79, 24. [Google Scholar]
- Aker Arctic Technology Inc. Ice Model Test with a Passenger Ferry for SSPA Sweden; AARC Report A-555; Aker Arctic Technology Inc.: Helsinki, Finland, 16 June 2017. [Google Scholar]
- ITTC. General Guidance and Introduction to Ice Model Testing; Technical Report; International Towing Tank Committee: Wuxi, China, September 2017. [Google Scholar]
- Croasdale, K.R.; Cammaert, A.B.; Metge, M. A method for the calculation of sheet ice loads on sloping structures. IAHR 94. In Proceedings of the 12th International Symposium on Ice, Trondheim, Norway, 23–26 August 1994; The Norwegian Institute of Technology: Trondheim, Norwegian, 1994; Volume 2, pp. 874–885. [Google Scholar]
- ISO/CD 19906. Petroleum and Natural Gas Industries—Arctic Offshore Structures; ISOTC 67/SC 7/WG 8 International Standard; International Standardization Organization: Geneva, Switzerland, 2010. [Google Scholar]
- Sodhi, D.S.; Takeuchi, T.; Nakazawa, N.; Akagawa, S.; Saeki, H. Medium-scale indentation tests on sea ice at various speeds. Cold Reg. Sci. Technol. 1998, 28, 161–182. [Google Scholar] [CrossRef]
- Sodhi, D.S. Crushing failure during ice–structure interaction. Eng. Fract. Mech. 2001, 68, 1889–1921. [Google Scholar] [CrossRef]
- Blanchet, D.; Kivisild, H.R.; Grinstead, J. Equations for local ice energy dissipations during ship ramming. Cold Reg. Sci. Technol. 1990, 18, 101–115. [Google Scholar] [CrossRef]
- Liu, J.; Lau, M.; Williams, F.M. Mathematical Modeling of Ice-Hull Interaction for Ship Maneuvering in Ice Simulations. ICE Tech. 2006, 845, 1–8. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).