1. Introduction
Projects ending later and costing more than planned are widespread phenomena in the construction industry [
1,
2]. Numerous causes were identified in the construction management literature [
3,
4,
5]. Among them, one cause that is persistently identified in late projects is poor planning and project control practices [
6].
Paradoxically, extensive research focused for quite some time on the development of enhanced project planning tools, such as the project evaluation and review technique (PERT) [
7], stochastic network analysis (SNA) [
8], and artificial intelligence and statistical learning techniques [
9]. Additionally, in recent years, project monitoring and control techniques also gained more research attention, including critical chain management [
10], earned value management [
11], and schedule risk analysis [
12].
However, most of the advanced techniques above were not successfully adopted by construction management practitioners [
13]. Currently, classical deterministic scheduling techniques such as the Gantt chart [
14] and the critical path method (CPM) [
15] still occupy a prominent position in the daily practice of construction management [
16]. Indeed, deterministic techniques have some important advantages. They are easier to learn, and their outputs are easier to understand and communicate. The amount of input information they require is generally much lower than other advanced techniques. Additionally, the calculations they involve are also significantly less computer-intensive and do not generally require advanced training to implement them.
However, deterministic scheduling techniques also suffer from serious limitations [
16]. In a recent study, Ballesteros-Pérez et al. [
17] broke down the core assumptions of some classical scheduling techniques and exemplified why they consistently underestimate the project duration even when accurate input information is available. Their findings were not new, but they emphasized that deterministic techniques’ major source of inaccuracy stems from neglecting and/or not properly handling activity duration variability. Duration variability is defined here as the difference between the actual (final) duration and the planned (initial) duration of a project activity.
Hence, the purpose of this paper is to propose some mathematical expressions that approximate the average project duration and the project duration standard deviation when its activities have some variability (virtually all real-life projects). Our estimates are compared against the analogous PERT project duration estimates. It is shown how, at the expense of minimal additional calculation and from the very same input information, our estimates largely outperform the PERT estimates. This allows bridging the accuracy gap that separates deterministic techniques from more complex techniques.
The paper is structured as follows:
Section 2 Background describes the activity duration variability and the merge event bias, which are the major source and consequence, respectively, of inaccuracy in all deterministic techniques. In
Section 3 Research methods, the mathematical expressions proposed are presented and all their subcomponents are justified.
Section 4 Application example describes how all the calculations can be easily implemented step by step.
Section 5 Analysis and
Section 6 Results describe how the two expressions were tested with a diverse and representative artificial network dataset.
Section 7 Discussions comments on how the expressions can be used in real contexts to improve the reliability of project management tasks in general, and the accuracy of some complementary scheduling techniques in particular. Then,
Section 8 Conclusions summarizes the paper’s contributions, highlighting the research limitations and proposing future avenues of research.
2. Background
The literature on project duration estimation is vast and cannot be representatively outlined here. Some of the most relevant scheduling techniques were presented in Introduction, and more are commented on later in the Discussions. This section considers in detail why activity duration variability is the major source of inaccuracy of all deterministic scheduling techniques and what can be done to (partially) overcome that problem.
Activities in all projects, construction projects included, suffer from some degree of duration variability [
18,
19]. Projects are unique, which means that, even when contractors have extensive experience, subsequent projects may differ regarding clients, contract type, location, regulations, labor, equipment, subcontractors, stakeholders, and weather [
20]. All these (and many other) factors constitute potential causes of uncertainty and, eventually, of activity duration variability [
21].
Deterministic scheduling techniques assume that activity durations are constant. In an attempt to draw up a representative execution plan, most project schedulers use the
average activity durations, expecting that such an approach will produce the
most likely project duration [
13]. However, such a schedule is often not reliable.
When two or more activities are performed in parallel, the average time it takes to complete all of them is not the maximum of the activity averages, but generally more. Indeed, this situation is identical to the problem of calculating the maximum of two or more random variables. Imagine two activities whose duration is modeled by a normal distribution. Half of the time, each activity ends early, and, half of the time, it ends late. However, when performing both activities in parallel, only in one out of four occasions will both activities finish early. In the other three occasions, either one of the activities will finish late, or both will be late. Hence, the maximum time of completion of these two activities will be higher than the average of the activity durations. This phenomenon is known as the merge event bias, and it is the reason why deterministic scheduling techniques generally underestimate the actual project duration.
The merge event bias is nothing but a manifestation of Jensen’s inequality [
22]. More precisely, the maximum of several random variables (each representing the activity durations) is a convex function. This means that,
on average, the maximum of several randomly generated activity durations will always be higher than, or at least equal to, the averages of those activity durations. Hence, the problem of obtaining the average project duration (also known as project makespan) is the same as obtaining the maximum of several random variables, and this was intensively studied in the field of stochastic network analysis (SNA).
In SNA, activity durations are modeled with different statistical distributions. One randomly generated duration value is generated for each activity in each simulation run, and then the project duration is computed by following the activities precedence network. This operation is repeated thousands of times until the sample of project durations is deemed representative. Then, the statistical project duration distribution can be represented, and its first two moments (the project duration average and the standard deviation) can be easily calculated.
However, as hinted above, there are
no analytical solutions to find (accurate) values of the average project duration in project network topologies that involve multiple parallel critical and subcritical paths. The only technique that provides reliable results when activities have variable durations is the Monte Carlo simulation, which is one of the most common in SNA [
23,
24,
25].
The main reason why there is no analytical solution in a schedule network is because there are no statistical distributions that are, at the same time, sum-stable and max-stable. When activities are in series, their durations are added (convoluted) to calculate the path durations. When activities are in parallel, the maximum of several path durations (distributions) has to be calculated instead. If the activity duration distributions of a schedule were sum-stable and max-stable, a distribution of the same family would result after calculating the project duration irrespective of whether the schedule mixed activities in series and parallel. Also, the parameters from such a distribution could be anticipated from the original activity duration distributions. However, as noted above, there are no sum-stable and max-stable distributions. The normal distribution is sum-stable, but not max-stable. The lognormal is product-stable, but neither sum- nor max-stable. Hence, in the absence of a distribution that can be used across a whole schedule involving activities in series and in parallel, approximate approaches must be used.
Precisely with the intention of allowing project managers to make probabilistic inferences about the likely project duration, the project evaluation and review technique (PERT) was proposed over 60 years ago [
7]. By means of three-point activity duration estimates (the well-known optimistic, most likely, and pessimistic durations of an activity), the average project duration is assimilated to the average duration of the (longest) critical path. Then, the project duration standard deviation is also assimilated to the duration standard deviation of that same longest critical path. The problem, however, is that PERT underestimates the average project duration and overestimates the project duration standard deviation [
26,
27]. Indeed, the PERT average project duration coincides with the one from a deterministic schedule. The project duration standard deviation, on the other hand, assumes that only a single critical path exists.
However, despite the limitations of PERT, it is a hugely popular technique in the field of project management. From the research standpoint, practically all its assumptions and calculation procedures were broken down and analyzed in pursuit of improvements from every possible perspective, for example, the activity duration distributions, the resulting project duration distribution, the accuracy of the three-point estimates, the inclusion of activity time–cost trade-offs, the inclusion of extra scheduling operations like minima of multiple paths, and activity self-loops, to cite just a few (see Ballesteros-Pérez [
13] for an extensive review).
Of particular interest, however, may be the work of Pritsker [
28]. He developed the graphical evaluation and review technique (GERT) in 1966. GERT attempted to overcome many of PERT’s fundamental problems, including the merge event bias. However, due to its mathematical complexity, its implementation was not possible without resorting to Monte Carlo simulation. More recently, some of GERT’s principles plus other convenient features were incorporated into M-PERT [
13]. This technique was proposed by Ballesteros-Pérez et al. and also allows manual calculation of the project duration average and standard deviation. Specifically, M-PERT recursively merges all project activities until there is one activity left which represents the project duration variability. For medium and big project networks, however, this technique can be come time consuming.
Hence, there is one common trait among almost all these PERT extensions. Those which (partially) overcome the merge event bias problem do so at the expense of (substantially) increasing the technique complexity and/or the time it takes to calculate the project duration average and standard deviation. That is why our aim here is to resort to a number of operations very similar to the original PERT technique, but which significantly improve its accuracy by allowing multiple critical and subcritical paths.
3. Materials and Methods
We assume that a project p corresponds to a network of activities connected by technological and/or resource precedence relationships. Any activity i in the schedule can have some duration variability which is modeled by a statistical distribution with mean μi and standard deviation σi. This does not preclude, however, the use of other non-location-scale or asymmetrical activity duration distributions later.
As discussed earlier, in stochastic network analysis (SNA), a representative sample of project durations are obtained by Monte Carlo simulation and eventually represented by a cumulative distribution function (CDF). Here, we are not interested in the analysis of the project duration CDF, but rather in proposing some mathematical expressions for estimating its first two moments. The first moment of the project duration distribution is the project duration mean (μp). The second moment is the project duration standard deviation (σp).
From now on, we generically refer to the distribution of all possible project durations as
real duration (
RD). This term is intentionally chosen in contrast with the
planned duration (
PD) which is generally associated with the (unique) project duration estimate coming from a deterministic schedule (a Gantt chart, for instance).
PD also coincides with the PERT estimate of the project duration average which, as described earlier, is prone to underestimations when activities have duration variability. Hence, we propose the following:
Finding approximated values of μp and σp is the aim of this research.
3.1. General Notation
In this subsection, we introduce the most relevant variables, subscripts, and sets.
Let be the set of all activities in the project schedule.
Let be the set of all critical activities in the project schedule, that is, those whose total slack is zero (noted later as si = 0).
Let be the set of all critical and subcritical activities in the project schedule (those whose slack , with τ being a cut-off slack value named slack admissibility threshold defined later).
From the definitions above, it is clear that K is always a subset of J, whereas J is always a subset of I, that is, .
Additionally, di, dk, and dj represent the duration of activities i (all), k (critical), or j (critical and subcritical), respectively. In deterministic schedules, they are assumed as static (constant) (generally, di = μi), even though they may actually have some variability σi.
si, sk, and sj represent the total slack (or floats) of an activity i (all), k (critical), or j (critical or subcritical) obtained from a deterministic schedule. The activity free slacks is not used. Furthermore, it is worth noting that, although PERT does not directly use the slack values in its calculations, they must be calculated anyway; otherwise, the critical activities cannot be identified.
Now, due to its practical interest, we need to take a closer look at the activity duration standard deviations. Like the activity duration means (
μi,
μk,
μj), the activity duration standard deviations (
σi,
σk,
σj) can be estimated in real contexts from the scheduler’s past experience, from the PERT three-point estimates, or even by analogy to similar projects. With the three-point estimates, for example, the values of the first two moments of each activity duration distribution (
μi and
σi) can be calculated with the following simple expressions:
where
Oi,
Li, and
Pi represent the optimistic (minimum), most likely (the mode), and pessimistic (maximum) duration of activity
i, respectively, to be elicited by the project scheduler. As can be seen, Equation (3) already includes a correction (the square root term) recently proposed by Herrerías-Velasco et al. [
29]. This extra term makes the
σi estimate more accurate and also unbiased.
Regarding the possibility of estimating
σi values by analogy, Ballesteros-Pérez et al. [
30] established that activity duration variability in construction projects is closely modeled by lognormal distributions with median zero and coefficients of variation (
CVi) of 0.10 (for activities with low variability), 0.20 (for medium variability), and 0.3 (for high variability). The coefficient of variation is the ratio of the activity duration standard deviation by the duration mean, that is,
CVi =
σi/
μi. However, Ballesteros-Pérez et al. [
30] measured the
log ratios of actual versus planned activity durations. If we want to calculate any activity
i’s duration in the first two moments in the natural scale (
μ’i and
σ’i), we must perform the following calculations (derived from the first two moments of a lognormal distribution):
where
CVi = 0.10, 0.20, and 0.30 for low, medium, and high activity duration variability, respectively. The coefficient 2.302 is added to change the base from 10 (the one used in Ballesteros-Pérez et al.’s [
30] study) to
e (the most common with lognormal distributions). The activity duration mean
μi is directly expressed in (natural) time units and can be calculated from the scheduler’s past experience or from Equation (2), for instance.
3.2. Expression for Estimating the Average Project Duration μp
As anticipated earlier, the calculation of μp involves screening out some initial activities and keeping only those activities which are either critical or subcritical. The explanations below illustrate the necessary calculations in the same exact order a practitioner should implement them.
We consider as critical or subcritical those activities whose total slack (
si) remains below a slack admissibility threshold (
τ), that is,
. The slack admissibility threshold
τ is calculated from the critical activities (
k), that is, those with
si = 0, with the following expression:
where
σK is an estimate of the critical path(s) duration standard deviation. It can be calculated with the following straightforward (but approximated) expression:
When there is a single critical path, the sum of all critical activity durations is equal to the (deterministic) duration of the whole project, that is, . In this case, and the value of σK is exact. Only in this case does σK coincide with the PERT estimate of the project duration standard deviation.
SP is the serial–parallel topological indicator, which can be calculated as follows:
where
m is the number of activities in the path with
more activities (not necessarily the longest in duration, that is, not necessarily the critical path);
ni is the total number of (initial) activities in the schedule.
The
SP measures how close a network is to a parallel network (
SP = 0 when all activities are in parallel) or a serial network (
SP = 1 when all activities are in series). Recent studies pointed out that most real-life project
SP values range from 0.3 to 0.7 [
31].
K0 is an empirical coefficient which represents the number of
σK multiples that define the overall cut-off value of
τ. Specifically, values of
K0 = 0 would only accept critical activities (no subcritical activities, that is, no activities with
si > 0). Conversely, values of
K0 > 3 (meaning three times
σK) would identify as subcritical activities with too big slacks. After some experimentation, it was found that values of
K0 within [
1,
2] generally lead to higher
R2 values when calculating
μp (Equation (9)) shown later). Consequently, most of the time, we just assume
K0 = 1.5.
The attentive reader would have noticed that the purpose of Equation (6) is just ruling out those activities with excessive slacks. This is simply because the paths to which those activities belong are more unlikely to extend the project duration and ultimately do not affect μp. Furthermore, the purpose of SP is to fine-tune the effectiveness of Equation (6) by considering the network macro-structure.
Therefore, once the value of
τ is known, it is possible to know which activities are critical and subcritical (the
J set). These are the activities whose total slack
si remains below the threshold defined by
τ. Only with those
j activities can the average project duration distribution (
μp) then be easily obtained with
For calculating Equation (9), we need the total number of critical + subcritical activities nj, the (deterministic) activity durations dj, the activity duration standard deviations σj, and the activity total slacks sj (to calculate S), and the deterministic project duration PD. This is the same input information that the PERT technique uses. Its components are outlined below.
K1 is another empirical coefficient whose recommended value is 1.12 when the activity duration distributions are symmetrical (for example, normal, uniform). If the activity duration distributions are asymmetrical (for example, lognormal, most triangular distributions), then we suggest taking a slightly higher value (K1 = 1.22). It must be borne in mind, however, that coefficients K0 and K1 are somehow in equilibrium with each other. If K0 in Equation (6) was higher (accept more activities as j), then K1 would have to be smaller (to account for a potentially lower impact of those j activities on μp), and vice versa. After some experimentation, we found the values proposed here for both coefficients seem to work well in almost all cases.
Np represents an estimate of the equivalent number of parallel critical + subcritical paths (assuming they all spanned from the project start to the project end). We calculate it as follows:
It is worth noting that, although the numerator and denominator of Np could have been integrated and simplified within Equation (9), they are presented separately for a reason; Np shows a high correlation on its own with μp, despite it not being linear. Future studies may want to improve our equations by revising, for example, how Np is mathematically included in Equation (9).
corresponds to the sum of all critical + subcritical activity duration standard deviations. We present it separately because, in cases where we were using coefficients of variation (CVj), we could easily replace this term with .
LN(·) corresponds to the natural (Euler’s) logarithm.
S is the slack tightness coefficient, whose values always remain in the range
; it is calculated as
S represents the average (total) slack per activity. When S = 1, all paths have to be critical (there is not a single activity with a slack ). When S = 0 (an extreme which is not mathematically possible), all subcritical paths would (theoretically) not be causing an impact on μp (impossible project duration extension beyond PD). Hence, like SP in Equation (6), the variable S allows fine-tuning the representativeness of Np by considering how loose the subcritical activities are.
With all these terms, Equation (9) for calculating μp was fully defined and can be easily implemented.
3.3. Justification of the Expression for Estimating μp
Equation (9) encompasses several terms, each in charge of one task. Let us review them in reverse order.
The maximum of n independent and identically distributed (iid) normal random variables has no analytical expression, but it is upper bounded by . This is important as, in our context, , the random variables represent the path durations (which converge to normal distributions as there are more activities in series by the Central Limit theorem), and their maximum coincides with the average project duration (μp).
This upper bound, however, largely overestimates μp for small values of n (for instance, when n < 50, the deviations are still above 20%). Most real projects have far fewer than 50 critical and subcritical parallel paths. That is why, from the upper bound , we kept the LN(n) term but reformulated it as K1·LN(S·Np). More precisely, the contribution of S was discussed in the paper, whereas K1 was adjusted to maximize the fit for Np < 5 paths (which approximately corresponds to projects with a serial–parallel indicator SP > 0.2, that is, most real projects as justified earlier). Consequently, in cases when Np > 5, Equation (9) slowly (but progressively) loses accuracy.
Next, the term
in Equation (9) represents the average activity duration coefficient of variation, that is, the average
CVj. In particular, this term is obtained from a weighted average of all activity coefficients of variation (
CVj) using the deterministic activity durations (
dj) as weights.
The ratio above is eventually multiplied by PD in Equation (9) which converts it into a proper standard deviation (in time units). The raison d’etre of this term is that, following the previous analogy, the maximum of n iid normally distributed random variables is always proportional to the duration standard deviation of the parallel paths to which those activities belong. This justifies why we need to include a term that represents the average activity duration standard deviation, or, in this case, the average activity coefficient of variation.
There is just one term left to justify from Equation (9); this is . This term provides an estimate of the average number of activities per critical and subcritical path. When n iid activities are in series, then . However, since we are working with the coefficient of variation here instead of variances, it means we need to divide the latter expression by the average activity duration, that is, . In this expression, CVj represents the term explained earlier. Hence, represents the reduction of CVj as more activities are located in the same path. In our case, the average number of critical and subcritical activities per path can be approximated by , then , exactly as in Equation (9).
3.4. Expression for Estimating the Project Duration Standard Deviation σp
Along with
μp, calculating an approximation of
σp allows a practitioner to make probabilistic inferences about how likely it is that a project will finish by different dates. Our expression for estimating
σp is
Most variables in Equation (12) are already known.
σK represents an estimate of the project duration standard deviation coming from the critical activities, as in Equation (7). Indeed,
σJ is quite similar to
σK. The only difference is that
σJ is calculated with all critical and subcritical activity durations, not just the critical ones. Hence,
K2 is another empirical coefficient whose value is suggested to be K2 = −0.22 when activity duration variability is predominantly coming from a symmetrical distribution (for example, normal distribution), and K2 = 0.07 when the activity duration variability is modeled with asymmetrical distributions (for example, lognormal).
3.5. Justification of the Expression for Estimating σp
Equation (12) takes an average path duration variance from σJ and σK. Then, it applies a correction factor that takes into account the reduction/increase (with K2 and S) as a function of the estimated total number of existing critical + subcritical paths (with Np).
As described earlier, in the PERT technique, the project duration standard deviation corresponds to the square root of the sum of all critical activity duration variances, that is, . This is exactly like our σK variable from Equation (7), but always assuming the existence of a single critical path (). However, as real projects may have more than one critical or subcritical path, this would significantly bias the σp estimate. In Equation (12), by averaging the variances of σK and σJ, it is more likely that our estimate of the actual project duration standard deviation will improve because the magnitude of σJ, in most cases, is lower than σK.
Finally, the term in Equation (12), constitutes a simplified linear regression of the σp reduction, as there are more paths in parallel. In this term, Np takes care of counting the number of those paths, and S takes care of reducing their importance as a function of how large their average slack is. K2 again just centers the regression expression to maximize accuracy for cases when Np < 5. As expected then, the estimate of σp keeps losing accuracy as Np grows beyond five.
3.6. A Final Note on Calculations with Non-Symmetrical Activity Duration Distributions
With the exception of the different values for coefficients K1 and K2, we made no distinction between how the expressions of μp and σp work when activity duration distributions are asymmetrical. In those cases, the scheduler must ensure that the deterministic activity durations (di) always correspond to their activity duration average. Indeed, this is also a requirement for symmetrical distributions as well; however, in those cases, choosing the average durations is the default option (as the median, mode, and mean coincide in all common symmetrical distributions). Hence, in the case of symmetrical activity duration distributions, di = μi always. However, in the case of asymmetrical distributions, then di = μ′i (as in Equation (4) for lognormal distributions, for instance). Only then will it be possible to calculate si, σi, and PD properly. If not done this way, the estimates of μp and σp may not be representative.
4. Application Example
In this section, we develop a manual example with a small project schedule. The purpose is to illustrate how μp and σp could be easily calculated by practitioners. All necessary auxiliary calculations and intermediate steps are also included. The results of the μp and σp are eventually compared with the PERT estimates and the (more accurate) estimates obtained by Monte Carlo simulation.
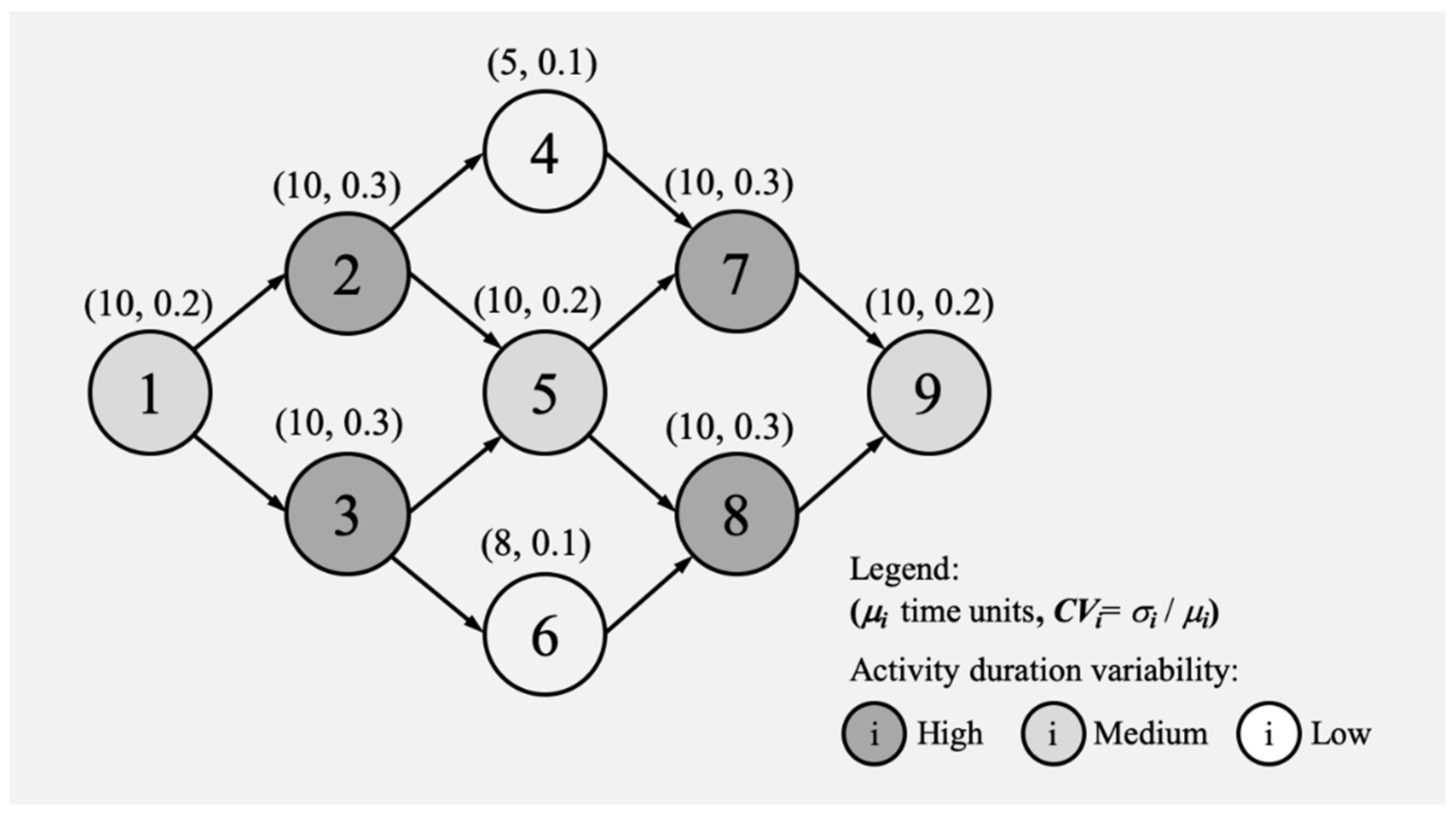
Let us refer to the nine-activity schedule network represented in
Figure 1. This project consists of activities with varied duration variabilities (represented by different gray tones).
Initially, we assume the activity duration variability is normally distributed. This way, the deterministic activity durations are
di =
μi, and the activity duration standard deviations are
σi =
μi·CVi. Both sets of values are represented for all activities in the leftmost part of
Table 1. From them, calculating the activity slacks is straightforward (indeed, all are equal to zero, apart from the slacks of activities 4 and 6, which are
s4 =
d5 −
d4 and
s6 =
d6 −
d5, respectively).
In this case, the deterministic project duration PD coincides with the sum of d1 + d2, d3 + d5 + d7, or d8 + d9 = 50 days (or time units).
From the initial set of all nine activities (i), we know that the critical activities (k) are those with si = 0, that is, K = {1, 2, 3, 5, 7, 8, 9} (all i other than activities 4 and 6).
The second step involves calculating the approximated critical path duration standard deviation
σK with Equation (7).
The longest chain of activities is five activities long; thus,
m = 5 and, since
ni = 9 activities (all initial activities), the value of the serial–parallel indicator with Equation (8) is
As
σK and
SP are known, we can calculate the slack admissibility threshold
τ with Equation (6). By assuming
K0 = 1.5, then
The only non-critical activity whose total slack is lower than 4.39 is activity 6 (s6 = 2 days). Activity 4 with a slack s4 = 5 > τ = 4.39 is not considered any further. Hence, the set of critical + subcritical activities is J = {1, 2, 3, 5, 6, 7, 8, 9}, that is, all but activity 4. The cardinality of J (the number of elements in the set) is then nj = 8.
Before calculating μp, it is necessary to calculate the value of a few more auxiliary variables.
nj = 8 act.; Σdj =7 × 10 + 8 = 78 days; Σσj =3 × 2 + 4 × 3 + 0.8 = 18.8 days; Σsj =7 × 0 + 2 = 2 days.
K1 = 1.12, as we are assuming symmetrical (normal) activity duration variability.
With all this information, we can now easily calculate
μp with Equation (9).
A much more accurate estimate of the average project duration with Monte Carlo simulation would be 53.4 days; that is, we miss it by 1.1 days. However, our estimate is substantially closer than the only estimate obtained (PD = 50 days, which is also the PERT estimate), and it was calculated manually.
Now, imagine we want to calculate the project duration standard deviation
σp. First, we need to calculate
σJ with Equation (13).
Then, assuming
K2 = −0.22 (symmetrical activity duration variability), we use Equation (12) to calculate
σp.
The project duration standard deviation obtained by simulation yields 4.88 days. We observe a deviation of just 0.36 days in this case. The only alternative estimate would have been the PERT one, but it does not offer a solution when there are multiple critical paths. If we assume that there is only a single critical path (as all critical paths intentionally had the same standard deviations in our example), then
which has a deviation of 0.59 days, that is, again worse than our
σp estimate.
Finally, the same calculations could have been replicated but assuming activity duration variability modeled with lognormal distributions. In this case, the values of
K1 and
K2 would change to 1.22 and 0.07, respectively. Additionally, before starting all calculations, the activity
di and
σi values would need to be calculated with Equations (4) and (5). The results of these variables for all activities are displayed in the rightmost part of
Table 1 under the
d′i and
σ′i columns. Then, the deterministic project duration (
PD = 58.7 days) and the activity slacks (
si) could have been calculated in the same way as normal activity duration variability. Indeed, the rest of the calculation process is exactly analogous to the previous example. The final results would have been as follows:
μp = 66.8 days (simulation estimate = 68.7 days) better than PD = 58.7 days.
σp = 18.3 days (simulation estimate = 18.4 days) better than PERT σK =18.9 days.
5. Analysis
In the previous section, we developed a manual example with the single purpose of illustrating how the expressions would be implemented by practitioners. In this section, a much wider and representative validation and performance analysis is conducted.
Our expressions depart from deterministic schedule information to estimate the first two moments of the project duration distribution (μp and σp). As in the manual example, we again employ Monte Carlo simulations to calculate the almost exact values of μp and σp. Then, the simulation estimates are compared with those obtained with our expressions. However, in order to draw valid conclusions, we use a wide benchmarking set of project schedules and model all their activities representatively.
5.1. Artificial Project Dataset
Network topology refers to the logical layout of a network (a project schedule). It defines the way different activities (often referred to as nodes) are placed and interconnected with each other. To test the quality of our
μp and
σp estimates, an artificial network dataset was used consisting of 4100 different networks (project schedules) with varied topologies. This dataset was developed by the Operations Research and Scheduling Research Group at Ghent University (Belgium). It can be downloaded from
http://www.projectmanagement.ugent.be/research/data (MT dataset in the “artificial project data” section (MT = measuring time)).
This set contains 4100 activity-on-node networks with 32 activities each. However, two activities out of the 32 are included simply to signpost the project start and end and are considered dummy activities (zero duration). The network dataset was generated with the RanGen2 algorithm. RanGen2 is a robust random network generator capable of generating a wide range of network topologies, which was validated in several studies [
32,
33]. Also, this very same network dataset was representatively used in other research studies on earned value management (for example, References [
31,
34,
35,
36]) and schedule risk analysis (for example, References [
11,
12,
37]).
In particular, the network dataset was generated under pre-set values of four topological indicators: the serial–parallel (
SP), the activity distribution (
AD), the length of arcs (
LA), and the topological float (
TF). These four topological indicators were initially proposed by Tavares et al. [
38] and later refined by Vanhoucke et al. [
33] and Vanhoucke [
11]. More precisely, the
SP indicator, introduced earlier, describes how close a network is to a serial or parallel network.
AD describes the distribution of activities in the different schedule paths.
LA measures the distance between two activities in the project network.
TF measures how dense a network is (the amount of topological slacks) at the topological level. The values of these indicators all range between 0% and 100%, and they are considered representative and accurate descriptors of a network topology. For the interested reader, the values of all these indicators for the 4100 networks can be found in Appendix B of the
Supplementary Materials (
μp and
σp regression results file).
5.2. Activity Duration Distribution
There were not many studies analyzing which statistical distribution is the most suitable to describe the distribution of the activity durations in a project schedule. Trietsch et al. [
39] suggested that both the activity duration distribution and the activity duration variability seemed to be fairly well approximated by lognormal distributions. Hence, we also predominantly use the lognormal distribution in our validation analysis. However, we also resorted to other distributions (e.g., normal, uniform) to explore whether our expressions worked equally well with them. The second column of
Table 2 includes the 12 different distribution combinations used.
To choose the parameter values of each dataset combination presented in
Table 2, a preliminary study was conducted of 101 real construction projects comprising over 6000 activities. The intention was to choose some distribution parameter values that emulated those of real projects. The 101 project schedules were retrieved from a real project dataset developed by Batselier and Vanhoucke [
40] and Vanhoucke et al. [
41]. These schedules contained both planned and actual (as-built) durations. From both sets of durations and from each project, activity
log duration values were taken and then their average and standard deviation calculated. Later, these two moments were used to generate activity duration distributions that seemed as realistic as possible in our simulations. In particular, they were used to generate the lognormally distributed (deterministic) activity duration values of the 30 non-dummy activities in the 4100 schedules. For the interested reader, the values of both moments (
μ and
σ) of the activity
log durations for the 101 real projects can be found in Appendix A of the
Supplementary Materials (Table S1). For further details about the real projects, the reader is referred to the individual project cards at OR-AS.be [
42].
5.3. Activity Duration Variability
Having set the (initial) activity durations, the activity duration variability was modeled with normal distributions and lognormal distributions predominantly (although a few simulations were also run using uniform distributions, see dataset XII in
Table 2). Normal distributions were used because they are the most common in academic settings and theoretical studies. Lognormal distributions were also used because, as explained earlier, this distribution seems to be the closest for modeling real construction project activities. Furthermore, building on the recent findings of Ballesteros-Pérez et al. [
30] for construction projects, we assumed that the median of our distributions would equal the initial (deterministic) activity durations defined in the previous subsection. This would ensure that half of the time the activities would end soon and half of the time late. This would avoid biasing the results toward predominantly early or late projects.
Next, activity duration variability was reproduced by randomly allocating a coefficient of variation between 0.10 (low variability) and 0.3 (high variability) to each activity as measured by Ballesteros-Pérez et al. [
30] (in log
10 scale). The median in the normal distribution is equal to the mean, which indicates that the stochastic activity duration values were generated with the following expression:
In the expression above, μi represents the default (deterministic) duration of each activity (defined in the previous subsection). Normal−1(·) represents the quantile function of the normal distribution, that is, the one in charge of generating the normally distributed stochastic values. CVi is the coefficient of variation randomly chosen for each activity in the range [0.1, 0.3]. It is worth noting that this range of CVi values in natural scale produces significantly less variability than in log scale (see Equation (15)). However, values of CVi > 0.3 are very likely to generate negative activity durations, which makes no sense and should be avoided.
In the case of lognormally distributed activity duration variability, the median does not coincide with the distribution mean unless it is transformed into a log scale first. That is why the following expression was adopted to generate thousands of (stochastic) activity duration values for each activity in the Monte Carlo simulations:
As before, the coefficient 2.302 is included in Equation (15) to change the base from 10 to e. Variables μi, Normal−1(·), and CVi are analogous to those in Equation (14).
5.4. Parameter Configuration Summary
In the proposed simulation framework, all activities were scheduled to start as soon as possible, and activity preemption was not allowed to avoid losing (simulation) control over the impact of activity duration variability on
μp or
σp. All activity precedence relationships were assumed to be finish–start. The latter choice, however, is not relevant, as the other three types of precedence (start–start, start–finish, and finish–finish) can be easily reformulated as a finish–start relationship (or the other way around) in any schedule (see Lu and Lam [
43] for a comprehensive treatment of precedence relationship transformations).
Hence, 13 different parametrizations of the same 4100-network dataset were finally used, with different activity duration distributions, and two activity duration variabilities per set. They are all summarized in
Table 2.
To summarize, the different simulation combinations differed in one or more of the following aspects:
By the distribution used to generate the initial (deterministic) activity duration values. Most of the time lognormal distributions were used (datasets I–VIII); sometimes, normal distributions (datasets IX–XI) were used, as well as a uniform (dataset XII), and even a constant distribution (dataset XIII, which assumed all activities lasted 10 days on average). Of particular interest are datasets V to VIII which approximately represent the maximum and minimum values found in the first two (log) moments of the 101 real projects.
By the number of activities in the schedule. In all cases other than dataset IV, the 30 non-dummy activities per network were used. However, a case with fewer activities was also considered to be sure that the network size (number of activities) did not affect the performance of our expressions.
By distribution (normal, lognormal, and uniform) and level of activity duration variability (
CVi). These are represented in the central and rightmost blocks of
Table 2. Some assumed
CVi = 0.1 always and some assumed
CVi = 0.3 always, whereas most assumed uniformly distributed
CVi values between a lower bound (
l = 0.1) and an upper bound (
u = 0.3).
Overall, the 13 dataset parametrizations seem to be representative of any possible real project. If our expressions for estimating μp and σp work well with these 13 datasets, then they must also work reasonably well in other contexts. For each of the 4100 projects in the 13 datasets, 10,000 simulations were run assuming normal activity duration variability and another 10,000 assuming lognormal duration variability. Results are discussed next.
6. Results
Table 3 and
Table 4 compare the actual values (obtained by simulation) with the estimated values (with our expressions) of
μp and
σp values in the form of ratios, that is,
μp/
PD and
σp/
σK. There are two reasons for this. Firstly, in this way, projects of different durations can be compared under the same scale. Secondly, we can also compare how much better our estimates perform compared to the PERT estimates. As described earlier,
PD is the deterministic project duration but also the PERT
μp estimate. The PERT project duration standard deviation estimate, on the other hand, cannot be produced with PERT when there is more than one critical path. That is why we assumed that the best possible PERT-like estimate would be
σK, although we ourselves proposed it for the first time in Equation (7).
Let us review all the information displayed in
Table 3 and
Table 4. The first column gives an indication of the dataset analyzed (by row). Each dataset contained 4100 projects and they were all analyzed under two different activity duration variabilities (central and rightmost blocks of
Table 3 and
Table 4). The first block (activity duration variability 1) mostly coincides with normally distributed duration variability except for dataset XII, which was uniformly distributed. The rightmost block (activity duration variability) always coincides with lognormally distributed activity duration variability. The bottom row in both tables displays the column averages for easier data interpretation.
Inside both the central and rightmost blocks, the same information is found. Pearson’s coefficient of correlation (
R) for
μp is in
Table 3 and that for
σp is in
Table 4, which shows the degree of linear correlation between the actual and estimated 4100
μp/
PD and
σp/
σK values, respectively, in each dataset. The coefficient of determination (
R2) quantifies the proportion of the (actual vs. estimated
μp/
PD and
σp/
σK) variability described by our empirical estimates.
R2 is, of course, the squared version of
R; however, as it offers complementary information, it was deemed useful to include both. Finally, the last two columns in the central and rightmost blocks display the mean absolute error (
MAE) and the mean squared error (
MSE), both in 10
−3 scale, calculated as follows:
where Equations (16) and (17) were calculated for the 13 datasets.
corresponds to the actual value of
μp (in
Table 3) or
σp (in
Table 4) for each project
p (all of them obtained by simulation).
corresponds to our estimated values of
μp (in
Table 3) or
σp (in
Table 4). In addition, all MAE and MSE values in
Table 3 and
Table 4 are also accompanied by an indication of the reduction achieved in MAE and MSE in percentage terms when using our
μp (in
Table 3) or
σp (in
Table 4) estimates, compared to using
PD or
σK, respectively. These values are included within parentheses.
Multiple readings can be made from
Table 3 and
Table 4. For the sake of clarity, we limit ourselves to the most essential. A quick inspection of the first columns of
Table 3 shows that values of
R > 0.90 are achieved for both duration variabilities.
R2 values are also very close to 90%. Overall, this means that there is a high degree of correlation between our estimates and the actual values. Also, in
Table 3, inspection of the MAE confirms that our expressions manage to reduce the variability from the PERT estimates by around two-thirds (63% and 69%). However, the reduction in the MSE is even higher (90% and 87%). This means that, when using our estimates, values can be expected to be around two-thirds closer to the actual values compared to the deterministic project duration estimates, but also that the amount of large deviations (measured by squared errors) would be significantly reduced.
Results in
Table 4 are still good, but clearly not as good as those in
Table 3. In this table, our project duration standard deviation estimates are not indisputably superior when compared to
σK (which, it must be borne in mind, are already better estimates than PERT’s). Still, in the case of normal variability (central block), we can observe
R > 0.80 and
R2 values again around two-thirds. The absolute errors are reduced by 40% on average and the squared errors by around 70%. As
σK is already better than the PERT estimate, we can expect our estimates to double (at the very least) PERT’s accuracy in absolute terms concerning its project duration standard deviation estimate. In squared terms, we could expect our estimates to improve PERT’s estimate by around 75% at least.
Results on the lognormal variability (rightmost block in
Table 4) also improve the
σK estimates, but not as much as hoped. Indeed, there are a couple of datasets (II and X) which worsen the
σK estimates (negative reduction values) in the MAE, MSE, or both. These datasets coincide with the configurations with lower activity duration variability (
CVi = 0.10). However, configurations with higher variability (datasets III and XIII, with
CVi = 0.3) do not report much better results compared to the case with average variability. Overall, this means that the expression for estimating
σp, although promising because of its decent correlation values, still needs some work. This is something we already disclosed when introducing it; however, this will probably come at the expense of complicating it numerically. This is an option for future research.
Table 3 and
Table 4 also contain two columns each reporting the values of coefficients
K1 and
K2. During the design stage, we experimented by letting these coefficients vary freely in order to minimize the MSE in every dataset. Results of these alternative scenarios can be found in Appendix D of the
Supplementary Materials (Tables S3 and S4). It can be seen, however, that the reduction from making coefficients
K1 and
K2 constant did not have a substantial impact on the expressions’ performance.
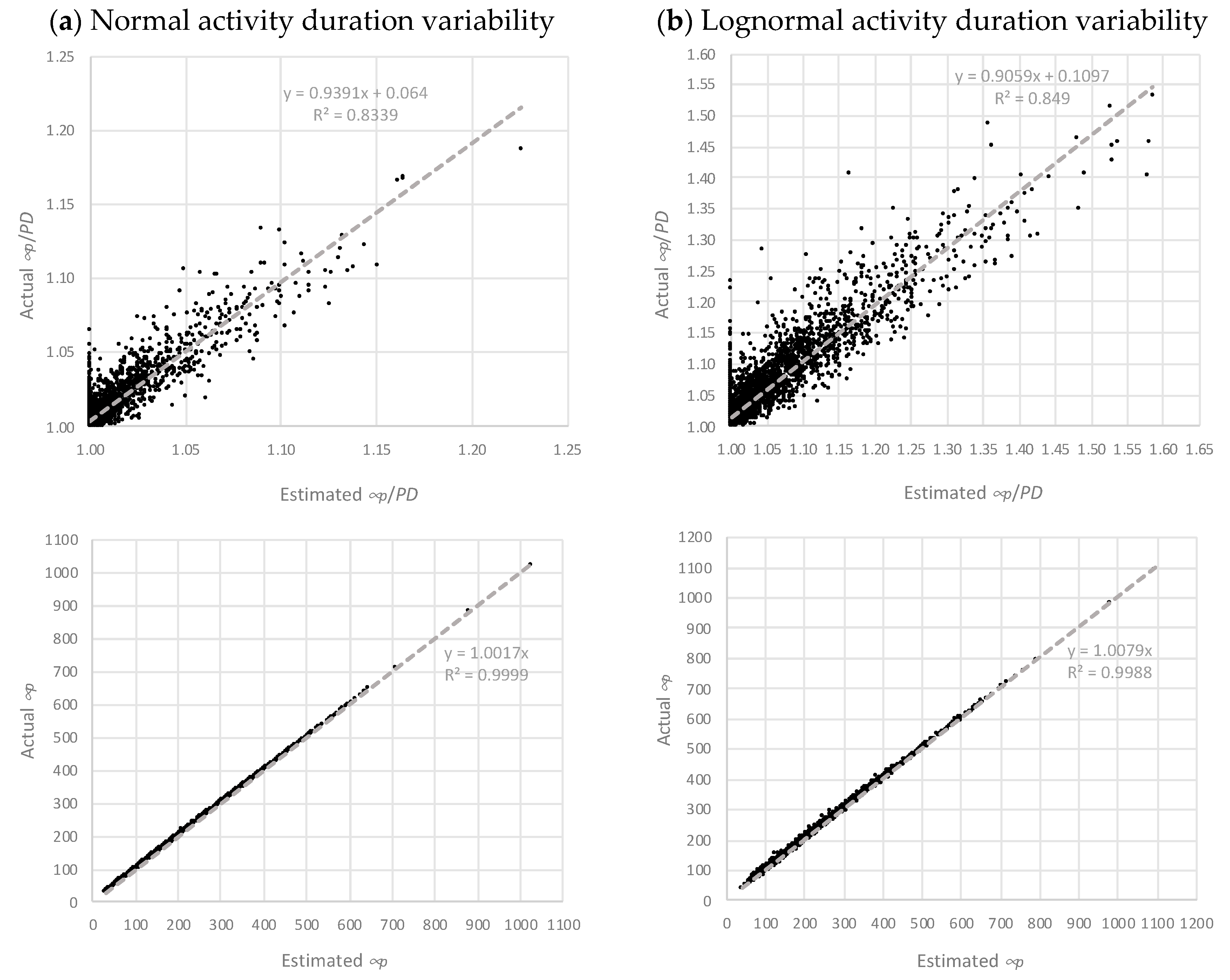
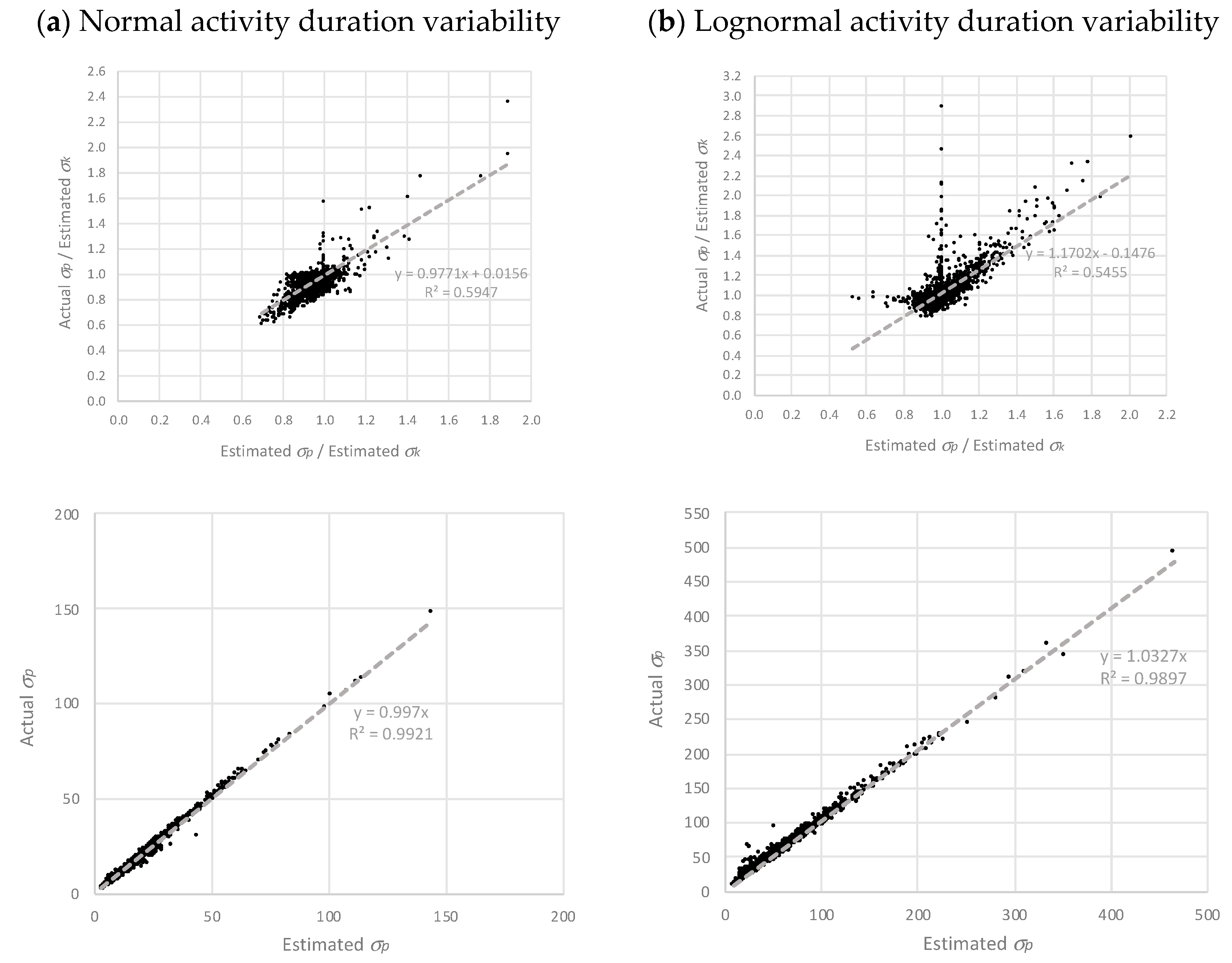
Finally, for those visual readers,
Figure 2 and
Figure 3 represent the regression graphs of the first dataset (dataset I). Dataset I can be considered the most representative of all datasets, as it approximately presents the average parameters and distribution configurations.
In
Figure 2 and
Figure 3, the top graphs represent the regression results in ratio scale. On observing the
μp estimates (in
Figure 2), it is evident that they are superior to the
σp estimates (in
Figure 3) as the datapoint clouds of the former follow a clearer bisector pattern. The other four graphs (the ones at the bottom of each figure), represent the correlations of estimated and actual
μp and
σp values in the natural scale instead of ratios (not homogenized by project duration). Arguably, the effect of the project size (duration) plays an important role as it gives the impression of obtaining higher correlations than in ratio scale. Still, these graphs show that the empirical expressions proposed in this paper work quite satisfactorily.
A final comment concerns the last two conditions of a representative regression analysis: independence of errors (normally distributed residuals) and constant variance of errors across observations (homoscedasticity). Regarding the first condition, we must be aware that our expressions are tested in a benchmark network dataset. The projects in this dataset do not follow a perfectly regular (random) pattern. For example, many of them (approximately one-third, but dependent on each dataset parameter configuration) did not produce a project duration extension at all (
μp =
PD). This means that, in those cases, there was a clearly dominant critical path, and our expressions anticipated it perfectly. However, although this aspect was intrinsically good (demonstrating that our expressions work as they are supposed to), it also artificially increased the residuals kurtosis (a higher than usual density of
μp/
PD = 1 and
σp/
σK =1 values). This artificially produced a slight departure from normality in the quantile–quantile (QQ) plots of some datasets (a sample of which is included in Appendix C of the
Supplementary Materials for dataset I). Still, all things considered, the QQ plots showed that the residual normality assumption was perfectly tenable.
Regarding the homoscedasticity check, the standardized estimates versus standardized residual graphs were also drawn for all datasets (Appendix C in the
Supplementary Materials shows some for dataset I). The gunshot pattern found in all of them evidenced an absence of datapoint directionality which eventually confirms that there was hardly any heteroscedasticity. Overall, all regression conditions were met, indicating that our estimates are unbiased and consistent.
7. Discussion
In this paper, we proposed several expressions that allow calculating the overall project duration average (
μp) and standard deviation (
σp) from purely deterministic schedule information. Calculations are quite straightforward and were exemplified step by step by means of a small project network in
Section 4. These calculations can be implemented either manually or in a simple spreadsheet. The only requirement is that the scheduler is familiar with the critical path algorithm. Basically, identifying the critical activities of a project involves the calculation of the activities’ earliest and latest start dates. The difference between earliest and latest start dates is equal to the activities’ total slacks (
si). Eventually, by comparing the size of
si against the slack admissibility threshold
τ from Equation (6), we can discriminate which activities are critical or subcritical. Hence, any basic spreadsheet that sequences activities departing from the activity durations and precedencies can implement the formulae proposed here. The only requirement is to follow the calculations in the same exact order used in the small project example. For those project schedulers who are not familiar with how to calculate the critical of bigger projects, it is always possible to resort to a commercial scheduling software (e.g., Microsoft Project, Oracle Primavera) to extract the values of the activity slacks (
si). Then, the rest of the calculations can be implemented in a spreadsheet, even manually.
However, beyond obtaining a more accurate estimate of the project duration average, there are other potentially interesting practical applications of the estimates proposed in this paper. Obviously, the first is the possibility of calculating a more accurate average project duration estimate (μp) from basic deterministic schedule information with hardly any extra effort. This improved estimate will allow project managers, for instance, to plan execution and resource allocation better with lower margins of error. Also, we anticipated that calculating both μp and σp values could allow us to make probabilistic inferences about any likely project duration (X). More precisely, we could say that . Then, assuming X follows a normal distribution, the value of z could be looked up in a standard normal distribution table and an (approximated) project completion date inferred.
There are other project management tools and techniques that can also benefit from more accurate
μp and
σp values. Earned value management (EVM), for example, is a deterministic project monitoring and control technique that also produces project duration forecasts, named
EAC(
t) (see Ballesteros-Pérez et al. [
31] for a recent and comprehensive comparison of the most relevant
EAC(
t) expressions). All possible parametrizations of
EAC(
t) include a deterministic estimate of the planned duration
PD which, after this research, could be replaced by
μp, enhancing their overall accuracy. Similarly, schedule risk analysis (SRA) is a proactive planning and monitoring technique which ranks project activities and determines their relative importance and exerts different levels of project control on them. SRA uses Monte Carlo simulations to calculate its metrics because, so far, there is no other way of calculating their parameters from deterministic schedule information. For example, the significance index (
SI) metric uses
E(
PD) (the expectation of the project duration) which is our
μp here. Also, the schedule sensitivity index (
SSI) and the criticality slack sensitivity index (CSS) both use
σp. There are still more variables to calculate (for example, the probability of an activity being critical), but the steps taken in this piece of research promise to avoid the use of computer-intensive simulations when calculating these metrics in the future.
On the other hand, a first apparent limitation of our performance measurement approach is that we predominantly tested our expressions with activity durations modeled by normal and lognormal distributions, and just testimonially with other distributions. The advanced reader may wonder whether the performance results from
Table 3 and
Table 4 might have differed significantly if other distributions were used. In this vein, Hajdu and Bokor [
44] concluded that the maximum project duration deviation when using alternative activity distributions was generally well below 10%. This finding resonated with observations from other earlier studies on PERT. For example, MacCrimmon and Ryavec [
45] showed in 1964 that, if triangular distributions for modeling activity durations were chosen instead of beta distributions, the probabilistic project duration would have produced almost identical results. All these results are also aligned with our
K1 coefficient values in Equation (9) for calculating
μp. It was observed that the regression coefficient values (
K1) that minimize the MSE were 1.12 and 1.22 for symmetrical and asymmetrical distributions, respectively. Hence, irrespective of the specific distribution modeling the activity duration variability, what matters is the order of magnitude of each activity’s first two moments (
μi and
σi). That is why they constitute the most relevant input information in our expressions.
Another practical limitation of our expressions would be how they can be used in real projects when no activity duration variability estimates (
σi) are available. In this regard, Ballesteros-Pérez et al. [
30] measured that the average activity duration variability in construction projects remains generally close to
CVi = 0.20. Hence, if only average activity duration values (
μi) are known, a project scheduler could assume that
σi =
CVi ·μi· = 0.20·
μi for all its activities in the case of symmetrical (for example, normal) duration variability. If they wanted to simulate more realistic (for example lognormal) asymmetrical activity variability, then they would need to resort to Equations (4) and (5) by replacing
CVi with 0.20 and proceeding as usual.
8. Conclusions
Deterministic scheduling techniques, such as the Gantt chart and the critical path method, are still the most common in practical settings these days. However, these techniques neglect activity duration variability which exacerbates a phenomenon known as the merge event bias. This bias is shared with the PERT duration estimates and is generally translated into average project durations being underestimated and standard deviations being overestimated. More recently, many advanced non-deterministic scheduling techniques were proposed. However, they are significantly more complex and highly computer-intensive, they require extensive precalibration information, and/or practitioners are not adequately trained to implement them. As a result, their adoption in practice is quite limited.
In this paper, we proposed a series of empirical expressions that allow construction project schedulers to come up with better estimates of the average project duration (μp) and the project duration standard deviation (σp). These estimates clearly outperform the analogous classical PERT estimates with the need for neither extra (deterministic) scheduling information nor a substantial additional calculation effort. For testing the superiority of our estimates, a wide and representative benchmark dataset containing 4100 networks (schedules) was employed. The activity durations and their variabilities were modeled with different statistical distributions and different parametrizations.
In this study, we commented on some apparent limitations of our estimates and how to overcome them. Finally, we also extensively discussed how the μp and σp estimates can be used in real construction contexts and/or in combination with other techniques (such as earned value management, and schedule risk analysis) to enhance accuracy or reduce calculation effort.
Future avenues of research are plentiful. For example, the current estimates work well with fewer than five critical and subcritical parallel paths (Np < 5). Future expressions may want to use higher-degree polynomials of the variable LN(Np) to improve the accuracy of our μp and σp estimates. Similarly, the accuracy of the σp estimate, when lognormal activity duration variability is assumed, could clearly be improved. Future research may want to consider extending the array of estimates that can be (deterministically) calculated. A fine example would be approximating the probability of an activity being critical (the criticality index) with deterministic calculations. This would greatly benefit the field of schedule risk analysis by allowing many metrics to be calculated with computer simulation.