1. Introduction
All products are transported between the production site and the consumer and are subject to vibration during transport, which shortens the product life and reduce the commodity value. Vibration during transport has large and small impacts from simple abrasion of the package to the collapse of the palletized unit-load owing to pallet destruction [
1]. Therefore, products in distribution should include protective packaging for adequate protection from vibration during transport [
2]. Both under-packaging and over-packaging are costly because the former increases the occurrence of damage incidents, and the latter increases the volume and weight of packages. Therefore, to reduce these costs, optimal packaging design should be developed to achieve product protection while minimizing the weight and size of the cushioning material [
3].
The first step in the development of product packaging is to simulate the physical stresses of vibration that occur during transport. However, both severe and moderate simulations are costly. The former guarantee the product’s integrity but leads to increased logistics expenses owing to excessive use of cushioning materials, and the latter cause economic losses to the enterprise due to product damage caused by insufficient protection of the product. Therefore, this simulation should be able to reproduce the vibrations produced by the vehicle accurately.
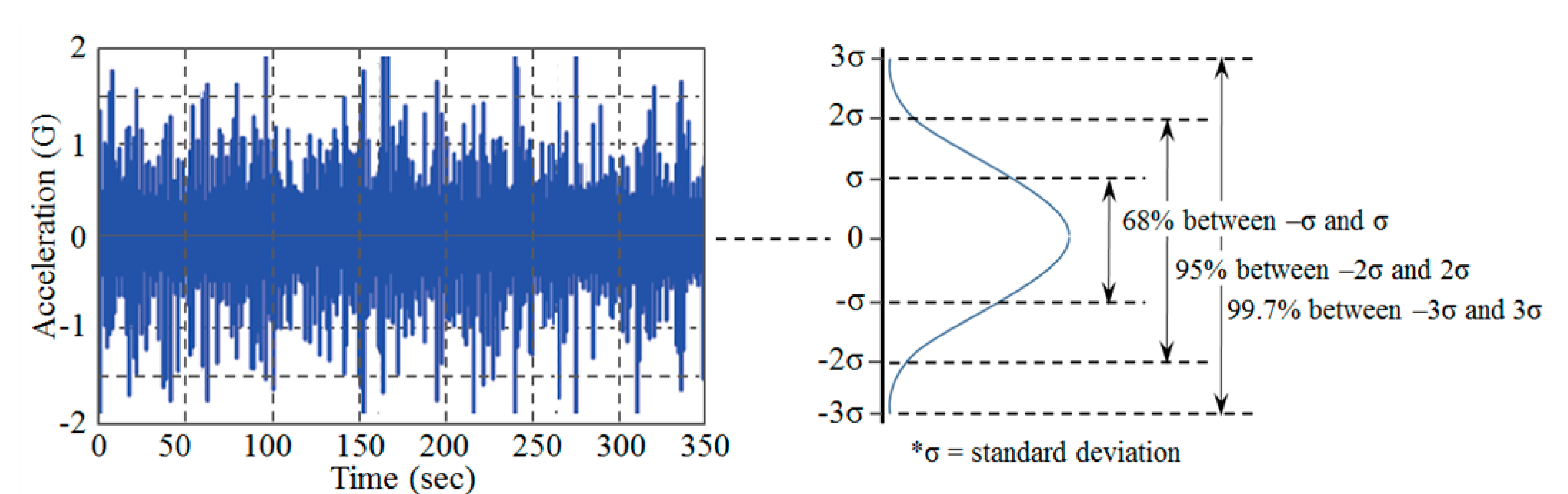
Because the vehicle speed and road pavement roughness vary throughout the journey, the vehicle vibration is non-stationary, in which statistical values such as the mean and root–mean–square acceleration (standard deviation; rms G or G
rms) of the events are not maintained over time. The non-stationarity of vehicle vibration causes the non-Gaussian distribution of vehicle vibration events [
4,
5]. However, vibration signals measured in a vehicle are characterized such that their average values remain relatively constant even if the vibration values for a particular frequency in the signal continue to change. This characteristic enables the vibration test equipment to reproduce the vibration behavior of the vehicle in a laboratory [
6]. Therefore, in the vibration analysis of the vehicle, the random vibration of the vehicle is a Gaussian distribution, and it is assumed that all measured events exist within three standard deviations (±3σ;
Figure 1).
Power spectral density (PSD) is measured vibration signals using the Fast Fourier Transform (FFT) algorithm, which represents the average intensity of the vibration. Some researchers [
4,
7,
8] have reported that the Gaussian distribution used in FFT at vibration test excludes values outside the normal distribution such as high-amplitude events in the vibration signal, which can have a significant effect on product damage. Therefore, reproducing actual vehicle vibrations through PSD-based simulation is limited [
5].
Because high-amplitude events owing to shocks during transport are included in the vibration signal, transport vibrations are not considered random vibration. Therefore, in research separating shock and vibration in the simulation of vehicle transport vibration, Lu et al. [
9] reported that when shock events more significant than 0.1 G were removed from the vibration data measured during truck transport, vibration level was close to a normal distribution. Such shock events are caused chiefly by road unevenness conditions such as roughness, metal joints, and sewer hole covers. Several researchers [
7,
10,
11,
12] developed PSD profiles for each by decomposing the signal into low-amplitude and high-amplitude events based on a rank of rms G. This method is based on the hypothesis that the low-level PSD profile represents the vehicle response to random variations in the road profile and that the high-level profile represents the response to transient events such as speed bumps, cracks, and potholes [
7]. Chonhenchob et al. [
10] and Singh et al. [
11] developed two PDS profiles based on 70% of vehicle vibration signals with the lowest acceleration levels and 30% with the highest. However, this method is too subjective for dividing the upper and lower ratios in the PSD calculation. For example, Wallin [
12] used an 80:20 percentage ratio, and Kipp [
7] used three-way split spectra of 70:25:5 for the signal. Even if the PSD is calculated by taking only the upper group of high-amplitude events, the distribution is still Gaussian, but the high-amplitude events included in the transport vibration signal are integrated at random points within the signal. Thus, this approach allows for better simulation of the overall distribution of vibration acceleration [
13].
In several geographic regions including North America [
11,
14,
15,
16], Australia [
17], Japan [
9,
17], China [
18], India [
19], Brazil [
20], Spain [
21], Thailand [
22] and Hungary [
23,
24,
25], vibration, and shock measured in representative vehicles in each country’s vehicle transport environment have been published. Also, many researchers have compared their measurement results with existing global standardized test protocols such as ASTM [
26], ISO [
27], and ISTA [
28].
The causes of vehicle transport vibration can be divided into three main categories: (1) the road roughness, (2) road surface aberrations such as cracks, speed bumps, and potholes, and (3) the vehicle drivetrain system including the wheels, drivetrain, and engine. Because the vibration level in vehicle transport depends on the interaction of the track-truck system, the vibration level is at least a function of road surface classification, terrain configuration, vehicle speed, vehicle suspension type and its conditions, load configuration, and tire pressure [
7,
8,
9,
11,
14,
18,
21,
22].
Lead by Singh and Marcondes [
15], several researchers [
11,
13,
19] have divided the vibration frequency of trucks into three significant ranges: (1) 3–4 Hz, representing the truck suspension response; (2) 15–20 Hz, representing the tire response; and (3) 40–55 Hz, representing the structure response. According to the results in the published literature, the vibration levels in air-ride trucks are significantly lower than those in leaf-spring trucks [
11,
15,
16,
18,
21,
29]. Pierce et al. [
16] stated that the vibration levels of leaf-spring trailers are at least 50% higher than those of air-ride trailers. However, Singh and Marcondes [
15] reported that a truck with damaged air-ride suspension result in significantly higher vibration levels than those with leaf-spring suspensions. They reported predominant suspension frequencies of air-ride and leaf-spring trailers of 2 Hz and 3–4 Hz, respectively; Garcia-Romeu-Martinez et al. [
21] reported similar results. Soleimani and Ahmadi [
30] reported that vibration peaks in leaf-spring and the air-ride suspension trucks occur at frequencies of 3 Hz and 4 Hz, respectively. The vibration level is shown to increase with an increase in vehicle travel speed, with a smaller the payload resulting in higher vibration levels [
8,
15,
18,
21,
31]. However, singh and marcondes [
15] stated that the vibration levels increase significantly in air-ride trailers because the air-ride suspension becomes stiffer as the trailer load increases. The vertical vibration level was shown to be larger than the lateral and longitudinal vibration levels [
11,
14,
31], and the vibration levels according to the location of the truck platform is more significant at the rear than at the front [
15,
29].
To apply PSD profiles obtained under various conditions to the simulation, a composite PSD profile with simplified breakpoints representing these conditions be determined. Generally, a smoothing process is valid for simplification of a single PSD profile [
12,
23]. However, two methods have been used to create a composite PSD profile representing several PSD profiles obtained under various conditions. The first is the average method of all recorded events under various conditions (the average composite spectra) [
15,
23], and the other connects the highest PSD level breakpoints by considering all various recorded PD spectra [
11,
23,
32]. In particular, the latter method produces conservative results that include all results measured under different conditions.
Research on the vehicle transport environment in Korea is at a rudimentary stage. In particular, no research on the vibration level for representative trucks and road types applied to Korea’s domestic freight transport is available. These studies are needed to compare domestic transport vibration levels with those presented by international standards (ASTM: West Conshohocken, USA, ISTA: Chicago, USA) and to simulate damage to packaged products by domestic transport environments. Therefore, we attempted to measure the dynamic vibration level of the distribution environment in Korea, construct the PSD profile for conducting the transport simulation in the lab and compare the results with the dynamic level of the distribution environment in other countries. The specific research objectives include:
- 1.
Analysis of the transport vibration levels for trucks and routes representative of Korea’s freight transport and development of a simulation protocol for this truck transport environment.
- 2.
Qualitative analysis of the characteristics of Korea’s truck transport environment by comparing the truck transport vibration levels measured in the pre-planned test route with exiting standardized test protocols.
- 3.
Proposal of optimum cushioning packaging design level of packaging products to prevent damage caused by vibration and shock during transport.
3. Results and Discussion
3.1. Transport Vibration Levels in the Pre-Planned Test Route
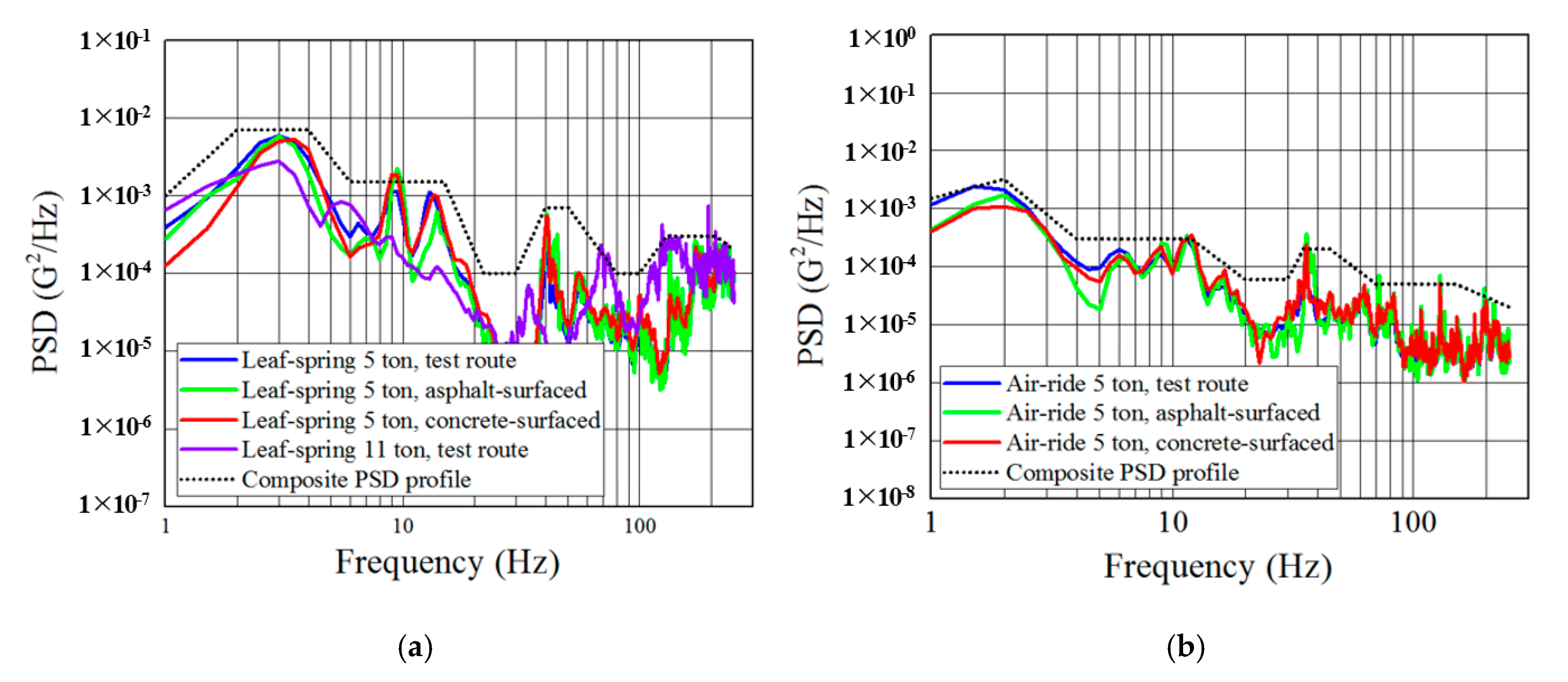
Figure 4 shows each PSD profiles for the tri-axial vibration records measured in three target trucks on the test route. As expected, the vibration levels were significantly higher in the vertical axis than in the lateral and longitudinal axes for all target tracks, and the change in the value of the longitudinal vibration level was smaller than that of the other two directions. In particular, the differences in directional vibration levels were more pronounced in the low-frequency range of 110 Hz. The vehicle’s overall rms G value at that frequency range was the largest in the vertical direction, followed by the lateral direction and the longitudinal direction (
Table 3).
For the overall frequency range of this study, 1–250 Hz, the values of the vertical overall rms G were approximately 2.6 and 3.0 times higher than those of the lateral and longitudinal directions, respectively, and the highest level of vibration in the vertical direction was the same as that of other countries.
The vibration level transmitted to products during truck transport is very large in the vertical direction; thus, the design of the cushioning packaging of the product depends on the vertical vibration level [
24,
25,
26,
34].
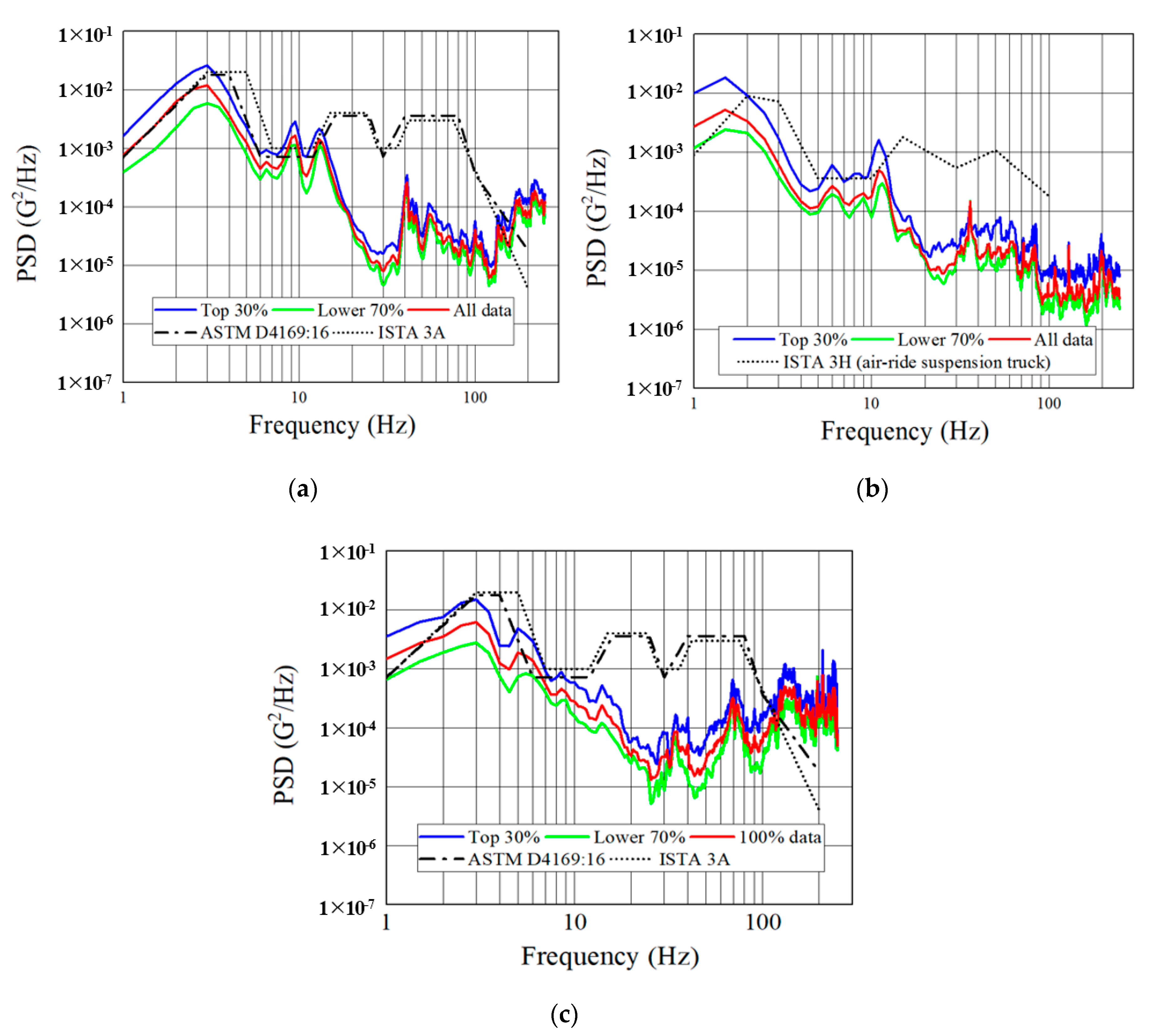
Figure 5 shows only the PSD profiles for the vertical direction. The overall rms G values of the leaf-spring truck in the low-frequency range of 1–10 Hz were about 1.5 times greater than those of the air-ride truck.
However, the value of the first PSD peak, which occurred as suspension’s response to external forces at the low-frequency region, was about two times smaller in the air-ride truck than in the leaf-spring truck, and its frequency was approximately 1.5 Hz and 3 Hz, respectively. The low frequency of the first PSD peak in the air-ride truck is considered as an effect of damping of the air-ride suspension (damped natural frequency
, where
ωn is the natural frequency, and
ζ is the damping ratio). The results of this study for the two suspension trucks agree well with the research results by Singh and Marcondes [
15] and Garcia-Romeu-Martinez et al. [
21]. Therefore, package designers should preferentially avoid designing ‘product + cushioning material’ system with natural frequencies between these ranges to avoid resonance during transport [
21].
Figure 5 also shows the analysis results of PSD from time-domain rms G data for the following three cases: (1) high-level PSD representing the top 30% of the recorded data, (2) low-level PSD representing the lower 70% of the data recorded, and (3) PSD representing all data recorded. The overall rms G value for each of the three classifications is shown in
Table 4.
The overall rms G value for the top 30% of the recorded data was approximately 0.31 G for the leaf-spring truck and 0.18 G for the air-ride truck, and that for the lower 70% of the data recorded, which was muted by averaging high-amplitude events included in the measured transport vibration signals, was approximately 0.18 G and 0.08 G, respectively (
Table 4). The overall rms G value for the lower 70% of the data recorded was approximately 42% less in the leaf-spring truck and 56% less in the air-ride truck than that for the top 30% of the data recorded. Therefore, because high-amplitude events that occur during truck transport have a significant impact on product damage [
3,
38], the high-amplitude events included in the measured transport vibration signal should not be excluded in the development of the PSD profile for lab-based simulation.
The overall shape of the PSD profile in the leaf-spring truck was higher in the low-frequency range of 1–10 Hz, lower in the medium-frequency range of 15–40 Hz, and again relatively higher in the high-frequency range of 40–250 Hz. However, in the case of the air-ride truck, the overall shape of the PSD profile was lower with increasing frequency. The shape of the PSD profile for the leaf-spring truck was similar to that reported by Zhou and Wang [
13].
In the low-frequency range of 1–10 Hz, the shape and peak intensity and frequencies of the high-level PSD profile of leaf-spring truck, representing the top 30% of the data recorded, were roughly similar to those of ASTM D4169:16 (medium level) [
26] and ISTA 3A (over-the-road trailer spectrum) [
28]. However, they showed significant differences in the higher-frequency regions. The shape and peak intensity and frequencies of the high-level PSD profile of the air-ride truck were roughly similar to those of the ISTA 3H (air-ride suspension truck) [
39], although significant differences were noted at the higher-frequency regions. The reason for the relatively substantial difference in these regions between the results of this study and the existing standardized test protocols is attributed mainly to the differences in test subjects and conditions [
40]. In addition, the results of this study were measured in unload conditions for general trucks, and there are many sudden speed changes of trucks during transport and the characteristics of national roads and highways in Korea having many curved routes.
3.2. Transport Vibration Level as a Function of Pavement Type and Travel Speed
The effects of travel speed and pavement type on the truck transport vibration level were analyzed by extracting the time zone data corresponding to the truck’s pre-planned travel speed and the pavement type from the vibration records measured on the test route configured for this study.
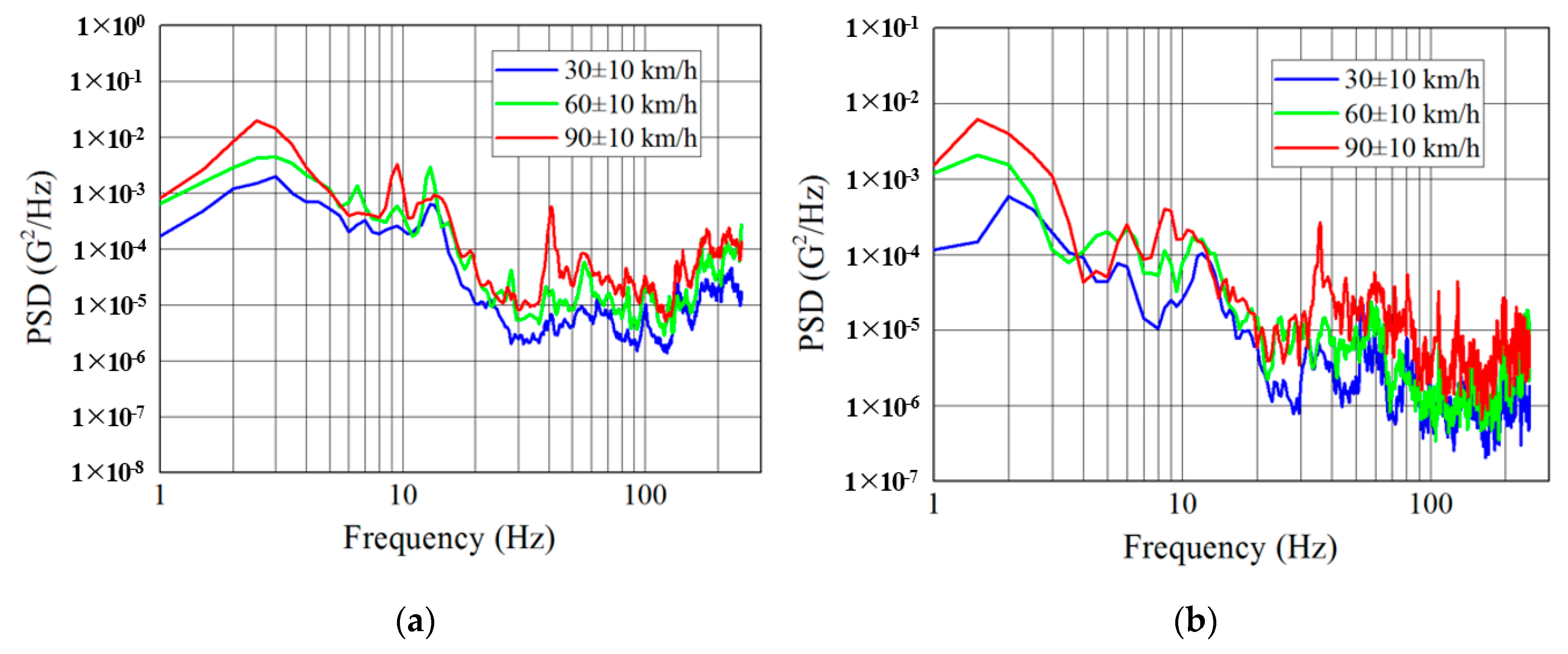
Figure 6 and
Table 5 show the vibration level according to the travel speed, with the vibration level increasing as the travel speed increased. Particularly in the low-frequency range of 1–10 Hz, the difference in the vibration level based on the travel speed clear (
Table 6). These results are similar to those reported by other researchers [
18,
21]. The increases in the vibration level of trucks with increases in travel speed indicate that the effects of road conditions on the truck’s vibration level are more sensitive as the travel speed increases [
18]. The increase rate of the vibration level according to travel speed in the air-ride truck was higher than that in the leaf-spring truck. This phenomenon is attributed to the more significant increase rate of the dynamic load acting on the air-ride truck as the travel speed increases, making the air-ride suspension stiffer. These results are similar to the research results of Singh and Marconds [
15], such that the air-ride suspension becomes thicker as the trailer load increases for air-ride trailers, resulting in higher vibration levels.
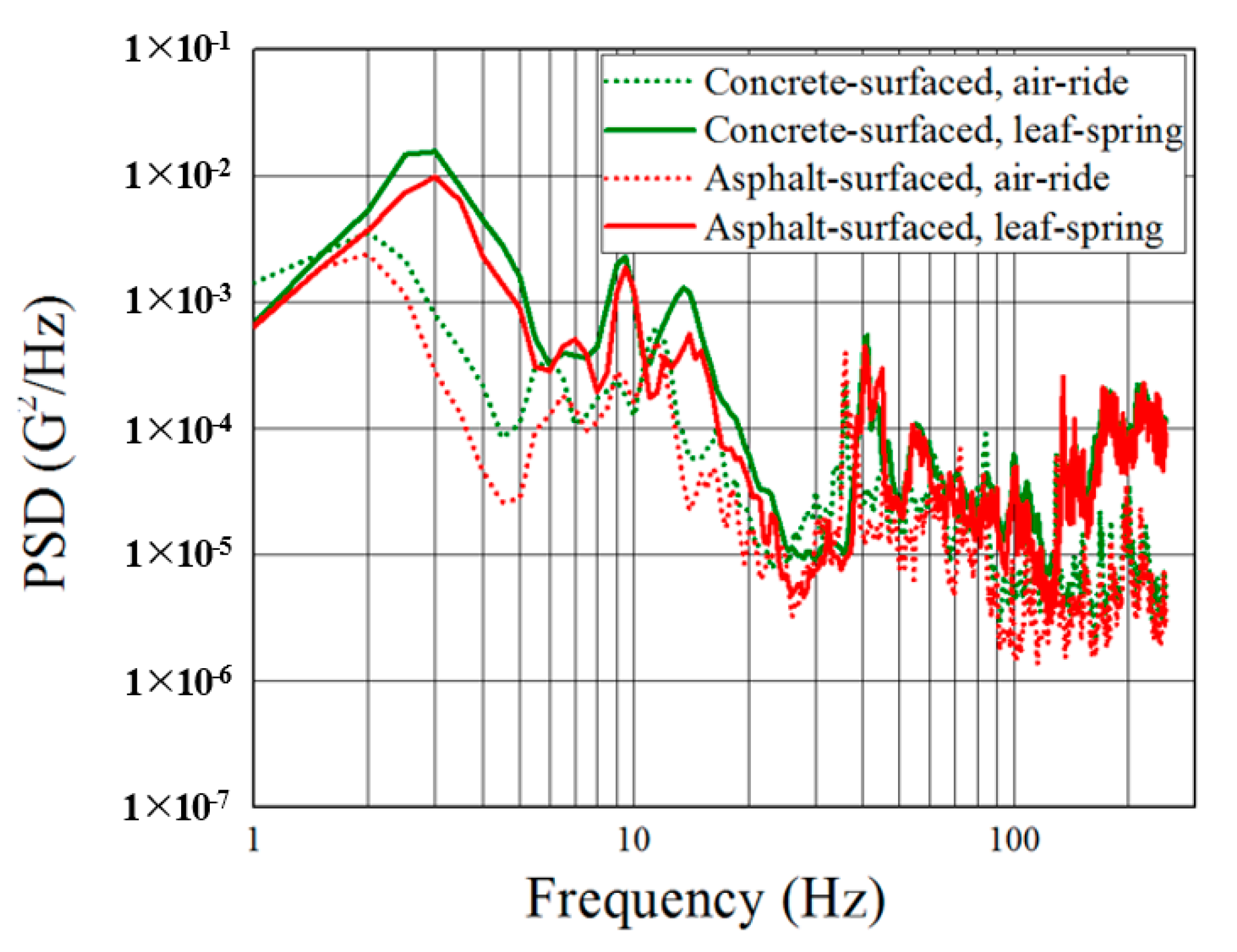
Figure 7 shows the vibration levels of trucks according to the highway pavement type; the results of the analysis are shown in
Table 5 and
Table 6. The vibration level of the air-ride truck within the overall frequency range of 1–250 Hz was approximately 50.0% on the concrete-surfaced highway and approximately 45.4% on the asphalt-surfaced highway compared with that of the leaf-spring truck. Moreover, the vibration level on the asphalt-surfaced highway was approximately 82.2% in the leaf-spring truck and approximately 74.5% in the air-ride truck compared with that on the concrete-surfaced highway. The difference in the vibration level by pavement type or suspension in the low-frequency range of 1–10 Hz showed the same tendency as that in the overall frequency range, although the difference was more significant. These results reflect the same travel speed in unloaded conditions; the results be different if the travel speed and payload are used as variables.
3.3. Statistical Characteristics of the Measured Truck Transport Vibration Events
The blue bars in
Figure 8 and
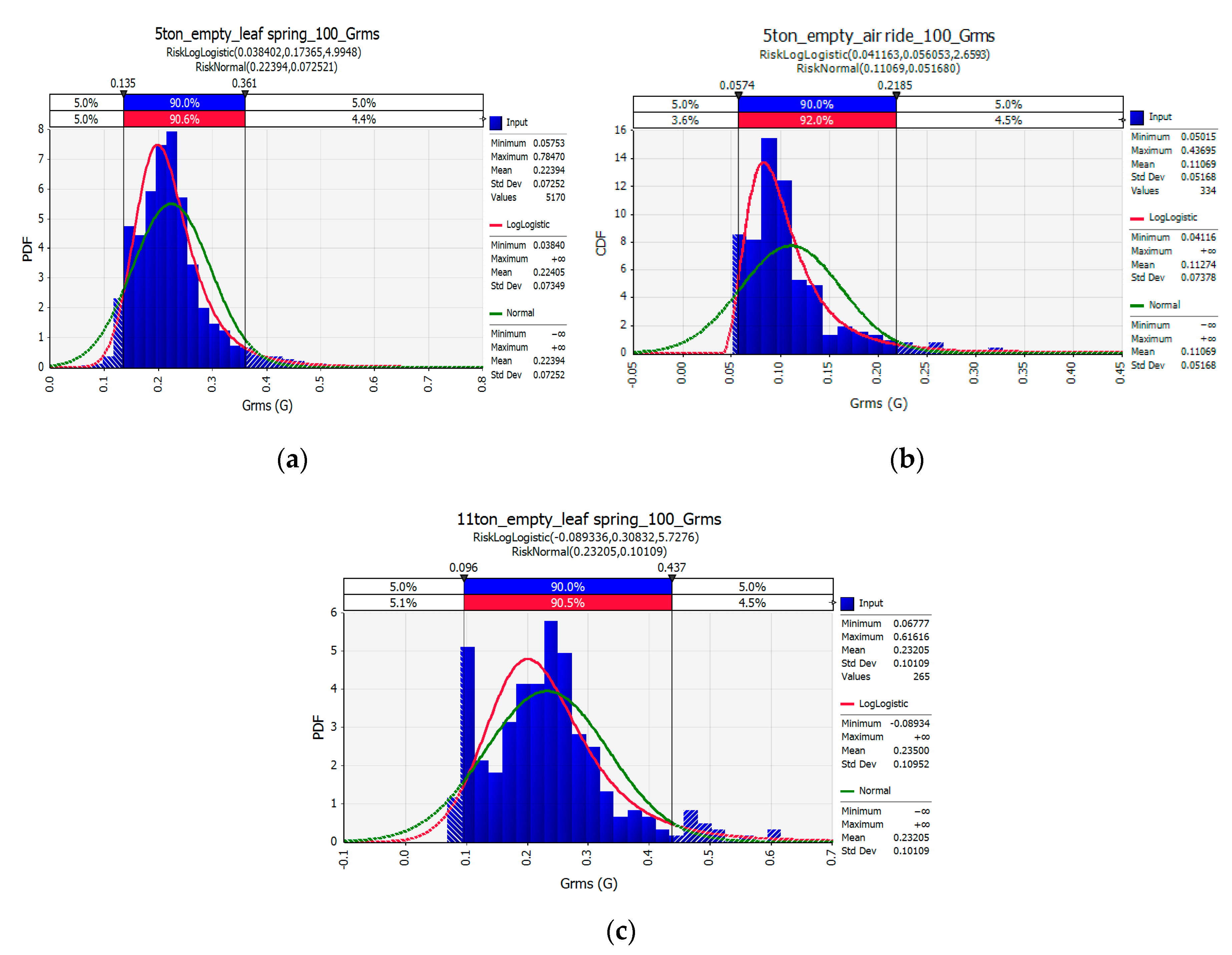
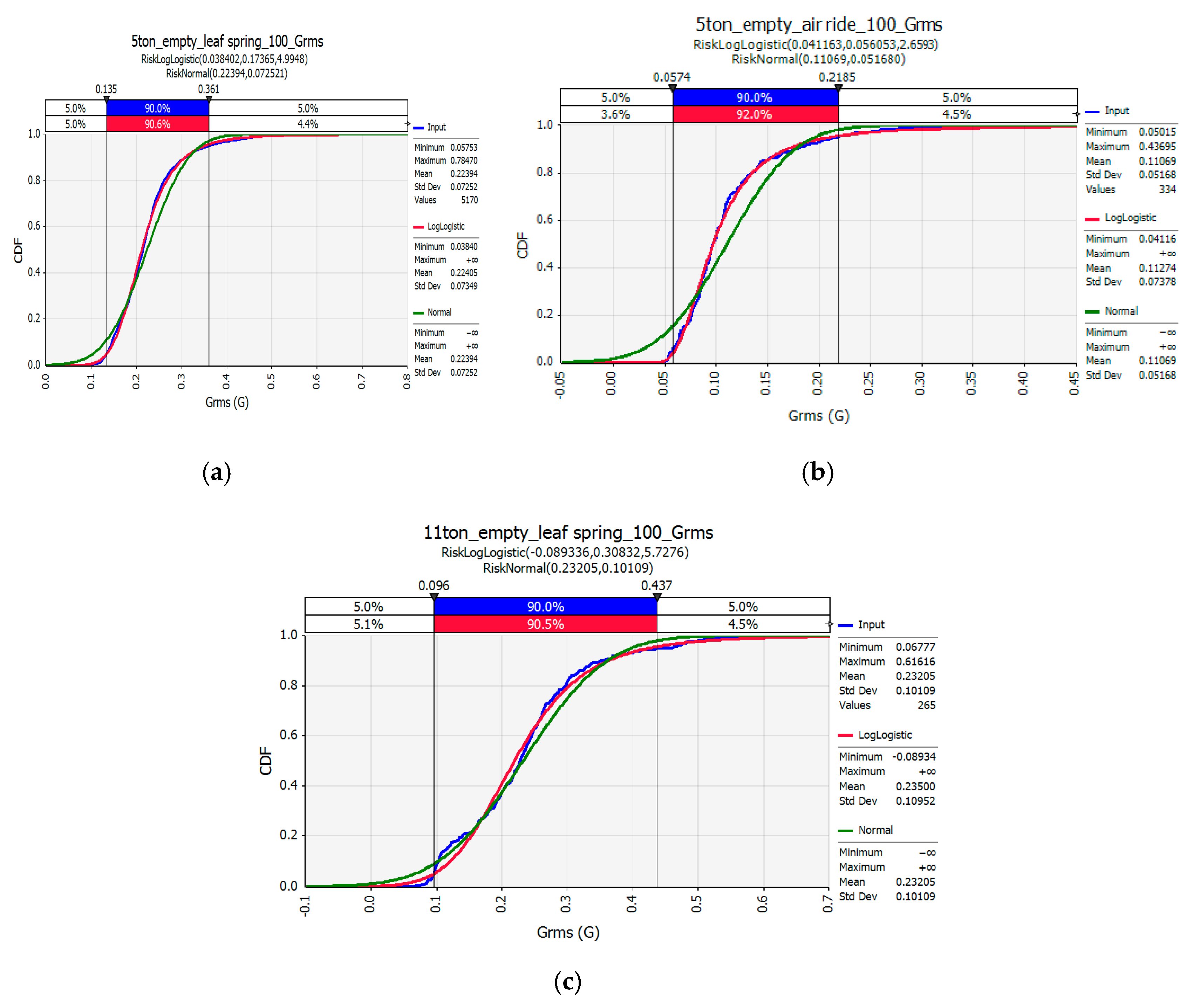
Figure 9 show the PDF and the cumulative distribution function (CDF), respectively, for the rms G of vertical transport vibration events. The green line in the figures represents the standard normal distribution, and the red line represents the log-logistics distribution Equations (5) and (6), which is the best-fit result for the measurement data based on the R-square and RMSE.
The kurtosis and skewness for this PDF were analyzed (
Table 7). The kurtosis values for all recorded data were more significant than 3 for all trucks of this study, which indicates a heavy-tailed distribution; therefore, the vibration events measured in Korea’s truck transport environment do not follow a normal distribution [
41]. However, the kurtosis for the lower 70% of data recorded was much closer to 3 and thus closer to normal distribution because the high-amplitude events included in the measured vibration signal, which exist outside normal distribution, were excluded.
Figure 9 shows the CDF for each condition. These values coincide with the log-logistics calculated values in 90% of the experimental data under all experimental conditions, but show some differences from the normal distribution values.
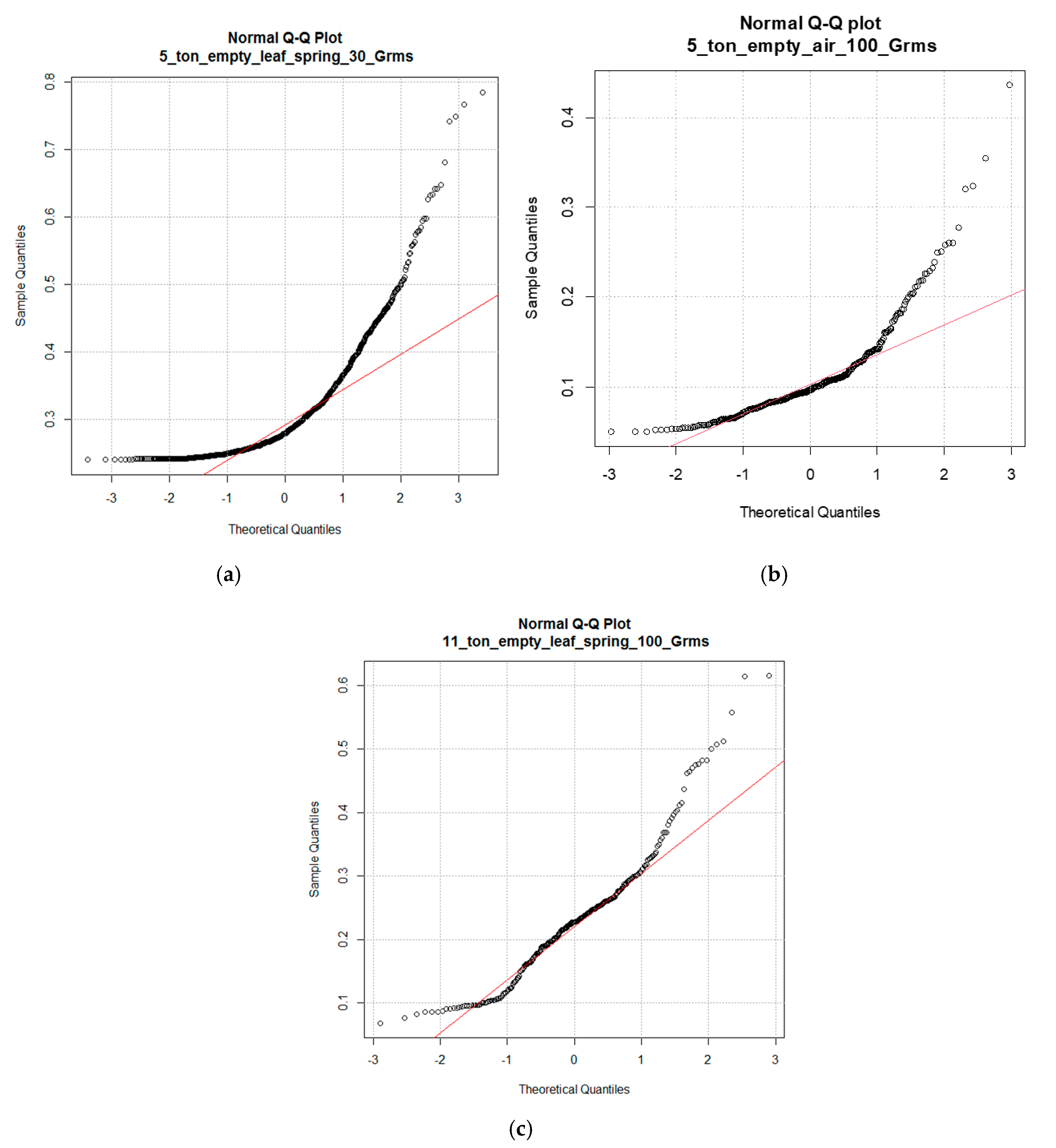
The heavy-tailed distribution characteristics of the vibration events measured in this study are also well illustrated by the normal quantile–quantile (Q-Q) analysis shown in
Figure 10. The normal Q-Q plot provides a diagnostic check on whether the data originate from a normal distribution and involve a plot of empirical quantiles against the corresponding quantile of normal distribution. A straight-line relationship suggests that the data are normally distributed. Q-Q plots are displayed in a curved shape, indicating that the distribution is skewed or has heavier tails than those in a normal distribution.
Moreover, the skewness values for all data recorded were 1–2.2 for all trucks. This indicates that the transport vibration events measured in the study were skewed to the right to cause, and many vibrations events with values higher than the mean. However, the kurtosis for the lower 70% of the data recorded was close to zero and thus close to symmetric distribution.
The CDF represents the percentage of events below a certain level of the data such as the rms G. The values for the parameters α (scale) and β (shape) that characterize this log-logistics distribution are shown in
Table 7 [
41].
The PDF of the log-logistics random variable is
and the CDF of the log-logistics random variable is
where
α > 0 is the scale parameter, and
β > 0 is the shape parameter of the distribution.
3.4. Composite PSD Profiles for the Measured Vibration Level in Truck Transport
In this study, the composite PSD profile for Korea’s truck transport environment was divided into four categories based on the transport vibration characteristics revealed through this study and the research results published by other researchers [
7,
10,
11,
12]: (1) high-level composite PSD profile representing the top 30% of the data recorded for leaf-spring trucks, (2) low-level composite PSD profile representing the lower 70% of the data recorded for leaf-spring trucks, (3) high-level composite PSD profile representing the top 30% of the data recorded for air-ride trucks, and (4) low-level composite PSD profile representing the lower 70% of the data recorded for air-ride trucks.
The method applied here to develop the composite PSD profile was previously presented by researchers [
32] of this study. This method divides each PSD profile into pre-planned groups. Each PSD profiles in each group are represented on a graph, and the breakpoints with relatively high-energy are connected to obtain a single comprehensive PSD profile. In the simplification process, the slope between breakpoints was suppressed by less than +25 dB/OCT or greater than −25 dB/OCT [
42,
43], ensuring the reproducibility of the developed composite PSD profile during the in-lab simulation. To meet this requirement, sharp peaks or deep valleys at about one-half their height (−3 dB) were selected [
42].
Figure 11 and
Figure 12 show the resultant high-level and low-level composite PSD profiles, respectively, for the top 30% and lower 70% of the data recorded in Korea’s truck transport environmental. The characteristics of these composite PSD profiles are shown in
Table 8 and
Table 9. The overall rms G of the developed high- and low-level composite PSD profiles were 0.47 and 0.32 for leaf-spring trucks, and 0.30 and 0.14 for air-ride trucks, respectively.
In Korea, vibration test machines are used a lot to simulate the vibration of truck-carrying products, and packaging engineers from each company are investing many time and money in proper cushion packaging of products to reduce costs. Until now, to simulate vibrations in transport environments, only the international standard (ASTM: West Conshohocken, USA, ISO: Geneva, Switzerland) transport environment has been used to analyze product damage and vibration behavior. Testing transport vibration simulation in Korea by applying foreign standards makes it difficult to achieve optimal cushion-packaging design of products. Previously, there was no research related to PSD development by transport routes of truck in Korea, but if PSD profiles measured in this paper are applied, proper cushion-packaging of products will be possible through vibration simulation tests on domestic distribution products.
Compared to the results of measurement of transport environment presented by existing researchers, parameters affecting vibration levels of domestic and foreign transport trucks (such as truck speed and road type) were similar results in low frequency bands below 15 Hz, but differed in higher frequencies. Generally, the frequency band associated with damage of packaged products in transit is the low frequency band. The difference in the high frequency band suggested by existing researchers is believed to be due to the road characteristics of Korea with many curves.